American Journal of Computational Mathematics
Vol. 2 No. 2 (2012) , Article ID: 20052 , 6 pages DOI:10.4236/ajcm.2012.22011
Nonstationary Wavelets Related to the Walsh Functions
Department of Mathematics, Russian State Geological Prospecting University, Moscow, Russia
Email: farkov@list.ru
Received March 29, 2012; revised April 25, 2012; accepted May 2, 2012
Keywords: Walsh Functions; Nonstationary Dyadic Wavelets; Fractal Functions; Adapted Multiresolution Analysis
ABSTRACT
Using the Walsh-Fourier transform, we give a construction of compactly supported nonstationary dyadic wavelets on the positive half-line. The masks of these wavelets are the Walsh polynomials defined by finite sets of parameters. Application to compression of fractal functions are also discussed.
1. Introduction
As usual, let 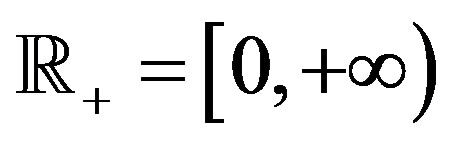 be the positive half-line,
be the positive half-line, 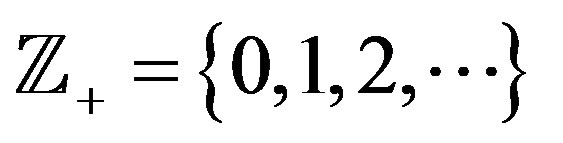 be the set of all nonnegative integers, and let
be the set of all nonnegative integers, and let  be the set of all positive integers. The first examples of orthogonal wavelets on
be the set of all positive integers. The first examples of orthogonal wavelets on 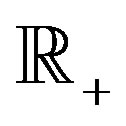 related to the Walsh functions and the corresponding wavelets on the Cantor dyadic group have been constructed in [1]; then, in [2] and [3], a multifractal structure of this wavelets is observed and conditions for wavelets to generate an unconditional basis in
related to the Walsh functions and the corresponding wavelets on the Cantor dyadic group have been constructed in [1]; then, in [2] and [3], a multifractal structure of this wavelets is observed and conditions for wavelets to generate an unconditional basis in 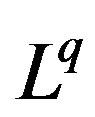 -spaces for all
-spaces for all 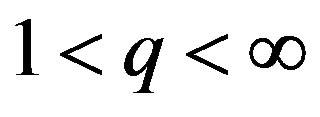 have been found. These investigations are continued in [4-10] where among other subjects the algorithms to construct orthogonal and biorthogonal wavelets associated with the generalized Walsh functions are studied. In the present paper, using the Walsh-Fourier transform, we construct nonstationary dyadic wavelets on
have been found. These investigations are continued in [4-10] where among other subjects the algorithms to construct orthogonal and biorthogonal wavelets associated with the generalized Walsh functions are studied. In the present paper, using the Walsh-Fourier transform, we construct nonstationary dyadic wavelets on 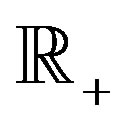 (cf. [11-13], [14, Ch.8]).
(cf. [11-13], [14, Ch.8]).
Let us denote by  the integer part of
the integer part of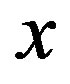 . For every
. For every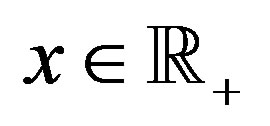 , we set
, we set
 where
where . Then
. Then
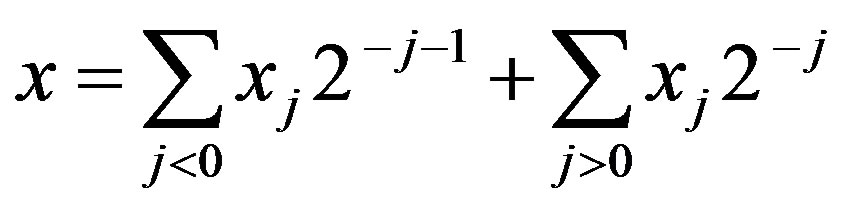 .
.
The dyadic addition on 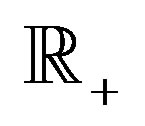 is defined as follows
is defined as follows
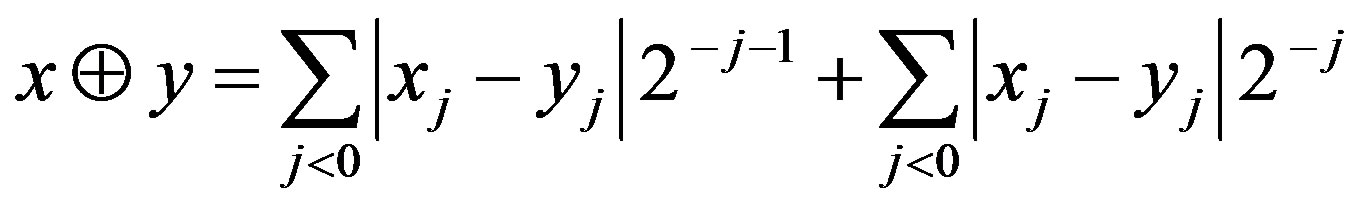 .
.
Further, we introduce the notations
 where
where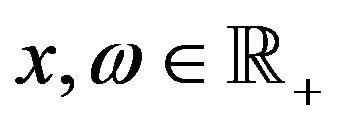 . Then the Walsh function
. Then the Walsh function  of order
of order 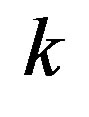 is
is  (see, e.g., [15]).
(see, e.g., [15]).
The Walsh-Fourier transform of every function 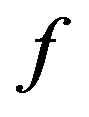 that belongs to
that belongs to  is defined by
is defined by
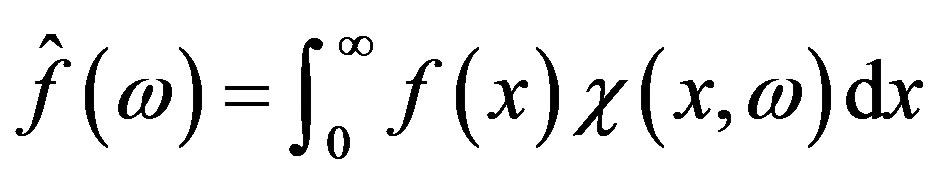 ,
,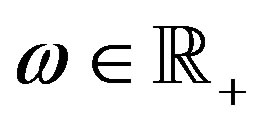 .
.
and extent to the whole space  in a standard way. The intervals
in a standard way. The intervals
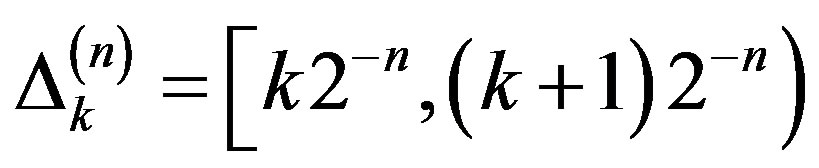 ,
, 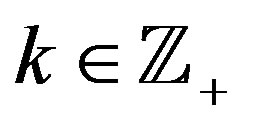 are called the dyadic intervals of range
are called the dyadic intervals of range . The dyadic topology on
. The dyadic topology on 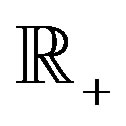 is generated by the collection of dyadic intervals. A subset
is generated by the collection of dyadic intervals. A subset  of
of 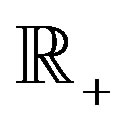 which is compact in the dyadic topology will be called W-compact.
which is compact in the dyadic topology will be called W-compact.
For any 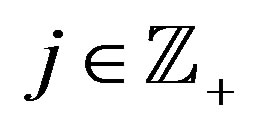 we define
we define 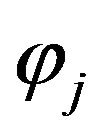 and
and 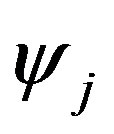 by the following algorithm:
by the following algorithm:
Step 1. For each 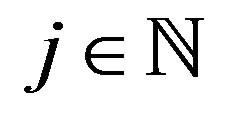 choose
choose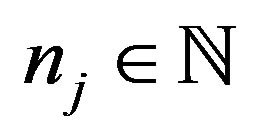 , and
, and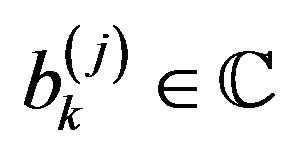 ,
, 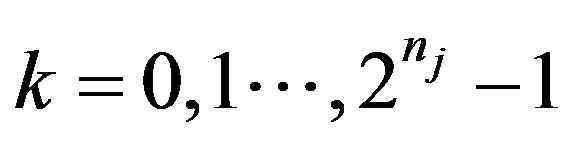 , such that
, such that
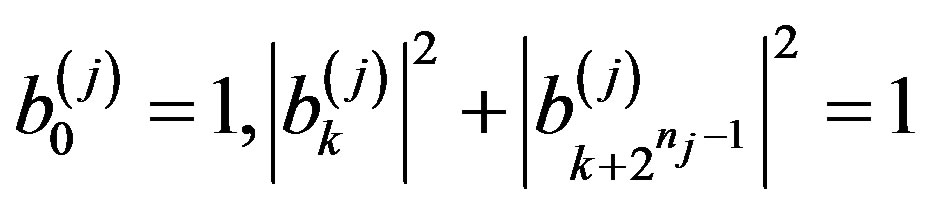 (1)
(1)
for all 
Step 2. Define the masks
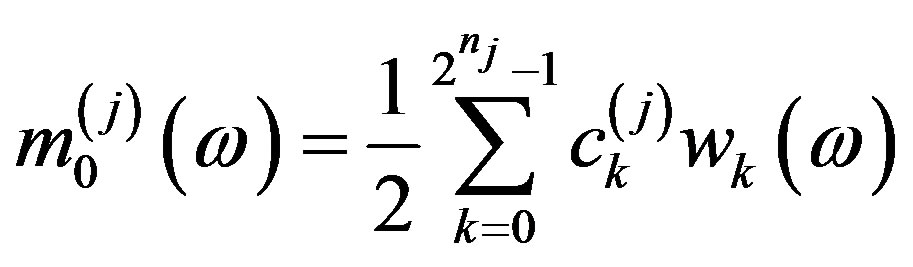 (2)
(2)
with the coefficients
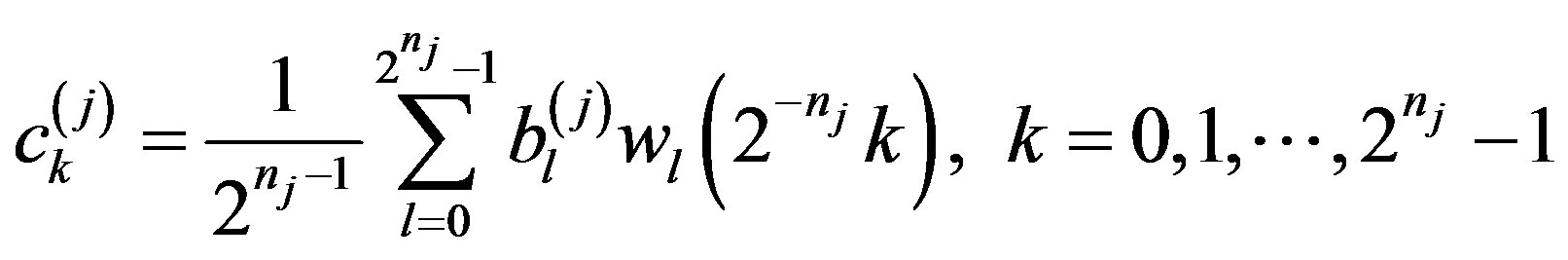 so that
so that  for all
for all 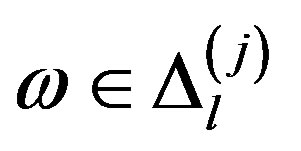 (cf. [15, Sect. 9.7]).
(cf. [15, Sect. 9.7]).
Step 3. For each 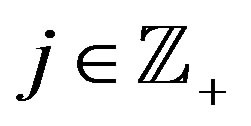 put
put
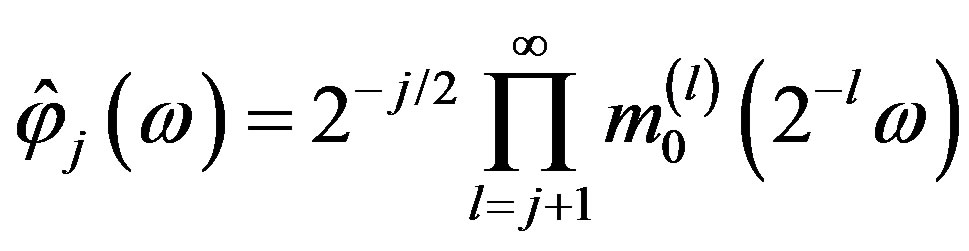 , (3)
, (3)
so that
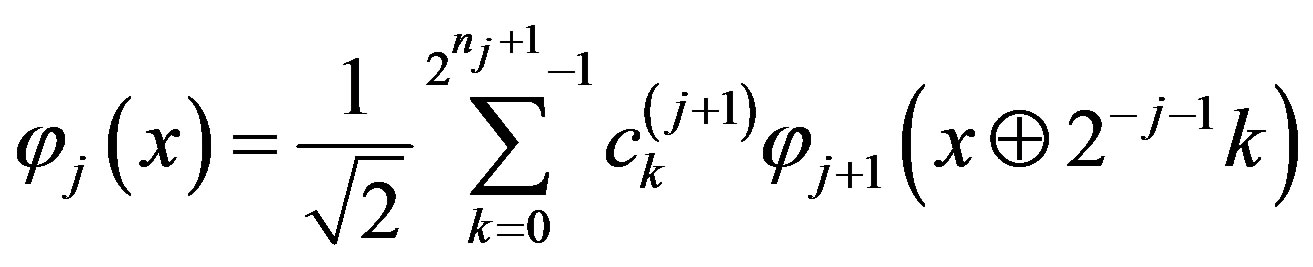 . (4)
. (4)
Step 4. Define  by the formula
by the formula
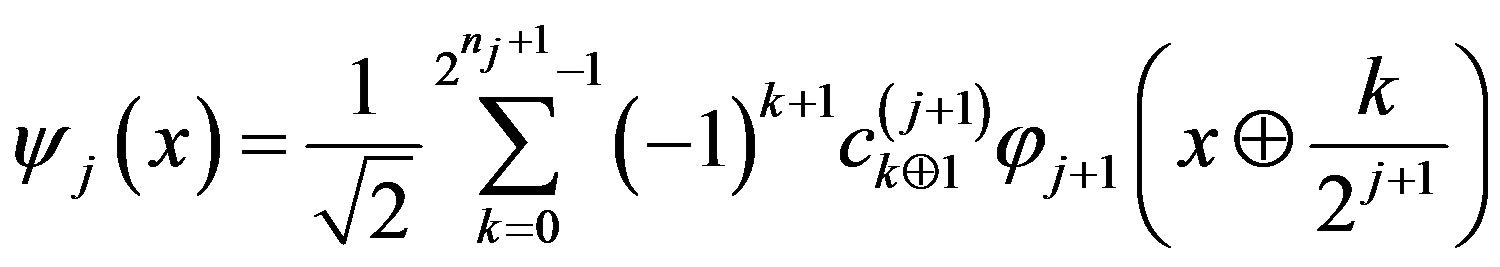 . (5)
. (5)
Further, let us define subspaces 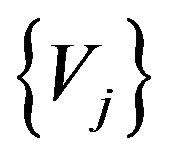 and
and  in
in 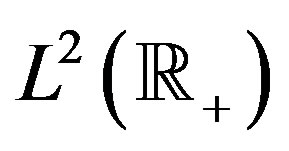 as follows
as follows
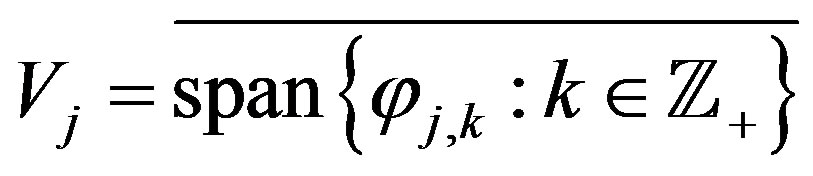 ,
,

for all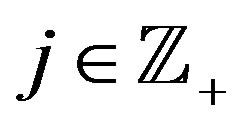 .
.
We say that a polynomial  satisfies the modified Cohen condition if there exists a W-compact subset
satisfies the modified Cohen condition if there exists a W-compact subset  of
of 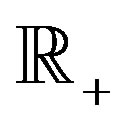 such that
such that
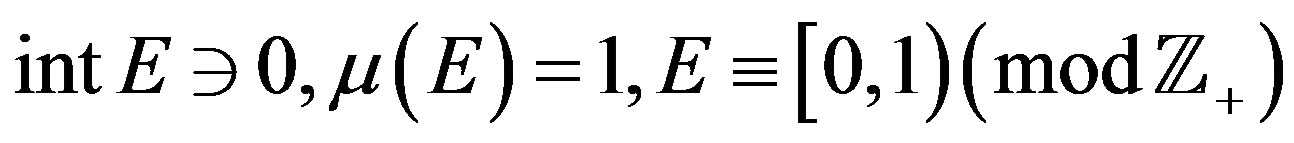
and
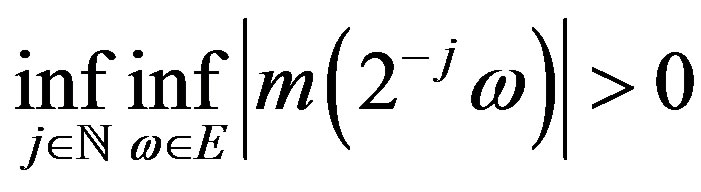 . (6)
. (6)
Theorem. Suppose that the masks  satisfy the modified Cohen condition with a subset
satisfy the modified Cohen condition with a subset  and there exists
and there exists  such that
such that
 for all
for all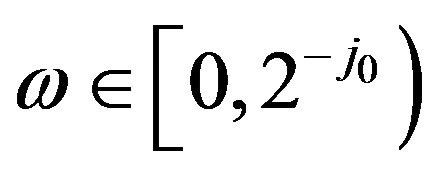 ,
,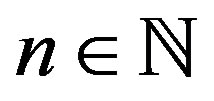 . (7)
. (7)
Then for any 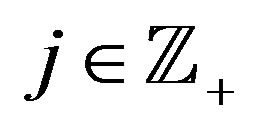 the following properties hold:
the following properties hold:
a) 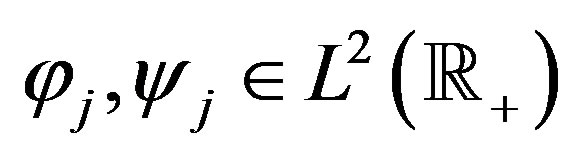 and
and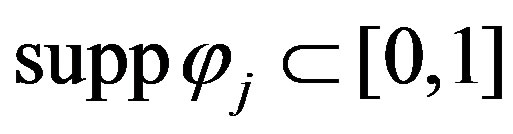 ;
;
b)  and
and  are orthonormal basis in
are orthonormal basis in 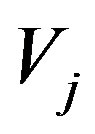 and
and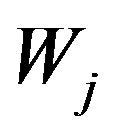 , respectively;
, respectively;
c)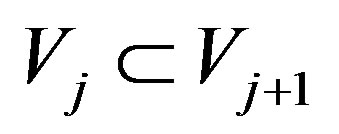 ,
,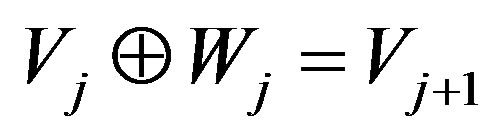 .
.
Moreover, we have
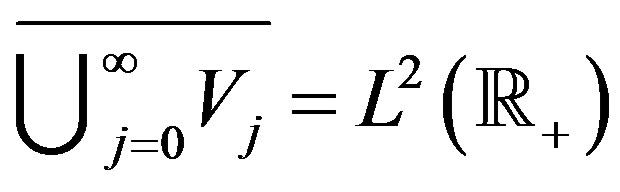 .
.
Corollary. The system
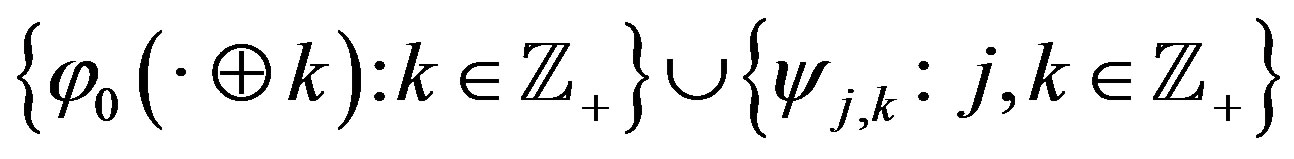
is an orthonormal basis in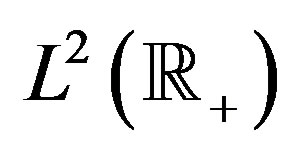 .
.
We prove this theorem in the next section. Then using the notion of an adapted multiresolution analysis suggested by Sendov [12], we discuss an application of the nonstationary dyadic wavelets to compression of the Weierstrass function and the Swartz function.
2. Proof of the Theorem
At first we prove the orthonormality of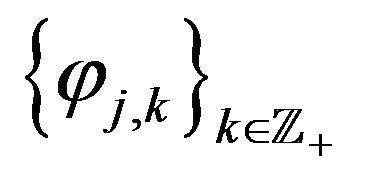 . In view of
. In view of
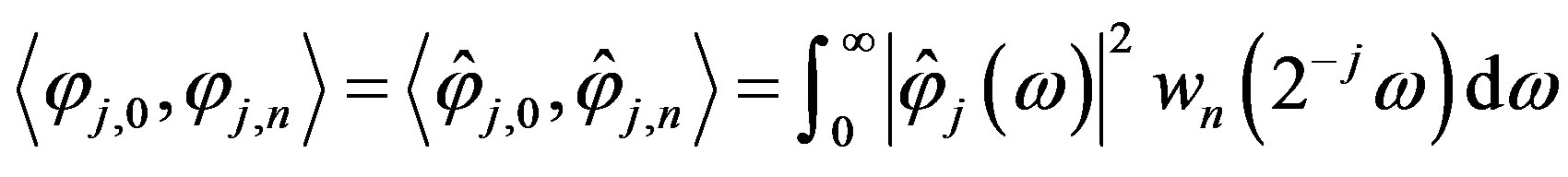 let us show that
let us show that
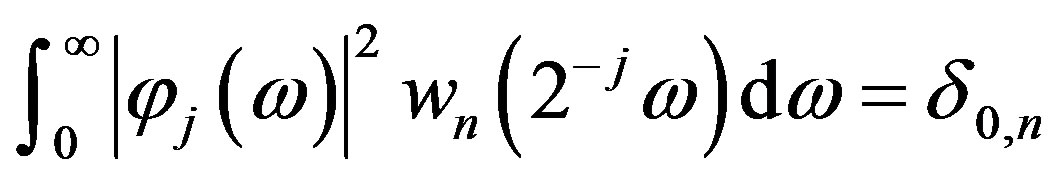 ,
,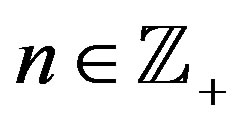 .
.
Denote by  the characteristic function of
the characteristic function of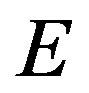 . For each
. For each  we define
we define

for 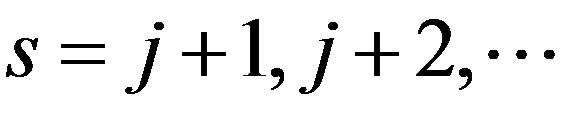 Since
Since 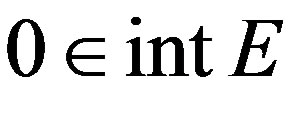 and, for all
and, for all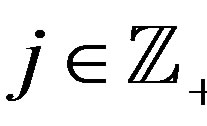 ,
, 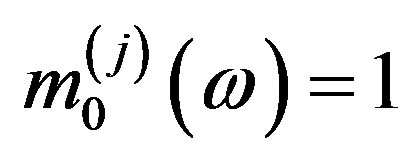 in some neighbourhood of zero, we obtain from Equation (3)
in some neighbourhood of zero, we obtain from Equation (3)
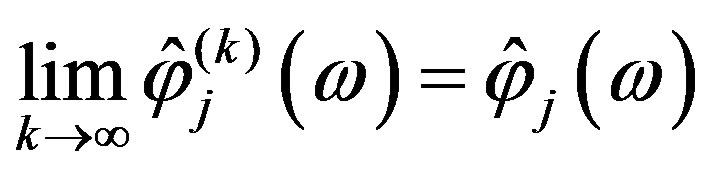 for all
for all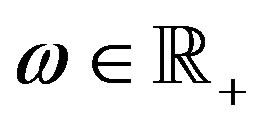 . (8)
. (8)
Let
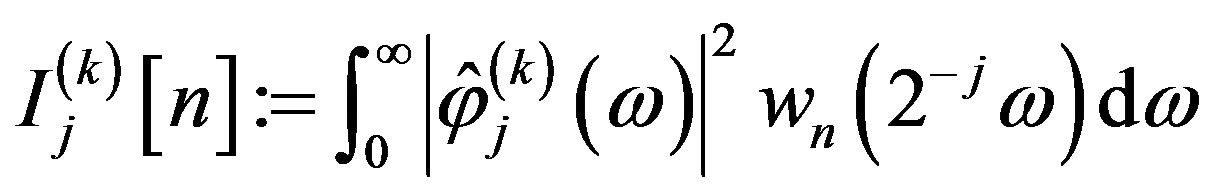 where
where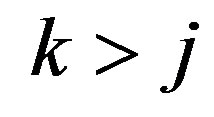 ,
,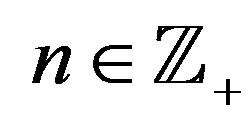 . Letting
. Letting , we have
, we have

that yields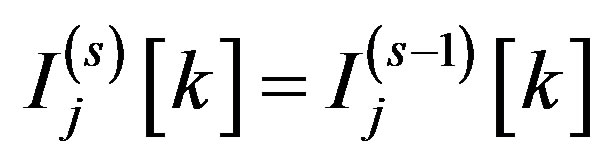 . By induction, we obtain
. By induction, we obtain
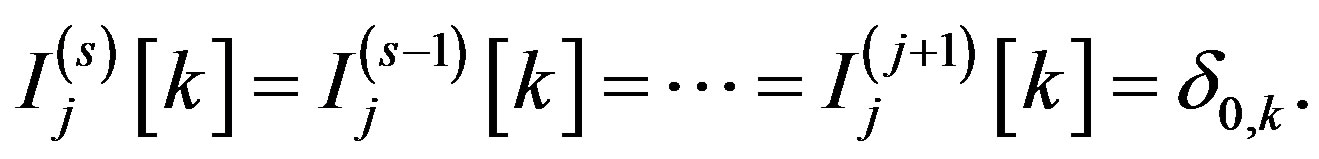
According to Equation (8), by Fatou’s lemma, we have
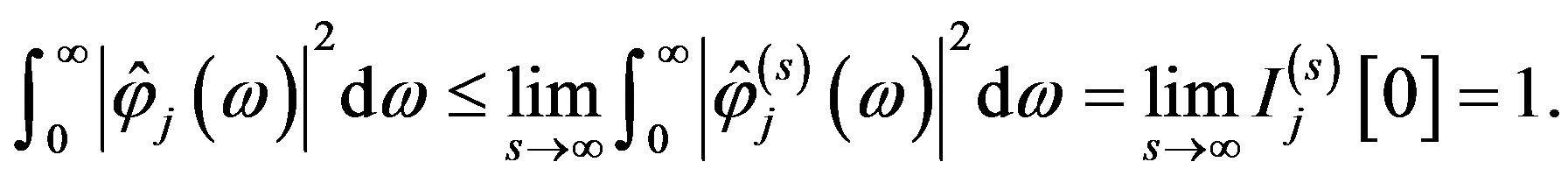 (9)
(9)
Consequently, 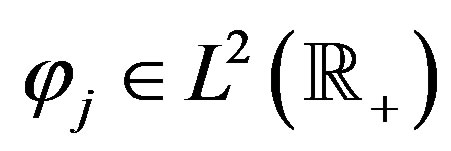 and, in view of Equation (5),
and, in view of Equation (5),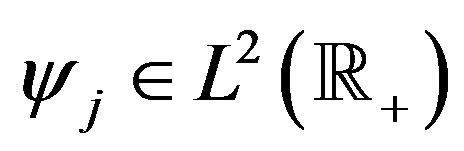 . It is known that if
. It is known that if 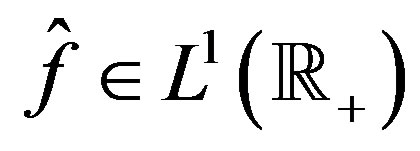 is constant on dyadic intervals of range
is constant on dyadic intervals of range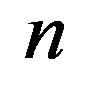 , then
, then  (see [16, Sect. 6.2]). Therefore, each function
(see [16, Sect. 6.2]). Therefore, each function 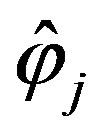 is constant on
is constant on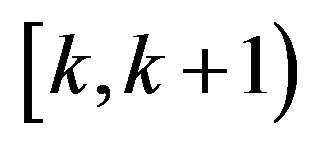 ,
, 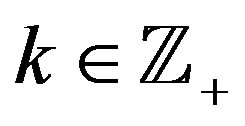 , which implies
, which implies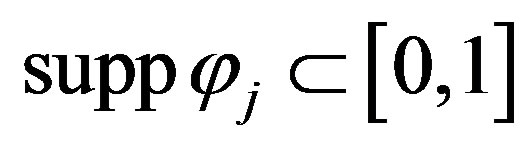 .
.
In view of Equation (7), there exists  such that
such that
 for all
for all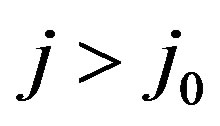 ,
, .
.
Hence, for ,
,
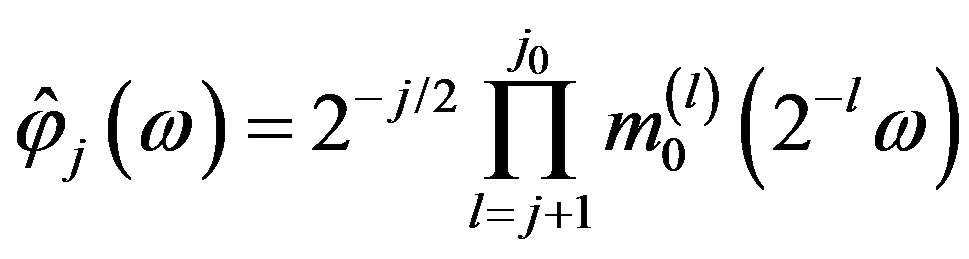 .
.
It follows from Equation (6) that for some 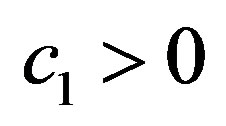
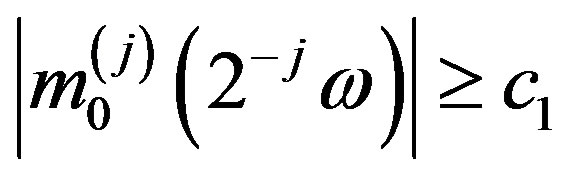 for
for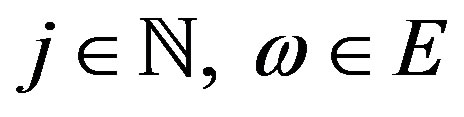 .
.
Since
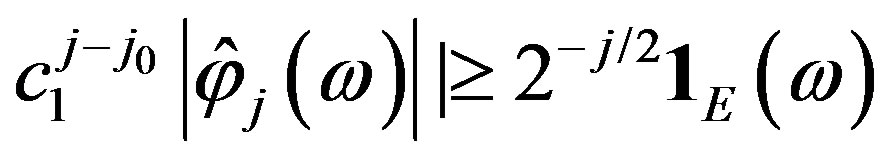 ,
,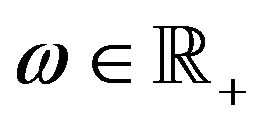 .
.
We have
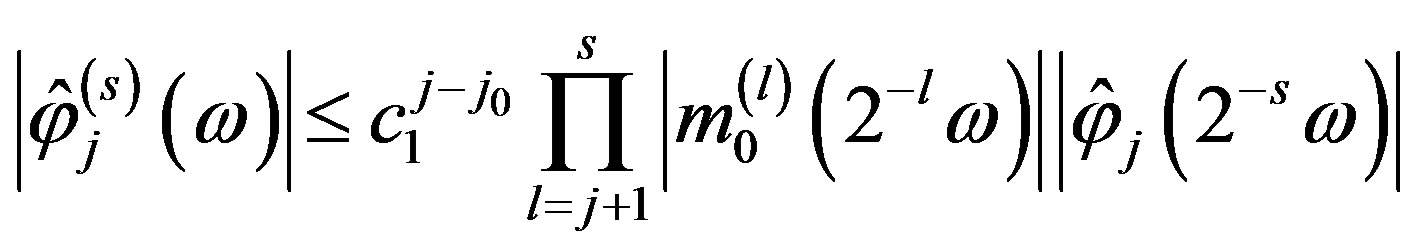 .
.
or, taking into account Equation (3),
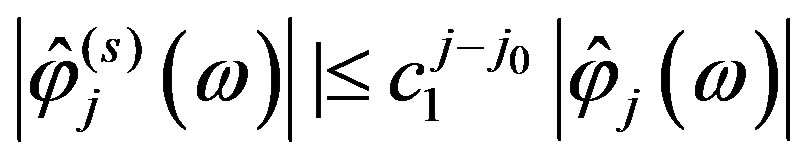 ,
, 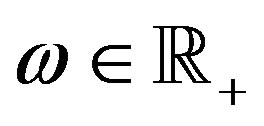
for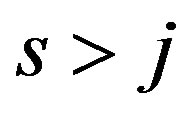 ,
,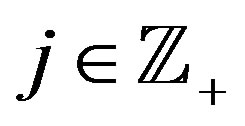 .
.
Applying the dominated convergence theorem we obtain

which means that 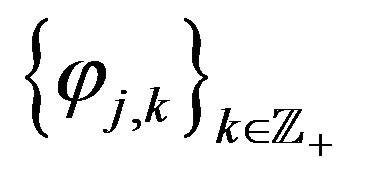 is an orthonormal system.
is an orthonormal system.
Now, let us prove an orthonormality of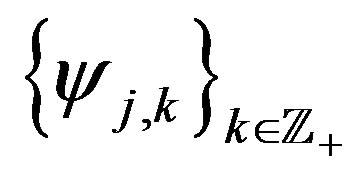 . For any
. For any  denote
denote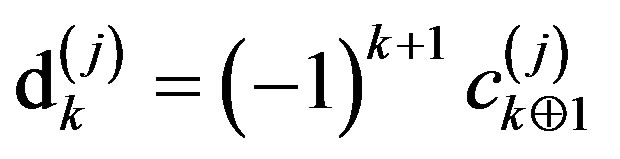 . Then
. Then
 . (10)
. (10)
Since
 We have
We have
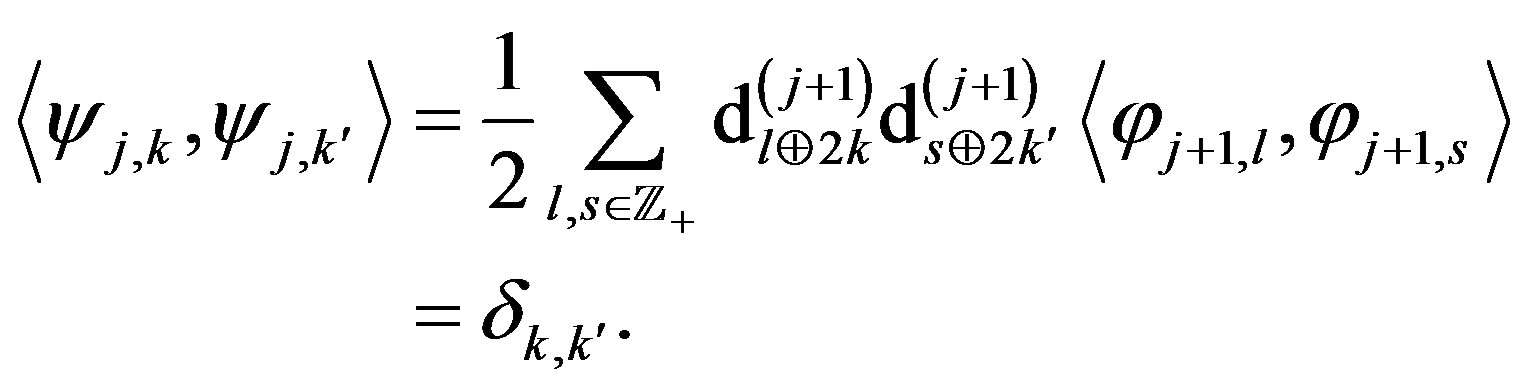
Then from Equation (10)
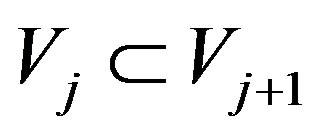 ,
, . (11)
. (11)
Let us define
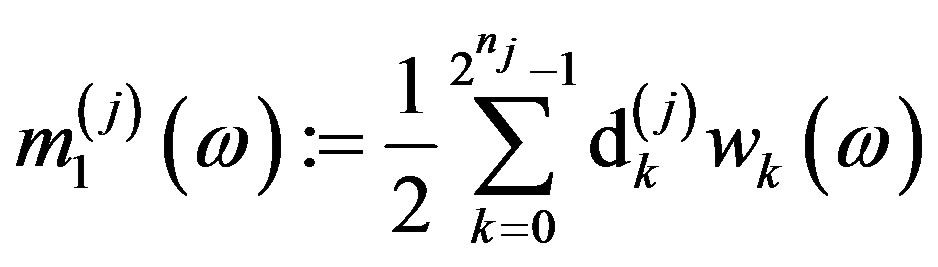 .
.
Denote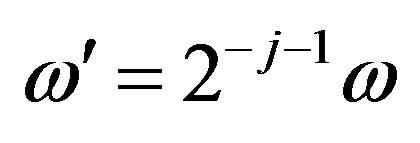 . Under the unitarity of the matrices
. Under the unitarity of the matrices
 We can write
We can write
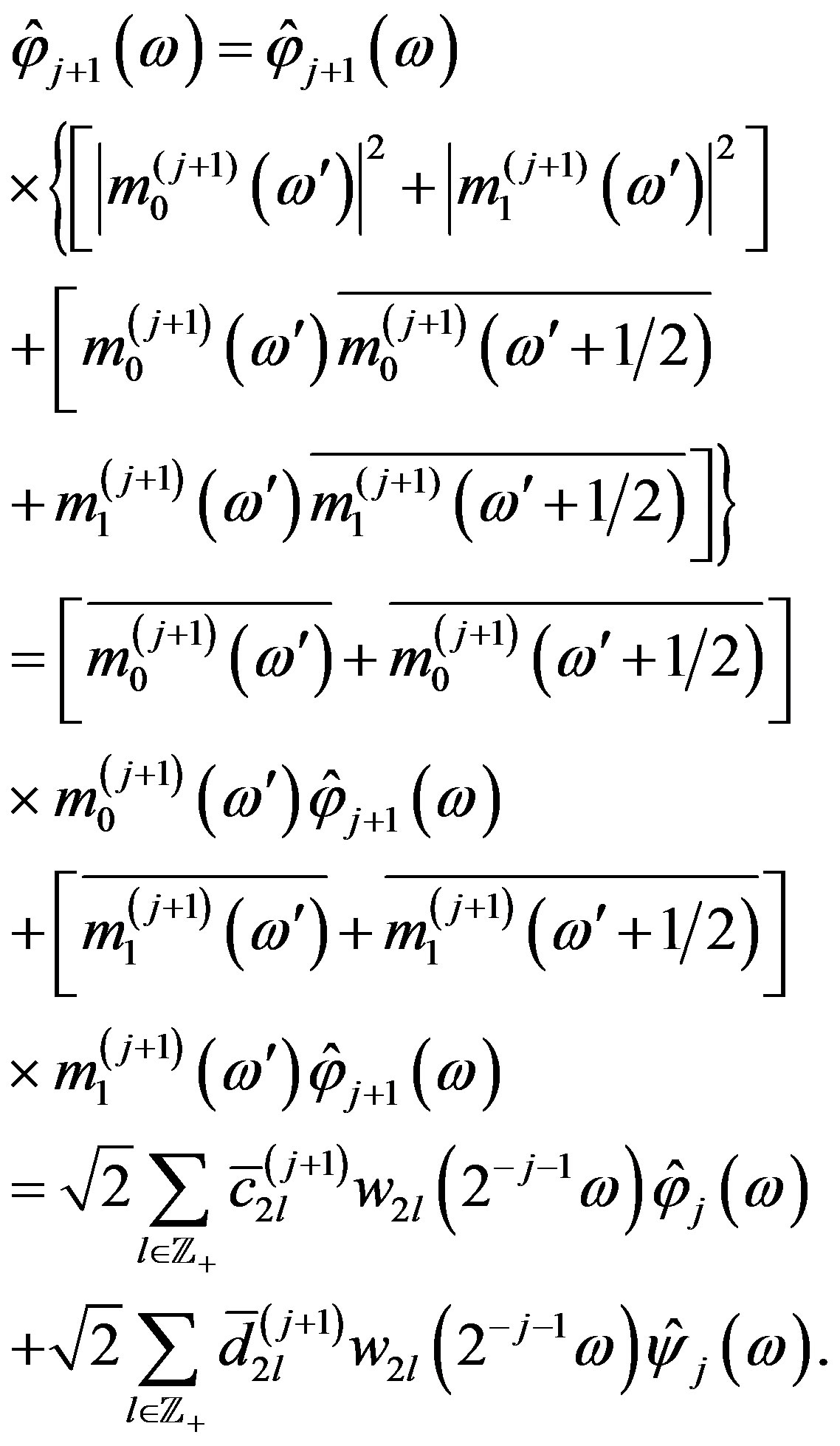
Using the inverse Fourier-Walsh transform, we have

or,
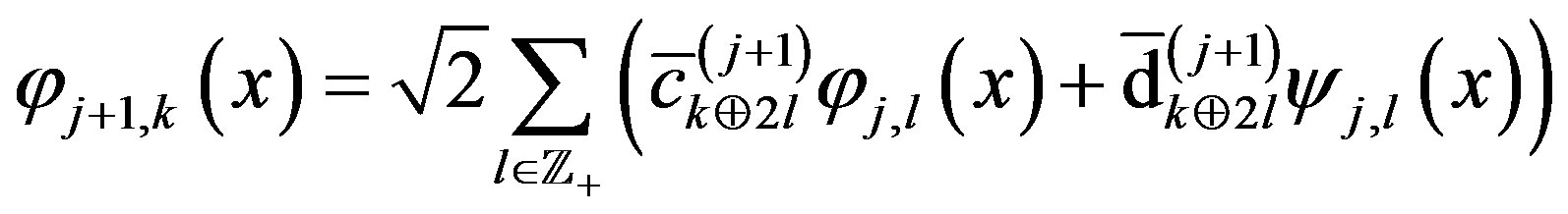 .
.
With Equation (11) it yields 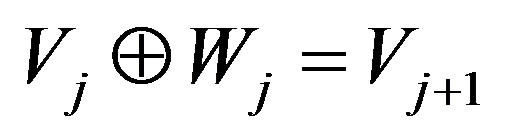
To conclude the proof it remains to show that
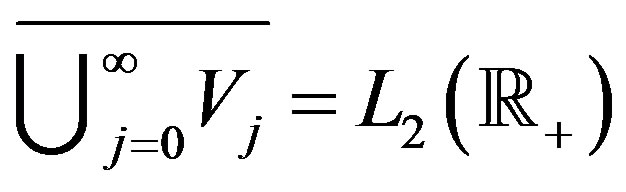 . (12)
. (12)
Note, that by Equation (7) for any  there exist
there exist  such that
such that 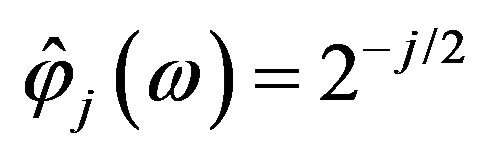 and, consequently,
and, consequently,
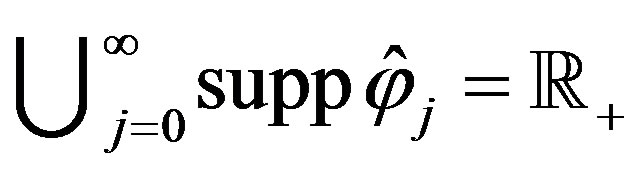 . (13)
. (13)
For any 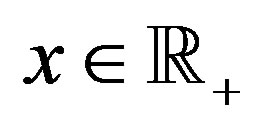 the subspace
the subspace 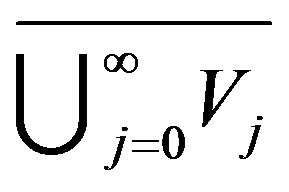 is invariant with respect to the shift
is invariant with respect to the shift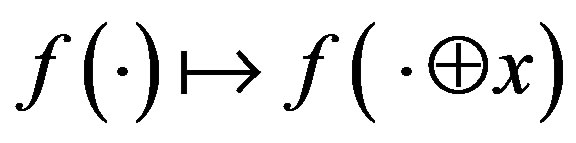 . Actually, an arbitrary
. Actually, an arbitrary  can be approximated by fractions
can be approximated by fractions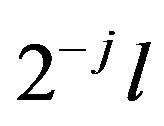 , with arbitrary large
, with arbitrary large . Besides, each
. Besides, each 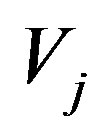 is invariant with respect to the shifts
is invariant with respect to the shifts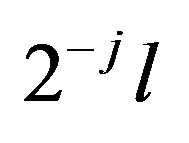 . By Equation (4) it is clear that
. By Equation (4) it is clear that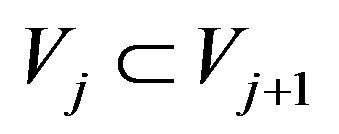 .
.
Let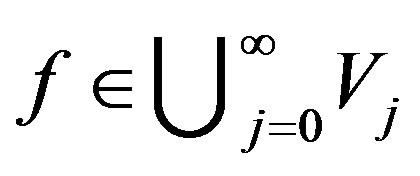 . There exist
. There exist  such that
such that 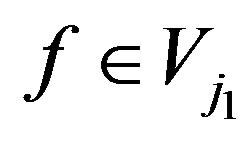
and hence 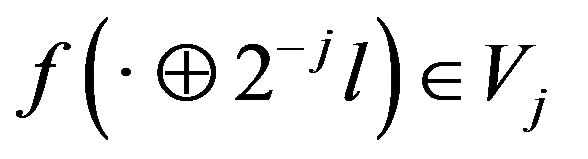 for all
for all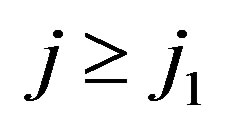 . The continuity of
. The continuity of 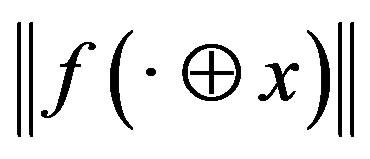 implies that
implies that . If
. If
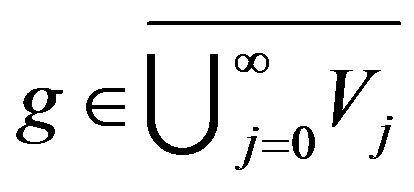 , then approximating
, then approximating  with
with 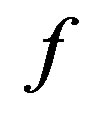 from
from
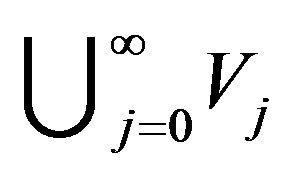 and using the invariance of a norm with respect to the shift, we obtain
and using the invariance of a norm with respect to the shift, we obtain .
.
Denote by 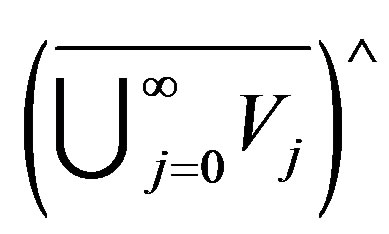 the set of all
the set of all 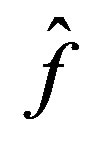 such that
such that
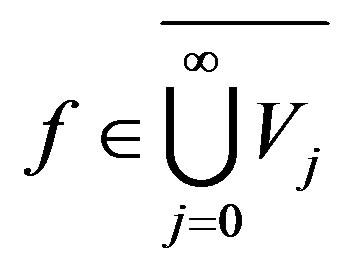 . By the Weiner’s theorem we can write
. By the Weiner’s theorem we can write
 , for some measurable
, for some measurable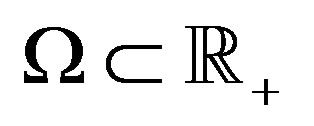 . It is clearly that
. It is clearly that 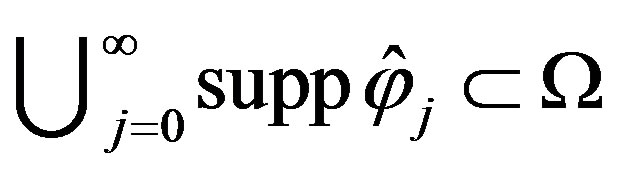 and, in view of Equation (13), we have
and, in view of Equation (13), we have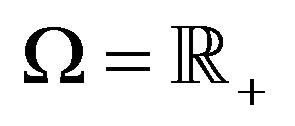 . Hence, the Equation (12) holds. The theorem is proved.
. Hence, the Equation (12) holds. The theorem is proved.
3. Numerical Experiments
For any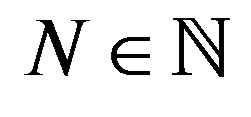 , let
, let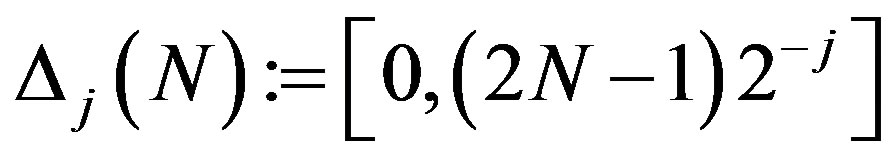 ,
,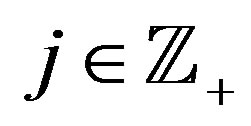 . According to [12] an adapted multiresolution analysis (AMRA) of rank
. According to [12] an adapted multiresolution analysis (AMRA) of rank  in
in 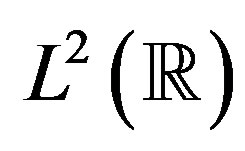 is a collection of closed subspaces
is a collection of closed subspaces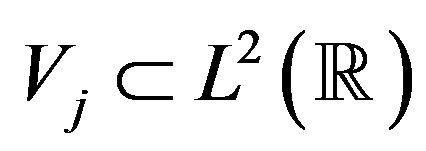 ,
, 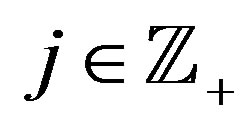 , which satisfies the following conditions:
, which satisfies the following conditions:
1) 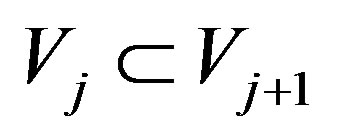 for all
for all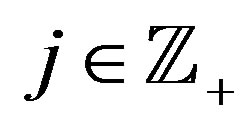 ;
;
2)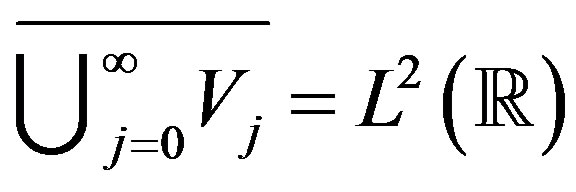 ;
;
3) for every 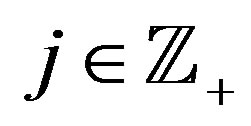 there is a function
there is a function 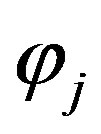 in
in 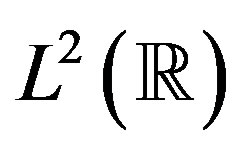 with a finite support
with a finite support  such that
such that
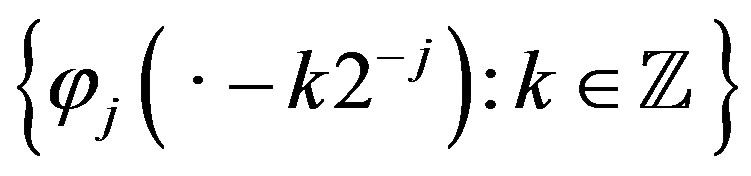 is an orthonormal basis of
is an orthonormal basis of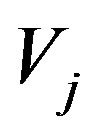 ;
;
4) for every 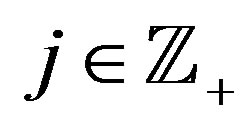 there exists a filter
there exists a filter
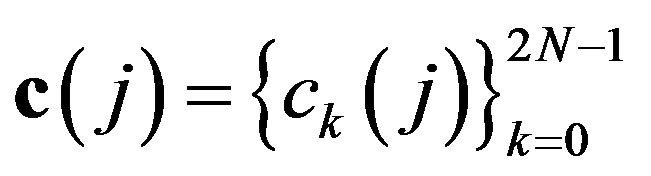
such that
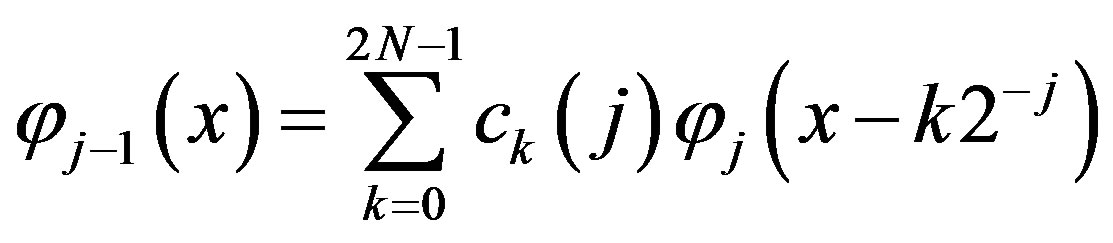 ,
,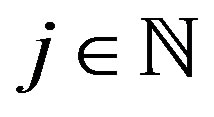 . (14)
. (14)
The sequence  from condition (4) is called a scaling sequence for given an AMRA. The corresponding a wavelet sequence
from condition (4) is called a scaling sequence for given an AMRA. The corresponding a wavelet sequence  can be defined by
can be defined by
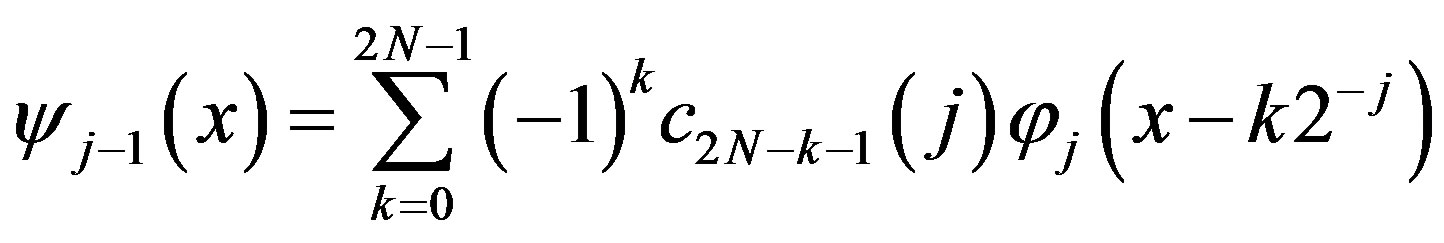 . (15)
. (15)
Denote by 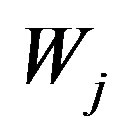 the orthogonal complement of
the orthogonal complement of 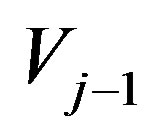 in
in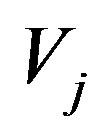 . It is known that, under some conditions, the system
. It is known that, under some conditions, the system 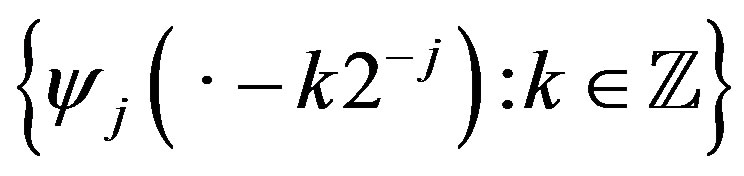 is an orthonormal basis of
is an orthonormal basis of
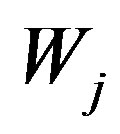 (for more details, see, e.g., [14, Sect. 8.1]). Moreover, if
(for more details, see, e.g., [14, Sect. 8.1]). Moreover, if 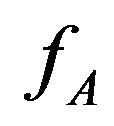 denotes the projection of a function
denotes the projection of a function 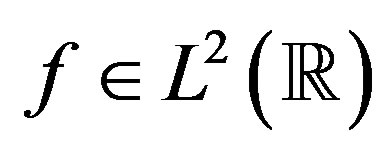 on the subset
on the subset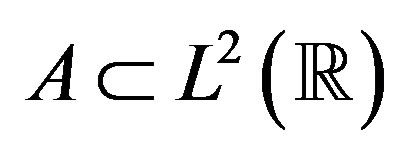 , then
, then
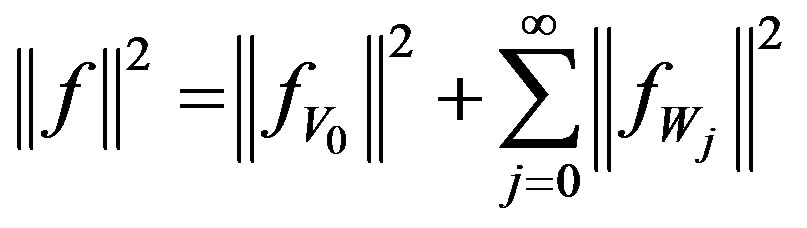
and
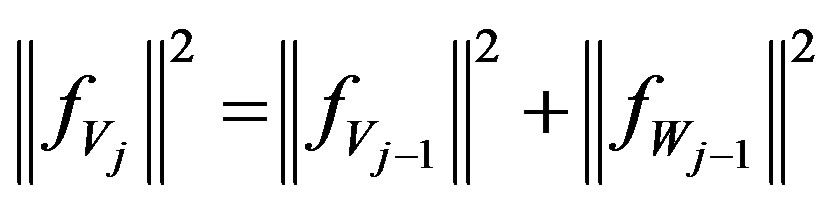 . (16)
. (16)
Let us denote
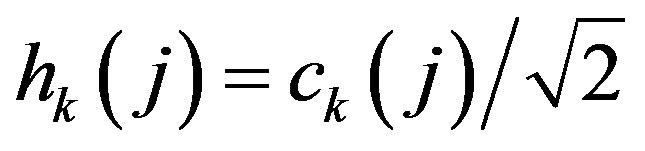
and
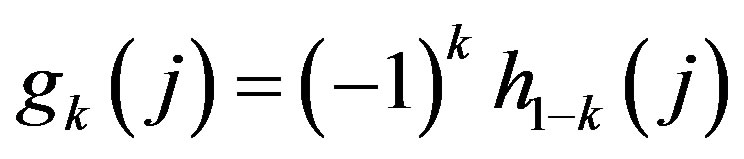 .
.
For a given array
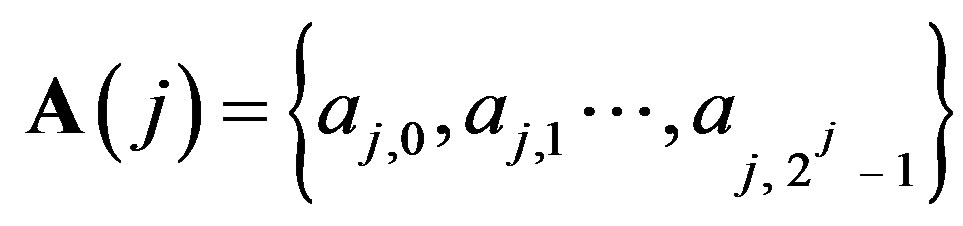 the direct non-stationary discrete wavelet transform
the direct non-stationary discrete wavelet transform
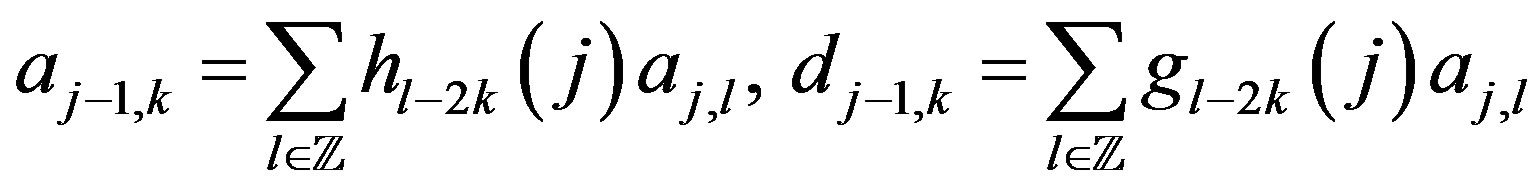 maps it into
maps it into
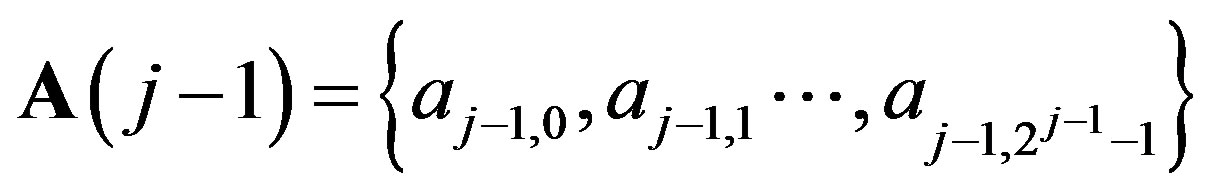
and
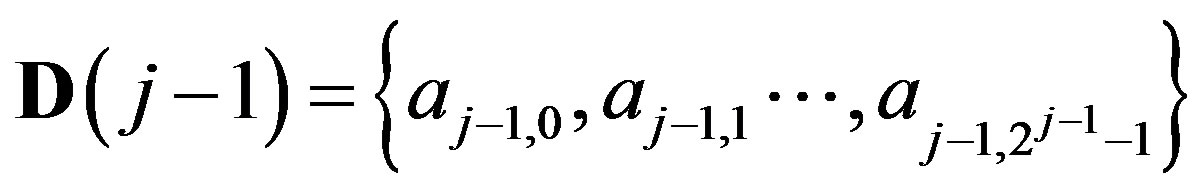 .
.
The inverse transform is defined as follows

and reconstructs  by
by 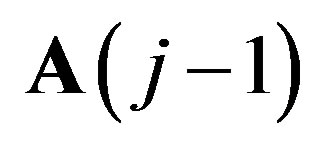 and
and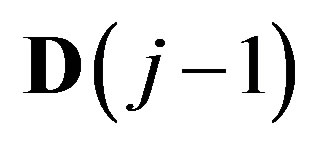 . According to [12] in order to choose the filter
. According to [12] in order to choose the filter  to maximize
to maximize 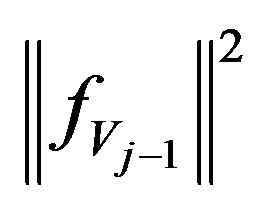 in Equation (16), we must solve the following problem.
in Equation (16), we must solve the following problem.
Problem 1. Let 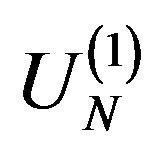 be the subset of the 2n-dimensional Euclidean space
be the subset of the 2n-dimensional Euclidean space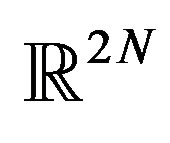 , which consists of the points
, which consists of the points 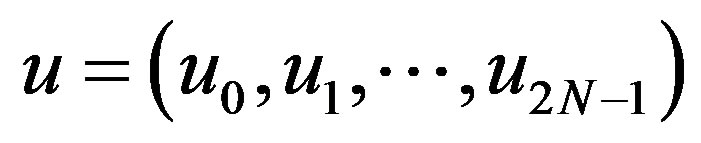 satisfying the conditions
satisfying the conditions
 . (17)
. (17)
for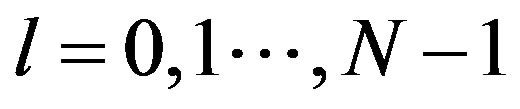 . Find a point
. Find a point 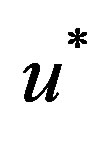 for which
for which
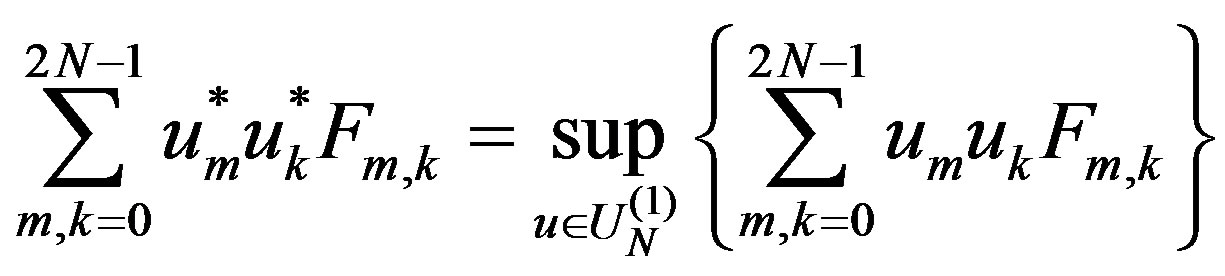 , (18)
, (18)
where  is a
is a 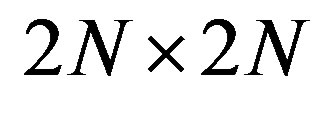 symmetric matrix.
symmetric matrix.
Problem 1 has a solution since 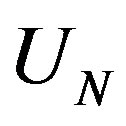 is a compact. But, as noted in [12], the numerical solution of this problem is not trivial even for
is a compact. But, as noted in [12], the numerical solution of this problem is not trivial even for .
.
Concerning the standard Haar and Daubechies (with 4 coefficients) discrete transforms see, e.g., [17]; we will denote them as SWTH and SWTD, respectively. We write NSWTH for the simplest case of a multiresolution analysis of rank 1 which is considered in [12, Sect. 3] (see also [13]). The nonstationary Daubechies discrete wavelet transform which corresponds an AMRA of rank 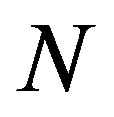 are defined in [12] and we will use the symbol NSWTDN to denote this transform (see NSWTD1 and NSWTD2 in the tables below).
are defined in [12] and we will use the symbol NSWTDN to denote this transform (see NSWTD1 and NSWTD2 in the tables below).
Method A associated with one of the mentioned above discrete wavelet transforms (cf. [17, Chap.7]) consists of the following steps:
Step 1. Apply the discrete wavelet transform  times to an input array
times to an input array 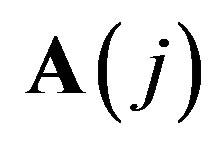 and get the sequence
and get the sequence
 .
.
Step 2. Allocate a certain percentage of the wavelet coefficients with lagest absolute value (we choose 10%) and nullify the remaining coefficients.
Step 3. Apply the inverse wavelet transform to the modified arrays of the wavelet coefficients.
Step 4. Calculate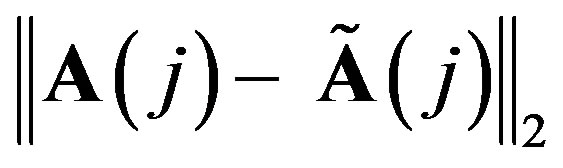 , where
, where  is a reconstructed array.
is a reconstructed array.
In Method B the second step is replaced on the uniform quantization and the forth step is replaced on the calculation of the entropy of a vector, obtained in the third step.
We recall that 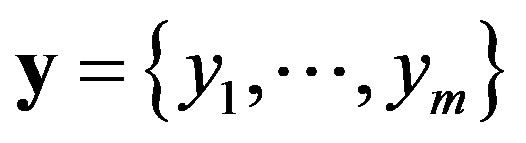 is a vector uniform quantization for given vector
is a vector uniform quantization for given vector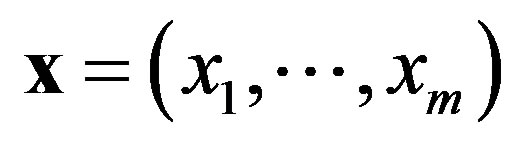 , if
, if

where  is the length of the quantization interval.
is the length of the quantization interval.
The value  will be calculated by
will be calculated by
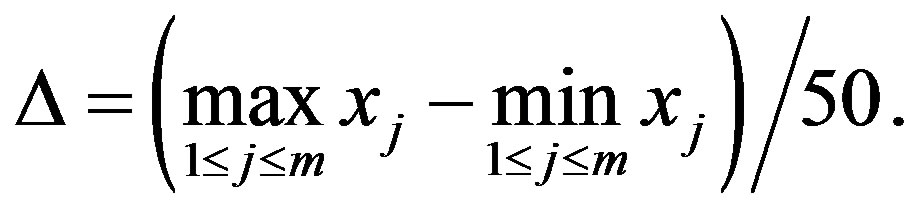
The Shannon entropy of  is defined by the formula
is defined by the formula
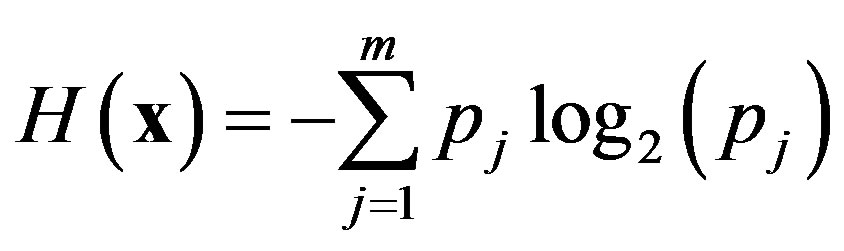 where
where 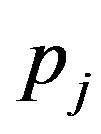 is frequency of the value
is frequency of the value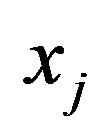 .
.
Let us consider a similar approach associated with the following problem:
Problem 2. Let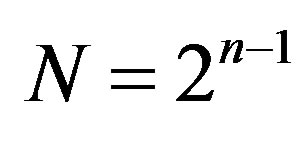 . Denote by
. Denote by 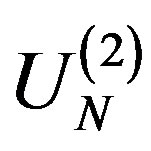 the set of all points
the set of all points 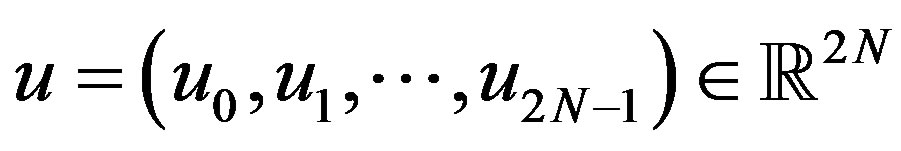 such that
such that
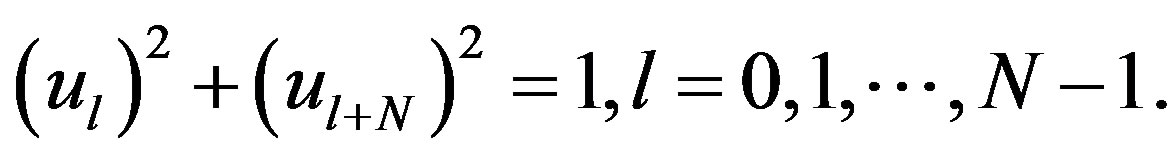
For every 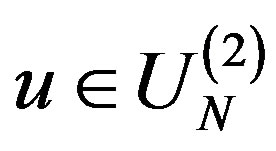 we define
we define
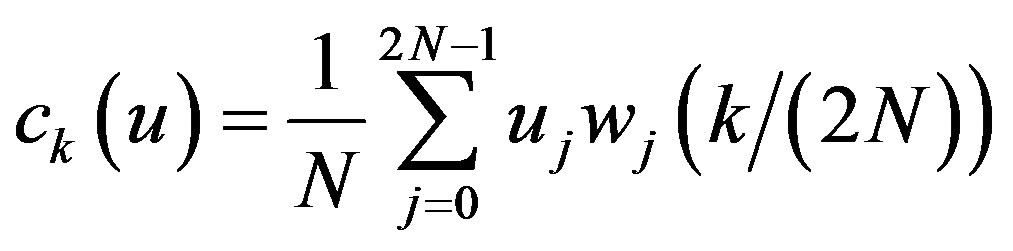
for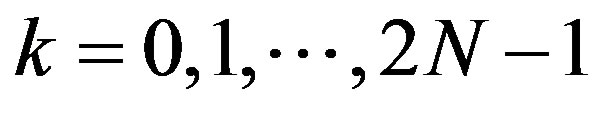 . Find a point
. Find a point 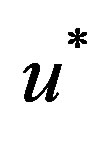 for which
for which
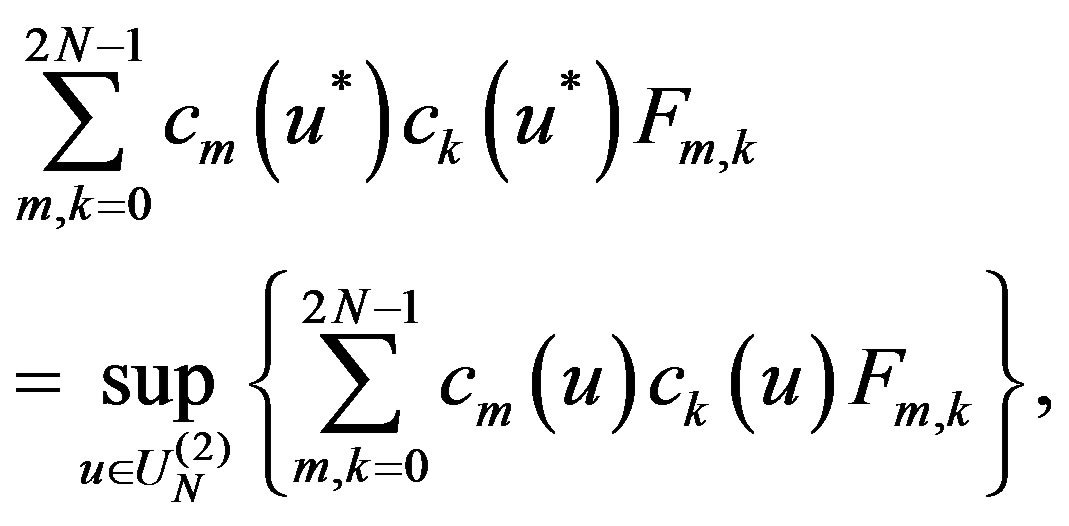 (19)
(19)
where 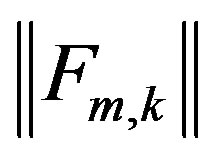 is a
is a 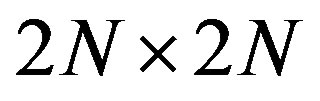 symmetric matrix.
symmetric matrix.
Given an array , we define the matrix
, we define the matrix 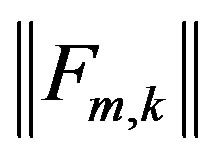 in Problem 1 and Problem 2 by
in Problem 1 and Problem 2 by

and
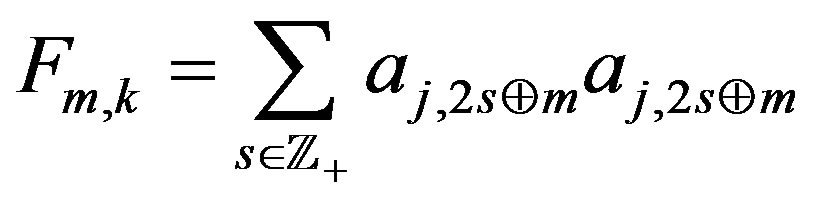 respectively. Here
respectively. Here  for
for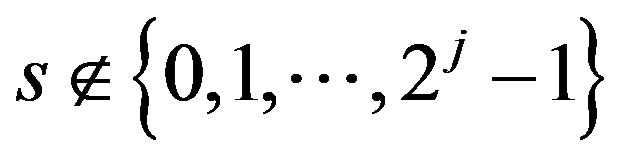 . Suppose that
. Suppose that 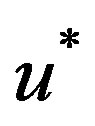 is a solution of Equation (19). Then the direct and inverse nonstationary discrete dyadic wavelet transforms are defined by
is a solution of Equation (19). Then the direct and inverse nonstationary discrete dyadic wavelet transforms are defined by
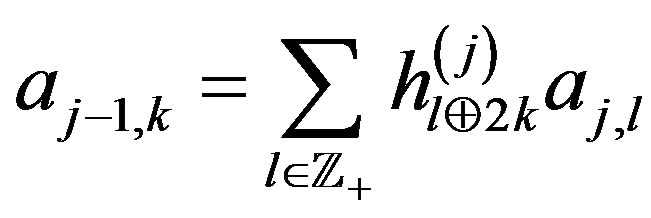 ,
, 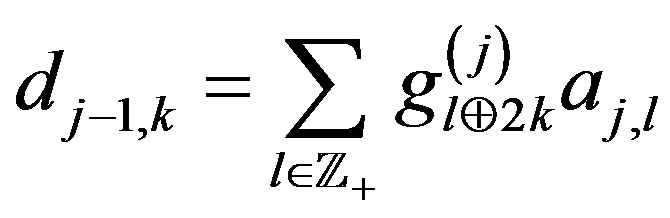 ,
,
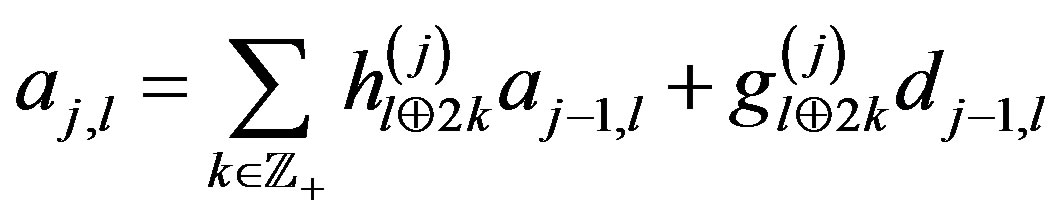 where
where 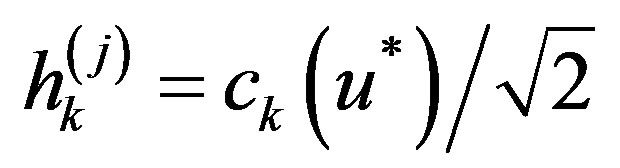 and
and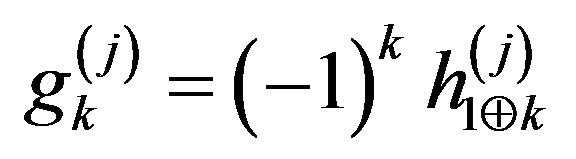 . We
. We
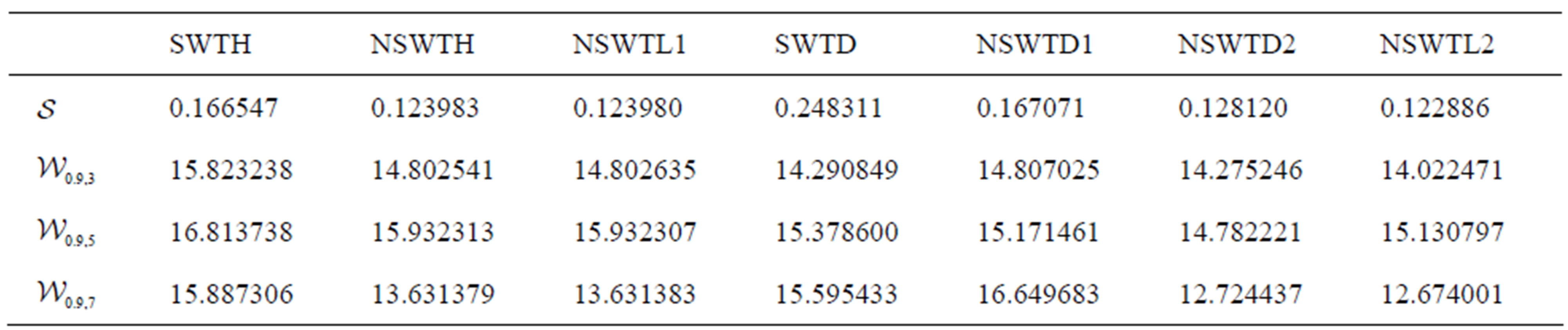
Table 1. Values of the square error corresponding to Method A.

Table 2. Values of the entropy obtained by Method B.
denote these discrete transforms as NSWTL1 if 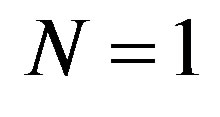 and as NSWTL2 if
and as NSWTL2 if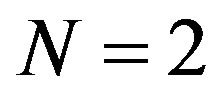 .
.
Let us recall that the Weierstrass function is defined as
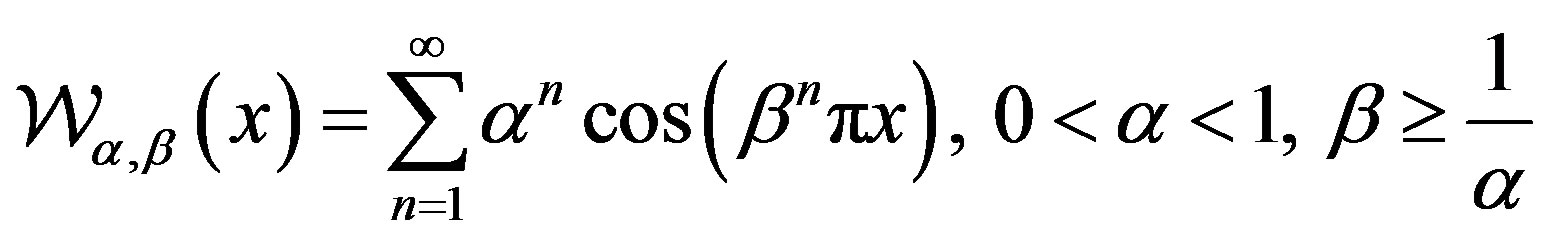 and the Swartz function is defined as
and the Swartz function is defined as
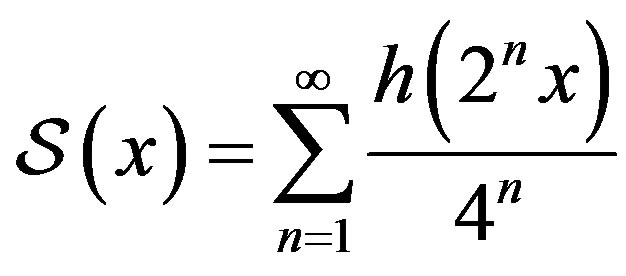 where
where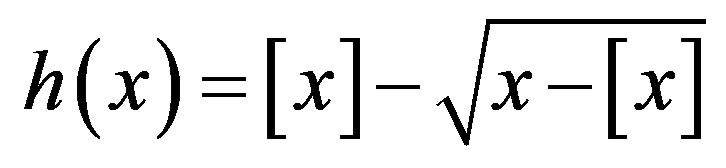 . We will consider arrays
. We will consider arrays 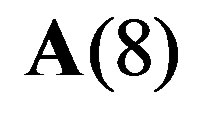 with elements a8,k =
with elements a8,k =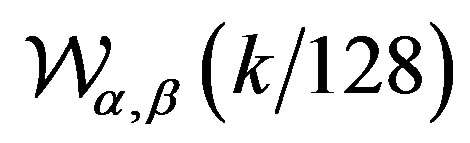 or a8,k =
or a8,k =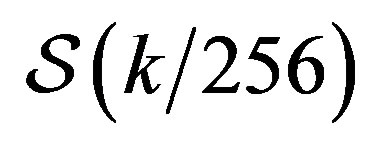 ,
, . Then we use the Matlab function fminsearch to solve the optimization problems in Equations (18) and (19). The results of these numerical experiments are presented in Tables 1 and 2. We see that in several cases the introduced nonstationary dyadic wavelets have an advantage over the classical Haar and Daubechies wavelets.
. Then we use the Matlab function fminsearch to solve the optimization problems in Equations (18) and (19). The results of these numerical experiments are presented in Tables 1 and 2. We see that in several cases the introduced nonstationary dyadic wavelets have an advantage over the classical Haar and Daubechies wavelets.
REFERENCES
- W. C. Lang, “Orthogonal Wavelets on the Cantor Dyadic Group,” SIAM Journal on Mathematical Analysis, Vol. 27, No. 1, 1996, pp. 305-312. doi:10.1137/S0036141093248049
- W. C. Lang, “Wavelet Analysis on the Cantor Dyadic Group,” Houston Journal of Mathematics, Vol. 24, No. 3, 1998, pp. 533-544.
- W. C. Lang, “Fractal Multiwavelets Related to the Cantor Dyadic Group,” International Journal of Mathematics and Mathematical Sciences, Vol. 21, No. 2, 1998, pp. 307-317. doi:10.1155/S0161171298000428
- Y. A. Farkov, “Orthogonal Wavelets with Compact Support on Locally Compact Abelian Groups,” Izvestiya: Mathematics, Vol. 69, No. 3, 2005, pp. 623-650. doi:10.1070/IM2005v069n03ABEH000540
- Y. A. Farkov, “Wavelets and Frames in Walsh Analysis,” In: M. del Valle, Ed., Wavelets: Classification, Theory and Applications, Chapter 11, Nova Science Publishers, New York, 2012, pp. 267-304.
- Y. A. Farkov and E. A. Rodionov, “Estimates of the Smoothness of Dyadic Orthogonal Wavelets of Daubechies Type,” Mathematical Notes, Vol. 82, No. 6, 2007, pp. 407-421. doi:10.1134/S0001434609090144
- Y. A. Farkov, A. Yu. Maksimov and S. A. Stroganov, “On Biorthogonal Wavelets Related to the Walsh Functions,” International Journal of Wavelets, Multiresolution and Information Processing, Vol. 9, No. 3, 2011, pp. 485- 499. doi:10.1142/S0219691311004195
- Y. A. Farkov and E. A. Rodionov, “Algorithms for Wavelet Construction on Vilenkin Groups,” P-Adic Numbers, Ultrametric Analysis, and Applications, Vol. 3, No. 3, 2011, pp. 181-195. doi:10.1134/S2070046611030022
- Y. A. Farkov, “Periodic Wavelets on the p-Adic Vilenkin Group,” P-Adic Numbers, Ultrametric Analysis, and Applications, Vol. 3, No. 4, 2011, pp. 281-287. doi:10.1134/S2070046611040030
- Y. A. Farkov and M. E. Borisov, “Periodic Dyadic Wavelets and Coding of Fractal Functions,” Russian Mathematics (Izvestiya VUZ. Matematika), No. 9, 2012, pp. 54- 65.
- I. Y. Novikov, “On the Construction of Nonstationary Orthonormal Infinitely differentiable Compactly Supported Wavelets,” Proceedings of the 12th International Association for Pattern Recognition, Jerusalem, 9-13 October 1994, pp. 214-215. doi:10.1109/ICPR.1994.577164
- B. Sendov, “Adapted Multiresolution Analysis,” Proceedings of Alexits Memorial Conference Functions, Series, Operators, Budapest, 9-14 August 1999, pp. 23-38.
- B. Sendov, “Adaptive Multiresolution Analysis on the Dyadic Topological Group,” Journal of Approximation Theory, Vol. 96, No. 2, 1998, pp. 21-45. doi:10.1006/jath.1998.3234
- I. Y. Novikov, V. Y. Protasov and M. A. Skopina, “Wavelet Theory,” American Mathematical Society, Providence, 2011.
- F. Schipp, W. R. Wade and P. Simon, “Walsh Series: An Introduction to Dyadic Harmonic Analysis,” Adam Hilger, Bristol, 1990.
- B. I. Golubov, A. V. Efimov and V. A. Skvortsov, “Walsh Series and Transforms,” Kluwer, Dordrecht, 1991.
- S. Welstead, “Fractal and Wavelet Image Compression Techniques,” SPIE Optical Engineering Press, Bellingham, 2002.

