American Journal of Computational Mathematics
Vol.2 No.1(2012), Article ID:17953,6 pages DOI:10.4236/ajcm.2012.21003
Computation of the Smith Form for Multivariate Polynomial Matrices Using Maple
Department of Mathematics and Statistics, Sultan Qaboos University, Muscat, Oman
Email: boudell@squ.edu.om
Received October 13, 2011; revised December 2, 2011; accepted December 15, 2011
Keywords: Smith Form; Unimodular; Equivalence; Quillen-Suslin Theorem; Maple
ABSTRACT
In this paper we show how the transformations associated with the reduction to the Smith form of some classes of multivariate polynomial matrices are computed. Using a Maple implementation of a constructive version of the Quillen-Suslin Theorem, we present two algorithms for the reduction to a particular Smith form often associated with the simplification of linear systems of multidimensional equations.
1. Introduction
Matrices whose elements are polynomials in more than one indeterminate have been studied by many authors. Such matrices arise in the mathematical treatment of the so-called multidimensional systems which can be considered as extensions of the ordinary differential or difference systems. These include delay-differential systems and partial differential systems. In particular the Smith normal form of a matrix plays an important role in many areas of mathematics such as the polynomial approach in control theory see for example Rosenbrock [1] and Kailath [2]. The problem of reducing an univariate polynomial matrix to its Smith form is well understood and the relevant algorithm is already implemented in most computer algebra systems. For the multivariate case, however the problem is still open. Despite that some necessary and/or sufficient conditions for the reduction of a matrix to its Smith form have been given in the literature, no algorithm has been given to show how the transformations involved in the reduction are actually computed. These transformations are important if the solutions of the reduced system are to be expressed in terms of the original variables. So far the computations associated with these conditions have been difficult if not impossible to carry out. Recently however, some progress has been made in symbolic computation in particular a QuillenSuslin Maple package [3] has been developed. This package which is a maple implementation of the Quillen-Suslin theorem provides an algorithm which computes a basis of a free module over a polynomial ring. In terms of matrices, this algorithm completes a unimodular rectangular matrix to an invertible matrix over the given polynomial ring with rational or integer coefficients (for more details see http://wwwb.math. rwth-aachen.de/QuillenSuslin/). In this paper, we show how this package can be used to compute the Smith form and the associated transformation for some classes of multivariate polynomial matrices. The classes of matrices considered can be regarded as those associated with linear determined systems of multidimensional equations which can be reduced to a single equation, thereby simplifying the analysis of such systems. The transformation used to obtain the Smith form is that of unimodular equivalence which will be defined later. First we need to introduce some definitions and a theorem which play a key role in this paper.
Definition 1 Let  be a ring. The general linear group
be a ring. The general linear group 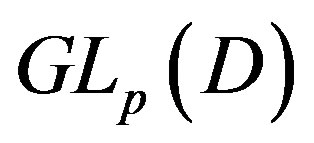 is defined by
is defined by
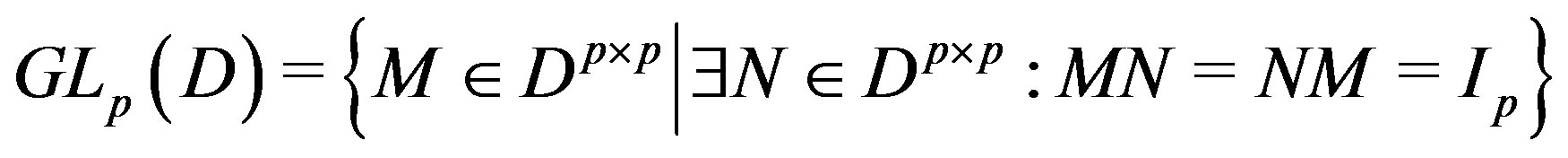
An element 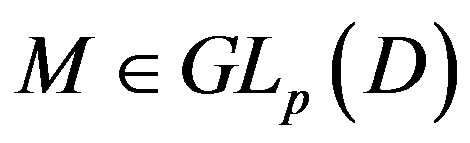 is called a unimodular matrix. In the case where
is called a unimodular matrix. In the case where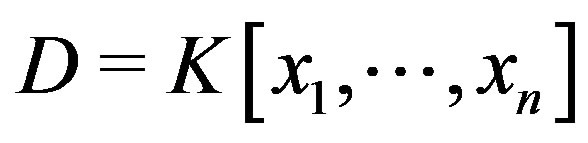 , a polynomial ring in the indeterminates
, a polynomial ring in the indeterminates 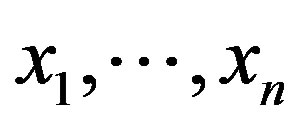 and coefficients in
and coefficients in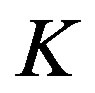 , the matrix
, the matrix  is unimodular if and only if the determinant of
is unimodular if and only if the determinant of 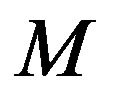 is invertible in
is invertible in , i.e., is a non-zero element of
, i.e., is a non-zero element of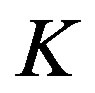 .
.
In the case when a matrix is rectangular we introduce the following concept of primeness.
Definition 2 A matrix 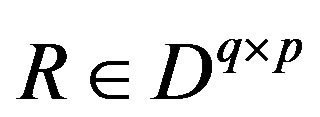 with
with 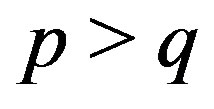 is said to be zero-left-prime
is said to be zero-left-prime  if it admits a right-inverse over
if it admits a right-inverse over . i.e., if there exists
. i.e., if there exists 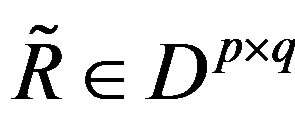 such that
such that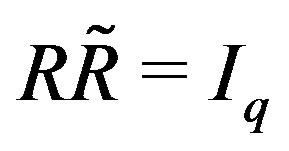 .
.
Similarly zero-right-primeness  can be defined by transposition for matrices where
can be defined by transposition for matrices where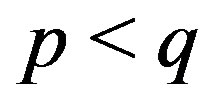 .
.
We now state the famous Quillen-Suslin Theorem. This theorem is at the centre of the proofs of the results presented in this paper and its Maple implementation is used in the computation of the transformations.
Theorem 1 (Quillen-Suslin [4,5]) Let 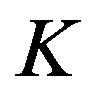 be a principal ideal domain and
be a principal ideal domain and 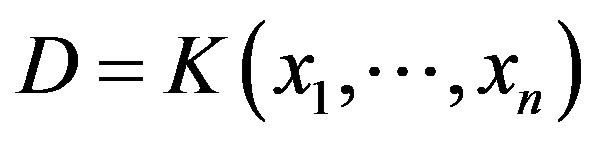 and let
and let 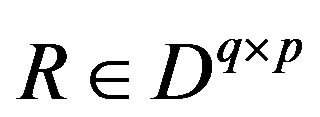 be a matrix which admits a right-inverse
be a matrix which admits a right-inverse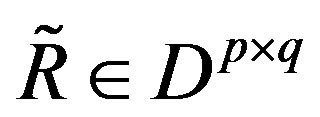 , i.e.,
, i.e.,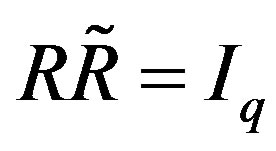 . Then there exists a unimodular matrix
. Then there exists a unimodular matrix 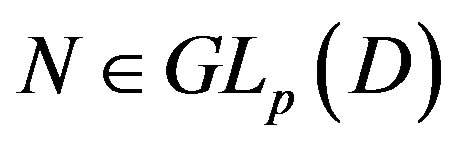 such that
such that
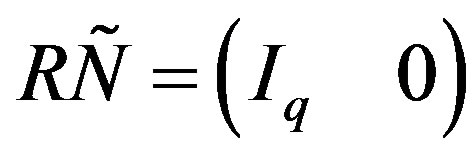 (1)
(1)
2. Equivalence to the Smith Form
The Smith form 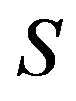 of a
of a 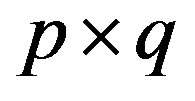 matrix
matrix 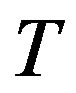 with elements in a ring
with elements in a ring  is usually the result of an equivalence transformation, i.e. a transformation of the form
is usually the result of an equivalence transformation, i.e. a transformation of the form
 (2)
(2)
where 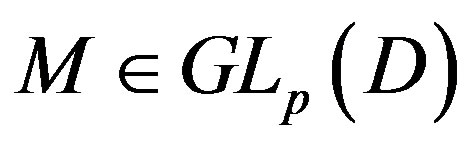 and
and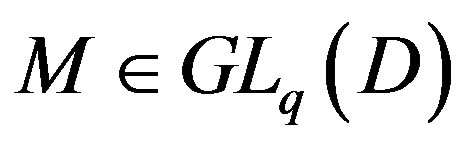 . The resulting Smith form S is given by the diagonal matrix formed by the invariant polynomials. The non-zero invariant polynomials
. The resulting Smith form S is given by the diagonal matrix formed by the invariant polynomials. The non-zero invariant polynomials 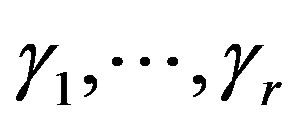 are defined by
are defined by 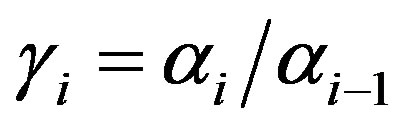 with
with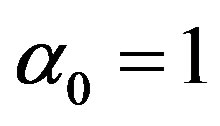 ,
, 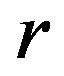 is the rank of
is the rank of  and
and 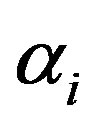 is the gcd of the
is the gcd of the  minors of
minors of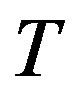 .
.
It is a fact that it is not always possible to reduce a matrix to its Smith form by an equivalence of the type (2). In order to show that any matrix can be brought by an equivalence transformation to its Smith form, it is usually required that  is a principal ideal or a Euclidean domain. In the case when
is a principal ideal or a Euclidean domain. In the case when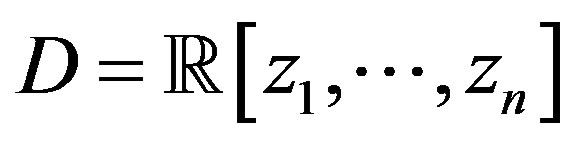 , the matrices may be treated as having elements in one of the indeterminates with coefficients that are rational forms in the other indeterminates e.g.
, the matrices may be treated as having elements in one of the indeterminates with coefficients that are rational forms in the other indeterminates e.g.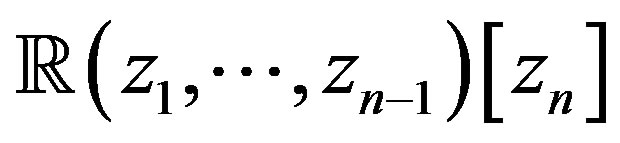 . This approach which involves a renormalization step has the disadvantage of yielding Smith forms which are not unique, see the work of Frost and Storey [6] and Morf et al. [7]. Conditions under which a matrix with elements in
. This approach which involves a renormalization step has the disadvantage of yielding Smith forms which are not unique, see the work of Frost and Storey [6] and Morf et al. [7]. Conditions under which a matrix with elements in 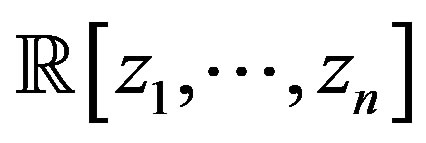 is equivalent to its Smith form have been given by a number of authors. For the ring
is equivalent to its Smith form have been given by a number of authors. For the ring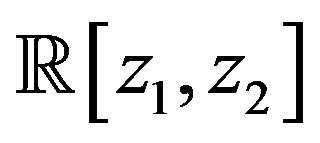 , Lee and Zak [8] proposed a necessary and sufficient condition in terms of the existence of solutions to certain polynomial equations. Frost and Boudellioua [9] gave a necessary and sufficient condition for a class of multivariate polynomial matrices in terms of the existence of a polynomial vector. Lin et al. [10] proposed a sufficient condition for a class of matrices whose determinant is linear in one of the indeterminates.
, Lee and Zak [8] proposed a necessary and sufficient condition in terms of the existence of solutions to certain polynomial equations. Frost and Boudellioua [9] gave a necessary and sufficient condition for a class of multivariate polynomial matrices in terms of the existence of a polynomial vector. Lin et al. [10] proposed a sufficient condition for a class of matrices whose determinant is linear in one of the indeterminates.
Theorem 2 (Boudellioua and Quadrat [11]) Let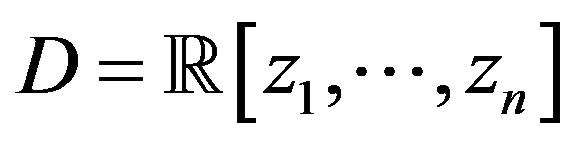 , a matrix
, a matrix 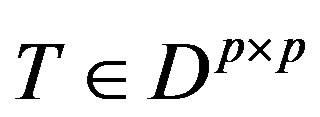 is equivalent to the Smith form:
is equivalent to the Smith form:
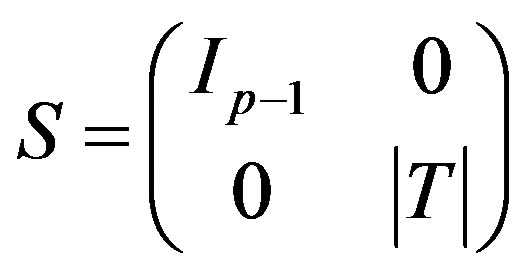 (3)
(3)
if and only if there exists a ZRP vector 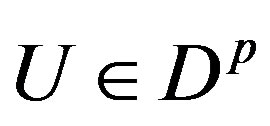 such that the matrix
such that the matrix 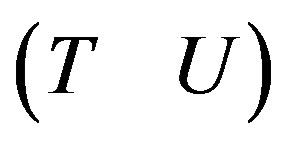 is ZLP.
is ZLP.
This is a particular type of Smith form where all the invariant polynomials are equal to 1 except the last one which is given by the determinant of the matrix. This form is important for simplification considerations, i.e. a system whose matrix is equivalent to the Smith form (3) is equivalent to a single equation in one unknown. Thus making it easier to analyse such a system either analyticcally or numerically. In order to express the conclusions and solutions made about the reduced system in terms of the original system, one has to compute the transformations (2) connecting the original system matrix to the Smith form. Suppose that such a vector is obtained then the transformations 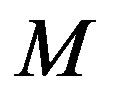 and
and 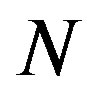 that reduce
that reduce 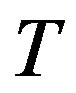 to the Smith form (3) can be obtained via the following Maple algorithm.
to the Smith form (3) can be obtained via the following Maple algorithm.
Ÿ 2.1. Algorithm 1
Ÿ Declare the path where the required Maple libraries such as QuillenSuslin are stored and load the packages LinearAlgebra and QuillenSuslin.
Ÿ Declare the ring over which the matrix is defined by declaring the indeterminates and the field of coefficients.
Ÿ Enter the elements of the matrices 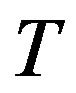 and
and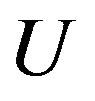 .
.
Ÿ Test the zero-primeness of the matrix 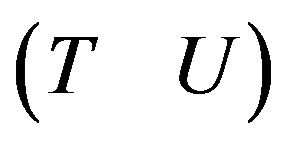 using the function IsUnimod.
using the function IsUnimod.
Ÿ Use the function QSAlgorithm to compute the square unimodular matrix 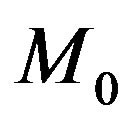 such that
such that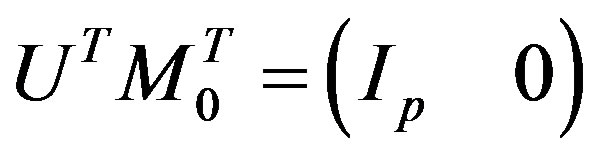 .
.
Ÿ Interchange the first and last column of 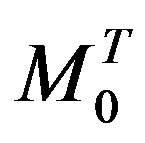 and transpose to obtain the matrix
and transpose to obtain the matrix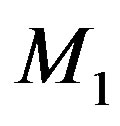 .
.
Ÿ Extract the matrices 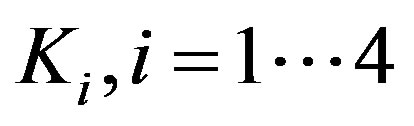 and
and 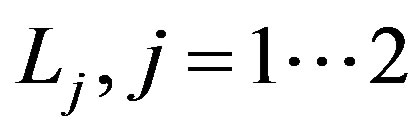 from
from 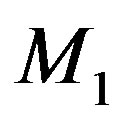 and
and 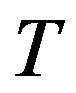 respectively.
respectively.
Ÿ Compute the matrix , where
, where
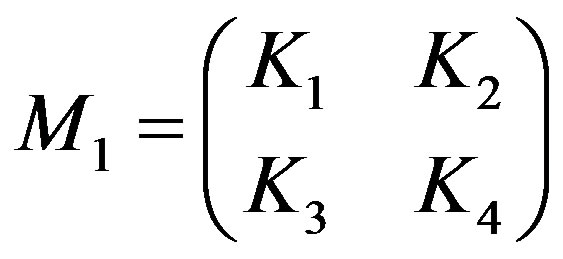 and
and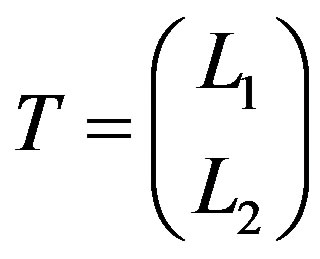 .
.
Ÿ Use the function QSAlgorithm to obtain the square unimodular matrix 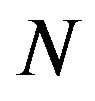 such that
such that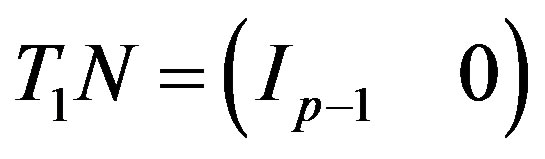 .
.
Ÿ Extract the submatrix 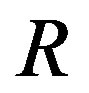 formed from the first row and the first
formed from the first row and the first 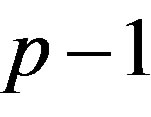 columns of the matrix
columns of the matrix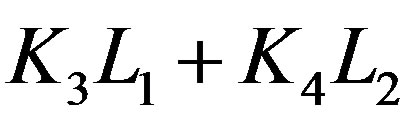 .
.
Ÿ Construct the matrix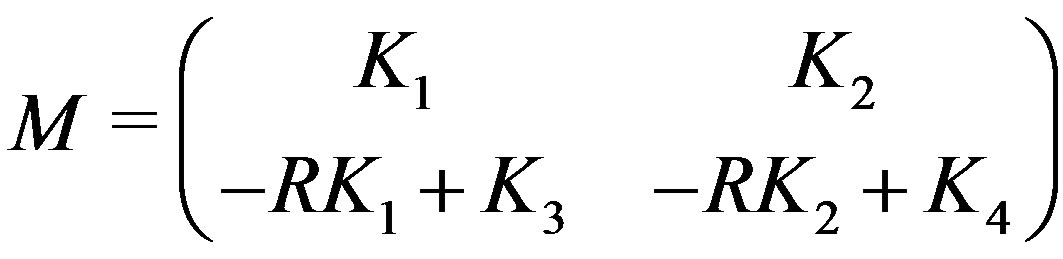 .
.
Ÿ Check that the Smith form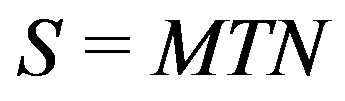 .
.
Another interesting result in the form of a sufficient condition for the reduction of class of linear multidimensional systems was given by Lin et al. [10]. This is the class of systems where the determinant of the system matrix is linear in one of the indeterminates. Such systems are also equivalent to a single equation. The result is given for the case when the determinant is linear in 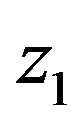 but it is equally valid for any indeterminate
but it is equally valid for any indeterminate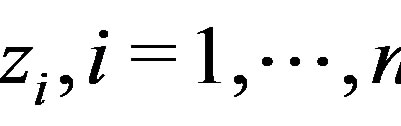 .
.
Theorem 3 (Lin et al. [10]) Let 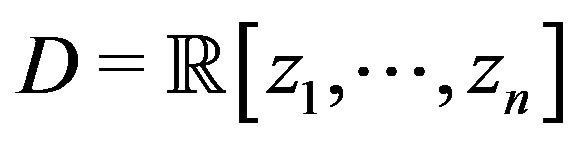 and
and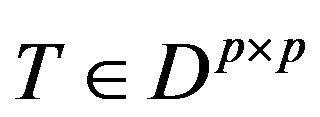 , then if
, then if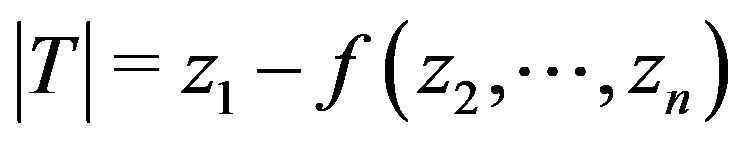 ,
, 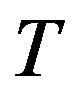 is equivalent to the Smith form:
is equivalent to the Smith form:
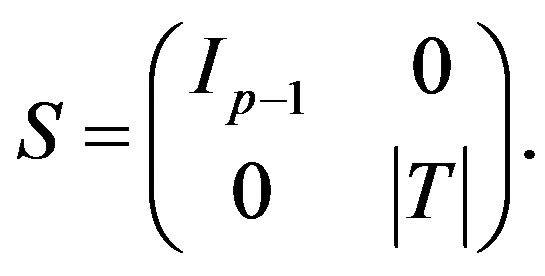 (4)
(4)
In the following we give an algorithm to find the unimodular matrices M and N that reduce the matrix T to the Smith form S.
Ÿ 2.2. Algorithm 2
Ÿ Declare the path where the required Maple libraries such as QuillenSuslin are stored and load the packages LinearAlgebra and QuillenSuslin.
Ÿ Declare the ring  over which the matrix is defined by declaring the indeterminates and the field of coefficients.
over which the matrix is defined by declaring the indeterminates and the field of coefficients.
Ÿ Enter the elements of the matrix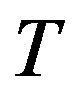 .
.
Ÿ Check that the determinant of 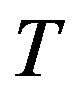 is linear in one of the indeterminates, say
is linear in one of the indeterminates, say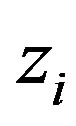 .
.
Ÿ Compute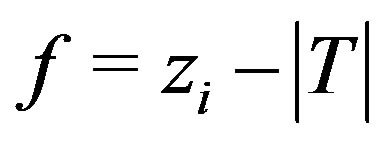 .
.
Ÿ Substitute 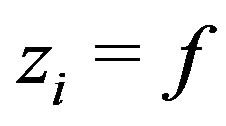 in
in 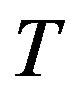 to obtain
to obtain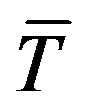 .
.
Ÿ Compute a ZRP vector 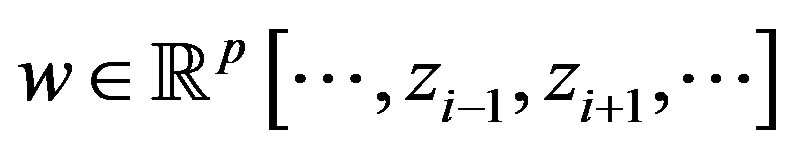 such that
such that  using the function SyzygyModule.
using the function SyzygyModule.
Ÿ Compute a matrix 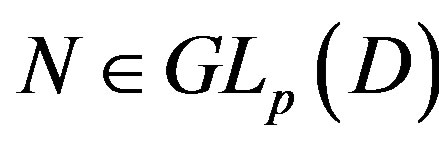 with last column given by
with last column given by 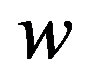 using the function CompleteMatrix.
using the function CompleteMatrix.
Ÿ Compute the matrix 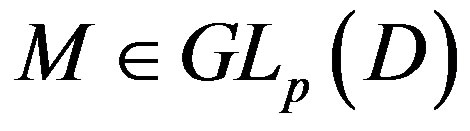 given by
given by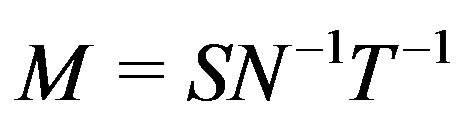 , where
, where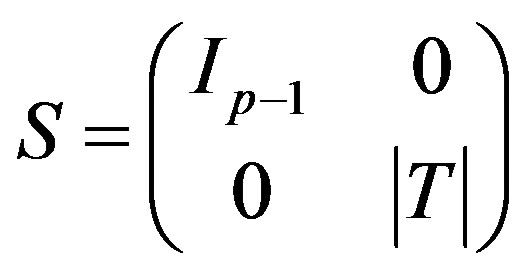 .
.
Ÿ Check that the Smith form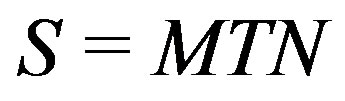 .
.
Example 1 (Frost and Boudellioua [9])
libname:=“C:/Involutive”, “C:/QuillenSuslin”, libname:
with (LinearAlgebra): with (QuillenSuslin):
Consider again the 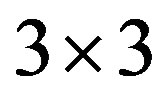 matrix
matrix 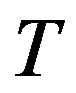 in Example 1 over the polynomial ring
in Example 1 over the polynomial ring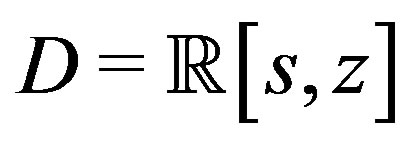 .
.
var := [s, z];

T := Matrix([[2*s*z^2 + z^3 + z^2 + 1,s*z^2 – s*z + s, 2*s*z + z^2], [2*s*z + z^2 + z, s*z – s, 2*s + z], [2*s^2*z + s*z^2 + s*z + z, s^2*z – s^2 – 1, 2*s^2 + s*z + 1]]); det_T := Determinant(T);
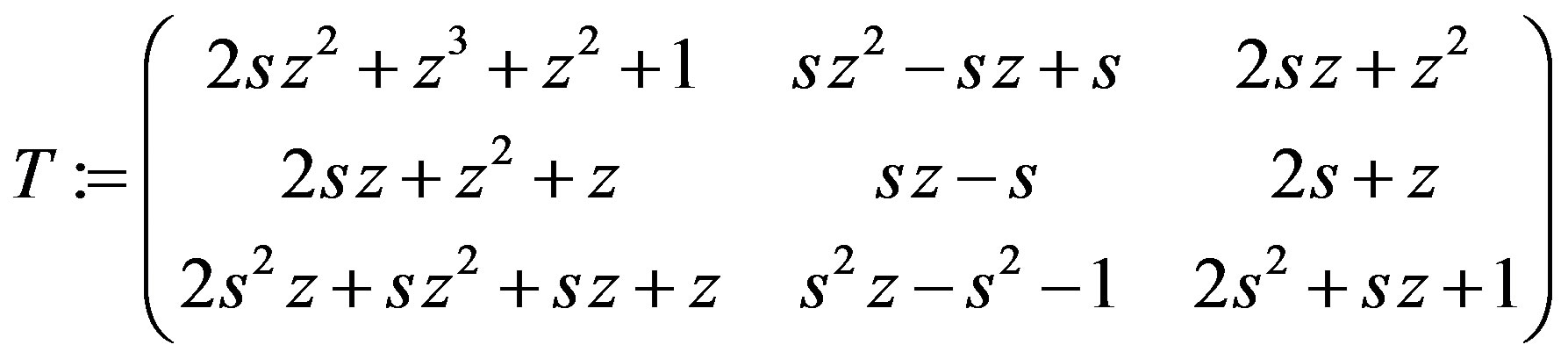
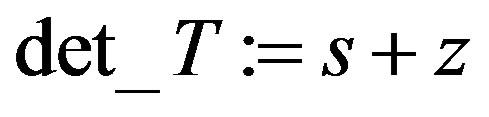
p := RowDimension(T);
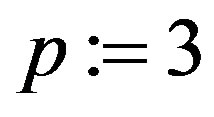
Now consider the column vector  satisfying the condition in Theorem 3U := Matrix([[z], [1], [s]]);
satisfying the condition in Theorem 3U := Matrix([[z], [1], [s]]);
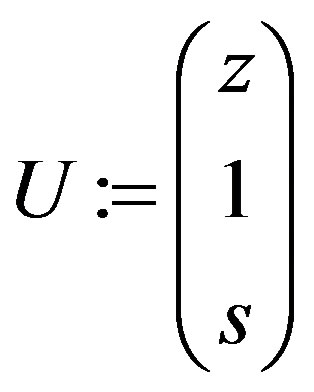
UT := Transpose(U);
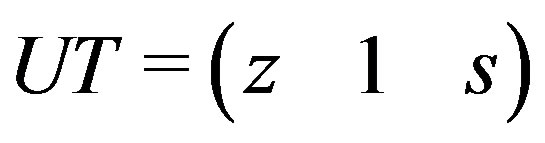
IsUnimod(UT, var, true);
TU := Matrix([T,U]);
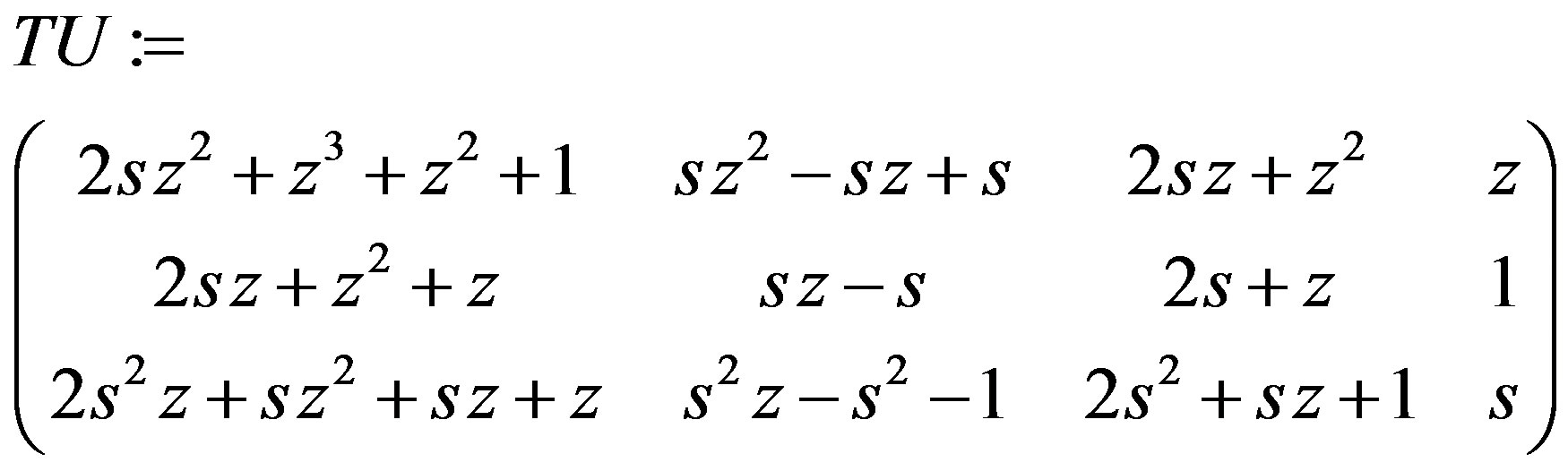
Let us check if the the matrix  is unimodular IsUnimod (TU, var, true);
is unimodular IsUnimod (TU, var, true);
Applying the QSAlgorithm procedure to the row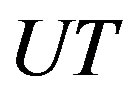 , we then obtain MT := QSAlgorithm(UT, var, true);
, we then obtain MT := QSAlgorithm(UT, var, true);
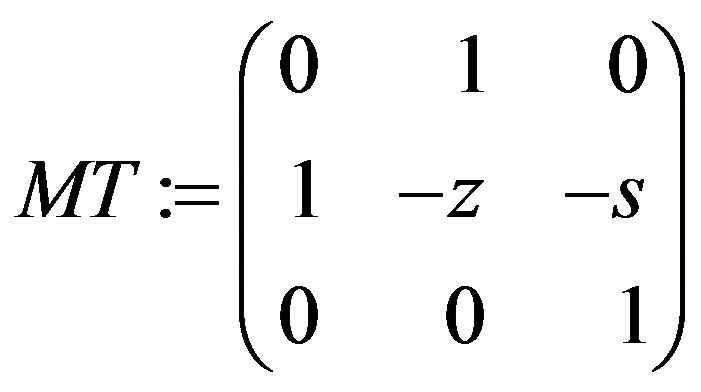
UTMT := simplify(Matrix(UT). MT);

Now we can check that  is the first row of the inverse of
is the first row of the inverse of :
:
MT_inv := CompleteMatrix(UT, var, true);
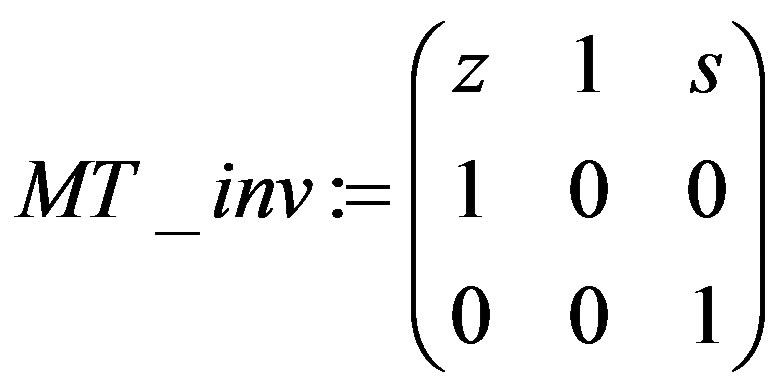
i.e., the matrix  is a completion of
is a completion of  to an invertible matrix over
to an invertible matrix over .
.
M1 := Transpose(ColumnOperation (Matrix(MT), [1, p]));
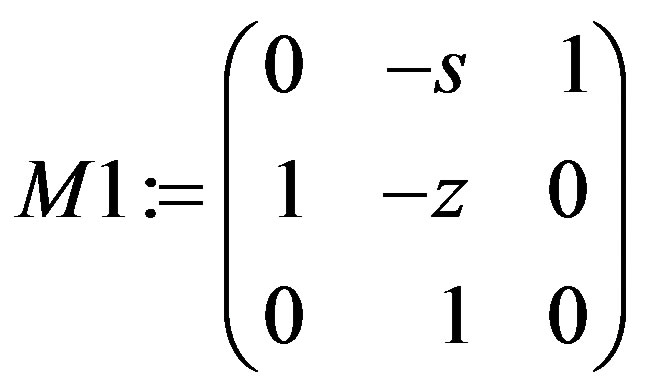
The matrix  and
and , where K1 := DeleteColumn(DeleteRow(M1, p), p); K2 := DeleteColumn(DeleteRow(M1, p), 1···p – 1); K3 := DeleteColumn(DeleteRow(M1, 1···p – 1), p); K4 := DeleteColumn(DeleteRow(M1, 1···p – 1), 1···p – 1);
, where K1 := DeleteColumn(DeleteRow(M1, p), p); K2 := DeleteColumn(DeleteRow(M1, p), 1···p – 1); K3 := DeleteColumn(DeleteRow(M1, 1···p – 1), p); K4 := DeleteColumn(DeleteRow(M1, 1···p – 1), 1···p – 1);
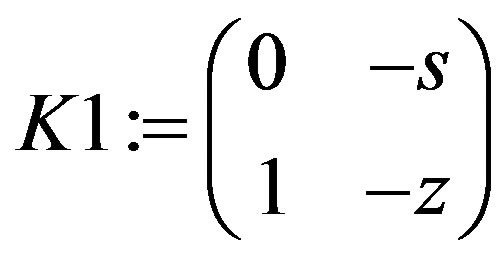

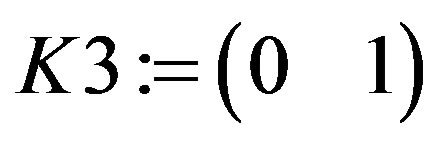
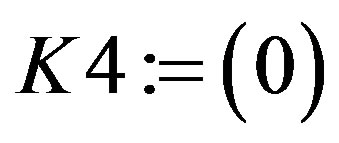
L1 := DeleteRow(T, p); L2: = DeleteRow(T, 1···p – 1);
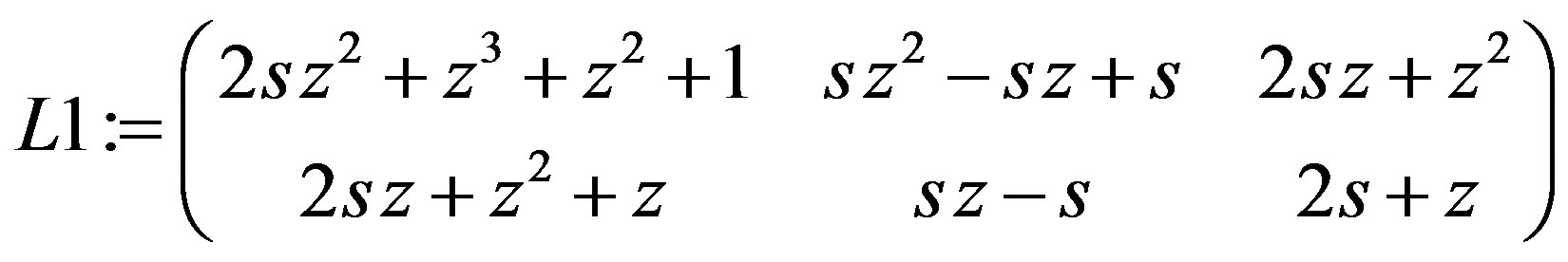
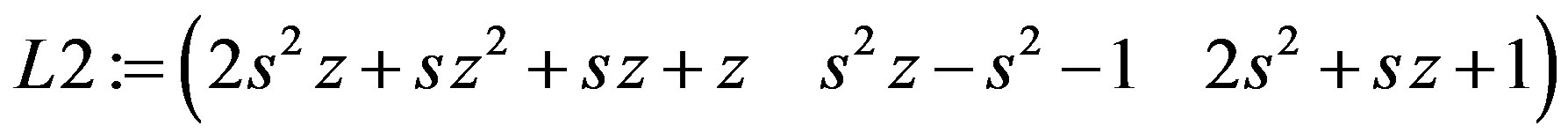
T1 := simplify(K1.L1 + K2.L2);
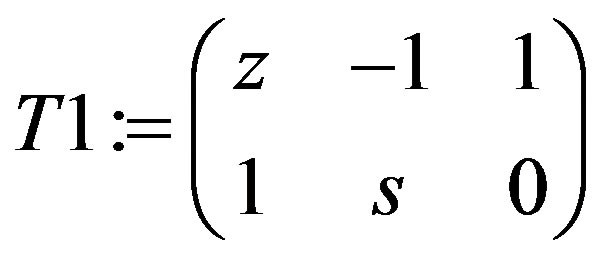
N := QSAlgorithm(T1, var, true);
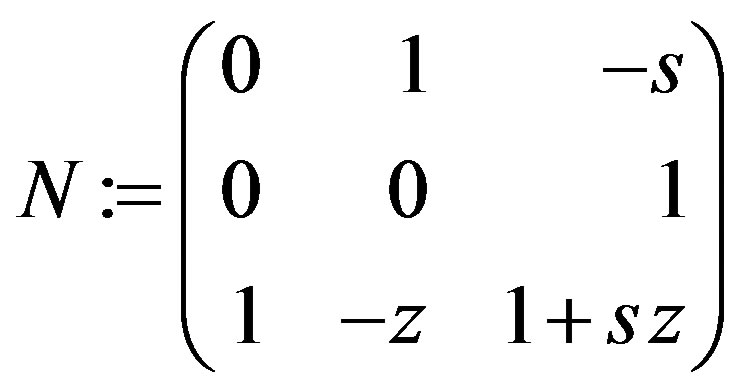
R := simplify(SubMatrix((K3.L1 + K4.L2). N, 1..1, 1..p – 1));
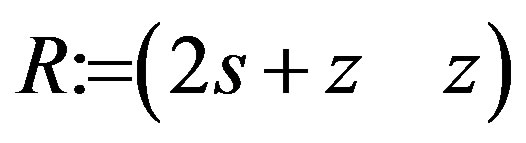
M := Matrix([[K1, K2], [–R.K1 + K3, –R.K2 + K4]]);
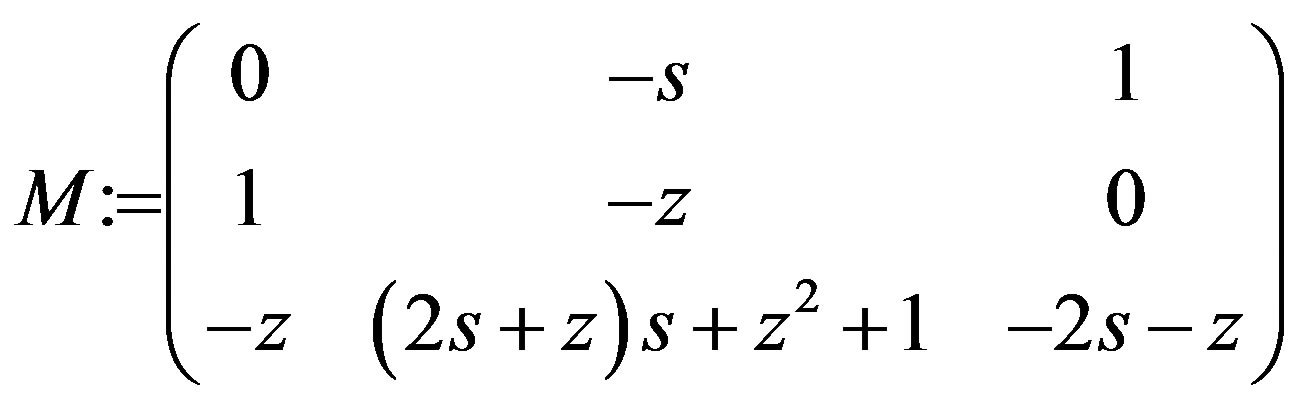
S := simplify(M.T.N);
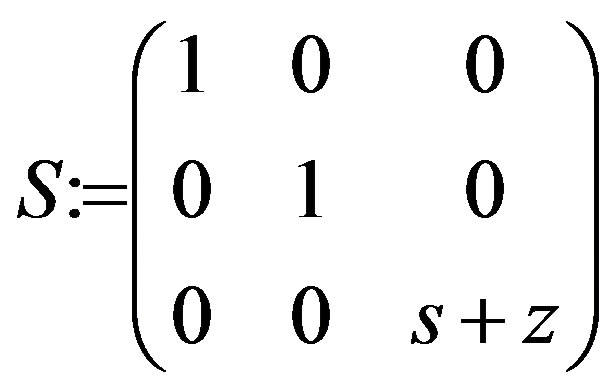
Example 2 (Frost and Boudellioua [9])
libname := “C: /Involutive”, “C: /QuillenSuslin”, libname:
with (LinearAlgebra): with (QuillenSuslin):
In the QuillenSuslin package all computations are performed over a commutative polynomial ring with rational coefficients if the last parameter param is set to true and with integer coefficients, if the parameter is set to false.
param := true:
The variables 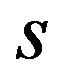 and
and 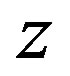 of the polynomial ring
of the polynomial ring 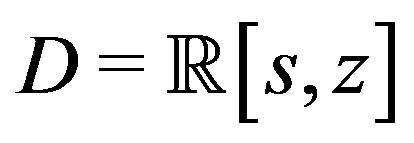 must be declared by setting:
must be declared by setting:
var := [s,z];
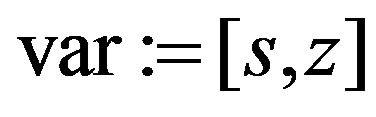
Now consider the 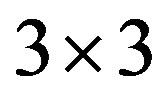 matrix
matrix 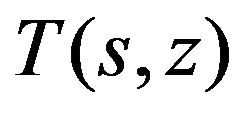 over the polynomial ring
over the polynomial ring .
.
T := Matrix([[2*s*z^2 + z^3 + z^2 + 1, s*z^2-s*z + s, 2*s*z + z^2],\ [2*s^2*z + s*z^2 + s*z + z, s^2*z – s^2 – 1, 2*s^2 + s*z + 1]]); det_T := Determinant(T);
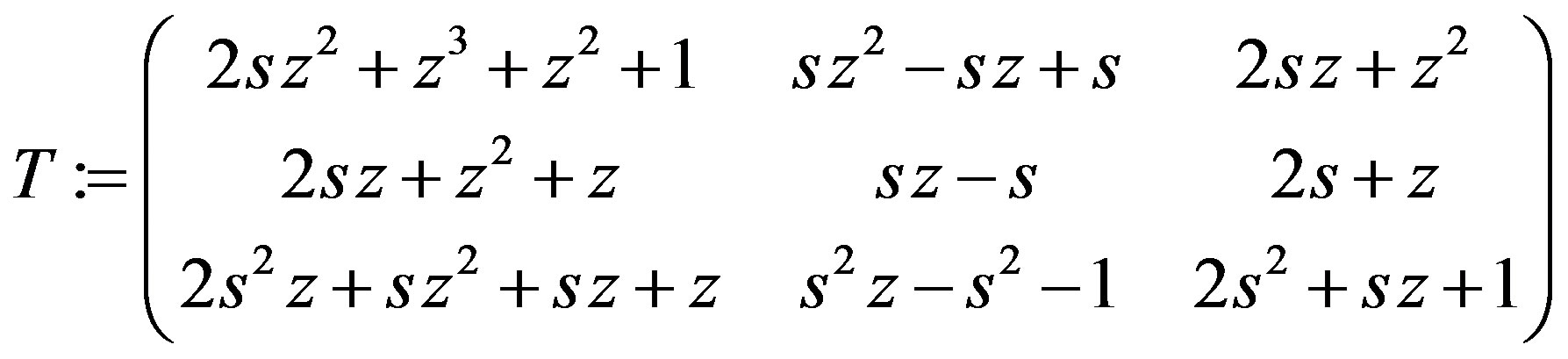
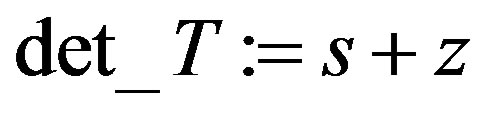
Clearly the determinant of 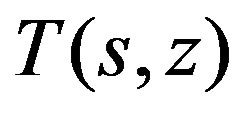 satisfies the condition in Theorem 3.
satisfies the condition in Theorem 3.
p := RowDimension(T);
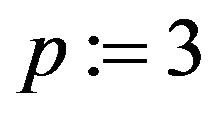
f := s-det_T;
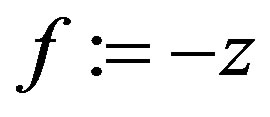
Evaluating 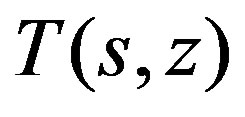 at
at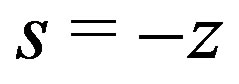 , i.e. computing
, i.e. computing 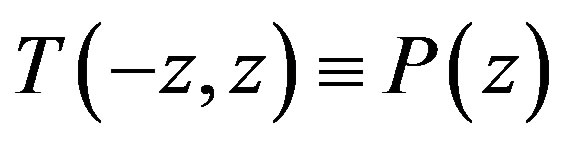 P := subs(s = f,T);
P := subs(s = f,T);
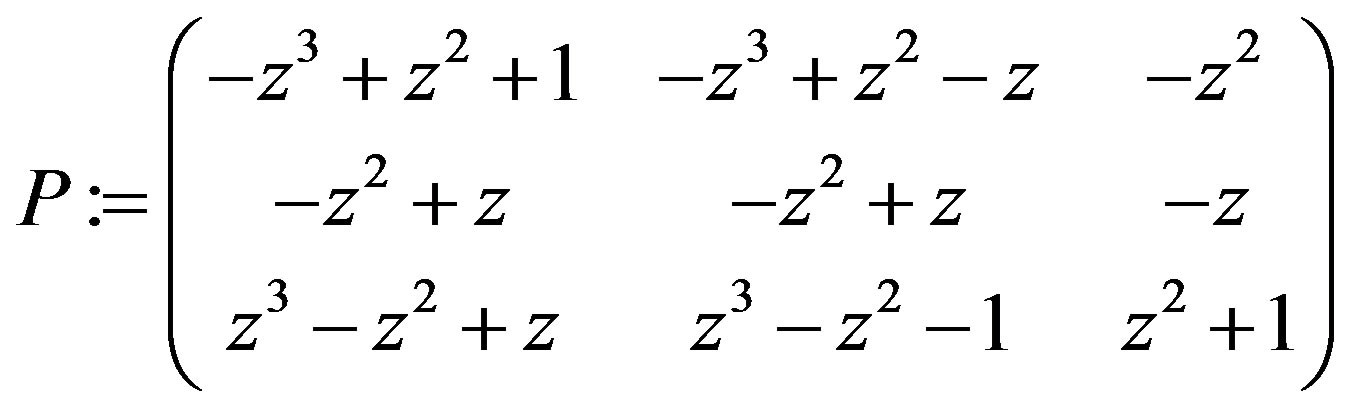
To find a unimodular column vector 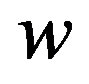 satisfying
satisfying 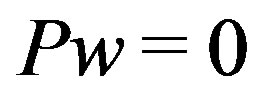 we need to find the row vector defining the syzygy module of
we need to find the row vector defining the syzygy module of 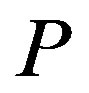 over
over .
.
w := Transpose(Matrix(SyzygyModule(Transpose(P), var)));
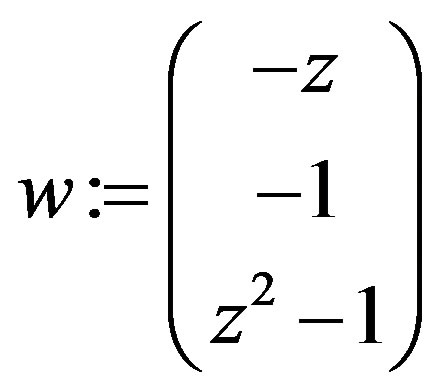
Testing that the vector 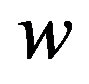 is unimodular and that
is unimodular and that .
.
IsUnimod (w,var,param);
true Now compute a matrix 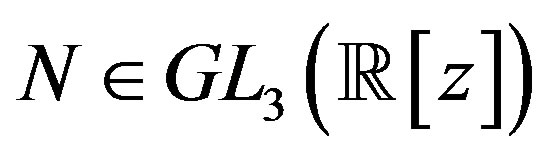 with last column given by
with last column given by 
N := ColumnOperation (Transpose(CompleteMatrix (Transpose(w),\
var,false)),[1,p]);
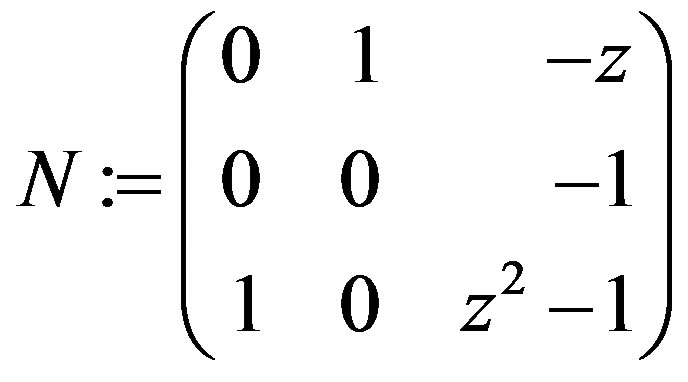
PN := simplify(P.N);
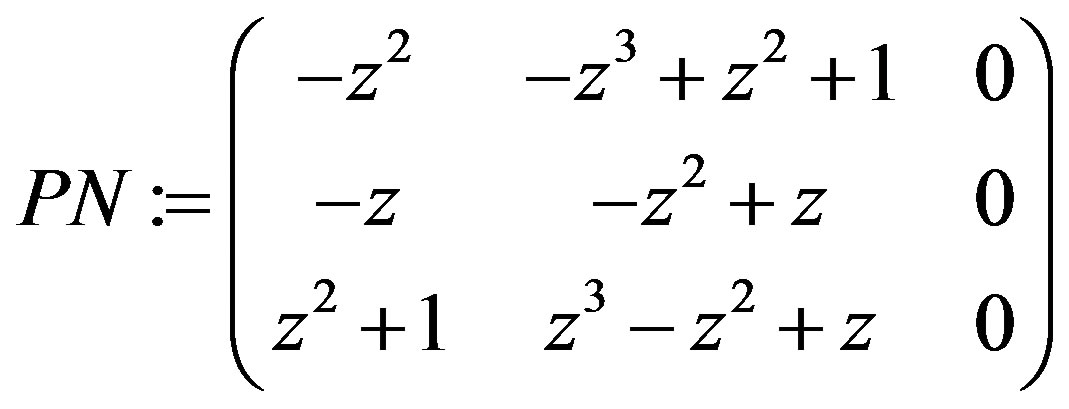
Computing the matrix  such that
such that
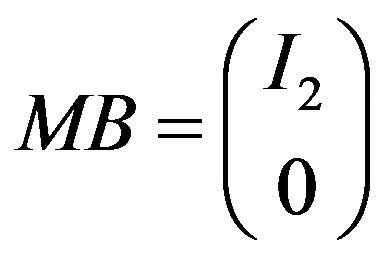 .
.
M := Transpose (QSAlgorithm(Transpose(B), var, true));
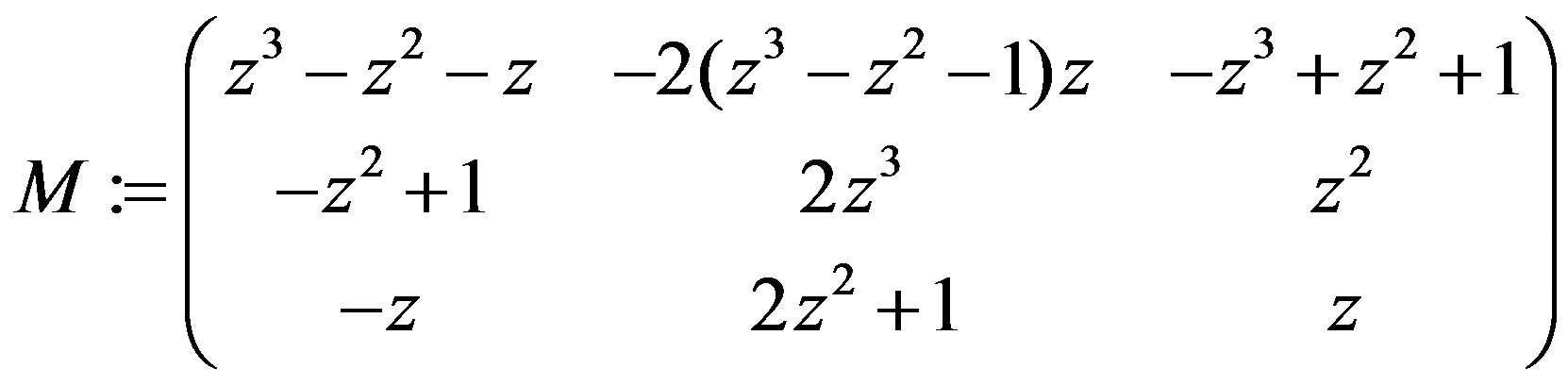
TN := simplify(T.N);
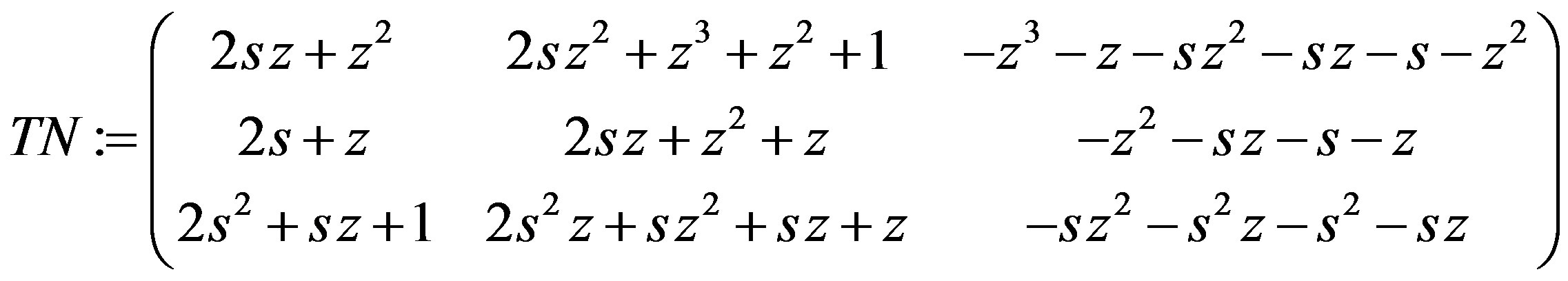
S := Matrix([[IdentityMatrix(p – 1), ZeroMatrix(p – 1,1)], \[ZeroMatrix(1, p – 1), det_T]]),
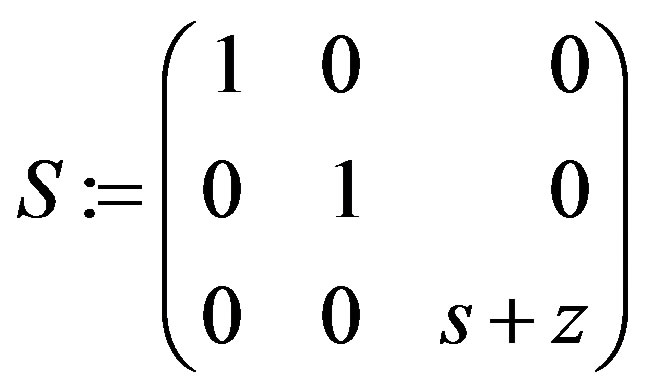
M := simplify(S.MatrixInverse(N). MatrixInverse(T)); “N” = N;
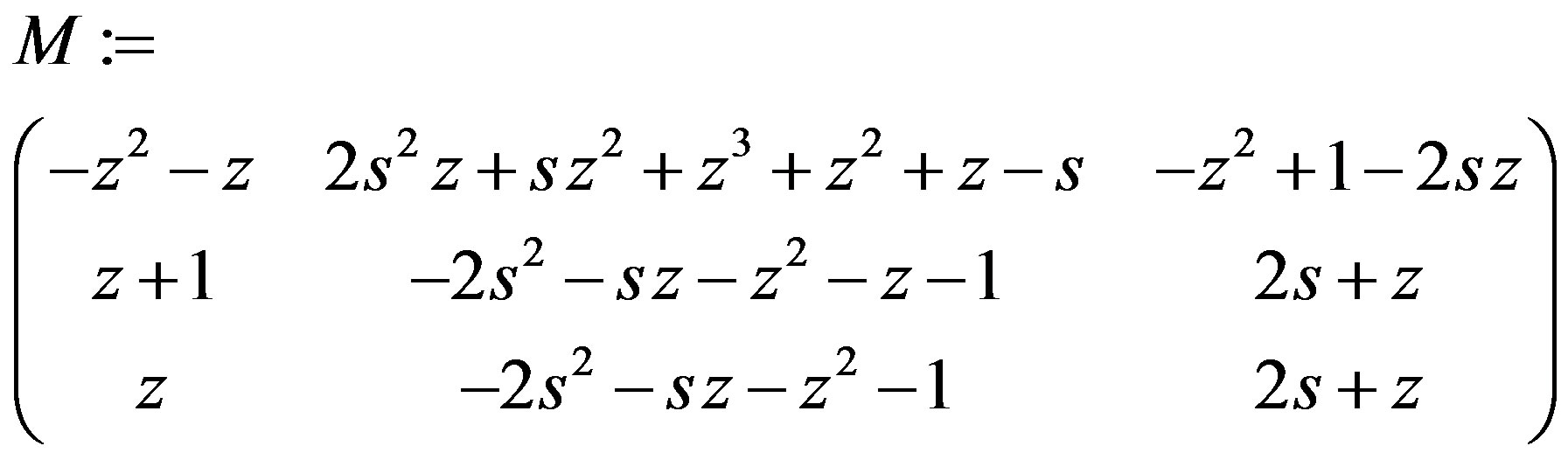
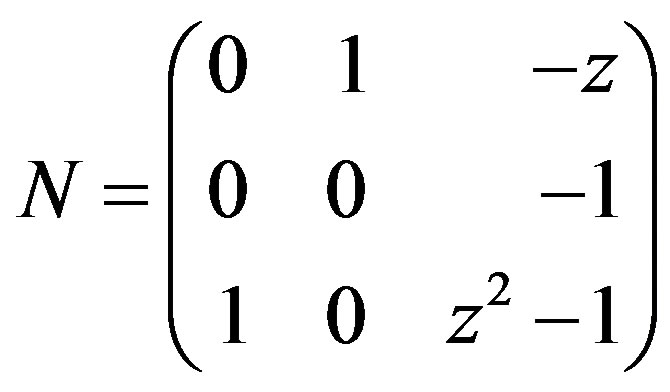
IsUnimod(M,var,true);
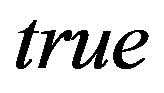
SS := simplify(M.T.N);
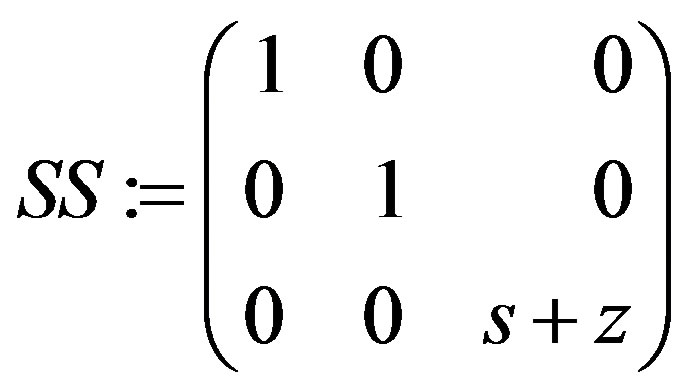
3. Conclusion
In this paper, we have shown that the recent implementation in Maple of a constructive version of the Quillen-Suslin Theorem can be used effectively to compute the Smith form and the associated unimodular transformations for a class of multivariate polynomial matrices. The classes of matrices considered are those arising from multidimensional systems amenable to be simplified to a single equation in one unknown. The case of underdetermined systems can also be treated in a similar fashion.
4. Acknowledgements
The author wishes to express his thanks to Sultan Qaboos University (Oman) for their support in carrying out this research and Dr. Alban Quadrat and Anna Fabianska for their help in providing the author with a copy of the QuillenSuslin Maple package.
REFERENCES
- H. H. Rosenbrock, “State Space and Multivariable Theory,” Nelson-Wiley, London, 1970.
- T. Kailath, “Linear Systems,” Prentice-Hall, Englewood Cliffs, 1980.
- A. Fabianska and A. Quadrat, “Applications of the Quillen-Suslin Theorem to Multidimensional Systems Theory,” Technical Report 6126, INRIA, Sophia Antipolis, 2007.
- D. Quillen, “Projective Modules over Polynomial Rings,” Inventiones Mathematicae, Vol. 36, 1976, pp. 167-171. doi:10.1007/BF01390008
- A. Suslin, “Projective Modules over Polynomial Rings Are Free,” Soviet Mathematics—Doklady, Vol. 17, No. 4, 1976, pp. 1160-1164.
- M. Frost and C. Storey, “Equivalence of a Matrix over R[s; z] with Its Smith Form,” International Journal of Control, Vol. 28, No. 5, 1979, pp. 665-671. doi:10.1080/00207177808922487
- M. Morf, B. Levy and S. Kung, “New Results in 2-D Systems Theory: Part I: 2-D Polynomial Matrices, Factorization and Coprimeness,” Proceedings of the IEEE, Vol. 65, No. 6, 1977, pp. 861-872. doi:10.1109/PROC.1977.10582
- E. Lee and S. Zak, “Smith Forms over R[z1; z2],” IEEE Transactions on Automatic Control, Vol. 28, No. 1, 1983, pp. 115-118. doi:10.1109/TAC.1983.1103118
- M. Frost and M. S. Boudellioua, “Some Further Results Concerning Matrices with Elements in a Polynomial Ring,” International Journal of Control, Vol. 43, No. 5, 1986, pp. 1543-1555. doi:10.1080/00207178608933558
- Z. Lin, M. S. Boudellioua and L. Xu, “On the Equivalence and Factorization of Multivariate Polynomial Matrices,” Proceedings of the 2006 International Symposium of Circuits and Systems, Island of Kos, 21-24 May 2006, p. 4914.
- M. S. Boudellioua and A. Quadrat, “Serre’s Reduction of Linear Functional Systems,” Mathematics in Computer Science, Vol. 4, No. 2, 2010, pp. 289-312. doi:10.1007/s11786-010-0057-y

