American Journal of Computational Mathematics
Vol. 1 No. 1 (2011) , Article ID: 4449 , 4 pages DOI:10.4236/ajcm.2011.11003
Conjugate Effects of Radiation and Joule Heating on Magnetohydrodynamic Free Convection Flow along a Sphere with Heat Generation
1Department of Mathematics, Dhaka Commerce College, Dhaka, Bangladesh
2Department of Mathematics, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh
3Department of Mathematics, Jahangirnagar University, Dhaka, Bangladesh
E-mail: mirajaknd@gmail.com, maalim@math.buet.ac.bd, sazzad67@hotmail.com
Received February 11, 2011; revised February 24, 2011; accepted March 1, 2011
Keywords: Natural Convection, Thermal Radiation, Prandtl Number, Joule Heating, Heat Generation, Magnetohydrodynamics, Nusselt Number
Abstract
The conjugate effects of radiation and joule heating on magnetohydrodynamic (MHD) free convection flow along a sphere with heat generation have been investigated in this paper. The governing equations are transformed into dimensionless non-similar equations by using set of suitable transformations and solved numerically by the finite difference method along with Newton’s linearization approximation. Attention has been focused on the evaluation of shear stress in terms of local skin friction and rate of heat transfer in terms of local Nusselt number, velocity as well as temperature profiles. Numerical results have been shown graphically for some selected values of parameters set consisting of heat generation parameter Q, radiation parameter Rd, magnetic parameter M, joule heating parameter J and the Prandtl number Pr.
1. Introduction
The conjugate effects of radiation and joule heating on magnetohydrodynamic (MHD) free convection boundary layer on various geometrical shapes such as vertical flat plate, cylinder, sphere etc, have been studied by many investigators and it has been a very popular research topic for many years. Nazar et al. [1], Huang and Chen [2] considered the free convection boundary layer on an isothermal sphere and on an isothermal horizontal circular cylinder both in a micropolar fluid. Molla et al. [3] have studied the problem of natural convection flow along a vertical wavy surface with uniform surface temperature in presence of heat generation or absorption. Miraj et al. [4] studied the effect of radiation on natural convection flow on a sphere in presence of heat generation. Amin [5] also analyzed the influences of both first and second order resistance, due to the solid matrix of non-darcy porous medium, Joule heating and viscous dissipation on forced convection flow from a horizontal circular cylinder under the action of transverse magnetic field. Hossain [6] studied viscous and joule heating effects on magnetohydrodynamic (MHD) free convection flow with variable plate temperature. Alam et al. [7] studied the viscous dissipation effects with MHD natural convection flow on a sphere in presence of heat generation.
In the present work, the effects of joule heating with radiation heat loss on natural convection flow around a sphere have been investigated. The governing partial differential equations are reduced to locally non-similar partial differential forms by adopting appropriate transformations. The transformed boundary layer equations are solved numerically using implicit finite difference method with Keller box scheme described by Keller [8] and later by Cebeci and Bradshaw [9]. The results have been shown in terms of the velocity, temperature profiles, the skin friction and surface heat transfer
2. Formulation of the Problem
A steady two-dimensional magnetohydrodynamic (MHD) natural convection boundary layer flow from an isothermal sphere of radius a, which is immersed in a viscous and incompressible optically dense fluid with heat generation and radiation heat loss is considered. The physical configuration considered is as shown in Figure 1.
Under the above assumptions, the governing equations for steady two-dimensional laminar boundary layer flow problem under consideration can be written as
 (1)
(1)
 (2)
(2)
 (3)
(3)
With the boundary conditions
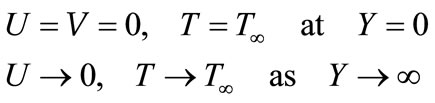 (4)
(4)
The above equations are further non-dimensionalised using the new variables:
 (5)
(5)
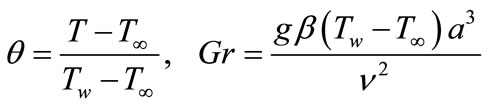 (6)
(6)
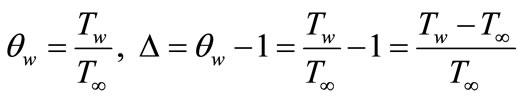 (7)
(7)
The radiation heat flux is in the following form
 (8)
(8)

Figure 1. Physical model and coordinate system.
Substituting (5), (6) and (7) into Equations (1), (2) and (3) leads to the following non-dimensional equations
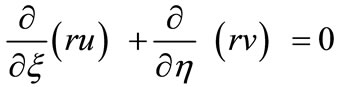 (9)
(9)
 (10)
(10)
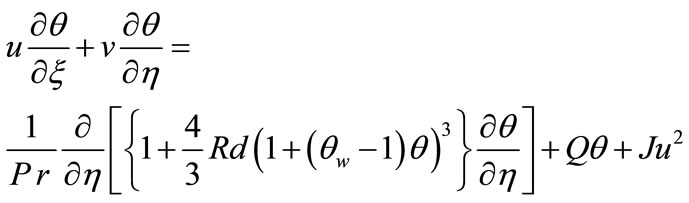 (11)
(11)
where  is the Prandtl number,
is the Prandtl number, 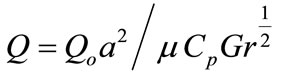 is the heat generation parameter,
is the heat generation parameter, 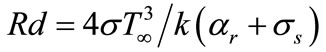 is the radiation parameter and
is the radiation parameter and  is the joule heating parameter.
is the joule heating parameter.
With the boundary conditions (4) become
 (12)
(12)
To solve Equations (10) and (11) with the help of following variables
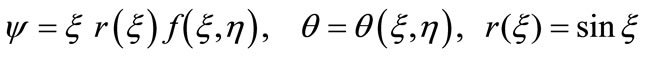 (13)
(13)
where y is the stream function defined by
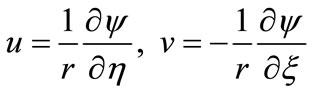 (14)
(14)
Equation (10) can be written as
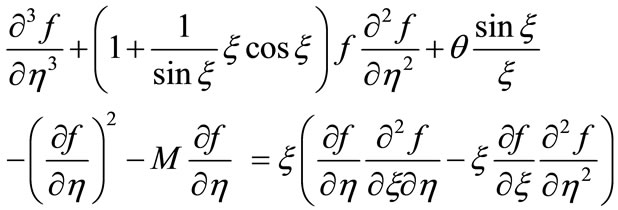 (15)
(15)
where  is the MHD parameter.
is the MHD parameter.
Equation (11) becomes
 (16)
(16)
Along with boundary conditions
 (17)
(17)
It can be seen that near the lower stagnation point of the sphere, i.e., ξ » 0, Equations (15) and (16) reduce to the following ordinary differential equations:
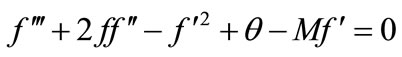 (18)
(18)
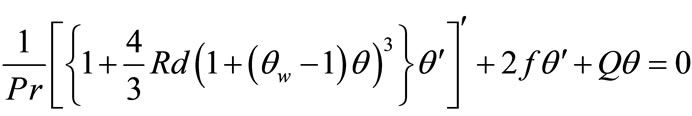 (19)
(19)
Subject to the boundary conditions
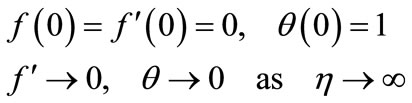 (20)
(20)
In practical applications, skin-friction coefficient Cf and Nusselt number Nu can be written in non-dimensional form as
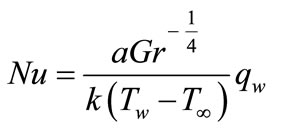 and
and 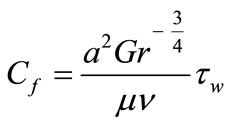 (21)
(21)
where, 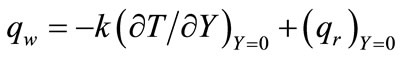 and
and 
Putting the above values in Equation (21), we have
 (22)
(22)
3. Results and Discussion
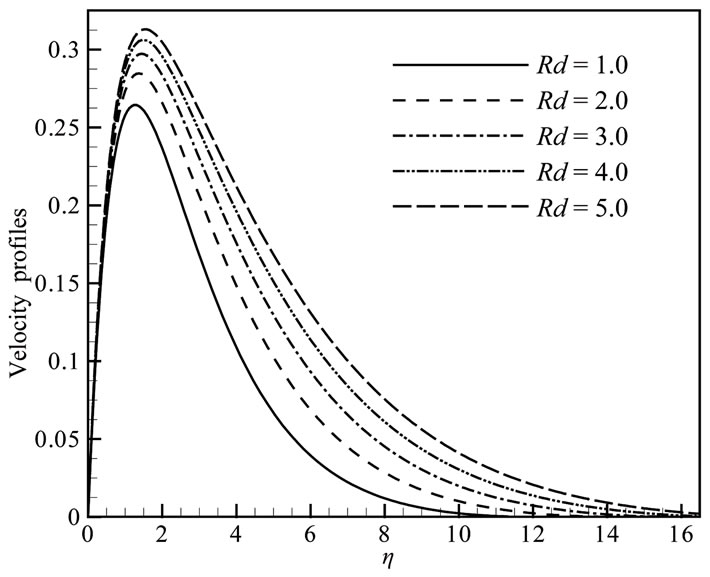
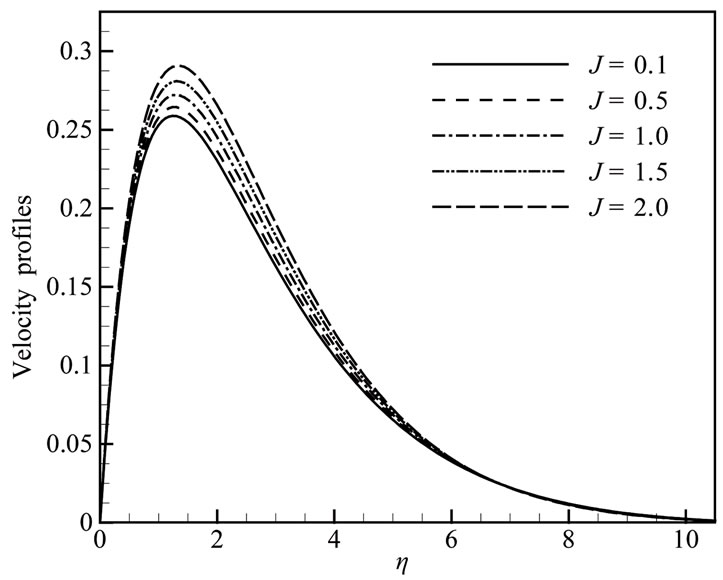
Solutions are obtained for some test values of Prandtl number Pr = 2.00, 5.00, 7.00, 9.00; radiation parameter Rd =1.00, 2.00, 3.00, 4.00, 5.00; heat generation parameter Q = 0.00, 0.05, 0.10, 0.15, 0.20; magnetic parameter M = 0.50, 1.00, 1.50, 2.00, 3.00 and joule heating parameter J = 0.10, 0.50, 1.00, 1.50, 2.00 in terms of velocity and temperature profiles, skin friction coefficient and heat transfer coefficient. The effects for different values of radiation parameter Rd the velocity and temperature profiles in case of Prandtl number Pr = 0.72, heat generation parameter Q = 0.10, magnetic parameter M = 2.00 and joule heating parameter J = 0.50 are shown in Figures 2(a) and 2(b). In Figures 3(a) and 3(b) are shown that when the Prandtl number Pr increases with radiation parameter Rd = 1.00, heat generation parameter Q = 0.10, magnetic parameter M = 2.00 and joule heating parameter J = 0.50, both the velocity and temperature profiles are decrease. For different values of heat generation parameter Q with radiation parameter Rd = 1.00, Prandtl number Pr = 0.72, magnetic parameter M = 2.00 and joule heating parameter J = 0.50 and display results in Figures 4(a,b) that as the heat generation parameter Q increases, the velocity and the temperature profiles increase.
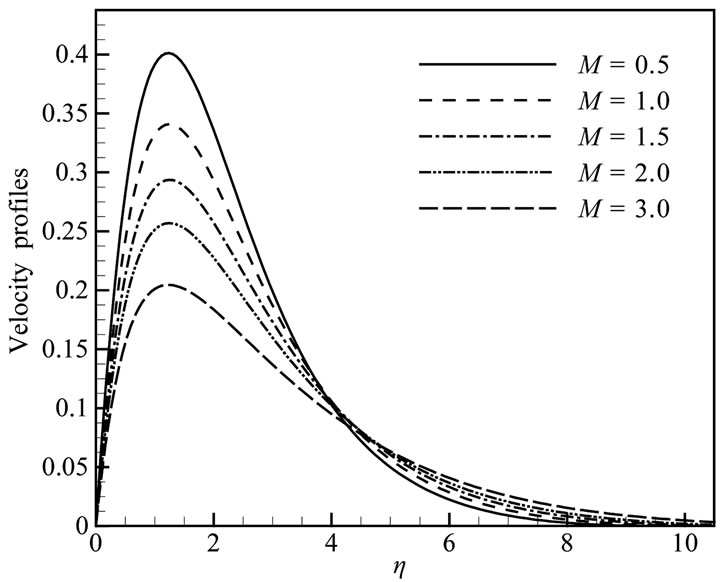
It has been seen from Figure 5(a) that as the magnetic parameter M increases, the velocity profiles decrease up to the position of h = 4.10555 after that position velocity profiles increase with the increase of magnetic parameter. We see that in Figure 5(b) temperature profiles increase for increasing values of magnetic parameter M with radiation parameter Rd = 1.00, Prandtl number Pr = 0.72, heat generation parameter Q = 0.10 and joule heating parameter J = 0.50. It has been seen from Figures 6(a,b) that as the joule heating parameter J increases, the velocity and the temperature profiles increase. In Figures 7(a,b) shown that the radiation parameter Rd increases, both the skin friction coefficient and heat transfer coefficient increase. The variation of the local skin friction coefficient Cf and local rate of heat transfer Nu for different values of Prandtl number Pr while radiation parameter Rd = 1.00, heat generation parameter Q = 0.10, magnetic parameter M = 2.00 and joule heating parameter J = 0.50 are shown in Figures 8(a) and 8(b). From
 (a)
(a)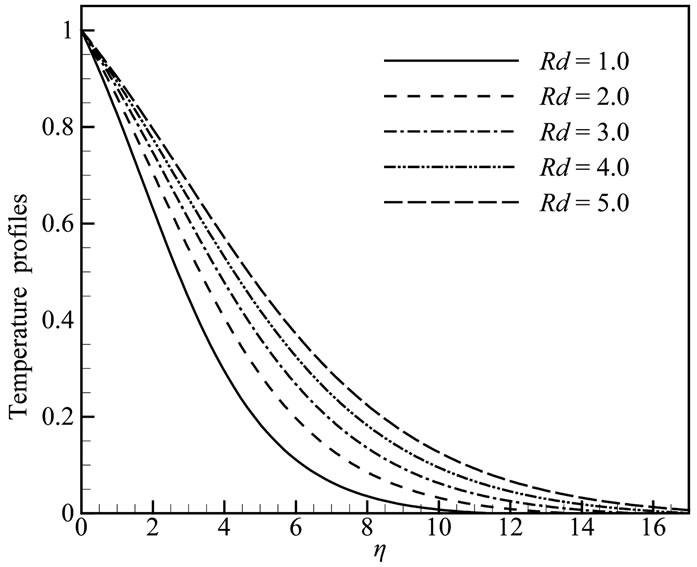 (b)
(b)
Figure 2. (a) Velocity and (b) Temperature profiles for different values of Rd when Pr = 0.72, Q = 0.1, M = 2.0 and J = 0.5.
 (a)
(a)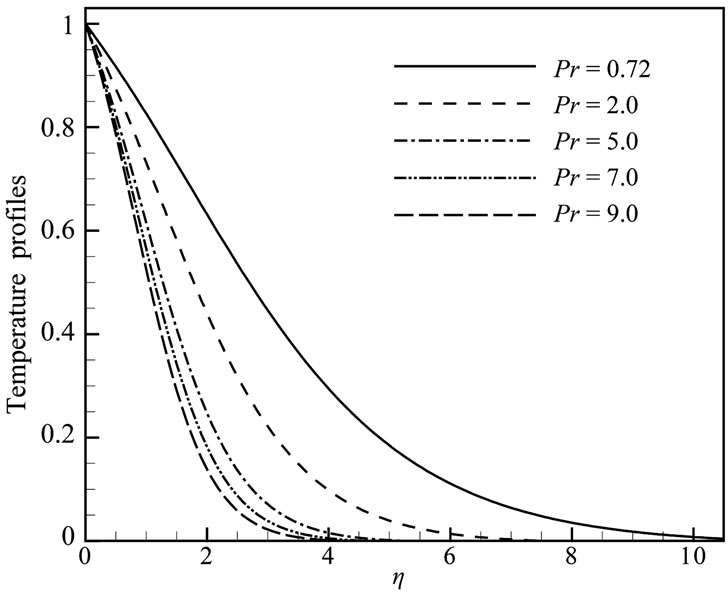 (b)
(b)
Figure 3. (a) Velocity and (b) Temperature profiles for different values of Pr when Rd = 1.0, Q = 0.1, M = 2.0 and J = 0.5.
 (a)
(a)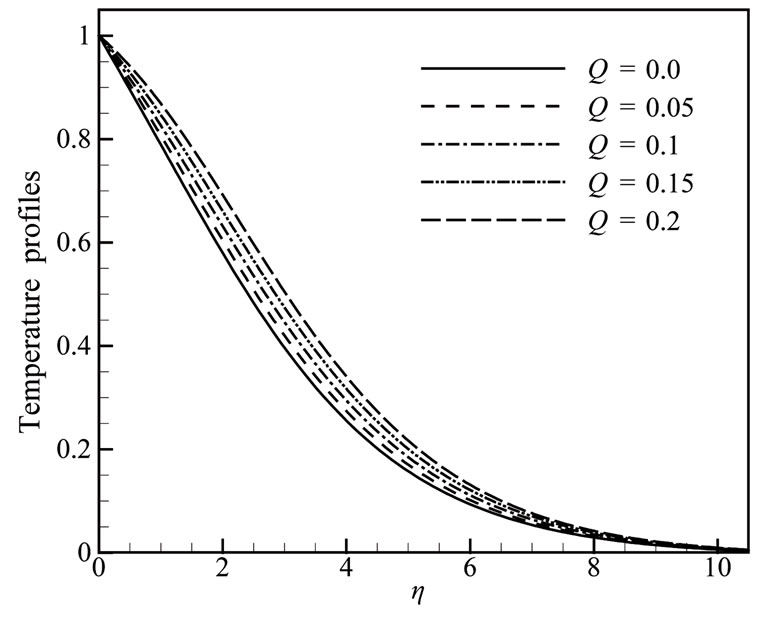 (b)
(b)
Figure 4. (a) Velocity and (b) Temperature profiles for different values of Q when Rd = 1.0, Pr = 0.72, M = 2.0 and J = 0.5.
 (a)
(a)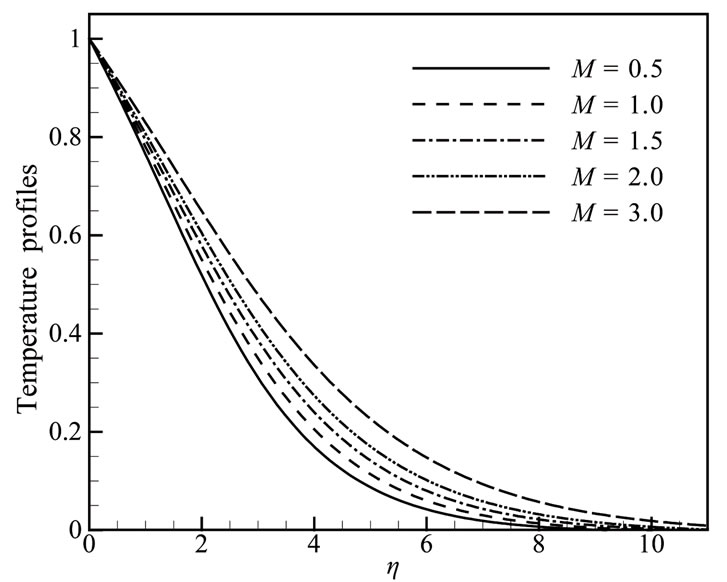 (b)
(b)
Figure 5. (a) Velocity and (b) Temperature profiles for different values of M when Rd = 1.0, Pr = 0.72, Q = 0.1 and J = 0.5.
 (a)
(a)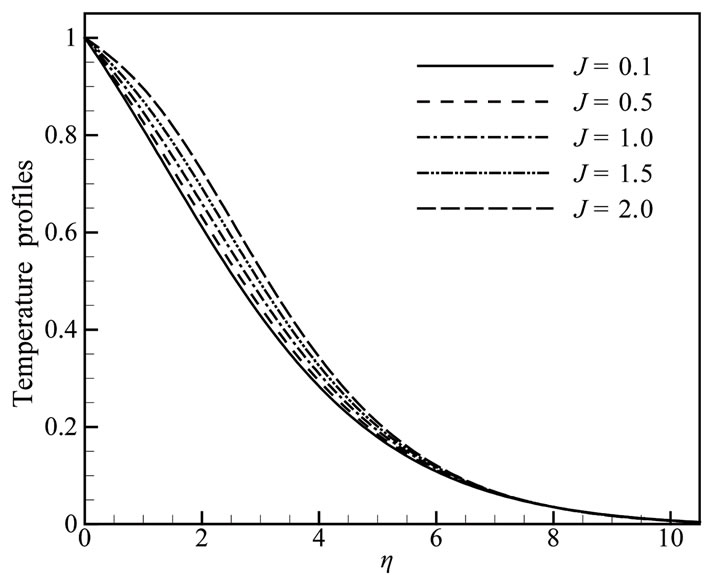 (b)
(b)
Figure 6. (a) Velocity and (b) Temperature profiles for different values of J when Rd = 1.0, Pr = 0.72, Q = 0.1 and M = 2.0.
 (a)
(a)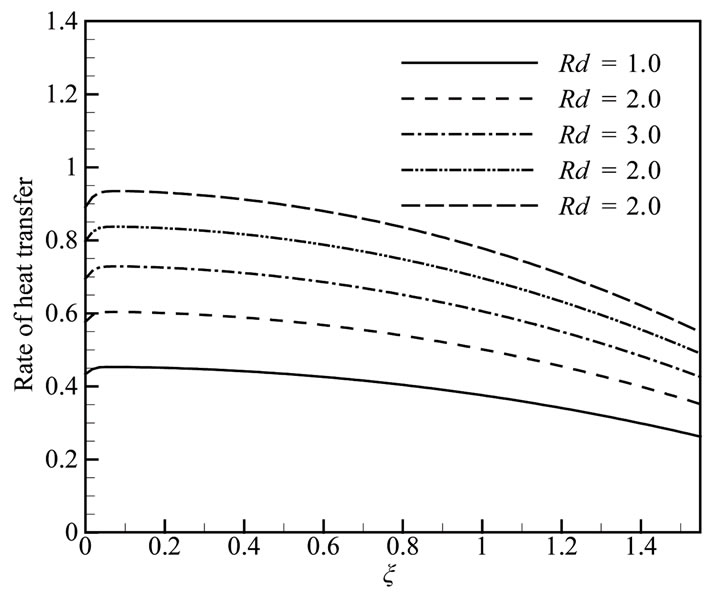 (b)
(b)
Figure 7. (a) Skin friction coefficient and (b) Rate of heat transfer for different values of Rd when Pr = 0.72, Q = 0.1, M = 2.0 and J = 0.5.
 (a)
(a) (b)
(b)
Figure 8. (a) Skin friction coefficient and (b) Rate of heat transfer for different values of Pr when Rd = 1.0, Q = 0.1, M = 2.0 and J = 0.5.
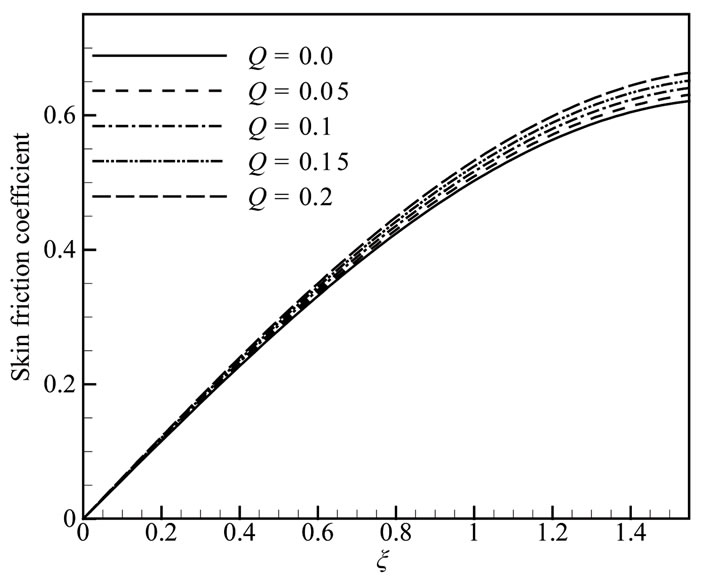
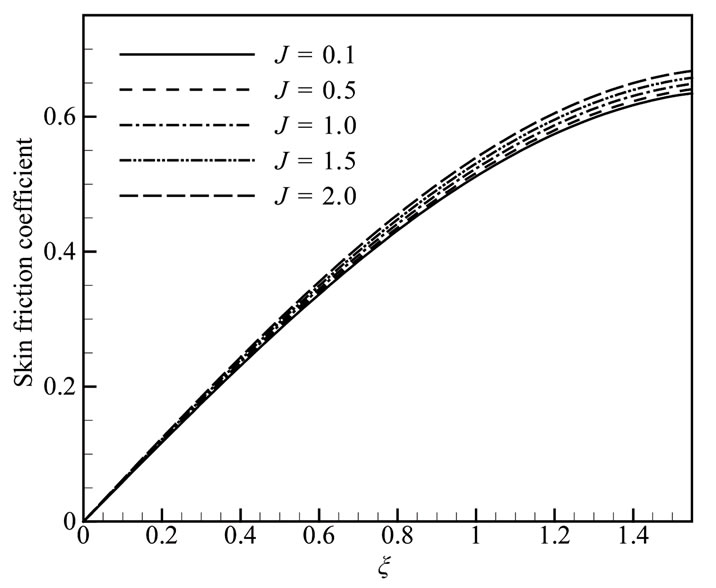
Figure 9(a) we observed that the skin friction coefficient Cf increases significantly as the heat generation parameter Q increases and Figure 9(b) show that heat transfer coefficient Nu decreases for increasing values of heat generation parameter Q with relevant parameters. It reveals that the rate of heat transfer decreases along the ξ direction from lower stagnation point to the downstream. Figures 10(a,b) shown that skin friction coefficient Cf and heat transfer coefficient Nu decrease for increasing values of magnetic parameter M while radiation parameter Rd = 1.00, Prandtl number Pr = 0.72,heat generation parameter Q = 0.10, and joule heating parameter J = 0.50. From Figure 11(a) we observed that the skin friction coefficient Cf increases and Figure 11(b) shown that heat transfer coefficient Nu decreases for increasing values of joule heating parameter J.
4 Conclusions
The conjugate effects of radiation and joule heating on magnetohydrodynamic free convection flow along a sphere with heat generation has been investigated for different values of relevant physical parameters including the magnetic parameter M. From the present investigation the following conclusions may be drawn:
All the velocity profile, temperature profile, the local skin friction coefficient Cf and the local rate of heat transfer Nu increase significantly when the values of radiation parameter Rd increases.
As joule heating parameter J increases, both the velocity and the temperature profiles increase and also the local skin friction coefficient Cf and the local rate of heat transfer Nu increase significantly.
 (a)
(a) (b)
(b)
Figure 9. (a) Skin friction coefficient and (b) Rate of heat transfer for different values of Q when Rd = 1.0, Pr = 0.72, M = 2.0 and J = 0.5.
 (a)
(a)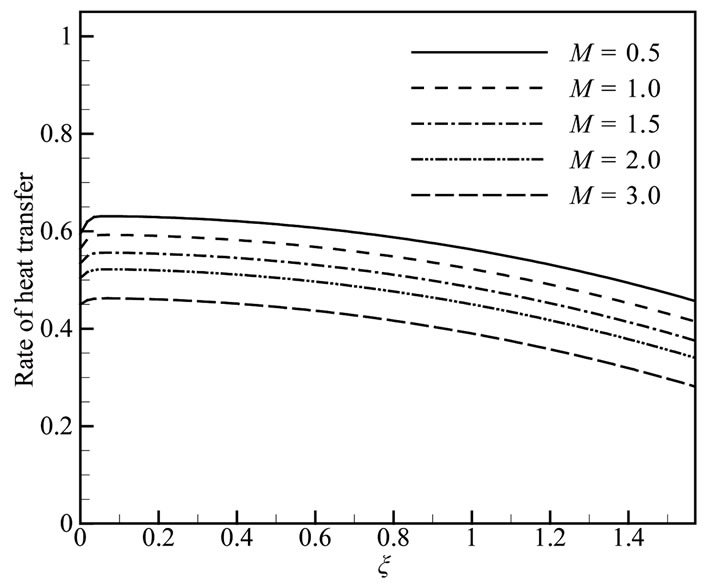 (b)
(b)
Figure 10. (a) Skin friction coefficient and (b) Rate of heat transfer for different values of M when Rd = 1.0, Pr = 0.72, Q = 0.1 and J = 0.5.
 (a)
(a)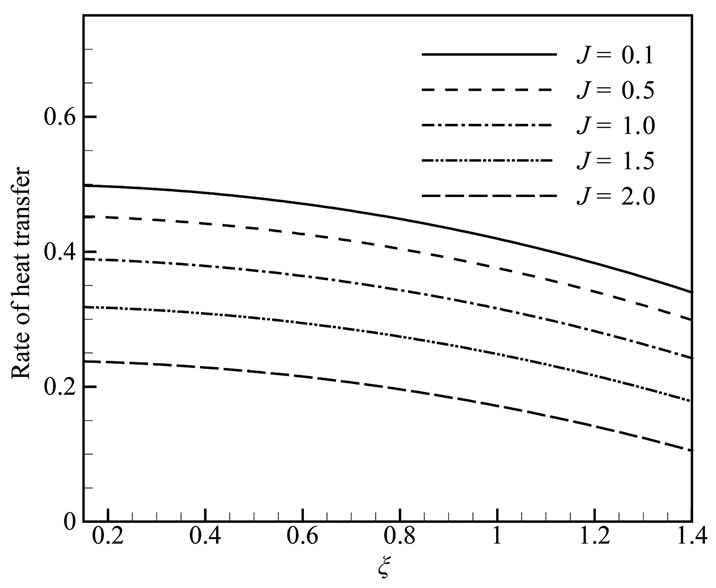 (b)
(b)
Figure 11. (a) Skin friction coefficient and (b) Rate of heat transfer for different values of J when Rd = 1.0, Pr = 0.72, Q = 0.1 and M = 2.0.
For increasing values of Prandtl number Pr leads to decrease the velocity profile, the temperature profile and the local skin friction coefficient Cf but the local rate of heat transfer Nu increases.
An increase in the values of M leads to decrease the velocity profiles but to increase the temperature profiles and also both the local skin friction coefficient Cf and the local rate of heat transfer Nu decrease.
5. References
- R. Nazar, N. Amin, T. Grosan and I. Pop, “Free Convection Boundary Layer on an Isothermal Sphere in a Micropolar Fluid,” International Communications in Heat and Mass Transfer, Vol. 29, No. 3, 2002, pp. 377-386. doi:10.1016/S0735-1933(02)00327-5
- M. J. Huang and C. K. Chen, “Laminar Free Convection from a Sphere with Blowing and Suction,” Journal of Heat Transfer, Vol. 109, 1987, pp. 529-532. doi:10.1115/1.3248117
- M. M. Molla, M. A. Taher, M. M. K. Chowdhury and Md. A. Hossain, “Magnetohydrodynamic Natural Convection Flow on a Sphere in Presence of Heat Generation,” Nonlinear Analysis: Modelling and Control, Vol. 10, No. 4, 2005, pp. 349-363.
- M. Miraj, M. A. Alim and M. A. H. Mamun, “Effect of Radiation on Natural Convection Flow on a Sphere in Presence of Heat Generation,” International Communications in Heat and Mass Transfer, Vol. 37, No. 6, 2010, pp. 660-665. doi:10.1016/j.icheatmasstransfer.2010.01.013
- M. F. El-Amin, “Combined Effect of Viscous Dissipation and Joule Heating on MHD Forced Convection over a Non-Isothermal Horizontal Cylinder Embedded in a Fluid Saturated Porous Medium,” Journal of Magnetism and Magnetic Materials, Vol. 263, No. 3, 2003, pp. 337-343. doi:10.1016/S0304-8853(03)00109-4
- M. A. Hossain, “Viscous and Joule Heating Effects on MHD-Free Convection Flow with Variable Plate Temperature,” International Journal of Heat and Mass Transfer, Vol. 35, No. 12, 1992, pp. 3485-3487. doi:10.1016/0017-9310(92)90234-J
- M. M. Alam, M. A. Alim and M. M. K. Chowdhury, “Viscous Dissipation Effects with MHD Natural Convection Flow on a Sphere in Presence of Heat Generation,” Nonlinear Analysis: Modelling and Control, Vol. 12, No. 4, 2007, pp. 447-459.
- H. B. Keller, “Numerical Methods in Boundary Layer Theory,” Annual Review of Fluid Mechanics, Vol. 10, 1978, pp. 417-433. doi:10.1146/annurev.fl.10.010178.002221
- T. Cebeci and P. Bradshaw, “Physical and Computational Aspects of Convective Heat Transfer,” Springer, New York, 1984.




