World Journal of Nuclear Science and Technology
Vol.07 No.04(2017), Article ID:78810,22 pages
10.4236/wjnst.2017.74020
Analysis of Residence Time in the Measurement of Radon Activity by Passive Diffusion in an Open Volume: A Micro-Statistical Approach
M. P. Silverman
Department of Physics, Trinity College, Hartford, CT, USA

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 12, 2017; Accepted: August 27, 2017; Published: August 30, 2017
ABSTRACT
Residence time in a flow measurement of radioactivity is the time spent by a pre-determined quantity of radioactive sample in the flow cell. In a recent report of the measurement of indoor radon by passive diffusion in an open volume (i.e. no flow cell or control volume), the concept of residence time was generalized to apply to measurement conditions with random, rather than directed, flow. The generalization, leading to a quantity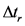 , involved use of a) a phenomenological alpha-particle range function to calculate the effective detection volume, and b) a phenomenological description of diffusion by Fick’s law to determine the effective flow velocity. This paper examines the residence time in passive diffusion from the micro-statistical perspective of single-particle continuous Brownian motion. The statistical quantity “mean residence time”
, involved use of a) a phenomenological alpha-particle range function to calculate the effective detection volume, and b) a phenomenological description of diffusion by Fick’s law to determine the effective flow velocity. This paper examines the residence time in passive diffusion from the micro-statistical perspective of single-particle continuous Brownian motion. The statistical quantity “mean residence time” 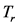 is derived from the Green’s function for unbiased single-particle diffusion and is shown to be consistent with
is derived from the Green’s function for unbiased single-particle diffusion and is shown to be consistent with . The finite statistical lifetime of the randomly moving radioactive atom plays an essential part. For stable particles,
. The finite statistical lifetime of the randomly moving radioactive atom plays an essential part. For stable particles, 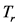 is of infinite duration, whereas for an unstable particle (such as 222Rn), with diffusivity D and decay rate
is of infinite duration, whereas for an unstable particle (such as 222Rn), with diffusivity D and decay rate ,
, 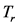 is approximately the effective size of the detection region divided by the characteristic diffusion velocity
is approximately the effective size of the detection region divided by the characteristic diffusion velocity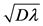 . Comparison of the mean residence time with the time of first passage (or exit time) in the theory of stochastic processes shows the conditions under which the two measures of time are equivalent and helps elucidate the connection between the phenomenological and statistical descriptions of radon diffusion.
. Comparison of the mean residence time with the time of first passage (or exit time) in the theory of stochastic processes shows the conditions under which the two measures of time are equivalent and helps elucidate the connection between the phenomenological and statistical descriptions of radon diffusion.
Keywords:
Radon, Diffusion, Brownian Motion, Random Walk, Residence Time, First-Passage Time, Exit Time

1. Introduction: Residence Time in the Measurement of Radon Activity
1.1. Measurement of Radon by Geiger-Mueller Detectors
Of the many sources and causes of airborne radioactive contamination [1] , the naturally occurring contaminant radon is perhaps the most pervasive, since it arises as one of the daughter products, and the only radioactive gas, in the decay series of uranium-238 (238U), uranium-235 (235U), and thorium-242 (242Th) dispersed widely in rocks and soils throughout the Earth. The radon isotope with the longest half-life, 222Rn, is of particular concern. The World Health Organization (WHO) reports 222Rn to be the leading cause of lung cancer among people who have never smoked, and to significantly increase the risk of lung cancer over that due to smoking alone in those who do smoke or have smoked in the past [2] . Although no level of indoor radon exposure is regarded as safe, the WHO recommends a reference level of 100 Bq/m3 to minimize health hazards (Ref [2] , p. ix). Similarly, the US Environmental Protection Agency (EPA) recommends a level of 4 pCi/L above which remedial action should be taken [3] . (For comparison, note that 1 picocurie per liter = 37 becquerel per cubic meter.) It is desirable, therefore, in view of the health risks posed by radon, to develop methods to measure indoor radon activity in a rapid, accurate, convenient, and inexpensive way.
In a recent paper [4] Silverman proposed and demonstrated the use of two pancake-style Geiger-Mueller (GM) counters to measure quantitatively the activity concentration, i.e. activity per unit volume, of radon-222 (222Rn) by passive diffusion without the requirement, common to virtually all other methods of radon measurement, of a fixed instrumental control volume. This new measurement protocol enables the user to determine radon concentration immediately after a short-term (e.g. 24 hour) sampling time, thereby eliminating the cost, delay, and sample loss of sending samples to an external testing laboratory for analysis. Application of the GM method yielded results of equivalent accuracy and higher precision, particularly in repeated short-term measurements, in comparison with results obtained concurrently with state-of-the-art certified commercial radon detectors also utilizing passive diffusion.
Briefly summarized, the reported GM method employed one GM detector to record counts of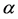 ,
, 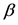 , and
, and 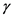 particles, and the other GM detector, covered with an alpha-blocking layer, to record just
particles, and the other GM detector, covered with an alpha-blocking layer, to record just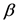 , and
, and 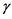 particles. The detectors were located so that the count-rate difference was exclusively attributable to alpha detection from 222Rn and its polonium progeny 218Po, 214Po in the room air―i.e. not contaminated by emissions from radioactive elements in the construction materials of surrounding surfaces. Theoretical analysis based on the physics of atomic diffusion in air and alpha particle interactions in matter provided the means to convert the alpha count rate (e.g. cpm = counts per minute) into a radon activity concentration (Bq/m3 or pCi/L).
particles. The detectors were located so that the count-rate difference was exclusively attributable to alpha detection from 222Rn and its polonium progeny 218Po, 214Po in the room air―i.e. not contaminated by emissions from radioactive elements in the construction materials of surrounding surfaces. Theoretical analysis based on the physics of atomic diffusion in air and alpha particle interactions in matter provided the means to convert the alpha count rate (e.g. cpm = counts per minute) into a radon activity concentration (Bq/m3 or pCi/L).
The methodology and accompanying analysis in [4] relied on the short range of alpha transmissivity in matter. For example, the 5.49 MeV alpha emitted in the decay of 222Rn to 218Po is about 4 cm in air (at 1 atm and 20˚C). Moreover, the energy loss of an alpha particle per collisional interaction is approximately a constant 35 eV for each ionizing encounter [5] , leading to a transmission probability that is essentially constant over the greater part of the particle’s range, then decreasing rapidly to zero after a total of about  interactions. It is this feature that enabled [4] to represent the alpha transmission through air (or a condensed medium like the thin mica window of the GM detector) by a phenomenological range function of the form
interactions. It is this feature that enabled [4] to represent the alpha transmission through air (or a condensed medium like the thin mica window of the GM detector) by a phenomenological range function of the form
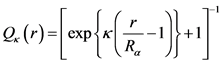 (1)
(1)
whose variation with distance r from the alpha point of origin is shown in the solid red plot of Figure 1 for the 5.49 MeV alpha in air. The red trace calculated from Equation (1) with alpha range parameter 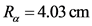 and fall-off parameter
and fall-off parameter 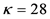 is visually indistinguishable from the empirical alpha transmissivity curve [6] . The mean range
is visually indistinguishable from the empirical alpha transmissivity curve [6] . The mean range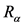 , marked by the dashed black vertical line is defined by the distance at which alpha transmission is 50%, as indicated by the dashed black horizontal line in the figure. The fluctuation in alpha range values about
, marked by the dashed black vertical line is defined by the distance at which alpha transmission is 50%, as indicated by the dashed black horizontal line in the figure. The fluctuation in alpha range values about 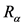 as the particle rapidly comes to rest is closely represented by a Gaussian distribution
as the particle rapidly comes to rest is closely represented by a Gaussian distribution 

Figure 1. Plot of 5.49 MeV alpha transmissivity in air (solid red) as modeled by range function 






1.2. Radon Transport as a Process of Macroscopic Diffusion
The measurement procedure described in [4] pertained primarily to the diffusive ingress of radon through a single external subterranean (or partly subterranean) wall, such as commonly occurs in the basements of residences and research labs. For purposes of mathematical modeling, these conditions entail one-dimensional atomic diffusion from a planar source. For atoms diffusing from the source at the wall through the room air and over the GM detectors, positioned so that the detector windows are horizontal (in the plane







Although the integrations are theoretically over the volume and cross section of the entire room (or, as a practical matter, over an infinite range for a room size



For measurements of radioactivity executed over a period of time in an open volume, it is necessary to determine the rate at which radioactive atoms pass through the region of detectability. This was accomplished in [4] by modeling the detection process as a radioactive flow measurement [8] , such as employed in high-performance radioactive liquid chromatography [9] , by defining an effective residence time

in which

is the flow velocity determined by the 222Rn diffusion coefficient [10] [11]

and decay rate [12]

In a conventional flow measurement, the sample consists of a stream that passes through a flow cell aligned perpendicular to the detector surfaces. The detectors, which are photomultiplier tubes in the case of flow scintillation counting, therefore sample the radioactive material only for the time that the atoms reside in the flow cell. This residence time is the ratio of the flow velocity and sample flow rate (in units of volume per time). In liquid chromatography the flow velocity is a well-defined, experimentally adjustable quantity, but in the diffusion of a radioactive gas it is a characteristic parameter of a stochastic process. Expression (5) was derived in [4] by solution of the one-dimensional steady-state diffusion equation with implementation of open-volume boundary conditions and account taken of loss by radioactive decay.
Although not reported in [4] , the integrals in Equations (2) and (3) upon substitution of range function (1) can be expressed in terms of known special functions yielding the following closed forms for the effective detection volume and area


in which

is the polylogarithm function. For index

Use of the preceding expressions (8) and (9) together with relations (4) and (5) leads to the following closed form expression for the residence time

Evaluation of relation (12) for passive diffusion of 222Rn in air yields a residence time
Although residence time defined in terms of the diffusive flow of a macroscopic current of radioactive gas resulted in values of radon concentration in accord with measurements by a calibrated standard, it is nevertheless of interest, both conceptually and practically, to examine the concept of residence time from a micro-statistical perspective of particle Brownian motion. For one, this latter approach avoids the adoption of a phenomenological range function with adjustable parameter
The development and investigation of such a micro-statistical model is the principal objective of this paper. This is accomplished in the following sections by calculating the exact time-dependent probability density (Green’s function) for Brownian motion of radon from a planar source and showing that a certain integral of this function over time provides the sought-for statistical expectation value corresponding to the residence time in the macro-statistical model developed in [4] . In this regard, Equations (8), (9), and (12) will be useful later in the comparison of the residence time as modeled in [4] with the mean residence time obtained from the micro-statistical treatment developed in this paper.
2. Micro-Statistical Calculation of Residence Time
2.1. Conditional Probability for Single-Particle Brownian Motion with Decay
The equation for the conditional probability 





and leads to the solution

The Green’s function expressed in Equation (14) is a three-dimensional Gaussian conditional probability density―i.e. a probability per unit volume―as indicated by the dimensionality 
In a coordinate system with vertical z-axis and horizontal x-axis directed normally outward from the particle source plane (





where 



The function 


Reduction of the problem of 3-dimensional diffusion from a planar source to diffusion from a point source on the horizontal axis is a consequence of the isotropic symmetry of Equation (14), which permits factorization into a product of three independent one-dimensional degrees of freedom. The isotropic symmetry itself comes from neglect of gravity, the effects of which are shown in Appendix 1 to be negligible under the circumstances of measuring radon activity by the method developed in [4] and elaborated further in this paper.
From Equation (15), one can calculate the cumulative probability 


Figure 2. Probability density of one-dimensional unconstrained Brownian motion (Equation (15)) as a function of displacement starting at the origin for times (s): (a) 20 (violet); (b) 50 (blue); (c) 100 (gold); (d) 200 (green); (e) 600 (red). Radon parameters:

region) during the time interval t begun when the particle was placed at 

The error function in Equation (16) is defined by

and is an anti-symmetric function of its argument.
The time interval 

in which

is the characteristic diffusion length. (See Ref. [4] , Appendix 1) For 222Rn, it follows from relations (6) and (7) that

In the limit that 




The mean value 



in which 




A procedure entirely equivalent to (21) for computing expectation values is to use the cumulative distribution function (cdf) 


It can then be shown (in Appendix 2) that the expectation value 

For a random variable defined on the positive real axis only, the second term on the right side of Equation (23) vanishes. This is the case for




where the second equality in Equation (24) follows from the definition (22) of the cumulative distribution function. Since 


2.2. Comparison of Phenomenological and Statistical Residence Time Functions
For purposes of comparison, the two expressions for residence time are collected below with substitution of the characteristic diffusion length (19)
Phenomenological:
Statistical:
Numerical evaluation of the statistical residence time (27) requires substitution of a specific length 





with the Taylor series expansion of relation (27) truncated at the lowest order of

For the two expressions (28) and (29) to yield the same residence time interval, the effective length of the detection volume L would be related to the mean alpha range by
Figure 3. Plot of range function 





For the case of a 5.49 MeV alpha in air with experimental mean range



which are in excellent accord.
From the definition (22) of the cdf, one obtains the corresponding pdf by application of the Leibniz rule [16] for differentiating an integral

It then follows from relation (24) that the pdf for the random variable T whose expectation is the residence time 

Figure 4 shows a plot of pdf (33) as a function of time for parameters characteristic of 222Rn with 



Figure 4. Probability density (Equation (33)) of the residence time of a particle in the region

simply by relation (25) or much more onerously from expression (21) with 

In the following section the residence time is obtained in a different way by examining stochastic events referred to as “first passage” or “first return”, which occur widely in problems involving Brownian motion with boundaries.
2.3. Comparison of Residence Time with First Passage Time to One Absorbing Boundary
The time of first passage (FPT) is the time for a particle undergoing Brownian motion to first reach a specified site. The problem has wide applicability in fields as diverse as physics, chemistry, biology, economics, and others [19] . Consider the first-passage of an unstable particle with decay rate 





Mathematically, it is required to find a probability density function 


The method of images entails placing an “anti-source” of particles at just such a location as to null the net probability at






The probability 


which is seen to be of identical form to the cumulative probability (16) of finding the particle in the region 

is identical under the stated circumstances to the residence time 


is identical to pdf (33) for
Figure 5. Probability density as a function of displacement of Brownian motion with initial location 

from the unconstrained pdf (15) mathematically and visually (as seen by comparing Figure 2 and Figure 5), the equivalence of the spatial integrals (16) and (35) follows by making the transformation of variable 

identical to probability (16).
A plot of the survival probability 



2.4. Comparison of Residence Time with First Passage Time to Two Absorbing Boundaries
From the analyses of the previous two sections one might expect that the residence time of radon within the detection region could also be modeled as the exit time or time of first passage of a particle to either of two absorbing boundaries representing the entrance and exit planes of the detection region. This inference would, in fact, be incorrect. It is instructive to understand why this latter system gives rise to a residence time of different functional form and entirely different magnitude.
Mathematically, it is now required to find a probability density function 



Figure 6. Survival probability (35) as a function of time (s) for the absorbing boundary and parameters of Figure 5.
again obtained by the method of images, where, in marked contrast to the simple solution (34) for the case of one absorbing boundary, an infinite number (




in which 

Figure 7 shows plots of pdf (39), truncated at






Figure 7. Probability density 

Figure 8. Probability density 

The survival probability that the particle has not reached either boundary within time t is given by

in which

The corresponding first-passage or exit time is

Performing the integrations and taking the limit in Equation (42) leads to an exit time

with diffusion length 



The difference between 






independent of the decay rate

The discrepancy between (44) and (45), which one might have thought described the same physical system―namely, a decaying particle initially at 

When a randomly moving particle reaches one or the other of the two absorbing boundaries it is removed from the system. This is not the case for radon diffusing through a region of width 






To understand the physical significance of the time interval (44) in the context of radon diffusion in an open volume (no boundaries) consider the temporal value at which pdf (33) for the residence time 






which, to within a numerical factor, has the same form as



It is worth noting here, although the derivation is given elsewhere [21] , that the mean exit time (referred to as time to capture) 


with implementation of appropriate boundary conditions. For a stable particle undergoing a one-dimensional random walk between absorbing boundaries at 


which reduces to 




In the case of an unstable particle with decay rate 

and leads to a solution that for 

3. Mutual Consistency of Brownian Motion and Mass Diffusion
1From a thermodynamic perspective, the potential responsible for diffusion is the chemical potential



The preceding sections have demonstrated the equivalence of residence times calculated from models of a) free diffusion of a macroscopic sample of radon gas under a concentration gradient, and b) unconstrained Brownian motion of individual radon atoms moving forward or backward independently with equal probability―i.e. oblivious to the concentration gradient. Since approach a) appears to involve directed motion attributable to a kind of force (i.e. gradient of a potential1) and approach b) clearly involves random motion in the absence of any force, it may not be immediately apparent why the two approaches actually describe the same physical process. Here, in brief, is an explanation, as illustrated schematically in Figure 9. Suppose there are 
Figure 9. Relation of Brownian motion to Fick’s law. Individual atoms (black dots) undergo a random walk to the left with probability p or to the right with probability q. For an unbiased walk,






For equal probabilities


that captures the physical content of Fick’s law. The greater transport of particles to the left does not arise because there is an asymmetric force acting on individual particles, but because of the greater number of particles to enter the region dx from the right (closer to the source) than from the left. For each particle, however, the two directions of motion are equally probable. The applicability of Fick’s law to radon diffusion has, in fact, been tested and confirmed experimentally [23] .
4. Conclusions
Implementation of the newly introduced procedure [4] to measure indoor radon activity concentration quantitatively and accurately by means of two GM detectors requires knowledge of the rate at which radon atoms pass through the open detection region, or, equivalently, the mean time spent by a radon atom within the detection region.
The analyses in this paper have established that one must exercise caution in adopting a stochastic model to describe the time spent by a radioactive atom in the detection region. For example, although it may seem reasonable to define (and presumably measure) the residence time as the mean time for an atom within the detection region to first reach either the entrance or exit plane, this choice is physically unsatisfactory. It ignores the possibility that the atom, having reached a boundary, can proceed away from or back into the detection region with equal probability. As a consequence, this first-passage or exit time, given approximately by

is too short and would lead to a measurement of radon concentration that is significantly lower than actual (see Equation (27) of Ref. [4] ). On the other hand, the present analysis has established the equivalence of defining the residence time as either a) the mean time spent by the atom between the entrance and exit planes of the detection region irrespective of how often the atom may pass through a boundary or b) the time the atom first reaches the exit plane of the detection region. The two times are identical mathematically and given approximately by

Given the system parameters D, 









Cite this paper
Silverman, M.P. (2017) Analysis of Residence Time in the Measurement of Radon Activity by Passive Diffusion in an Open Volume: A Micro-Statistical Approach. World Journal of Nuclear Science and Technology, 7, 252-273. https://doi.org/10.4236/wjnst.2017.74020
References
- 1. Andersson, K.G. (2009) Airborne Radioactive Contamination in Inhabited Areas. Elsevier, Amsterdam, 1-20.
- 2. Zeeb, H. and Shannoun, F., Eds. (2009) WHO Handbook on Indoor Radon: A Public Health Perspective, Summary Statistics at http://www.who.int/phe/radiation/backgrounder_radon/en/
- 3. A Citizen’s Guide to Radon (2012) US Environmental Protection Agency EPA-402/K-12/002. http://www.epa.gov/radon
- 4. Silverman, M.P. (2016) Method to Measure Indoor Radon Concentration in an Open Volume with Geiger-Mueller Counters: Analysis from First Principles. World Journal of Nuclear Science and Technology, 6, 232-260. https://doi.org/10.4236/wjnst.2016.64024
- 5. Lapp, R.E. and Andrews, H.L. (1972) Nuclear Radiation Physics. 4th Edition, Prentice-Hall, Englewood Cliffs, NJ, 198-200.
- 6. Annunziata, M.F. (1998) Handbook of Radioactivity Analysis. Academic Press, New York, 6-8.
- 7. Tsoulfanidis, N. and Landsberger, S. (1995) Measurement & Detection of Radiation. 2nd Edition, Taylor & Francis, Washington DC, 106.
- 8. Hull, D.E. (1958) The Total-Count Technique: A New Principle in Flow Measurement. International Journal of Applied Radiation and Isotopes, 4, 1-15.https://doi.org/10.1016/0020-708X(58)90020-6
- 9. Reeve, D.R. and Crozier, A. (1977) Radioactivity Monitor for High-Performance Liquid Chromatography. Journal of Chromatography, 137, 271-282.https://doi.org/10.1016/S0021-9673(00)81350-3
- 10. Nazaroff, W.W. and Nero Jr., A.V. (Eds.) (1988) Radon and Its Decay Products in Indoor Air. Wiley, New York, 65-69.
- 11. Environmental Science Division, Argonne National Laboratory. Effective Radon Diffusion Coefficient. http://web.ead.anl.gov/resrad/datacoll/radon.htm
- 12. Bellotti, E., Broggini, C., Di Carlo, G., Laubenstein, M. and Menegazzo, R. (2015) Precise Measurement of the 223Rn Half-Life: A Probe to Monitor the Stability of Radioactivity. Physics Letters B, 743, 526-530.
- 13. Wallace, P.R. (1984) Mathematical Analysis of Physical Problems. Dover, New York, 355-383.
- 14. Lea, S.M. (2004) Mathematics for Physicists. Brooks/Cole, Belmont, 354.
- 15. Feller, W. (1957) An Introduction to Probability Theory and Its Applications. Vol. 1, Wiley, New York, 304-305, 368-370.
- 16. Franklin, P. (1964) A Treatise on Advanced Calculus. Dover, New York, 347-349.
- 17. Hughes, B.D. (1995) Random Walks and Random Environments. Vol. 1, Random Walks. Oxford University Press, Oxford, 205-206.
- 18. Krapivsky, P., Redner, S. and Ben-Naim, E. (2010) A Kinetic View of Statistical Physics. Cambridge University Press, Cambridge, 32-35. https://doi.org/10.1017/CBO9780511780516
- 19. Redner, S. (2007) A Guide to First Passage Processes. Cambridge University Press, Cambridge.
- 20. Carslaw, H. and Jaeger, J. (1959) Conduction of Heat in Solids. 2nd Edition, Oxford University Press, Oxford, 273-281.
- 21. Berg, H.C. (1993) Random Walks in Biology. Princeton University Press, Princeton, 42-47.
- 22. Silverman, M.P. (2017) Unpublished Work in Preparation for Publication.
- 23. Sasaki, T., Gunji, Y. and Iida, T. (2007) Transient-Diffusion Measurements of Radon: Fick’s Law Confirmation and 218Po/214Po Behavior Determination. Journal of Nuclear Science and Technology, 44, 1330-1336. https://doi.org/10.1080/18811248.2007.9711379
- 24. Goody, R. and Walker, J. (1972) Atmospheres. Prentice-Hall, Englewood Cliffs, 4-11.
- 25. Tabor, D. (1979) Gases, Liquids, and Solids. 2nd Edition, Cambridge University Press, Cambridge, 43-51.
- 26. Vardavas, I. and Taylor, F. (2011) Radiation and Climate: Atmospheric Energy Budget from Satellite Remote Sensing. Oxford University Press, Oxford, 42-48.
Appendix 1:
Density Profile of Radon Gas in a Uniform Gravitational Field
The point at issue is whether the vertical density profile of radon gas is affected by gravity over a dimension of order of the alpha-particle range
The barometric law for equilibrium gas pressure 

where 

where 

(A) Isothermal Atmosphere (Constant Temperature
Elimination of pressure by substitution of Equation (56) into (55) leads to a logarithmic differential equation for density whose solution is

with scale parameter

In the second equality of (58) M is the radon molar mass and 
For 222Rn (M = 0.222 kg) at room temperature (




(B) Adiabatic Atmosphere (Constant Entropy)
Although a room (e.g. a laboratory) or a building may be kept under isothermal conditions, the lowest section of the Earth’s atmosphere (the troposphere) is not isothermal, but more accurately described by the adiabatic constitutive relation [26]

where 


with the scale parameter 




It is to be concluded, therefore, that gravity has a negligible effect on the equilibrium density profile of radon within the detection volume, and that use of the isotropic Green’s function for calculating the radon residence time is justified.
Appendix 2:
Use of the Cumulative Distribution Function to Calculate Expectation Values
If 



Integration by parts of the two integrals on the second line of (61) yields

where use was made of the properties



It then follows from (61) that

For an intrinsically positive variable X the second term on the right side of (63) vanishes. In that case, the same procedure can be used to show that the variance of X is given by














