World Journal of Nuclear Science and Technology
Vol.06 No.03(2016), Article ID:68130,7 pages
10.4236/wjnst.2016.63015
Fluorine Assessment of Igneous Rocks by Neutron Activation Analysis
Abdelrazig Mohmed Abdelbagi1,2
1Physics Department, Science College, Shaqra University, Da wadami, Kingdom of Saudi Arabia
2Faculty of Science, Omdurman Islamic University, Omdurman, Sudan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2016; accepted 8 July 2016; published 11 July 2016
ABSTRACT
The main goal of the current study was to determine the fluorine in the rock samples coal (SARM- 18, SARM-19, and SARM-20), opal glass NBS91 and phosphate rock NBS694 using neutron activation analysis. Neutrons energy of 14 MeV used for irradiation was produced by bombardment of a water-cooled titanium tri-tide target with a beam of deuterons accelerated to a potential of 350 KV to develop a neutron flux (108 n∙cm−2∙s−1) on the sample at the neutron generator in the ECN (Netherlands Energy Research Foundation) Petten. This new approach contributes to the existing knowledge of fluorine measurement by the coincidence channels investigation of the positron energy with respect to decay time for each radionuclide element. The present study was designed to determine the fluorine by fast neutron through the reaction of F19 (n, 2n) F18. Interference was treated by irradiating the standard of these elements and reasonable selection of the decay time between the end of irradiation and beginning of counting time. The results of this method indicate that the concentration of fluorine is agreed fairly with literatures.
Keywords:
Fluorine, New Method, Rock Samples, Neutron Generator, Activation Analysis, Spectroscopy

1. Introduction
Fluorine is a common element in the earth’s crust formed in minerals and rocks as fluorides. It’s present in the composition of volcanic rocks and in some area in underground water, which is soluble element of water and it’s leaching from the host rock of high concentrations of natural origin (up to 6 ppm) [1] . The height concentration of fluorine content was measured in alluvial soils and the lowest amount found in cambisols soils that determined by M. Jakovljević, S. Blagojević and Svetlana Antić-Mladenović, which was in the normal range of fluorine content in the soil (150 - 400 ppm), also, formed in igneous rocks and the sandy soils that were confirmed by Kabata-Pendias and Pendias (1989) [2] .
Fluorine is an essential element for animals and inclusion in minerals and plants. It is presented naturally in almost all food, drinking water and ocean water, but it’s a toxic element at higher concentration. Therefore, fluorine is playing an important role in the health of human and animals and the control of fluorine concentration is essential for growing and breeding, which has impacted on bone illnesses and the tooth serious infections at a higher level [3] [4] . The Environmental Protection Agency (EPA) of US is set by regulation for maximum contamination water level of fluorine 4.0 ppm and the optimum level of 0.7 ppm in 2011. In addition, to respond to the recent regulations of the Department of Health and Human Services for the Water Research Foundation, fluorine was added to drinking water treatment to provide public protection from dental caries from the lack of fluorine [5] .
Fluorine is determined using various methods such as chemical methods due to the loss or gain of fluorine during chemical reaction and incomplete extraction of fluorine from solid samples into solution [4] . The lower energies and a limit of detection of fluorine are affecting the sensitivity of the measurement of fluorine using the X-ray fluorescence method. Mainly fluorine is determined by fluoride-ion selective electrode method and mineral supplements decomposition prior to fluorine and the conductivity of the sample [6] [7] . The gamma ray of 6.13 MeV via reaction 19F (p, αγ)16O has been used to determine fluorine in various types of tea leaves, basaltic volcanic rocks TB4 and rabbit bones using 5 MeV protons produced by cyclotron in Melbourne University, which measured by M. A. Chaudhrit, J. L. Rouse and B. M. Spicer [5] . Fluorine determination using thermal neutron activation analysis can measured through 19F(p, αγ)16O reaction, which is a convenient detection method for fluorine assessing for gammas of 6.13 MeV energy that can influence with the short-life radionuclides from the various reactions due to increased backgrounds [7] .
The fast neutron generator that produces 14 MeV of energy is used in neutron activation produces. Fluorine can be assessed through the nuclear reactions, the F19(n, p)O19, F19(n, α)N16 and F19(n, 2n)F18, so that the F19(n, p)O19 reaction is affected by the high Compton background and possible interference in the low energy region of gamma-ray [8] . Fluorine activated by the F19(n, α)N16 reaction has the interference of oxygen O16(n, p)N16 that produces the same N16 radionuclide [9] . Fast neutron techniques are activating many elements through reaction (n, 2n) that produces positrons emission photo peaks of 511 KeV. However, it is employed in this method for fluorine determination in the rock samples that emit 511 KeV photo peak induced by the F19(n, 2n)F18 [10] .
2. Methodology
The fluorine F18 half-life time is 110 minutes and the elements of (n, 2n) reaction, which were irradiated under the same condition used for fluorine and the elements of short-life time less than F18 allowed to decay before sample counting time start [10] .
Therefore, the possible removal or greatly reduce the interference of these elements with fluorine is by reasonable selection of the irradiation time, counting and decay time between the end of irradiation and beginning of count time measurement. Moreover, most of these elements are not pure-emitting energy in spectrum region, by a survey of the spectrum of the sample between 100 KeV and 1800 KeV energies that possible to detect any photo peaks of these elements interfere with photo peak 511 KeV [11] .
The radionuclide F18 is the pure emits positron, which annihilates in the sample to form two 511 KeV gamma-rays. The concentration of fluorine in the unknown sample is then determined by comparison with fluorine standard. The decay correction formula of the counts of these elements has been taken due to the fluorine decay times.
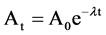
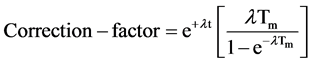
where, Ao is initial activity, At is activity after waiting time, t is waiting time, Tm is measuring time, λ is decay constant.
The formula below was used for calculating the standard deviation of net photo-peak area of fluorine with the interference of the peak of Na24.

where, σF511 is a fluorine standard deviation, E.T511 is peak error in total 511 KeV according to the formula, E.Na1368 is a peak error in 1368 KeV according to the formula, a σ1368 is the standard deviation of peak 1368 KeV and α is the ratio of peak 511 KeV to peak 1368 KeV of Na24 [12] [13] .
The system for detection is needed for activation analysis that depends on the complexity of the problem under consideration. However, positron annihilation photons are detected by two oppositely placed sodium iodide crystal NaI(TI) and the positron counts is registered when coincident 511 KeV annihilation gamma-ray pulses occur in each detector. The channels of the coincidence counting of the annihilation quanta rejected all radiation from the sample that interacted in the crystal and detect the positrons, so that the relevant gamma energy of the radionuclide can be easily selected [14] .
The sodium iodide crystal NaI(TI) (put crystal) detector with source mounted in the center of shielding lead, has been used to measure the efficiency of the detection equipment, which was shielded against background radiation by lead and efficiency calculation by using the sum-peak method [15] [16] .
3. NaI(TI) Detector Efficiency
The purpose of this technique is to calculate the photo-peak detection efficiency for 511 KeV gamma-radiations by using the sum-peak method with a small radionuclide Na22 (half-life 2.6 years) that illustrates in the decay scheme below.

An examination of the spectrum shows that the annihilation photo-peak at the 511 KeV was appearing with the peak at 1277 KeV and the sum-peak at 1788 KeV [15] [16] .
The efficiency for the detection of the annihilation can be now calculated as follows formula.

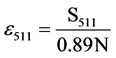
where, N is number of disintegration per present counting time, T is the total content of γ-ray spectrum minus the natural background, S511 is the area under the annihilation photo-peak at 511 KeV, S1277 is the area under the annihilation photo-peak at 1277 KeV, S1788 is the area under the annihilation Photo-peak at 1788 KeV, ε511 is efficiency for the detection of the annihilation radiation [10] [16] .
4. Experimental Method
An experimental demonstration of this gamma ray of 511 KeV was first measured by NaI(TI) scintillation crystal detector with the head mounted in the center (put-crystal). A small source of Na22 (weight = 10 mg) was used to perform the detector efficiency of the experiment. A ten series of measurements on Na22 source with counting time of 10 minutes was computed that followed by 10 hours counting time of the natural background.
The neutron flux monitor equipment system consists of U238 detector and preamplifier is located near the irradiation position and the neutron flux was corrected with standard of 105 counts per 2 minutes. All samples were packed in cylindrical polyethylene container (12.5 × 29.5 mm), so that sample was transferred through a single aluminum pneumatic tube between irradiation position and counting stations.
This method is particularly useful in determining of fluorine in igneous rock samples with adjacent of fluorine standard concentration measurement. Fast neutrons from neutron generator were used to irradiate rock samples and fluorine standard using energy of 14 MeV. The rock samples and different concentration of p-fluoro-benzoic acid or (4-Fluorobenzoic acid, C7H5FO2) are organic compound acid were used to determine the fluorine concentration; subsequently both sample types were irradiated for 10 min to produce sufficient activities for the measurement.
The gamma-ray detector is two 3 × 3 inches NaI(TI) scintillation crystal of distance between two surfaces of the crystal and the axis of the sample container, which is perpendicular to the crystal of 11 mm distance.
Multi-channel analyzer (Nuclear Data) with 512 channels pulse high analyzer on coincidence technique setting is connected to detectors. The detector calibration was performed using the standard Na22 positron source surveying for more interference with coincident 511 KeV annihilation gamma-rays standard CO60 source [16] .
Standard CO57 source and standard silicon were irradiated in the neutron generator used for assessing the spectrum between 100 KeV and 1800 KeV for the interferences. The gamma-rays of 511 KeV are produced when positrons annihilation photo-peak appear as characteristic of the radionuclide in the spectrum. The magnesium and Aluminum concentrations were measured for interference correction with fluorine in some samples using the reactor power of 30 KW.
5. Results
The concentrations of the fluorine in the samples are calculated compared to the standards after the background and flux corrections have been applied to the both standards and samples. The neutron flux during irradiation may decrease from the beginning of the measurement to the end of irradiation. Therefore, the difference in the neutron flux has been corrected due to mean flux of all samples and standards only small variations are observed. Also, extend of any interference was measured as described below, to obtain the best accuracy in fluorine determination.
In the present work in some rock samples aluminum and magnesium concentration influence with fluorine concentration on photo-peak 511 KeV of the Na24 (half-life, 15 hours) induce by the reaction Al27(n, α)Na24 and Mg24(n, p)Na24.
Subsequently, aluminum standard is a white crystalline double sulfate or ammonium aluminum sulfate, formula (NH4)Al(SO4)2・12H2O was irradiated and measured under the same condition of fluorine (F18), then the 511 KeV photo-peak was corrected for by taking the ratio of the 511 KeV peak to the 1368 KeV peak of Na24. In particular, the formula below has been used for the correction.
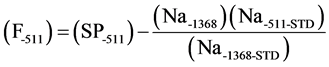
(F-511) is fluorine net area; (Sp-511) is 511 KeV photo-peak areas in the sample. (Na-1368) is 1368 photo-peak area of Na24 in the sample, (Na-511-STD) is 511 KeV photo-peak area of Na24 in the standard and (Na-1368-STD is 1368 KeV photo-peak area of Na24 in the standard.
In some samples the peak of 1368 KeV was not resolved by the Multi-channel analyzer. For this problem the 511 KeV net area of fluorine was corrected due to the aluminum and magnesium concentration in the sample. The aluminum standards and magnesium standard (MgSO4.7H2O) were irradiated under the same condition of F18. The following formula has been applied for that correction.
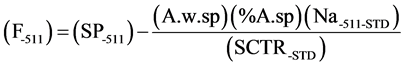
where, (A.w.sp) is element weight in the sample, (% A.sp) is the element concentration in the sample, (SCTR-STD) is the specific count rate of element in the standard.
Table 1 presents the result of the determination of fluorine in the rock samples by fast neutron and possible interferences of Al and Mg, which are resolved with the cross check measurement in Table 2 and Table 3 by using low flux reactor (30 KW power). Table 4 shows measurement parameters and the physical constant for possible interference with fluorine in rocks by positron annihilation through reaction (n, 2n) [8] [10] [12] .
Table 1. Fluorine concentration in rock samples.
Table 2. Low flux reactor of power (30 Kw) and SARM20 (Coal) and reaction (n, α).
Table 3. Low flux reactor of power (30 Kw) and SARM18 (Coal) and reaction (n, α).
Table 4. Reactions (n, 2n) of radionuclides elements and measurement parameters with neutron generator, (Neutron flux = 108/cm2∙s, Irradiation time (t1) = 10 minutes, Waiting time (t2) = 110 minutes, Counting time (t3) = 10 minutes).
6. Discussion
The method of the present study was designed to determine the fluorine concentration with precise quantitative analysis and evaluating fluorine observed consistent results on whether some difficulty facing the other methods. The finding of this experiment using sum-peak calculation the efficiency was considered to be 14.25% that in very good agreed with literatures [16] . This study set out with the aim of assessing the importance of fluorine is effect on human life and animals at very low concentration. Contrary to expectations, this study did not conclude a significant difference between fluorine in rocks compared to the literatures. It is apparent from this method that very little variation in fluorine concentration in coal SARM (18-19-20) compared to the literatures and values obtained [17] . A possible explanation for this might be that from coincidence detection techniques show interference of radionuclide Na24 peak energy. The reactor power in the present study was used to determine the Mg and Al concentration in coal samples for Na24 effect and alteration of fluorine determination. Further research should be made to resolve the interference of Na24 via detector peak for coincident in positron annihilation technique. Some of the issues emerging from this finding relate specifically to additional work is required to establish the viability of new approached methods through computer software for routine analysis of fluorine in all types of samples.
6. Conclusion
The new approach in activation analysis was designed to determine the fluorine in rock samples using a neutron generator. The experiment confirmed that fluorine could be measured using a technique based on coincidences 511 KeV peaks and the decay time of radionuclide. The present study makes a noteworthy contribution to the measurement of fluorine spectroscopy determination. One of the more significant findings to emerge from this efficiency measurement is [16] , which is agreed fairly with literatures values. The method has gone some way towards enhancing our understanding technique of measurement, calculation and assessment of fluorine in rock samples. The major limitation of this study is the influence of Na24 peak, which can be resolved using the measurement of possible Aluminum and Magnesium known concentration. The most striking result to emerge from the data is that the concentration of fluorine agrees fairly with standards of known rocks in the literatures [17] .
Acknowledgements
I very much appreciate the support of A.H.D as that is leading to these results and Energy Research Centre of the Netherlands, ECN, Petten, the Netherlands and gratefully acknowledge for financial support from the IAEA and Sudan Atomic Energy Commission.
Cite this paper
Abdelrazig Mohmed Abdelbagi,1 1, (2016) Fluorine Assessment of Igneous Rocks by Neutron Activation Analysis. World Journal of Nuclear Science and Technology,06,140-146. doi: 10.4236/wjnst.2016.63015
References
- 1. Haamer, K. and Karroa, E. (2006) Tartu, High Fluorine Content of K-Bentonite Beds in Estonian Paleozoic Carbonate Rocks, Fluoride. Research Report, 39, 132-137.
- 2. Jakovljević, M., Blagojević, S. and Antić-Mladenović, S. (2002) Fluorine Content in Soils of Northern Pomoravlje. Journal of Agricultural Sciences, 47, 121-128.
- 3. Campbell, A.D. (1987) Determination of Fluorine in Various Matrices. Pure and Applied Chemistry, 59, 695-702.
- 4. Chaudhrit, M.A., Rouse, J.L. and Spicer, B.M. (1975) Determination of Fluorine in Tea, Bones and Rocks through the Reaction Using a Cyclotron, 19F(p, αγ)16O. Proceedings of the 7th International Conference on Cyclotrons and Their Applications, Zürich, Switzerland, 19-22 August 1975, 522-523.
http://dx.doi.org/10.1007/978-3-0348-5520-4_110 - 5. Tokalioglu, S. Kartal, S. and Sahin, U. (2004) Determination of Fluoride in Various Samples and Some Infusions Using a Fluoride Selective Electrode. Turkish Journal of Chemistry, 28, 203-211.
- 6. Farzaneh, A. and Troll, G. (1977) Pyrohydrolysis for the Rapid Determination of Small and Large Amounts of Fluorine in Fluorides, Silicate Minerals and Rocks Using an Ion-Selective Electrode. Geochemical Journal, 11, 177-181.
- 7. Taflik, T., Duarte, F.A., Flores, é.L.M., Antes, F.G., Paniz, J.N.G., Flores, é.M.M. and Dressler, V.L. (2012) Determination of Bromine, Fluorine and Iodine in Mineral Supplements Using Pyrohydrolysis for Sample Preparation. Journal of the Brazilian Chemical Society, 23, 488-495.
http://dx.doi.org/10.1590/S0103-50532012000300016 - 8. Prud’homme, J.T. (1964) Texas Nuclear Corporation; Neutron Generators. Texas Nuclear Corp., Austin.
- 9. Moses, A.J., Belcher, R. and Gordon, L. (1963) Analytical Chemistry of the Actinide Elements. Elsevier Inc.
- 10. Lyon, W.S. (1964) Guide to Activation Analysis. Van Nostrand, Princeton, NJ.
- 11. Van der Mark, W. and Das, H.A. (1973) The Determination of Fluorine in the Bone by Fast Neutron Activation Analysis. Journal of Radio-Analytical Chemistry, 13, 62-107.
- 12. Moses, A.J., Belcher, R. and Gordon, L. Analytical Chemistry of the Actinide Elements. Vol. 9, International Series of Monographs on Analytical Chemistry.
http://www.sciencedirect.com/science/book/9780080099156 - 13. Cuypers, M. and Cuypers, J. (1968) Gamma Ray Spectra and Sensitivities for 14 MeV Neutron Activation Analysis. Journal of Radio-Analytical Chemistry, 1, 243-264.
http://dx.doi.org/10.1007/BF02514041 - 14. Weber, G. and Guillaume, M. (1971) Fast and precise Determination of Fluorine in Geological Samples by 14 MeV Neutron Activation Analysis. Journal of Radio-Analytical and Nuclear Chemistry, 7, 271-280.
- 15. Perdijon, J. (1967) Experimental Sensitivities in Neutron Activation and Spectrometry with a 150 KeV Accelerator. Analytical Chemistry, 39, 448-456.
http://dx.doi.org/10.1021/ac60248a024 - 16. Akkurt, I., Gunoglu, K. and Arda, S.S. (2014) Detection Efficiency of NaI(Tl) Detector in 511–1332 keV Energy Range. Science and Technology of Nuclear Installations, 2014, Article ID: 186798.
- 17. Van Der Sloot, H.A. and Zonderhuis, J. (2007) Instrumental Neutron Activation Analysis of 37 Geochemical Reference Samples. Geostandards Newsletter, 3, 185-193.


