Journal of Encapsulation and Adsorption Sciences
Vol.2 No.3(2012), Article ID:23086,11 pages DOI:10.4236/jeas.2012.23006
On Damped Wave Diffusion of Oxygen in Pancreatic Islets: Parabolic and Hyperbolic Models
Advanced Technology Center & Biotechnology Institute, Lone Star College, CYFair, Cypress, TX & Department of Physics, Texas Southern University, Houston, USA
Email: jyoti_kalpika@yahoo.com
Received June 19, 2012; revised July 24, 2012; accepted August 12, 2012
Keywords: C Type I Diabetes; Simultaneous Reaction and Diffusion; Michaelis and Menten Kinetics; Damped Wave Diffusion; Relativistic Transformation; Hyperbolic Models; Parabolic Models; Islets of Langerhans
ABSTRACT
Damped wave diffusion effects during oxygen transport in islets of Langerhans is studied. Simultaneous reaction and diffusion models were developed. The asymptotic limits of first and zeroth order in Michaelis and Menten kinetics was used in the study. Parabolic Fick diffusion and hyperbolic damped wave diffusion were studied separately. Method of relativistic transformation was used in order to obtain the solution for the hyperbolic model. Model solutions was used to obtain mass inertial times. Convective boundary condition was used. Sharma number (mass) may be used in evaluating the importance of the damped wave diffusion process in relation to other processes such as convection, Fick steady diffusion in the given application. Four regimes can be identified in the solution of hyperbolic damped wave diffusion model. These are: 1) Zero Transfer Inertial Regime, 0 ; 2) Rising Regime during times greater than inertial regime and less than at the wave front, Xp > t; 3) at Wave front , t = Xp; 4) Falling Regime in open Interval, of times greater than at the wave front, t > Xp. Method of superposition of steady state concentration and transient concentration used in both solutions of parabolic and hyperbolic models. Expression for steady state concentration developed. Closed form analytic model solutions developed in asymptotic limits of Michaelis and Menten kinetic at zeroth order and first order. Expression for Penetration Length Derived-Hypoxia Explained. Expression for Inertial Lag Time Derived. Solution was obtained by the method of separation of variables for transient for parabolic model and by the method of relativistic transformation for hyperbolic models. The concentration profile was expressed as a sum of steadty state and transient parts.
; 2) Rising Regime during times greater than inertial regime and less than at the wave front, Xp > t; 3) at Wave front , t = Xp; 4) Falling Regime in open Interval, of times greater than at the wave front, t > Xp. Method of superposition of steady state concentration and transient concentration used in both solutions of parabolic and hyperbolic models. Expression for steady state concentration developed. Closed form analytic model solutions developed in asymptotic limits of Michaelis and Menten kinetic at zeroth order and first order. Expression for Penetration Length Derived-Hypoxia Explained. Expression for Inertial Lag Time Derived. Solution was obtained by the method of separation of variables for transient for parabolic model and by the method of relativistic transformation for hyperbolic models. The concentration profile was expressed as a sum of steadty state and transient parts.
1. Introduction
Diffusion of oxygen in pancreatic islets in an important consideration during development of models of viability and function of the islets of Langerhans (Figure 1). Islets of Langerhans are spheroidal aggregate of cells located in pancreas. They secrete harmones such as insulin during glucose metabolism. These islets are transplanted in order to effect cure for Type I diabetes and are often encapsulated in devices. Islets that are removed from pancreas loose their internal vascularization. The cure is depends on diffusion of oxygen from external environment.
Avgoustiniatos et al. [1] and Colton et al. [2] developed a method for estimation of maximum oxygen consumption rate and the oxygen permeability in the tissue in a suspension of spherical aggregates from measurements of partial pressure of oxygen in batch experiments. A simultaneous reaction and diffusion model was used. Williams et al. [3] discuss a dramatic diffusion barrier that
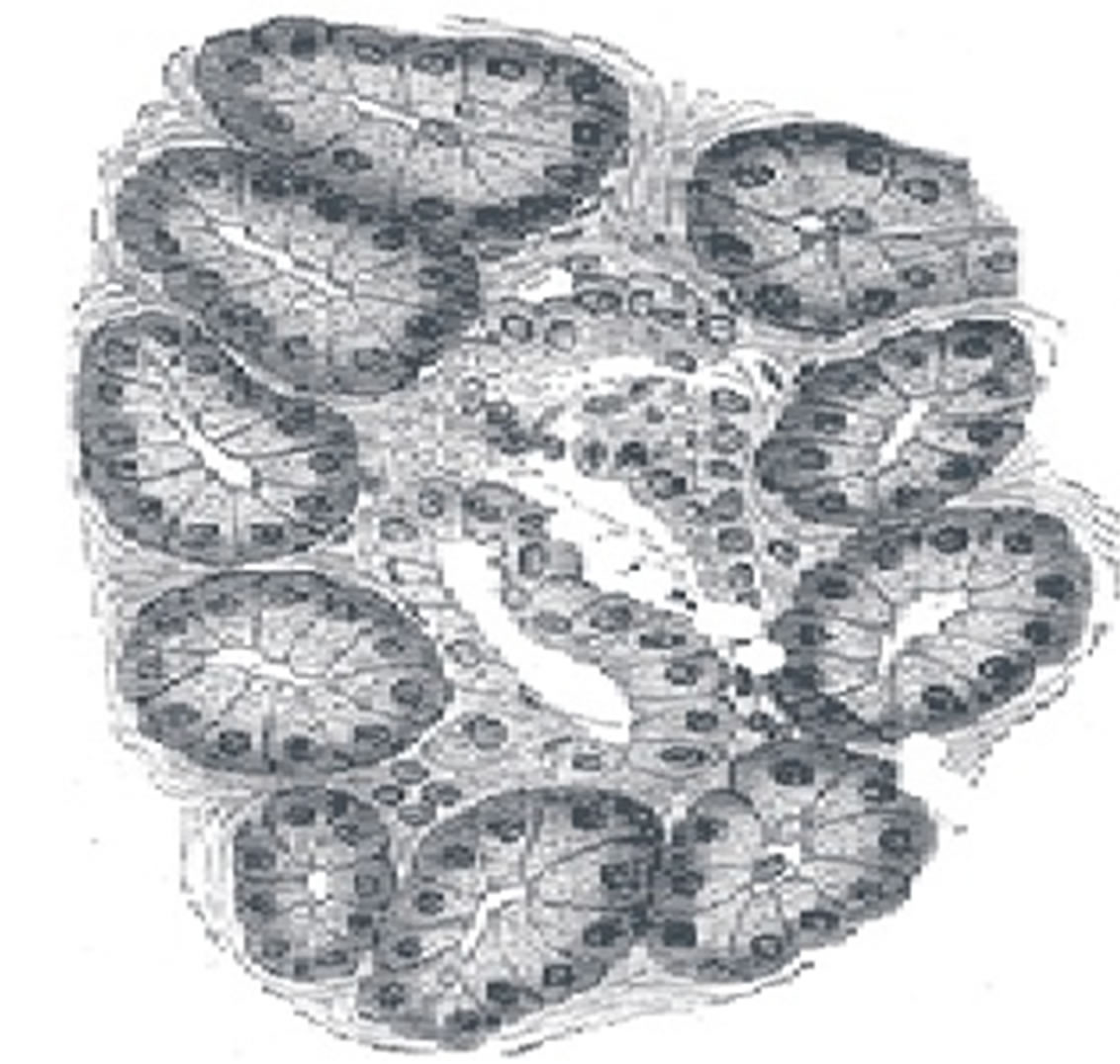
Figure 1. Islets of Langerhans.
leads to core cel death during islet transplantation as cure for Type I diabetes. They attempted to measure the diffusion barrier in intact human islets and deterimine its role in cessation of insulin secretion. They monitored impeded diffusion into iselts using fluorescent destran beads. They linked the poor diffusion properties with necrosis and not apoptosis. The Fick diffusion model was used in the analysis of [1-3]. Sharma [4,5] has shown that nonFick damped wave diffusion effects can become significant at short time scales. Bounded solutions from hyperbolic models can be obtained when final time condition and physically reasonable initial time rate of change conditions are used. In this study, damped wave diffusion effects during the diffusion of oxygen in islets of Langerhans is accounted for in detail.
The metabolic process becomes diffusion limited. Oxygen availability becomes limited in some regions of the tissue. The metabolic rate in the cells and demand for oxygen is greater than the oxygen that has diffused to that region. Growth of multicellular systems over 100 mm cease to happen. A condition called hypoxia has been observed in Brockman bodies in fish. During islet transplantation, lack of oxygen supply may restrict graft function especially when encapsulated tissue is used.
Oxygen partial pressure were measured in the islet organs of Osphronemus gorami (Brockmann bodies) placed in culture. A microelectrode was used to detect oxygen partial pressure in the surrounding region of the islet organ that is 800 mm in diameter and within the cells. This was achieved in a radial track. Within a distance of 100 mm for the case of no convection (Schrezenmeir et al. [6]),  is close to zero. A condition called necrosis is reached where the cells begin to die without sufficient oxygen supply. The experiments with convection showed increased
is close to zero. A condition called necrosis is reached where the cells begin to die without sufficient oxygen supply. The experiments with convection showed increased  at the surface and core regions of the islet. The experiments were conducted in a thermostatically controlled measuring chamber at 37˚C.
at the surface and core regions of the islet. The experiments were conducted in a thermostatically controlled measuring chamber at 37˚C.
Oxygen supply in addition to diffusion also comes about by the circulatory system and by hemoglobin molecule. Oxygen is carried in the blood by convection to capillaries by the circulatory system. Islets of Langerhans (Figure 1) are spheroidal aggregates of cells that are located in the pancreas. The metabolic requirement of the cells require oxygen to diffuse from the external envirnonment and through the oxygen-consuming islet tissue. The oxygen supply is a critical limiting factor for the functionality and feasibility of islets that are encapsulated, placed in devices for implantation, cultured, used in aneorobic conditions. Theoretical models are needed to describe the oxygen diffusion. The parameters of the model require knowledge of the consumption rate of oxygen, oxygen solubility, effective diffusion coefficient to oxygen in the tissue.
2. Theory
Avgoustiniatos et al. [1] developed a oxygen reaction and diffusion model. They assumed that the islet preparation is a suspension of tissue spheres that can be divided into m groups. Each sphere in group i has the same equivalent radius, Ri that varies from group to group. The tissue is assumed to be uniform with constant physical properties that is invariant in space. The governing equation for oxygen diffusion and reaction in spherical coordinates with azimuthal symmetry accounting for Fick’s diffusion can be written as:
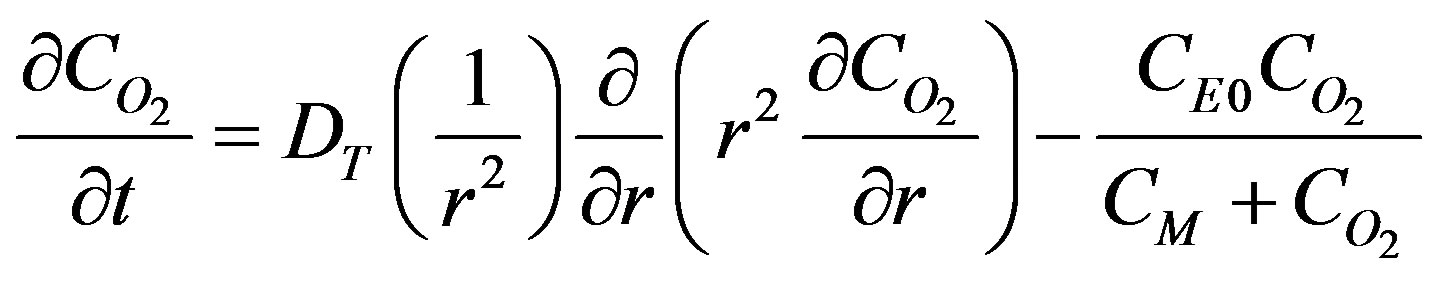 (1)
(1)
where DT is the diffusion coefficient in the tissue, CE0 is the total enzyme or complexation species concentration and CM is the Michaelis constant. The oxygen consumption rate is assumed to obey the Michaelis-Menten kinetics. Equation (1) describes the interplay of transient diffusion and metabolic consumption of oxygen in the tissue in spherical coordinates. The concentration of oxygen, 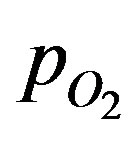 can be expressed in terms of its partial pressure,
can be expressed in terms of its partial pressure,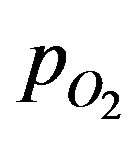 . This is obtained by using the Bunsen solubility coefficient, at such that:
. This is obtained by using the Bunsen solubility coefficient, at such that:
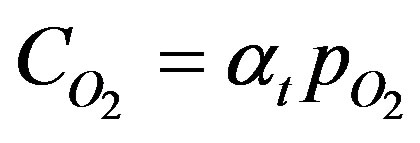 (2)
(2)
Substituting Equation (2) in Equation (1), Equation (1) becomes:
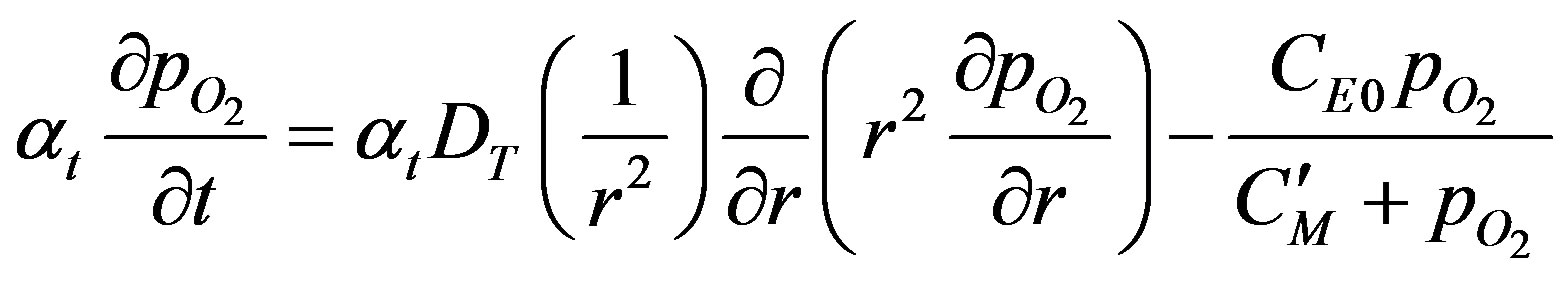 (3)
(3)
The product atDT can be seen to the product of solubility and diffusivity and hence is the permeability of oxygen in the tissue. The Michaelis constant CM, is also modified, C'M expressed in units of mm Hg. The initial condition can be written as:
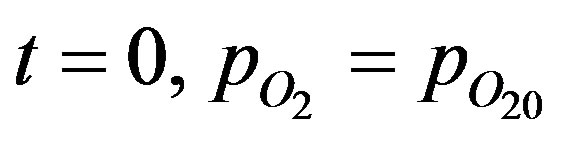 (4)
(4)
From symmetry at the center of the sphere:
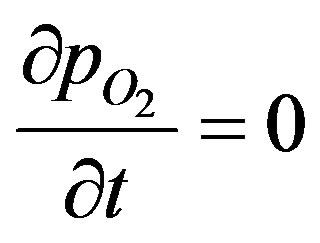 (5)
(5)
At the surface the oxygen diffusive transport from within the sphere must be equal to the oxygen transport by convection across the boundary layer surrounding each sphere:
 (6)
(6)
where the partial pressure of oxygen at the surface is given by  (Ri), the mass transfer coefficient between the surrounding space and the surface of the sphere is given by ki and the oxygen solubility in the surrounding space is given by am. Total rate of oxygen transfer N from the surrounding space to all of the spheres can be summed up as:
(Ri), the mass transfer coefficient between the surrounding space and the surface of the sphere is given by ki and the oxygen solubility in the surrounding space is given by am. Total rate of oxygen transfer N from the surrounding space to all of the spheres can be summed up as:
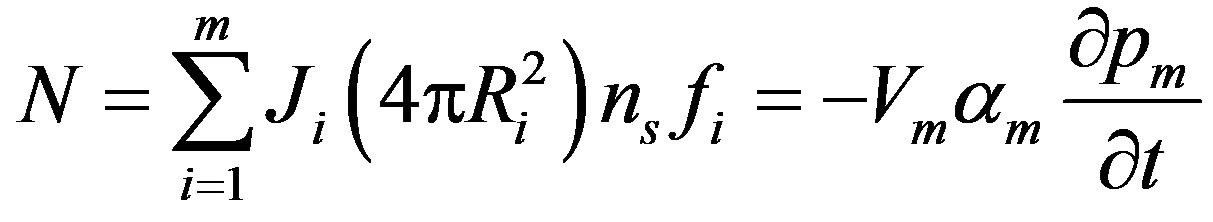 (7)
(7)
where the volume of the surrounding space is given by Vm, the total number of spheres is ns and the fraction of spheres in group i is given by fi. The initial condition for surrounding space is:
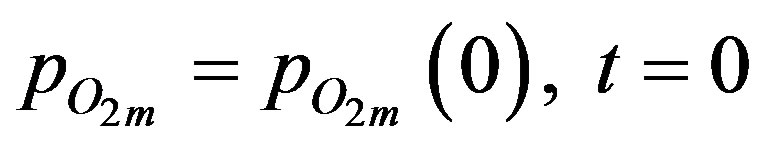 (8)
(8)
The mass transfer coefficient can be obtained from suitable Sherwood number correlations. For instance the mass transfer coefficient for spherical particles in an agitated tank in the islet size range of 100 - 300 mm can be written as:
 (9)
(9)
where e is the power input per unit fluid mass, f is the function that has to be obtained form experimental data.
Numerical methods are needed to obtain the solution to Equation (3). This is because of the nonlinearity of Michaelis-Meten kinetics.
2.1. Asymptotic Limits of Michaelis-Menten Kinetics
Closed formed analytical solutions to Equation (3) can be obtained in the asymptotic limits of:
1) high concentration of oxygen, the rate is independent of Po2 (zeroth order);
2) low concentration of oxygen, the rate is first order with respect to Po2.
The reasons for choosing the asymptotic limits is elucidated in Figure 2. It can be seen that at low reactant concentrations the rate is linear [7]. At high enzyme or complexing agent concentration the rate is invariant with respect to concentration. Hence a zeroth order can be assumed at high concentrations and first order at low reactant concentrations.
Thus, at high reactant concentrations Equation (3) becomes,
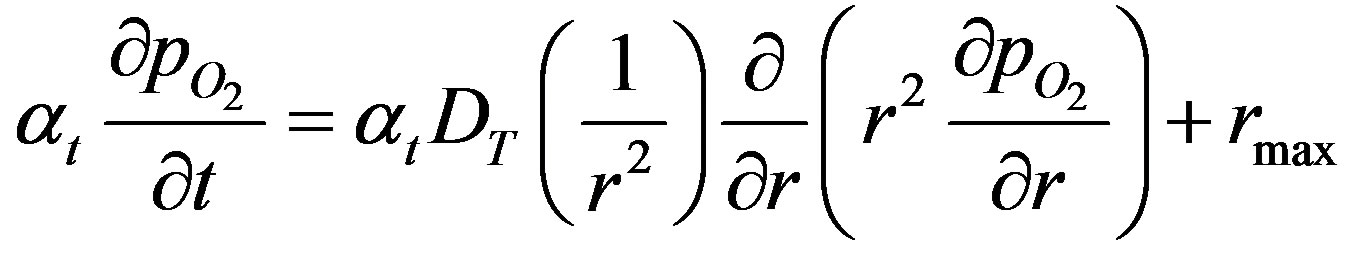 (10)
(10)

Figure 2. Rate-concentration curve obeying Michaelis-Menten kinetics.
Equation (10) can be non-dimensionalized as follows:
Let, 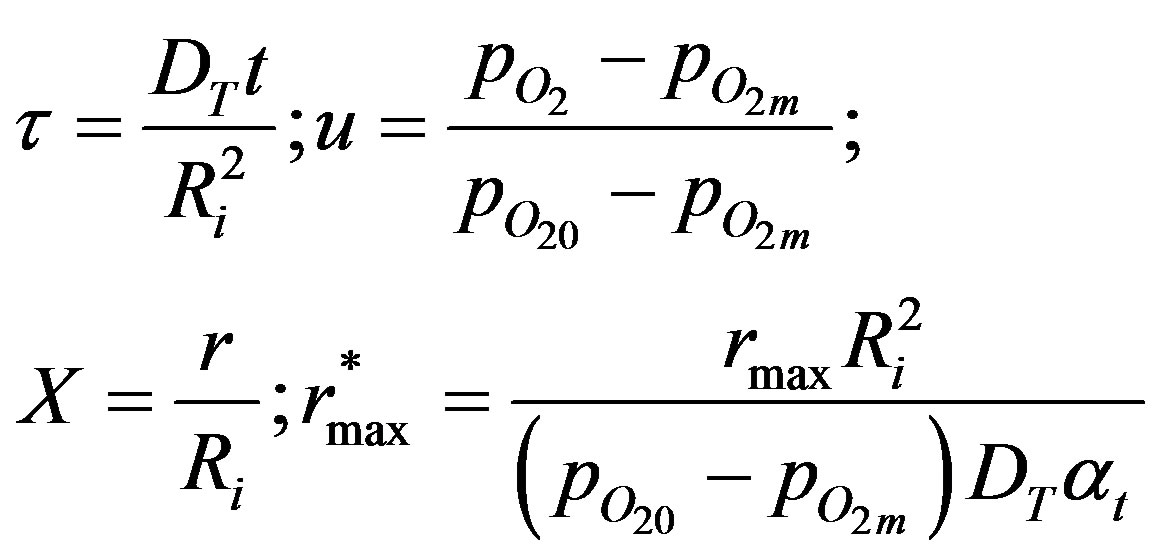 (11)
(11)
Equation (10) becomes:
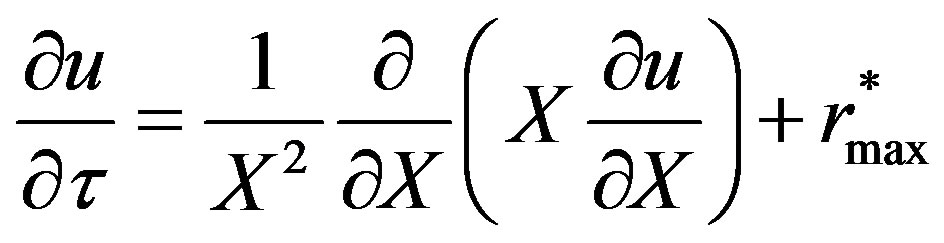 (12)
(12)
2.2. Parabolic Fick Diffusion and Reaction Model
The zeroth order reaction at high concentrations of oxygen is a heterogeneity in the partial differential equation. Systems such as this can be solved for by assuming that the solution consists of a steady state part and a transient part; Let
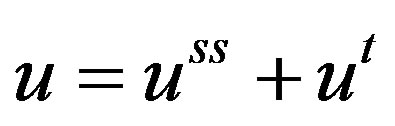 (13)
(13)
Substituting Equation (13) in Equation (12), Equation (12) becomes:
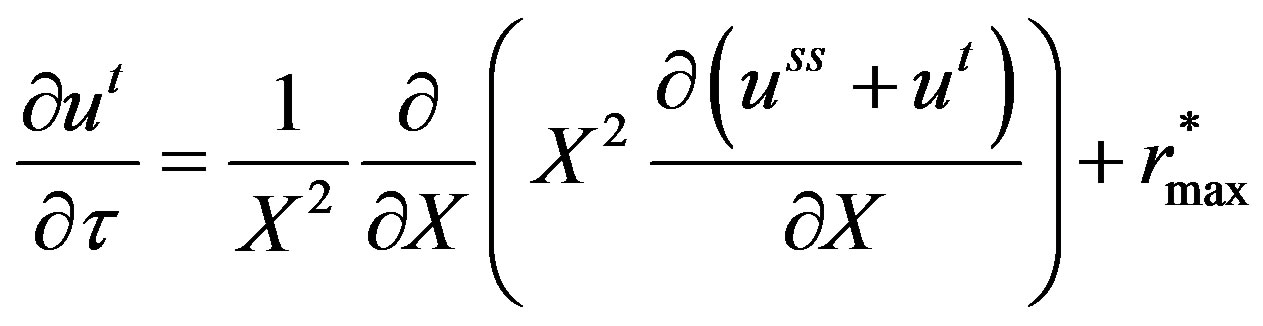 (14)
(14)
Equation (14) holds good when,
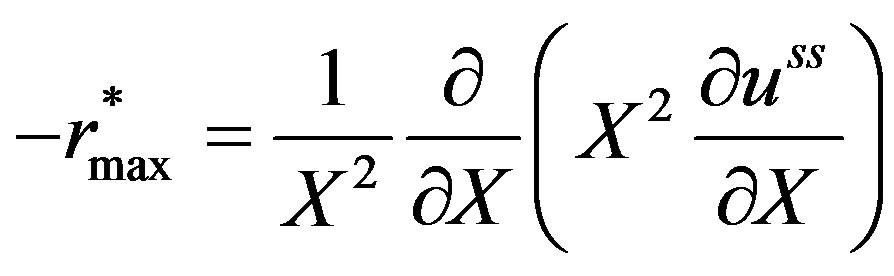 (15)
(15)
and
 (16)
(16)
Equation (16) can be integrated twice and the boundary condition given by Equation (5) applied to yield:
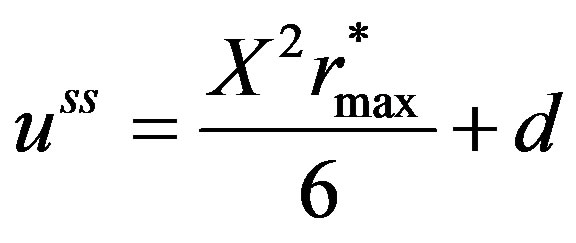 (17)
(17)
In order to obtain the solution of the integration constant d in Equation (17), the boundary condition given by Equations (5) and (6) needs to be modified. Assuming that after attainment of steady state, the surface concentration of the sphere would have reached the surrounding space concentration, d can be solved for the solution for the 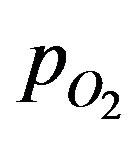 at steady state written as:
at steady state written as:
 (18)
(18)
The solution to Equation (16) may be obtained by separation of variables as follows:
Let ut = V(t)g(X). Then Equation (16) becomes:
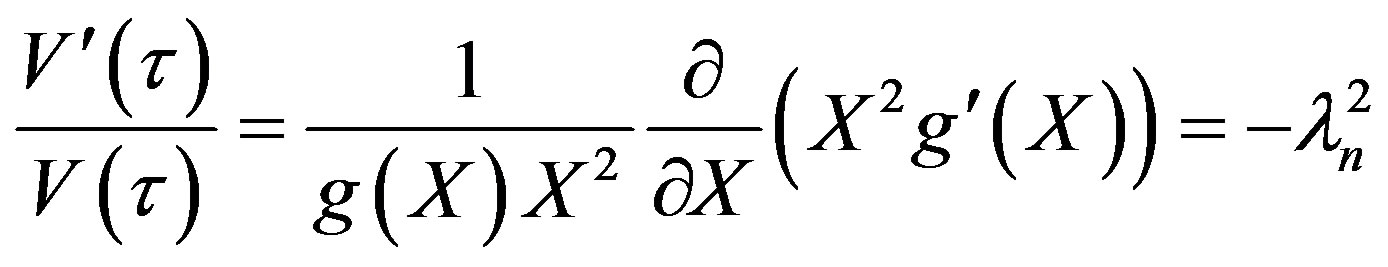 (19)
(19)
Hence, (20)
(20)
 (21)
(21)
Comparing Equation (21) with the generalized Bessel function [8]:
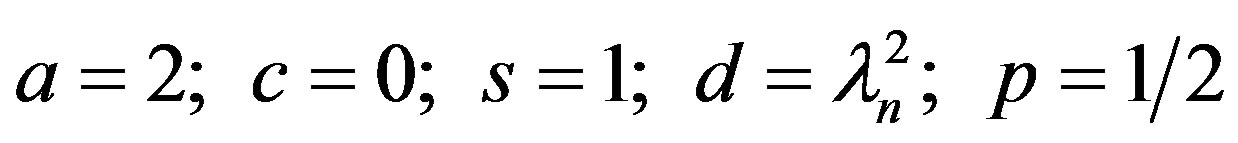
The solution to Equation (21) can be seen to be:
 (22)
(22)
From the boundary condition given by Equations (5) and (6), it can be seen that d1 can be set to 0 and,
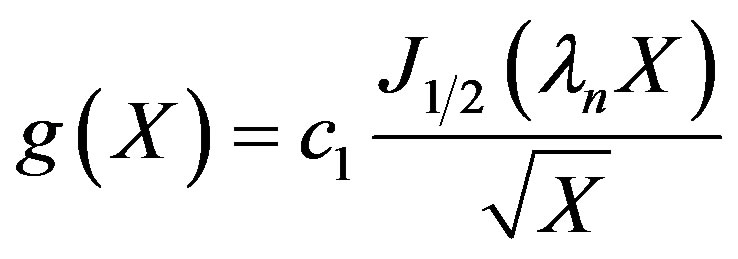 (23)
(23)
The eigenvalues ln can be solved for from the boundary condition given by Equation (6).
In the dimensionless form Equation (6) may be written as:
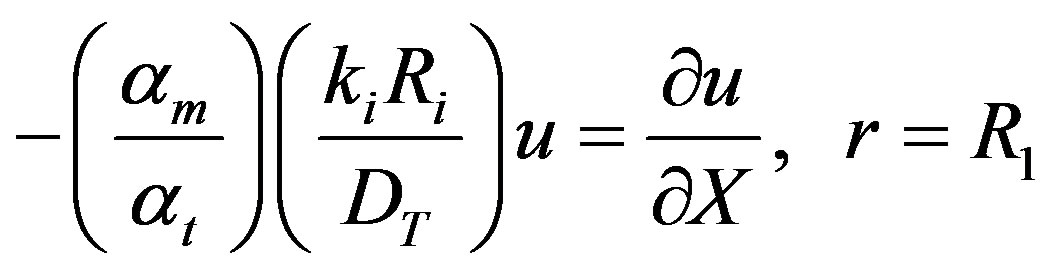 (24)
(24)
where

the Biot number (mass). This represents the ratio of mass transfer from the surrounding space and the diffusion within the sphere. To simplify matters from a mathematical standpoint, Equation (22) can be written in terms of elementary trigonomentric functions as;
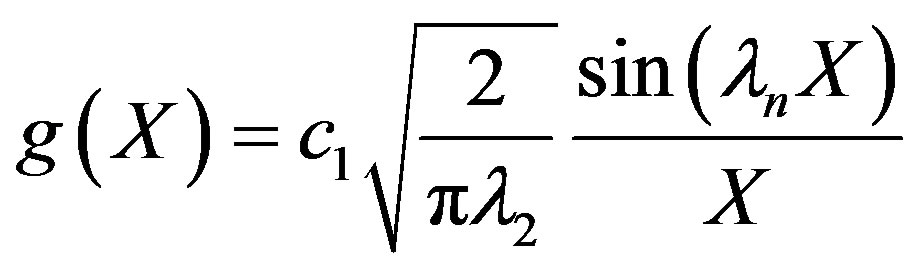 (25)
(25)
The Eigenvalues can be obtained from the solution of the following trancedental equation:
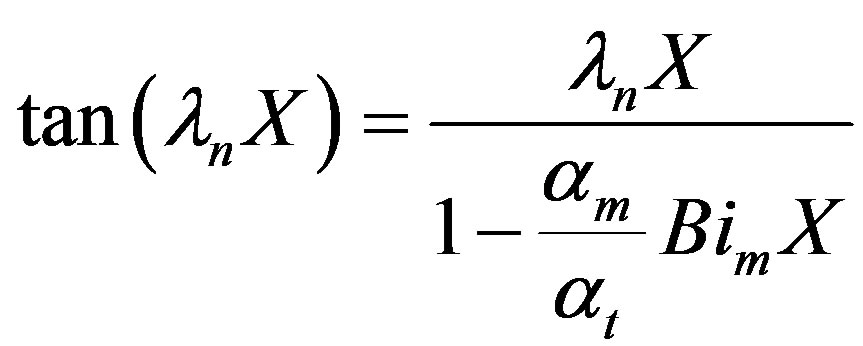 (26)
(26)
The general solution for the dimensionless 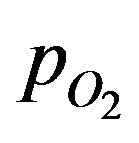 can be written as:
can be written as:
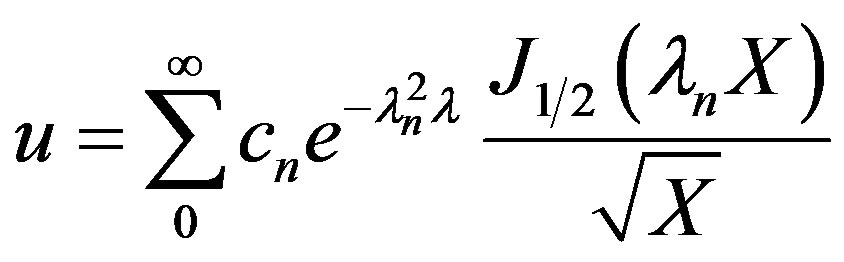 (27)
(27)
The Eigen values are given by Equation (26). The cn can be solved for from the initial condition given by Equation (4) using the principle of orthogonality and
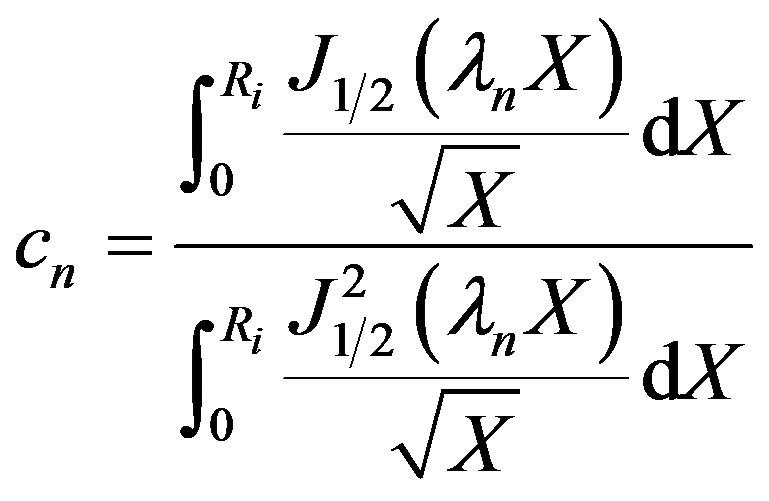 (28)
(28)
Thus the oxygen concentration profile at high oxygen concentration is obtained. At low concentration of oxygen the rate of consumption of oxygen is first order. The governing equation, Equation (3) can be written as
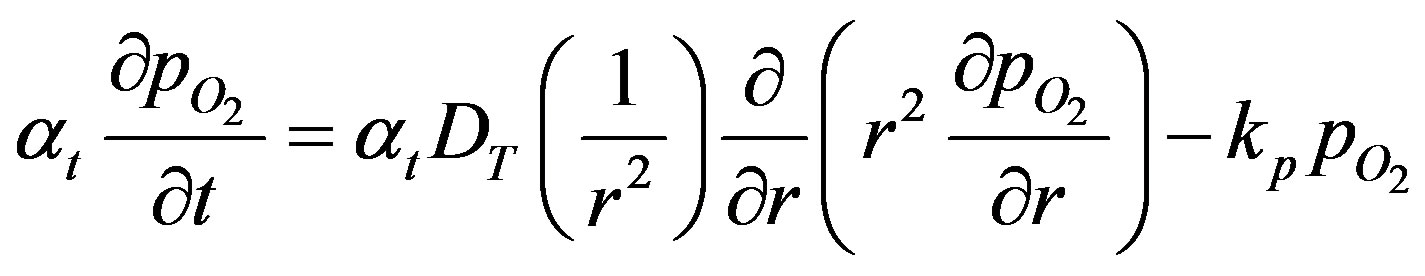 (29)
(29)
Obtaining the dimensionless form of Equation (29)
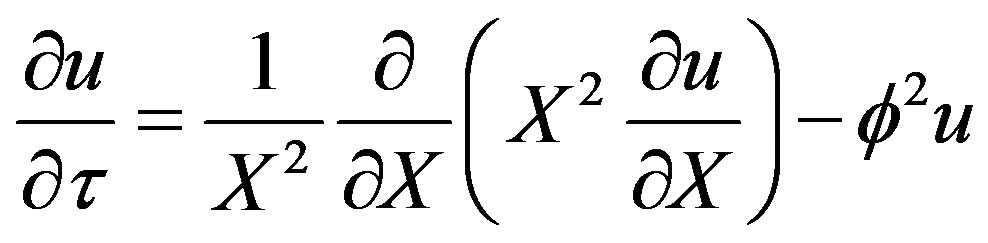 (30)
(30)
where,
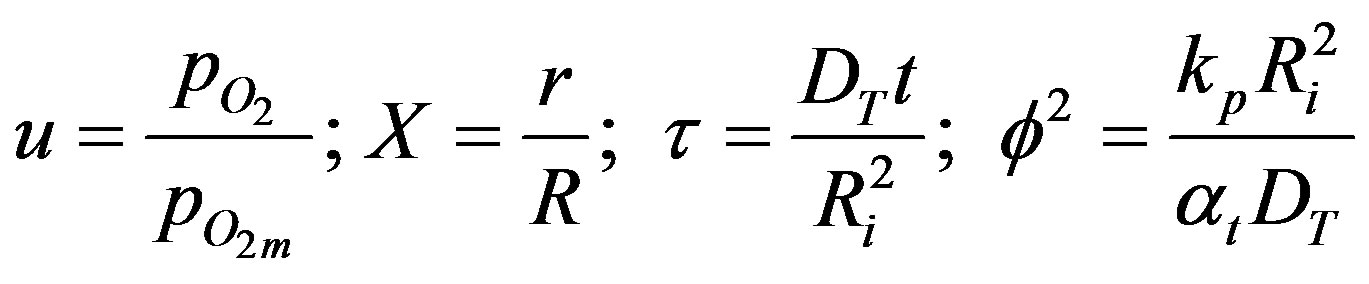 (31)
(31)
It can be recognized that f is the thiele modulus. Equation (30) can be solved for by the method of separation of variables. Let u = V(t)g(X).
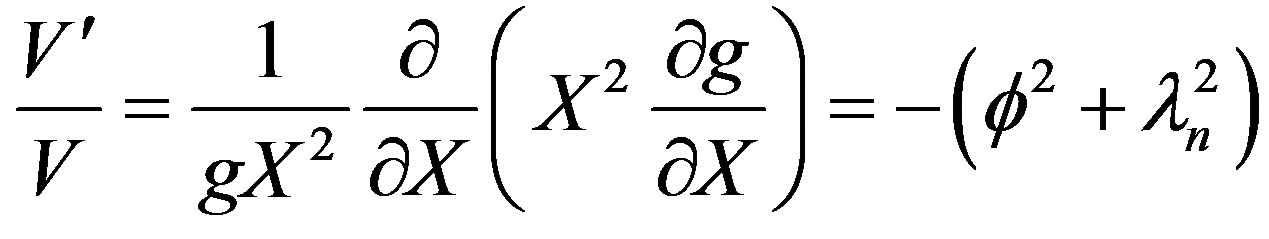 (32)
(32)
The solution in time domain can be seen to be;
 (33)
(33)
The solution in space domain can be seen to be
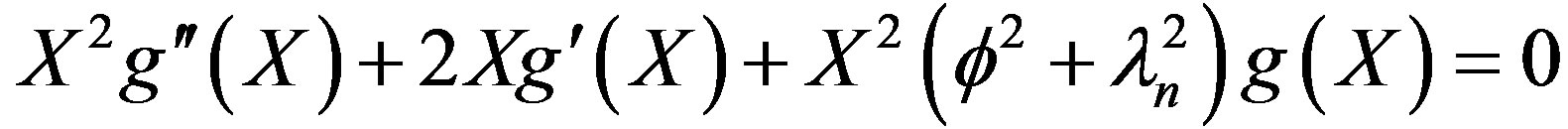 (34)
(34)
Comparing Equation (34) with the generalized Bessel function [8].

The solution to Equation (34) can be seen to be
 (35)
(35)
From the boundary condition given by Equation (5), it can be seen that d1 can be set to 0 and,
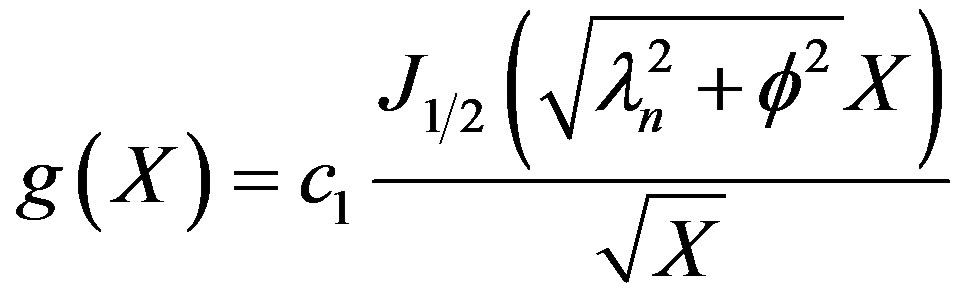 (36)
(36)
The Eigenvalues ln can be solved for from the boundary condition given by Equation (6).
In the dimensionless form Equation (6) may be written as
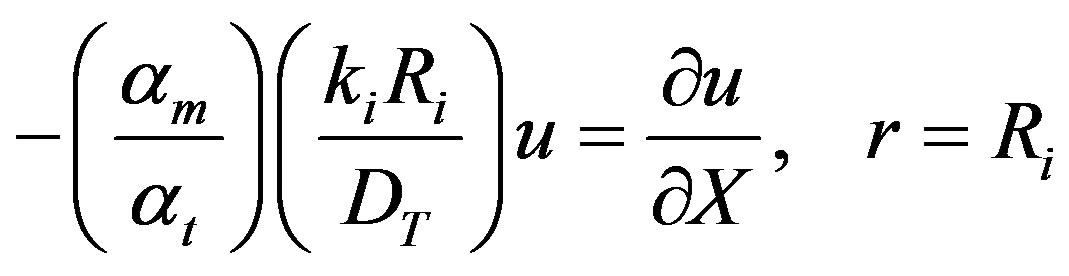 (37)
(37)
where
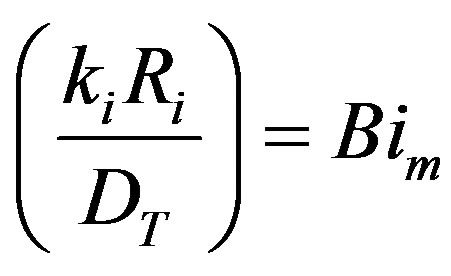
the Biot number (mass). This represents the ratio of mass transfer from the surrounding space of the diffusion within the sphere. To simplify matters from a mathematical standpoint, Equation (35) can be written in terms of elementary trigonomentric functions as:
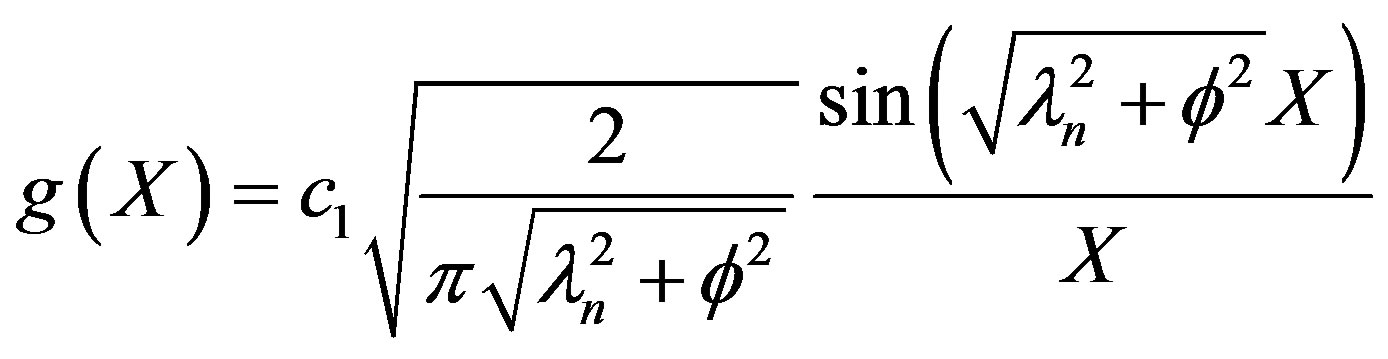 (38)
(38)
The eigenvalues can be obtained from the solution of the following trancedental equation.
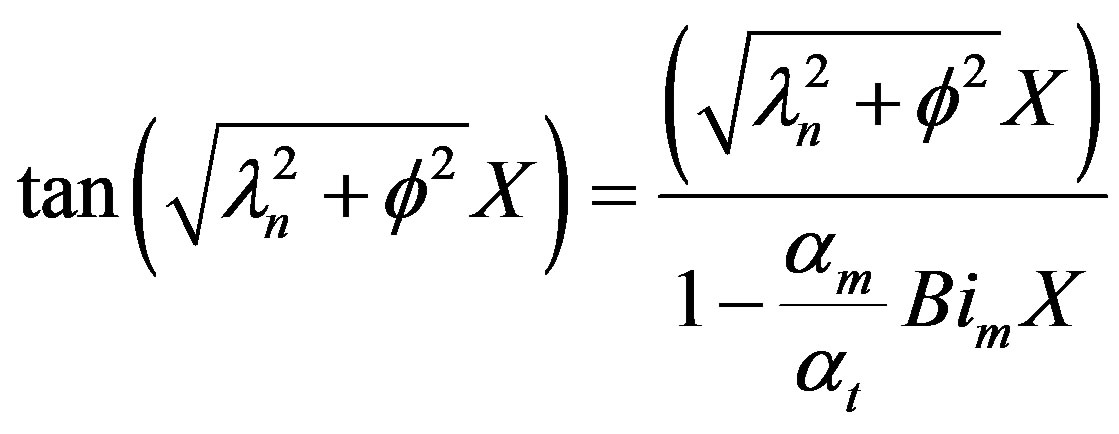 (39)
(39)
The general solution for the dimensionless Po2 can be written as
 (40)
(40)
The Eigen values are given by Equation (39). The cn can be solved for from the initial condition given by Equation (4) using the principle of orthogonality and
 (41)
(41)
Thus the oxygen concentration profile at low oxygen concentration is obtained.
2.3. Damped Wave Diffusion and Reaction Hyperbolic Model
The times associated with oxygen consumption are low. Oxidation reactions are fast. Recent experimental reports of relaxation times in biological materials by Mitra et al. [9] are in ther order of 16 seconds. Hence in times associated with the oxygen consumption (~10−3 - 1 s) the finite speed of diffusion effects cannot be ignored. The damped wave diffusion and relaxation effects may be included in the following manner.
At low oxygen concentration a first order rate of reaction can be assumed. A semi-infinite medium of tissue is considered. A step change in concentration is given at the surface. At times zero the concentration of oxygen is at a initial value. At infinite distances the concentration of oxygen would be unchanged at the initial value. The mass balance equation for oxygen can be written as;
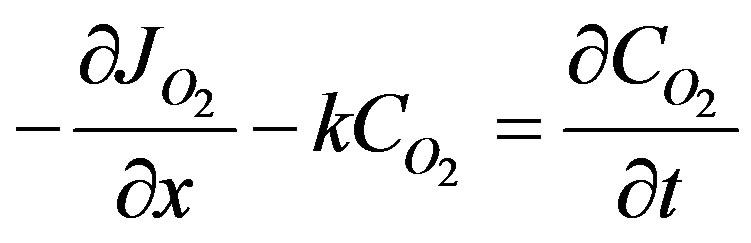 (42)
(42)
where k is the lumped first order reaction rate constant. Combining Equation (42) with the damped wave diffusion and relaxation equation given below in Equation (43):
 (43)
(43)
the governing equation is obtained.tmr is the mass relaxation time. When it is zero Equation (44) reverts to the Fick’s law of diffusion. When the rate of mass flux is greater than an exponential rise the wave regime would be more dominant mechanism of transport compared with the Fick regime. Equation (43) is differentiated by x and Equation (42) is differentiated by t and the cross term 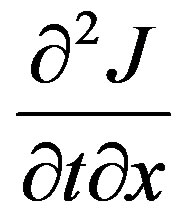 eliminated between the two equations and the governing equation obtained as follows:
eliminated between the two equations and the governing equation obtained as follows:
 (44)
(44)
The governing equation for oxygen concentration in the tissue is obtained in the dimensionless form by the following substitutions.
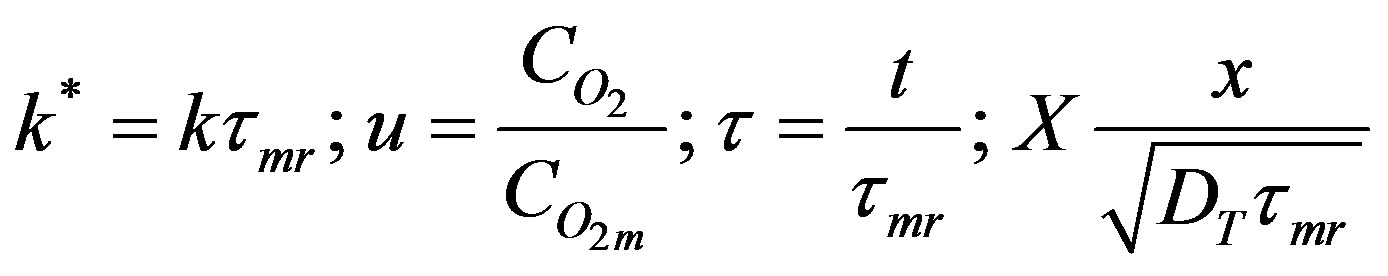 (45)
(45)
The governing equation is a partial differential equation of the hyperbolic type. It is second order with respect to time and second order with respect to space.
 (46)
(46)
The Equation (46) can be solved by a recently developed method given in Sharma [2] called relativistic transformation of coordinates. The expression for the transient temperature during damped wave conduction and relaxation developed by Baumeister and Hamill [10] by the method of Laplace transforms was further integrated in Sharma [11]. Chebysheve polynomial approximation was used for the integrand. The integrand was a modified Bessel composite function of the first order in space and time. Telescoping power series was used in order to develop a more useful expression for the model solution. By another method named relativistic transformation the transient temperature during damped wave conduction and relaxation was derived. The solution exhibited a convev concave pattern. This is different from the parabolic solutions that are concave in nature. The convex to concave transition is an interesting phenomena. This can be the point where damped wave conduction and relaxation reverts to Fourier conduction. Four regimes can be identified in the solution of hyperbolic damped wave diffusion model. These are: 1) Zero Transfer Inertial Regime, 0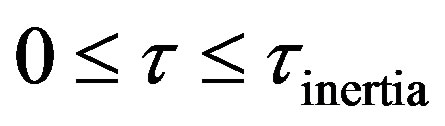 ; 2) Rising Regime during times greater than inertial regime and less than at the wave front, Xp > t; 3) At Wave front , t = Xp; 4) Falling Regime in open Interval, of times greater than at the wave front, t > Xp. The solution for the transient temperature from the method of retavistic transformation was compared side by side with the solution for transient temperature from Chebyshev economization. Both solutions were withing 12% of each other. For conditions close to the wave front the method of Chebyshev economization is expected to be closer to the exact solution. The solutions from methods of Chebyshev economization and relativistic transformation was found to be within 2% of each other. Far from the wave front the numerical error in the method of Chebyshev economization is expected to become significant. This was illustrated using an example. For t > 0.5 the solutions for transient surface heat flux from both parabolic and hyperbolic models were found to be within 10% of each other. A “blow-up” is found in the parabolic model as t ® 0. The hyperbolic model solution is devoid of any singularities. At large times the model solution from the method of Chebysveb economization was found to be withing 25% of the error function solution of the parabolic model. A penetration distance beyond which there is no effect of the step change at the boundary is derived using method of relativistic transformation.
; 2) Rising Regime during times greater than inertial regime and less than at the wave front, Xp > t; 3) At Wave front , t = Xp; 4) Falling Regime in open Interval, of times greater than at the wave front, t > Xp. The solution for the transient temperature from the method of retavistic transformation was compared side by side with the solution for transient temperature from Chebyshev economization. Both solutions were withing 12% of each other. For conditions close to the wave front the method of Chebyshev economization is expected to be closer to the exact solution. The solutions from methods of Chebyshev economization and relativistic transformation was found to be within 2% of each other. Far from the wave front the numerical error in the method of Chebyshev economization is expected to become significant. This was illustrated using an example. For t > 0.5 the solutions for transient surface heat flux from both parabolic and hyperbolic models were found to be within 10% of each other. A “blow-up” is found in the parabolic model as t ® 0. The hyperbolic model solution is devoid of any singularities. At large times the model solution from the method of Chebysveb economization was found to be withing 25% of the error function solution of the parabolic model. A penetration distance beyond which there is no effect of the step change at the boundary is derived using method of relativistic transformation.
The method of relativistic transformation of coordinated has been shown [11] to bounded solutions close to the integrated expression of exact solution presented by other investigators. This method of analysis is used in this study, The damping term is first removed by Equation (46) by ent. Choosing
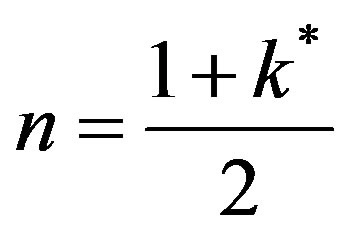 and let
and let  Equation (46) becomes:
Equation (46) becomes:
 (47)
(47)
The significance of W is it that this can be recognized as the wave concentration. During the transformation of Equation (46) to Equation (47) the damping term has vanished. Now let us define a spatio-temporal symmetric substitution (relativistic transformation),
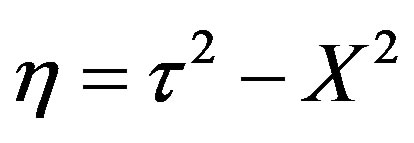 for
for  (48)
(48)
Equation (47) becomes:
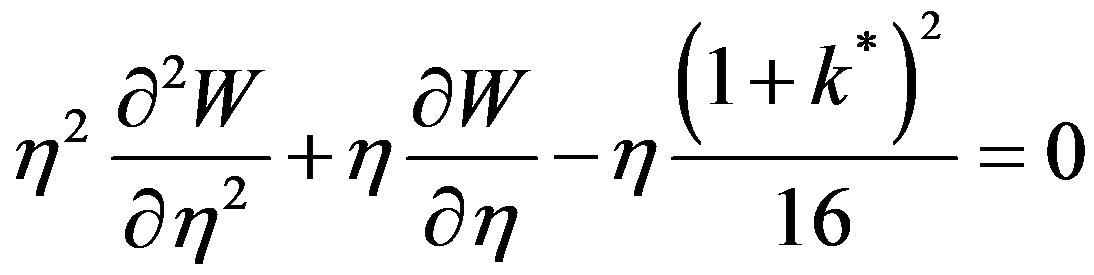 (49)
(49)
Comparing Equation (49) with the generalized Bessel equation [8]
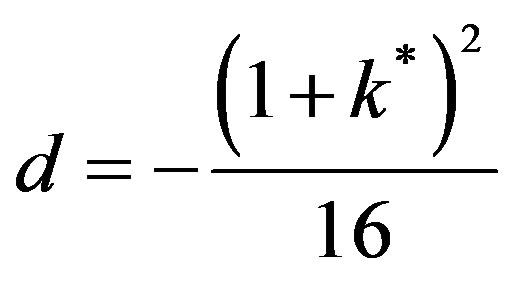

The order p = 0,
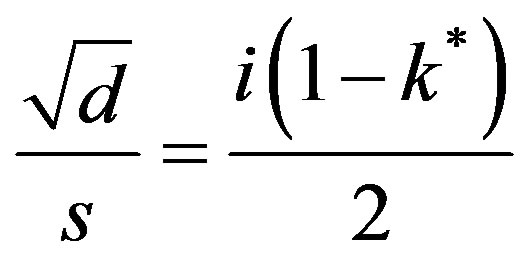
and is imaginary. Hence the solution is:
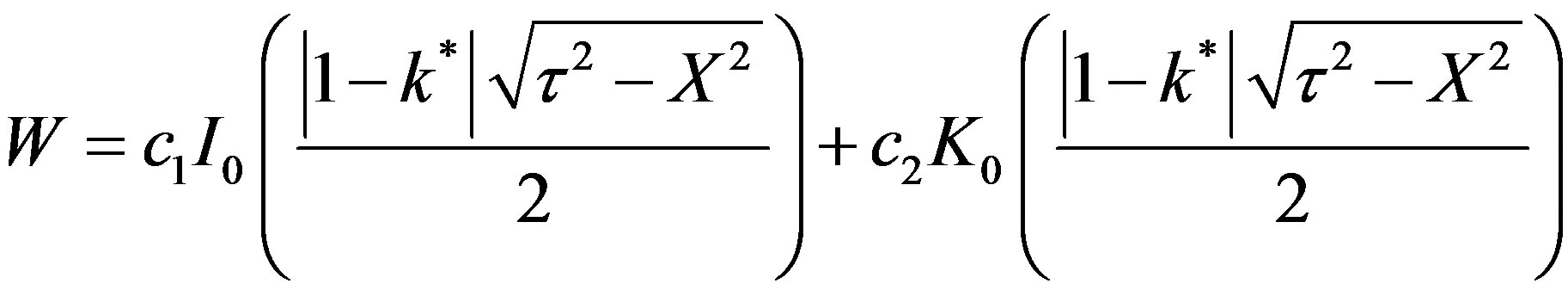 (50)
(50)
c2 can be seen to be zero from the condition that at h = 0, W is finite.
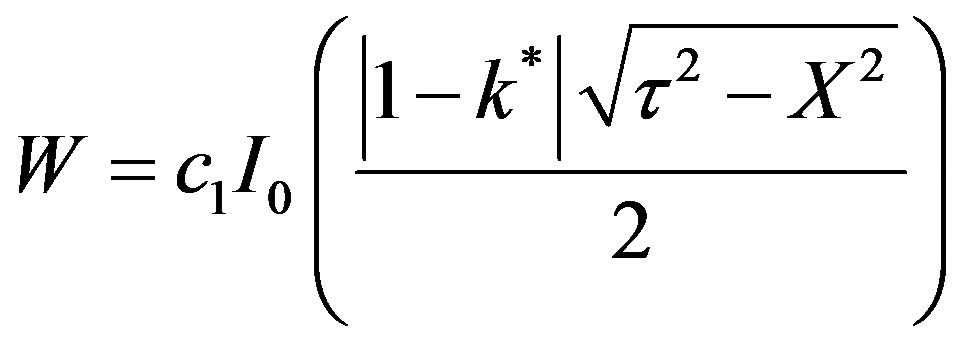 (51)
(51)
From the boundary condition at X = 0,
 (52)
(52)
c1 can be eliminated between Equations (51) and (52) in order to yield:
 (53)
(53)
This is valid for for t > X, k* ¹ 1. For X > t,
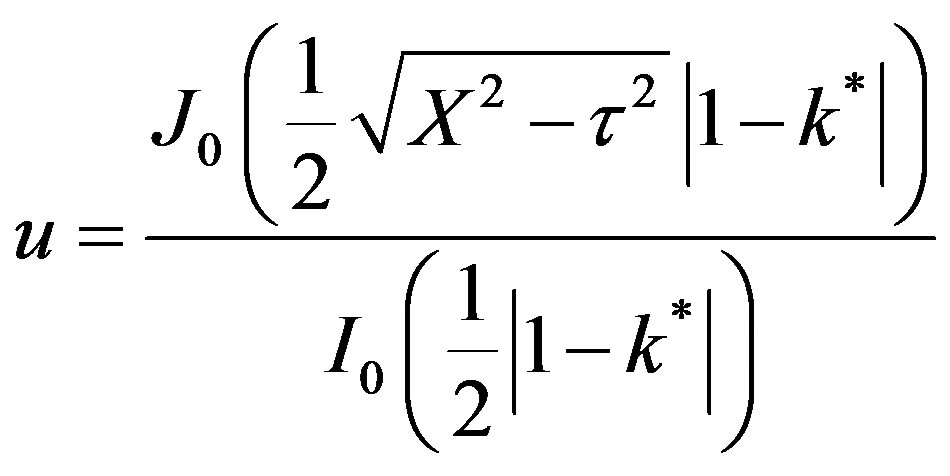 (54)
(54)
At the wavefront , t = X,
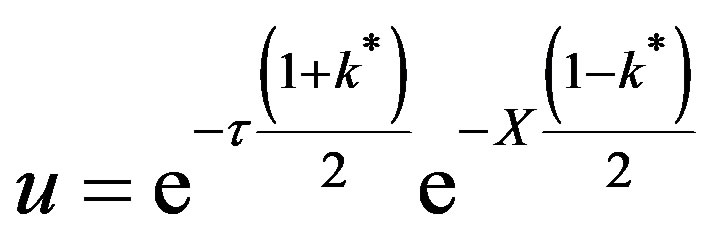 (55)
(55)
3. Results
The mass inertia can be calculated from the first zero of the Bessel function at 2.4048. Thus,
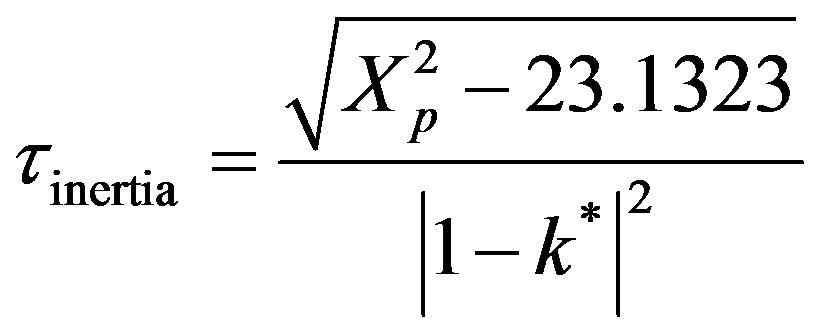 (56)
(56)
A de no vo dimensionless group called Sharma Number (Mass) was introduced [12]. This can be written as follows:
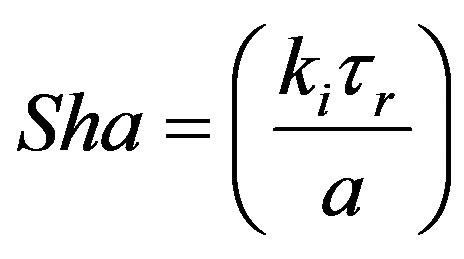 (57)
(57)
It is the ratio of mass transfer rate to the transport taking place by damped wave diffusion. This can be seen to a product of Maxwell number and Sherwood number.
 (58)
(58)
Maxwell number (mass) as given by Equation (58) can be seen to be the Fick number with the relaxation time substituted for time, t. This gives the ratio of the square of the speed of mass 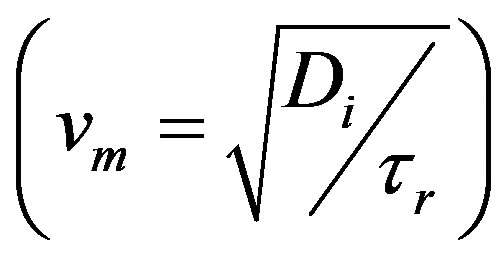 by damped wave diffusion divided by the square of a characteristic speed (a/tr).
by damped wave diffusion divided by the square of a characteristic speed (a/tr).
The Sherwoord number, Sh can be written as:
 (59)
(59)
The product of Maxwell number (mass) and Sherwood number can be seen to yield the Sharma number (mass) as follows:
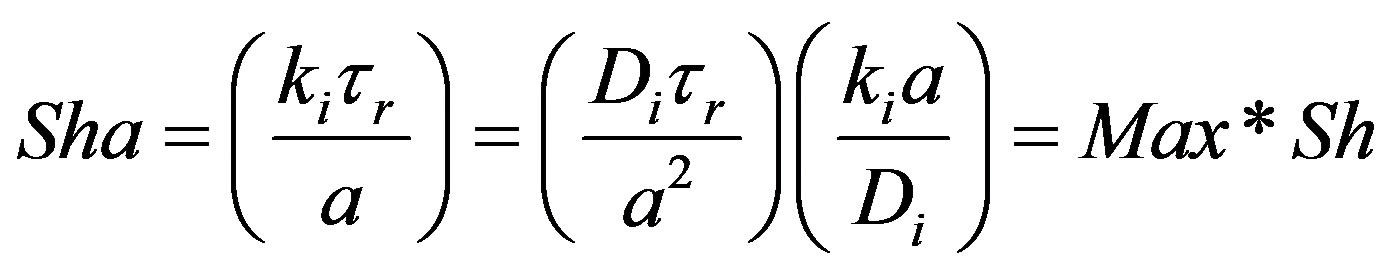 (60)
(60)
Sharma number (mass) may be used in evaluating the importance of the damped wave diffusion process in relation to other processes such as convection, Fick steady diffusion in the given application.
The concentration at a interior point in the semi-infinite medium is shown in Figure 3. Four regimes can be identified. These are:
• Zero Transfer Inertial Regime, 0 ;
;
• Times greater than inertial regime and less than at the wave front, Xp > t;
• Wave front , t = Xp;
• Open Interval, of times Greater than at the wave front, t > Xp.
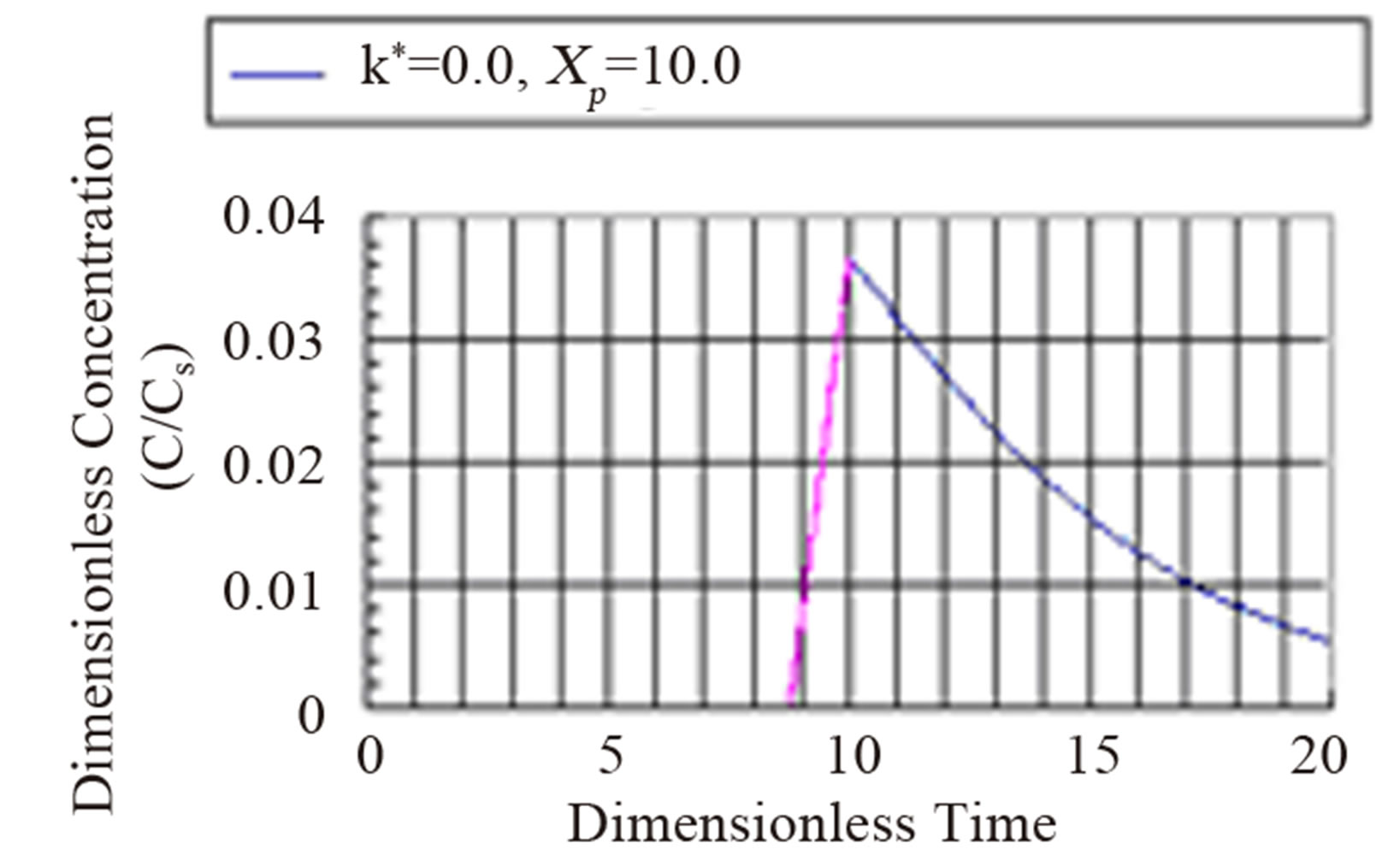
Figure 3. Dimensionless concentration at a interior point Xp = 10 in a semi-infinite medium during simultaneous reaction and diffusion. k* = 0.5.
During the first regime of mass inertia there is no transfer of mass upto a certain threshold time at the interior point Xp = 10. The second regime is given by Equation (53) represented by a Bessel composite function of the first kind and zeroth order. The rise in dimensionless concentration proceeds from the dimensionless time 2.733 upto the wave front at Xp = 10.0. The third regime is at the wave front. The dimensionless concentration is described by Equation (54).
The fourth regime is described by Equation (53) and represents the decay in time of the dimensionless concentration. It is given by the modified Bessel composite function of the first kind and zeroth order. In Figure 4 is shown the three regimes of the concentration when k* = 2.0. It can be seen from Figure 4 that the mass inertia time has increased to 8.767. The rise is nearly a jump in concentratin at the interior point Xp = 10.0. When k* = 0.25 as shown in Figure 5 the inertia time is 7.673. In Figure 6, the three regimes for the case when k* = 0.0 is plotted. In Table 1 the mass inertia time for various values of k* for the interior point Xp = 10.0 is shown. k* needs to be sufficiently far from 1 to keep the inertia time positive.
The steady state solution for Equation (46) can be written as:
 (61)
(61)
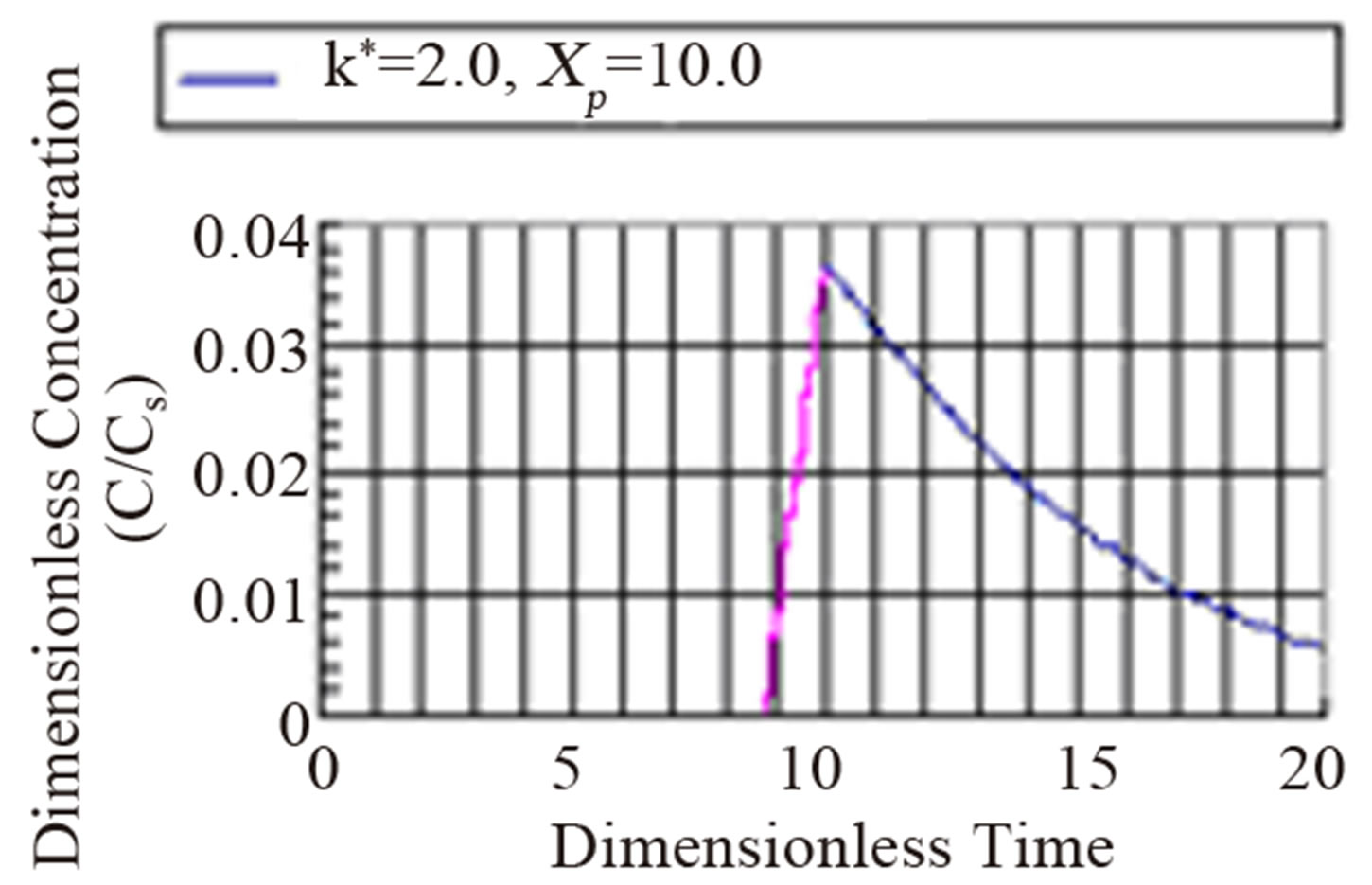
Figure 4. Dimensionless concentration at a interior point Xp = 10 in a semi-infinite medium during simultaneous reaction and diffusion for k* = 2.0.
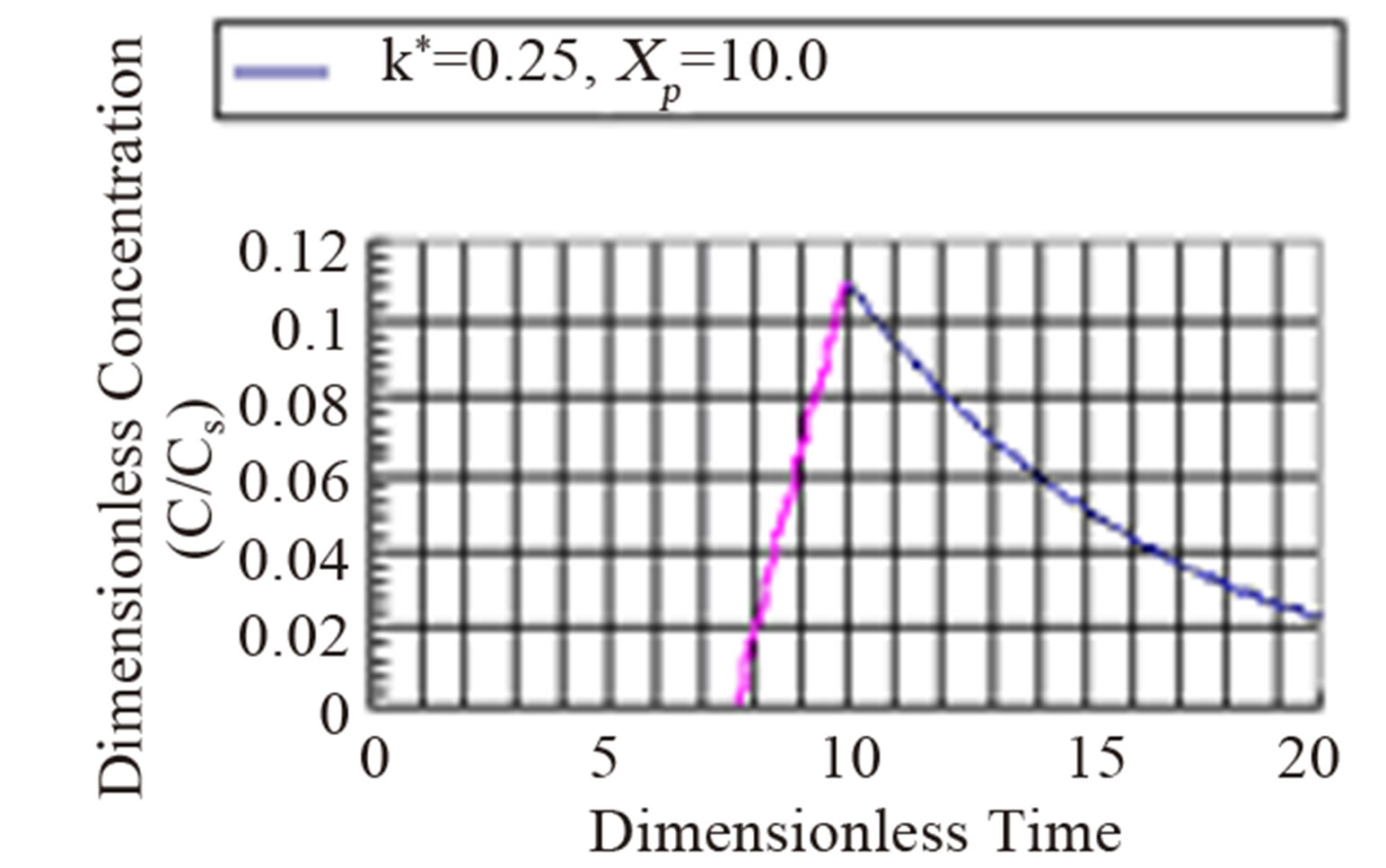
Figure 5. Dimensionless concentration at a interior point Xp = 10 in a semi-infinite medium during simultaneous reaction and diffusion. k* = 0.25

Figure 6. Dimensionless concentration at a interior point Xp = 10 in a semi-infinite medium during simultaneous reaction and diffusion. k* = 0.0.
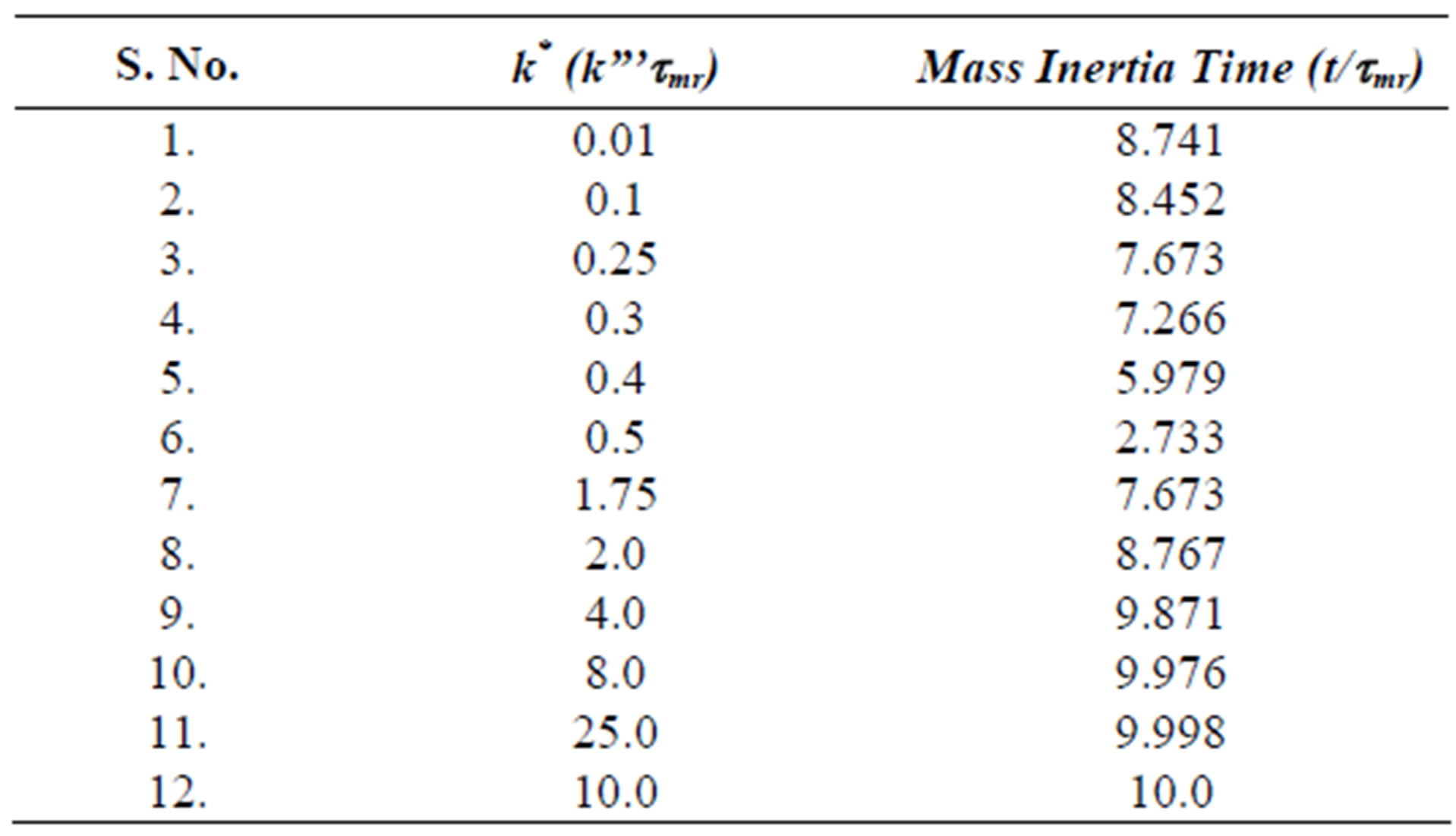
Table 1. Mass inertia time vs k* for Interior Point Xp = 10.0.
1) 4. Conclusions
2) Diffusion and Reaction in Islets of Langerhans was studied using Parabolic and Hyperbolic Models. This is needed to better treat Type I diabetes by the transplantation method.
3) Sharma number can be used to evaluate when the wave term becomes important in the application. It represents the ratio of Mass Transfer in Bulk to Relaxational Transfer.
4) Sharma number (mass) may be used in evaluating the importance of the damped wave diffusion process in relation to other processes such as convection, Fick steady diffusion in the given application.
5) Four regimes can be identified in the solution of hyperbolic damped wave diffusion model. These are; i) Zero Transfer Inertial Regime, 0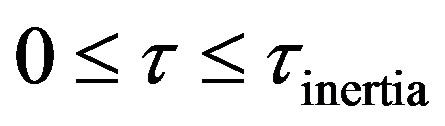 ; ii) Rising Regime during times greater than inertial regime and less than at the wave front, Xp > t; iii) at Wave front , t = Xp; iv) Falling Regime in Open Interval, of times greater than at the wave front, t > Xp.
; ii) Rising Regime during times greater than inertial regime and less than at the wave front, Xp > t; iii) at Wave front , t = Xp; iv) Falling Regime in Open Interval, of times greater than at the wave front, t > Xp.
6) Method of superposition of steady state concentration and transient concentration used in both solutions of parabolic and hyperbolic models.
7) Expression for steady state concentration developed.
8) Closed form analytic model solutions developed in asymptotic limits of Michaelis and Menten kinetic at zeroth order and first order.
9) Expression for Penetration Length Derived-Hypoxia Explained.
10)Expression for Inertial Lag Time Derived.
11)Solution within bounds of Second Law of Thermodynamics.
12)No Overshoot Phenomena observed.
5. Acknowledgements
Acknowledements are extended to K. N. Somasekaran, Dean, School of Chemical and Biotechnology, SASTRA University, Thanjavur, India for assigning me to instruct Biofluid Dynamics from Spring 2004 - Spring 2007. Special mention to Elsevier, Amsterdam, Netherlands and McGraw Hill Professional, New York, NY as I brought to book form the diffusion issues during gas transport in tissue. Thanks to the funds provided by Prairie View A & M University, Roy G. Perry College of Engineering, Prairie View, TX for travel to Salt Lake City, UT, November 2010 and San Francisco, CA, March 2010 and conference paper presentation on related material. Vote of thanks for the inspiration from a circle developed at work and home who had sugar problem.
REFERENCES
- E. S. Avgoustiniatos, K. E. Dionne, D. F. Wilson, M. L. Yarmush and C. K. Colton, “Measurements of the Effective Diffusion Coefficient of Oxygen in Pancreatic Islets,” Industrial & Engineering Chemistry Research, Vol. 46, No. 19, 2007, pp. 6157-6163.
- A. S. Johnson, E. O. ’Sullivan, L. N. D’Aoust, A. Omer, S. Bonner-Weir, R. J. Fisher, G. C. Weir and C. K. Col- ton, “Quantitative Assessment of Islets of Langerhans Encapsulated in Alginate,” Tissue Engineering Part C: Methods, Vol. 17, No. 4, 2011, pp. 435-449.
- S. J. Williams, T. Schwasinger-Schmidt, D. Zamierowsk and L. Stehno-Bittel, “Diffusion into Human Islets in Limited to Molecules below 10 kDa,” Tissue and Cell, Vol. 44, No. 5, 2012, pp. 332-341. doi:10.1016/j.tice.2012.05.001
- K. R. Sharma, “Damped Wave Transport and Relaxation,” Elsevier, Amsterdam, 2005.
- K. R. Sharma, “Transport Phenomena in Biomedical Engineering: Artificial Organ Design and Development and Tissue Design,” McGraw Hill Professional, New York, 2010.
- J. Schrezenmeir, J. Kirchgessner, L. Gero, L. A. Kuz, J. Beyer and W. Mueller-Klieser, “Effect of Microencapsulation on Oxygen Distribution in Isets Organs,” Transplantation, Vol. 57, No. 9, 1994, pp. 1308-1314.
- O. Levenspiel, “Chemical Reaction Engineering,” Third Edition, John Wiley and Sons, New York, 1999.
- A. Varma and M. Morbidelli, “Mathematical Methods in Chemical Engineering,” Oxford University Press, Oxford, 1997.
- K. Mitra, S. Kumar, A. Vedavarz and M. K. Moallemi, “Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat,” ASME Journal of Heat Transfer, Vol. 117, No. 3, 1995, pp. 568-573.
- K. J. Baumeister and T. D. Hamill, “Hyperbolic Heat Conduction Equation: A Solution for the Semi-Infinite Body Problem,” ASME Journal of Heat Transfer, Vol. 93, No. 1, 1971, pp. 126-128.
- K. R. Sharma, “Comparison from Parabolic and Hyperbolic Models for Transient Heat Conduction in Semi-Infinite Medium”, International Journal of Thermophysics, Vol. 20, No. 5, 2009, pp. 1671-1687.
- K. R. Sharma, “On Damped Wave Diffusion of Oxygen in Islets of Langerhans: Part I. Comparison of Parabolic and Hyperbolic Models in a Finite Slab,” 102nd AIChE Annual Meeting, Salt Lake City, November 2010.

