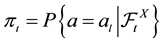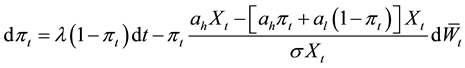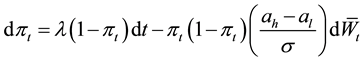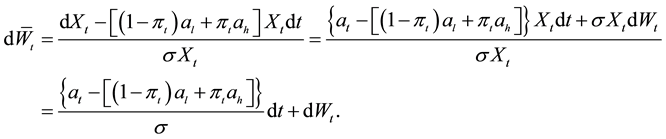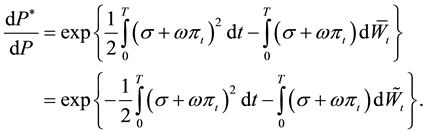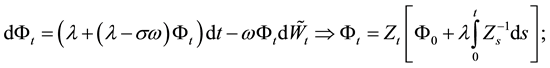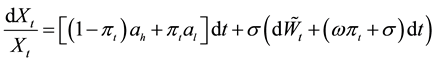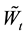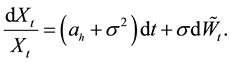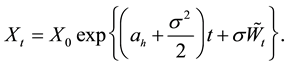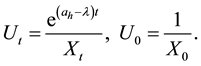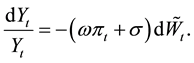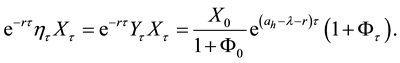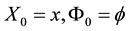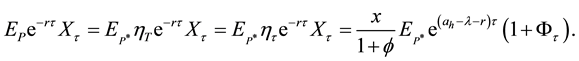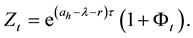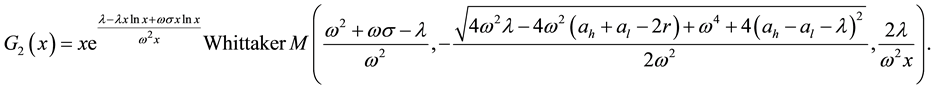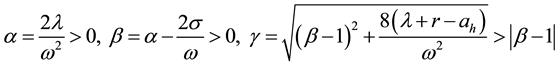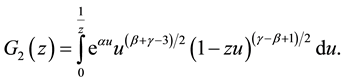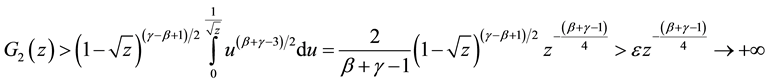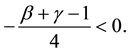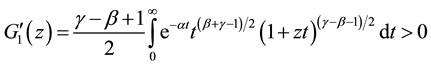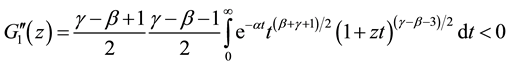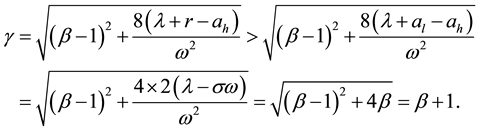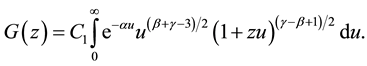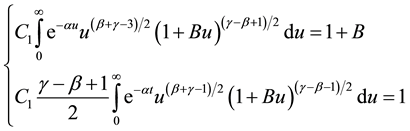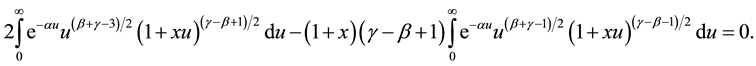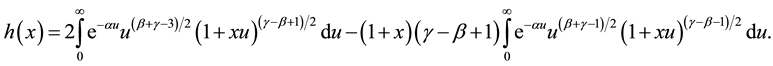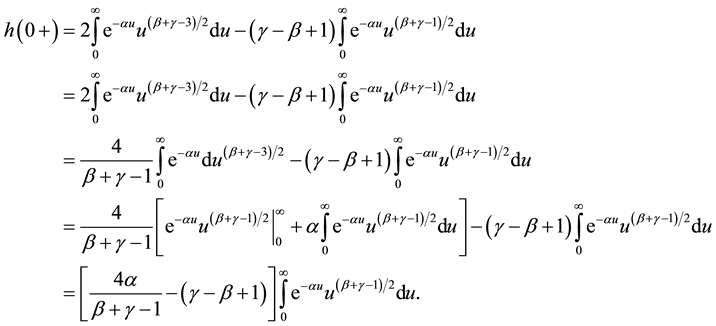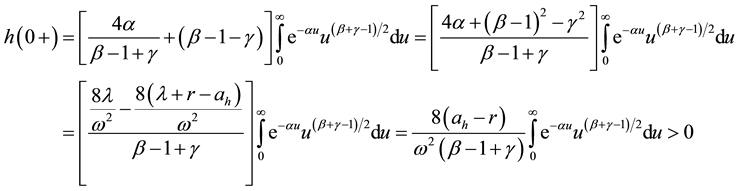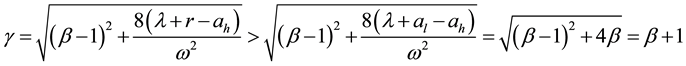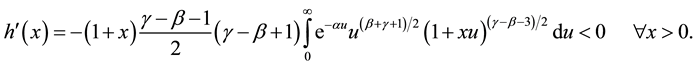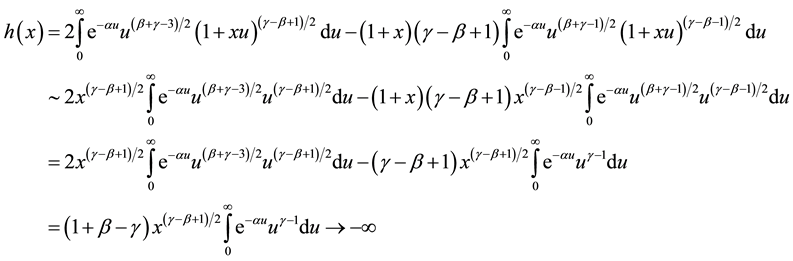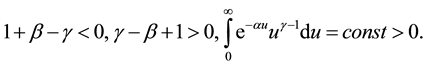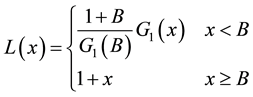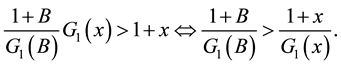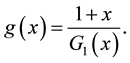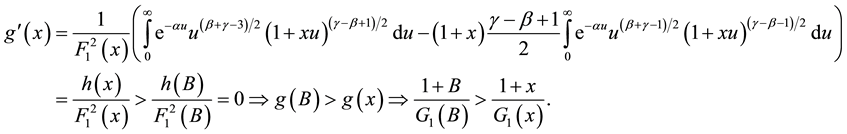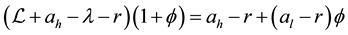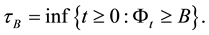American Journal of Operations Research
Vol.05 No.06(2015), Article ID:60989,12 pages
10.4236/ajor.2015.56040
When to Sell an Asset Where Its Drift Drops from a High Value to a Smaller One
Pham Van Khanh
Institute of Economics and Corporate Group, Hanoi, Vietnam

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 28 June 2015; accepted 8 November 2015; published 11 November 2015

ABSTRACT
To solve the selling problem which is resembled to the buying problem in [1] , in this paper we solve the problem of determining the optimal time to sell a property in a location the drift of the asset drops from a high value to a smaller one at some random change-point. This change-point is not directly observable for the investor, but it is partially observable in the sense that it coincides with one of the jump times of some exogenous Poisson process representing external shocks, and these jump times are assumed to be observable. The asset price is modeled as a geometric Brownian motion with a drift that initially exceeds the discount rate, but with the opposite relation after an unobservable and exponentially distributed time and thus, we model the drift as a two-state Markov chain. Using filtering and martingale techniques, stochastic analysis transform measurement, we reduce the problem to a one-dimensional optimal stopping problem. We also establish the optimal boundary at which the investor should liquidate the asset when the price process hit the boundary at first time.
Keywords:
Optimal Stopping Time, Posterior Probability, Threshold, Markov Chain, Jump Times, Martingale, Brownian Motion

1. Introduction
In this paper we consider the following problem: How to find the optimal stopping time to sell a stock (or an asset) when the expected return of a stock is assumed to be a constant larger than the discount rate up until some random, and unobservable, time τ, at which it drops to a constant smaller than the discount rate.
An investor wants to hold the position as long as the inertia is present by taking advantage of the drift which is exceeding the discounted rate (or interest rate). On the other hand, when the inertia disappears the investor would like to exit the position by selling the asset.
The under study problem in this paper was also addressed in [1] where the buying problem with the same assumption was solved. The results of [1] showed that the optimal buying time was the first passage time over some unknown level for the a posteriori probability process
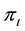 defined below and by simulating it was found that the optimal time to buy an asset was the time which the asset price process had just passed the trough.
defined below and by simulating it was found that the optimal time to buy an asset was the time which the asset price process had just passed the trough.
The author of [2] studied a problem of finding an optimal stopping strategy to liquidate an asset with unknown drift; more exactly he wanted to find the best time to sell a stock when its drift was a discrete random variable which took the given values. The first time the posterior mean of the drift passes below a non-decreasing boundary that is the unique solution of a particular integral equation is shown to be optimal.
Some classical optimal stopping time problem has been considered in [3] . These are applied in mathematical finance but these are basic problem, and it is difficult to apply in real world.
For related studies of stock selling problems, see [4] [5] and for studies of basic optimal stopping problems see [3] . The method we use to study in this paper is the martingale theory, the transformation theory of measuring and the optimal stopping time is referenced in the literature [3] [6] [7] .
In this paper, the asset price is modeled as a linear Brownian motion with a drift that drops from one constant to a smaller constant at some unobservable time. This drift is modeled as a Markov chain with two states which are denoted by 0 and 1 where 0 is denoted for price decrease and 1 is denoted for price increase.
We define the asset price model in Section 2, and the optimal selling problem is set up. In Section 3, we study the simulation to examine our studies and finally, Section 4 is conclusion.
2. The Model
We take as given a complete probability space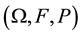 . On this probability space, let the change-point τ be a random variable with distribution
. On this probability space, let the change-point τ be a random variable with distribution
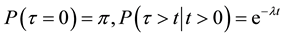
where λ is the intensity of the transition from state 1 to state 0 and assume that λ is positive and that belongs to [0; 1). Denote the drift of the price process at, t ≥ 0, can be modeled as a Markov chain with two states al denoted by state 0 and ah denoted by state 1 such that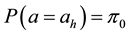 ;
;
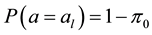 at time 0, al < r < ah where r is discounted rate which is a given constant and process at, t ≥ 0 can only transit from state 1 to state 0
at time 0, al < r < ah where r is discounted rate which is a given constant and process at, t ≥ 0 can only transit from state 1 to state 0
with transition density matrix as follows
 Next, let W be a Brownian motion which is indepen-
Next, let W be a Brownian motion which is indepen-
dent of τ. The asset price process X is modeled by a geometric Brownian motion with a drift that drops from ah to al at time τ. More precisely,
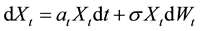
and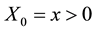 , where
, where
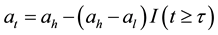 i.e.
i.e.
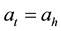 if
if
 and
and
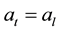 if
if
 the volatility
the volatility
 is a constant.
is a constant.
At the time of
 we define the a posteriori probability process
we define the a posteriori probability process
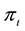
where
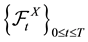
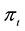
Find
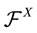
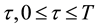
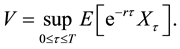
Similar the buying problem, posterior probability process
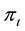
or
where
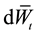

Moreover, in terms of
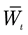
Processes
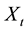
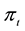
Put
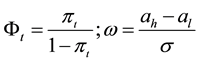
We define new process
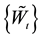
and a new measure
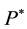
By Girsanov theorem,
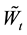
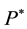
where
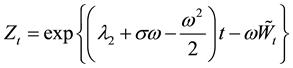
The price process

or in term of
The solution of this stochastic equation is
Now we consider the process:
then

Let
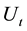
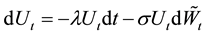
Put
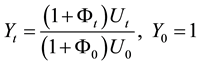
From this we have

Denote
then
To solve the problem (2.1) we solve the following auxiliary problem:
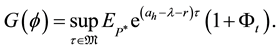
Put
The optimal stopping time is the first hitting time of the process
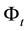



where
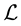
Differential equation in (2.3) has the general solution as follows:
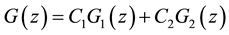
Changing variables and using some analytic transformations we obtain:
then
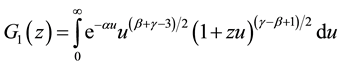
We also have
as
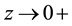
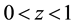
We have
since
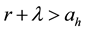
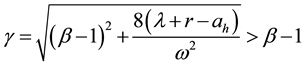
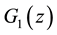
Moreover
since
These mean that the function
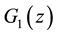
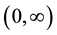
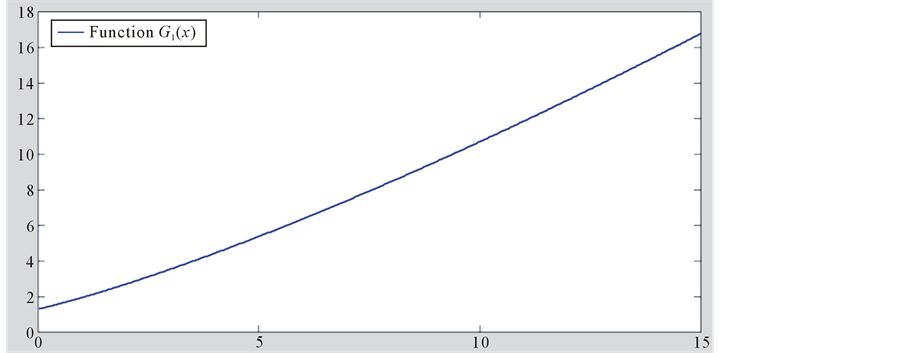
Figure 1 shows the graph of function
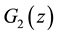
But
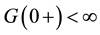
According to (2.3) we have
Figure 1. Graph of the function
Figure 2. Graph of the function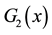
So B is the solution of the following equation:

Lemma 2.1. The free boundary Equation (2.4) has unique positive solution B.
Proof: The Equation (2.4) is equivalent to
Denote:
The graph of

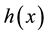
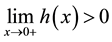

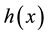
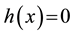
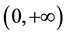
We have
Figure 3. Graph of the function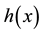
It follows that
Because
and
we obtain
We will prove that
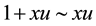
since
Consequently,
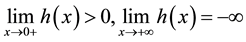
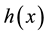
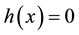
solution on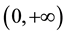
Theorem 2.2. Stopping time
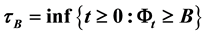
Proof: Let
and we will prove that
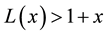
Now, we examine the function
Take the derivative we obtain
This follows
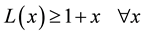
Using the Dynkin’s formula to the process
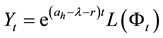
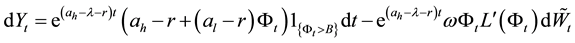
Because B satisfying
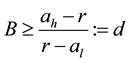
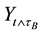

By
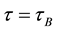
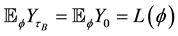

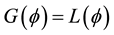
We will show that B satisfy the condition: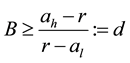
with positive value will be in continuation area
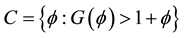
The optimal stopping time is the first hitting time of
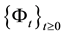
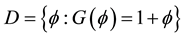
Thus function G satisfy the following condition:
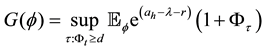
We define the function:
Now, we assume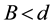
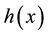
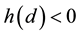
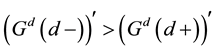
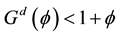
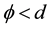

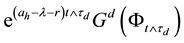
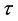
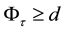
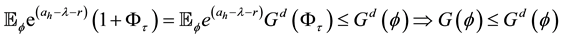
This contradicts to the existence of
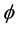

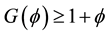
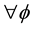

The optimal stopping time
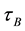
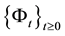
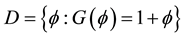
But
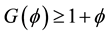
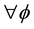
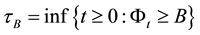
by this, we have finished the provement.
3. Simulation Study
To make visual for the above theory we simulate the asset price process, the posterior probability process
process
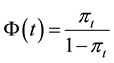
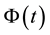

parameters is used in our simulating are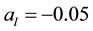
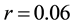

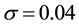
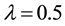
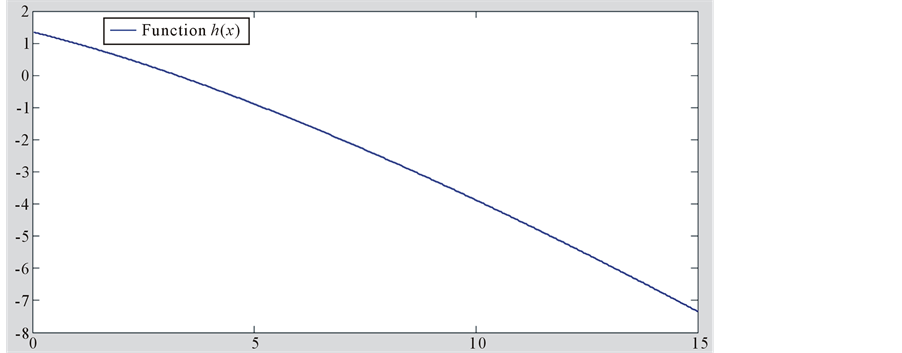
As can be seen in the figures from 4 to 8 if the price is increasing then the
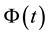
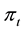
Figure 4 shows the price process has increased since the time 0.2 so the
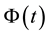
Figure 5 simulate a price process which is fluctuated from time 0 to 0.14 and decrease dramatically at the time 0.14 so the process
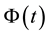
Another simulation is shown in Figure 6. Clearly, whenever the price process is increasing, the
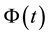
Figure 4. A simulation of asset price process, the posterior probability process, process Φ(t), the threshold probability and the optimal stopping time. In this case, the process Φ(t) always under the threshold probability so the optimal stopping time is the final time 1.
Figure 5. A simulation of asset price process, the posterior probability process, process Φ(t), the threshold probability and the optimal stopping time. In this case, the first time that the process Φ(t) over passes the threshold probability at the time 0.17 so the optimal stopping time is 0.17.
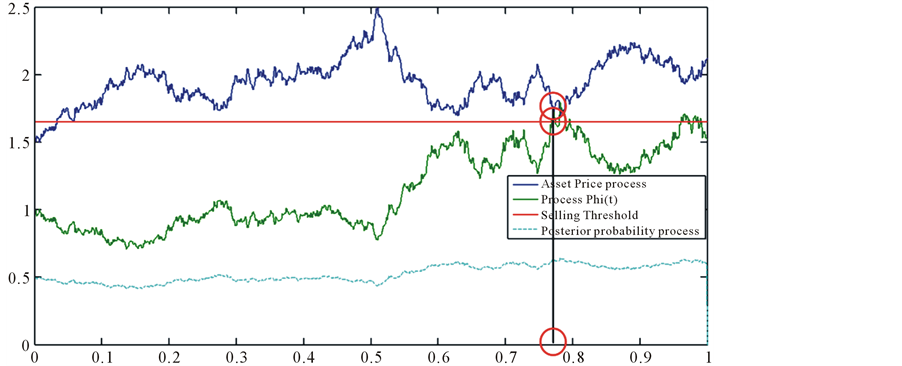
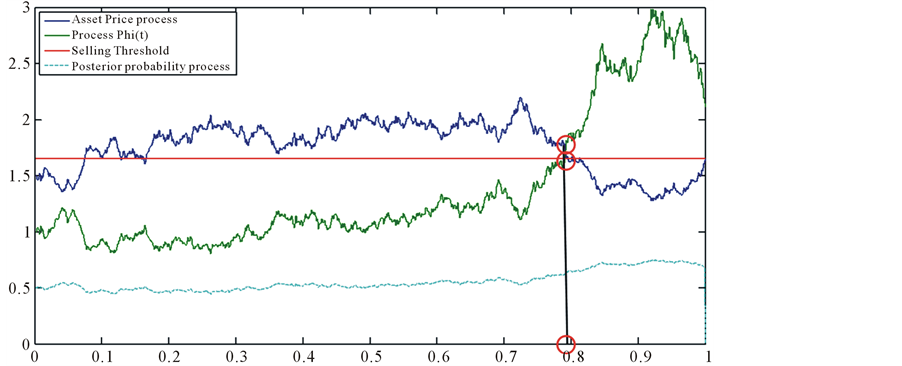
In Figure 7, we can see the same scenario with the simulation in Figure 6. The time to liquidate in this case is 0.795, the price is about 1.75 whereas the started price was 1.5. We can see

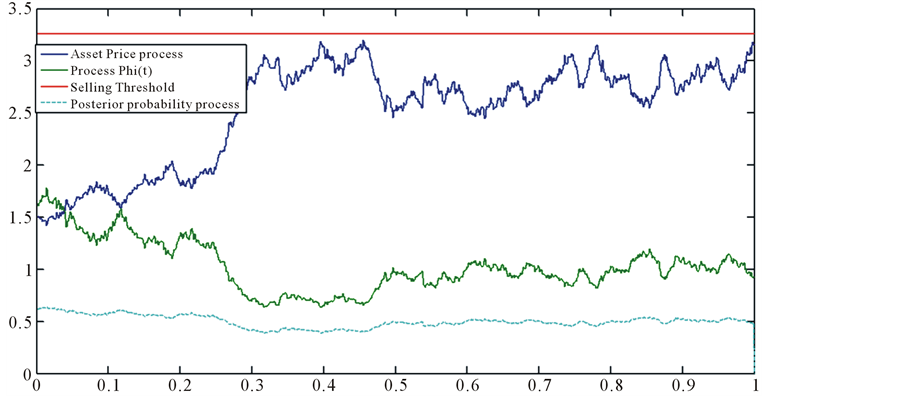
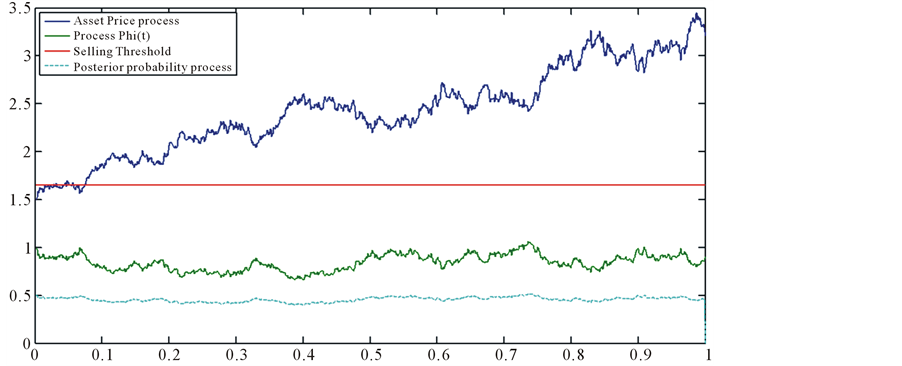
The same scenario with the simulation in Figure 1, the simulation results in Figure 8 show the price illustrates an uptrend from time 0 to the end that the process
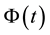
4. Conclusion
This research considers the problem of how to find the optimal time to liquidate an asset when the asset price is modeled by the geometric Brownian motion which has a change point. In particular, the drift of the process drops from a high value to a smaller one and this drift process can be modeled as two-state Markov process. The results of this research indicate that a optimal selling decision is made when the probability of downtrend surpassed some certain threshold. We also simulate the price process with a number of parameters and conduct
Figure 6. A simulation of asset price process, the posterior probability process, process Φ(t), the threshold probability and the optimal stopping time. In this case, the first time that the process Φ(t) over passes the threshold probability at the time 0.77 so the optimal stopping time is 0.77.
Figure 7. A simulation of asset price process, the posterior probability process, process Φ(t), the threshold probability and the optimal stopping time. In this case, the first time that the process Φ(t) over passes the threshold probability at the time 0.795 so the optimal stopping time is 0.795.
Figure 8. A simulation of asset price process, the posterior probability process, process Φ(t), the threshold probability and the optimal stopping time. In this case, the process Φ(t) always under the threshold probability so the optimal stopping time is the final time 1, the same with the case in Figure 4.
numerical solution to the experimental selling threshold. In next studies, we will consider problems in which the price growth rate is a Markov process which has more than 2 states and establish some properties as well as distribution of stopping time.
Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 10103-2012.17.
Cite this paper
PhamVan Khanh, (2015) When to Sell an Asset Where Its Drift Drops from a High Value to a Smaller One. American Journal of Operations Research,05,514-525. doi: 10.4236/ajor.2015.56040
References
- 1. Khanh, P. (2014) Optimal Stopping Time to Buy an Asset When Growth Rate Is a Two-State Markov Chain. American Journal of Operations Research, 4, 132-141.
http://dx.doi.org/10.4236/ajor.2014.43013 - 2. Khanh, P. (2012) Optimal Stopping Time for Holding an Asset. American Journal of Operations Research, 4, 527-535.
http://dx.doi.org/10.4236/ajor.2012.24062 - 3. Peskir, G. and Shiryaev, A.N. (2006) Optimal Stopping and Free-Boundary Problems (Lectures in Mathematics ETH Lectures in Mathematics. ETH Zürich (Closed)). Birkhäuser, Basel.
- 4. Shiryaev, A.N., Xu, Z. and Zhou, X.Y. (2008) Thou Shalt Buy and Hold. Quantitative Finance, 8, 765-776.
http://dx.doi.org/10.1080/14697680802563732 - 5. Guo, X. and Zhang, Q. (2005) Optimal Selling Rules in a Regime Switching Model. IEEE Transactions on Automatic Control, 9, 1450-1455.
http://dx.doi.org/10.1109/TAC.2005.854657 - 6. Lipster, R.S. and Shiryaev, A.N. (2001) Statistics of Random Process: I. General Theory. Springer-Verlag, Berlin, Heidelberg.
- 7. Shiryaev, A.N. (1978) Optimal Stopping Rules. Springer Verlag, Berlin, Heidelberg.