American Journal of Operations Research
Vol.4 No.3(2014), Article ID:45569,8 pages DOI:10.4236/ajor.2014.43012
Assessing Chinese Commercial Bank Technical Efficiency with a Parametric Hyperbolic Distance Function
Xuan Fang*, Feng Yang
School of Management, University of Science and Technology of China, Hefei, China
Email: *fangxuan@mail.ustc.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 26 February 2014; revised 26 March 2014; accepted 3 April 2014
ABSTRACT
This paper contributes to the literatures about Chinese commercial banks technical efficiency. In order to eliminate the deviation of efficiency scores caused by an undesirable output that is represented by banks’ non-performing loans, the estimation is based on an enhanced parametric hyperbolic distance function which considers not only desirable outputs but also undesirable outputs. Furthermore, we extend the model to divide the factors that affecting technical efficiency into direct factors and indirect factors and exclude the influence of the latter when analyzing the determiners of banks technical efficiency. The validity of this model is examined by a panel of bank data from 2004-2010.
Keywords:Parametric Distance Functions, Chinese Bank Efficiency, Undesirable Outputs

1. Introduction
Banks in China have been the focus of research. Despite the contribution of previous studies, two issues remain unaddressed. First, for all we know, there is no one study that adopts an enhanced hyperbolic distance function to analyze Chinese commercial banks efficiency. Cuesta et al. [1] developed an enhanced hyperbolic distance function that is stochastic and parametric simultaneously. Second, factors affecting the banking efficiency are not divided into direct control and indirect control factors in the existing papers about banks efficiency. Macroeconomic and bank-specific variables are always regarded as direct control factors.
These two problems motivate us to employ the enhanced hyperbolic distance function to estimate Chinese banks efficiency. We treat the non-performing loans as the undesirable output in the productive process of banks and extend the model which developed by Cuesta to deal the indirect impacts of macroeconomic variables and some bank characteristics on technical efficiency. What’s more we unearth the direct determiners of efficiency. These determiners are under the control of banks.
The rest of this paper is organized as follow. Section 2 gives a literature review about bank efficiency. We discuss the method employed in this paper in Section 3. Section 4 describes and analyzes the data. Section 5 presents the empirical results and discussion. Conclusions and implications of this paper are shown in Section 6.
2. Literature Review
Most of the studies on the technical efficiency of bank employ the mathematical programming technique-data envelopment analysis (DEA). Another method is stochastic frontier analysis. Battese et al. [2] found that there were great technical inefficiency effects for labor use in the Swedish banks from 1984 to 1995. Pasiouras et al. [3] examined the influence of the regulatory and supervision framework on bank efficiency. Kumbhakar and Wang [4] evaluated the performance of banks in China during the reform period. Jiang et al. [5] adopted a stochastic distance function and suggested that foreign competition is beneficial to China’s on-going bank reform. Heffernan and Fu [6] estimated the efficiency of different types of Chinese banks from 1999 to 2006 and determined the efficiency factors.
Researchers have made great efforts to manage undesirable outputs. Akther et al. [7] used a slacks-based inefficiency measure and the directional distance function to examine nineteen commercial banks in Bangladesh. However researchers do not make great progress with parametric approaches which can deal with undesirable outputs until 2005 Färe et al. [8] made a breakthrough in this field. Later, Cuesta et al. [1] developed the method to an enhanced hyperbolic distance function that taking accounting into undesirable outputs.
3. Method
We regard a bank as a productive unit that transforms input vector 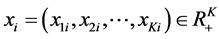 into desirable output vector
into desirable output vector 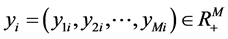 and undesirable output vector
and undesirable output vector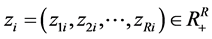 , and where the subscript
, and where the subscript ![]() is the set of observed banks. This productive technology is defined below
is the set of observed banks. This productive technology is defined below
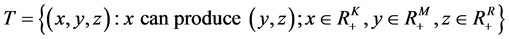 (1)
(1)
This compact production possibility set satisfies the axioms of production showed in Färe and Primont [9] . The technology can also be represented by an enhanced hyperbolic distance function 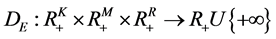
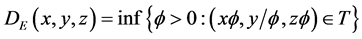 (2)
(2)
which is developed by Cuesta et al. [1] from the hyperbolic distance function. The range of the hyperbolic distance function is![]() , and it thus can play a role in measuring technical efficiency. If
, and it thus can play a role in measuring technical efficiency. If![]() , the bank is said to be technical inefficient and it could improve its performance by decreasing undesirable outputs and inputs and increasing production of desirable outputs simultaneously. On the contrary, if
, the bank is said to be technical inefficient and it could improve its performance by decreasing undesirable outputs and inputs and increasing production of desirable outputs simultaneously. On the contrary, if![]() , the productive unit is supposed to be efficient.
, the productive unit is supposed to be efficient.
Suppose the technology meets the customary axioms, then the enhanced hyperbolic distance function satisfies the following properties (Cuesta et al. [1] ): 1) it is homogeneous,  ; 2) non-decreasing in desirable outputs,
; 2) non-decreasing in desirable outputs, ![]() ; 3) non-increasing in undesirable outputs,
; 3) non-increasing in undesirable outputs, 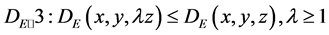 ; 4) non-increasing in inputs,
; 4) non-increasing in inputs,![]() .
.
In order to make the function meet the demand of homogeneity, Cuesta et al. [1] define a function ![]() that is almost homogeneous of degrees k1, k2, k3, and k4 if
that is almost homogeneous of degrees k1, k2, k3, and k4 if
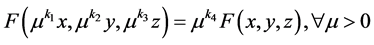 (3)
(3)
Using the extended Euler Theorem, they assume that ![]() is continuously differentiable, and to be almost homogeneous it must satisfy
is continuously differentiable, and to be almost homogeneous it must satisfy
 (4)
(4)
According to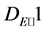 , we can know that k1 = −1, k2 = 1, k3 = −1, and k4 = 1 in the case of the enhanced hyperbolic distance function.
, we can know that k1 = −1, k2 = 1, k3 = −1, and k4 = 1 in the case of the enhanced hyperbolic distance function.
 (5)
(5)
The translog form of ![]() is presented by
is presented by
 (6)
(6)
Substituting the partial derivatives of x, y and z of Equation (6) into Equation (5) obtains
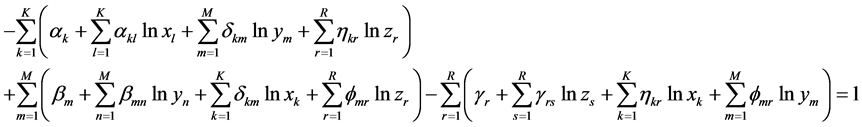 (7)
(7)
Simplifying Equation (7), we can get (1+K+M+R) restrictions to ensure the homogeneity below
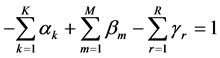 (8)
(8)
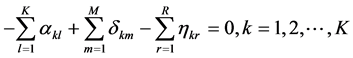 (9)
(9)
 (10)
(10)
 (11)
(11)
Through a modifying process we impose the Equation (8), Equation (9), Equation (10), Equation (11) and Equation (4) on the enhanced hyperbolic distance function and yield
![]() (12)
(12)
As a productive unit, the outputs and inputs of commercial banks are being discussed in the banking literature. Two main ways for the selection of inputs and outputs is proposed by Berger and Humphrey [10] . These are the intermediation approach and the production approach. The former regards banks as financial institutions which servicing for savers and investors, the latter perceives loans and deposits as banks outputs, labor and capital as banks inputs. However, Berger and Humphrey [10] pointed out that no one better than another and neither of them is perfect. There is a heated controversy over the role of deposits in banks performance. Researchers do not agree on the role of the deposits so far, but reach agreement on the selection of inputs and outputs. For example, the common inputs are personnel and interest expense; the outputs are loans and other earning assets.
In our paper, we assume that banks are productive units. The inputs are interest expense (x1) and business and management costs (x2), the desirable outputs are loans (y1), deposits (y2) and securities (y3), and the undesirable output is non-performing loans (z1). Thus the enhanced hyperbolic distance function of banks for i = 1, 2… N, in t = 1, 2… T time periods can be represented
 (13)
(13)
When taking the logarithm of output term![]() , it is equal to null. This is the interpretation why the summations involving
, it is equal to null. This is the interpretation why the summations involving ![]() in the model are 2.
in the model are 2. ![]() is the kth observed input of banks.
is the kth observed input of banks. ![]() is the mth desirable output of the ith bank at year t.
is the mth desirable output of the ith bank at year t. ![]() is the rth undesirable output.
is the rth undesirable output. ![]() is the symmetric time-varying stochastic error and is independent of inputs and independently identically distributed, i.e.,
is the symmetric time-varying stochastic error and is independent of inputs and independently identically distributed, i.e., .
.
The main innovation of this study is to measure the efficiencies after controlling for the individual traits and different macroeconomic characteristics over the observed periods. We extend this model by defining
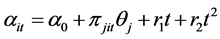 (14)
(14)
 is a constant.
is a constant. 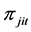 is the jth of observed macroeconomic and bank-sector characteristics which are out of control of banks and can influence the efficiency. Three macroeconomic variables are used in our study, GDP, CPI and industrial output value (IOV). We also investigate two features of banks. Firstly, listed banks have an advantage in financing, enjoy a better organizational structure and keep the high quality management personnel. Secondly, all banks set up a great number of branches which help to enlarge the scope of business and acquire more clients for banks.
is the jth of observed macroeconomic and bank-sector characteristics which are out of control of banks and can influence the efficiency. Three macroeconomic variables are used in our study, GDP, CPI and industrial output value (IOV). We also investigate two features of banks. Firstly, listed banks have an advantage in financing, enjoy a better organizational structure and keep the high quality management personnel. Secondly, all banks set up a great number of branches which help to enlarge the scope of business and acquire more clients for banks.
We also employ linear and quadratic time trends as it is next to impossible that technology keeps unchanged over time.
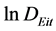 corresponds to the one-side term
corresponds to the one-side term![]() . In this study, not only do we estimate the inefficiency, but we check the direct determinants of it. Battese and Coelli [11] have discussed a two-step approach to embody the elements which influencing the efficiency by assuming that
. In this study, not only do we estimate the inefficiency, but we check the direct determinants of it. Battese and Coelli [11] have discussed a two-step approach to embody the elements which influencing the efficiency by assuming that ![]() is obtained by truncation of the normal distribution with mean,
is obtained by truncation of the normal distribution with mean, 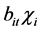 , and a constant variance,
, and a constant variance,![]() .
. ![]() is a vector of explanatory variables associated with technical inefficiency. We adopt this method and select bank size, the ratio of returns to average assets, the ratio of loan loss provisions to loans and market shares as variables.
is a vector of explanatory variables associated with technical inefficiency. We adopt this method and select bank size, the ratio of returns to average assets, the ratio of loan loss provisions to loans and market shares as variables.
4. Empirical Study
4.1. Data
Chinese banking system has many types of financial intuitions, including four state-owned commercial banks, three policy banks, twelve joint-venture commercial banks, a great amount of city and rural commercial banks, rural cooperative banks, rural credit cooperatives and some foreign banks. According to statistics published by China Banking Regulatory Commission from 2004 to 2010, the state-owned commercial banks account for about half of the bank market share. Obviously, they have great advantages over other financial intuitions. In contrast, rural commercial banks, rural cooperative banks and rural credit cooperatives enjoy such a small share that can be ignored because their business scope is limited to local. With a short history in China, foreign banks are subject to various restrictions on business. Therefore, our sample is selected from joint-venture and city commercial banks. Furthermore, it is convenient to choose listed banks to collect data. The data in the analysis is obtained from the China Statistical Yearbook, and the annual reports of the sample. The observed period is 2004-2010.
The macroeconomic variables include GDP (π1), industrial output value (π2) and the inflation (π3). In our observed period 2004-2010, GDP and IOV increase rapidly. On the whole, the macro environment is favorable to the banks performance. We take account into a dummy (π4) for whether listed or not. A dummy is equal one for a listed bank, null otherwise. We designate (π5) as the number of branches. Generally, city commercial banks acquire a lot less branches than joint-venture banks. Intuitively, the former win a larger market share than the latter.
Two inputs are specified in the model, they are interest expenses (x1), business and management costs (x2). As a financial institution, banks pay interest to corporations and individuals to absorb deposits. It accounts for a large part of the bank expenditure according to the Table 1. Business and management costs include not only staff salaries but also other operation costs such as welfare expense, publicity expenses and travelling expense.
Among other the undesirable outputs-the non-performing loans (z1), there are three desirable outputs: the normal loans (y1), securities (y2) and deposits (y3). Banks offer capital to firms or individuals to sustain their projects and achieve loan interest. It is the main part of profits and is about five times of other outputs in Table 2. On the other side, in order to avoid market risk, banks will invest other assets. Transaction financial liabilities and derivatives are two preferable financial instruments. We define securities as the sum of these two products. For banks employ their resources such as personnel and fixed assets to produce deposits, it is better to give deposits a kind of role of outputs.
The model also allows us to investigate how the selected directive variables affect the bank inefficiency. Previous studies have made great efforts in this field. Sizes, profitability, loans to assets are the most common factors (Ataullah and Le, [12] ; Ariff and Can, [13] ). We follow the prior research and choose size (b1), return on average assets (b2), the ratio of loan loss provisions to loans (b3) and market shares (b4) in this model. We choose the total assets as the proxy of size, and the ratio of bank deposits to national total deposits as the index of market share.
4.2. Empirical Results
In Table 4, we show our results obtained from maximum likelihood estimation. The macroeconomic and bank-specific characteristics’ parameter estimates are 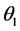 to
to . As we expected, the parameters of CPI, industrial output value have the positive sign and past the t-test. It confirms the hypothesis that macro environment affect banks performance positively. The parameter of the listed dummy has a positive sign. It means that banks which have gone to public possess advantages that aforementioned. As we have stated that banks which with a wide number of branches have a greater business scope, but they have to spend more efforts to manage their branches. In this case, banks may perform worse than small counterparts. In Table 3,
. As we expected, the parameters of CPI, industrial output value have the positive sign and past the t-test. It confirms the hypothesis that macro environment affect banks performance positively. The parameter of the listed dummy has a positive sign. It means that banks which have gone to public possess advantages that aforementioned. As we have stated that banks which with a wide number of branches have a greater business scope, but they have to spend more efforts to manage their branches. In this case, banks may perform worse than small counterparts. In Table 3,  shows a negative sign. The sign of the estimated coefficient
shows a negative sign. The sign of the estimated coefficient 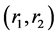 of the linear trend effect t and the quadratic trend t2 is both positive. This reflects the fact that the distance to the frontier is decrease as time passes.
of the linear trend effect t and the quadratic trend t2 is both positive. This reflects the fact that the distance to the frontier is decrease as time passes.
Table 1. Sample of banks.
Table 2. Descriptive statistics of inputs and outputs.
Table 3. Descriptive statistics of efficiency factors.
The coefficients of inputs  in Table 3 show the expected negative sign. The negative signs in here mean that the decrease of inputs can cut down the distance to the given frontier. The desirable outputs parameters
in Table 3 show the expected negative sign. The negative signs in here mean that the decrease of inputs can cut down the distance to the given frontier. The desirable outputs parameters 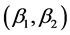 have the opposite effects. Similarly, banks produce the more outputs with a fixed number of inputs have the shorter distance to the frontier. The coefficient
have the opposite effects. Similarly, banks produce the more outputs with a fixed number of inputs have the shorter distance to the frontier. The coefficient 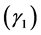 of the undesirable output has the negative sign. We can conclude that the non-performing loans play an adverse role in the productive process of banks.
of the undesirable output has the negative sign. We can conclude that the non-performing loans play an adverse role in the productive process of banks.
The variables that in the one-side error term show a negative sign except the coefficient of the ratio of loan loss provisions to loans. The negative sign indicates a positive influence of variables on bank technical efficiency because the dependent variable is technical inefficiency. From the Table 4, we can summarize that banks which have more total assets and a larger market share are likely to be more technical efficient.
Banks technical efficiency scores are shown in Table 5. The mean technical efficiency of sample is 0.823. The Bank of Nanjing achieves the highest score in the observed period. As one of city commercial banks, it has the least branches in our sample and is the smallest bank according to the total size. These traits make it more convenient to operate to get high technical efficiency. China Citic Bank, Hua Xia Bank, Industrial Bank and the city commercial banks go to public during the observed period, but the advantages are not demonstrated clearly by the technical efficiency term. Perhaps, the favorable effects are hysteretic and will show in a long run.
And on average, the city commercial banks have a mean efficiency of 0.842 that is more efficient than the joint-venture banks which have a mean efficiency of 0.815. We suppose some explanations for this phenomenon: 1) city commercial banks conduct banking business in the local primarily and can work out appropriate strategies to response to market change rapidly; 2) they attract foreign investment and adopt foreign advanced management methods such as the strategy of streamlining staffing and network scale, forge development in service to strengthen the functions of Treasury Department, Product Development Department; 3) they have begun to step towards other provinces to enlarge their business. Bank of Ningbo has established branches in other cities outside of Ningbo.
We also show the minimum and maximum efficiency score of banks in our sample. The China Minsheng Banking has the largest gap. It means that the bank experienced a faster increase process during the period than others. This phenomenon may come from the reform of the operation. The standard deviation is also listed in Table 5 which represents the dispersion of the efficiency. Obviously, the performance of Bank of Nanjing is most stable in the sample. In our opinion, stable operating environment is useful to improve the technical efficiency. As shown in the table, the mean efficiency score of Nanjing bank is the highest.
Table 4. Parameter estimates and t-statistic of the model.
Table 5. Efficiency scores.
5. Conclusions
In this paper, eight joint-venture banks and three city commercial banks performances in China are examined by the modification of the enhanced parametric hyperbolic distance function. We make a breakthrough in the classification of the determiners of technical efficiency. In our point of view, banks are incapable of controlling all kinds of influencing variables. It is better to divide the factors that affecting technical efficiency into direct factors and indirect factors and exclude the influence of the latter when analyzing the determiners of banks technical efficiency.
A number of results are found in this study. Generally speaking, the indirect factors have a positive effect on technical efficiency. A good macro environment is beneficial to the operation of banks for enterprises that need to borrow more money from banks to expand their business and reproduce. The bank-specific characteristics do not make contribution to the banks performance. As shown in the empirical results, listed banks do not enjoy great advantages in the current. What’s more, banks with more branches have to throw more energy to run and suffer a reduction in technical efficiency.
References
- Cuesta, R.A., Lovell, C.A.K. and Zofio, J.L. (2009) Environmental Efficiency Measurement with Translog Distance Functions: A Parametric Approach. Ecological Economics, 68, 2232-2242. http://dx.doi.org/10.1016/j.ecolecon.2009.02.001
- Battese, G.E., Heshmati, A. and Hjalmarsson, L. (2000) Efficiency of Labour Use in the Swedish Banking Industry: A Stochastic Frontier Approach. Empirical Economics, 25, 623-640. http://dx.doi.org/10.1007/s001810000037
- Pasiouras, F., Tanna, S. and Zopounidis, C. (2009) The Impact of Banking Regulations on Bank’s Cost and Profit Efficiency: Cross-Country Evidence. International Review of Financial Analysis, 18, 294-302. http://dx.doi.org/10.1016/j.irfa.2009.07.003
- Kumbhakar, S.C. and Wang, D. (2007) Economic Reforms, Efficiency and Productivity in Chinese Banking. Journal of Regulatory Economics, 32, 105-129. http://dx.doi.org/10.1007/s11149-007-9028-x
- Jiang, C., Yao, S. and Zhang, Z.Y. (2009) The Effects of Governance Changes on Bank Efficiency in China: A Stochastic Distance Function Approach. China Economic Review, 20, 717-731. http://dx.doi.org/10.1016/j.chieco.2009.05.005
- Heffernan, S.A. and Fu, X.Q. (2010) Determinants of Financial Performance in Chinese Banking. Applied Financial Economics, 20, 1585-1600. http://dx.doi.org/10.1080/09603107.2010.505553
- Akther, S., Fukuyama, H. and Weber, W.L. (2012) Estimating Two-Stage Network Slacks-Based Inefficiency: An Application to Bangladesh Banking. Omega, 41, 88-96. http://dx.doi.org/10.1016/j.omega.2011.02.009
- Färe, R., Grosskopf, S., Noh, D.-W. and Weber, W.L. (2005) Characteristics of a Polluting Technology: Theory and Practice. Journal of Econometrics, 126, 469-492. http://dx.doi.org/10.1016/j.jeconom.2004.05.010
- Färe, R. and Primont, D. (1995) Multi-Output Production and Duality: Theory and Applications. Kluwer Academic Publishers, Dordrecht. http://dx.doi.org/10.1007/978-94-011-0651-1
- Berger, A.N. and Humphrey, D.B. (1997) Efficiency of Financial Institutions: International Survey and Directions for Future Research. European Journal of Operational Research, 98, 175-212. http://dx.doi.org/10.1016/S0377-2217(96)00342-6
- Battese, G.E. and Coelli, T.J. (1995) A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data. Empirical Economics, 20, 325-332. http://dx.doi.org/10.1007/BF01205442
- Ataullah, A. and Le, H. (2006) Economic Reforms and Bank Efficiency in Developing Countries: The Case of the Indian Banking Industry. Applied Financial Economics, 16, 653-663. http://dx.doi.org/10.1080/09603100500407440
NOTES

*Corresponding author.


