New Journal of Glass and Ceramics
Vol.05 No.03(2015), Article ID:57481,8 pages
10.4236/njgc.2015.53006
Optical Basicity and Polarizability of Nd3+-Doped Bismuth Borate Glasses
Beena Bhatia, S. L. Meena, Vishal Parihar, Monika Poonia
Ceramics Laboratory, Department of Physics, Jai Narain Vyas University, Jodhpur, India
Email: drbeenabhatia@rediffmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 April 2015; accepted 26 June 2015; published 29 June 2015
ABSTRACT
This paper reports on different physical and optical properties of Nd3+-doped bismuth borate glasses. The glasses containing Nd3+ in (25 − x)Bi2O3:20Li2O:20ZnO:35B2O3:xNd2O3 (where x = 1, 1.5, 2 mol%) have been prepared by melt-quenching method. The amorphous nature of the glasses was confirmed by X-ray diffraction studies. The physical parameters like dielectric constant, refractive index, ionic concentration, oxygen-packing density, inter ionic distance, polaronradius, reflection loss, energy gap, molar refractivity, molar polarizability, electronic polarizability, optical basicity and field strength are computed. On the basis of the measured values of the density and refractive index, the Nd3+ ion concentration in glasses, the polarizability of oxide ions and optical basicity were theoretically determined. The theoretical value of average electronic polarizability and oxide ion polarizability were calculated by using Lorentz-Lorenz formula. Theoretical optical basicity of the glasses is evaluated based on equation proposed by Duffy and Ingram. The metallization criterion has also been calculated on the basis of refractive index and energy gap. The large value of metallization criterion indicates that the glass materials are insulators. The results obtained predict the nature of bonding in the present glasses and provide basis for developing new nonlinear optical material.
Keywords:
Neodymium Based Glass, Optical Basicity, Polarizability, Metallization Criterion

1. Introduction
Bismuth oxide (Bi2O3) based glasses for their high polarizability has fascinated much attention of glass researchers because of their nonlinear optical properties which have importance for the development of optical information processing technology [1] -[5] . Hence there has been an increasing interest in the synthesis, physical properties of heavy metal oxide (HMO) glasses. Bismuth glass is one of the most important amongst the heavy metal oxide.
Recently many researchers study glasses as switching and memory devices, superior insulators and dielectrics. Thus glass becomes an ordinary electronic material [6] [7] .
Recently, Dimitrov and Komatsu [8] have investigated the polarizability approach of numerous oxide glasses by estimating the electronic oxide ion polarizability, optical basicity and metallization criterion based on the refractive index and energy gap. Since the optical nonlinearity is the cause of electronic polarization of the glass upon exposure to intense light beams, polarizability is the most important properties which govern the nonlinearity response of the glass. That is why knowledge of the state of polarization of ions in different crystalline and amorphous materials is of significant interest.
The aim of the present study is to prepare the Nd3+-doped bismuth borate glass with different Nd2O3 concentrations and to study the effect of Nd2O3 content on various physical parameters such as density, molar volume, and refractive index. In addition the optical basicity and polarizability were theoretically determined. Glass containing neodymium oxide has been used because of its high hardness and excellent chemical durability [9] [10] .
2. Experimental Techniques
Sample Preparation
The following Nd3+-doped bismuth borate glass system (25 − x)Bi2O3:20Li2O:20ZnO:35B2O3:Nd2O3 (where x = 0, 1, 1.5, 2) have been prepared by melt-quenching method. Analytical reagent grade chemical used in the present study consist of Bi2O3, Li2O, ZnO, B2O3 and Nd2O3. They were thoroughly mixed by using an agate pestle mortar.
Then melted at 1060˚C by an electrical muffle furnace for 2 hours, After complete melting, the melts were quickly poured in to a preheated stainless steel mould and annealed at temperature of 350˚C for 2 hours to remove thermal strains and stresses. Every time fine powder of cerium oxide was used for polishing the samples. The glass samples so prepared were of good optical quality and were transparent. The chemical compositions of the glasses with the name of samples are summarized in Table 1 ZnLiBiB (Nd)-Represents Nd3+-doped Zinc Lithium Bismuth Borate glass specimens.
3. Results and Discussion
3.1. XRD Measurement
Figure 1 presents the XRD pattern of the samples shows no sharp Bragg’s peak, but only a broad diffuse hump around low angle region. This is the clear indication of amorphous nature within the resolution limit of XRD instrument.
3.2. Physical Properties
Density and molar volume measurements
Density is an effective tool to explore the degree of structural compactness modification of the geometrical configurations of the glass network. The density of all glasses was measured by using Archimedes principle with xylene as immersing liquid. The relation used is
 (1)
(1)
Table 1. Chemical composition of the glasses.
Figure 1. X-ray diffraction pattern of Bi2O3:Li2O:ZnO:B2O3:Nd2O3 glasses.
where 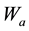 is the weight of glass sample in air,
is the weight of glass sample in air, 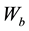 is the weight of glass sample when immersed in xylene and
is the weight of glass sample when immersed in xylene and  is the density of xylene (0.86 m/cm3).
is the density of xylene (0.86 m/cm3).
The molar volume of the glass samples can be calculated from following expression:
 (2)
(2)
where ρ is the density of the sample and MT is the total molecular weight of the multi-component glass system given by
 (3)
(3)
where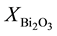 ,
, 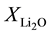 ,
,  ,
,  ,
,  are the molar fraction of the constituent oxides and
are the molar fraction of the constituent oxides and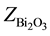 ,
,  ,
, 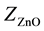 ,
, 

Refractive index measurement
Refractive index is another important property to be considered with respect to the optical features of glass. Therefore, a large number of researchers have carried out investigations to ascertain the relation between refractive index and glass composition. The refractive index was measured by using an Abbe refractometer.
Reflection loss
The reflection loss from the glass surface was computed from the refractive index using Fresnel’s formula [11]

where n is the refractive index.
Molar refraction
The molar refraction, (Rm) of the glass samples were calculated using the formula which is well known as Volf and Lorentz-Lorenz formula [12]

where n is the refractive index of the glass sample, ρ is the density and M is the molecular weight of the glass samples. M/ρ is called the molar volume, (Vm).
Energy gap
According to duffy the energy gap is given by [13]

Molar electronic polarizability
The molar refraction is related to the structure of the glass and it is proportional to the molar electronic polarizability of the material (αm) according to the relation [14]

Dielectric constant
The dielectric constant was calculated using refractive index of the glass [15]

where n is the refractive index.
Optical dielectric constant
The optical dielectric constant of the glass [16] .

where є is the dielectric constant.
Electronic polarizability
The electronic polarizability was calculated using the formula [17] .

where AV is the Avogadro number.
Oxide ions polarizability
The electronic polarizability of oxide ions has been calculated using the equation proposed by Dimitrov and Sakka [18] .

where 

Ionic concentrations
The ionic concentrations of the glass samples are determined using the following relation [19] .

Polaron radius
The polaron radius was calculated using the formula [20]

where N is the number of neodymium ions per unit volume.
Inter-ionic distance
Inter-ionic distance of the glass samples is given as [20]

where N is the number of neodymium ions per unit volume.
Field strength
The field strength was calculated using the formula [21]

where Z is the thickness of the samples.
Oygen packing density
The oxygen packing density of the glass samples were calculated using the following relation [22] .

where ρ the density of desired glass samples, M is the molecular weight of the sample and n is the number of oxygen atoms in the composition.
Optical basicity
The optical basicity addresses the ability of oxide glass in contributing the negative charges in the glass matrix. In other words it defines the electron donating power of the oxygen in the oxides glass. The theoretical optical basicity can be calculated by the equation proposed by duffy and Ingram [23]

where 

The measured density, molar volume and refrective index of Nd3+ doped zinc lithium bismuth borate glass samples for different concentrations are shown in Table 2. Based on the measurement of density, molar volume and refrective index various physical parameters e.g. electronic polarizability, ionic concentrations, polaron radius, molar refraction, Inter-ionic distance and field strength, etc. are calculated and are also listed in Table 2.
The density increases with the addition of content of Nd2O3 into the network. This indicates that replacing Bi2O3 by addition of small amount of Nd2O3 results in the increase in the average molecular weight of oxide ions in the glass. The molar volume depends on both the rate of change of density and molecular weight. However, when the Nd2O3 concentration is increased the increasing rate of molecular weight is greater than that of density. It may be assumed that the increase in Nd2O3 concentration at the expense of Bi2O3 cause the opened glass network structure.
Thus the increase in density (ρ) & electronic polarizability (αe) is due to higher molecular weight of Nd2O3 compared to that of Bi2O3.
In the present glass sample refractive index also increases with the increase in electronic polarizability. [Figure 2] of oxide ions as a result of increase in the non-bridging oxygen to bridging oxygen ratio.
Oxygen packing density is another important parameter in explaining the structure of glass. The increase of oxygen packing density may cause a decrease of molar volume and hence an increase of mass density of these glass samples.
It is clear from Table 2 and Figure 3 that the optical basicity increases linearly when Bi2O3 is replaced by Nd2O3 Increasing basicity results in increasing negative charge on the oxygen atom and thus, increasing covalency in the cation-oxygen bonding. Also it has been found that the value of optical basicity increases with increase in refractive index [Figure 4].
Insulating nature
Based on the theory of metallization of condensed matter explained by Herzfeld, refractive index turn to be infinite in the condition of Rm/Vm = 1 from the Lorentz-Lorenz equation. This is in accordance to the metallization of covalent solid materials [24] . Dimitrov and Komatsu explained on predicting the nature of solids which is metallic or non-metallic based on the condition of or Rm/Vm < 1 (non metal) and Rm/Vm > 1 (metal). Subtracting by 1 gives the metallization criterion (M)

Figure 2. Variation of electronic polarizability with refractive index.
Table 2. The physical properties of Bi2O3:Li2O:ZnO:B2O3:Nd2O3 glasses.
The small value of M means that the width of both valence and conduction bands become large, resulting in a narrow band gap and increased the metallicity of the solid [Figure 5].
Figure 3. Variation of optical basicity with Nd2O3 concentration.
Figure 4. Variation of optical basicity with refractive index.
Figure 5. Variation of metallization criterion with energy gap.
4. Conclusion
The Nd3+-doped zinc lithium bismuth borate gasses were prepared at various doping concentrations of Nd2O3 and characterized for their physical properties. The density and refractive index increases with an increase in concentration of Nd2O3. The other two properties of polarizability and optical basicity also rise over the doping concentration. Increase in optical basicity results in increasing ability of oxide ions to donate electrons to surrounding cation. This suggests that the present glasses are more basic. The electrons polarizability shows a general trend of increase with increase in refractive index. The metallization parameter values of the present glasses are found to be less than one, and thus they exhibit insulating behaviour.
References
- Zhou, S., Jiang, N., Zhu, B., Yang, H., Ye, S., Laksminarayana, G., Hao, J. and Qiu, J. (2008) Multifunctional Bismuth-Doped Nanoporous Silica Glass: From Blue-Green, Orange, Red, and White Light Sources to Ultra-Broadband Infrared Amplifiers. Advanced Functional Materials, 181, 407-1413.
- Meng, X., Qiu, J., Pen, M., Chen, D., Zhao, Q., Jiang, X. and Zhu, C. (2005) Near Infrared Broadband Emission of Bismuth-Doped Aluminophosphate Glass. Optics Express, 13, 1628-1634. http://dx.doi.org/10.1364/OPEX.13.001628
- Wang, Y., Dai, S., Chen, F., Xu, T. and Nie, Q. (2009) Physical Properties and Optical Band Gap of New Tellurite Glasses within the TeO2-Nb2O5-Bi2O3 System. Materials Chemistry and Physics, 113, 407-411. http://dx.doi.org/10.1016/j.matchemphys.2008.07.117
- Opera, I., Hesse, H. and Betzler, K. (2004) Optical Properties of Bismuth Borate Glasses. Optical Materials, 26, 235- 237. http://dx.doi.org/10.1016/j.optmat.2003.10.006
- Zhao, X., Wang, X., Lin, H. and Wang, Z. (2007) Correlation among Electronic Polarizability, Optical Basicity and Interaction Parameter of Bi2O3-B2O3 Glasses. Physica B, 390, 293-300. http://dx.doi.org/10.1016/j.physb.2006.08.047
- Khor, S.F., Talib, Z.A., Sidek, H.A.A., Daud, W.M. and Ng, B.H. (2009) Effects of ZnO on Dielectric Properties and Electrical Conductivity of Ternary Zinc Magnesium Phosphate Glasses. American Journal of Applied Sciences, 6, 1010-1014. http://dx.doi.org/10.3844/ajassp.2009.1010.1014
- Varshneya, A.K. (1994) Fundamentals of Inorganic Glasses. Academic Press, Boston, 570.
- Dimitrov, V. and Komatsu, T. (2005) Classification of Oxide Glasses: A Polarizability Approach. Journal of Solid State Chemistry, 178, 831-846. http://dx.doi.org/10.1016/j.jssc.2004.12.013
- Mohana, S., Thind, K.S., Sharma, G. and Gerward, L. (2008) Spectroscopic Investigations of Nd3+-Doped Flouro- and Chloro-Borate Glasses. Spectrochimica Acta Part A, 70, 1173-1179. http://dx.doi.org/10.1016/j.saa.2007.10.038
- Moorthy, L.R., Rao, T.S., Jayasimhadri, M., Radhapathy, A. and Murthy, D.V.R. (2004) Spectroscopic Investigation of Nd3+-Doped Alkali Chloroborophosphate Glasses. Spectrochimica Acta Part A, 60, 2449-2458. http://dx.doi.org/10.1016/j.saa.2003.12.022
- Ohishi, Y., Mitachi, S., Kanamori, T. and Manabe, T. (1983) Optical Absorption of 3d Transition Metal and Rare Earth Elements in Zirconium Fluoride Glasses. Physics and Chemistry of Glasses, 24, 135-140.
- Shelby, J.E. and Ruller, J. (1987) Properties of Barium Gallium Germanate Glasses. Physics and Chemistry of Glasses, 28, 262.
- Weber, M.J. (1967) Probabilities for Radiative and Nonradiative Decay of Er3+ in LaF3. Physical Review, 157, 262- 272. http://dx.doi.org/10.1103/PhysRev.157.262
- Zhao, X.Y., Wang, X.L., Lin, H. and Wang, Z.Q. (2007) Electronic Polarizability and Optical Basicity of Lanthanide Oxides. Physica B, 392, 132-136. http://dx.doi.org/10.1016/j.physb.2006.11.015
- Bendow, B., Benerjee, P.K., Drexhage, M.G. and Lucas, J. (1985) Journal of the American Ceramic Society, 65, C92- C95.
- Schroeder, J. (1980) Brillouin Scattering and Pockels Coefficients in Silicate Glasses. Journal of Non-Crystalline Solids, 40, 549-566. http://dx.doi.org/10.1016/0022-3093(80)90129-5
- Klinokowski, A. (1985) Non-Monotonic Variations of Some Parameters in Vitreous R2O SiO2 and R2O Al2O3 SiO2 Systems. Journal of Non-Crystalline Solids, 72, 117-137.
- Dimitrov, V. and Sakka, S. (1996) Electronic Oxide Polarizability and Optical Basicity of Simple Oxide. Journal of Applied Physics, 79, 1736-1740. http://dx.doi.org/10.1063/1.360962
- Shaker, A., Dasgupta, A., Babsu, B. and Paul, A. (1983) Journal of Materials Science Letters, 4, 697.
- Ahmed, M.M., Hogarth, C.A. and Khan, M.N. (1984) A Study of the Electrical and Optical Properties of the GeO2- TeO2 Glass System. Journal of Materials Science, 19, 4040-4044. http://dx.doi.org/10.1007/BF00980769
- Chimalawong, P., Kaewkhao, J., Kedkaew, C. and Limsuwan, P. (2010) Optical and Electronic Polarizability Investigation of Nd3+-Doped Soda-Lime Silicate Glasses. Journal of Physics and Chemistry of Solids, 71, 965-970. http://dx.doi.org/10.1016/j.jpcs.2010.03.044
- Saritha, D., Markandeya, Y., Salagram, M., Vithal, M., Singh, A.K. and Bhikshamaiah, G. (2008) Effect of Bi2O3 on Physical, Optical and Structural Studies of ZnO-Bi2O3-B2O3 Glasses. Journal of Non-Crystalline Solids, 354, 5573- 5579. http://dx.doi.org/10.1016/j.jnoncrysol.2008.09.017
- Duffy, J.A. and Ingram, M.D. (1991) Optical Properties of Glass. The American Ceramic Society, Westerville, 159- 184.
- Herzfeld, K.F. (1927) On Atomic Properties Which Make an Element a Metal. Physical Review, 29, 701-705. http://dx.doi.org/10.1103/PhysRev.29.701







