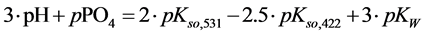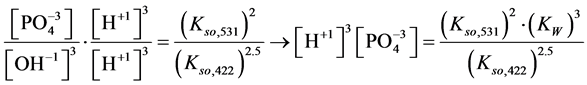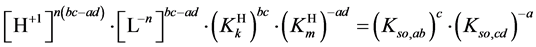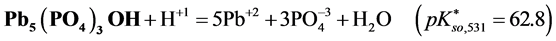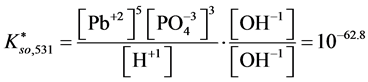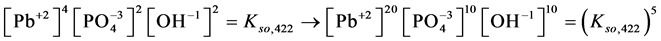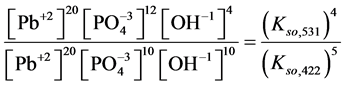Journal of Analytical Sciences, Methods and Instrumentation
Vol.04 No.03(2014), Article ID:49567,7 pages
10.4236/jasmi.2014.43012
Evaluation of Transition Points between Different Solid Phases in Aqueous Media
Anna M. Michałowska-Kaczmarczyk1, Tadeusz Michałowski2*
1Department of Oncology, The University Hospital in Cracow, Cracow, Poland
2Faculty of Engineering and Chemical Technology, Technical University of Cracow, Cracow, Poland
Email: *michalot@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 July 2014; revised 3 August 2014; accepted 10 August 2014
ABSTRACT
A uniform procedure is suggested for calculation of the pHt value(s) separating equilibrium solid phases in pH scale, at an excess of the precipitating agent. The pHt value, related to pairs of precipitates formed from the species 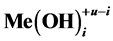
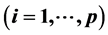 and
and 
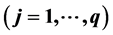 , fulfils the relation
, fulfils the relation , where F is a constant value involving pKso’s for solubility products (
, where F is a constant value involving pKso’s for solubility products (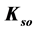 ’s) of these precipitates, and the equilibrium data, related to the species composing these precipitates.
’s) of these precipitates, and the equilibrium data, related to the species composing these precipitates.
Keywords:
Electrolytic Systems, Precipitates, pH-Intervals

1. Introduction
Some species are able to form different solid phases in aqueous media whose composition depends on pH-val- ue of these media. In particular, this was indicated for the systems obtained after introducing the ternary salts such as struvite [1] or dolomite [2] into pure water or aqueous solution of a strong base in presence/absence of CO2, originating e.g. from air. Full physicochemical knowledge was involved in the algorithms used for calculations made according to iterative computer programs related to redox or non-redox, mono- or two-phase systems [3] - [8] .

*Corresponding author.
This paper concerns calculations related to two-phase systems, and made with use of Excel spreadsheets. It refers to location of different equilibrium solid phases within defined pH-intervals [9] - [11] . The search of these pH-intervals is based on the simplified calculation procedure. The pH-values separating these intervals are named as transition  points, and denoted as
points, and denoted as .
.
2. Formulation of the Transition Points
Let the precipitates  and
and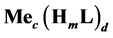 , characterized by solubility products:
, characterized by solubility products:
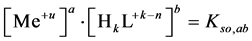 (1)
(1)
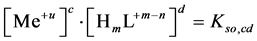 (2)
(2)
be two equilibrium solid phases formed in an aqueous system involving  and
and 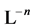 ions, together with the
ions, together with the 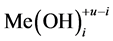


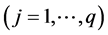


We assume that the Me-species are precipitated with an excess of the L-species; this excess is expressed by the molar concentration:

If the protonated species do not exist, then

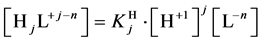
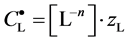
where

and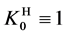
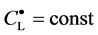
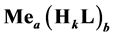


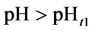
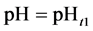
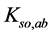
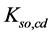
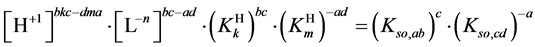
Applying in (8) the relations (3) and (4), we have 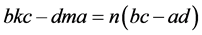

where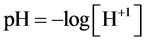
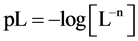

are valid simultaneously at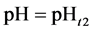

Note that 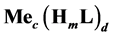




Equations (8) and (10) involve the term 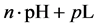


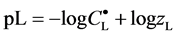
and then

In each case, 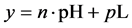

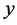


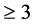
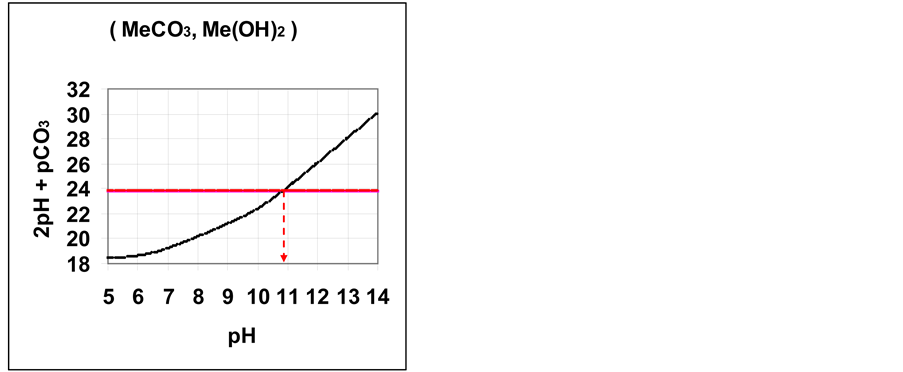
3. Transition Point for Carbonates
Many divalent cations form sparingly soluble carbonates MeCO3 






The curve of 



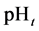
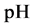


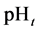
Figure 1. Location of 
Table 1. The 
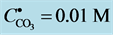

4. Transition Points for Lead Phosphates
For
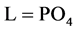


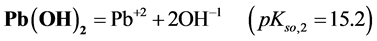
In this system, the physicochemical data related to another solid phases: Pb5(PO4)3OH and Pb4O(PO4)2 as precipitates are also cited in literature [12] [13] ; however, the solubility products for these species are formulated there in an unconventional manner. The unification of the solubility products to conventional notation will be the first, preparatory step for further considerations. The expressions for solubility products, formulated unconventionally, will be denoted as 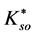
and then
The values:
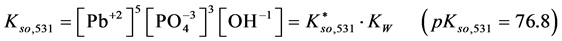
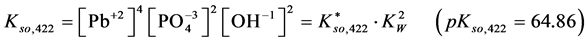
refer to the reactions:
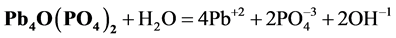
At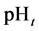
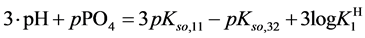
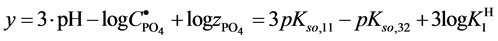
where (see Equation (7))

and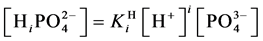

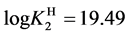
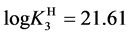
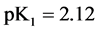
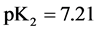
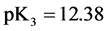

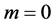

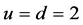

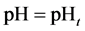
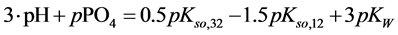
The complete set of values for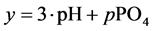

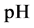
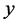




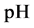

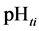
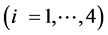

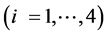

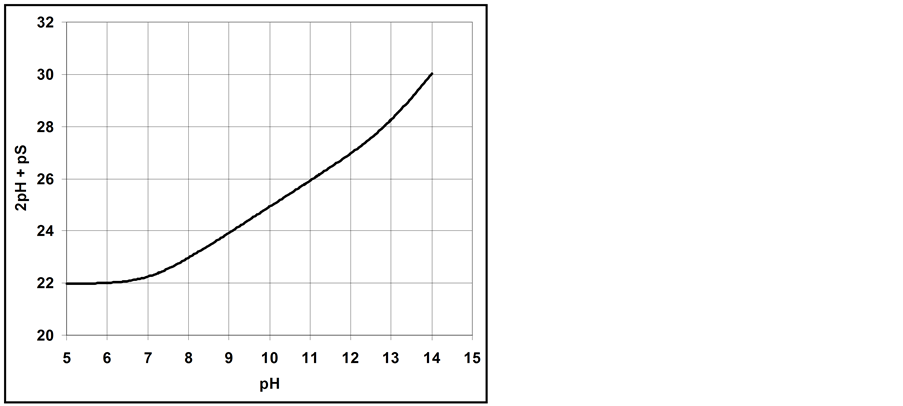
The curve of 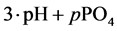

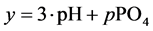

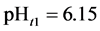

5. Crossing the pH Scale
In some cases, the precipitate of sparingly soluble salt is characterized by a relatively small solubility product value. Consequently, the 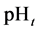

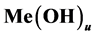

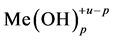
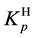



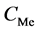

Table 2. Expressions for 

As an example, let us take the precipitates: ZnS 
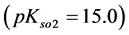
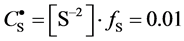






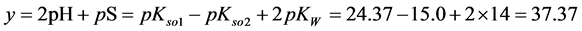

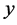
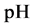
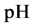


Another example is the system with precipitates: CaC2O4 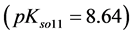




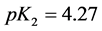



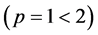
Figure 2. The curve 

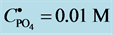
Figure 3. The curve 

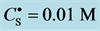
Figure 4. The curve 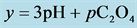
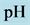
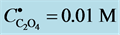
6. Final Comments
A simple, uniform method for determining the pH ranges of different precipitates as the equilibrium solid phases in aqueous systems with Me- and L-species is presented. The systems with two or more precipitates thus formed are discussed, together with the problem of ordering of appropriate precipitates along the pH scale. The above issues are applicable to the systems where soluble complexes of the 

Solubility products can be defined in different ways. The lack of awareness of this fact can be a source of confusion, as results from examples taken from the literature. In particular, for the solubility product 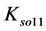

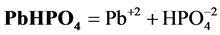
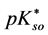

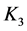

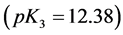
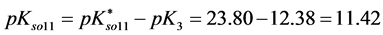
References
- Michałowski, T. and Pietrzyk, A. (2006) A Thermodynamic Study of Struvite + Water system. Talanta, 68, 594-601. http://dx.doi.org/10.1016/j.talanta.2005.04.052
- Michałowski, T. and Asuero, A.G. (2012) Thermodynamic Modeling of Dolomite Behavior in Aqueous Media. Journal of Thermodynamics, 2012, Article ID 723052. http://www.hindawi.com/journals/jtd/2012/723052/cta/
- Michałowski, T. (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non- Equilibrium Electrolytic Systems. In: Michałowski, T., Ed., Applications of MATLAB in Science and Engineering, Chapter 1, InTech, Rijeka, 1-34. http://www.intechopen.com/books/show/title/applications-of-matlab-in-science-and-engineering
- Michałowski, T. and Lesiak, A. (1994) Formulation of Generalized Equations for Redox Titration Curves. Chemia Anali-Tyczna (Warsaw), 39, 623-637.
- Michałowski, T., Ponikvar-Svet, M., Asuero, A.G. and Kupiec, K. (2012) Thermodynamic and Kinetic Effects Involved with pH Titration of As(III) with Iodine in a Buffered Malonate System. Journal of Solution Chemistry, 41, 436-446. http://dx.doi.org/10.1007/s10953-012-9815-6
- Michałowski, T., Asuero, A.G., Ponikvar-Svet, M., Toporek, M., Pietrzyk, A. and Rymanowski, M. (2012) Principles of Computer Programming Applied to Simulated pH-Static Titration of Cyanide According to a Modified Liebig-De- nigès Method. Journal of Solution Chemistry, 41, 1224-1239. http://dx.doi.org/10.1007/s10953-012-9864-x
- Michałowski, T., Toporek, M., Michałowska-Kaczmarczyk, A.M. and Asuero, A.G. (2013) New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta, 109, 519-531. http://dx.doi.org/10.1016/j.electacta.2013.07.125
- Michałowski, T., Michałowska-Kaczmarczyk, A.M. and Toporek, M. (2013) Formulation of General Criterion Distinguishing between Non-Redox and Redox Systems. Electrochimica Acta, 112, 199-211. http://dx.doi.org/10.1016/j.electacta.2013.08.153
- Michałowski, T. (1982) Solubility Diagrams and Their Use in Gravimetric Analysis. Chemia Analityczna, 27, 39.
- Dirkse, T.P., Michałowski, T., Akaiwa, H. and Izumi, F. (1986) Copper, Silver, Gold and Zinc, Cadmium, Mercury Oxides and Hydroxides. Pergamon Press, Oxford. http://search.library.wisc.edu/catalog/ocm12945958
- Michałowski, T., Janecki, D., Lechowicz, W. and Meus, M. (1996) pH Intervals for Precipitates in Two-Phase Systems. Chemia Analityczna (Warsaw), 41, 687-695.
- Crannell, B.S., Eighmy, T.T., Krzanowski, J.E., Eusden Jr., J.D. Shaw, E.L. and Francis, C.A. (2000) Heavy Metal Stabilization in Municipal Solid Waste Combustion Bottom Ash Using Soluble Phosphate. Waste Management, 20, 135-148. http://dx.doi.org/10.1016/S0956-053X(99)00312-8
- Viellard, P. and Tardy, Y. (1984) Thermochemical Properties of Phosphates. In: Nriagu, J.O. and Moore P.B., Eds., Phosphate Minerals, Springer-Verlag, Berlin, 171-198. http://dx.doi.org/10.1007/978-3-642-61736-2_4
- Inczédy, J. (1976) Analytical Applications of Complex Equilibia. Horwood, Chichester.
- Saisa-ard, O. and Haller, K.J. (2012) Crystallization of Lead Phosphate in Gel Systems. Engineering Journal, 16, 161- 168. http://dx.doi.org/10.4186/ej.2012.16.3.161
Appendix
As an example, let us consider the pair of precipitates defined by Equations (22) and (23). We have, by turns,