Journal of Analytical Sciences, Methods and Instrumentation
Vol.4 No.1(2014), Article ID:44199,8 pages DOI:10.4236/jasmi.2014.41003
Ultrafast Laser Energy Density and Retinal Absorption Cross-Section Determination by Saturable Absorption Measurements
Alfons Penzkofer1*, Meike Luck2, Tilo Mathes2,3, Peter Hegemann2
1Faculty of Physics, University of Regensburg, Regensburg, Germany
2Institute of Biology/Experimental Biophysics, Humboldt University to Berlin, Berlin, Germany
3Department of Exact Sciences/Biophysics, Vrije Universiteit, Amsterdam, The Netherlands
Email: *alfons.penzkofer@physik.uni-regensburg.de
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 7 January 2014; revised 7 February 2014; accepted 15 February 2014
Abstract
Laser pulse nonlinear transmission measurements through saturable absorbers of known absorption parameters allow the measurement of their energy density. On the other hand, nonlinear transmission measurements of laser pulses of known energy density through absorbing media allow their absorption parameter determination. The peak energy density w0P of second harmonic pulses of a mode-locked titanium sapphire laser at wavelength λP = 400 nm is determined by nonlinear energy transmission measurement TE through the dye ADS084BE (1,4-bis(9-ethyl-3-carbazovinylene)-2-methoxy-5-(2’-ethyl-hexyloxy)-benzene) in tetrahydrofuran. TE(w0P) calibration curves are calculated for laser pulse peak energy density reading w0P from measured pulse energy transmissions TE. The ground-state absorption cross-section σP and the excited-state absorption cross-section σex at λP, and the number density N0 of the retinal Schiff base isoform RetA in pH 7.4 buffer of the blue-light adapted recombinant rhodopsin fragment of the histidine kinase rhodopsin HKR1 from Chlamydomonas reinhardtii were determined by picosecond titanium sapphire second harmonic laser pulse energy transmission measurement TE through RetA as a function of laser input peak energy density w0P. The complete absorption cross-section spectrum σ(λ) of RetA was obtained by absorption coefficient spectrum measurement α(λ) and normalization to the determined absorption cross-section σP at λP [σ(λ) = α(λ)σP/αP].
Keywords:Laser Pulse Peak Energy Density Determination; Ground-State Absorption Cross-Section Determination; Excited-State Absorption Cross-Section Determination; Saturable Absorption; ADS084BE Dye; Histidine Kinase Rhodopsin HKR1; Retinal Schiff Base RetA Cofactor; Number Density Determination

1. Introduction
Saturable absorption measurements may be used to determine the peak intensity or peak energy density of laser pulses [1] . For peak intensity detection saturable absorbers with ground-state absorption recovery time τA short compared to the laser pulse duration ΔtP are appropriate. For peak energy density detection saturable absorbers (dyes) with fluorescence lifetime τF long compared to the laser pulse duration are suited. The fast saturable absorber technique was applied to determine the peak intensity of picosecond Nd:glass lasers at 1054 nm [2] (saturable absorber: mode-locking dye A9860 in 1,2-dichloroethane) and ruby lasers [3] (saturable absorber DDI in methanol). The slow saturable absorber technique was applied to measure the peak pulse energy density of Nd:glass lasers (fundamental: BDN I in 1,2-dichloroethane, second harmonic: rhodamine 6G in ethanol, third harmonic: dimethyl POPOP in cyclohexane, fourth harmonic: 9,10-dimethylanthracene in cyclohexane) and ruby lasers (fundamental: DDI in glycerol, second harmonic: dimethyl POPOP in cyclohexane) [4] .
Here the peak energy density w0P of picosecond second harmonic pulses of a mode-locked Ti:sapphire laser (wavelength λP = 400 nm, pulse duration ΔtP ≈ 5 ps) was measured using the dicarbazavinylene-MEH-benzene dye ADS084BE (from American Dye Source Inc., Quebec, Canada) in tetrahydrofuran (THF). The structural formula of ADS084BE is shown in Figure 1. Its absorption cross-section spectrum is shown in Figure 2 (from [5] ). Further relevant parameters of ADS084BE required for the calculation of the energy transmission TE versus input pump pulse peak energy density w0P are collected in Table 1 (from [5] ). Two curves of TE(w0P) were determined for two different small-signal transmissions T0 of ADS084BE in THF.
The energy transmission, TE(w0P), of picosecond titanium sapphire second harmonic laser pulses (λP = 400 nm, ΔtP ≈ 5 ps) through retinal Schiff base RetA in pH 7.4 HEPES/DDM buffer (20 mM 2-[4-(2-hydroxyethyl)- 1-pipererazin-1-yl]ethansulfonic acid, 100 mM NaCl, 10 vol-% glycerol containing 0.03 m/v-% DDM (n-dodecyl-ß-D-maltoside)) of the blue-light adapted rhodopsin fragment of the histidine kinase rhodopsin HKR1 from Chlamydomonas reinhardtii [6] was measured to determine its ground-state absorption cross-section σP, excited state absorption cross-section σex, and number density N0 (concentration C0 = N0/NA where NA is the Avogadro constant). Knowing the absolute absorption cross-section of RetA at the fixed wavelength λP, its whole absorption cross-section spectrum is obtained by measuring the absorption coefficient spectrum α(λ) with a conventional spectrophotometer and calculation of the absorption cross-section spectrum by the relation ![]() since the number density of RetA is given by
since the number density of RetA is given by![]() . The absorp
. The absorp
Table 1 . Parameters of reference dye ADS084BE in THF and of blue-light adapted cofactor RetA of HKR1 in HEPES/DDM pH 7.4 buffer used for saturable absorption calculations.
a: of HKR1 rhodosin. b: mean excited-state lifetime ![]() [7] . Abbreviations: Mm: molar mass. η: viscosity. ρ: mass density. Vm: molecule volume. J: temperature. kB: Boltzmann constant. λP: pump laser wavelength. Δtp: pump laser pulse duration (FWHM). σp: ground-state absorption cross-section at pump laser wavelength. σex: excited-state absorption cross-section at pump laser wavelength. τF: fluorescence lifetime. τFC: Franck-Condon relaxation time. τex: higher excited-state lifetime. τor: molecular reorientation time.
[7] . Abbreviations: Mm: molar mass. η: viscosity. ρ: mass density. Vm: molecule volume. J: temperature. kB: Boltzmann constant. λP: pump laser wavelength. Δtp: pump laser pulse duration (FWHM). σp: ground-state absorption cross-section at pump laser wavelength. σex: excited-state absorption cross-section at pump laser wavelength. τF: fluorescence lifetime. τFC: Franck-Condon relaxation time. τex: higher excited-state lifetime. τor: molecular reorientation time.

Figure 1. Structural formulae of ADS084BE (1,4-bis(9-ethyl-3-carbazovinylene)-2-methoxy-5-(2’- ethyl-hexyloxy)-benzene) and of retinal Schiff base isoform RetA with lysine residue coupled to rhodopsin.
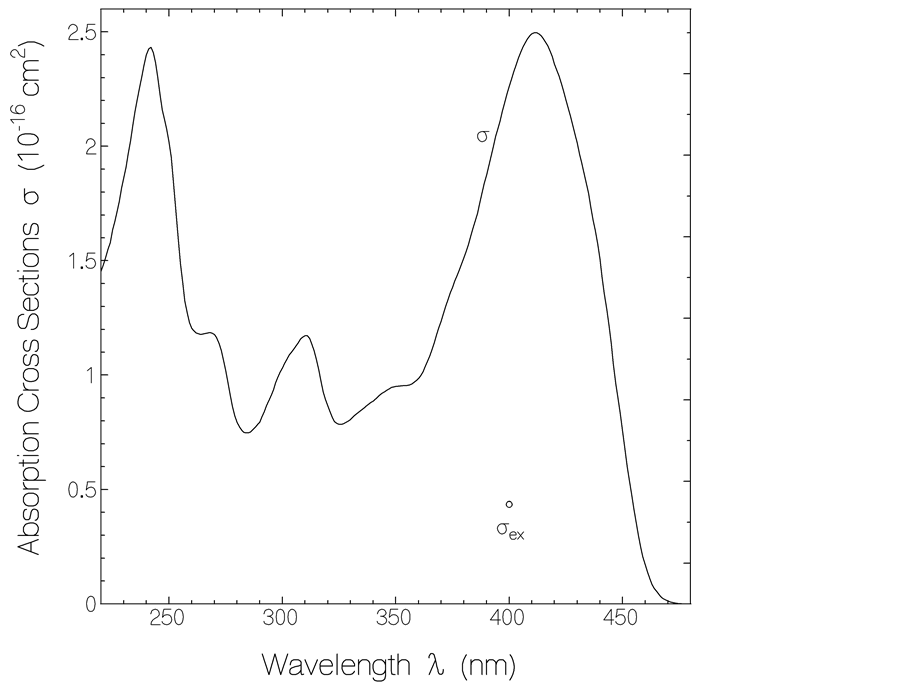
Figure 2. Absorption cross-section spectrum σ(λ) of the absorber ADS084BE in THF. Circle: determined excited-state absorption cross-section σex at λP = 400 nm.
tion cross-section spectrum of RetA was needed in the analysis of the photo-dynamics of HKR1 rhodopsin [7] . The structural formula of RetA is displayed in Figure 1. Relevant parameters of RetA cofactor in HKR1 rhodopsin for the absorption cross-section determination are collected in Table 1 (from [6] [7] ). Detailed information on the histidine kinase rhodopsin HKR1 from Chlamydomonas reinhardtii and its retinal Schiff base cofactor isoforms is found in [6] [7] and is not repeated here.
2. Experimental
The nonlinear energy transmission measurements were carried out with a mode-locked titanium sapphire laser oscillator–regenerative amplifier system (Hurricane from Spectra Physics). The experimental arrangement is sketched in Figure 3. The laser was operated at wavelength of 800 nm and pulse duration of ≈ 5 ps. The laser pulses were frequency doubled in a BBO crystal (phase-matched β-BaB2O4 crystal, from Eksma, crystal length: 3 mm). The fundamental laser light was blocked off (filter BF) and the second harmonic light passed to the sample S. The second harmonic laser pulse intensity at the sample position S was varied by working with and without lens L1 and with and without neutral density filters NF. The second harmonic laser pulse input pulse signal height SP,in was measured with the silicon photodiode PD1, and the transmitted pulse signal height SP,out was measured with the silicon photodiode PD2. The energy transmission TE through the sample was obtained by the ratio TE = SP,out/SP,in. The fused silica sample cell S of 2 mm path length was either filled with the dye ADS084BE in THF or the HKR1 rhodopsin in pH 7.4 HEPES/DDM buffer. The laser was operated in singleshot mode. It was fired every 10 seconds. Each energy transmission data point shown in Figures 5 and 6 was obtained as an average over about 30 laser shots. The retinal cofactor in HKR1 rhodopsin was brought and kept in the RetA isoform by continuous sample irradiation at 470 nm with an intensity of Iexc = 1.5 mW cm−2 using a light emitting diode LED (from Thorlabs).
The absorption dynamics was simulated by using the absorber energy level scheme of Figure 4. Level 1 describes the S0 ground-state. Its population number density is N1. Level 2’ is the excited Franck-Condon state in the S1 band (population number density N2’). Level 2 is the thermally relaxed state in the S1 band (population number density N2). Level 3 is a higher excited state in the singlet band Sn (population number density N3). σP indicates the ground state absorption cross-section at the pump laser at wavelength λP (frequency 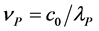 where c0 is the vacuum light velocity). σex denotes the excited absorption cross-section for S1-Sn transition of the pump laser at the wavelength λP. τFC is the Franck-Condon relaxation time within the S1 band. τF is the ground-state absorption recovery time constant (fluorescence lifetime). The picosecond pump pulse temporal and spatial intensity distribution is assumed to be Gaussian shaped (
where c0 is the vacuum light velocity). σex denotes the excited absorption cross-section for S1-Sn transition of the pump laser at the wavelength λP. τFC is the Franck-Condon relaxation time within the S1 band. τF is the ground-state absorption recovery time constant (fluorescence lifetime). The picosecond pump pulse temporal and spatial intensity distribution is assumed to be Gaussian shaped (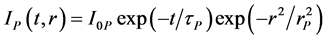 ,
,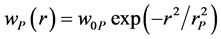 . The pump pulse energy transition through the sample is defined as
. The pump pulse energy transition through the sample is defined as
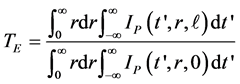 , (1)
, (1)

Figure 3. Schematic of experimental setup. ps Laser: mode-locked titanium sapphire oscillator–amplifier system. SHG: second harmonic generation. BF: fundamental laser blocking filter. NF: neutral density filter. L1, L2: lenses. S: sample. PD1, PD2: photo-detectors. LED: light emitting diode (LED 470 nm for blue-light adaptation of HKR1 rhodopsin).
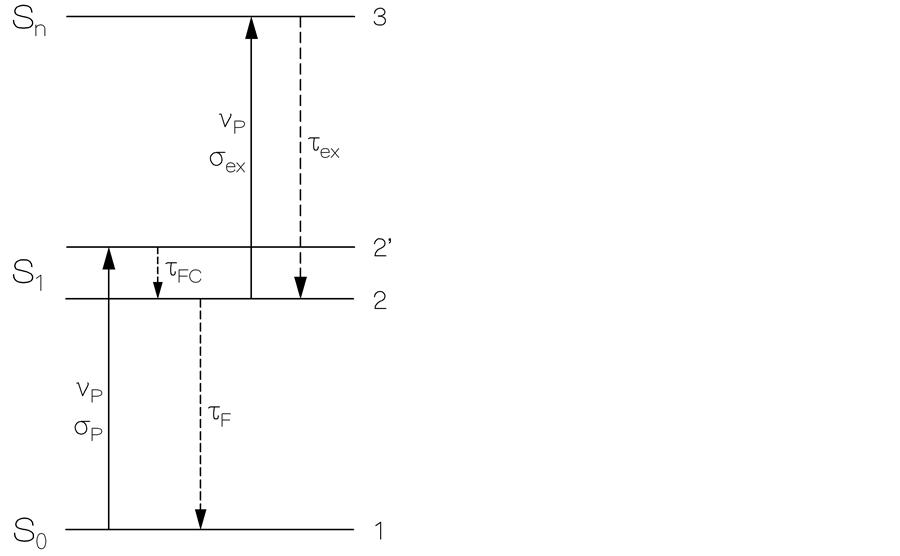
Figure 4. Energy level scheme. σP: ground-state absorption cross-section. σex: excited-state absorption cross-section. τF: ground-state absorption recovery time. τFC: Franck-Condon relaxation time in first excited state. τex: higher excited-state relaxation time. νP: pump laser frequency.
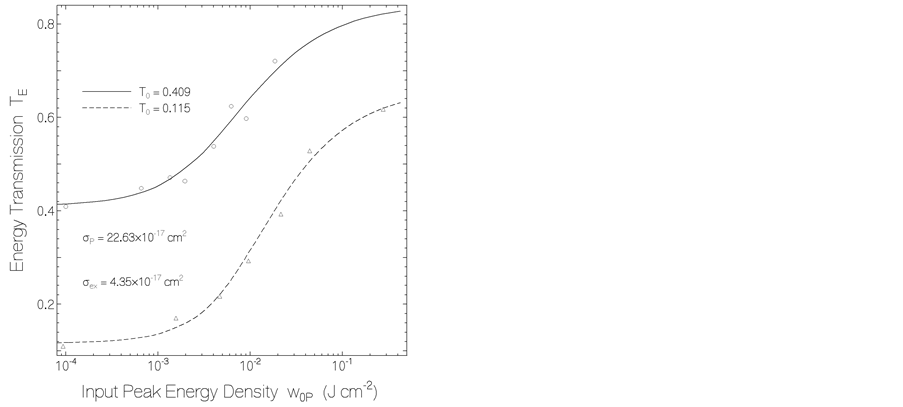
Figure 5. Energy transmission TE versus input peak energy density w0P through ADS084BE in THF. Circles and solid curve belong to sample length of l = 2 mm and small signal transmission of T0 = 0.409. Triangles and dashed curve belong to l = 2 mm and T0 = 0.115. Marks are experimental data. Curves are calculated. Applied parameters are collected in Table1
where ℓ is the sample length. The equation system for the level populations and the nonlinear pump pulse transmission through the sample is given in [8] and is not repeated here. It was solved numerically. The applied parameters in the calculations are collected in Table1
3. Results and Discussion
3.1. Calibration Curves for Pump Pulse Peak Energy Density Determination
In Figure 5 two calculated energy transmission curves belonging to the dye ADS084BE in THF are shown for two different small-signal transmissions T0 (ground-state absorption cross-section σP = 2.236 × 10−16 cm2, sample length ℓ = 0.2 cm). The dye parameters used in the calculations are listed in Table1 The excited state absorption cross-section σex of ADS084BE in THF was fitted to the experimental energy transmission results. For this purpose the TE energy transmission data points were determined with the two photodiodes, PD1 and PD2, as a function of the photodiode signal height SP,in of PD1. TE(SP,in) was scaled to the input peak energy density abscissa w0P. In the calculations σex was varied until the best agreement between the shapes of experimental TE(SP,in) data and calculated TE(w0P) curves was obtained. The best fit was found for σex = 4.35 × 10−17 cm2.
After having the calculated calibration curves, the procedure of input pump pulse energy density determination is now the following: A sample of ADS094BE in THF is prepared with small-signal transmission of T0(lP) = 0.115 or 0.409, then the energy transmission TE is measured and w0P is read from the relevant curve (w0P abscissa to TE ordinate).
3.2. Absorption Cross-Section and Number Density Determination of RetA
The energy transmission measurement results on a HKR1 rhodopsin sample with the retinal Schiff base cofactor in the RetA isoform (blue-light adapted) are displayed in Figure 6. The input peak energy densities for the data points were obtained by subsequent energy transmission measurements under the same experimental conditions on the dye ADS084BE. The solid curves in Figure 6 are calculated energy transmission curves with the fixed parameters of Table 1 for RetA and the varied parameters listed in the caption. Thereby the small signal transmission was set to the experimental value of T0 = 0.695 and the limiting high pump pulse energy transmission of Te = 0.79. A comparison of the calculated energy transmission curves with the experimental data gives σP = (2.0 ± 0.3) × 10−16 cm2 and σex = (1.29 ± 0.2) × 10−16 cm2. The molar absorption coefficients [9] are 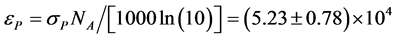 dm3∙mol−1∙cm−1 and
dm3∙mol−1∙cm−1 and ![]() dm3∙mol−1∙cm−1. The RetA number density of the used sample is obtained by the relation
dm3∙mol−1∙cm−1. The RetA number density of the used sample is obtained by the relation ![]() (sample length ℓ = 0.2 cm) giving N0 = 9.1 × 1015 cm−3 (concentration C0 = 1.51 × 10−5 mol∙dm−3).
(sample length ℓ = 0.2 cm) giving N0 = 9.1 × 1015 cm−3 (concentration C0 = 1.51 × 10−5 mol∙dm−3).
The complete absorption cross-section spectrum σ(λ) of RetA is shown in Figure 7. It was obtained by measuring the transmission spectrum T(λ) of RetA with a spectrophotometer (Cary 50 from Varian), transferring it to the absorption coefficient spectrum α(λ) by the relation  where ℓ is the sample length, and finally converting α(λ) to σ(λ) by the relation
where ℓ is the sample length, and finally converting α(λ) to σ(λ) by the relation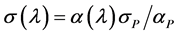 .
.
4. Conclusions
The presented laser pulse peak energy density calibration curves for ADS084BE at λP= 400 nm were calculated for a pulse duration of ΔtP = 5 ps. But the energy transmission is nearly independent of the pulse duration as long as the laser pulse duration ΔtP is short compared to the absorption recovery time τF and the molecular reorientation time τor, and longer than the higher excited-state relaxation time τex. Therefore they may be used with reasonable accuracy in the laser pulse duration range of 100 fs < ΔtP < 50 ps (see ADS084BE parameters of Table 1).
The described method of ground-state absorption cross-section σP, excited-state absorption cross-section σex, and absorbing entity number density N0 determination by TE(w0P) measurement and numerical TE(w0P) simulation of the excitation an relaxation dynamics for the level-system of Figure 4 with known ground-state absorption recovery time τF,, approximate molecular reorientation time τor and approximate higher excited-state recovery time τex is generally applicable. It works for samples with σP > σex (saturable absorption [10] ) and for samples with σP < σex (reverse saturable absorption [11] ). It only fails for samples with σP ≈ σex since in this case, the energy transmission is approximately independent of the pump pulse energy density (TE(w0P) ≈ T0).

Figure 6. Energy transmission TE(w0P) of 5 ps laser pulses at 400 nm through sample of RetA in HEPES/DDM buffer at pH 7.4. Sample length l = 2 mm. Small-signal transmission T0 = 0.695. Data fit to limiting high input energy density transmission of Te = TE(∞) = 0.79. The calculated curves belong to: (1) σP = 4 × 10−16 cm2 and σex = 2.58 × 10−16 cm2 giving 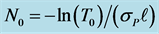 = 4.55 × 1015 cm−3; (2) σP = 3 × 10−16 cm2, σex = 1.94 × 10−16 cm2, N0 = 6.06 × 1015 cm−3; (3) σP = 2 × 10−16 cm2, σex = 1.29 × 10−16 cm2, N0 = 9.1 × 1015 cm−3; (4) σP = 1.5 × 10−16 cm2, σex = 9.69 × 10−17 cm2, N0 = 1.21 × 1016 cm−3; (5) σP = 1 × 10−16 cm2, σex = 6.46 × 10−17 cm2, N0 = 1.82 × 1016 cm−3.
= 4.55 × 1015 cm−3; (2) σP = 3 × 10−16 cm2, σex = 1.94 × 10−16 cm2, N0 = 6.06 × 1015 cm−3; (3) σP = 2 × 10−16 cm2, σex = 1.29 × 10−16 cm2, N0 = 9.1 × 1015 cm−3; (4) σP = 1.5 × 10−16 cm2, σex = 9.69 × 10−17 cm2, N0 = 1.21 × 1016 cm−3; (5) σP = 1 × 10−16 cm2, σex = 6.46 × 10−17 cm2, N0 = 1.82 × 1016 cm−3.
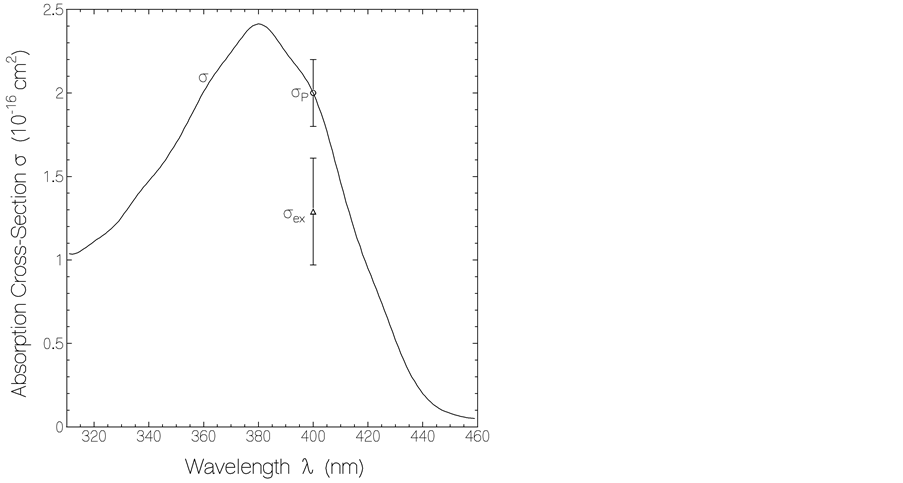
Figure 7. Absorption cross-section spectrum of RetA cofactor of HKR1 rhodopsin in pH 7.4 HEPES/DDM buffer. Experimental data points of sP (circle) and sex (triangle) at lP = 400 nm are included.
Acknowledgements
The work was supported by the Deutsche Forschungsgemeinschaft (DFG, HE3824/19-1 and HE3824/29-1 to P. H.). A. P. thanks Prof. F. J. Gießibl for his kind hospitality.
References
References
Penzkofer, A. (1988) Passive Q-Switching and Mode-Locking for the Generation of Nanosecond to Femtosecond Pulses. Applied Physics B, 46, 43-60. http://dx.doi.org/10.1007/BF00698653
Penzkofer, A. von der Linde, D., Laubereau A. and Kaiser, W. (1972) The Intensity of Short Light Pulses Determined with Saturable Absorbers. Optics Communications, 4, 377-379. http://dx.doi.org/10.1016/0030-4018(72)90082-X
Blau, W. Reber, R. and Penzkofer, A. (1982) S1-S0 Relaxation Time of Saturable Absorber DDI. Optics Communications, 43, 210-214. http://dx.doi.org/10.1016/0030-4018(82)90348-0
Grönninger G. and Penzkofer, A. (1984) Determination of Energy and Duration of Picoseconds Light Pulses by Bleaching of Dyes. Optical and Quantum Electronics, 16, 225-233. http://dx.doi.org/10.1007/BF00619377
Bansal, A.K. Holzer, W., Penzkofer, A. and Kley, E.B. (2008) Spectroscopic and Lasing Characterisation of a Dicarbazovinylene-MEH-Benzene Dye. Optics Communications, 281, 3806-3819. http://dx.doi.org/10.1016/j.optcom.2008.03.032
Luck, M. Mathes, T., Bruun, S., Fudim, R., Hagedorn, R., Nguyen, T.M.T., Kateriya, S., Kennis, J.T.M., Hildebrandt, P. and Hegemann, P. (2012) A Photochromic Histidine Kinase Rhodopsin (HKR1) that is Bimodally Switched by Ultraviolet and Blue Light. Journal of Biological Chemistry, 287, 40083-40090. http://dx.doi.org/10.1016/j.optcom.2008.03.032
Penzkofer, A. Luck, M., Mathes, T. and Hegemann, P. (2014) Bistable Retinal Schiff Base Photo-Dynamics of Histidine Kinase Rhodopsin HKR1 from Chlamydomonas reinhardtii. Photochemistry and Photobiology, in print. http://dx.doi.org/10.1111/php.12246
Holzer, W. Gratz, H., Schmitt, T., Penzkofer, A., Costela, A., García-Moreno, I., Sastre, R. and Duarte, F.J. (2000) Photo-Physical Characterization of Rhodamine 6G in a 2-Hydroxyethyl-Methacrylate Methyl-Methacrylate Copolymer. Chemical Physics, 256, 125-136. http://dx.doi.org/10.1016/S0301-0104(00)00101-4
Valeur, B. (2002) Molecular Fluorescence. Principles and Applications, Wiley-VCH, Weinheim, Germany.
Hercher, M. (1967) An Analysis of Saturable Absorbers. Applied Optics, 6, 947-954. http://dx.doi.org/10.1364/AO.6.000947
Bentivegna, F. Canva, M., Georges, P., Brun, A., Chaput, F., Malier, L. and Boilot, J.-P. (1993) Reverse Saturable Absorption in Solid Xerogel Matrices. Applied Physics Letters, 62, 1721-1723. http://dx.doi.org/10.1063/1.109585
Fischer, H. Polikarpov, I. and Craievich, A. (2004) Average Protein Density is a Molecular-Weight-Dependent Function. Protein Science, 13, 2825-2828. http://dx.doi.org/10.1110/ps.04688204
Penzkofer, A. Falkenstein, W. and Kaiser, W. (1976) Vibronic Relaxation in the S1-State of Rhodamine Dye Solutions. Chemical Physics Letters, 44, 82-87. http://dx.doi.org/10.1016/0009-2614(76)80414-9
Graf F. and Penzkofer, A. (1985) Sn-State Lifetime Determination of Dyes. Optical and Quantum Electronics, 17, 53-68. http://dx.doi.org/10.1007/BF00619994
NOTES

*Corresponding author.


