Materials Sciences and Applications, 2010, 1, 223-246
doi:10.4236/msa.2010.14035 Published Online October 2010 (http://www.SciRP.org/journal/msa)
Molar Binding Energy of Zigzag and Armchair
Single-Walled Boron Nitride Nanotubes
Levan Chkhartishvili1, Ivane Murusidze2
1Department of Physics, Georgian Technical University, Tbilisi, Georgia; 2Institute of Applied Physics, Ilia State University, Tbilisi,
Georgia.
Received August 4th, 2010; revised August 27th, 2010; accepted September 6th, 2010.
ABSTRACT
Molar binding energy of the boron nitride single-walled zigzag and armchair nanotubes is calculated within the
quasi-classical approach. We find that, in the range of ultra small radii, the binding energy of nanotubes exhibit an
oscillatory dependence on tube radius. Nanotubes (1,1), (3,0), and (4,0) are predicted to be more stable species among
single-walled boron nitride nanotubes. The obtained binding energies of BN single-walled nanotubes corrected with
zero-point vibration energies lies within the interval (12.01-29.39) eV. In particular, molar binding energy of the ul-
tra-large-radius tube is determined as 22.95 eV. The spread of the molar zero-point vibration energy of BN nanotubes
itself is (0.25-0.33) eV and its limit for ultra-large-radius tubes is estimated as 0.31 eV. The binding energy peak lo-
cated at 2.691 Å corresponds to the equilibrium structural parameter of all realized stable BN nanotubular structures.
Keywords: Binding Energy, Zigzag and Armchair Nanotubes, BN
1. Introduction
Boron nitride with the chemical formula BN can be
found in the form of one-dimensional diatomic molecules,
two-dimensional nanotubes and fullerenes, three-dimen-
sional crystals like the layered hexagonal h-BN and
rhombohedral r-BN as well as turbostratic t-BN, cubic
zinc-blende c-BN and wurtzite w-BN modifications as
well as their nanostructures etc. Boron and nitrogen at-
oms are surrounded tetrahedrally in both denser c-BN
and w-BN crystals.
Any constituent atom of an h-BN crystal, which is be-
lieved to correspond to the boron nitride ground state,
may be considered as a 3-coordinated atom because the
strong chemical binding (covalent with some deal of
ionic) occurs only within the layers, while weak van der
Waals forces seem to be responsible mostly for interlayer
binding. The h-BN crystal has a “graphitic” structure
with a two-layer stacking sequence (r-BN is character-
ized by a three-layer stacking). These layers consist of
regular hexagons (i.e., 6-membered atomic rings) with
vertexes alternatively occupied by B and N atoms. In the
h-BN crystal, B atoms are placed directly above N atoms
and vice versa. Therefore one might suppose that the
ionicity contributes to interlayer bonding as well. How-
ever, actually, the electrostatic component is insignificant
due to the large interlayer distances. It is argued also by
the existence of a layered r-BN crystal, in which each
subsequent layer is turned around an angle of /3

, and
also by the isolated plane defects and their bundles in-
cluded in real h-BN crystals, in which any given atom
can be placed above the same atom. In addition, it is pos-
sible to obtain turbostratic t-BN and amorphous struc-
tures in the form of mixes of various boron nitride crys-
talline phases, and multi-walled nanotubular and multi-
shelled fullerene-like BN structures. Strong chemical
bonding between atoms in a given layer and weak inter-
layer interaction in layered boron nitrides specify an op-
portunity of physical and chemical intercalations by
various atoms and molecules.
Based upon the similarity of structures of the boron
nitride layered phases with graphite, it was assumed [1]
that along with carbon C nanotubes, stable BN nanotubes
– fragments of hexagonal or mixed BN layers wrapped
into cylinders – could also exist.
Indeed, by means of arc discharge BN nanotubes had
been obtained both from carbon nanotubes [2] and in
carbon-free plasma [3]. The arc discharge methods were
used to produce BxCyNz nanotubular structures identified
by the high-resolution transmission-electron-microscopy

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 224
(TEM) together with K-edge electron-energy-loss-spec-
trometry (EELS) determining the local atomic composi-
tion, while, in a carbon-free plasma discharge area be-
tween a BN-packed W-rod and a cooled Cu-electrode,
multi-walled pure BN tubes were produced with inner
diameters on the order of 1 to 3 nm and with lengths up
to 200 nm; EELS of individual tubes yielded B/N ratio of
approximately 1.
At present various methods of synthesis of the BN
nanotubular structures are developed.
The arc discharge in a molecular nitrogen atmosphere
between electrodes made of graphite and refractory bo-
ron compounds, e.g., hafnium diboride HfB2, forms BN-C
nanotubes with strong phase separation between BN and
C layers along the radial direction [4,5]. If both elec-
trodes are made of HfB2 rods, single- or double-walled
chemically pure BN nanotubes are formed with a struc-
ture close to stoichiometric B/N ~1 [6]. Most obtained
tube ends are closed by flat layers perpendicular to the
tube axis. A closure by a triangular facet resulting from
three 120-disclinations was proposed to account for this
specific shape. For the most part, the multi-walled BN
nanotubes are formed with electrodes made of zirconium
diboride ZrB2 [7,8]. In this case most of the nanotubes
have diameters from 3 to 40 nm and lengths on the order
of 100 nm. Single-layer tubes with diameters of 2 to 5
nm are also formed rarely. The morphology of the tube
tips suggests the presence of pentagons and heptagons
which are energetically less favorable compared with
squares.
A laser melting of the solid-state BN (of any crystal
structure, not only layered but also amorphous) at high
nitrogen pressure, (5-15) GPa, forms nanotubes free from
inclusions, containing from 3 up to 8 walls, and having a
characteristic outer diameter of (3-15) nm [9].
BN nanotubes have been also obtained by pyrolysis of
the molecular precursor with the use of Co catalysts [10].
Bundles of single-walled (or containing few layers)
BN nanotubes with almost stoichiometric structure can
be formed in substitution reactions – by thermal treat-
ment of a mixture of boron trioxide or trichloride, and
bundles of single-walled C-nanotubes at high tempera-
tures, (1250-1350)℃, in a nitrogen flow [11,12].
BN nanotubes also grow in solid-state process that in-
volves neither deposition from the vapor phase nor che-
mical reactions [13]. The nanotubes were produced by
first ball-milling of the layered h-BN powder to generate
highly disordered or amorphous nanostructures and fo-
llowed by the product annealing at temperatures up to
1300℃. The annealing leads to the nucleation and growth
of hexagonal BN nanotubes both of cylindrical and bam-
boo-like morphologies.
Multi-walled BN nanotubes have been obtained by
carbothermal reduction of the ultra-dispersive amorphous
boron oxide B2O3 at simultaneous nitriding at high tem-
peratures, (1100-1450)℃ [14,15]. For large tubes, it is
found that the ratio of length to radius is preserved.
Besides of arc-melting, pyrolysis, and chemical reac-
tions, boron nitride nanotubular structures were created
by means of ballistic nuclear displacements caused in a
h-BN layered crystal structure by electron irradiation in
TEM [16,17].
High growth temperatures (above 1100℃), a low pro-
duction yield, and impurities have prevented progress in
applications of BN nanotubes in the past decade. Rather
recently, it has been shown that these tubes can be grown
on substrates at lower temperatures (of about 600℃) [18].
High-order tubular structures were constructed, which
can be used without further purification.
For synthesizing BN nanotubular material, some meth-
ods were inspired from carbon. In particular, these in-
clude techniques such as laser ablation and non-ablative
laser heating [19]. Transformation of the compressed
powders of the fine-grained h-BN into nanotubular form
can be induced [20] by the concentrated light energy in
nitrogen flow. Fiber-like clusters synthesized by evapo-
ration of the layered BN in a nitrogen atmosphere and
obtained in powders formed on substrate or chamber
surfaces contained nanotubes with diameters and lengths
equal to (0.05-200) and (100-3000) m, respectively.
Applying TEM, there were obtained their associations in
tree- and coral-like aggregates.
BN nanotubes can be grown from a nanococoon seed
as well [21].
Recently the development of a new method for pro-
ducing long, small-diameter, single- and few-walled, BN
nanotubes in macroscopic quantities has been reported
[22]. The pressurized vapor/condenser (PVC) method
produces highly crystalline, very long, small-diameter
nanotubes without catalysts. Their palm-sized, cotton-
like masses of raw material were grown by this technique
and spun directly into centimeters-long yarn. Nanotube
lengths were observed to be ~100 times that of those
grown by the most closely related method.
Soon after synthesizing the first BN nanotubes, it was
proposed a number of their possible applications in tech-
nique [3]. For example, a system of the collinear BN
nanotubes forms a boron nitride fiber. At the same time,
the theory [23] developed for structural and electronic
properties of nanotubular heterojunctions, in which one
of the layers is nanotubular boron nitride (namely, for
C/BN and BC2N/BN systems), leads to a conclusion that
on basis of it a different electronic devices can be de-
signed. In particular, nanostructures with C-layers both in
the center and at the periphery separated by a few BN-
layers may allow the creation of sandwich nanotubular

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 225
devices [4]. Within the special semiempirical approach
[24] C/BN superlattices and isolated junctions have been
investigated as specific examples by the wide variety of
electronic devices that can be realized using such nano-
tubes. The bottom of the conduction bands in pure BN
nanotubes is controlled by a nearly-free-electron-state
localized inside the tube suggesting interesting electronic
properties under doping.
Other opportunities of application of the BN nanotubes
are connected with the features of their phonon spectrum
[25]. Such dielectric tubes without inversion center can
be used as a phonon laser in GHz − THz range or hyper-
sound quantum generator. Because of the presence of
special nanotubular oscillatory modes, there is a strong
enhancement of electron-phonon interaction in compari-
son with a bulk material. It is not excluded that close-
packed one-dimensional BN nanotubes will serve as
high-temperature superconductors. The GHz oscillatory
behavior of double-walled BN nanotubes was also pre-
dicted [26,27]. This system can also be employed for
making good shock absorbers because application of low
pressure leads to its significant compression.
The band gap progression with BN nanotube diameter
(which is of crucial importance for device applications)
was presented and analyzed in detail in [28]. In zigzag
BN nanotubes, radial deformations that give rise to
transverse pressures decrease the gap from 5 to 2 eV,
allowing for optical applications in the visible range [29].
Importantly, both the zigzag and armchair tubes are
found [30] (see also [31]) to exhibit large second-order
nonlinear optical behavior with the second-harmonic
generation and linear electro-optical coefficients being
up to 15-times larger than that of bulk BN in both denser
zinc-blende and wurtzite structures. This indicates that
BN nanotubes are promising materials for nonlinear op-
tical and optoelectronic applications.
The electronic structure of BN nanotubes can be tuned
within a wide range through covalent functionalization
[32] (see also [33]). The ultraviolet (UV) and visible ab-
sorption spectra indicate that their electronic structure
undergoes drastic changes under functionalization. First
principle calculations revealed that the covalently func-
tionalized BN nanotubes can be either n- or p-doped de-
pending on the electronegativity of molecules attached.
Their energy gap can be adjusted from UV to visible
optical range by varying concentration of functionalizing
species.
One-dimensional crystals of potassium halides, inclu-
ding KI, KCl, and KBr, were inserted into BN nanotubes
[34]. High-resolution TEM and energy-dispersive X-ray
spectrometry were used to characterize their microstruc-
tures and compositions. The fillings are usually single
crystals with lengths up to several m. The wetting
properties (static contact angles of the liquids and surface
tension) of individual BN nanotubes were studied [35]
experimentally using a nanotube-based force to measure
the interactions between nanotubes and liquids in situ.
First principles simulations on the interaction of mo-
lecular hydrogen H2 with the native and substitutional
defects in small-diameter (8,0) BN nanotubes were per-
formed in [36]. The adsorption of H2 in structures found
to be endothermic with respect to dissociation, with the
small-diameter nanotube possessing the smaller barrier.
Although chemisorption along the tube axis is energeti-
cally preferred, the barrier for dissociation is lower for
chemisorption across the tube axis. This implies that
chemisorbed hydrogen can be kinetically trapped in a
higher energy state. Dopants that maximize the localiza-
tion of the higher-occupied-molecular-orbital (HOMO)
and lower-unoccupied-molecular-orbital (LUMO) states
maximize hydrogen binding energies. C-dopants do not
enhance H2 binding, whereas Si-dopants substituting for
N provide H2 binding energies of 0.8 eV, at the upper
end of the range required for hydrogen storage. The for-
mation energy of most defects is reduced with increasing
curvature except for the C-substitutionals. Vacancies do
not reduce the barriers for H2 dissociation for strongly
curved nanotubes. The surface stress induced by the
nanotube curvature boosts the hydrogen storage capabili-
ties of vacancies with the nitrogen vacancy chemisorbing
4H and allowing a H2 molecule to enter the interior of the
tube. The hydrogen binding properties of BN systems
strongly depend on existing defects and dopants. Pre-
treating of these systems so as to partially remove nitro-
gen should enhance H2 adsorption properties. The hy-
drogen absorption capacity of Ti-covered single-walled
BN nanotube was investigated using first principles
plane-wave (PW) method [37]. The weak interaction of
H2 molecules with the outer surface of bare nanotube can
be significantly enhanced upon functionalization by Ti
atoms: each Ti atom adsorbed on tube can bind up to four
H2 molecules with average binding energy suitable for
room temperature storage.
The morphology of BN nanotubes with a collapsed
structure has been discovered by a metal-catalyzed
treatment [38]. The collapse causes the dramatic enlarge-
ment of a specific surface area of BN nanotubes and re-
markably enhances the hydrogen storage capacity of BN
nanotubes.
It was reported [39] that proteins are immobilized on
boron nitride nanotubes. There is a natural affinity of a
protein to BN nanotube: it can be immobilized on tube
directly, without using of an additional coupling reagent.
Besides, boron nitride nanotubes may be dissolved in
organic solvents by wrapping them with a polymer [40].

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 226
It was proposed [41] that BN polymers, having the
structures similar to organic polymers, can serve as a
cheap alternative to inorganic semiconductors in design-
ing modern electronic devices. Some related potential
innovations, including band gap tuning, were also dem-
onstrated.
The observed giant Stark effect significantly reduces
the band gap of BN nanotubes and thus greatly enhances
their utility for nanoscale electronic, electromechanical,
and optoelectronic applications [42]. In particular, this
effect may be important for tuning the band gap of BN
nanotubes for applications as a nanoscale field-effect-
transistor (FET).
Boron nitride nanotubes have also manifested stable
currents in field emission geometry and may be more stable
than carbon nanotubes at high temperatures [43,44].
As it was mentioned, boron nitride nanotubes exhibit
many similarities with the carbon ones (such as high
Young modulus etc.) and might have superior unique
mechanical, thermal, and electronic properties [45]. In
addition, BN nanotubes are characterized by chemical
inertness and poor wetting [46].
The factor that distinguishes BN from C is partial het-
eropolarity of the chemical bonding. For this reason, one
more sphere of possible applications of BN nanotubes
can be new pyroelectric and piezoelectric materials
promising for applications in nanometer-scale sensors
and actuators. The 3-fold symmetry of a BN sheet, the
III-V analog to graphite, prohibits an electric polarization
in its ground state. However, this symmetry is broken
when the sheet is wrapped to form a BN tube. It was
shown [47] that this leads to an electric polarization
along the nanotube axis which is controlled by the quan-
tum-mechanical boundary conditions of its electronic
states around the tube circumference. Thus, the macro-
scopic dipole moment has an intrinsically nonlocal quan-
tum-mechanical origin from the wrapped dimension.
Combining first principles, tight-binding methods and
analytical theory, the piezoelectricity of heteropolar (in
particular, BN) nanotubes was found [48] to depend on
their chirality and radius. This effect can be understood
starting from the piezoelectric response of an isolated
sheet along with a structure specific mapping from the
sheet onto the tube surface. It was demonstrated that a
linear coupling between the uniaxial and shear deforma-
tions occurs for chiral nanotubes, and the piezoelectricity
of nanotubes is fundamentally different from its coun-
terpart in a bulk material. First principles calculations of
the spontaneous polarization and piezoelectric properties
of BN nanotubes have shown [49] that they are excellent
piezoelectric systems with response values larger than
those of piezoelectric polymers. The intrinsic chiral sy-
mmetry of the nanotubes induces an exact cancellation of
the total spontaneous polarization in ideal, isolated
nanotubes of arbitrary indexes. But the breaking of this
symmetry by the intertube interaction or elastic deforma-
tions induces spontaneous polarization comparable to
that of wurtzite bulk semiconductors [50].
Multielement nanotubes comprising multiple SiC-core,
an amorphous SiO2-intermediate layer, and outer shells
made of BN and C layers separated in the radial direction
with diameters of a few tens of nm and lengths up to 50
m were synthesized by means of reactive laser ablation
[51]. They resemble a coaxial nanocable with a semi-
conductor-insulator-semiconductor (SIS) geometry and
suggest applications in nanoscale electronic devices that
take advantage of this self-organization mechanism for
multielement nanotube formation.
A theoretical description of electron irradiation of sin-
gle-walled BN nanotubes was presented in [52]. As a
first step, the anisotropy of the atomic emission energy
threshold was obtained within extended molecular-dyna-
mical (MD) simulations based on the density-functional-
theory (DFT) tight-binding method. As a second step,
total cross section for different emission sites as a func-
tion of the incident electron energy was numerically de-
rived. Two regimes were then described: at low irradia-
tion energies (below 300 keV), atoms are ejected mostly
from the upper and lower parts of the tube while at high
energies (above 300 keV) atoms are ejected mostly from
the side walls. Typical values of the total cross section of
knock-on processes are obtained to vary from a fraction
of barn (at side wall for 150 keV electrons) up to around
20 barns (for 1 MeV electrons). In BN nanotubes, the
emission energy threshold maps were reported to show B
sputtering to be more favorable for low irradiation ener-
gies, while N sputtering is more favorable at high ener-
gies. These calculations of the total knock-on cross sec-
tion for nanotubes can be used as a guideline for TEM
experimentalists using high energy focused beams to
shape nanotubes, and also, more generally, if electron
irradiation is used to change nanotube properties such as
their optical behavior or conductivity.
Such wide field of possible technical and technological
applications of boron nitride nanotubes makes useful
theoretical research determining their main physical
characteristics. In particular, for purposeful design of
some materials and devices based on nanotubular BN,
like the fibrous composites, tubular heterojunctions,
other nanoelectronic devices, nanoreservoirs for hydro-
gen storage etc, it is very important to be able to predict
reliably values of the ground-state parameters, especially,
the molar binding energies and sizes of the nanotubes
with given indexes and their relative stability. In present
work, this task is solved for the most stable – achiral
(zigzag and armchair) – single-walled forms.

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 227
Paper is organized as follows. In Section 1, we have
introduced methods of synthesis of the boron nitride
nanotubes and their technological applications. Section 2
is a brief summary of the structural and binding data
available on nanotubular boron nitride. In Section 3, the
theoretical approach based on the quasi-classical ap-
proximation to the binding energy calculation and ge-
ometries is presented. In Section 4, results of the per-
formed calculations are presented in the form of curves
“molar binding energy – structural parameter”. Section 5
is devoted to estimation of the nanotube lattice zero-point
vibration energy. And finally, Section 6 discusses rela-
tive stability of the boron nitride nanotubes of various
radii and makes an attempt to generalize the obtained
results.
2. Structural and Binding Data
Let us start with a brief overview of the structural and
binding data available on a boron nitride diatomic mole-
cule, isolated sheet, and nanotubular form.
2.1. Molecular Boron Nitride
The diatomic molecule BN can be considered as a sim-
plest (degenerated) form for boron nitride nanotubes. In
general, electronic theory of substance considers a dia-
tomic molecule as a special problem for its intermediate
structural and, consequently, electronic properties be-
tween mono- and polyatomic systems. Peculiarities are
related mainly with the system axial symmetry and
uniqueness of the structural parameter – interatomic dis-
tance d. Unlike the solid state or nanoscale boron ni-
trides, which are materials with a diversity of technical
and industrial applications, BN molecule, which exists
under the extreme conditions, is only of academic inter-
est as a “building block” for two- and three-dimensional
boron nitride structures. From the standard thermoche-
mical data, the energy of B–N bond at the equilibrium
length is known to be considerably higher compared with
those of B–B and N–N bonds. In addition, any stable
regular BN structure is a network of atomic rings with
alternating atoms such that the nearest-neighbor envi-
ronment of both B and N atoms consists of only B–N
bonds. Therefore, the B–N bond length is a key intera-
tomic distance in the analysis of boron-nitrogen binding.
There are known some old first principles and
semiempirical investigations for boron–nitrogen interac-
tion (see [53,54]). Applying a self-consistent-field (SCF)
procedure to the BN molecule in [55], it was calculated
molecular orbitals (MOs) in order to minimize total en-
ergy of the diatomic system. Then using the spectro-
scopic data available for the corresponding ground state,
the BN molecule dissociation energy value E was
found to be 4.6 eV. According to the original theoretical
approach of [56], the equilibrium interatomic distance in
this molecule equals to 1.307 Å. At the same time, spec-
troscopic parameters characterizing the calculated bo-
ron–nitrogen interaction potential curve lead to the dis-
sociation energy estimation of 5.05 eV. Nearly the same
theoretical value for the bond length of 1.320 Å was
suggested in [57]. In [58], a short-ranged classical-force-
field (CFF) modeling of BN modifications was per-
formed on the basis of experimental and first principles
solid-state and diatomic-molecular data. In particular,
assuming that CFF can be correctly determined by a sum
of only two-body interaction terms, the B−N potential
energy had been expressed analytically via Morse poten-
tial, which gave 1.32521d

Å and 5.0007EeV.
However, it was noted [25] that standard forms of
the pair interatomic potentials, such as the Morse,
Mee–Grüneisen, Buckingham, and other potentials, con-
verge slowly and, therefore, a cutoff procedure should be
used. But, in such a case a non-physical jump on the po-
tential radial function can arise. In order to eliminate this
problem, based on the embedded atom method, a new
B−N interatomic potential was designed which fulfills
the conditions for smooth end: the potential function and
its derivative (i.e., the interatomic force) vanish at the
cutoff radius. The equilibrium bond length of 1.4457 Å
and binding energy of 4.00 eV were found to reproduce
correctly relative stabilities of the boron nitride layered
structures.
We also suggested [59] a theoretical, namely, quasi-
classical method of calculation of the dependence the
B–N interatomic binding energy E upon the bond
length d. The constructed ()EEd curve was shown
to be useful for estimations of BN crystalline structures
cohesion parameters as well. This function reveals stan-
dard behavior characteristic for the central pair potentials.
(0)E

 , and () 0Ed

if d is equal or greater
than the sum of B and N quasi-classical atomic radii
() 2.30r

and () 1.70r

Å, i.e., ()() 4.00dr r


Å (note that quasi-classical B−N interatomic potential
automatically fulfills the conditions for the smooth end at
() ()
dr r



), while within the intermediate region
() ()
0dr r



 it is an oscillating function with sev-
eral maxima. Among these maxima only one is available
kinetically and, therefore, it corresponds to the equilib-
rium. Analysis of the piece of the quasi-classical
()EEd

curve for BN diatomic molecule, in the vicin-
ity of this maximum, yields the values of bond length of
1.55 Å and binding energy of 4.51 eV. Same dependence
determined earlier [60,61] within the frames of another
quasi-classical parameterization scheme (for this purpose
the screening factor of the potential affecting the given
electron in interacting atom was approximated by the

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 228
radial polynomial, not by the constant) is relatively flat
and leads to the estimations of 1.58 Å and 4.79 eV.
Thus, the spread in theoretical and semiempirical val-
ues for BN molecule binding energy is (4.0-5.5) eV,
which overlaps with the recommended [62] experimental
dissociation energy value of (4.0 ± 0.5) eV. The available
first principles and semiempirical calculations and ther-
mochemical experimental data lead to the binding energy
values of about (4-7) eV per B−N bond for various, dif-
ferently coordinated, BN modifications (for sheet and
nanotubular structures see below). Such kind of estima-
tions may be considered to be in qualitative agreement
with the quasi-classically calculated B–N bond energy as
the ground state energetic parameters are quite sensitive
to the atomic coordination. For this reason, we focus our
attention on the differences in the bond length values
between BN molecular and crystalline phases.
The quasi-classical values for the isolated B−N bond
length and other relevant theoretical and semiempirical
data, which lie over the range (1.307-1.580) Å, are overes-
timated in comparison with 1.281 Å measured in 11B14N
molecule [63]. An explanation may be that BN molecular
spectra [64] verify triplet ground state, but at the same
time reveal a low-lying singlet state with longer bond.
Quasi-classically calculated interatomic vibration en-
ergy in a B−N diatomic system of 0.178 eV/mole (the
corresponding vibration quantum equals to 1435 cm1)
was found by fitting the quasi-classical B–N potential
curve with parabola [60,65]. This value is in good agree-
ment (accurate within 5 %) with the values experimen-
tally obtained for a neutral BN molecule of 0.187 (1514.6)
[63] and 0.188 eV/mole ((1519.0 ± 0.2) cm1, from the
absorption spectra Fourier analysis for laser-induced
molecular fluorescence) [64].
According to the SCF theoretical method of [56], the
ground state vibration energy in molecular BN estimated
as 0.179 eV/mole (1446 cm1), which is almost the quasi-
classical result.
In [57], it was suggested the higher theoretical value of
0.217 (1750), what is close with 0.216 eV/mole (1740
cm1) measured in ionized molecule BN+ [66].
Studies of more complex molecular clusters of B and
N are also interesting to get deeper insight into the defect
formation processes in boron nitride nanotubes. High-
temperature Knudsen cell mass spectrometry was used to
study the equilibria involving the B2N molecule [67].
The thermal functions necessary to evaluate the mass
spectrometric equilibrium data had been calculated from
available experimental and theoretical molecular pa-
rameters. In particular, in some B2N formation reactions
changes in enthalpy have been measured. Room tem-
perature atomization and formation enthalpies were de-
termined to be 10.84 and 5.71 eV, respectively. At the
same time, first-principles calculations were performed
to estimate the electronic parameters of B2N, such as
ionization energy and electron affinity.
Mixed clusters of B and N atoms – B2N, BN2, B3N,
B4N, B2N2, and B3N2 – can be produced by sputtering of
a solid state BN [68]. Atom ordering in assumed linear
species had been derived from measurements of the mass
distribution of both the positive and the negative prod-
ucts from the fragmentation of the anionic clusters in a
gas target. As for neutral configurations, they were cal-
culated. A tendency was found that a structure with the
highest number of B−N bonds is most stable both in neu-
tral and anionic species (an exception is the BN2 mole-
cule). In contrast to this, the species with the highest
number of adjacent same atoms (except for triatomic
chains) had the largest electron affinity.
2.2. Boron Nitride Sheet
The facts that boron nitride layered crystals and nano-
tubes may be prepared suggest the necessity of analyzing
the hypothetic isolated infinite hexagonal layer, i.e., the
BN sheet. Corresponding two-dimensional BN crystal is
represented as a planar layer composed of regular hexa-
gons with vertexes alternately occupied by B and N at-
oms. Classification and discussion of the BN haeckelite
sheet structures, consisting of not only hexagonal atomic
rings but also other even-membered rings, one can find
in [69].
For the first time, the truncated crystal approach in the
form of two semiempirical (standard and extended itera-
tive Hückel) methods was applied to a two-dimensional
hexagonal boron nitride structure [70]. The bond length
was found to be 1.48 or 1.50 Å. However, when semiem-
pirical calculations were performed on a two-dimensional
periodic small cluster of the h-BN layer the equilibrium
B−N distance was computed as 1.441 Å [71]. In [72], the
3-coordinated B12N12 network of 6-membered atomic
rings was examined theoretically. Namely, the total en-
ergy calculated using Hartree–Fock (HF) approach and
DFT in local and gradient-corrected forms was mini-
mized with respect to the B−N bond length. But, “graph-
itic” isomer B12N12 is only a fragment of the BN sheet
and its geometry appears to be somewhat distorted be-
cause of finite sizes. As is to be expected, slight devia-
tions of the bonds’ angles from the ideal value of 120
were observed for the bonds of atoms forming the central
hexagon: −(2.52-2.65) for B atoms and +(2.52-2.65) for
N atoms. There were also obtained number of unequal
bond lengths: (1.266-1.283), (1.371-1.378), (1.427-1.442),
(1.434-1.444), (1.520-1.536), and (1.553-1.576) Å. The
finiteness of the quasi-classical atomic radii allowed us
to obtain the B−N bond length for an infinite boron ni-
tride sheet within the initial quasi-classical approxima-

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 229
tion [73]. The calculated dependence of the molar bind-
ing energy on the lattice constant exhibits a maximum of
23.0 eV at 2.64 Å, which should correspond to the equi-
librium state for an isolated hexagonal layer (analytical
optimization [74] of the lattice parameter using the bind-
ing energy calculated in quasi-classical approximation,
which is possible only by neglecting the vibration energy,
yields slightly different values: 23.2 eV and 2.66 Å, re-
spectively). The lattice constant of 2.64 Å implies B−N
bond length of 1.52 Å. Correction in energy introduced
by zero-point vibrations was estimated as 0.242 eV/mole
[65,73].
The quasi-classical bond length of 1.52 Å in an iso-
lated BN sheet is in reasonable agreement (accurate
within 4.6 %) with the bond length of 1.45 Å observed in
layers of real h-BN crystals. At first glance, the surpris-
ing thing is that the theoretical result for the isolated
layer is in better agreement (with the accuracy of (2.6-3.8)
%) with the bond lengths in tetrahedrally coordinated
modifications c-BN (1.57 Å) and w-BN (1.56 and 1.58
Å). However, it is worth noting that to a certain extent
two-dimensional boron nitride looks like three-dimen-
sional crystals c-BN and w-BN: these three structures do
not contain weak interlayer bonds, which occur in the
h-BN layered modification. The lengths of (1.52-1.54)
and (1.55-1.58) Å obtained in [72] for the bonds of atoms
forming the central (almost undistorted) hexagon in B12N12
plane-fragment are also in good agreement with the
quasi-classical result found for an idealized infinite BN
sheet. Another quasi-classical approach using a different
scheme of parameterization, employed to calculate h-BN
binding and zero-point vibration energies, slightly un-
derestimates the intralayer bond length [75]. The plausi-
ble reason may be that the crystalline equilibrium con-
figuration was selected to maximize its static binding
energy with respect only to the layer lattice parameter,
while the interlayer distance was fixed.
Summarizing other theoretical and semiempirical re-
sults concerning intralayer bond lengths in h-BN (and
r-BN), one can state that all of them are in agreement
with the experimental value of 1.446 Å [76]. For instance,
in [77] the total energy of h-BN crystal as a function of
unit cell volume V had been calculated using orthogo-
nalized linear-combinations-of-atomic-orbitals (LCAOs)
method within the local-density-approximation (LDA).
The equilibrium was found at exp
/ 0.998VV , where
exp
V is the experimental value of V. Such result corre-
sponds to the intralayer B−N distance of 1.438 Å. The
calculations of [78] were also based on DFT within LDA,
but PW expansion was used both for the pseudo-
potential (PP) and the wave-function. The computed total
energies and, consequently, the intralayer bond lengths in
h-BN and r-BN were nearly the same: 1.441 and 1.439 Å,
respectively. The short-ranged CFF modeling of boron
nitrides leads to exactly the same intralayer B–N bond
lengths in both layered structures: 1.454 Å [58]. The re-
sults presented show satisfactory accuracy for the quasi-
classically determined boron-nitrogen binding character-
istics: accuracies of quasi-classical approach to deter-
mine isolated B−N bond length and length of bonds in
solid state structure amount a few percents, 7.2 and 5.1 %,
respectively. Thus, the quasi-classically obtained B–N
binding curve and its parameters mentioned above
(namely, equilibrium bond length, binding energy, and
vibration frequency) would be useful for investigations
of compounds containing B−N bonds and, especially, BN
nanosystems.
As for the BN sheet binding and vibration energies, it
is also reasonable to analyze correctness of the given
predictions by comparing them with data available on the
cohesion characteristics of h-BN layered crystals. As
follows from standard thermochemical data, the binding
energy of h-BN equals to 13.0 eV/mole [79]. The binding
energies of 14.5, 16.0, and 14.4 eV/mole were deter-
mined from semiempirical calculations performed using
two variants of the semiempirical LCAOs method and an
approach based on a periodic small-sized cluster [70,71].
Within the CFF potential model, the lower semiempirical
estimate of 11.5 eV/mole was obtained [58]. In the
framework of DFT, optimization of the structural pa-
rameters led to the theoretical binding energy of 12.5
eV/mole [78]. Therefore, it can be expected that the mo-
lar binding energy for h-BN layered crystal lies in the
range from 11.5 to 16.0 eV. The binding energy of 23.0
eV/mole found by the quasi-classical method for the iso-
lated layer is considerably higher. However, when com-
paring these energies, one should take into account that
interlayer bonds are substantially weaker than intralayer
ones and that each atom in layered BN structures is in-
volved in the formation of 5 bonds, of which only 3 are
intralayer bonds. Consequently, if the interlayer energy is
ignored as compared to the intralayer energy, we can
assume that the binding energy per B−N bond of similar
modifications is equal to 3/5 of the molar binding energy
of the isolated layer. Making use of the result 23.0
eV/mole for layer, we find the molar binding energy of
3/5  23.0 eV = 13.8 eV. Indeed, this energy is close to
the midpoint (13.75 eV) of the aforementioned energy
range. On the other hand, the vibration energies of the
isolated layer and layered crystals can be directly com-
pared because the atoms of the low-dimensional system
can execute vibrations in three independent directions in
physical space. The quasi-classical result of 0.242 for
two-dimensional BN agrees well with analogous calcula-
tions of 0.266 [65], with the semiempirical estimate of
0.225 for zero-point vibrations energy in h-BN [58], and

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 230
coincides in order of magnitude with the estimate of 0.350
eV/mole from the theoretical phonon spectrum [78].
A few words about the defects in BN layer. Using PP
and expanded unit cell methods, it was found that N-
vacancies in BN sheet, as well as di- and trivacancional
clusters including neighbor defects in BN layer, are
characterized by small binding energies [80]. Calculated
spectra and oscillator strengths allow to interpret local
bands of the optical absorption in pyrolitic h-BN crystals
before and after irradiation by fast-neutrons, protons, and
C-ions. By first-principles calculations the 20 structures
BxCyNz, derived from a hexagonal layer by placing B, N,
or C atoms on each site, were considered [81] to investi-
gate their relative stabilities. First-principles simulations
of the interaction of molecular hydrogen H2 with the na-
tive and substitutional defects of a single hexagonal BN
sheet were performed in [36]. The adsorption of H2 on
structures found to be endothermic with respect to disso-
ciation. Vacancies reduce the barriers for H2 dissociation.
The geometries of haeckelite BN sheets were con-
structed by DFT [82]. Their molar energy of cohesion is
found to be higher (by ~0.6 eV/mole) than that of regular
one.
2.3. Nanotubular Boron Nitride
The elementary form of a BN nanotube is a wrapped
closed hexagonal surface inscribed in the cylinder. Such
BN nanotubes can be found in regular – achiral, i.e., zig-
zag (n,0) or armchair (n,n), and also in chiral (n,m) forms,
0mn. Here n and m are the tube indexes. Their
symmetry operators have been identified in [83]: each
type belongs to different family of the non-symmorphic
rod groups; armchair tubes with even n are found to be
centro-symmetric. The types and structures of the non-
carbon, in particular, BN nanotubes were reviewed in
[84]. In addition, the deformed regular or haeckelite
nanotubes can exist. Concerning the haeckelite structures
of BN tubes, a variety of chiral angles, including zigzag
and armchair types, were observed. Depending on the
structure formation kinetics characteristic for a given
technology, BN nanotubes quite often take the bamboo-
like morphology, form of a nanoarch (i.e., half-tube at
the ends closed by planes) etc. Real nanotubular struc-
tures are not infinite in length: they are definitely trun-
cated.
The three main different possible morphologies of the
cylindrical tube closing with flat [8], conical, and amor-
phous ends, as observed in experiments, were shown [85]
to be directly related to the tube chirality. There are also
possible rectangular BN nanotubes with linear defects on
edges and with tips in the form of triangular flags. Such
kinds of morphologies suggest the presence of energeti-
cally unfavorable odd-membered atomic rings (i.e., pen-
tagons and heptagons) in addition to favorable even-mem-
bered rings (e.g. squares).
As the growth of BN nanotubes cannot be directly ob-
served and, consequently, the underlying microscopic
mechanism is a controversial subject, in [86] first-prin-
ciples MD simulation of the single-walled nanotube edges
was performed. The behavior of growing BN nanotubes
was found to strongly depend on the nanotube network
chirality. In particular, open-ended zigzag tubes close
rapidly into an amorphous tip, preventing further growth.
In the case of armchair tubes, formation of squares traps
the tip into a flat cap presenting a large central even-
membered ring. This structure is meta-stable and is able
to revert to a growing hexagonal framework by incorpo-
rating incoming atoms. These findings are directly re-
lated to frustration effects, namely that B−N bonds are
energetically favored over B–B and N–N bonds.
The expressions of radii, (,0)n
R and (,)nn R, of the zig-
zag and armchair, (n,0) and (n,n), BN nanotubes in terms
of the index and the structure parameter a were ob-
tained [87]. The parameter a corresponds to the lattice
constant of the boron nitride layered crystals, i.e., intra-
layer B–B or N–N bonds lengths. Therefore, the B–N
bond length d equals to /3a. The nanotube index
1,2,3,...n

determines the number of atoms as nano-
tube unit cell consists of 2n formula units BN. The
estimations of radii of the single-walled BN nanotubes,
for their part, can be used for predicting their most prob-
able combinations in multi-walled structures.
Analyzing this problem, it is necessary to take into
account that actually the question involves the average
radii. A detailed study using the generalized tight-binding
MD method has revealed [85] that, as a result of the dy-
namical relaxation, the structure acquires a wave-like or
“rippled” surface in which B atoms are displaced inward,
while N atoms are displaced outward. This relaxation is
similar to the reconstruction occurring at clean surfaces
of III-V type crystalline semiconductors. However a
general feature of BN nanotubular systems is that
stronger surface potentials are associated with regions of
higher curvature [88]. Thus, the interlayer interaction in
BN nanotubes differs from bonding in three-dimensional
layered crystals. However, most probably, these distinc-
tions for nanotubular BN are weak enough to change
essentially the equilibrium interlayer distances which are
observed in h-BN and r-BN crystals. This conclusion is
also confirmed by the results of an experimental study of
the multi-walled nanotubes by high-resolution electronic
microscopy [89]. In these structures, like in three-dimen-
sional layered BN crystals, hexagonal and rhombohedral
stacking sequences can freely coexist in nanotube wall-
assembly. There are also possible some different cross-

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 231
section flattening, as well as ordering of layers in non-
spiral zigzag. According to first-principles total-energy
calculations [90], the most favorable double-walled BN
nanotubes are structures in which the inter-wall distances
are about 3 Å, i.e., as interlayer distances in layered BN
crystals. Therefore, due to the weakness of the interlayer
van der Waals forces, various types of multi-walled BN
nanotubes can exist. Consequently, it is more probable
the formation of such multi-walled BN nanotubes in
which the difference between the radii of adjacent regu-
lar nanotubes is close to the interlayer distance in a lay-
ered h-BN crystal, i.e., to half of the height of the hex-
agonal unit cell 6.6612c Å [91]. Thus, the similarity
between types of the adjacent nanotubes has no crucial
importance.
In view of these factors, from the calculated single-
walled nanotubes [87] pairs most suitable for the forma-
tion of the stable double-walled BN nanotubes have been
chosen. Remaining small divergences in sizes of the
neighboring regular nanotubes can be compensated by
defects and small chiral distortions. Such transformations
of the zigzag and armchair nanotubes into chiral one will
be accompanied, respectively, by the increase and de-
crease in their radii. If the difference in radius between
regular nanotubes is more (less) than /2c, the realiza-
tion of structure in which the internal wall will be zigzag
(armchair) and external – armchair (zigzag) is more
probable. Hence, based on estimations of sizes of the
single-walled BN nanotubes, it is possible to predict
successfully the most stable double-walled forms. But,
how can be solved the same problem for multi-walled
nanotubes? A few words on the task. In this case, all over,
it will be necessary to calculate radii of nanotubes with
high indexes to choose sequences of single-walled nano-
tubes, whose radii are close to terms of arithmetic pro-
gression with common difference of /2c. However,
now only geometrical considerations will be insufficient.
The point is that unlike double-walled nanotubes in
multi-walled ones there are also medial layers. For this
reason, the choice of the most stable multi-walled struc-
ture should be based on the comparison between the
gains in energy, which are caused by the deviation from
the equilibrium interlayer distance, on the one hand, and
by chiral distortions, on the other hand.
We can mention some theoretical results available on
binding properties and stabilities of BN nanotubes. Sta-
bilities of the boron nitride nanotubular structures were
studied by means of non-orthogonal tight-binding for-
malism [92]. The radii and energies of the BN nanotubes
also were estimated by MD simulation [25] within the
embedded atom model in which parameter d took the
experimental value 1.4457 Å of the intralayer B–N bond
length in real h-BN crystals. In [69], the binding energy
of the regular BN nanotubes has been calculated within
the DFT in generalized gradient approximation (GGA).
Seeking equilibrium values of B–N bond length and radii,
the geometry of the tubular 32-atom supercell was opti-
mized. For (8,0), (10,0) and (4,4) tubes, it has been found
1.46d

Å, and for (5,5) tube, 1.45d Å. Within the
frame of semiempirical calculations of the nanotubular
piezoelectric characteristics performed by the method of
modified neglecting of diatomic overlapping (MNDO)
[50], their radii also were determined. In this case the
dependence of energies on the bond length was calcu-
lated for the molecular fragments containing 3 or 4 ele-
mentary layers (presumably, in this work for d the
empirical value known for h-BN crystals was fixed as an
equilibrium value).
The possible contribution of ionicity of bonds in boron
nitride structures is important to explain the binding dif-
ferences between BN tubes and similar C tubes [1]. In
order to facilitate understanding and prediction of nano-
tube interactions in a multi-walled structure, the electro-
static potentials on both outer and inner surfaces of some
single-walled BN nanotubes have been calculated at a
HF Slater-type-orbital level [88]. Structures were opti-
mized computationally. Fictitious hydrogen atoms were
introduced at the ends of the open tubes to satisfy the
unfulfilled valences. It was found that BN tubes have
stronger and more variable surface potentials than graph-
itic ones. There are characteristic patterns of positive and
negative sites on the outer lateral surfaces, while the in-
ner ones are markedly positive.
The binding and vibrations in small-radius single-
walled BN nanotubes in [93] were studied by DFT using
LDA. The results show that the chirality preference ob-
served in experiments may be explained from the relative
stability of the corresponding BN strips: the zigzag strips
have larger binding energies and thus may be more easily
formed. The smallest stable BN nanotube is found to be
the (5,0) zigzag nanotube. The dependence of the tube
deformation energy on its radius R was approximated
by the formula E

[eV/mole] 2.09 5.82 /R [Å]. The
phonon dispersions of BN nanotubes were calculated and
the frequency of the radial breathing mode was found to
be inversely proportional to the nanotube radius. The
geometries of the BN nanotubes were also constructed in
DFT [82]. Based on DFT calculations [69], it was found
that the energies of haeckelite BN nanotubes exceed by ~
0.6 eV/mole those of corresponding hexagonal nanotubes.
They are less stable in comparison with corresponding
haeckelite sheets as well. However, still they are stable
and can be synthesized. Energy of deformation (i.e., en-
ergy needed to wrap nanotube from its sheet prototype)
for large haeckelite BN tubes extrapolated by the formula
~/CR

, where R is the tube radius, with different

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 232
parameters C and 2

 for different structures.
Using the symmetry properties in [83], it was deter-
mined the numbers of Raman- and infrared (IR)-active
vibrations in single-walled BN nanotubes. In contrast to
the regular carbon nanotubes, zigzag boron nitride tubes
possess almost twice as many vibrations as armchair
ones. An extensive first principles study of the phonons
in BN nanotubes using perturbation DFT in the LDA was
performed in [94], where, based on the non-symmorphic
rod group symmetry of tubes, the Raman- and IR-active
modes at the point of the one-dimensional Brillouin zone
were evaluated. For zigzag and chiral nanotubes, the set
of IR-active modes is a subset of the Raman-active
modes. In particular, the radial breathing mode is not
only Raman-, but also IR-active. However, for armchair
tubes, the sets of IR- and Raman-active modes are dis-
joint. The frequencies of the active modes of zigzag,
chiral, and armchair tubes were presented as a function
of the tube diameter. They were compared with the fre-
quencies obtained by the zone-folding method (i.e., by
rolling of a BN sheet into a tube). Except for the high-
frequency tangential modes, the zone-folding results are
in very good agreement with the first principles calcula-
tions. The radial breathing mode frequency can be de-
rived by folding a sheet of finite width. Finally, the ef-
fects of bundling on the phonon frequencies are shown to
be small. First principles calculations of the nonresonant
Raman spectra of zigzag and armchair BN nanotubes
were presented in [95]. In comparison, a generalized
bond-polarizability model, where the parameters are ex-
tracted from first principles calculations of the polariza-
bility tensor of a BN sheet, was implemented. For light
polarized parallel to the tube axis, the agreement between
model and first principles spectra is almost perfect, but
for perpendicular polarization, depolarization effects
have to be included in the model in order to reproduce
Raman intensities.
The possible dislocation dipoles as defect nuclei under
tension in BN nanotubes were identified by dislocation
theory and MD simulations [96]. Formation energies of
the dipoles evaluated by gradient-corrected DFT are high
and remain positive at large strains, thus suggesting great
yield resistance of BN nanotubes. The dipole appears to
be more favorable in spite of its homoelemental B−B and
N−N bonds. The resonant photoabsorption and vibration
spectroscopy combined with scanning tunneling micros-
copy unambiguously identify the presence of Stone–Wales
defects in BN nanotubes [97]. Based on extensive time-
dependent DFT calculations, it was proposed to reso-
nantly photoexcite such defects in the IR and UV re-
gimes as a means of their identification. Intrinsic defects
in zigzag BN nanotubes, including single vacancy, diva-
cancy, and Stone–Wales defects, were systematically
investigated using DFT calculation in [98]. It was found
that the structural configurations and formation energies
of the topological defects are dependent on tube diameter.
The results demonstrate that such properties are origi-
nated from the strong curvature effect in BN nanotubes.
The scanning tunneling microscope images of intrinsic
defects in the BN nanotubes also were predicted. The
defected BN tubes with C-substitutions were considered
in [50].
The theoretical studies of the elastic properties of sin-
gle-walled BN nanotubes, carried out using the total
-energy non-orthogonal tight-binding parameterization,
were reported in [99]. Tubes of different diameters,
ranging from 0.5 to 2 nm, were examined. The study
found that in the limit of large diameters the mechanical
properties of nanotubes approach those of the graph-
ite-like sheet. The stiffness and plasticity of BN nano-
tubes was investigated [100] using generalized tight-
binding MD and first principles total-energy methods.
Due to the B−N bond rotation effect, the compressed
zigzag nanotubes were found to undergo anisotropic
strain release followed by anisotropic plastic buckling.
The strain is preferentially released toward N atoms in
the rotated B−N bonds. The tubes buckle anisotropically
toward only one end when uniaxially compressed from
both ends. Based on these results, a skin-effect-model of
smart nanocomposite materials is proposed, which local-
izes the structural damage toward the surface side of the
material. B−N bond-rotation mode of plastic yield in BN
nanotubes in [101] was investigated combining first
principles computations with a probabilistic rate approa-
ch to predict the kinetic and thermodynamic strength. BN
nanotubes yield defects have low activation, but high
formation energies. In [50], elastic characteristics of BN
nanotubes also were calculated applying MNDO method.
3. Theoretical Basis
Our calculations are based on the quasi-classical expres-
sion for binding molar energy of a substance, on the one
hand, and on the geometric characterization of nano-
tubular boron nitride, on the other hand.
3.1. Quasi-Classical Binding Energy of
Substance
Under the term ‘substance’ we imply polyatomic struc-
tures at the ground state, i.e., molecules, various clusters,
and crystals. Consequently, any substance is considered
as a non-relativistic electron system affected by the static
external field of nuclei, which are fixed at the sites in
structure, and the averaged SCF of electrons. Because of
singularities at the points, where the nuclei are located,
and electron shell effects as well the inner potential of

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 233
substance does not satisfy the standard Wentzel–Kramers–
Brillouin (WKB) quasi-classical condition of spatial
smoothness. Nevertheless, beginning from Bohr’s fun-
damental work ‘On the constitution of atoms and mole-
cules’ up to the present the semi-classical analysis of the
electronic spectrum has been widely used for light atoms
and their small complexes. Besides, heavy atoms, large
molecules, and crystals can be treated within the LDA
using the total energy functional in the form of quasi-
classical expansion. Success of quasi-classical approa-
ches can be attributed to the diffuseness of atomic poten-
tials. The expression for bounded electron states energies
obtained by Maslov yields that precise and quasi-classi-
cal spectra are close to each other if the characteristic
values of potential 0
 and the radius of its action 0 R
meet requirement 2
00
21R (here and below all rela-
tions are given in atomic units). For atomic potential
0~/
Z
R and 0~RR where 1
Z
 is the atomic
number and R is the radius of electron cloud. Therefore,
in case of atoms it is required that 21
Z
R . Even for
light atoms their radii are several times larger than Bohr
radius, 1R. Thus atoms and all polyatomic struc-
tures indeed are quasi-classical electron systems and their
structural and electronic characteristics can be calculated
based on the quasi-classically parameterized electric
charge density and electrical field potential distributions
in atoms.
The values of i-th electron classical turning point ra-
dii i r and i r , ii rr

, are obtained by solving the
equations
2
(1)
() 1,2,3,...,
2
ii
ii
ll
Eri Z
r

,
where r denotes the distance from the center of atom,
()
ir is the potential affecting the given electron,
0
i
E and i l are its energy and orbital quantum num-
ber, respectively.
In the ground state the inner classical turning point for
relative motion of atomic nucleus and electron cloud
coincides with the center of system. As for the corre-
sponding outer classical turning point radius r
, it is
obtained by solving the equation
()EZ r
,
where 0E
 denotes the energy associated with rela-
tive motion and
2
1
1
() ()
1
iZ
i
i
Z
rr
Zr








is the electron cloud potential affecting the nucleus.
In particular, using the quasi-classical parameteriza-
tion based on the Coulomb-like atomic potentials ()
ir

i
Z
r

we are able to get exact formulas


2(1)
iii ii
i
i
nnn ll
rZ

,


2(1)
iiiii
i
i
nnnll
rZ

,
2
22
1
2( 1)
iZ
i
i
Z
r
ZZ Z








,
2
32
1
2
2( 1)
iZ
i
i
ZZ Z
EZ






 

.
Here 2
ii i
Z
nE is the effective charge of the
screened nucleus and i
n is the principal quantum num-
ber of i-th electron. The numerical values of i
Z
, E
,
i
r

, i r

 and r  can be found by fitting the quasi-classical
energy levels i
E to ab initio (for instance HF) ones.
Quasi-classical limit implies the truncation of electron
states charge densities outside the classical turning points
and space-averaging within the range between them. In
this case i-th electron partial charge density is approxi-
mated by the piecewise-constant radial function
33
()0
3
4( )
0
ii
ii
ii
i
rrr
rrr
rr
rr


 



 



.
As for the nucleus charge density, it should be aver-
aged inside the r
-sphere:
3
3
() 0
4
0
Z
rrr
r
rr







.
Consequently, the full atomic charge density is ex-
pressed by the step-like radial function
1
() ()()
iZ
ik
i
rr r




 


1 1,2,3,..., kk
rrrk q


 ,
where k
r and k

denote known constants which de-
pend on parameters i
r

, i r

 and r ,
012
0q rrr r

, 2qZ is the number of
different homogenous-charge-density spherical layers in
atom.
Using the Poisson equation, the radial dependence of
the full atomic potential also can be approximated by the

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 234
step-like function,
22 55
11
33 33
11
3()3()
() 2( )5( )
kk kkk k
kk
kk kk
ar rbrr
rc
rr rr






1 1,2,3,..., kk
rrrk q
 ,
33 3
111
1
4( )4
33
ik ii ikk
k
i
rrr
a
 
 



,
2
3
k
k
b


 ,
22 2
1
1
2( )2
iq
kiiikk
ik
crrr  




,
if it is substituted by the space-averaged values inside
each of the 1kk rrr
 intervals.
In the region q rr, both the charge density and po-
tential vanish identically, () 0r

 and () 0r


. Thus
finite parameter q r acquires a meaning of the quasi-
classical atomic radius.
Based on the presented step-like parameterization of
the charge density and potential distributions in an atom,
its quasi-classical total energy can be expressed in the
following form:
33
() 1
1
()0
3
iq
Atomk kkk
k
Err






.
Note that it includes the non-physical energy of self-
action, () 0
Atom SelfAction
E which arises from substitut-
ing the charge density for the probability density. Its
value can be easily calculated in the quasi-classical appro-
ximation and then excluded from the total energy.
When the molecular or crystalline charge densities and
potentials are expressed by the superposition of the step-
like atomic charge densities and potentials, respectively,
the molar (i.e., per chemical formula unit of the sub-
stance) ground state static energy and its zero-point vi-
bration correction are calculated as
()( )
()( )
()( )()()
() 1 ()111
1()0
4
ik
jq lq
iNkN
Staticijk likjlik t
ti kj l
EVr 





 
,
()( )
()( )()()()()( )( )
/
() 1() 111() () ()
()
30.
22
ik
jq lq
iN kNijk lk lijikjlikt
Vibration
itkjl iik tik t
Vr
EMr r
 









Here the primed summation symbol denotes the
elimination of the terms with 0t
 and ik

; in-
dexes in parentheses ()i and ()k denote the atoms
in the molecule or crystal unit cell, N is the full
number of atoms, ()i
M
is the mass of i-th atom, t

is the crystal translational vector – in case of a mole-
cule 0t


, ()ik t r

is a distance between atomic sites
and
()()( )()1( )1()( )1()1( )
()()() () ()
()(,,)(,,)(,,)(,,)
ikjli jkli jkli jkli jkl
ik tik tik tik tik t
VrVrrrVrrrVr rrVrrr
 
 
 
.
We have introduced an universal geometric function
12 12
(, ,)VR RD which expresses the volume of the inter-
section of two spheres as a function of their radii 1 R
and 2 R, and the inter-center distance 12 D. 12 12 (, ,)VR RD
and its partial derivative 1 21212 (, ,)/VR RDD

 both are
continuous piecewise algebraic functions as follows:
3
1
12 12
4
(, ,)3
R
VRR D

 122 1 DRR

,
3
2
4
3
R 
 1212 DRR

,
2222
121212 121 122
12
()(()4( ))
12
RRD RRDRRRR
D
  
 1212 12 ||RR DRR

,
0

12 12 RRD

;
12 12
12
(,,) 0 VRR D
D


 122 1
DRR

,
0

1212 DRR

,
2222
1212 1212
2
12
(())(())
4
RRDD RR
D
  
 1212 12 ||RR DRR

,
0

12 12 RR D

.
In the lowest quasi-classical approximation, the equi-
librium structure of substance is obtained by maximizing
the molar binding energy of expected structures.
()
() ()
() 1
()
()0
iN
Bindingii SelfAction
i
StaticSelf ActionVibration
EEE
EE E









Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 235
with respect to their structural parameters.
However, neglecting the insignificant redistribution of
valence electrons arisen from association of atoms into a
molecular or crystalline structure, the quasi-classical self-
action energy of the substance is approximated by the
sum of self-action energies of constituent atoms:
()
()
() 1
iN
SelfActioni SelfAaction
i
EE



.
And consequently, the binding energy approximately
can be calculated without excluding of the self-action
terms in advance:
()
()
() 1
0
iN
BindingiStatic Vibration
i
EEEE



.
The expected errors of the quasi-classical approach
can be estimated for the model inner potential in the form
of the analytical solution of the Thomas–Fermi (TF) equ-
ation for the semi-classical atomic potential: structural
and energy parameters of the electronic system deter-
mined within the initial quasi-classical approximation are
shown to differ from their exact values by factors
1/3
(10 / 3)1.02~ 1   and 2/3 (3/10)0.96 ~ 1  , respe-
ctively. Thus the expected errors of the quasi-classical
approach amount to a few percents. Even more, within
the initial quasi-classical approximation there are no un-
controllable calculation errors due the finiteness of quasi-
classical atomic radii − the pair interactions without se-
ries termination are truncated at the distances exceeded
the sums of atomic radii.
A complete quasi-classical theory of substance in-
cluding calculation schemes for structural and binding, as
well as for electronic spectrum characteristics, one can
find in [102,103]. These schemes have been applied suc-
cessfully for Na molecular and crystalline structures
[104], various diatomic molecules [60,61], boron nano-
tubes [105,106], and mainly for one-, two- and three-
dimensional structural modifications of boron nitride –
diatomic molecule, isolated plane sheet, hexagonal h-BN,
cubic c-BN, and wurtzite-like w-BN crystals [59,60,64,
73-75,107,108].
3.2. Geometries of the Boron Nitride Regular
Single-Walled Nanotubes
Summarizing previous subsection, one can conclude that
equilibrium structural and binding parameters of the bo-
ron nitride nanotubes can be calculated quasi-classically
based on analytical expressions describing their geome-
tries. This task has been solved in [87,108,109] for regu-
lar (achiral), i.e., zigzag (n,0) and armchair (n,n) BN
nanotubes. A model of regular nanotubes used here as-
sumes that all atomic sites are located on cylindrical sur-
face at the vertexes of regular hexagons broken along
B–N or B–B and N–N diagonals, i.e., the expected small
differences in bond length distinguished by their orienta-
tion toward the tube axis are neglected.
Namely, radii (,0)n
R and (,)nn R of the zigzag and
armchair nanotubes have been obtained [87,108] in terms
of the nanotube index 1,2,3,... n

and the structure
parameter a:
(,0) 4sin /2 n
a
Rn

,
(,)
54cos/2
43sin /2
nn
na
Rn



.
As it was mentioned, the parameter a corresponds to
a lattice constant of the boron nitride layered crystals, i.e.,
to an intralayer B–B or N–N bond lengths. Therefore, the
B–N bond length d equals to /3a. The nanotube
index n determines the number of atoms, as a nanotube
unit cell consists of 2n formula units, B2nN2n.
Detailed regular geometries of zigzag and armchair
BN nanotubes have been described in [108,109] using
cylindrical coordinates (,,)z

 , which are useful for
calculating binding energy.
A unit cell of zigzag nanotubes consists of 4 atomic
rings in parallel planes perpendicular to the axis. There
are 2 pairs of rings, each consisting of 2 planes with n
boron or n nitrogen atoms. Obviously, the cylindrical
coordinate

for all atomic sites equals to the tube ra-
dius:
(,0)n
R



.
As for the coordinates

and z in the first and sec-
ond pairs of atomic rings, they equal to
2/ln




,
(61)/ 23zma
 ,
(61)/ 23zma
,
and
(21) /ln




 ,
(31) /3zma
 ,
(31) /3zma
,
respectively. Here 0,1, 2,...,1ln

 and 0,1,2,...m
number atomic pairs in a given pair of the atomic rings
and these rings themselves, respectively.
The unit cell of armchair nanotubes consists of 2 ato-
mic rings in parallel planes perpendicular to the tube axis.
For its part, each ring consists of n boron and n ni-
trogen atoms. The coordinate

for all atomic sites
again equals to the tube radius:
(,)nn
R



,

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 236
while the rest cylindrical coordinates in the first and
second atomic rings equal to
12/ln


 ,
12/ln


,
zzma

,
and
12
22/ln


 ,
12
22/ln


 ,
(21)/ 2zz ma

 ,
respectively. Here
1
2sin /2
sin 54cos/2
n
n


,
2
sin/2
sin 54cos/2
n
n


,
and 0,1,2,...,1ln and 0, 1,2,...m

 number B or
N atoms in atomic rings and these rings themselves.
Based on the above discussion, the distances between
a given atomic site and the sites in the so-called central
atomic pairs (with 0 lm) in zigzag and armchair
nanotubes have been found.
For zigzag (0 lm: 0


,B/2 3za,
and N/23za ) tubes
00 22
(,0) (,0)2
22
(1 1)sin/3
4sin /2
lm
nn ln m
an


 
,
00 222
(,0) (,0)
22
(2 1)
sin(21)/23(21)
4
4sin /2
lm
nn lnm
an


 

,
00 222
(,0)(,0)
22
(1 1)
sin/(3 1)
3 4sin /2
lm
nn lnm
an


 

,
00 222
( ,0)( ,0)
22
(2 1)
sin(21)/ 2(61)
12
4sin /2
lm
nn lnm
an


 

,
00 222
(,0) (,0)
22
(1 1)sin/(3 1)
3 4sin /2
lm
nn lnm
an


 

,
00 222
( ,0)( ,0)
22
(2 1)
sin(21)/ 2(61)
12
4sin /2
lm
nn lnm
an


 
 ,
00 22
(,0)(,0)2
22
(1 1)
sin /3
4sin /2
lm
nn ln m
an



,
00 222
(,0) (,0)
22
(2 1)
sin(21)/23(21)
4 4sin /2
lm
nn lnm
an


 

.
For armchair (0 lm:1

,1

, and
0zz

) tubes,
00 22
(,) (,)2
22
(1 1)
(54cos/2)sin/
12sin/ 2
lm
nn nnnln
m
an


 

,
00 2
(,) (,)
2
22
2
(2 1)
(54cos/2)sin (21)/2(21)
4 12sin/ 2
lm
nn nn
a
nl nm
n


 


.
00 2
(,) (,)
2
2
2
2
(1 1)
(2sin(21)/ 2sin/)
12sin/ 2
lm
nn nn
a
lnln
m
n


 


,
00 2
(,) (,)
2
22
2
(2 1)
(sin(21)/22sin/)(21)
4
12sin/ 2
lm
nn nn
a
lnlnm
n


 
 

,
00 2
(,) (,)
2
2
2
2
(1 1)
(2sin(21)/ 2sin/)
12sin/ 2
lm
nn nn
a
lnln
m
n


 


,
00 2
(,) (,)
2
22
2
(2 1)
(sin(21)/ 22sin/)(21)
4
12sin/ 2
lm
nn nn
a
lnlnm
n


 
 

,
00 22
(,) (,)2
22
(1 1)
(54cos/ 2)sin/
12sin/ 2
lm
nn nnnln
m
an


 

,
00 2
(,) (,)
2
22
2
(2 1)
(54cos/ 2)sin(21)/ 2(21)
4
12sin/ 2
lm
nn nn
a
nl nm
n


 


.
4. Binding Energies in Dependence on
Structural Parameter
At first, based on the above stated relations and HF val-
ues of the atomic electron energy-levels tabulated in
[110], the required quasi-classical parameters k r, k

,
and k

for constituent atoms B and N have been calcu-
lated. They are given in Tables 1 and 2, respectively.
Here the values are shown in atomic units with 7 sig-
nificant digits in accordance with the accuracy of input
data (HF energies). Such high accuracy is useful in in-
terim calculations. As for the final results, they should be
expressed in rounded figures with 3 or 4 significant digits
(in Å or eV for structure or energy parameters, respec-
tively) because it corresponds to the usual experimental
errors when determining structure and energy parameters
of a substance, and the relative errors of the semi-classical
calculations aimed at finding theoretically these parame-
ters for polyatomic systems amount to a few percents.

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 237
Table 1. Quasi-classical parameters of step-like radial distributions of electron-charge-density and electric-field-potential in
boron atom (in a.u.).
k 1 2 3 4 5
k
r 2.758476E − 02 5.098016E − 01 7.441219E − 01 4.021346E + 00 4.337060E + 00
k

5.686514E + 04 −3.610951E + 00 −7.342212E − 03 −1.028341E − 02 −2.941197E − 03
k

2.105468E + 02 8.882329E + 00 3.652920E + 00 2.060720E − 01 6.135348E − 04
Table 2. Quasi-classical parameters of step-like radial distributions of electron-charge-density and electric-field-potential in
nitrogen atom (in a.u.).
k 1 2 3 4 5
k
r 9.446222E − 03 3.577244E − 01 5.498034E − 01 2.909074E + 00 3.204489E + 00
k

1.982589E + 06 −1.044967E + 01 −1.939444E − 02 −4.126981E − 02 −2.187537E − 02
k

8.784581E + 02 2.022523E + 01 8.464698E + 00 5.096684E − 01 3.993358E − 03
Using these parameters and expressions for the com-
ponents of the quasi-classical molar binding energy and
squared interatomic distances in zigzag and armchair BN
nanotubes (Figures 1 and 2), their binding energies were
calculated versus the structural parameter a with spac-
ing of 0.001 a.u., i.e., within the accuracy of 4 significant
digits. The vibration energy is assumed to be zero when
radicand in its formula becomes negative.
In order to carry out these massive calculations, a spe-
cial computer code has been designed. Calculations were
performed within the range of the structure parameter a
which varied from 1 to 13 a.u. with a step 0.001a
a.u. (that is quite enough to cover values having any
physical sense). The nanotube indexes varied from 1n

,
covering zigzag and armchair nanotubes up to (18,0) and
(10,10), respectively. The radii of the largest calculated
species are approximately equal. They are sufficiently
large for the tube molar binding energy to almost reach
the “saturation” value, which is given by the binding
energy of the planar hexagonal BN sheet. In order to
make sure that such “saturation” indeed takes place, test
species with very large indexes (45,0) and (26,26) (again
with approximately equal radii) have also been calcu-
lated.
Figures 3-6 show ()
Binding
Ea curves (and their trends
near the peaks) for some zigzag and armchair BN nano-
tubes, respectively. One can see that at sufficiently small
interatomic distances binding energy might take a large
negative value that implies that the structure is unstable,
while at sufficiently large interatomic distances the binding
energy always equals to zero which reveals atomization
of a structure. As for the intermediate distances, the mo-
lar binding energy is positive that is a signature of struc-
tural stability. In this case, general trend in binding en-
ergy value is decreasing. However, ()
Binding
Ea curves
are not monotonous, but with several extremes. Such
kind of oscillatory behavior of the molar biding energy of
Figure 1. Structure of a zigzag BN nanotube.
Figure 2. Structure of an armchair BN nanotube.

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 238
(a)
(b)
Figure 3. Molar binding energy of zigzag BN nanotubes vs.
structural parameter a for different nanotube indexes n.
any atomic structure against the inter-atomic distances
reflects electron-shell-structure of the constituent atoms
(note that the interaction between particles of matter with
forces non-monotonously decreasing with distance was
foreseen as early as in 18th century by Boscovich [111],
whose atomic theory was based only on abstract philoso-
phical speculations).
Figures 7 and 8 show the binding energies for the two
types of achiral nanotubes with the same index n (na-
mely (3,0) and (3,3) nanotubes).
Let us discuss which of the peaks in these figures cor-
respond to the equilibrium structure. The first peak from
the right is lower than the successive one. This second
peak for all tubes located at 5.085a a.u. (2.691 Å)
seems to correspond to the realized stable BN nanotubu-
lar structures (the detailed behavior of ()
Binding
Ea curves
in its vicinity is shown in Figures 4, 6 and 8). The next
peak, even being higher than this, can not been reached
kinetically in standard laboratory conditions because they
correspond to lower interatomic distances and these two
peaks are separated by very deep and sufficiently wide
(a)
(b)
Figure 4. Molar binding energies of zigzag BN nanotubes
with different indexes n near the peak a = 2.691 Å.
Figure 5. Molar binding energy of armchair BN nanotubes
vs structural parameter a for different nanotube indexes n.
minima, i.e., by high and wide potential barriers which
can be overcome only at ultrahigh temperatures or tun-
neled only at ultrahigh pressures.
The obtained equilibrium binding energies of BN nano-
tubes of both achiral types are summarized in Table 3.

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 239
Figure 6. Molar binding energies of armchair BN nanotubes
with different indexes n near the peak a = 2.691 Å.
Figure 7. Dependence of molar binding energies of zigzag
and armchair BN nanotubes with the nanotube index n = 3
on the structural parameter a.
together with their radii calculated from formulas for
equilibrium value of the structural parameter 2.691a

Å.
Thus, the molar binding energies of small-sized nano-
tubes, both zigzag and armchair have peaks at (3,0) and
(2,2), respectively. Then for large indexes the binding
energies decrease toward the same constant value (see
Figures 9 and 10).
Figure 11 presents the dependence of the molar bind-
ing energy of achiral BN nanotubes on their radii R. It
reveals pairs of minima at (1,0) and (2,0), and maxima at
(1,1) and (3,0), i.e., all the extremes are located in low-
radii-region. At higher radii, the molar binding energy
slowly decreases to the value of 23.26 eV, which, appar-
ently, corresponds to that of the plane hexagonal BN
sheet.
The obtained dependence ()
Binding
Ea in its domain
of monotonicity seems to be quite smooth. It allows us
to extrapolate this curve also to chiral BN nanotubes
(Figure 12) because the radius of a chiral tube (, )nm R
Figure 8. Molar binding energies of zigzag and armchair BN
nanotubes with the index n = 3 near the peak a = 2.691 Å.
Figure 9. Molar binding energy of zigzag BN nanotubes for
different nanotube indexes n at the peak a = 2.691 Å.
Figure 10. Molar binding energy of armchair BN nanotubes
for different nanotube indexes n at the peak a = 2.691 Å.
(0mn

) and radii of the corresponding achiral tubes
always meet the condition (,0) (,) (,)nnmnn RR R .
The results of the carried out calculations are pre-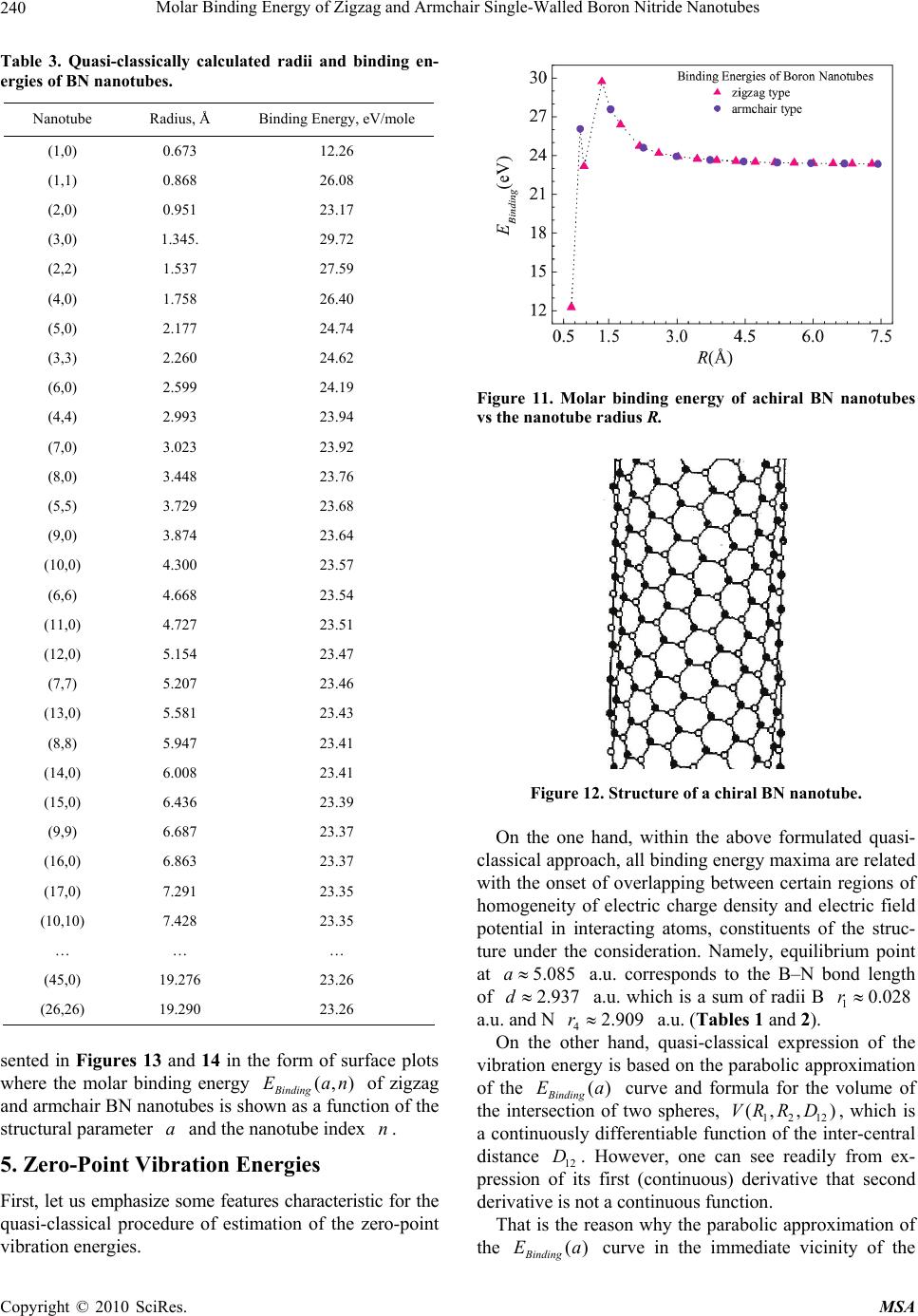

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 240
Table 3. Quasi-classically calculated radii and binding en-
ergies of BN nanotubes.
Nanotube Radius, Å Binding Energy, eV/mole
(1,0) 0.673 12.26
(1,1) 0.868 26.08
(2,0) 0.951 23.17
(3,0) 1.345. 29.72
(2,2) 1.537 27.59
(4,0) 1.758 26.40
(5,0) 2.177 24.74
(3,3) 2.260 24.62
(6,0) 2.599 24.19
(4,4) 2.993 23.94
(7,0) 3.023 23.92
(8,0) 3.448 23.76
(5,5) 3.729 23.68
(9,0) 3.874 23.64
(10,0) 4.300 23.57
(6,6) 4.668 23.54
(11,0) 4.727 23.51
(12,0) 5.154 23.47
(7,7) 5.207 23.46
(13,0) 5.581 23.43
(8,8) 5.947 23.41
(14,0) 6.008 23.41
(15,0) 6.436 23.39
(9,9) 6.687 23.37
(16,0) 6.863 23.37
(17,0) 7.291 23.35
(10,10) 7.428 23.35
… … …
(45,0) 19.276 23.26
(26,26) 19.290 23.26
sented in Figures 13 and 14 in the form of surface plots
where the molar binding energy (,)
Binding
Ean of zigzag
and armchair BN nanotubes is shown as a function of the
structural parameter a and the nanotube index n.
5. Zero-Point Vibration Energies
First, let us emphasize some features characteristic for the
quasi-classical procedure of estimation of the zero-point
vibration energies.
Figure 11. Molar binding energy of achiral BN nanotubes
vs the nanotube radius R.
Figure 12. Structure of a chiral BN nanotube.
On the one hand, within the above formulated quasi-
classical approach, all binding energy maxima are related
with the onset of overlapping between certain regions of
homogeneity of electric charge density and electric field
potential in interacting atoms, constituents of the struc-
ture under the consideration. Namely, equilibrium point
at 5.085a

a.u. corresponds to the B–N bond length
of 2.937d

a.u. which is a sum of radii B 10.028r

a.u. and N 42.909r

a.u. (Tables 1 and 2).
On the other hand, quasi-classical expression of the
vibration energy is based on the parabolic approximation
of the ()
Binding
Ea curve and formula for the volume of
the intersection of two spheres, 12 12 (, ,)VR RD, which is
a continuously differentiable function of the inter-central
distance 12 D. However, one can see readily from ex-
pression of its first (continuous) derivative that second
derivative is not a continuous function.
That is the reason why the parabolic approximation of
the ()
Binding
Ea curve in the immediate vicinity of the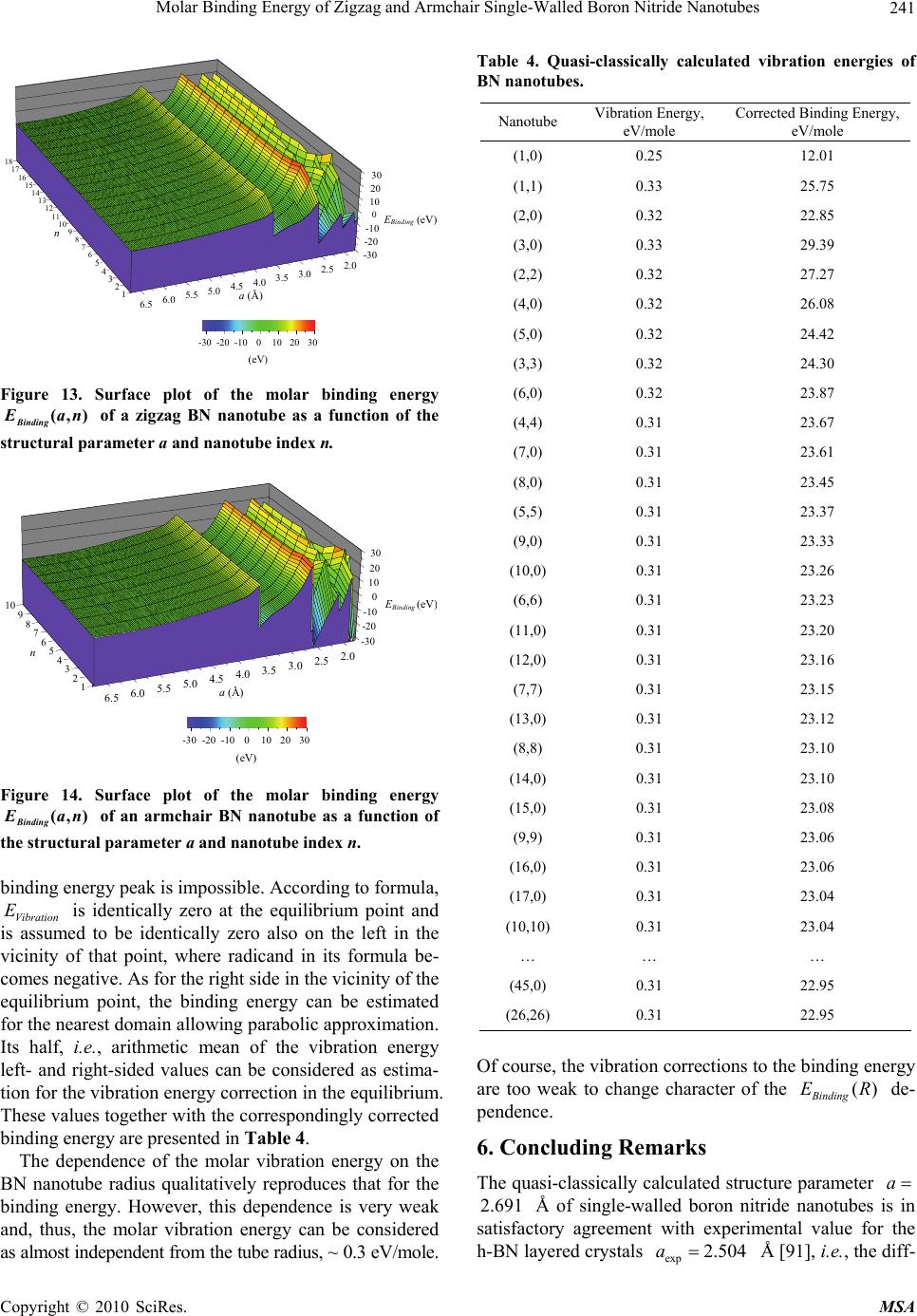

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 241
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
n
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
6.5 a (Å)
-30
-20
-10
0
10
20
30
EBind ing (eV
)
-30 -20 -10 0 10 20 30
(
e
V
)
Figure 13. Surface plot of the molar binding energy
(,)
Binding
E
an of a zigzag BN nanotube as a function of the
structural parameter a and nanotube index n.
1
2
3
4
5
6
7
8
9
10
n 2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
6.5 a (Å)
-30
-20
-10
0
10
20
30
E
Binding (eV
)
-30 -20 -100 10 20 30
(eV)
Figure 14. Surface plot of the molar binding energy
(,)
Binding
E
an of an armchair BN nanotube as a function of
the structural parameter a and nanotube index n.
binding energy peak is impossible. According to formula,
Vibration
E is identically zero at the equilibrium point and
is assumed to be identically zero also on the left in the
vicinity of that point, where radicand in its formula be-
comes negative. As for the right side in the vicinity of the
equilibrium point, the binding energy can be estimated
for the nearest domain allowing parabolic approximation.
Its half, i.e., arithmetic mean of the vibration energy
left- and right-sided values can be considered as estima-
tion for the vibration energy correction in the equilibrium.
These values together with the correspondingly corrected
binding energy are presented in Table 4.
The dependence of the molar vibration energy on the
BN nanotube radius qualitatively reproduces that for the
binding energy. However, this dependence is very weak
and, thus, the molar vibration energy can be considered
as almost independent from the tube radius, ~ 0.3 eV/mole.
Table 4. Quasi-classically calculated vibration energies of
BN nanotubes.
Nanotube Vibration Energy,
eV/mole
Corrected Binding Energy,
eV/mole
(1,0) 0.25 12.01
(1,1) 0.33 25.75
(2,0) 0.32 22.85
(3,0) 0.33 29.39
(2,2) 0.32 27.27
(4,0) 0.32 26.08
(5,0) 0.32 24.42
(3,3) 0.32 24.30
(6,0) 0.32 23.87
(4,4) 0.31 23.67
(7,0) 0.31 23.61
(8,0) 0.31 23.45
(5,5) 0.31 23.37
(9,0) 0.31 23.33
(10,0) 0.31 23.26
(6,6) 0.31 23.23
(11,0) 0.31 23.20
(12,0) 0.31 23.16
(7,7) 0.31 23.15
(13,0) 0.31 23.12
(8,8) 0.31 23.10
(14,0) 0.31 23.10
(15,0) 0.31 23.08
(9,9) 0.31 23.06
(16,0) 0.31 23.06
(17,0) 0.31 23.04
(10,10) 0.31 23.04
… … …
(45,0) 0.31 22.95
(26,26) 0.31 22.95
Of course, the vibration corrections to the binding energy
are too weak to change character of the ()
Binding
ER de-
pendence.
6. Concluding Remarks
The quasi-classically calculated structure parameter a

2.691 Å of single-walled boron nitride nanotubes is in
satisfactory agreement with experimental value for the
h-BN layered crystals exp 2.504a

Å [91], i.e., the diff-

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 242
erence is about 7%. As is mentioned above the overesti-
mations in the structural parameter is characteristic for
the quasi-classical approach. However, at least partially,
this overestimation seems to be related with expansion of
lattice of the single hexagonal layer (plane or cylindrical)
if compared with that of the three-dimensional layered
crystal.
It is also instructive to analyze the obtained spread of
the molar zero-point vibration energy of BN nanotubes
(0.25-0.33) eV and, in particular, its limit for ultra-large-
radius tubes 0.31 eV using the data available on the vi-
bration characteristics of h-BN layered crystal. The vi-
bration energies of an isolated tubular layer and layered
crystals can be directly compared as the atoms of the
low-dimensional system can execute vibrations in three
independent directions in physical space. Our quasi-classical
estimations made for BN nanotubes agree well with ana-
logous calculations (but in tight-binding approximation)
for BN plane sheet of 0.27, the semiempirical estimate of
0.23 for zero-point vibrations energy in h-BN, and the
estimate of 0.35 eV/mole from the theoretical phonon
spectrum (see Subsection 2.2).
We have found that the binding energies of BN sin-
gle-walled nanotubes corrected with zero-point vibration
energies lies within the interval (12.01-29.39) eV. In par-
ticular, the calculated corrected binding energy of the
ultra-large-radius tube is predicted as 22.95 eV. Previous
quasi-classical calculations (but in tight-binding appro-
ximation) performed for BN isolated plane sheet have
given the binding energy 23.00 eV/mole, which coin-
cides in order of magnitude with this interval and agrees
very well with present result obtained for large tubes. As
it was demonstrated in Subsection 2.2, for its part the
binding energy ~23 eV/mole for single-layer boron ni-
tride structures should be in good agreement with bind-
ing energy data available for BN multi-layered structures.
Summarizing the obtained results, it should be empha-
sized that a complex dependence of the BN nanotube
molar binding energy on its radius is found out, though
all the binding energy values are found to be positive, i.e.,
all tubes should be stable. However, they have rather
different degrees of stability.
On the one hand, ultra-small-radius BN nanotubes (1,0)
and (2,0) seem to be meta-stable, though their molar
binding energies are positive, they are less than that for
isolated hexagonal boron nitride layer. Especially the
smallest (1,0) tube structure degenerated in zigzag ato-
mic strip should be meta-stable because its binding en-
ergy is only about half of this value. Such a structure can
be realized only as an inner wall in a multi-walled tube.
On the other hand, the formation probabilities for BN
tubes with indexes (1,1), (3,0), and (4,0) should exceed
that for isolated sheet. Among them the (3,0) tube is well
pronounced, formation of which is predicted to be ener-
getically most preferable than the layer growth. Molar
binding energies for other BN nanotubes slightly exceed
that of sheet and their formation probabilities should be
almost same as for layered crystal growth.
Finally, it should be noted that, in addition to the en-
ergy considerations concerning the relative stability of
tubular structure, it is also necessary to take into account
features characteristic to BN nanosystems, in view of the
general equations derived for energy fluctuations of
small completely open (incompressible) systems [112].
They show that the fluctuations should be unusually
large because there are no constraints on the size of a
system and, in addition, the fluctuations of the total or
partial number of atoms in binary systems indirectly con-
tribute to the fluctuations in their energy.
7. Acknowledgements
L. Chkhartishvili acknowledges the financial support from
the Georgia National Science Foundation (GNSF) under
the Project # GNSF/ST 08/4-411-Geometry of the boron
nitride nanostructures.
REFERENCES
[1] A. Rubio, J. L. Corkill and M. L. Cohen, “Theory of
Graphitic Boron Nitride Nanotubes,” Physical Review B,
Vol. 49, No. 7, 1994, pp. 5081-5084.
[2] Z. Weng-Sieh, K. Cherrey, N. G. Chopra, X. Blasé, Y.
Miyamoto, A. Rubio, M. L. Cohen, S. G. Louie, A. Zettl
and R. Gronsky, “Synthesis of BxCyNz Nanotubules,”
Physical Review B, Vol. 51, No. 16, 1995, pp. 11229-
11232.
[3] N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M.
L. Cohen, S. G. Louie and A. Zettl, “Boron-Nitride Nano-
tubes,” Science, Vol. 269, No. 5226, 1995, pp. 966-967.
[4] K. Suenaga, C. Colliex, N. Demoncy, A. Loieseau, H.
Pascard and F. Willaime, “Synthesis of Nanoparticles and
Nanotubes with Well-Separated Layers of Boron Nitride
and Carbon,” Science, Vol. 278, No. 5338, 1997, pp. 653-
655.
[5] K. Suenaga, F. Willaime, A. Loieseau and C. Colliex.
“Organization of Carbon and Boron Nitride Layers in
Mixed Nanoparticles and Nanotubes Synthesized by Arc
Discharge,” Applied Physics A, Vol. 68, No. 3, 1999, pp.
301-308.
[6] A. Loiseau, F. Willaime, N. Demoncy, G. Hug and H.
Pascard, “Boron Nitride Nanotubes with Reduced Num-
bers of Layers Synthesized by Arc Discharge,” Physical
Review Letters, Vol. 76, No. 25, 1996, pp. 4737-4740.
[7] Y. Saito, M. Maida and T. Matsumoto, “Structures of
Boron Nitride Nanotubes with Single-Layer and Multi-
Layers Produced by Arc Discharge,” Japanese Journal of
Applied Physics, Vol. 38, No. 1A, 1999, pp. 159-163.
[8] Y. Saito and M. Maida, “Square, Pentagon, and Heptagon

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 243
rings at BN Nanotube Tips,” Journal of Physical Chem-
istry A, Vol. 103, No. 10, 1999, pp. 1291-1293.
[9] D. Golberg, Y. Bando, M. Eremets, K. Takemura, K.
Kurashima and H. Yusa “Nanotubes in Boron Nitride
Laser Heated at High Pressure,” Applied Physics Letters,
Vol. 69, No. 14, 1996, pp. 2045-2047.
[10] R. Sen, B. C. Satishkumar, A. Govindaraj, K. R. Hariku-
mar, G. Raina, J.-P. Zhang, A. K. Cheetham and C. N. R.
Rao, “B-C-N, C-N and B–N Nanotubes Produced by the
Pyrolysis of Precursor Molecules over Co Catalysts,”
Chemical Physics Letters, Vol. 287, No. 5-6, 1998, pp.
671-676.
[11] D. Golberg, Y. Bando, W. Han, K. Kurashima and T.
Sato, “Single-Walled B-Doped Carbon, B/N-Doped Car-
bon, and BN Nanotubes Synthesized from Single-Walled
Carbon Nanotubes through a Substitution Reaction,”
Chemical Physics Letters, Vol. 308, No. 3-4, 1999, pp.
337-342.
[12] D. Golberg, W. Han, Y. Bando, L. Bourgeois, K. Kura-
shima and T. Sato, “Fine Structure of Boron Nitride
Nanotubes Produced from Carbon Nanotubes by a Sub-
stitution Reaction,” Journal of Applied Physics, Vol. 86,
No. 4, 1999, pp. 2364-2366.
[13] Y. Chen, L. T. Chadderton, J. F. Gerald and J. S. Wil-
liams, “A Solid-State Process for Formation of Boron Ni-
tride Nanotubes,” Applied Physics Letters, Vol. 74, No.
20, 1999, pp. 2960-2962.
[14] T. S. Bartnitskaya, G. S. Oleinik, V. V. Pokropivnyi, N.
V. Danilenko, V. M. Vershchaka and A. V. Kotko, “Na-
notubes from Graphite-Like BN,” Superhard Materials,
No. 6, 1998, pp. 71-74.
[15] T. S. Bartnitskaya, G. S. Oleinik, A. V. Pokropivnyi and
V. V. Pokropivnyi, “Synthesis, Structure, and Formation
Mechanism of Boron Nitride Nanotubes,” JEPT Letters,
Vol. 69, No. 2, 1999, pp. 163-168.
[16] C. Colazo-Davila, E. Bengu, L. D. Marks and M. Kirk,
“Nucleation of Cubic Boron Nitride Thin Films,” Dia-
mond Related Materials, Vol. 8, No. 6, 1999, pp. 1091-
1100.
[17] T. Oku, T. Hirano, M. Kuno, T. Kusunose, K. Niihara and
K. Suganuma, “Synthesis, Atomic Structures, and Proper-
ties of Carbon and Boron Nitride Fullerene Materials,”
Materials Science and Engineering B, Vol. 74, No. 1-3,
2000, pp. 206-217.
[18] J. Wang, V. K. Kayastha, Y. K. Yap, Z. Fan, J. G. Lu, Z.
Pan, I. N. Ivanov, A. A. Puretzky and D. B. Geohegan,
“Low Temperature Growth of Boron Nitride Nanotubes
on Substrates,” Nano Letters, Vol. 5, No. 12, 2005, pp.
2528-2532.
[19] L. L. Sartinska, S. Barchikovski, N. Wagenda, B. M.
Rud’ and I. I. Timofeeva, “Laser Induced Modification of
Surface Structures,” Applied Surface Science, Vol. 253,
No. 9, 2007, pp. 4295-4299.
[20] L. L. Sartinska, A. A. Frolov, A. Yu. Koval’, N. A.
Danilenko, I. I. Timofeeva and B. M. Rud’, “Transforma-
tion of Fine-Grained Graphite-Like Boron Nitride In-
duced by Concentrated Light Energy,” Materials Chem-
istry and Physics, Vol. 109, No. 1, 2008, pp. 20-25.
[21] M. V. P. Altoe, J. P. Sprunck, J.-C. P. Gabriel and K.
Bradley, “Nanococoon Seeds for BN Nanotube Growth,”
Journal of Materials Science, Vol. 38, No. 24, 2003, pp.
4805-4810.
[22] M. W. Smith, K. C. Jordan, C. Park, J.-W. Kim, P. T.
Lillehei, R. Crooks and J. S. Harrison, “Very Long Sin-
gle- and Few-Walled Boron Nitride Nanotubes via the
Pressurized Vapor/Condenser Method,” Nanotechnology,
Vol. 20, No. 50, 2009, pp. 505604-505610.
[23] X. Blasé, J.-C. Charlier, A. de Vita and R. Car, “Theory
of Composite BxCyNz Nanotube Heterojunctions,” Ap-
plied Physics Letters, Vol. 70, No. 2, 1997, pp. 197-199.
[24] X. Blasé, J.-C. Charlier, A. de Vita and R. Car, “Struc-
tural and Electrical Properties of Composite BxCyNz
Nanotubes and Heterojunctions,” Applied Physics A, Vol.
68, No. 3, 1999, pp. 293-300.
[25] V. V. Pokropivnyj, V. V. Skorokhod, G. S. Oleinik, A. V.
Kurdyumov, T. S. Bartnitskaya, A. V. Pokropivnyj, A. G.
Sisonyuk and D. M. Sheichenko, “Boron Nitride Analogs
of Fullerenes (the Fulborenes), Nanotubes, and Fullerites
(the Fulborenites),” Journal of Solid State Chemistry, Vol.
154, No. 1, 2000, pp. 214-215.
[26] J. H. Lee, “A Study on a Boron-Nitride Nanotube as a
Gigahertz Oscillator,” The Journal of the Korean Physi-
cal Society, Vol. 49, No. 1, 2006, pp. 172-176.
[27] V. Verma and K. Dharamvir, “BNNT in Contact with
h-BN Sheet and Other BNNT and DW-BNNT as GHz
Oscillator,” International Journal of Nanosystems, Vol. 1,
No. 1, 2008, pp. 27-34.
[28] B. Baumeier, P. Krüger and J. Pollmann, “Structural,
Elastic, and Electronic Properties of SiC, BN, and BeO
Nanotubes,” Physical Review B, Vol. 76, 2007, p. 085407.
[29] Y.-H. Kim, K. J. Chang and S. G. Louie, “Electronic
Structure of Radially Deformed BN and BC3 Nanotubes,”
Physical Review B, Vol. 63, 2001, p. 205408.
[30] G. Y. Guo and J. C. Lin, “Second-Harmonic Generation
and Linear Electro-Optical Coefficients of BN Nano-
tubes,” Physical Review B, Vol. 72, 2005, p. 075416.
[31] G. Y. Guo and J. C. Lin, “Erratum: Second-Harmonic
Generation and Linear Electro-Optical Coefficients of BN
Nanotubes,” Physical Review B, Vol. 77, 2008, p. 049901
(E).
[32] C. Zhi, Y. Bando, C. Tang and D. Golberg, “Engineering
of Electronic Structure of Boron-Nitride Nanotubes by
Covalent Functionalization,” Physical Review B, Vol. 74,
2006, p. 153413.
[33] C. Zhi, Y. Bando, C. Tang and D. Golberg, “Publisher’s
Note: Engineering of Electronic Structure of Boron-Ni-
tride Nanotubes by Covalent Functionalization,” Physical
Review B, Vol. 74, 2006, p. 199902 (E).
[34] W.-Q. Han, C. W. Chang and A. Zettl, “Encapsulation of
One-Dimensional Potassium Halide Crystals within BN
Nanotubes,” Nano Letters, Vol. 4, No. 7, 2004, pp. 1355-
1357.
[35] K. Yum and M.-F. Yu, “Measurement of Wetting Proper-

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 244
ties of Individual Boron Nitride Nanotubes with the Wil-
helmy Method Using a Nanotube-Based Force Sensor,”
Nano Letters, Vol. 6, No. 2, 2006, pp. 329-333.
[36] S. A. Shevlin and Z. X. Guo, “Hydrogen Sorption in De-
fective Hexagonal BN Sheets and BN Nanotubes,” Physi-
cal Review B, Vol. 76, 2007, p. 024104.
[37] E. Durgun, Y.-R. Jang and S. Ciraci, “Hydrogen Storage
Capacity of Ti-Doped Boron-Nitride and B/Be-Substitut-
ed Carbon Nanotubes,” Physical Review B, Vol. 76, 2007,
p. 073413.
[38] C. Tang, Y. Bando, X. Ding, S. Qi and D. Golberg,
“Catalyzed Collapse and Enhanced Hydrogen Storage of
BN Nanotubes,” Journal of the American Chemical Soci-
ety, Vol. 124, No. 49, 2002, pp. 14550-14551.
[39] C. Zhi, Y. Bando, C. Tang and D. Golberg. “Immobiliza-
tion of Proteins on Boron Nitride Nanotubes,” Journal of
the American Chemical Society, Vol. 127, No. 49, 2005,
pp. 17144-17145.
[40] C. Zhi, Y. Bando, C. Tang, R. Xie, T. Sekiguchi and D.
Golberg, “Perfectly Dissolved Boron Nitride Nanotubes
Due to Polymer Wrapping,” Journal of the American
Chemical Society, Vol. 127, No. 46, 2005, pp. 15996-
15997.
[41] M. Côté, P. D. Haynes and C. Molteni, “Boron Nitride
Polymers: Building Blocks for Organic Electronic De-
vices,” Physical Review B, Vol. 63, 2001, p. 125207.
[42] M. Ishigami, J. D. Sau, Sh. Aloni, M. L. Cohen and A.
Zettl, “Observation of the Giant Stark Effect in Bo-
ron-Nitride Nanotubes,” Physical Review Letters, Vol. 94,
2005, p. 056804.
[43] J. Cumings and A. Zettl, “Mass-Production of Boron
Nitride Double-Wall Nanotubes and Nanococones,”
Chemical Physics Letters, Vol. 316, No. 3-4, 2000, pp.
211-216.
[44] Y. Chen, J. Zou, S. J. Campbell and G. le Caer, “Boron
Nitride Nanotubes: Pronounced Resistance to Oxidation,”
Applied Physics Letters, Vol. 84, No. 13, 2004, pp. 2430-
2432.
[45] E. Bengu and L. D. Marks, “Single-Walled BN Nanos-
tructures,” Physical Review Letters, Vol. 86, No. 11, 2001,
pp. 2385-2387.
[46] C. Tang, Y. Bando, Y. Huang, S. Yue, C. Gu, F. F. Xu
and D. Golberg, “Fluorination and Electrical Conductivity
of BN Nanotubes,” Journal of the American Chemical
Society, Vol. 127, No. 18, 2005, pp. 6552-6553.
[47] E. J. Mele and P. Král, “Electric Polarization of Heter-
opolar Nanotubes as a Geometric Phase,” Physical Re-
view Letters, Vol. 88, 2002, p. 056803.
[48] N. Sai and E. J. Mele, “Microscopic Theory for Nanotube
Piezoelectricity,” Physical Review B, Vol. 68, 2003, p.
241405.
[49] S. M. Nakhmanson, A. Calzolari, V. Meunier, J. Bernholc
and M. Buongiorno Nardelli, “Spontaneous Polarization
and Piezoelectricity in Boron Nitride Nanotubes,” Physi-
cal Review B, Vol. 67, 2003, p. 235406.
[50] N. G. Lebedev and L. A. Chernozatonskiĭ, “Quantum-
Chemical Calculations of the Piezoelectric Characteristics
of Boron Nitride and Carbon Nanotubes,” Physics of the
Solid State, Vol. 48, No. 10, 2006, pp. 2028-2034.
[51] Y. Zhang, K. Suenaga, C. Colliex and S. Iijima, “Coaxial
Nanocable: Silicon Carbide and Silicon Oxide Sheathed
with Boron Nitride and Carbon,” Science, Vol. 281, No.
5379, 1998, pp. 973-975.
[52] A. Zobelli, A. Gloter, C. P. Ewels, G. Seifert and C. Col-
liex, “Electron Knock-on Cross Section of Carbon and
Boron Nitride Nanotubes,” Physical Review B, Vol. 75,
2007, p. 245402.
[53] I. V. Weiz, “Supplement II,” In: K.-P. Huber and G.
Herzberg, Constants of Diatomic Molecules, Part 2:
Molecules N2–ZrO, Mir, Moscow, 1984, pp. 295-366.
[54] O. I. Bukhtyarov, S. P. Kurlov and B. M. Lipenskikh,
“Calculation of the Structure and Physicochemical Prop-
erties of B-Based Systems by the Computer Modeling
Method,” In: Abstracts of the 8th International Sympo-
sium on Boron, Borides, Carbides, Nitrides, and Related
Compounds, Tbilisi, October 1984, pp. 135-136.
[55] J. L. Masse and M. Bärlocher, “Etude par la Méthode du
Autocohérent (Self-Consistent) de la Molécule BN,”
Helvetica Chimia Acta, Vol. 47, No. 1, 1964, pp. 314-
318.
[56] Y. G. Khajt and V. I. Baranovskij, “Ab Initio Calcula-
tions of the BN Molecule,” Journal of Structural Chem-
istry, Vol. 21, No. 1, 1980, pp. 153-154.
[57] H. Bredohl, J. Dubois, Y. Houbrechts and P. Nzo-
habonayo, “The Singlet Bands of BN,” Journal of Phys-
ics B, Vol. 17, No. 1, 1984, pp. 95-98.
[58] C. M. Marian, M. Gastreich and J. D. Gale, “Empirical
Two-Body Potential for Solid Silicon Nitride, Boron Ni-
tride, and Borosilazane Modifications,” Physical Review
B, Vol. 62, No. 5, 2000, pp. 3117-3124.
[59] L. Chkhartishvili, “Quasi-Classical Analysis of Boron-
Nitrogen Binding,” In: Proceedings of the 2nd Interna-
tional Boron Symposium, Eskişehir, Turkey, September
2004, pp. 165-171.
[60] L. Chkhartishvili, D. Lezhava, O. Tsagareishvili and D.
Gulua, “Ground State Parameters of B2, BC, BN, and BO
Diatomic Molecules,” Transactions of the AMIAG, Vol. 1,
1999, pp. 295-300.
[61] L. Chkhartishvili, D. Lezhava and O. Tsagareishvili,
“Quasi-Classical Determination of Electronic Energies
and Vibration Frequencies in Boron Compounds,” Jour-
nal of Solid State Chemistry, Vol. 154, No. 1, 2000, pp.
148-152.
[62] A. Gaydon, “Dissociation Energies and Spectra of Dia-
tomic Molecules,” Chapman & Hall, London, 1947.
[63] K. P. Huber and G. Herzberg, “Molecular Spectra and
Molecular Structure: IV. Constants of Diatomic Mole-
cules,” van Nostrand Reinhold Co, New York, 1979.
[64] M. Lorenz, J. Agreiter, A. M. Smith and V. E. Bondybey,
“Electronic Structure of Diatomic Boron Nitride,” Jour-
nal of Chemical Physics, Vol. 104, No. 8, 1996, pp. 3143-
3146.

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 245
[65] L. Chkhartishvili, “Zero-Point Vibration Energy within
Quasi-Classical Approximation: Boron Nitrides,” Pro-
ceedings of the TSU (Physics), Vol. 40, 2006, pp. 130-138.
[66] V. I. Vedeneev, L. V. Gurvich, V. N. Kondrat’ev, V. A.
Medvedev and E. A. Frankevich, “Chemical Bonds
Breaking Energies, Ionization Potentials and Electron Af-
finities,” Academy of Sciences of USSR, Moscow, 1962.
[67] G. Meloni, M. Sai Baba and K. A. Gingerich, “Knudsen
Cell Mass Spectrometric Investigation of the B2N Mole-
cule,” Journal of Chemical Physics, Vol. 113, No. 20,
2000, pp. 8995-8999.
[68] R. Vanderbosch, “Gas-Phase Anions Containing B and
N,” Physical Review A, Vol. 67, 2003, p. 013203.
[69] S. V. Lisenkov, G. A. Vinogradov, T. Y. Astakhova and
N. G. Lebedev, “Non-Spiral ‘Haeckelite-Type’ BN-Nano-
tubes,” JETP Letters, Vol. 81, No. 7, 2005, pp. 431-436.
[70] A. Zunger, “A Molecular Calculation of Electronic Prop-
erties of Layered Crystals: I. Truncated Crystal Approach
for Hexagonal Boron Nitride,” Journal of Physics C, Vol.
7, No. 1, 1974, pp. 76-95.
[71] A. Zunger, “A Molecular Calculation of Electronic Prop-
erties of Layered Crystals: II. Periodic Small Cluster
Calculation for Graphite and Boron Nitride,” Journal of
Physics C, Vol. 7, No. 1, 1974, pp. 96-106.
[72] D. L. Strout, “Structure and Stability of Boron Nitrides:
Isomers of B12N12,” Journal of Physical Chemistry A, Vol.
104, No. 15, 2000, pp. 3364-3366.
[73] L. S. Chkhartishvili, “Quasi-Classical Estimates of the
Lattice Constant and Band Gap of a Crystal: Two-Di-
mensional Boron Nitride,” Physics of the Solid State, Vol.
46, No. 11, 2004, pp. 2126-2133.
[74] L. S. Chkhartishvili, “Analytical Optimization of the Lat-
tice Parameter Using the Binding Energy Calculated in
the Quasi-Classical Approximation,” Physics of the Solid
State, Vol. 48, No. 5, 2006, pp. 846-853.
[75] L. Chkhartishvili and D. Lezhava, “Zero-Point Vibration
Effect on Crystal Binding Energy: Quasi-Classical Cal-
culation for Layered Boron Nitride,” Transactions of the
GTU, Vol. 439, 2001, pp. 87-90.
[76] K.-H. Hellwege and O. von Madelung, Eds., “Boron Ni-
tride (BN),” In: Landolt-Börnstein, Numerical Data and
Functional Relationships in Science and Technology,
New Series, Group III: Crystal and Solid State Physics,
Volume 17: Semiconductors, Subvolume g: Physics of
Non-Tetrahedrally Bonded Binary Compounds III,
Springer-Verlag, Berlin, 1982.
[77] Y.-N. Xu and W. Y. Ching, “Calculation of Ground-State
and Optical Properties of Boron Nitrides in the Hexagonal,
Cubic, and Wurtzite Structures,” Physical Review B, Vol.
44-I, No. 15, 1991, pp. 7784-7798.
[78] K. Albe, “Theoretical Study of Boron Nitride Modifica-
tions at Hydrostatic Pressures,” Physical Review B, Vol.
55-II, No. 10, 1997, pp. 6203-6210.
[79] D. D. Wagmann, W. H. Evans, V. B. Parker, J. Halow, S.
M. Bairly and R. H. Shumn, Eds., Selected Values of
Chemical Thermodynamic Properties, National Bureau of
Standards, Washington, 1968.
[80] S. N. Grinyaev, F. V. Konusov and V. V. Lopatin, “Deep
Levels of Nitrogen Vacancy Complexes in Graphite-Like
Boron Nitride,” Physics of the Solid State, Vol. 44, No. 2,
2002, pp. 286-293.
[81] M. S. C. Mazzoni, R. W. Nunes, S. Azevedo and H.
Chacham, “Electronic Structure and Energetics of BxCyNz
Layered Structures,” Physical Review B, Vol. 73, 2006, p.
073108.
[82] S. V. Lisenkov, G. A. Vonogradov, T. Y. Astakhova and
N. G. Lebedev, “Geometric Structure and Electronic
Properties of Planar and Nanotubular BN Structures of
the Haeckelite Type,” Physics of the Solid State, Vol. 48,
No. 1, 2006, pp. 192-198.
[83] O. E. Alon, “Symmetry Properties of Single-Walled Bo-
ron Nitride Nanotubes,” Physical Review B, Vol. 64, 2001,
p. 153408.
[84] V. V. Pokropivnyi, “Non-Carbon Nanotubes (Review). 2.
Types and Structure,” Powder Metallurgy and Metal Ce-
ramics, Vol. 40, No. 11-12, 2002, pp. 582-594.
[85] M. Menon and D. Srivastava, “Structure of Boron Nitride
Nanotubes: Tube Closing Versus Chirality,” Chemical
Physics Letters, Vol. 307, No. 5-6, 1999, pp. 407-412.
[86] J.-C. Charlier, X. Blase, A. de Vita and R. Car, “Micro-
scopic Growth Mechanisms for Carbon and Boron-Ni-
tride Nanotubes,” Applied Physics A, Vol. 68, No. 3, 1999,
pp. 267-273.
[87] L. S. Chkhartishvili, “On Sizes of Boron Nitride Nano-
tubes,” In: Proceedings of the 18th International Sympo-
sium ‘Thin Films in Optics in Nanoelectronics’, Kharkiv,
October 2006, pp. 367-373.
[88] Z. Peralta–Inga, P. Lane, J. S. Murray, S. Boyd, M. E.
Grice, C. J. O’Connor and P. Politzer, “Characterization
of Surface Electrostatic Potentials of Some (5,5) and (n,1)
Carbon and Boron/Nitrogen Model Nanotubes,” Nano
Letters, Vol. 3, No. 1, 2003, pp. 21-28.
[89] D. Golberg, Y. Bando, L. Bourgeois, K. Kurashima and T.
Sato, “Insights into the Structure of BN Nanotubes,” Ap-
plied Physics Letters, Vol. 77, No. 13, 2000, pp. 1979-
1981.
[90] S. Okada, S. Saito and A. Oshiyama, “Inter-Wall Interac-
tion and Electronic Structure of Double-Walled BN
Nanotubes,” Physical Review B, Vol. 65, No. 16, 2002, p.
165410.
[91] Y. B. Kuz’ma and N. F. Chaban, “Boron Containing Bi-
nary and Ternary Systems: Handbook,” Metallurgiya,
Moscow, 1990.
[92] E. Hernández, C. Goze, P. Bernier and A. Rubio, “Elastic
properties of C and BxCyNz Composite Nanotubes,”
Physical Review Letters, Vol. 80, No. 20, 1998, pp. 4502-
4505.
[93] H. J. Xiang, J. Yang, J. G. Hou and Q. Zhu, “First-Prin-
ciples Study of Small-Radius Single-Walled BN Nano-
tubes,” Physical Review B, Vol. 68, 2003, p. 035427.
[94] L. Wirtz, A. Rubio, R. A. de la Concha and A. Loiseau,
“Ab initio Calculations of the Lattice Dynamics of Boron

Molar Binding Energy of Zigzag and Armchair Single-Walled Boron Nitride Nanotubes 246
Nitride Nanotubes,” Physical Review B, Vol. 68, 2003, p.
045425.
[95] L. Wirtz, M. Lazzeri, F. Mauri and A. Rubio, “Raman
Spectra of BN Nanotubes: Ab Initio and Bond-Polari-
zability Model Calculations,” Physical Review B, Vol. 71,
2005, p. 241402 (R).
[96] H. F. Bettinger, T. Dumitrică, G. E. Scuseria and B. I.
Yakobson, “Mechanically Induced Defects and Strength
of BN Nanotubes,” Physical Review B, Vol. 65, 2002, p.
041406.
[97] Y. Miyamoto, A. Rubio, S. Berber, M. Yoon and D. To-
mánek, “Spectroscopic Characterization of Stone–Wales
Defects in Nanotubes,” Physical Review B, Vol. 69, 2004,
p. 121413 (R).
[98] G. Y. Gou, B. C. Pan and L. Shi, “Theoretical Study of
Size-Dependent Properties of BN Nanotubes with Intrin-
sic Defects,” Physical Review B, Vol. 76, 2007, p.
155414.
[99] E. Hernandez, C. Goze, P. Bernier and A. Rubio, “Elastic
Properties of Single-Wall Nanotubes,” Applied Physics A,
Vol. 68, No. 3, 1999, pp. 287-292.
[100] D. Srivastava, M. Menon and K.-J. Cho, “Anisotropic
Nanomechanics of Boron Nitride Nanotubes: Nanostruc-
tured “Skin” Effect,” Physical Review B, Vol. 63, 2001, p.
195413.
[101] T. Dumitrică and B. I. Yakobson, “Rate Theory of Yield
in Boron Nitride Nanotubes,” Physical Review B, Vol. 72,
2005, p. 035418.
[102] L. Chkhartishvili, “Quasi-Classical Theory of Substance
Ground State,” Technical University Press, Tbilisi, 2004.
[103] L. Chkhartishvili, “Quasi-Classical Method of Calcula-
tion of Substance Structural and Electronic Energy Spec-
trum Parameters,” Tbilisi University Press, Tbilisi, 2006.
[104] L. Chkhartishvili, “Selection of Equilibrium Configura-
tions for Crystalline and Molecular Structures Based on
Quasi-Classical Inter-Atomic Potential,” Transactions of
the GTU, No. 427, 1999, pp. 13-19.
[105] L. Chkhartishvili, “On Quasi-Classical Estimations of
Boron Nanotubes Ground-State Parameters,” Journal of
Physics: Conference Series, Vol. 176, 2009, p. 012013.
[106] L. Chkhartishvili, “Molar Binding Energy of the Boron
Nanosystems,” In: Proceedings of the 4th International
Boron Symposium, Osmangazi University Press, Eskişe-
hir, Turkey, 2009, pp. 153-160.
[107] L. Chkhartishvili, “Ground State Parameters of Wurtzite
Boron Nitride: Quasi-Classical Estimations,” In: Pro-
ceedings of the 1st International Boron Symposium,
Dumlupinar University Press, Kütahya, 2002, pp. 139-
143.
[108] L. Chkhartishvili, “Boron Nitride Nanosystems of Regu-
lar Geometry,” Journal of Physics: Conference Series,
Vol. 176, 2009, p. 012014.
[109] L. S. Chkhartishvili, “Equilibrium Geometry of Ultra-
Small-Radius Boron Nitride Nanotubes,” Material Sci-
ence of Nanostructures, No. 1, 2009, pp. 33-44.
[110] Ch. Froese–Fischer, “The Hartree–Fock Method for At-
oms: A Numerical Approach,” Wiley, New York, 1977.
[111] R. J. Boscovich, “Philosophiae Naturalis Theoria Redacta
ad Inicam Legem Vitium in Natura Existentiam,” Colle-
gio Romano, Milano, 1758.
[112] T. L Hill and R. V. Chamberlin, “Fluctuations in Energy
in Completely Open Small Systems,” Nano Letters, Vol.
2, No. 6, 2002, pp. 609-613.