Materials Sciences and Applications, 2010, 1, 177-186
doi:10.4236/msa.2010.14028 Published Online October 2010 (http://www.SciRP.org/journal/msa)
177
Electrical Conductivity, Magnetoconductivity and
Dielectric Behaviour of (Mg,Ni)-Ferrite below
Room Temperature
Somenath Ghatak1, Ajit Kumar Meikap1, Manika Sinha2, Swapan Kumar Pradhan2
1Department of Physics, National Institute of Technology, Deemed University, Durgapur, India; 2Department of Physics, University
of Burdwan, Burdwan, India.
Received March 19th, 2010; revised June 17th, 2010; accepted October 9th, 2010.
ABSTRACT
We report a comprehensive study of electrical transport properties of stoichiometric (Mg,Ni)-ferrite in the temperature
range 77 ≤ T ≤ 300 K, applying magnetic field upto 1T in the frequency range 20 Hz-1 MHz. After ball milling of MgO,
NiO and  -Fe2O3 and annealing at 1473 K, a (Mg,Ni)-ferrite phase is obtained. The temperature dependency of dc re-
sistivity indicates the prevalence of a simple hopping type charge transport in all the investigated samples. The activa-
tion energy decreases by annealing the samples by 1473 K. The dc magnetoresistivity of the samples is positive, which
has been explained by using wave function shrinkage model. The frequency dependence of conductivity has been de-
scribed by power law and the frequency exponent ‘s’ is found to be anomalous temperature dependent for ball milling
and annealing samples. The real part of the dielectric permittivity at a fixed frequency was found to follow the power
law 
/(f,T)
 Tn. The magnitude of the temperature exponent ‘n’ strongly depends on milling time and also on annealing
temperature. The dielectric permittivity increases with milling and also with annealing. An analysis of the complex im-
pedance by an ideal equivalent circuit indicates that the grain boundary contribution is dominating over the grain con-
tribution in conduction process.
Keywords: Ferrites, Chemical Synthesis, X-Ray Scattering, Transport Properties
1. Introduction
Small ferri-magnetic oxides, technically known as fer-
rites have attracted considerable attention not only from a
fundamental scientific interest but also from a practical
point of view for growing applications in the magnetic,
electronic and microwave fields [1-7]. Simultaneous
presence of magnetic and dielectric nature of ferrites is
vastly exploited in a variety of applications at different
frequencies. The special feature of these materials is that
the properties can be tailored over wide ranges by appro-
priate substitution of various ions in the chemical for-
mula unit and control of processing procedures. Ferrites
are extensively used in magnetic recording, information
storage, colour imaging, bio-processing, magnetic refrig-
eration and in magneto optical devices [5-7]. Ferrites also
have great promise for atomic engineering of materials
with functional magnetic properties. The formation of
corrosion product on the out of core surfaces in pressur-
ized heavy water reactors (PHWRs) are major problem.
Ferrite having spinal structure such as magnetic and nickel
etc play a major role to prevent such problem. Thus at-
tempts are being made to study the various ferrites to
evaluate the impact of substitution of the divalent metal
ions to modify the properties of these oxides.
Spinals are characterized by a very compact oxygen
array with cations in tetrahedral (A) and octahedral (B)
coordination and may be described by the IV(A1-iBi)
VI(B2-iAi)O4 structural formula, where IV and VI repre-
sent tetrahedrally and octahedrally coordinated sites, A
and B are cations with variable valency and i the inver-
sion parameter. Normal spinal are those with i = 0, in-
verse spinals those with i = 1.
Different synthetic roots are employed in preparation
of ferrites [8-10]. High energy ball milling is a very suit-
able solid state processing technique for the preparation
of nanocrystalline ferrite powder exhibiting new and un-
usual properties [11-14]. The objectives of the present
work are 1) to prepare the Mg-Ni ferrite by ball milling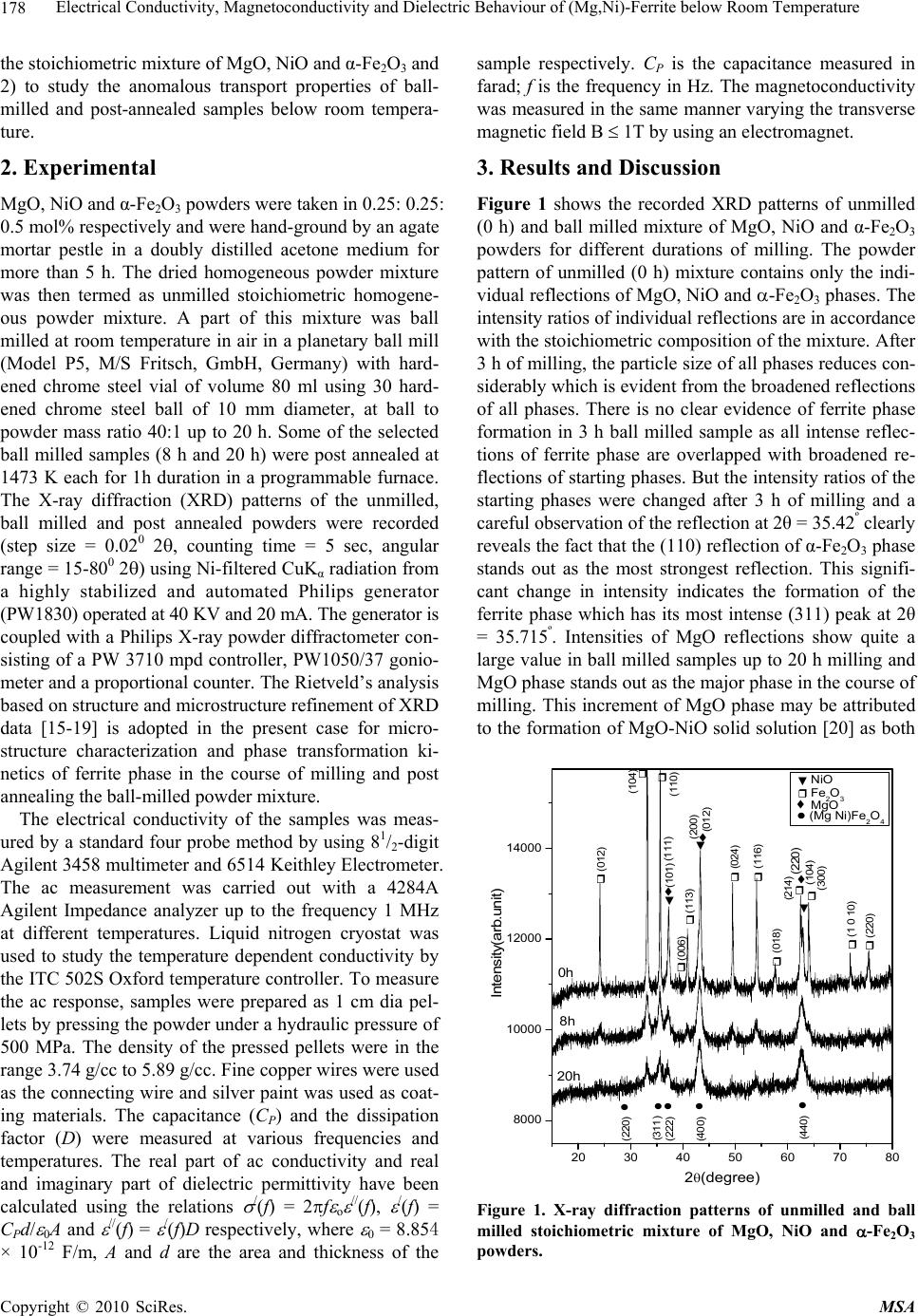

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 178
the stoichiometric mixture of MgO, NiO and α-Fe2O3 and
2) to study the anomalous transport properties of ball-
milled and post-annealed samples below room tempera-
ture.
2. Experimental
MgO, NiO and α-Fe2O3 powders were taken in 0.25: 0.25:
0.5 mol% respectively and were hand-ground by an agate
mortar pestle in a doubly distilled acetone medium for
more than 5 h. The dried homogeneous powder mixture
was then termed as unmilled stoichiometric homogene-
ous powder mixture. A part of this mixture was ball
milled at room temperature in air in a planetary ball mill
(Model P5, M/S Fritsch, GmbH, Germany) with hard-
ened chrome steel vial of volume 80 ml using 30 hard-
ened chrome steel ball of 10 mm diameter, at ball to
powder mass ratio 40:1 up to 20 h. Some of the selected
ball milled samples (8 h and 20 h) were post annealed at
1473 K each for 1h duration in a programmable furnace.
The X-ray diffraction (XRD) patterns of the unmilled,
ball milled and post annealed powders were recorded
(step size = 0.020 2, counting time = 5 sec, angular
range = 15-800 2) using Ni-filtered CuKα radiation from
a highly stabilized and automated Philips generator
(PW1830) operated at 40 KV and 20 mA. The generator is
coupled with a Philips X-ray powder diffractometer con-
sisting of a PW 3710 mpd controller, PW1050/37 gonio-
meter and a proportional counter. The Rietveld’s analysis
based on structure and microstructure refinement of XRD
data [15-19] is adopted in the present case for micro-
structure characterization and phase transformation ki-
netics of ferrite phase in the course of milling and post
annealing the ball-milled powder mixture.
The electrical conductivity of the samples was meas-
ured by a standard four probe method by using 81/2-digit
Agilent 3458 multimeter and 6514 Keithley Electrometer.
The ac measurement was carried out with a 4284A
Agilent Impedance analyzer up to the frequency 1 MHz
at different temperatures. Liquid nitrogen cryostat was
used to study the temperature dependent conductivity by
the ITC 502S Oxford temperature controller. To measure
the ac response, samples were prepared as 1 cm dia pel-
lets by pressing the powder under a hydraulic pressure of
500 MPa. The density of the pressed pellets were in the
range 3.74 g/cc to 5.89 g/cc. Fine copper wires were used
as the connecting wire and silver paint was used as coat-
ing materials. The capacitance (CP) and the dissipation
factor (D) were measured at various frequencies and
temperatures. The real part of ac conductivity and real
and imaginary part of dielectric permittivity have been
calculated using the relations 
/(f) = 2f

o

//(f),

/(f) =
CPd/ 
0A and

//(f) =

/(f)D respectively, where

0 = 8.854
× 10-12 F/m, A and d are the area and thickness of the
sample respectively. CP is the capacitance measured in
farad; f is the frequency in Hz. The magnetoconductivity
was measured in the same manner varying the transverse
magnetic field B  1T by using an electromagnet.
3. Results and Discussion
Figure 1 shows the recorded XRD patterns of unmilled
(0 h) and ball milled mixture of MgO, NiO and α-Fe2O3
powders for different durations of milling. The powder
pattern of unmilled (0 h) mixture contains only the indi-
vidual reflections of MgO, NiO and -Fe2O3 phases. The
intensity ratios of individual reflections are in accordance
with the stoichiometric composition of the mixture. After
3 h of milling, the particle size of all phases reduces con-
siderably which is evident from the broadened reflections
of all phases. There is no clear evidence of ferrite phase
formation in 3 h ball milled sample as all intense reflec-
tions of ferrite phase are overlapped with broadened re-
flections of starting phases. But the intensity ratios of the
starting phases were changed after 3 h of milling and a
careful observation of the reflection at 2θ = 35.42º clearly
reveals the fact that the (110) reflection of α-Fe2O3 phase
stands out as the most strongest reflection. This signifi-
cant change in intensity indicates the formation of the
ferrite phase which has its most intense (311) peak at 2θ
= 35.715º. Intensities of MgO reflections show quite a
large value in ball milled samples up to 20 h milling and
MgO phase stands out as the major phase in the course of
milling. This increment of MgO phase may be attributed
to the formation of MgO-NiO solid solution [20] as both
20 30 40 50 60 70 80
8000
10000
12000
14000
(111)

(440)
(400)
(222)
(311)
(220)




(Mg Ni)Fe
2
O
4

(220)

(200)

MgO

Fe
2
O
3

NiO

(104)

(012)
(101)



(220)

(1 0 10)

(300)

(214)

(018)

(116)

(024)





(006) (113)
(110)
(104)
(012)
0h
8h
20h
Int ens i t y( ar b. un i t )
2  (degree)
Figure 1. X-ray diffraction patterns of unmilled and ball
milled stoichiometric mixture of MgO, NiO and -Fe2O3
powders.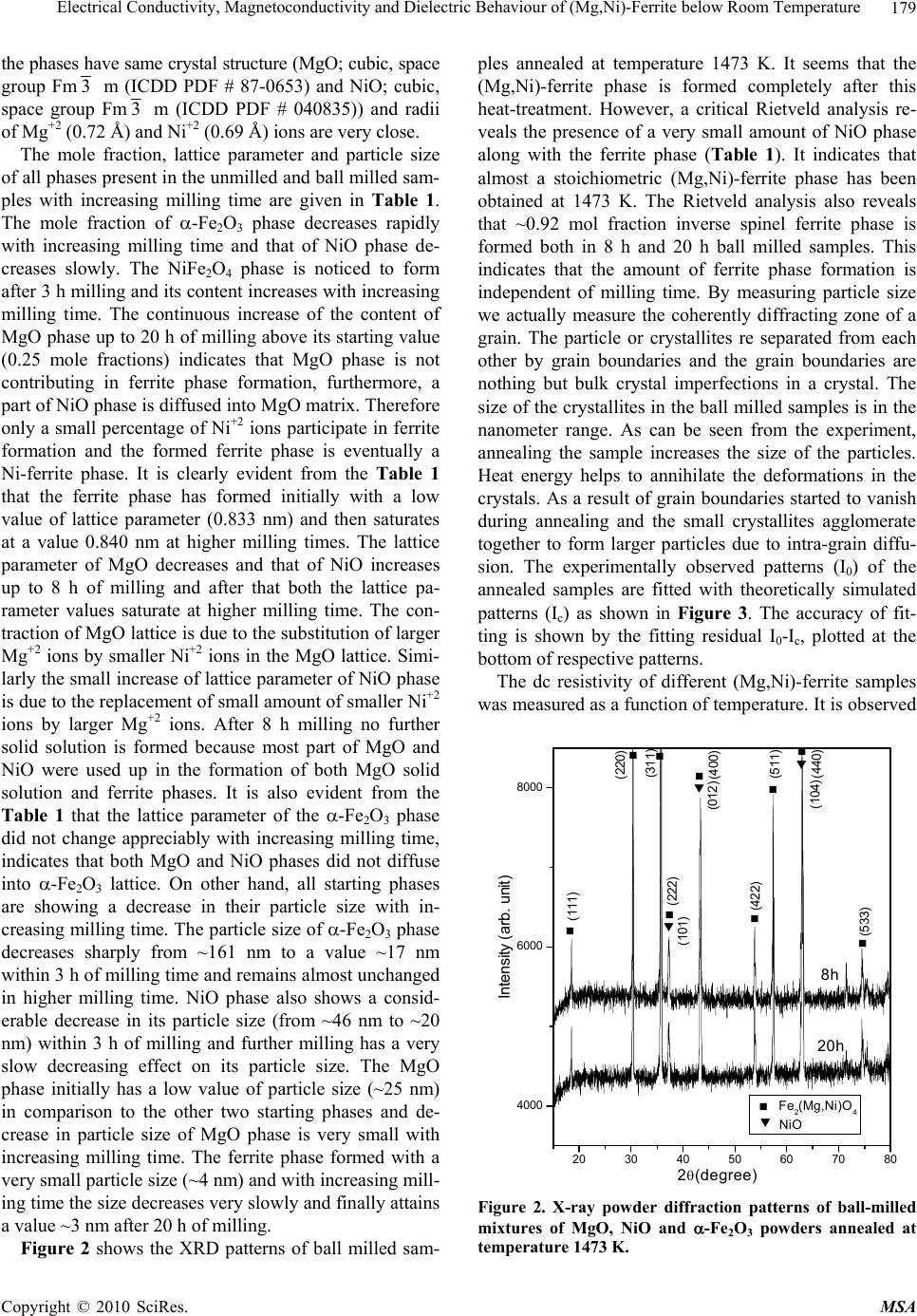

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 179
the phases have same crystal structure (MgO; cubic, space
group Fm3 m (ICDD PDF # 87-0653) and NiO; cubic,
space group Fm3 m (ICDD PDF # 040835)) and radii
of Mg+2 (0.72 Å) and Ni+2 (0.69 Å) ions are very close.
The mole fraction, lattice parameter and particle size
of all phases present in the unmilled and ball milled sam-
ples with increasing milling time are given in Table 1.
The mole fraction of -Fe2O3 phase decreases rapidly
with increasing milling time and that of NiO phase de-
creases slowly. The NiFe2O4 phase is noticed to form
after 3 h milling and its content increases with increasing
milling time. The continuous increase of the content of
MgO phase up to 20 h of milling above its starting value
(0.25 mole fractions) indicates that MgO phase is not
contributing in ferrite phase formation, furthermore, a
part of NiO phase is diffused into MgO matrix. Therefore
only a small percentage of Ni+2 ions participate in ferrite
formation and the formed ferrite phase is eventually a
Ni-ferrite phase. It is clearly evident from the Table 1
that the ferrite phase has formed initially with a low
value of lattice parameter (0.833 nm) and then saturates
at a value 0.840 nm at higher milling times. The lattice
parameter of MgO decreases and that of NiO increases
up to 8 h of milling and after that both the lattice pa-
rameter values saturate at higher milling time. The con-
traction of MgO lattice is due to the substitution of larger
Mg+2 ions by smaller Ni+2 ions in the MgO lattice. Simi-
larly the small increase of lattice parameter of NiO phase
is due to the replacement of small amount of smaller Ni+2
ions by larger Mg+2 ions. After 8 h milling no further
solid solution is formed because most part of MgO and
NiO were used up in the formation of both MgO solid
solution and ferrite phases. It is also evident from the
Table 1 that the lattice parameter of the -Fe2O3 phase
did not change appreciably with increasing milling time,
indicates that both MgO and NiO phases did not diffuse
into -Fe2O3 lattice. On other hand, all starting phases
are showing a decrease in their particle size with in-
creasing milling time. The particle size of -Fe2O3 phase
decreases sharply from ~161 nm to a value ~17 nm
within 3 h of milling time and remains almost unchanged
in higher milling time. NiO phase also shows a consid-
erable decrease in its particle size (from ~46 nm to ~20
nm) within 3 h of milling and further milling has a very
slow decreasing effect on its particle size. The MgO
phase initially has a low value of particle size (~25 nm)
in comparison to the other two starting phases and de-
crease in particle size of MgO phase is very small with
increasing milling time. The ferrite phase formed with a
very small particle size (~4 nm) and with increasing mill-
ing time the size decreases very slowly and finally attains
a value ~3 nm after 20 h of milling.
Figure 2 shows the XRD patterns of ball milled sam-
ples annealed at temperature 1473 K. It seems that the
(Mg,Ni)-ferrite phase is formed completely after this
heat-treatment. However, a critical Rietveld analysis re-
veals the presence of a very small amount of NiO phase
along with the ferrite phase (Table 1). It indicates that
almost a stoichiometric (Mg,Ni)-ferrite phase has been
obtained at 1473 K. The Rietveld analysis also reveals
that ~0.92 mol fraction inverse spinel ferrite phase is
formed both in 8 h and 20 h ball milled samples. This
indicates that the amount of ferrite phase formation is
independent of milling time. By measuring particle size
we actually measure the coherently diffracting zone of a
grain. The particle or crystallites re separated from each
other by grain boundaries and the grain boundaries are
nothing but bulk crystal imperfections in a crystal. The
size of the crystallites in the ball milled samples is in the
nanometer range. As can be seen from the experiment,
annealing the sample increases the size of the particles.
Heat energy helps to annihilate the deformations in the
crystals. As a result of grain boundaries started to vanish
during annealing and the small crystallites agglomerate
together to form larger particles due to intra-grain diffu-
sion. The experimentally observed patterns (I0) of the
annealed samples are fitted with theoretically simulated
patterns (Ic) as shown in Figure 3. The accuracy of fit-
ting is shown by the fitting residual I0-Ic, plotted at the
bottom of respective patterns.
The dc resistivity of different (Mg,Ni)-ferrite samples
was measured as a function of temperature. It is observed
20 30 40 5060 70 80
4000
6000
8000
(104)
(012)
(222)
(101)












(533)
(440)
(422)
(511)
(400)
(311)
(220)
(111)
NiO
Fe2(Mg,Ni)O4


8h
20h
Intensity (arb. unit)
2(degree)
Figure 2. X-ray powder diffraction patterns of ball-milled
mixtures of MgO, NiO and -Fe2O3 powders annealed at
temperature 1473 K.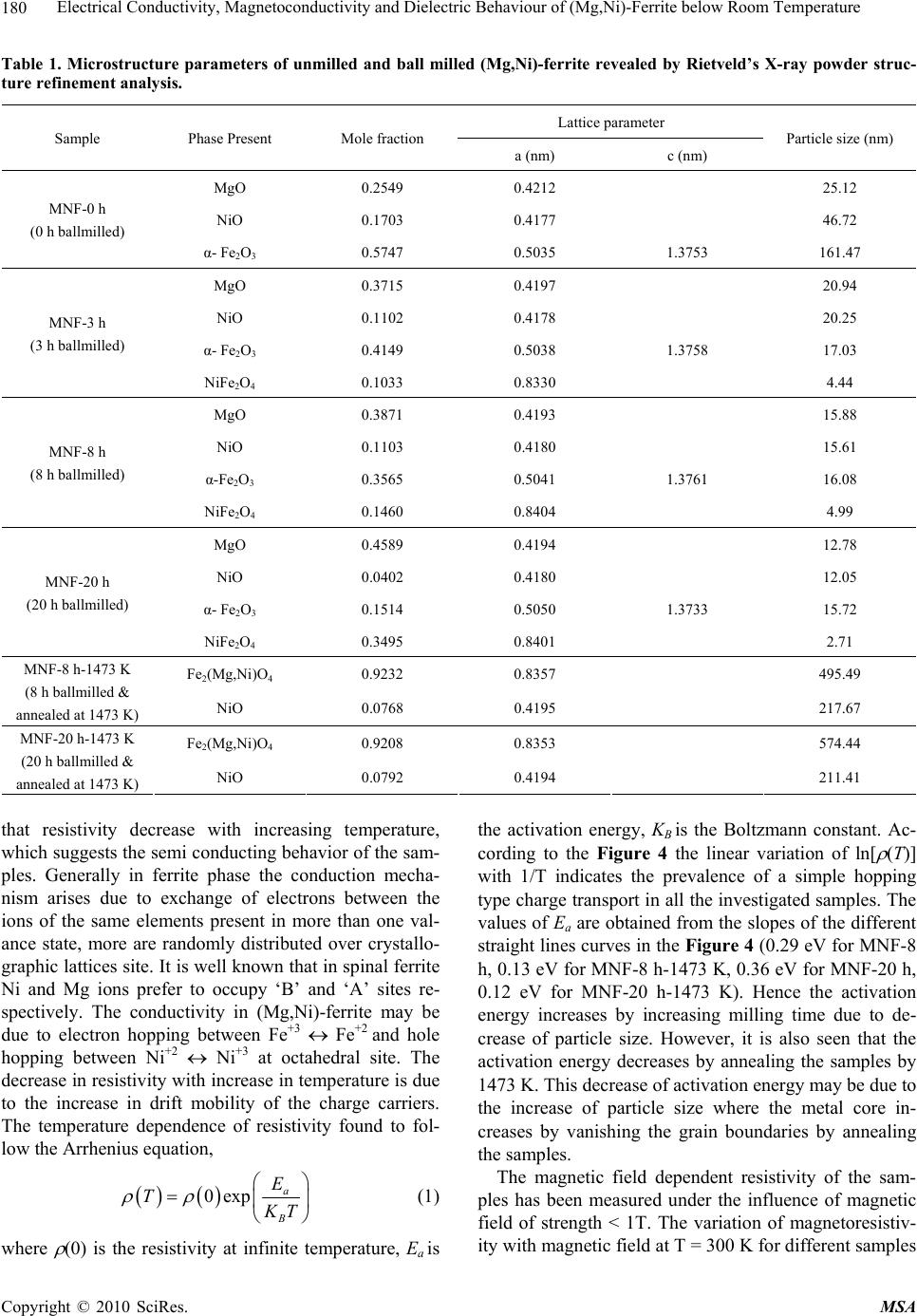

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 180
Table 1. Microstructure parameters of unmilled and ball milled (Mg,Ni)-ferrite revealed by Rietveld’s X-ray powder struc-
ture refinement analysis.
Lattice parameter
Sample Phase Present Mole fraction
a (nm) c (nm)
Particle size (nm)
MgO 0.2549 0.4212 25.12
NiO 0.1703 0.4177 46.72
MNF-0 h
(0 h ballmilled)
α- Fe2O3 0.5747 0.5035 1.3753 161.47
MgO 0.3715 0.4197 20.94
NiO 0.1102 0.4178 20.25
α- Fe2O3 0.4149 0.5038 1.3758 17.03
MNF-3 h
(3 h ballmilled)
NiFe2O4 0.1033 0.8330 4.44
MgO 0.3871 0.4193 15.88
NiO 0.1103 0.4180 15.61
α-Fe2O3 0.3565 0.5041 1.3761 16.08
MNF-8 h
(8 h ballmilled)
NiFe2O4 0.1460 0.8404 4.99
MgO 0.4589 0.4194 12.78
NiO 0.0402 0.4180 12.05
α- Fe2O3 0.1514 0.5050 1.3733 15.72
MNF-20 h
(20 h ballmilled)
NiFe2O4 0.3495 0.8401 2.71
Fe2(Mg,Ni)O4 0.9232 0.8357 495.49
MNF-8 h-1473 K
(8 h ballmilled &
annealed at 1473 K) NiO 0.0768 0.4195 217.67
Fe2(Mg,Ni)O4 0.9208 0.8353 574.44
MNF-20 h-1473 K
(20 h ballmilled &
annealed at 1473 K) NiO 0.0792 0.4194 211.41
that resistivity decrease with increasing temperature,
which suggests the semi conducting behavior of the sam-
ples. Generally in ferrite phase the conduction mecha-
nism arises due to exchange of electrons between the
ions of the same elements present in more than one val-
ance state, more are randomly distributed over crystallo-
graphic lattices site. It is well known that in spinal ferrite
Ni and Mg ions prefer to occupy ‘B’ and ‘A’ sites re-
spectively. The conductivity in (Mg,Ni)-ferrite may be
due to electron hopping between Fe+3  Fe+2 and hole
hopping between Ni+2  Ni+3 at octahedral site. The
decrease in resistivity with increase in temperature is due
to the increase in drift mobility of the charge carriers.
The temperature dependence of resistivity found to fol-
low the Arrhenius equation,
 
0exp a
B
E
T
K
T




(1)
where  (0) is the resistivity at infinite temperature, Ea is
the activation energy, KB is the Boltzmann constant. Ac-
cording to the Figure 4 the linear variation of ln[  (T)]
with 1/T indicates the prevalence of a simple hopping
type charge transport in all the investigated samples. The
values of Ea are obtained from the slopes of the different
straight lines curves in the Figure 4 (0.29 eV for MNF-8
h, 0.13 eV for MNF-8 h-1473 K, 0.36 eV for MNF-20 h,
0.12 eV for MNF-20 h-1473 K). Hence the activation
energy increases by increasing milling time due to de-
crease of particle size. However, it is also seen that the
activation energy decreases by annealing the samples by
1473 K. This decrease of activation energy may be due to
the increase of particle size where the metal core in-
creases by vanishing the grain boundaries by annealing
the samples.
The magnetic field dependent resistivity of the sam-
ples has been measured under the influence of magnetic
field of strength < 1T. The variation of magnetoresistiv-
ity with magnetic field at T = 300 K for different samples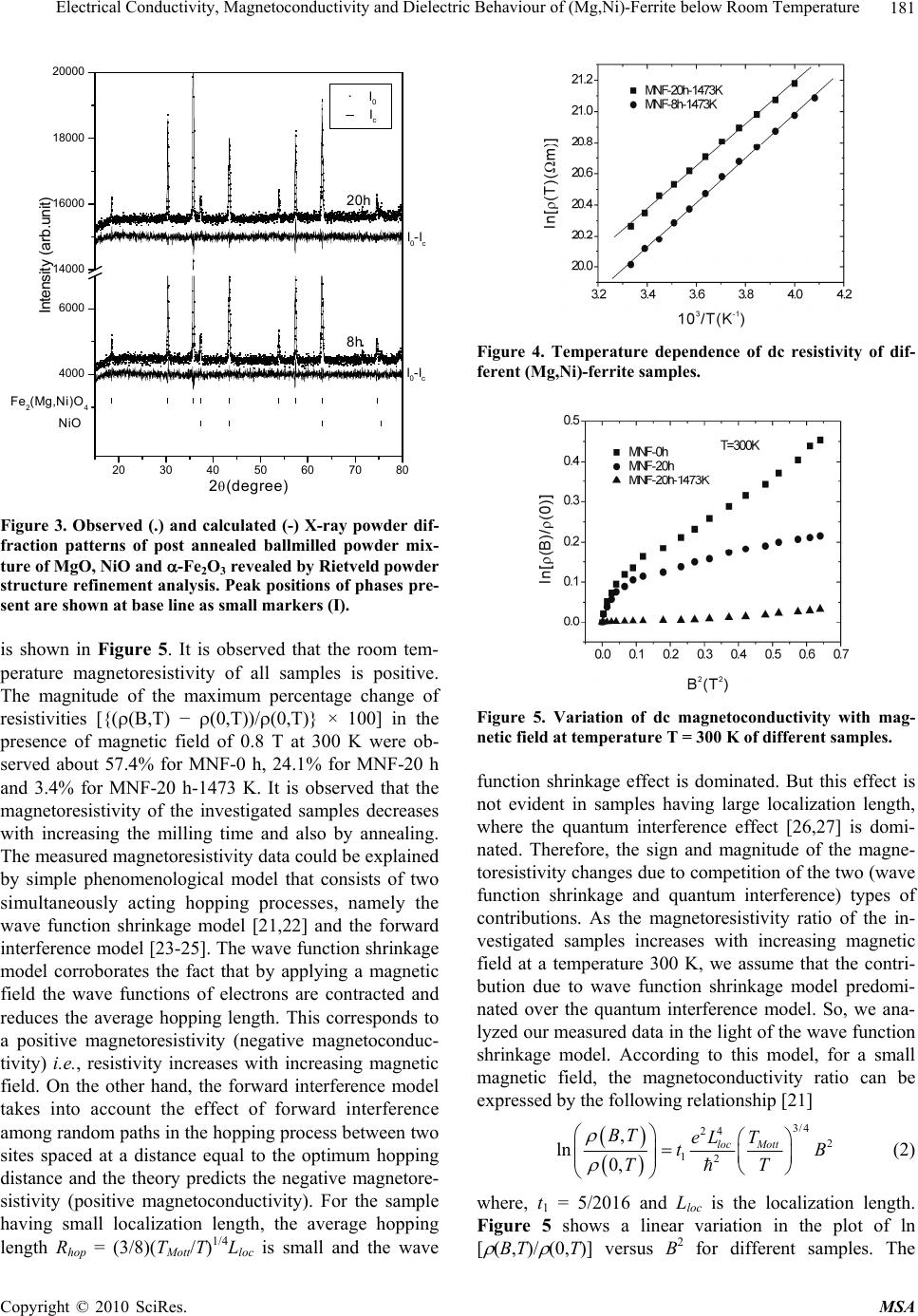

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 181
20 3040 50 60 7080
4000
6000
14000
16000
18000
20000
NiO
Fe2(Mg,Ni)O4
_
.
Ic
I0
I0-Ic
I0-Ic
8h
20h
Intensity (arb.unit)
2(degree)
Figure 3. Observed (.) and calculated (-) X-ray powder dif-
fraction patterns of post annealed ballmilled powder mix-
ture of MgO, NiO and -Fe2O3 revealed by Rietveld powder
structure refinement analysis. Peak positions of phases pre-
sent are shown at base line as small markers (I).
is shown in Figure 5. It is observed that the room tem-
perature magnetoresistivity of all samples is positive.
The magnitude of the maximum percentage change of
resistivities [{((B,T) − (0,T))/(0,T)} × 100] in the
presence of magnetic field of 0.8 T at 300 K were ob-
served about 57.4% for MNF-0 h, 24.1% for MNF-20 h
and 3.4% for MNF-20 h-1473 K. It is observed that the
magnetoresistivity of the investigated samples decreases
with increasing the milling time and also by annealing.
The measured magnetoresistivity data could be explained
by simple phenomenological model that consists of two
simultaneously acting hopping processes, namely the
wave function shrinkage model [21,22] and the forward
interference model [23-25]. The wave function shrinkage
model corroborates the fact that by applying a magnetic
field the wave functions of electrons are contracted and
reduces the average hopping length. This corresponds to
a positive magnetoresistivity (negative magnetoconduc-
tivity) i.e., resistivity increases with increasing magnetic
field. On the other hand, the forward interference model
takes into account the effect of forward interference
among random paths in the hopping process between two
sites spaced at a distance equal to the optimum hopping
distance and the theory predicts the negative magnetore-
sistivity (positive magnetoconductivity). For the sample
having small localization length, the average hopping
length Rhop = (3/8)(TMott/T)1/4Lloc is small and the wave
Figure 4. Temperature dependence of dc resistivity of dif-
ferent (Mg,Ni)-ferrite samples.
Figure 5. Variation of dc magnetoconductivity with mag-
netic field at temperature T = 300 K of different samples.
function shrinkage effect is dominated. But this effect is
not evident in samples having large localization length,
where the quantum interference effect [26,27] is domi-
nated. Therefore, the sign and magnitude of the magne-
toresistivity changes due to competition of the two (wave
function shrinkage and quantum interference) types of
contributions. As the magnetoresistivity ratio of the in-
vestigated samples increases with increasing magnetic
field at a temperature 300 K, we assume that the contri-
bution due to wave function shrinkage model predomi-
nated over the quantum interference model. So, we ana-
lyzed our measured data in the light of the wave function
shrinkage model. According to this model, for a small
magnetic field, the magnetoconductivity ratio can be
expressed by the following relationship [21]


3/ 4
24
2
12
,
ln 0,
loc Mott
BT eL T
tB
TT


 

 
 

 (2)
where, t1 = 5/2016 and Lloc is the localization length.
Figure 5 shows a linear variation in the plot of ln
[  (B,T)/  (0,T)] versus B2 for different samples. The

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 182
points are the experimental data while the solid lines
represent the best fits obtained on the basis of the wave
function shrinkage model. It is evident from the Figure 5
that the experimental data can be well described by the
theory as indicated in (2). It is observed from the fitting
that the slope of the curves are 0.59 for MNF-0 h, 0.19
for MNF-20 h and 0.07 for MNF-20 h-1473 K samples.
The slope of unmilled MNF-0 h sample is much greater
than the ballmilled and annealed samples. This is because
in unmilled sample, the individual phases of oxides of Fe,
Ni and Mg contribute the magnetoresistivity. However in
ballmilled and annealed samples, ferrite phases exist and
by milling, the particle size decreases and more disorder
presents in the sample. Since, in sample with higher dis-
order, electronic wave functions are more localized within
smaller regions resulting smaller localization length.
Therefore, the lowering of slope arises due to reduction
of localization length.
The ac conductivity of Mg-Ni ferrite samples are in-
vestigated in the frequency range 20 Hz to 1 MHz and in
the temperature range 77  T  300 K. The measured
data showed that the variation of conductivity with fre-
quency at a particular temperature is prominent at higher
frequencies, whereas at low frequencies it is almost in-
dependent with frequencies, this could be attributed to
the dc contribution. A general feature of amorphous
semiconductors or disordered systems is that the fre-
quency dependent conductivity

ac(f) obeys a power law
with frequency. The total conductivity 
/(f) at a particular
temperature over a wide range of frequencies can be ex-
pressed as [28-30]
/() ()
s
dc acdc
f
ff

   (3)
where 
dc is the dc conductivity,  is the temperature
dependent constant and the frequency exponent s < 1.
The value of 
ac(f) has been determined upon subtraction
of the dc contribution from the total frequency dependent
conductivity 
/(f). Figure 6 shows the linear variation of
ln[ 
ac(f)] with ln(f) at different temperatures for the sam-
ple MNF-20 h-1473 K. Similar behavior was observed for
all other samples. The value of ‘s’ at each temperature
has been calculated from the slope of ln[ 
ac(f)] versus
ln(f) plot for each temperature. The trend of change in ‘s’
with temperature is shown in Figure 7 for different sam-
ples. The temperature dependency of ‘s’ of disordered
systems has been explained by two physical processes
such as correlated barrier hopping (CBH) [30] and quan-
tum mechanical tunneling (QMT) like electron tunneling
(ET) [31], small polaron tunneling (SPT) [30] and large
polaron tunneling (LPT) [29]. As the nature of tempera-
ture dependency of ‘s’ for different conduction processes
are different, the exact nature of charge transport may be
obtained experimentally from the temperature variation
Figure 6. Frequency dependent ac conductivity at different
temperatures of MNF-20 h-1473 K sample.
of the frequency exponent ‘s’. According to the corre-
lated barrier hopping model ‘s’ increases with the de-
crease in temperature. From the trend of change in ‘s’
with temperature for unmilled sample (MNF-0 h), it is
presumed that the correlated barrier hopping is suitable.
According to this model, the charge carrier hops between
the sites over the potential barrier separating them and
the frequency exponent ‘s’ is given by the expression
[30].
0
6
11
ln
B
HB
kT
s
WkT


 


(4)
where WH is the effective barrier height and 
o is the
characteristic relaxation time. According to (4), for large
values of WH/kBT, the variation of ‘s’ with frequency is
so small that it is effectively independent of frequency
[32]. On the other hand, the linear variation of ln[ 
ac(f)]
vs ln(f) in Figure 6 supports that ‘s’ is independent of
frequency in our investigated samples. Therefore, we
fitted experimental data with (4) as function of tempera-
ture alone with WH and

o as fitting parameters. In Fig-
ure 7 the points represent the experimental data whereas
solid lines are the theoretical best fit values obtained
from (4) for MNF-0 h sample and the best fitted values
of the parameters WH and

o (at a fixed frequency of f =
10 KHz) are 1.16 eV and 5.97 × 10-13 S. The value of WH
are, as expected, higher than the activation energy meas-
ured from dc contribution and the values of the cha-
racteristic relaxation time 
o are comparable with those
that would be expected for typical inverse phonon fre-
quency. Therefore, it may be concluded that the ac con-
ductivity of MNF-0 h sample can be described by CBH
model. But for MNF-20 h sample, ‘s’ has to increase first
upto T < 150 K and then decrease with further increasing
of temperature (T > 150 K). Similar trend was observed
in annealed (MNF-20 h-1473 K) sample with weaker
temperature dependency. Hence, the anomalous behavior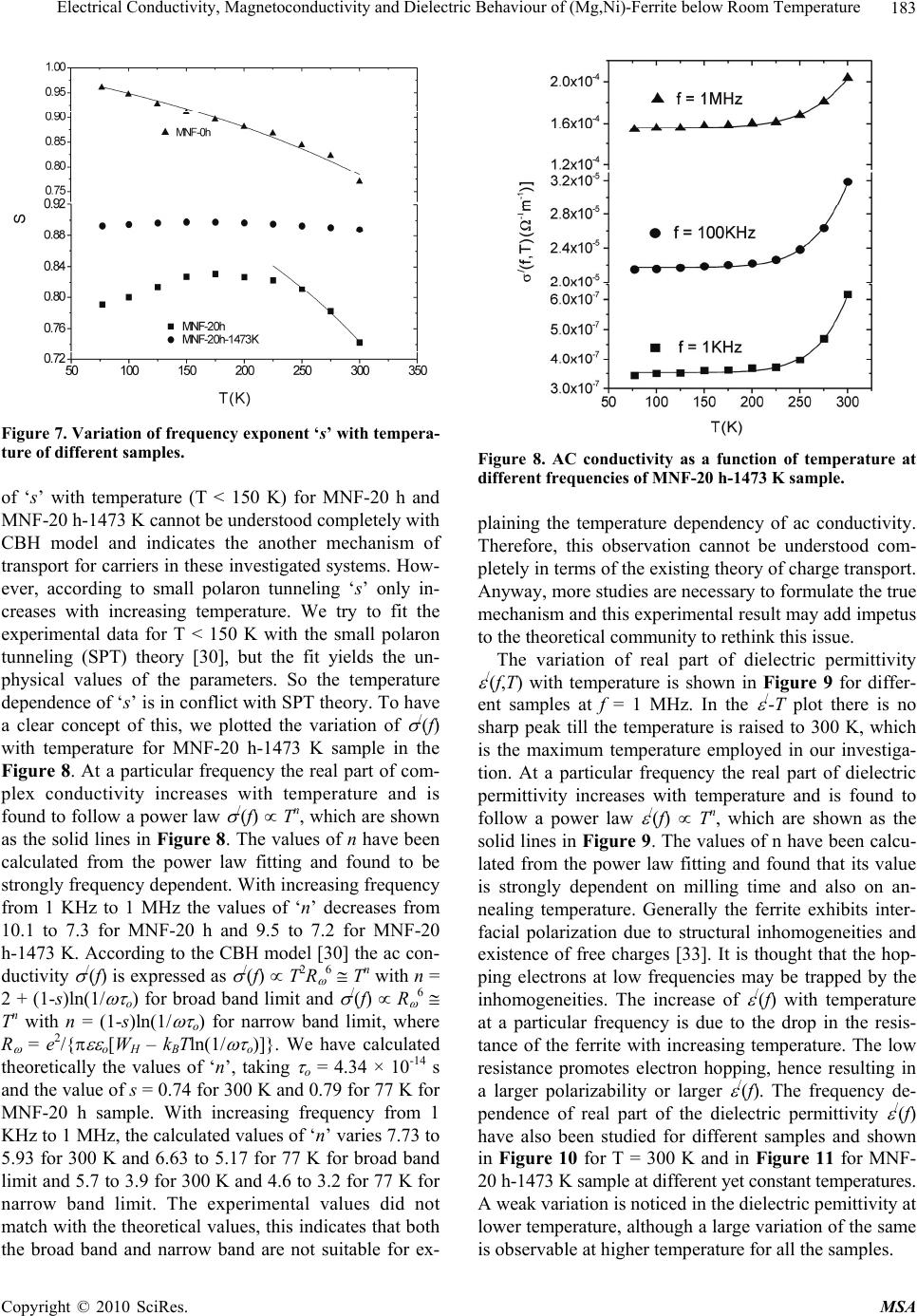

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 183
Figure 7. Variation of frequency exponent ‘s’ with tempera-
ture of different samples.
of ‘s’ with temperature (T < 150 K) for MNF-20 h and
MNF-20 h-1473 K cannot be understood completely with
CBH model and indicates the another mechanism of
transport for carriers in these investigated systems. How-
ever, according to small polaron tunneling ‘s’ only in-
creases with increasing temperature. We try to fit the
experimental data for T < 150 K with the small polaron
tunneling (SPT) theory [30], but the fit yields the un-
physical values of the parameters. So the temperature
dependence of ‘s’ is in conflict with SPT theory. To have
a clear concept of this, we plotted the variation of 
/(f)
with temperature for MNF-20 h-1473 K sample in the
Figure 8. At a particular frequency the real part of com-
plex conductivity increases with temperature and is
found to follow a power law 
/(f)  Tn, which are shown
as the solid lines in Figure 8. The values of n have been
calculated from the power law fitting and found to be
strongly frequency dependent. With increasing frequency
from 1 KHz to 1 MHz the values of ‘n’ decreases from
10.1 to 7.3 for MNF-20 h and 9.5 to 7.2 for MNF-20
h-1473 K. According to the CBH model [30] the ac con-
ductivity 
/(f) is expressed as

/(f)  T2R

6  Tn with n =
2 + (1-s)ln(1/ 
o) for broad band limit and

/(f)  R

6 
Tn with n = (1-s)ln(1/ 
o) for narrow band limit, where
R

= e2/{ 
o[WH – kBTln(1/

o)]}. We have calculated
theoretically the values of ‘n’, taking 
o = 4.34 × 10-14 s
and the value of s = 0.74 for 300 K and 0.79 for 77 K for
MNF-20 h sample. With increasing frequency from 1
KHz to 1 MHz, the calculated values of ‘n’ varies 7.73 to
5.93 for 300 K and 6.63 to 5.17 for 77 K for broad band
limit and 5.7 to 3.9 for 300 K and 4.6 to 3.2 for 77 K for
narrow band limit. The experimental values did not
match with the theoretical values, this indicates that both
the broad band and narrow band are not suitable for ex-
Figure 8. AC conductivity as a function of temperature at
different frequencies of MNF-20 h-1473 K sample.
plaining the temperature dependency of ac conductivity.
Therefore, this observation cannot be understood com-
pletely in terms of the existing theory of charge transport.
Anyway, more studies are necessary to formulate the true
mechanism and this experimental result may add impetus
to the theoretical community to rethink this issue.
The variation of real part of dielectric permittivity

/(f,T) with temperature is shown in Figure 9 for differ-
ent samples at f = 1 MHz. In the 
/-T plot there is no
sharp peak till the temperature is raised to 300 K, which
is the maximum temperature employed in our investiga-
tion. At a particular frequency the real part of dielectric
permittivity increases with temperature and is found to
follow a power law 
/(f)  Tn, which are shown as the
solid lines in Figure 9. The values of n have been calcu-
lated from the power law fitting and found that its value
is strongly dependent on milling time and also on an-
nealing temperature. Generally the ferrite exhibits inter-
facial polarization due to structural inhomogeneities and
existence of free charges [33]. It is thought that the hop-
ping electrons at low frequencies may be trapped by the
inhomogeneities. The increase of 
/(f) with temperature
at a particular frequency is due to the drop in the resis-
tance of the ferrite with increasing temperature. The low
resistance promotes electron hopping, hence resulting in
a larger polarizability or larger 
/(f). The frequency de-
pendence of real part of the dielectric permittivity 
/(f)
have also been studied for different samples and shown
in Figure 10 for T = 300 K and in Figure 11 for MNF-
20 h-1473 K sample at different yet constant temperatures.
A weak variation is noticed in the dielectric pemittivity at
lower temperature, although a large variation of the same
is observable at higher temperature for all the samples.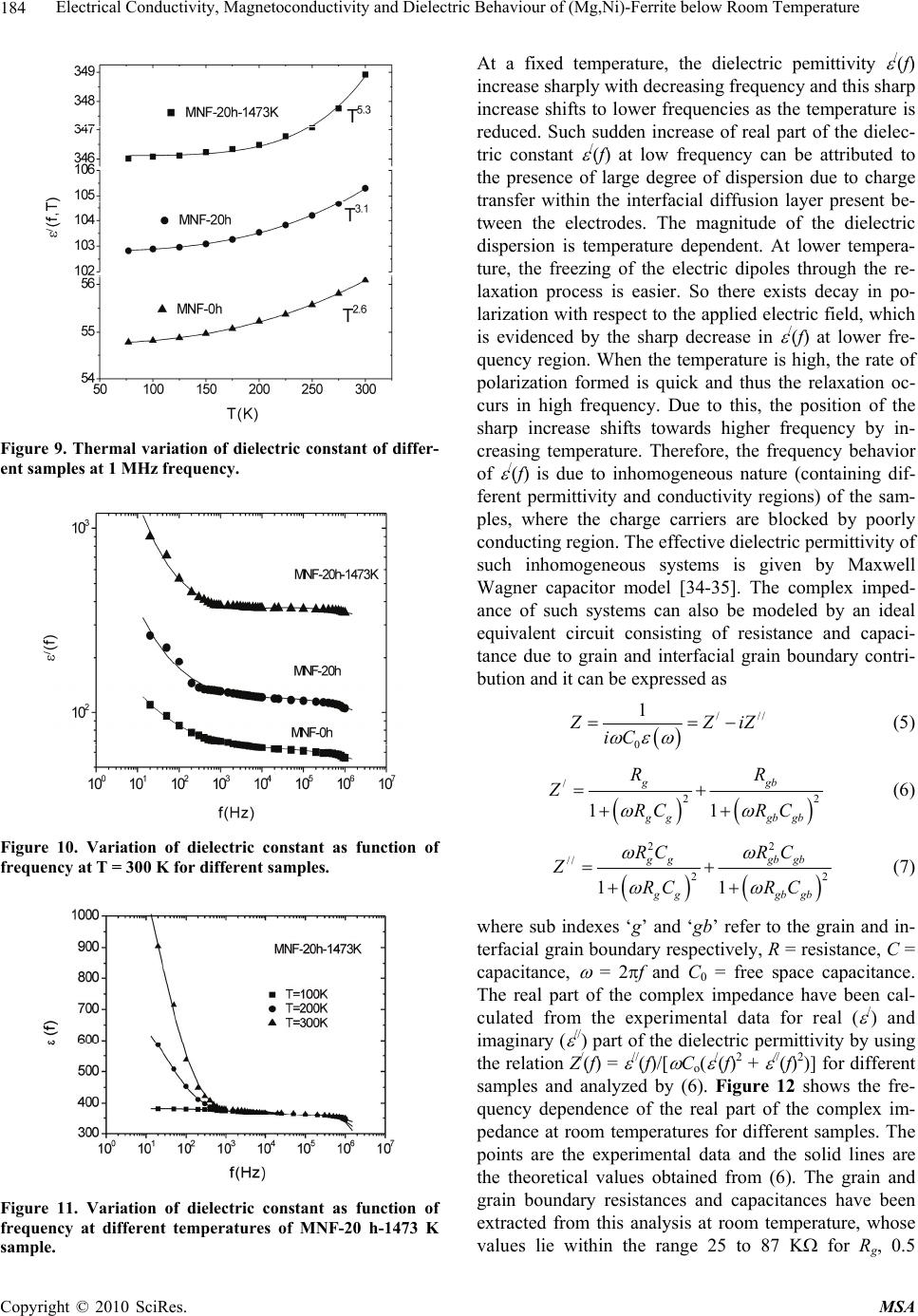

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 184
Figure 9. Thermal variation of dielectric constant of differ-
ent samples at 1 MHz frequency.
Figure 10. Variation of dielectric constant as function of
frequency at T = 300 K for different samples.
Figure 11. Variation of dielectric constant as function of
frequency at different temperatures of MNF-20 h-1473 K
sample.
At a fixed temperature, the dielectric pemittivity 
/(f)
increase sharply with decreasing frequency and this sharp
increase shifts to lower frequencies as the temperature is
reduced. Such sudden increase of real part of the dielec-
tric constant

/(f) at low frequency can be attributed to
the presence of large degree of dispersion due to charge
transfer within the interfacial diffusion layer present be-
tween the electrodes. The magnitude of the dielectric
dispersion is temperature dependent. At lower tempera-
ture, the freezing of the electric dipoles through the re-
laxation process is easier. So there exists decay in po-
larization with respect to the applied electric field, which
is evidenced by the sharp decrease in

/(f) at lower fre-
quency region. When the temperature is high, the rate of
polarization formed is quick and thus the relaxation oc-
curs in high frequency. Due to this, the position of the
sharp increase shifts towards higher frequency by in-
creasing temperature. Therefore, the frequency behavior
of

/(f) is due to inhomogeneous nature (containing dif-
ferent permittivity and conductivity regions) of the sam-
ples, where the charge carriers are blocked by poorly
conducting region. The effective dielectric permittivity of
such inhomogeneous systems is given by Maxwell
Wagner capacitor model [34-35]. The complex imped-
ance of such systems can also be modeled by an ideal
equivalent circuit consisting of resistance and capaci-
tance due to grain and interfacial grain boundary contri-
bution and it can be expressed as

///
0
1
Z
ZiZ
iC 
 (5)

/
22
11
ggb
gggb gb
RR
Z
RCR C 


(6)

22
//
22
11
gggb gb
gggb gb
RCR C
Z
RCR C




(7)
where sub indexes ‘g’ and ‘gb’ refer to the grain and in-
terfacial grain boundary respectively, R = resistance, C =
capacitance,  = 2f and C0 = free space capacitance.
The real part of the complex impedance have been cal-
culated from the experimental data for real ( 
/) and
imaginary ( 
//) part of the dielectric permittivity by using
the relation Z/(f) = 
//(f)/[
 Co( 
/(f)2 +

//(f)2)] for different
samples and analyzed by (6). Figure 12 shows the fre-
quency dependence of the real part of the complex im-
pedance at room temperatures for different samples. The
points are the experimental data and the solid lines are
the theoretical values obtained from (6). The grain and
grain boundary resistances and capacitances have been
extracted from this analysis at room temperature, whose
values lie within the range 25 to 87 K for Rg, 0.5

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 185
Figure 12. The real part of the complex impedance versus
frequency at T = 300 K of different samples.
to 1.02 M for Rgb, 0.63 to 1.56 nF for Cg and 0.43 to
0.92 nF for Cgb for different samples. It is observed from
the Figure 12 that the experimental data are reasonably
well fitted with the theory. It is observed that the grain
capacitance (Cb) are comparable with the grain boundary
capacitance (Cgb) for the investigated samples. However,
the resistance due to interfacial grain boundary is much
larger in compare to the grain resistance. This implies
that the grain boundary contribution dominates over the
grain contribution. Since the ferrites are semiconductors,
the conduction process can be explained by hopping
mechanism, where the carrier mobility is dominated by a
factor that increases with temperature exponentially. This
temperature dependent factor is controlled by thermal
activation in order to overcome the potential barrier be-
tween the sites by hopping.
4. Conclusions
The above experimental observations suggest the foll-
owing facts: 1) A Ni-ferrite phase and MgO-NiO solid
solution is obtained in ball milling the powder mixtures
of MgO, NiO and -Fe2O3; 2) Ni-ferrite phase is ob-
tained in the ball milling process is a non-stoichiometric
phase with a number of cation vacancies; 3) Particle size
of Ni-ferrite phase reduces to ~3 nm within 20 h of mill-
ing; 4) After annealing at 1473 K, ~0.92 mol fraction of
(Mg,Ni)-ferrite phase is obtained. The dc resistivity de-
creases with increasing temperature and the same follows
a hopping type charge transport. The magnetoresistivity
is positive and its magnitude reduces with increasing the
milling time and also by annealing and it can be ex-
plained by the wave function shrinkage model. The real
part of the complex ac conductivity was found to follow
the power law 
/(f)  T pf s. The magnitude of the tem-
perature exponent ‘p’ strongly depends on frequency and
its value decreases with increasing frequency. A detailed
analysis of the temperature dependence of the universal
dielectric response parameter ‘s’ revealed that the corre-
lated barrier hopping is the dominating charge transport
mechanism for only unmilled sample, however, anoma-
lous temperature dependency has been observed for ball
milling and annealing samples, which cannot be ex-
plained in terms of existing theory of charge transport.
Anyway, more studies are necessary to formulate the true
mechanism and this experimental result may add impetus
to the theoretical community to think about this issue. At
a particular frequency the real part of the dielectric per-
mittivity was found to follow the relation

/(f,T)  Tn.
The magnitude of the temperature exponent ‘n’ strongly
depends on milling time and also on annealing tempera-
ture. The frequency dependent real part of the dielectric
permittivity shows large degree of dispersion at low fre-
quency, but rapid polarization at high frequencies, which
can be interpreted by Maxwell-Wagner capacitor model.
The complex impedance of such systems can also be
modelled by an ideal equivalent circuit consisting of re-
sistance and capacitance due to grain and interfacial
grain boundary contribution. The details analysis of this
indicates that the grain and grain boundary capacitances
are comparable with each other; however, the resistance
due to interfacial grain boundary is much larger in com-
pare to the grain resistance.
5. Acknowledgements
This work has been carried out under Grant nos. F.27-1/
2002. TS.V dated 19.03.2002 and F.28-1/2003.TS.V dated
31-03.2003 sanctioned by the MHRD, Government of
India. The authors gratefully acknowledge the principal
assistance received from the above organization during
this work.
REFERENCES
[1] I. Anton., I. D. Dabata and L. Vekas, “Application Orien-
tated Researches on Magnetic Fluids,” Journal of Mag-
netism and Magnetic Materials, Vol. 85, No. 1-3, 1990,
pp. 219-226.
[2] R. D. McMickael, R. D. Shull, L. J. Swartzendruber, L. H.
Bennett and R. E. Watson, “Magnetocaloric Effect in Su-
perparamagnets,” Journal of Magnetism and Magnetic
Materials, Vol. 111, No. 1-2, 1992, pp. 29-33.
[3] D. L. Leslie-Pelecky and R. D. Rieke,” Magnetic Proper-
ties of Nanostructures Materials,” Chemistry of Materials,
Vol. 8, No. 8, 1996, pp. 1770-1783.
[4] T. Hirai, J. Kobayashi and I. Koasawa, “Preparation of
Acicular Ferrite Fine Particles Using an Emulsion Liquid

Electrical Conductivity, Magnetoconductivity and Dielectric Behaviour of (Mg,Ni)-Ferrite below Room Temperature 186
Membrane System,” Langmuir, Vol. 15, No. 19, 1999, pp.
6291-6298.
[5] R. H. Kodama, “Magnetic Nanoparticles,” Journal of
Magnetism and Magnetic Materials, Vol. 200, No. 1-3,
1999, pp. 359-372.
[6] K. V. P. M. Shafi, Y. Koltypin, A. Gedanken, R. Pro-
zorov, J. Balogh, J. Lendvai and I. Felner, “Sonochemical
Preparation of Nanosized Amorphous NiFe2O4 Particles,”
The Journal of Physical Chemistry B, Vol. 101, No. 33,
1996, pp. 6409-6414.
[7] D. Niznansky, M. Drillon and J. L. Renspinger, “Prepara-
tion of Magnetic Nanoparticles (γ-Fe2O3) in the Silica
Matrix,” IEEE Transaction on Magnetics, Vol. 30, No. 2,
1994, pp. 821-823.
[8] J. M. Yang, W. J. Tsuo and F. S. J. Yen, “Preparation of
Ultrafine Nickel Ferrite Powder Using Ni and Fe Tar-
trates,” Journal of Solid State Chemistry, Vol. 145, No. 1,
1999, pp. 50-57.
[9] Y. Shi, J. Ding, X. Liu and J. Wang, “NiFe2O4 Ultrafine
Particles Prepared by Co-Precipitation/Mechanical Al-
loying,” Journal of Magnetism and Magnetic Materials,
Vol. 205, No. 2-3, 1999, pp. 249-254.
[10] P. Druska, U. Steinike and V. Sepelak, “Surface Structure
of Mechanically Activated and of Mechanosynthesized
Zinc Ferrite,” Journal of Solid State Chemistry, Vol. 146,
No. 1, 1999, pp. 13-21.
[11] V. Sepelak, K. Tkacova, V. V. Boldyrev and U. Steinike,
“Crystal Srtucture Refinement of the Mechanically Acti-
vated Spinel-Ferrite,” Materials Science Forum, Vol.
228-231, 1996, pp. 783-788.
[12] V. Sepelak, A. Yu, U. Rogachev, D. Steinike, C. Uecker,
S. Wibmann and K. D. Becker, “Structure of Nanocrys-
talline Spinel Ferrite Produced by High Energy
Ballmilling Method,” Acta Crystallographica A, Vol. A
52, No. (Suppl.), 1996, p. C367
[13] V. Sepelak, A. Yu, U. Rogachev, D. Steinike, C. Uecker,
F. Krumcich, S .Wibmann and K. D. Becker, “The Syn-
thesis and Structure of Nanocrystalline Spinel Ferrite Pro-
duced by High Energy Ball-Milling Method,” Materials
Science Forum, Vol. 235-238, 1997, pp. 139-144.
[14] V. Sepelak, U. Steinike, D. C. Uecker, S. Wibmann and
K. D. Becker, “Structural Disorder in Mechanosynthe-
sized by Zinc Ferrite,” Journal of Solid State Chemistry,
Vol. 135, No. 1, 1998, pp. 52-58.
[15] H. M. Rietveld, “Line Profile of Neutron Powder Diffrac-
tion Peaks for Structure Refinement,” Acta Crystal-
lographica, Vol. 22, 1967, pp. 151-152.
[16] H. M. Rietveld, “A Profile Refinement Method for Nu-
clear and Magnetic Structures,” Journal of Applied Crys-
tallography, Vol. 2, 1969, pp. 65-71.
[17] R. A. Young, “The Rietveld Method,” Oxford University
Press, Oxford, 1996.
[18] L. Lutterotti, P. Scardi and P. Maistrelli, “LSI-a Com-
puter Program for Simultaneous Refinement of Material
Structure and Microstructure,” Journal of Applied Crys-
tallography, Vol. 25, No. 3, 1992, pp. 459-462.
[19] L. Lutterotti, “MAUD Version 2.046.” http://www.ing.
unitn. it/~luttero/maud
[20] W. D. Kingery, H. K. Bowen and D. R. Uhlmann, “In-
troduction to Ceramics,” 2nd Edition, John Wiley and
Sons, New York, 1976.
[21] B. I. Shklovskii, “Positive Magnetoresistance in the Vari-
able Range Hopping Conduction Regimes,” Soviet Phys-
ics Semiconductors, Vol. 17, 1983, p. 1311.
[22] B. I. Shklovskii and A. L. Efros, “Electronic Properties of
Doped Semiconductors,” Springer, Berlin, 1994.
[23] V. L. Nguyen, B. Z. Spivak and B. I. Shklovskii, “Tunnel
Hops in Disordered Systems,” Soviet Physics-JETP, Vol.
62, 1985, p. 1021.
[24] U. Sivan, O. Entin-Wohiman and O. Imry, “Orbital Mag-
netoconduction in the Variable-Range-Hopping Regime,”
Physical Review Letters, Vol. 60, No. 15, 1988, pp.
1566-1569.
[25] R. Rosenbaum, A. Milner, S. Hannens, T. Murphy, E.
Palm and B. Brandt, “Magnetoresistance of an Insulating
Amorphous Nickel-Silicon Film in Large Magnetic
Fields,” Physica B, Vol. 294-295, 2001, pp. 340-346.
[26] M. S. Fuhrer, W. Holmes, P. L. Richards, P. Delaney, S.
G. Louie and A. Zettl, “Nonlinear Transport and Local-
ization in Single Walled Carbon Nanotubes,” Synthetic
Metals, Vol. 103, No. 1-3, 1999, pp. 2529-2532.
[27] Y. Yosida and I. Oguro, “Variable Range Hopping Con-
duction in Bulk Samples Composed of Single Walled
Carbon Nanotubes,” Journal of Applied Physics, Vol. 86,
No. 2, 1999, pp. 999-1003.
[28] N. F. Mott and E. Davis, “Electronic Process in Noncrys-
talline Materials,” 2nd Edition, Clarendon, Clarendo,
1997.
[29] A. R. Long, “Frequency-Dependent Lossin Amorphous
Semi-Conductors,” Advances in Physics, Vol. 31, No. 5,
1982, pp. 553-637.
[30] S. R. Elliott, “a.c. Conduction in Amorphous Chalco-
genide and Pnictide Semiconductors,” Advances in Phys-
ics, Vol. 36, No. 2, 1987, pp. 135-217.
[31] A. L. Efros, “On the Theory of a.c. Conduction in Amor-
phous Semiconductors and Chalcogenide Glasses,” Phi-
losophical Magazine B, Vol. 43, No. 5, 1981, pp. 829-838.
[32] M. Ghosh, A. Barman, S. K. De and S. Chatterjee,
“Transport Properties of Hcl Doped Polyaniline and Poly-
aniline-Methyl Cellulose Dispersion,” Journal of Applied
Physics, Vol. 84, No. 2, 1998, pp. 806-811.
[33] B. G. Soares, M. E. Leyva, G. M. O. Barra and D. Khast-
gir, “Dielectric Behaviour of Polyaniline Synthesized by
Different Techniques,” European Polymer Journal, Vol.
42, No. 3, 2006, pp. 676-686.
[34] S. S. Suryavanshi, S. R. Patil, S. A. Patil and S. R. Sa-
want, “d.c. Conductivity and Dielectric Behaviour of Ti4+
Substituted Mg-Zn Ferrites,” Journal of the Less-Com-
mon Metals, Vol. 168, No. 2, 1991, pp. 169-174..
[35] J. C. Maxwell, “A Treatise on Electricity and Magnet-
ism,” Vol. 1, Oxford University Press, Oxford, 1988.