Vol.2, No.10, 1171-1179 (2010) Natural Science
http://dx.doi.org/10.4236/ns.2010.210145
Transient response of multilayered hollow cylinder
using various theories of generalized thermoelasticity
Daoud S. Mashat1, Aahraf M. Zenkour1,2*, Khaled A. Elsibai3
1Department of Mathematics, Faculty of Science, King AbdulAziz University, Jeddah, Saudi Arabia; *Corresponding Author:
2Department of Mathematics, Faculty of Science, Kafrelsheikh University, Kafr El-Sheikh, Egypt;
3Department of Mathematics, Faculty of Applied Science, Umm Al-Qura University, Holy Makkah, Saudi Arabia.
Received 7 March 2010; revised 12 April 2010; accepted 16 April 2010.
ABSTRACT
The present paper deals with thermoelastic pro-
blems of finitely long hollow cylinder composed
of two different materials with axial symmetry.
The medium is traction-free, with negligible bo-
dy forces and with internal and external heat
generations. The governing equations for dif-
ferent theories of the generalized thermoelas-
ticity are written in terms of displacement and
temperature increment. The exact solution of
the problem, using different theories of gener-
alized thermoelasticity, has been deduced. The
analytical expressions for displacements, tem-
perature and stresses are found in final forms,
and a numerical example has been taken to
discuss the effect of the relaxation times. Finally,
the results have been illustrated graphically to
find the responses of different theories.
Keywords: Multilayered Hollow Cylinder;
Generalized Theories of Thermoelasticity;
Relaxation Times
1. INTRODUCTION
The governing equations for displacement and tempe-
rature fields in the linear dynamical theory of classical
thermoelasticity consist of the coupled partial differen-
tial equation of motion and Fourier’s law of heat con-
duction equation. The equation for displacement field is
controlled by a wave type hyperbolic equation, whereas
that for the temperature field is a parabolic diffusion
type equation. This amounts to the remark that the clas-
sical thermoelasticity predicts a finite speed for pre-
dominantly elastic disturbances but an infinite speed for
predominantly thermal disturbances, which are coupled
together. This means that a part of every solution of the
equations extends to infinity.
Biot [1] formulated the theory of coupled thermoelas-
ticity (named as C-D theory) to eliminate the paradox
inherent in the classical uncoupled theory of thermoelas-
ticity that the elastic changes have no effect on the tem-
perature. But, the classical dynamical coupled theory of
thermoelasticity still based on a parabolic heat equation,
which predicts an infinite speed for the propagation of
heat wave, contradicts the physical facts. Generalized
theories of thermoelasticity have been developed that are
free from this paradox. Lord and Shulman [2] (L-S the-
ory) introduced the theory of generalized thermoelastic-
ity based on a new law of heat conduction by incorpo-
rating a flux rate term and involved a hyperbolic type of
heat transport equation (called the generalized thermoe-
lasticity with one relaxation time). The L-S theory was
extended by Dhaliwal and Sherief [3] to the case of ani-
sotropic media. Uniqueness of the solution for the gen-
eralized thermoelasticity with one relaxation time under
a variety of conditions was proved by Ignaczak [4] and
Sherief and Dhaliwal [5] respectively. Generalized the-
ory of thermoelasticity with two relaxation time pa-
rameters has also been proposed. Based on a generalized
inequality of thermodynamics, Green and Lindsay [6]
developed the theory of thermoelasticity with two re-
laxation time parameters (named as G-L theory). The
G-L theory doesn’t violate the Fourier’s law of heat con-
duction when the body under consideration has a center
of symmetry. In this theory, both the equations of motion
and heat conduction are hyperbolic but the equation of
motion is modified and differs from that of the classical
dynamical coupled theory of thermoelasticity.
The axisymetric multilayered hollow cylinder prob-
lems have been discussed by some researchers in the un-
coupled, coupled and generalized thermoelasticity in the
recent years. Jane and Lee [7] considered the thermoe-
lasticity of multilayered cylinders subjected to known
temperatures at traction-free boundaries by using Lap-
lace transform and the finite difference method. Kandil

D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
1172
[8] studied the effect of steady-state temperature and
pressure gradient on compound cylinders fitted together
by shrink fit. Sherief and Anwar [9] discussed the prob-
lem of an infinitely long elastic circular cylinder whose
inner and outer surfaces are subject to known tempera-
ture and traction free. Yang and Chen [10] discussed the
transient response of one-dimensional quasi-static cou-
pled thermoelasticity problems of an infinitely long an-
nular cylinder composed of two different materials. Lee
[11] solved the two-dimensional, quasi-static coupled,
thermoelastic problem of finitely long hollow cylinder
composed of two different materials with axial symmetry.
Chen et al. [12,13] discussed also the transient response
of one-dimensional quasi static coupled and uncoupled
thermoelasticity problems of multilayered hollow cylin-
der. Allam et al. [14] solved the problem of an infinite
body with a circular cylindrical hole in a harmonic field
in the context of the generalized theory of thermoelastic-
ity. In a recent article, Zenkour et al. [15] presented the
static bending response for a simply supported function-
ally graded rectangular plate subjected to a through-the-
thickness temperature field under the effect of various
theories of generalized thermoelasticity with relaxation
times.
In the present article, the analytical expressions for
displacements, temperature and stresses of finitely long
hollow cylinder composed of two different materials
with axial symmetry are found in final forms. Numerical
examples have been taken to discuss the effect of the
relaxation times. Finally, the results have been illustrated
graphically to find the differences between the different
generalized theories of thermoelasticity.
2. FORMULATION OF THE PROBLEM
Through this area of research, we consider the fol-
lowing boundary value problem. We deal with a problem
of finitely long hollow cylinder composed of three lay-
ered of two different materials with axial symmetry. The
length of the multilayered hollow cylinder is L, and the
inner and outer radii of the cylinder are denoted by i
r
and o
r, respectively (see Figure 1).
We assume that, the hollow cylinder is taken to be
heated suddenly at the inner and outer surface under
temperature i

and o

, respectively. We take into ac-
count that the body forces are absent, and then the fun-
damental equations of the boundary value problem in the
context of the different theories of generalized thermoe-
lasticity, in the case of quasi-static, can be written as:
1) Equilibrium equations for the cylinder along r and z
directions:
,0










z
r
r
rrzr
r (1)
.0






r
r
z
rrzz
rz



(2)
where ij

are the components of stress tensor and
),,( zr

are the cylindrical coordinate system.
2) General heat conduction equation in the context of
generalized thermo-elasticity theories:


































rrozr t
t
tt
t
t
c
zrrr





32
2
2
2
2
11 ,11 33 

























zz t
t
tt
t
t


(3)
in which 0
 is the temperature and 0

is the
reference temperature; i

are the components of strain
tensor; 2
t and 3 t are the second and third thermal
relaxation times;



,
r and z

are the thermal con-
ductivity;

is the density; and

c is the specific heat
at constant deformation. The components of the ther-
moelastic tensor are given by
 ,)()()1(
1
zzrrzzrzzrrzzrr EEE





 ,)()1()(
1
zrzrzzzrrzrrzzr EEE





 ,)1()()(
1
zrrzrzrzzrzrrzzz EEE
  

.21 rzzrrzzrzzrr















(4)
where



rrz , and z 

are Poisson’s ratios;

EEr,
and z E are Young’s moduli; and



,
r and z

are
linear thermal expansion coefficients.
3) Duhamel-Neumann’s relations for layer number k:
,1 1131211 














t t
z
U
c
r
U
c
r
U
cr
zrr
r

(5)
,1 1232212 














t t
z
U
c
r
U
c
r
U
czrr
 
(6)
r
z
Figure 1. The three-layer hollow cylinder and its coordinate
sys te m.

D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
117
1173
,1 1332313














t t
z
U
c
r
U
c
r
U
cz
zrr
z

(7)
,
55 










z
U
r
U
crz
rz

(8)
where 1 t is the first thermal relaxation time and i U
are the components of displacement vector. The elastic
constants ij c are given by
,
)1(
,
)1(
2211 




zrrzzzr E
c
E
c


,
)1(
33


rrz
E
c


,,
)()(
552112 rz
zrzrrrzzr Gcc
EE
c








,
)()(
3113 c
EE
czrrzzrzzrr













.
)()(
3223 c
EE
crrzzzrrzz 













(9)
The full system equations for the different theories of
generalized thermoelasticity will appear by the following
instructions:
1) ,0
321



ttt C-D theory,
2) 123 0, 0,ttt

 L-S theory,
3) 123 0,0, 0,tt t

 G-L theory.
3. SOLUTION OF THE PROBLEM
Substituting Eq s. 5- 8 into Eqs.1-3, we get the follow-
ing system of partial differential equations:
zr
U
cc
z
U
c
r
U
c
r
U
r
c
r
U
czrrrr










2
5513
2
2
55
2
2211
2
2
11 )(
1
,01
1
)(1
1
)( 112313 























 t t
rt
t
rz
U
r
cc rr
z


(10)
2
2
3355
2
5513
2
2
55
1
)( z
U
c
r
U
r
c
zr
U
cc
r
U
czzrz











,01
1
)( 15523  













 t t
zz
U
r
cc z
r

(11)








































rrozr U
t
t
trt
t
t
c
z
rr
r3
2
2
2
2
2
2
11 




.11
1
3
2
3

























zzr U
t
t
tz
U
t
t
tr


(12)
Eqs.10 and 11 represent the equations of equilibrium
for the hollow cylinder along the r and z directions, re-
spectively, while Eq.12 represents the coupled transient
heat conduction equation for the kth layer of the axi-
symmetric hollow cylinder. The boundary and interface
conditions of the present composite hollow cylinder are
given by:
3.1. Boundary Conditions
.at,0
,0at,0
,at0,0
,at,0
3
2
1
LzU
zU
rr
r
UU
rrUU
zrz
zrz
ozr
izr










(13)
3.2. Interface Conditions
.),,,,,,(),,,,,,( 1  krzzrzrkrzzrzr UUUU 

(14)
3.3. Initial Conditions
0
2
1 at t = 0. (15)
To solve the above equations, we introduce the fol-
lowing dimensionless quantities:
,,,,
1
2
*
1
2























c
r
t
t
c
r
t
L
z
Z
r
r
Rr
o
i
i
r
o o
,,,3,2,1
11

















 





cr
U
U
cr
U
Ui r
o
z
z
r
o
r
r
,
)(
,,,
)( 101 r
r
r
o
i
i
r
ij
ij T
r
r
R





 


 
,
)(
,
)(
,
)(11111 c
c
cij
ij
r
z
z
r
 








,
)(
,
)(
,
)(
,
)( 1111

















c
c
c
r
z
z
rr
r
r 
,, 0
1
11
0
1
11


















cc B
cc
Brr
rr









D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
1174
.
0
1
11









cc Br
zz




Note that, the index “1” represents the thermome-
chanical properties of layer 1. Substituting the above
dimensionless quantities into Eqs.10-12, we get
ZR
U
L
r
cc
Z
U
L
r
c
R
U
c
R
U
R
c
R
U
czororrr

























2
5513
2
2
2
55
2
2211
2
2
11 )(
1

 













Tt
R
B
Z
U
RL
r
cc r
zo

12313 1
1
)(
,01
1
)( 1 







  Tt
R
BBr


(16)
2
2
2
3355
2
5513
2
2
55
1
)( Z
U
L
r
c
R
U
R
c
ZR
U
L
r
cc
R
U
cz
o zr o z























,01
1
)( 15523 














 

 Tt
ZL
r
B
Z
U
RL
r
cco
z
r
o

(17)



































TtcT
Z
L
r
RR
R
o
zr






2
2
2
2
2
2
1
 






















rrrUt
R
Ut
R 



33
2
1
1
1.1 3
2 










z
o
zUt
ZL
r


(18)
The dimensionless stresses are also given by
,1 1131211
















Tt
Z
U
L
r
c
R
U
c
R
U
cr
z
o
rr
r



(19)
,1 1232212
















Tt
Z
U
L
r
c
R
U
c
R
U
cz
o rr



 (20)
,1 1332313
















Tt
Z
U
L
r
c
R
U
c
R
U
cz
z o rr
z



(21)
,
55 















Z
U
L
r
R
U
cr
o
z
rz
 (22)
where
.
1
2
0









r
ij
ij
c
c
c


(23)
The solution of Eqs.16-18 may be given by using the
following substitutions of 
r
UT , and 
z
U that satisfy
the boundary conditions given in Eq.13:
),sin()()(
),cos()()(
),cos()()(
2
2
1
ZRfwU
ZRfuU
ZRfT
z
r









(24)
where the functions 1
f and 2 f are given, respectively,
by:
).1)((
,)1()1(
2
22
1


RRRf
RRf
i
i (25)
Using Eq.23 into Eqs.15 -17, one can get
,
d
d
1
d
d
d
d
1
d
d
d
d
1
d
d
,0
d
d
1 ,0
d
d
1
21039387
65143211








































tAwtAutAA
wAuAtAwAuAtA
(26)
where
,
d
d1
11
1
21 f
RR
B
R
f
BA 




 ,
d
d
d
d1
2
2
55
2
222
2
2
112 f
L
r
c
R
f
cf
RRR
cAo













 

,
d
d1
d
d1
25523133 fc
RR
c
RR
c
L
r
Ao










 

,
134 fB
L
r
Ao


,
d
d1
d
d1
21323555 fc
RR
c
RR
c
L
r
Ao










 

,
d
d
d
d1
2
2
332
2
2
556 f
L
r
cf
RRR
cA o













 


D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
117
1175
,
d
d1
d
d
1
2
2
2
7f
L
r
RRR
Ao
zr












 



,
1
d
d
28 f
RR
Ar




 

 ,
29 f
L
r
Az
o
 

.
110 fcA 


 (27)
The solution of the above system of first-order differ-
ential equations may be easily given for all theories. The
corresponding solutions for C-D, L-S and G-L theories
are also obtained from the general one.
4. NUMERICAL EXAMPLES
In order to illustrate the results graphically, the ge-
ometry and thermoelastic constants for the two materials
of the hollow cylinder are given in Table 1. The cylinder
is composed of three layers of two distinct materials
with the same thickness of each layer. Layers 1 and 3
have properties of the same material. So, the two inter-
faces are given at R = 0.5 and R = 0.75, respectively. The
various non-dimensional parameters used are:
,,10
1
3
1
2
1






















cr
U
Uu
cr
U
Uu r
o
z
z
r
o
r
r
,
)(
,
)(
,
1
2
1
1
0rr
r
r
TT











 
.
)(
,
)(1
5
1
3
r
rz
rz
r
z
z





  
The numerical results are plotted in Figures 2-17. The
values of 0  and  are taken to have the same value
as .5
0 The values of i
 and o

and ,, 21 
and 3

are given, respectively, in terms of 0

and
. The ratio of the outer radius of the cylinder to its
length is given by .2.0/ Lro In addition, the * is
dropped, for simplicity, from the dimensionless relaxa-
tion times.
Figure 2 illustrates the variation of dimensionless
temperature T through axial parameter Z, for value of
the dimensionless time namely 8

and at the second
interface of the dimensionless radial direction (R = 0.75).
The computations were carried out for C-D, L-S and
G-L theories of thermoelasticity. Figure 3 shows the
variation of dimensionless radial stress 1

through the
axial parameter Z. The values of dimensionless time and
radial direction are chosen to be 8 and 0.75, respectively.
The results were calculated for L-S and G-L theories.
In what follows, we restrict our attention to the results
of L-S theory. Figures 4,6,8,10,12,14 and 16 illustrate,
respectively, the variation of dimensionless radial and
axial displacements, 1 u and 3 u; the dimensionless
temperature T; and the dimensionless stresses ,
1

,, 32


and 5

through the radial direction of the
multilayered hollow cylinder for different values of the
dimensionless time ,7,5

and 9 with the relaxation
time 20
23  tt . Similar results are plotted in Figures
5,7,9,11,13,15, and 17 through the radial direction of the
Table 1. The geometry and material constants of a finitely long
hollow cylinder.
Material 1 Material 2








2
m
N
Er 6
1050  6 1058






2
m
N
E

6
1015 6 1022






2
m
N
Ez 6
1015 6 1018






2
m
N
Grz 5
1015 6 1020 






K.m
watt
r
 18 22






K.m
watt

 12 15






K.m
watt
z
 15 20
rr 
  0.2 0.2
zrrz
  0.1 0.1
zz 
  0.15 0.15






K
1
z


6
103   6 103  






K
1
r
 6
104   6 104  






3
m
kg
 0.095 0.095








K
ckg
kj

0.31 0.31
1
0.8
0.6
0.4
0.2
0
Axial parameter Z
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5
Temperature T
L-S
G-L
C-D
Figure 2. Variation of dimensionless temperature T through the
axial direction of the hollow cylinder for various thermoelas-
ticity theories (

= 8; R = 0.75).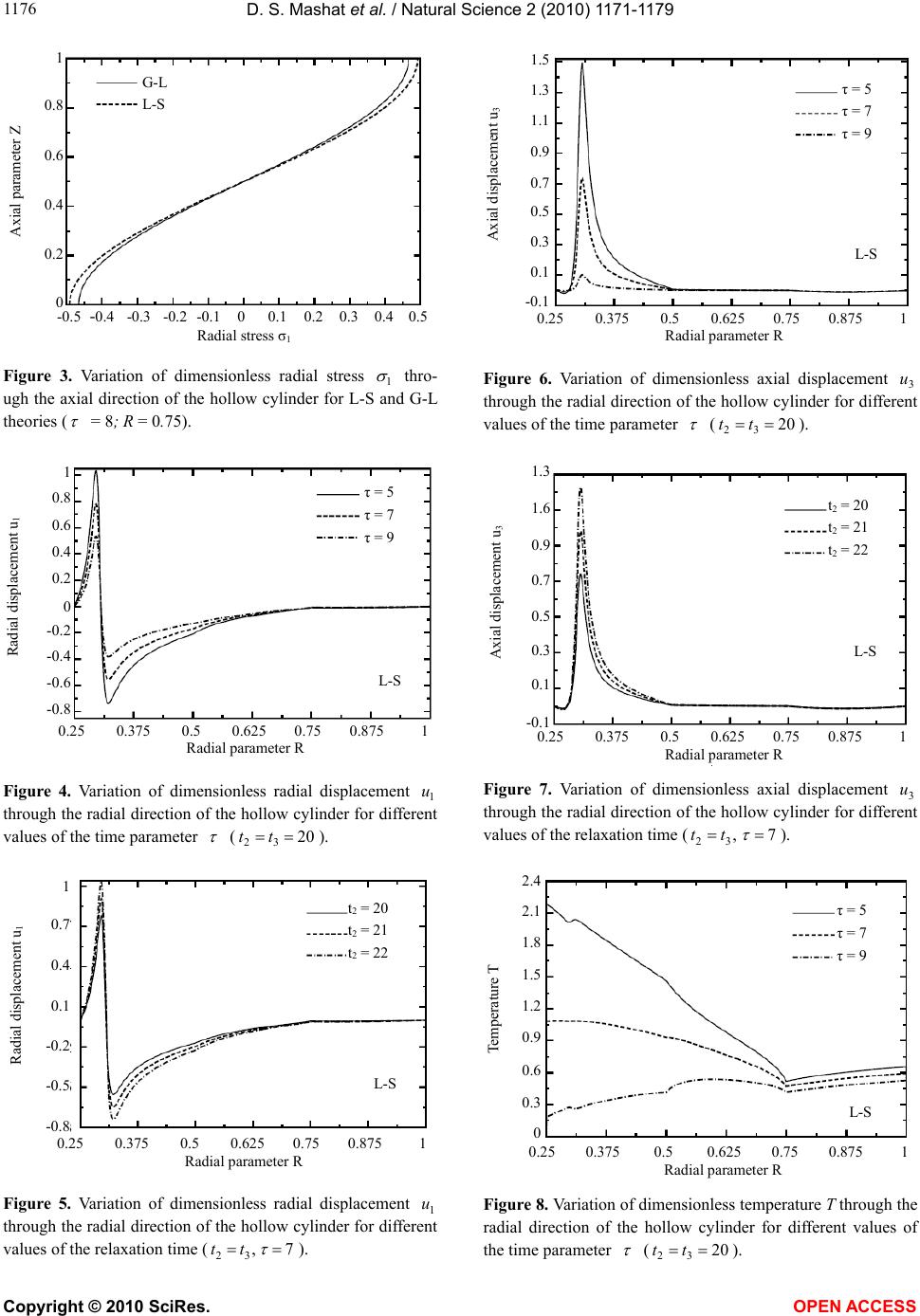

D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
1176
1
0.8
0.6
0.4
0.2
0
Axial parameter Z
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5
Radial stress σ
1
G-L
L-S
Figure 3. Variation of dimensionless radial stress 1

thro-
ugh the axial direction of the hollow cylinder for L-S and G-L
theories (

= 8; R = 0.75).
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
Radial displacement u
1
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
τ = 5
τ = 7
τ = 9
L-S
Figure 4. Variation of dimensionless radial displacement 1 u
through the radial direction of the hollow cylinder for different
values of the time parameter

(20
32 tt ).
1
0.7
0.4
0.1
-0.2
-0.5
-0.8
Radial displacement u
1
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
t
2
= 20
t
2
= 21
t
2
= 22
L-S
Figure 5. Variation of dimensionless radial displacement 1 u
through the radial direction of the hollow cylinder for different
values of the relaxation time (7,
32 


tt ).
1.5
1.3
1.1
0.9
0.7
0.5
0.3
0.1
-0.1
Axial displacement u
3
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
τ = 5
τ = 7
τ = 9
L-S
Figure 6. Variation of dimensionless axial displacement 3 u
through the radial direction of the hollow cylinder for different
values of the time parameter

(20
32tt ).
1.3
1.6
0.9
0.7
0.5
0.3
0.1
-0.1
Axial displacement u
3
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
t
2
= 20
t
2
= 21
t
2
= 22
L-S
Figure 7. Variation of dimensionless axial displacement 3 u
through the radial direction of the hollow cylinder for different
values of the relaxation time (7,
32

tt ).
Temperature T
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
L-S
τ = 5
τ = 7
τ = 9
2.4
2.1
1.8
1.5
1.2
0.9
0.6
0.3
0
Figure 8. Variation of dimensionless temperature T through the
radial direction of the hollow cylinder for different values of
the time parameter

(20
32tt ).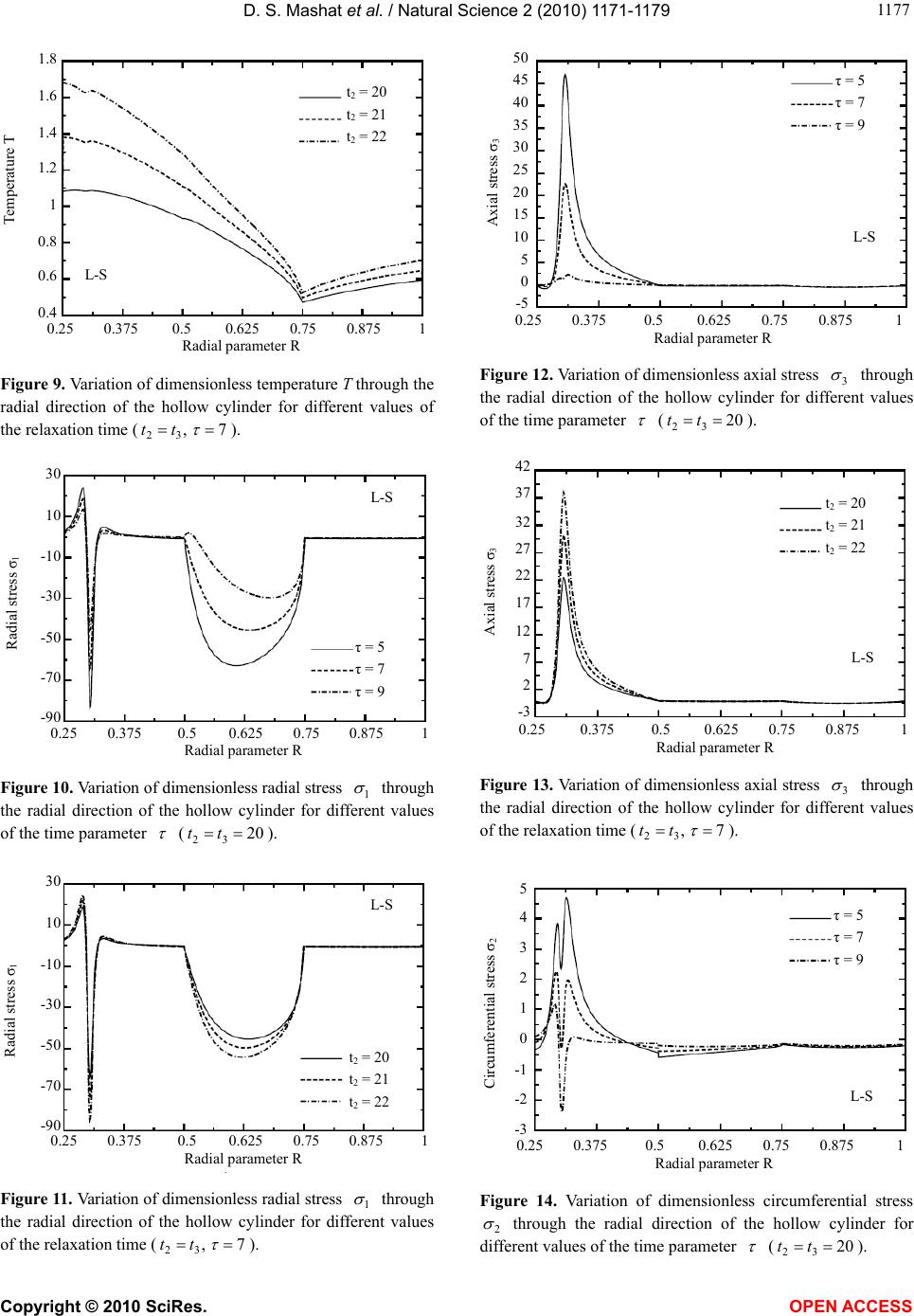

D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
117
1177
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
Temperature T
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
t
2
= 20
t
2
= 21
t
2
= 22
L-S
Figure 9. Variation of dimensionless temperature T through the
radial direction of the hollow cylinder for different values of
the relaxation time (7,
32

tt ).
30
10
-10
-30
-50
-70
-90
Radial stress σ1
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
τ = 5
τ = 7
τ = 9
L-S
Figure 10. Variation of dimensionless radial stress 1

through
the radial direction of the hollow cylinder for different values
of the time parameter

(20
32

tt ).
30
10
-10
-30
-50
-70
-90
Radial stress σ
1
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
L-S
t
2
= 20
t
2
= 21
t
2
= 22
Figure 11. Variation of dimensionless radial stress 1  through
the radial direction of the hollow cylinder for different values
of the relaxation time (7,
32
 tt ).
50
45
40
35
30
25
20
15
10
5
0
-5
Axial stress σ3
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
τ = 5
τ = 7
τ = 9
L-S
Figure 12. Variation of dimensionless axial stress 3

through
the radial direction of the hollow cylinder for different values
of the time parameter

(20
32tt ).
42
37
32
27
22
17
12
7
2
-3
Axial stress σ
3
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
t
2
= 20
t
2
= 21
t
2
= 22
L-S
Figure 13. Variation of dimensionless axial stress 3

through
the radial direction of the hollow cylinder for different values
of the relaxation time (7,
32


tt ).
5
4
3
2
1
0
-1
-2
-3
Circumferential stress σ
2
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
τ = 5
τ = 7
τ = 9
L-S
Figure 14. Variation of dimensionless circumferential stress
2
 through the radial direction of the hollow cylinder for
different values of the time parameter

(20
32tt ).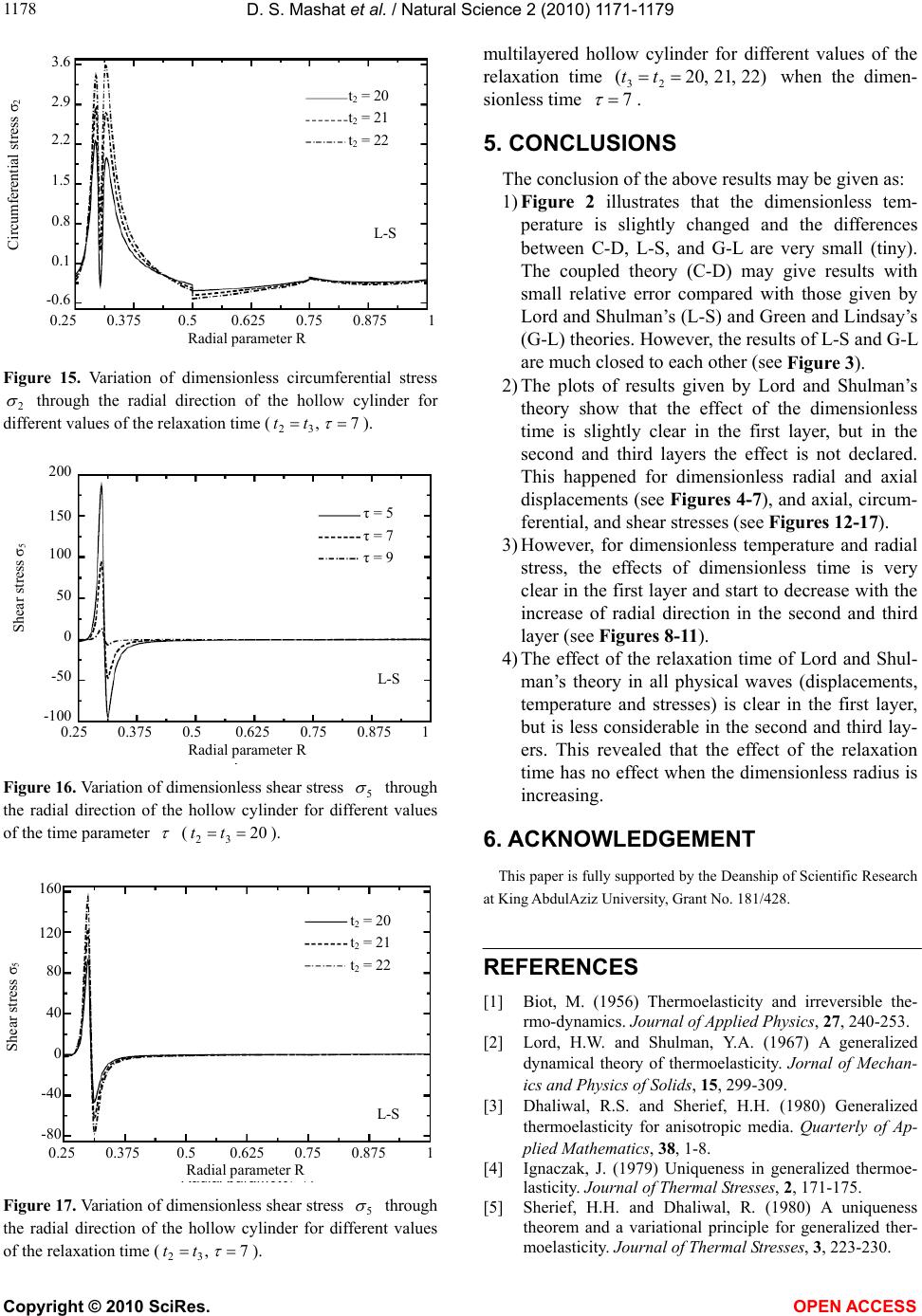

D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
1178
3.6
2.9
2.2
1.5
0.8
0.1
-0.6
Circumferential stress σ
2
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
t
2
= 20
t
2
= 21
t
2
= 22
L-S
Figure 15. Variation of dimensionless circumferential stress
2

through the radial direction of the hollow cylinder for
different values of the relaxation time (7,
32

tt ).
200
150
100
50
0
-50
-100
Shear stress σ
5
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
τ = 5
τ = 7
τ = 9
L-S
Figure 16. Variation of dimensionless shear stress 5

through
the radial direction of the hollow cylinder for different values
of the time parameter

(20
32

tt ).
160
120
80
40
0
-40
-80
Shear stress σ
5
0.25 0.375 0.5 0.625 0.75 0.875 1
Radial parameter R
t
2
= 20
t
2
= 21
t
2
= 22
L-S
Figure 17. Variation of dimensionless shear stress 5

through
the radial direction of the hollow cylinder for different values
of the relaxation time (7,
32

tt ).
multilayered hollow cylinder for different values of the
relaxation time )22,21,20( 23


tt when the dimen-
sionless time 7


.
5. CONCLUSIONS
The conclusion of the above results may be given as:
1) Figure 2 illustrates that the dimensionless tem-
perature is slightly changed and the differences
between C-D, L-S, and G-L are very small (tiny).
The coupled theory (C-D) may give results with
small relative error compared with those given by
Lord and Shulman’s (L-S) and Green and Lindsay’s
(G-L) theories. However, the results of L-S and G-L
are much closed to each other (see Figure 3).
2) The plots of results given by Lord and Shulman’s
theory show that the effect of the dimensionless
time is slightly clear in the first layer, but in the
second and third layers the effect is not declared.
This happened for dimensionless radial and axial
displacements (see Figures 4-7), and axial, circum-
ferential, and shear stresses (see Figures 12-17).
3) However, for dimensionless temperature and radial
stress, the effects of dimensionless time is very
clear in the first layer and start to decrease with the
increase of radial direction in the second and third
layer (see Figures 8-11).
4) The effect of the relaxation time of Lord and Shul-
man’s theory in all physical waves (displacements,
temperature and stresses) is clear in the first layer,
but is less considerable in the second and third lay-
ers. This revealed that the effect of the relaxation
time has no effect when the dimensionless radius is
increasing.
6. ACKNOWLEDGEMENT
This paper is fully supported by the Deanship of Scientific Research
at King AbdulAziz University, Grant No. 181/428.
REFERENCES
[1] Biot, M. (1956) Thermoelasticity and irreversible the-
rmo-dynamics. Journal of Applied Physics, 27, 240-253.
[2] Lord, H.W. and Shulman, Y.A. (1967) A generalized
dynamical theory of thermoelasticity. Jornal of Mechan-
ics and Physics of Solids, 15, 299-309.
[3] Dhaliwal, R.S. and Sherief, H.H. (1980) Generalized
thermoelasticity for anisotropic media. Quarterly of Ap-
plied Mathematics, 38, 1-8.
[4] Ignaczak, J. (1979) Uniqueness in generalized thermoe-
lasticity. Journal of Thermal Stresses, 2, 171-175.
[5] Sherief, H.H. and Dhaliwal, R. (1980) A uniqueness
theorem and a variational principle for generalized ther-
moelasticity. Journal of Thermal Stresses, 3, 223-230.

D. S. Mashat et al. / Natural Science 2 (2010) 1171-1179
117
1179
[6] Green, A. and Lindsay, K. (1972) Thermoelasticity. Jour-
nal of Elasticity, 2, 1-7.
[7] Jane, K.C. and Lee, Z.Y. (1999) Thermoelasticity of mul-
tilayered cylinder. Journal of Thermal Stresses, 22, 57-74.
[8] Kandil, A. (1975) Investigation of stress analysis in com-
pound cylinders under high pressure and temperature.
M.Sc. Thesis, CIT Helwan.
[9] Sherief, H.H. and Anwar, M.N. (1988) A problem in
generalized thermoelasticity for an infinitely long annu-
lar cylinder. International Journal of Engineering Sci-
ence, 26, 301-306.
[10] Yan, Y.C. and Chen, C.K. (1986) Thermoelastic transient
response of an infinitely long annular cylinder com-
posed of two different materials. International Journal of
Engineering Science, 24, 569-581.
[11] Lee, Z.-Y. (2006) Generalized coupled transient response
of 3-D multilayered hollow cylinder. International Com-
munications in Heat and Mass Transfer, 33, 1002-1012.
[12] Chen, C.K., Hung, C.I. and Lee, Z.Y. (2001) Transient
thermal stresses analysis of multilayered hollow cylinder.
Acta Mechanica, 151, 75-88.
[13] Chen, C.K., Hung, C.I. and Lee, Z.Y. (2001) Thermoe-
lastic transient response of multilayered hollow cylinder
with initial interface pressure. Journal of Thermal Str-
esses, 24, 987-1006.
[14] Allam, M.N., Elsibai, K.A. and Abouelregal, A.E. (2002)
Thermal stresses in a harmonic field for an infinite body
with a circular cylindrical hole without energy dissipa-
tion. Journal of Thermal Stresses, 25, 57-67.
[15] Zenkour, A.M., Mashat, D.S. and Elsibai, K.A. (2009)
Bending analysis of functionally graded plates in the
context of different theories of thermoelasticity. Mathe-
matical Problems in Engineering, 2009, Article ID 962351,
1-15.