Journal of Software Engineering and Applications, 2013, 6, 67-72
doi:10.4236/jsea.2013.63b015 Published Online March 2013 (http://www.scirp.org/journal/jsea)
67
Modeling of Objects Using Conic Splines
Muhammad Sarfraz1, Malik Z. Hussain2, Munazah Ishaq2
1Department of Information Science, Kuwait University, Adailiya Campus, Safat, Kuwait; 2Department of Mathematics, University
of the Punjab, Lahore, Pakistan.
Received 2013
ABSTRACT
This paper contributes towards modeling for the designing of objects in the areas of Computer Graphics (CG), Com-
puter-Aided Design (CAD), Computer-Aided Manufacturing (CAM), and Computer-Aided Engineering (CAE). It pro-
vides a modeling technique for the designing of objects. The model is based on a conic-like curve (rational quadratics)
method and provides an extra degree of freedom to the user to fine tune the shape of the design to the satisfactory level.
The 2D curve model has then been extended for the designing of 3D objects to produce fancy objects. The scheme has
been also extended to automate the degree of freedom when a reverse engineering is required for images of the objects.
A heuristic technique of genetic algorithm is applied to find optimal values of shape parameters in the description of
conics.
Keywords: Computer Graphics; CAD; CAM; CAE; Splines
1. Introduction
Object modeling is an important area of Computer
Graphics (CG), Computer-Aided Design (CAD), Computer-
Aided Manufacturing (CAM), and Computer-Aided
Engineering (CAE). No matter, it is designing of an
aircraft or an outline of a font, most of the objects are
being designed through computers. This area of study has
attracted many scientists to work for different industries
including engineering works, medical, entertainment, etc.
Since the advent of computers, numerous authors have
discovered various methodologies in various disciplines.
This research is mainly concerned for the designing of
2D objects composed of curve outlines and then it is ex-
tended for the 3D objects based on rectangular domain. It
is in continuatio n of the spline introdu ced in [27]. Spline
curves and surfaces [1-27] play significant role in the
construction and re-construction of objects. The splines
including Beta-splines [18-24], Nu-splines [5], and
weighted Nu-splines [5] make a good contribution to CG,
CAD, CAM, CAE, and Geometric Modeling. A reason-
able amount of literature is available (see [1-27]) on this
subject. Various other forms of splines are also available
in the literature. For example, conic presentation can be
found in [10-11], cubic flavor can be seen in [5,7-8,12],
and B-splines work can be searched in [14-16]. The use-
fulness of rational splines can also not be denied, much
of work has been done in this direction. For brevity, the
reader is referred to [1-2,4,13].
In [14], rational cubic spline, with derivatives based on
control points, was discovered. This spline method has
the feature of local interval shape control. This paper has
used a different alternative interpolant which is rational
quadratic in its description, but serves in the same man-
ner as the rational cubic spline [14]. It is computationally
economical and achieves equivalently fine results. All
the features of cubic or rational cubic splines can be
characterized by this quadratic method. Particularly, it
holds the feature of local interval shape control as in [14].
Thus, any type of plane or space curve can be designed
with having a strong control over the intervals of control
points. In addition, the scheme has the following proper-
ties which may lead to a more useful approach to curve
design in CAD, CAM, CAE, Computer Graphics, and
Geometric Modeling:
(1) The curve has 1 C continuity.
(2) This scheme is rational quadratic and hence is
simpler than the rational cubic scheme in [14].
(3) This scheme is an extended work done in [27].
(4) The method is local, i.e. the interval tension
applied by shape control parameters will affect very
small neighborhood of interval.
(5) This scheme is as suitable as any cubic or
rational cubic method for space curves and hence can be
generalized to surfaces.
(6) Any part of the rational quadratic spline
method is a conic and can be made straight line using the
same interpolant.

Modeling of Objects Using Conic Splines
68
(7) The rational quadratic curve scheme is
extendable to its rational bi-quadratic counterpart for the
designin g or re-design ing of 3D objects.
The paper, in addition to curve design method, also
proposes a surface design scheme. This has been
achieved by extending the proposed rational quadratic
curve scheme to its rational bi-quadratic co unterpart. The
presentation of surface model is mainly a tensor product
surface model. It is simple in its description and useful
for the designing of 3D objects.
The outline of the remainder of the pa per is as follo ws.
The mention of the piecewise rational quadratic interpo-
lant is made in Section 2. This section describes the pa-
rametric rational quadratic spline interpolation scheme.
Analysis of the design curve, regarding various geomet-
ric features, is made in Section 3. The effect of shape
control analysis is described in Section 4. The construc-
tion of 3D surfaces has been briefly explained pictorially
in Section 5. Section 6 concludes the paper.
2. Design Curve
In this section, piecewise rational quadratic func tions are
presented to be used for curve designing and fitting. The
rational quadratic is targeted to provide 1 C continuity.
It is also required that the quadratic curve presentation is
extended towards its surface designing counterpart.
2.1. Rational Quadratic Function
The objective of this research is to provide design
curve scheme which
 is composed of conics like curve (see Figure 1) the
following:
  
 
22
22
121
121
012
bwbb
Fw


 
  (1)
 interpolates the data points
 possesses ideal geometric properties like convex hull
and variation diminishing properties
Figure 1. Demonstration of rational quadratic function.
 can handle the inflection points like cubic or rational
cubic spline curves
 provides freedom to the designer for further shape
control
 is reasonably smooth
2.2. Rational Quadratic Spline
Let FiRm,i = 0,1,….n, (2)
be a given set of data points at the distinct knots ti  R,
with unit interval sp acing. Let
*11
()/2, and .
iii iii
ttt htt


 (3)
Also let
Ui, Wi, ViRm,i = 0,1,….n-1, (4)
be the control points. Then, we define a parametric
piecewise rational quadratic function P: R  Rm, com-
posed with two conic representations (see Figures 2(a)
and (b)) of the form (1), as follows:
Figure 2. Rational quadratic representations: (a) Conic piece in (6), (b) Conic piece in (7), (b) Conic spline curve in (5).

Modeling of Objects Using Conic Splines
69
*
1,
**
2, 1
(),()2()/,[, ],
() (),()2()/,[,]
iiiii
i
iiiii
Pttthttt
Pt Pttthttt
 


 

 


(5)
where
  
 
2 2
2
22
,1 11
11





i
i i ii
iWUF
tP (6)
and
  

2
21
2
22
,2 11
11





i
i i ii
iFVW
tP (7)
It can be seen that the rational quadratic curve (5) is
0
C as the followings hold:




*
,2
*
,1 iiii tPtP and
 
itPtP iiii   ,. (8)
Let ()Pt be the curve over the given knot partition
and passing through the given set of points (2). Let us
denote the first derivatives at the knot position as:
 iDtP ii  ,
)1( (9)
Since 0
C curve is not ideal as far as smoothness is
concerned, we need higher order of continuity. To obtain
1
C order of continuity, we need to impose the following
constraints:



 









itPtP
tPtP
ii
ii
,
)1()1(
*
)1(
*
)1(
(10)
These 1
C constraints, after some analysis and simpli-
fications, yield the following:










i
ii
ii
i
ii
i i
Dh
FV
Dh
FU


2
2
1
1
(11)
and


i
i i i i i ii
iDDhFF
VU
W
 422 11 




 (13)
3. Design Curve Analysis
This section describes the parametric rational quadratic
spline interpolation scheme. Analysis of the design curve,
regarding parameterization, derivative estimation, shape
parameters and various geometric features, is made in
this section. It also demonstrates design curves with
various practical examples.
3.1. Parameterization
Number of parameterization techniques can be found in
literature for instance uniform parameterization, linear or
chord length parameterization, parabolic parameterize-
tion and cubic parameterization. In this paper, chord
length parameterization is used to estimate the parametric
value t associated with each point. It can be observed that
i

is in normalized form and varies from 0 to 1. Conse-
quently, in our case, i h is always equal to 1.
3.2. Estimation of Tangent Vectors
A distance based choice of tangent vectorsDi’s at Fi’s is
defined as:






01020
12
11
22
22
1,1,2,..., 1
nnnnn
iiiiii i
DFFFF
DFFFF
DaFFaF Fin


 

 


 

For close curves:

1111
11
,
1, 0,1,...,
nn
iiiiiii
FFF F
D
aF FaFFin


 


 


where
1
11
, 0,1,...,
ii
i
iiii
FF
ain
FFFF




 .
4. Shape Analysis
This section is concerned about the shape design aspects
to achieve a model curve. The parameters 
i may be used
to control the shape of the curve. The parameters 
i are
mainly meant to be used freely to control the shape of the
curve. At the same time, for the convenient of the de-
signer, it is also required that the ideal geometric proper-
ties of the curve are not lost. The geometric properties
like variation diminishing, convex hull, and positivity are
the ones which needed to be present in the description of
the design curve.
One can see that each conic representation in (5-7) is
of Bernstein Bezier form, provided the weight functions
are positive. This is possible if the shape parameters are
constrained as i
i

,0

. Thus following the Bernstein
Bezier theory, the pieces of curves  tP i,1 and

 tP i,2
lie in the convex hulls of


i i iWUF ,, and


1
,, i
i iFVW respectively. They also follow the varia-
tion diminishing properties within their convex hulls.
Similarly, due to 1 C imposition, the equations (8-10)
lead to the followings:



tPilies in the convex hull of


1
,,,, i
i i i iFVWUF ,
i

, see Figure 3.



tPisatisfies the variation diminishing property
[22]. That is any straight line crossing the control
polygon of


1
,,,, i
i i i iFVWUF does not cross the
curve more than its control polygon.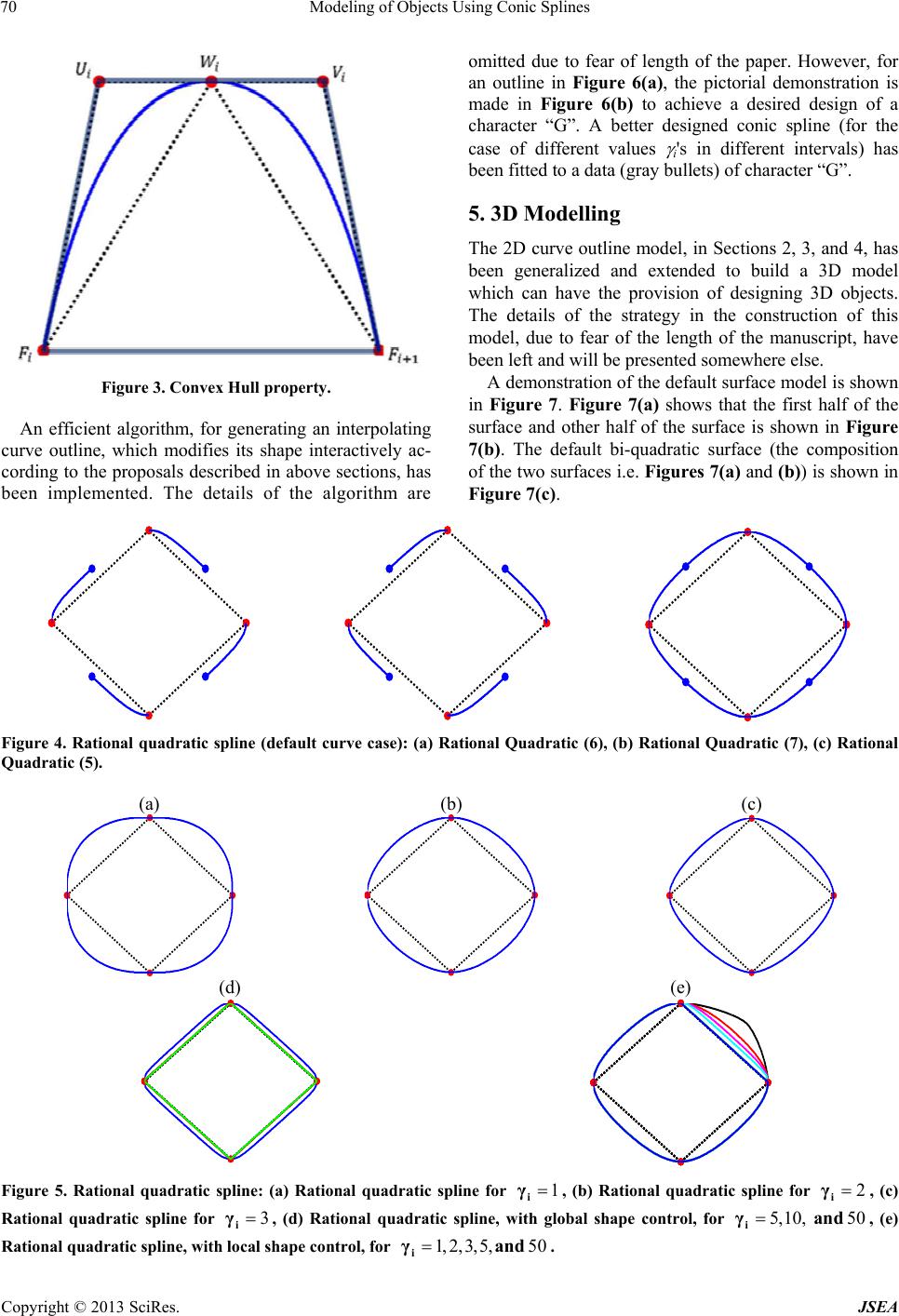

Modeling of Objects Using Conic Splines
70
Figure 3. Convex Hull property.
An efficient algorithm, for generating an interpolating
curve outline, which modifies its shape interactively ac-
cording to the proposals described in above sections, has
been implemented. The details of the algorithm are
omitted due to fear of length of the paper. However, for
an outline in Figure 6(a), the pictorial demonstration is
made in Figure 6(b) to achieve a desired design of a
character “G”. A better designed conic spline (for the
case of different values

i's in different intervals) has
been fitted to a data (gray bullets) of character “G”.
5. 3D Modelling
The 2D curve outline model, in Sections 2, 3, and 4, has
been generalized and extended to build a 3D model
which can have the provision of designing 3D objects.
The details of the strategy in the construction of this
model, due to fear of the length of the manuscript, have
been left and will be presented somewhere else.
A demonstration of the default surface model is shown
in Figure 7. Figure 7(a) shows that the first half of the
surface and other half of the surface is shown in Figure
7(b). The default bi-quadratic surface (the composition
of the two surfaces i.e. Figures 7(a) and (b)) is shown in
Figure 7(c).
Figure 4. Rational quadratic spline (default curve case): (a) Rational Quadratic (6), (b) Rational Quadratic (7), (c) Rational
Quadratic (5).
(a) (b) (c)
(d) (e)
Figure 5. Rational quadratic spline: (a) Rational quadratic spline for 1

i
γ, (b) Rational quadratic spline for 2

i
γ, (c)
Rational quadratic spline for 3
i
γ, (d) Rational quadratic spline, with global shape control, for 5,10, 50
i
γand , (e)
Rational quadratic spline, with local shape control, for 1, 2, 3, 5,50

i
γand .

Modeling of Objects Using Conic Splines
71
Some more pictorial demonstrations are made as fol-
lows. A wire frame model, with u-lines is constructed, as
the first step in the Figure 8(a) of a bottle. Secondly,
uv-lines are drawn to provide a complete wire frame
model (see Figure 8(b)). Thirdly, visibility detection
method is used to provide a realistic view of the picture
(see Figure 8(c)). Another feature built in the 3D model
is the local shape control like in the 2D models demon-
strated in Section 3.3. This feature can be seen in Fig-
ures 8(a-c) at the neck of the bottle showing interval
tension.
Another pictorial example of a vase is shown in Fig-
ure 9. The wire frame model is shown in Figure 9(a)
and its shaded model is demonstrated in Figure 9(b). A
variety of shape control has been applied at different
places to achieve the shown model.
(a) (b)
Figure 6. Rational quadratic spline: (a) Rational quadratic
spline for 2
i
γ, (b) Rational quadratic spline for varying
values of i
γ in different intervals.
(a) (b) (c)
Figure 7. Rational bi-quadratic spline interpolant: (a) Ra-
tional bi-quadratic 1.(b) Rational bi-quadratic 2, (c) Ra-
tional bi-quadratic.
(a) (b) (c)
Figure 8. Rational bi-quadratic spline for the design of a
bottle: (a) A wire frame model, with u-lines, (b) A wire
frame model with uv-lines, (c) A wire frame model with
uv-lines and hidden surface removal.
(a) (b)
Figure 5. A bi-conic Spline model for a Vase: left one is a
wire-frame model, right one is the shaded model.
6. Conclusion and Future Work
A shape controlling piecewise rational quadratic interpo-
lation scheme, to design 2D and 3D objects, has been
proposed. The scheme offers a possible and feasible way
in which the shape of the objects may be altered by the
user. Such a scheme can make a useful addition to an
interactive design package in a CG/CAD/CAM/CAE
environment. It provides the users complete control over
the curve segments and surface patches to modify the
shape to achieve a model object. The changes will be
local and that the shape will change in a stable manner.
The scheme is quite simple, easy to implement and
computationally economical as compared to its cubic and
bi-cubic counter parts. The authors are thinking to extend
the scheme for various applications including font de-
signing, image outline capture, modeling animation paths,
and others.
7. Acknowledgements
This work was supported by Kuwait University.
REFERENCES
[1] J. A. Gregory, and P.K. Yuen, An arbitrary mesh network
scheme using rational splines, in: T. Lyche and L.L.
Schumaker (eds.), Mathematical Methods in Computer
Aided Geometric Design II, Academic Press, 321-329,
1992.
[2] J. A. Gregory, M. Sarfraz, and P.K. Yuen, Curves and
Surfaces for Computer Aided Design using Rational Cu-
bic Splines, Engineering with Computers, 11:94-102,
1995.
[3] J. Hoschek, Circular splines, Computer-Aided Design,
24:611-618, 1992.
[4] M. Sarfraz, M. Hussain, and Z. Habib, Local convexity
preserving rational cubic spline curves, Proceedings of

Modeling of Objects Using Conic Splines
72
IEEE Conference on Information Visualization, IV'97,
London, 211-218, 1997.
[5] T. A. Foley and H. S. Ely, Interpolation with interval and
point tension controls using cubic weighted Nu-splines,
ACM Transactions on Mathematical Software, 13(1):
68-96, 1987.
[6] L. Piegl, and W. Tiller, The NURBS Book, Springer,
1995.
[7] Sarfraz, M., Al-Mulhem, M., Al-Ghamdi, J., and Hussain,
A., Quadratic Representation to a C1 Rational Cubic
Spline with Interval Shape Control, Proc International
Conference on Imaging Science, Systems, and Technol-
ogy (CISST'98), USA, 322-329, 1998.
[8] J. S. Kouh, and S. W. Chau, Computer-aided geometric
design and panel generation for hull forms based on ra-
tional cubic Bezier curves, , Computer Aided Geometric
Design, 10:537-549, 1993.
[9] V. Pratt, Techniques for conic splines, Proceedings of
SIGGRAPH, 151-159, 1985.
[10] T. Pavlidis, Curve fitting with conic splines, ACM
Transactions on Graphics, 1-31, 1983.
[11] M. Plass and Maureen Stone, Curve-fitting with Piece-
wise Parametric Cubics, Computer Graphics, 17(3):
229-239, 1983.
[12] G. Nielson, Rectangular Nu-splines, IEEE Computer
Graphics and Applications, 35-40, 1986.
[13] J. A. Gregory and M. Sarfraz, A rational cubic spline with
tension, Computer Aided Geometric Design, 7:1-13,
1990.
[14] T. A. Foley and H. S. Ely, Interpolation with interval and
point tension controls using cubic weighted Nu-splines,
ACM Transactions on Mathematical Software, 13(1):
68-96, 1987.
[15] M. Paluszny and R. Patterson, A family of tangent conti-
nous cubic algebraic splines, ACM Transactions on
Graphics, 12(3):209-232, 1993.
[16] J. C. Beatty R. Bartels and K. S. Booth, Experimental
comparision of splines using the shape-matching para-
digm, ACM Transactions on Graphics, 12(3):179-208,
1993.
[17] B. A. Barsky, Computer Graphics and Geometric Mod-
eling using Beta-Splines, Springer-verlag, 1986, Tokyo.
[18] T. N. T. Goodman, Properties of Beta-Splines, Journal of
Approximation Theory, 44(2):132-153, 1985.
[19] B. Barsky and J. Bea tty, Lo cal contr ol of bia s and tens ion
in Beta-Splines, ACM Transactions on Graphics,
2(2):73-77, 1983.
[20] D. Joe, Multiple knot and rational cubic beta-splines,
ACM Transactions on Graphics, 8(2):100-120, 1989.
[21] T. N. T. Goodman and K. Unsworth, Manipulating shape
and producing geometric continuity in beta-splines curves,
IEEE Computer Graphics and Applications, 6(2):50-56,
1986.
[22] M. Sarfraz, Interactive curve modeling with applications
to computer graphics, vision and image processing.
Springer, 2008.
[23] M. Sarfraz, M. Hussain, M. Irshad, and A. Khalid, Ap-
proximating boundary of bitmap characters using genetic
algorithm, Seventh International Conference on Com-
puter Graphics, Imaging and Visualization (CGIV'10),
2010, 671-680.
[24] Z.R. Yahya, A.R.M Piah and A.A. Majid, G1 continuity
conics for curve fitting using particle swarm optimization,
E. Banissi et al. (Eds.) 15th International Conference on
Information Visualization,. IV, 2011, 497-501.
[25] M. Sarfraz, S. Raza and M. Baig, Capturing image out-
lines using soft computing approach with conic splines,
International Conference of Soft Computing and Pattern
Recognition, 2009, 289-294.
[26] P. Priza, S. M. Shamsuddin and A. Ali, Differential evo-
lution optimization for Bezier curve fitting, Seventh In-
ternational Conference on Computer Graphics, Imaging
and Visualization, 2010, 68-72.
[27] M. Sarfraz, M. Al-Mulhem, J. Al-Ghamdi, and A. M.
Hussain, Representing a C1 Rational Quadratic Spline
with Interval Shape Control, Proceedings of International
Conference on Imaging Science, Systems, and Technol-
ogy (CISST'98), Las Vegas, Nevada, USA, CSREA Press,
USA, 322-329, 1998.