Open Journal of Civil Engineering, 2013, 3, 29-44
http://dx.doi.org/10.4236/ojce.2013.31005 Published Online March 2013 (http://www.scirp.org/journal/ojce)
The Compactions of Elasto-Plastic and Visco-Plastic
Granular Assemblies
Pengfei He, Yuching Wu, Huiliang Chen
College of Civil Engineering, Tongji University, Shanghai, China
Received November 16, 2012; revised December 18, 2012; accepted December 30, 2012
ABSTRACT
In this paper, the compactions of the elasto-plastic and the visco-plastic granular assemblies are simulated using the
finite element method. Governing equations for motion and deformation for particles, including coupling of rigid body
motion and deformation for deformable bodies, are investigated. An implicit discrete element method for block systems
is developed to make visco-plastic analysis for the assemblies. Among particles, three different contact types, cohering,
rubbing and sliding, are taken into account. To verify accuracy and efficiency of the numerical method, some numerical
example is simulated and the results are in a satisfactory agreement with the solutions in literatures. The effects of fric-
tional condition , the initial solid volume ratio, the number of particles in the assembly, and different types of co mpact-
tion on the compaction of the elasto-plastic and the visco-plastic aggregates are investigated. It is demonstrated that the
effect of frictional condition, the initial solid volume ratio, the number of particles in the assembly, and different types
of compaction on the global behavior of the elasto-plastic the visco-plastic granular assemblies under compacting are
considerable. The numerical model is extended to simulate the compaction of aggregates consisting of mixed particles
of different viscous incompressible materials. It is indicated that, with minor modification, the method could be used in
a variety of problems that can be represented using granular media, such as asphalt, polymers, aluminum, snow, food
product, etc.
Keywords: Compaction; Elasto-Plastic; Visco-Plastic; Granular Assembly; Finite Element Method
1. Introduction
Researches focused on particulate materials were devel-
oped rapidly in the past 20 years. In the 1990s, basic
physics of particle material characteristics were de-
scribed in detail by Jaeger and Nagel [1], and fundamen-
tal theory of mechanics of granular materials was devel-
oped. At the same time, the load distribution for two-
dimensional aggregates compaction was studied by Lud-
ing [2]. For the issue of the particle shape, two-dimen-
sional quasi-static analysis for circular particle compres-
sion state was made by Bashir and Goddard [3]. The fric-
tional pressure of oval particles was taken into accoun t in
theoretical analysis and numerical simulation by Tzafer-
opoulos [4]. Coppersmith et al. [5] studied the problem
of bead-like particles model. Matuttis [6] simulated two-
dimensional hexagonal particle under distributed loading.
Satake [7] presented a random distribution method to
define particle position based on theoretical and numeri-
cal analysis. Emeriault et al. [8] proposed a uniform
method to create a structure consisting of the oval-shaped
particles. Antony et al. [9] investigated limit state of
compression and impact of aggregates consisting of the
flat round, round and elong ated spherical particles. I t was
demonstrated that the effect of particle shape on the final
result was little. The same particle samples under differ-
ent pressure distribution were studied. In the final state of
compression of the particles, it was indicated that the
shape and distribution of particles had little effect on the
global elastic deformation resulted from rigid body
movement of particles.
In addition, some scholars have begun to investigate
compaction of particles of non-spherical shape. Wu [10]
simulated compaction of adhesive polygonal particles in
different size. A step-by-step incremental numerical
model was developed to simulate the compaction of
granular system of non-spherical nonlinear visco-plastic
particles. The nonlinear visco-plastic constitutive law of
each particle was derived based on the generalized
Maxwell model that the material property of each ele-
ment was treated as a series connection of a linear elastic
matter to the other nonlinear visco-plastic media. The
mesh upgrade scheme, consisting of contact detection
algorithms, mesh update algorithms, concave four-node
element modification, and locking preven tion subroutine,
was generated based on a mixed triangular and quadric-
C
opyright © 2013 SciRes. OJCE

P. F. HE ET AL. 30
lateral mesh system [11,12]. However, these researches
only focused on a perfectly plastic material and the use
of particle equations for the nonlinear viscous process
was not taken into account.
In this paper, uni-axial compaction of two-dimensional
mixed non-linear v iscous po lygon al particles is ex amined.
A numerical model is developed to anatomize the prob-
lem. It provides a theoretical basis and numerical model
for engineering design related to particulate matter. This
research mainly includes the following four sections.
First of all, a non-linear numerical model is established
to analyze amass made up of elastic-plastic and visco-
plastic particles under densification. Secondly, This me-
thod is applied to an alyze the relationship between stress
and density of the metal powder or asphalt material dur-
ing the process of compaction in different directions.
Next, the effects of the distribution of particles, particle
density throughout the structure, particle size and shape,
and friction among particles on the stress distribution of
the entir e structure a re inspected. Finally, the defects and
limitations of the numerical model are examined to es-
tablish a better model.
2. Geometrically Nonlinear Finite Element
Formulations
The incremental finite element method is usually used to
solve geometrically nonlinear problems. The main pur-
pose is to identify speed, displacement, stress, strain and
other parameters of kinematics and static of objects in a
series of discrete time points. Assume that all variables at
time t are known, all solutions of the problem can be
obtained by solving all parameters at time t + t and re-
peating the procedure. For the incremental method, and
the principle of virtual work at time t + t can be ex-
pressed as
d
d,
tt
k k
tttt
ttk k
uS
tt
tt
tt tt
tt
S
V
Wt
f
uV




tt


 






 (1)
where t+tW is the virtual work of th e loading at time t +
t. δuk is virtual displacement at time t + t. tt
k
f


tt
and
tt
t

k tt
V
 S
are body force and surface traction at time t + t,
respectively. , and
tt tt

 are volume area
and density of the object at time t + t, respectively.
After linearization, the total Lagrangian formulation
can be written as
0
0
00 0
0
00
d
ijkl kl ij
V
tt t
ij ij
V
DeeV
WSe 





0
00
00
dd
t
ij ij
V
S V
V

dd
d,
t
ttt
ij t ij
V
V
V

ij
e
, (2)
The updated Lagrangian formulation can be written as
t
t
tijkltkltij
V
ttt t
ijt ij
V
DeeV
We





 (5)
where tt

 is the corresponding infinitesimal strain
written as

,,
1
2
ttijttij ttji
euu 
 


00
11
1
,,
,1,2,3
nn
kt tk
ikiiki
kk
n
tt ttk
iki
k
. (6)
If the isoparametric element is used for solving the dis-
crete domain, the coordinates of each element and the
displacement of its nodes can be interpolated as follows.
x
Nx xNx
xNxi

 






11
,,1,2,3
nn
ttk k
ikiiki
kk
uNuuNui



tk
i
, (3)
, (4)
where
x
is the component of node k at time t in i di-
rection, i is the displacement component of node k at
time t in i direction. k is the shape function of node k.
n is the num ber of nodes.
tk
u
N
Substitution of Equations (3) and (4) to Equation (2)
yields the total Lagrangian formulation given as


00 0
tt ttt
LNL
K
Ku QF


u
0
t
, (5)
where is nodal incremental displacement vector.
0
t0 t
L
K
,
N
L
K
and
F
can be expressed as
00 0000
d
e
ttTt
LLL
V
e
K
BDB V


00 0000
d
e
ttTtt
NLNL NL
V
e
, (6)
K
BSB V


00 000
ˆd
e
ttTt
L
V
e
, (7)
F
BSV


t
, (8)
here 0
L
B0
t
and
N
L are the transformation matrix of
linear strain 0ij and nonlinear strain 0ij
B
e

, respectively.
0 is the constitutive matrix. 0 and 0 is the se-
cond Piola-Kirchhoff stress matrix and vector, respec-
tively. All of these parameters are measured from the
initial configuration corresponding to the shape and posi-
tion at time t.
DtSˆ
tS
Using the modified Newton-Raphson iteration, suffi-
ciently accurate solution of Equation (9) can be obtained.
That is


 

000 0, 1,2,
ll
tttt tt
LNL
KKuQ Fl
 
 
 
1lll
tt tt
uuu

 

 
00 000
ˆd
llTl
tttt tt
L
V
, (9)
where
, (10)
F
BSV
 
. (11)
Similarly, subsititution of Equations (6)-(8) to Equa-
tion (3) yields the updated Lagrangian formulation given
as

P. F. HE ET AL. 31

tt
tL tNL
ttt
t
K
Ku QF


d
Ttt
LttL
, (12)
where
te
tt
tL t
V
e
K
BDB V
d
Tttt
NL tNL
, (13)
te
tt
tNLt
V
e
K
BBV 
0ˆd
e
tTtt
tL
V

t
, (14)
t
e
F
BV 
t

t
tL
B B
, (15)
here and t
tNL
are transformation matrix of linear
strain tij
and nonlinear strain ij e

, respectively. t is
constitutive matrix. t
D

and tˆ

are Cauchy stress ma-
trix and vector, respectively. All of these parameters are
measured from the current configuration corresponding
to the shape and pos ition at time t.
Using the modified Newton-Raphson iteration, suffi-
ciently accurate solution of Equation (16) can be obtain-
ed. That is


tL tNL
l
tttt
tt
KK
QF
 





0, 1,2,
l
tt u
l
 
ˆd
llTll
tttttt tt
(16)
where
tt tt ttL
V
F
BV 
 
d
tttttttt tt
I c
eVWWW 



  
. (17)
3. Finite Element Methods for Contact
Problems
In the contact problems, the interfacial conditions be-
tween two objects can be classified into two types, touch
and separation. And the situations of touch can also be
classified into two types, sticking and sliding. Assuming
the object A and the object B as the two domains, the
equivalent principle of virtual displacement can be ex-
pressed as
,d
0
tt
ttr
ij ttijL
V
AB
ttr rtt
ijttij
V
r
tt rtt rtt r
LI c
eV
WWW




 


  



 


tt
(18)
where
L
W
 tt
,
I
W

c
W

and tt are the virtual work
of external forces, inertial forces and contact forces load-
ed on the configuration at time , respectively.
tt
If there is friction between two contact surfaces, the
virtual work is expresse d as






1, 2
tt
c
cC P NN
S
AB
NNJT J
uu uu u
J
  

  


d
ttAB t
NN
tt
AB
J
Wuug
u S




 




0
(19)
For the situation without friction, we can let


to
get the corresponding equation.
Next, the corresponding finite ele ment models are gen-
erated as follows. The total Lagrangian formulation in
matrix form can be given as


00 0
tt ttttttt
LNLc L
uK KuQQF
 
 

M
, (20)
and the total Lagrangian formulation in matrix form can
be given as


tt ttttttt
tL tNLcL t
uK KuQQF
 


M
, (21)
where
L
Q is equivalent nodal loading vector.
For sticking situation, the Lagrang ian multiplier model
can be written in T.L. form as
00
0
0
tt
tt LNLc
tt T
c
tt t
L
t
u KKK
Mu K
QF
g


















(22)
in U.L. form,
0
tt
tt tL tNLc
tt T
c
tt t
Lt
t
u
KKK
Mu K
QF
g


















(23)
For sliding situation, the Lagrangian multiplier model
can be written in T.L. form as
00
0
0
,
tt
tt LNLc
tt
N
cu
tt t
L
t
N
u
KKK
Mu K
QF
g

















(24)
in U.L. form,
0
.
tt
tt tL tNLc
tt
N
cu
tt t
Lt
t
N
u
KKK
Mu K
QF
g

















(25)
Similarly, using the penalty method, the corresponding
finite element formulation in matrix form can be written
in T.L. form as


00
0,
tt tt
LNLc
tt ttt
Lc
M
uKKKu
QQF


 


 (26)
in U.L. form,


,
tt tt
tL tNLc
tt tt t
Lct
M
uK KKu
QQF


 


 (27)

P. F. HE ET AL. 32
where

1
1
c
cc
k
n
tt tt
cc
k
KK
QQ


 





1
,,
.
cc
nn
cc
kk
k
k
uu



(28)
4. Verification
Compaction of the rigid elliptical particles has been si-
mulated by Tzaferopoulos [4]. In this section, one of his
numerical examples is simulated using the present nume-
rical model. Results of both models are in a satisfactory
agreement.
The finite element mesh of the numerical example is
presented. Since in the original literatu re particles are set
to be of rigid body. The elastic modulus in the numerical
model is set as 2 × 1010 MPa, and Poisson’s ratio 0.5. At
the same time, the friction coefficient of contacts among
25 particles is set to be 0.1. Relation of particles to the
surrounding rigid surface is set as contact state. The
boundaries on the side and the bottom are fixed. The
boundary on the top goes down in uniform velocity until
it can not continu e going down.
Final configurations from the present numerical model
and literature are shown in Figure 1. It is indicated that
final positions of particles are a little bit different be-
tween two results. However, layout and location of parti-
cles are very close to literature especially on the circled
areas. It is demonstrated that the present numerical model
is accurate and efficient.
5. Numerical Experiments
In this section, first of all, elasto-plastic analyses of alu-
minum granular materials are made using the proposed
numerical model to get some properties of behavior of
the aggregates in the compaction process. Next, visco-
plastic analyses of asphalt aggregates are made to invest-
tigate the global constitutive law. Then, mixed visco-
(a) (b)
Figure 1. Final configurations from (a) literature and (b)
the present numerical model.
plastic analyses for assembles of three types of asphalt
are made to offer some reference data for asphalt Indus-
try.
5.1. The Elasto-Plastic Analysis
A series of elasto-plastic analyses of aluminum granular
materials are made using the proposed numerical model
to get some rules in the compaction process. The linear
hardening elastic-plastic model is used as material model
in the cases of temperature from 20˚C to 250˚C. It can be
simplified to the ideal elastic-plastic model at tempera-
ture higher than 250˚C. The stress-strain relation of alu-
minum alloy at 250˚C is given in Table 1. In the elastic
section elastic modulus is 64.1 GPa, and Poisson’s ratio
0.3.
The compaction for two-dimensional assembly of 20
particles is simulated. The particles are placed on the
border of 1 meter square in area. The initial grain bound-
ary area is around 65% of the total area. The simulation
is regarded as a plane strain calculation. The compactions
of two-dimensional aggregates of twenty particles can be
classified as three types, the lateral compaction, the ver-
tical compaction, and the bi-axial compaction. Friction
between particles and wall is neglected. The inward
movement of walls is of 10 mm/s in velocity. Relation-
ship of the wall pressure to solid ratio is obtained.
5.1.1. The Lateral Compaction
In this simulation, the total loading time is set to be 40 s,
with a total of 130 time steps. In the 124th step, the as-
sembly is compacted to 98.43% of the initial area. The
compaction process is shown in Figure 2.
Figure 3 shows the relationship between the wall pres-
sure and the solid ratio. The value of lateral pressure be-
gins to increase when the solid ratio is about 0.77. A
large increase in slope occurs when the solid ratio is
close to 1. When the solid ratio is 98.43%, the average
values of the left and right wall pressure is 290 MPa, and
the one of the top and bottom wall pressure 224.8 MPa.
For the same solid ratio, the left-right pressure is less
than the up-down pressure. At the same time, it is shown
that the curve is oscillated rather than smooth. It is re-
sulted from the complex interaction among the particles.
5.1.2. The Vertical Com p action
In this simulation, the total loading time is set to be 50 s,
with a total of 170 time steps. In the 128th step, the as-
sembly is compacted to 97.90% of the initial area. The
Table 1. The stress-strain relation of aluminum alloy at
250˚C.
Strain (%) 0 0.11 0.31 0.87 1.60
Stress (MPa)0 70.5 111.2 129.1 130.2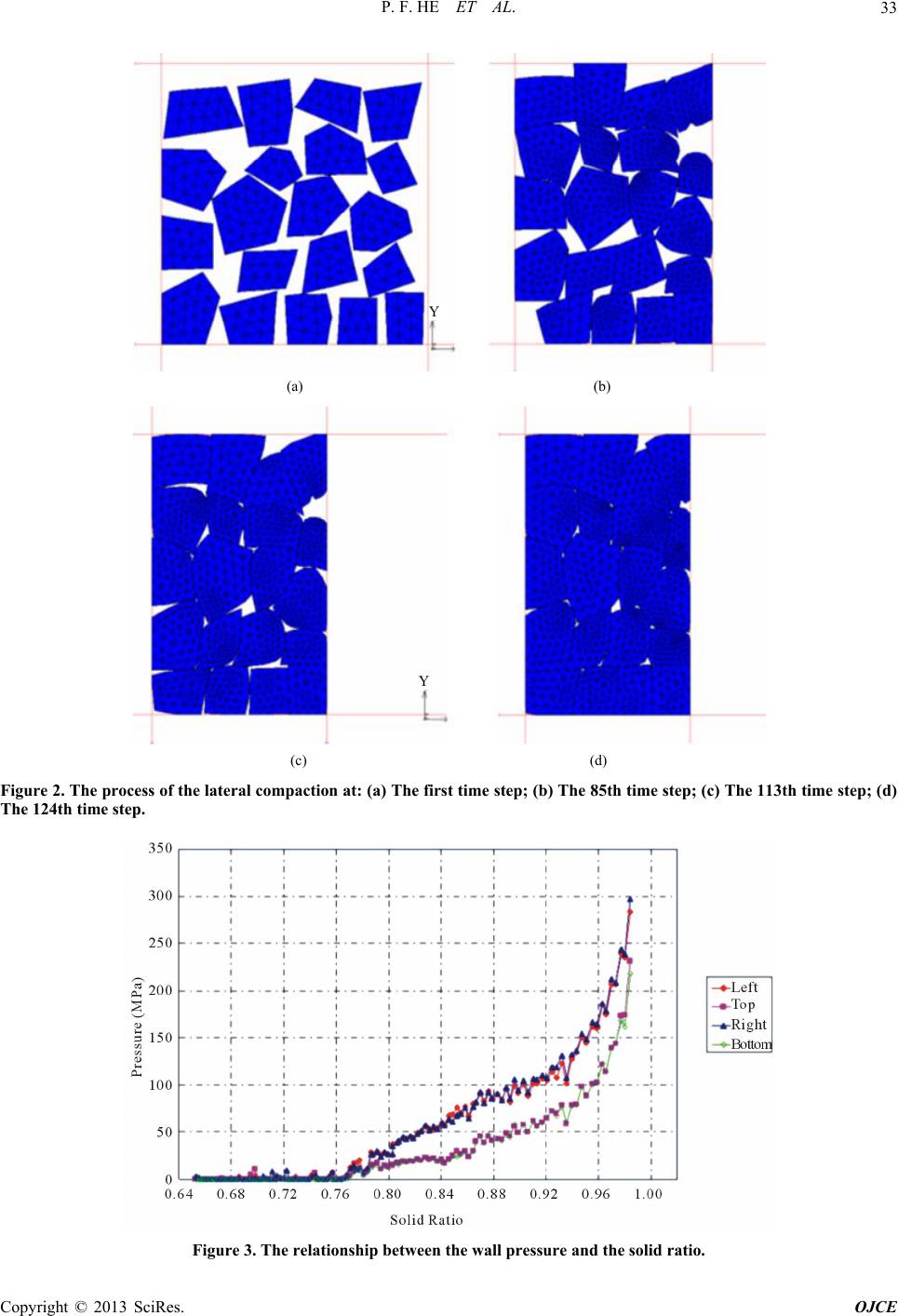

P. F. HE ET AL. 33
Y
(a) (b)
Y
(c) (d)
Figure 2. The process of the lateral compaction at: (a) The first time step; (b) The 85th time step; (c) The 113th time step; (d)
The 124th time step.
Figure 3. The relationship between the wall pressure and the solid ratio.

P. F. HE ET AL. 34
compaction process is shown in Figure 4.
Figure 5 shows the relationship between the wall pres-
sure and the solid ratio. The value of lateral pressure be-
gins to increase when the solid ratio is about 0.79. A
large increase in slope occurs when the solid ratio is
close to 1. When the solid ratio is 97.9%, the average
values of the left and right wall pressure is 290.8 MPa,
and the one of the top and bottom wall pressure 228.9
MPa. For the same solid ratio, the left-right pressure is
less than the up-down pressure. At the same time, it is
shown that the curve is os cillated rather than smooth. It is
resulted from the complex interaction among the parti-
cles.
5.1.3. The Biaxial Compaction
In this simulation, the total loading time is set to be 40 s,
with a total of 130 time steps. In the 89th step, the as-
sembly is compacted to 99.37% of the initial area. The
compaction process is shown in Figure 6.
Figure 7 shows the relationship b etween the wall pres-
sure and the solid ratio. The value of lateral pressure be-
gins to increase when the solid ratio is about 0.79. A
large increase in slope occurs when the solid ratio is close
to 1. When the solid ratio is 99.3 7%, the values of the left
wall pressure is 290.9 Mpa, the one of the right wall
pressure is 309.9 MPa, the one of th e top wall pressure is
280.3 MPa, and the one of the bottom wall pressure is
297.2 MPa. For the same solid ratio, the left-right pres-
sure is less than the up-down pressure. At the same time,
it is shown that the curve is oscillated rather than smooth.
It is resulted from the complex interaction among the
particles.
5.2. The Visco-Plastic Analysis
In this section, a series of visco-plastic analyses of as-
phalt aggregates are made to investigate the global con-
stitutive law. Here asphalt is used as the granular matter.
Y
Y
(a) (b)
YY
(c) (d)
Fi gu r e 4. T h e p r oc e s s of t h e v er t i c al c o m pa c t ion at: (a) The first time step; (b) The 82nd time st e p; ( c ) T h e 1 13 t h ti m e s te p ; (d)
The 128th time step.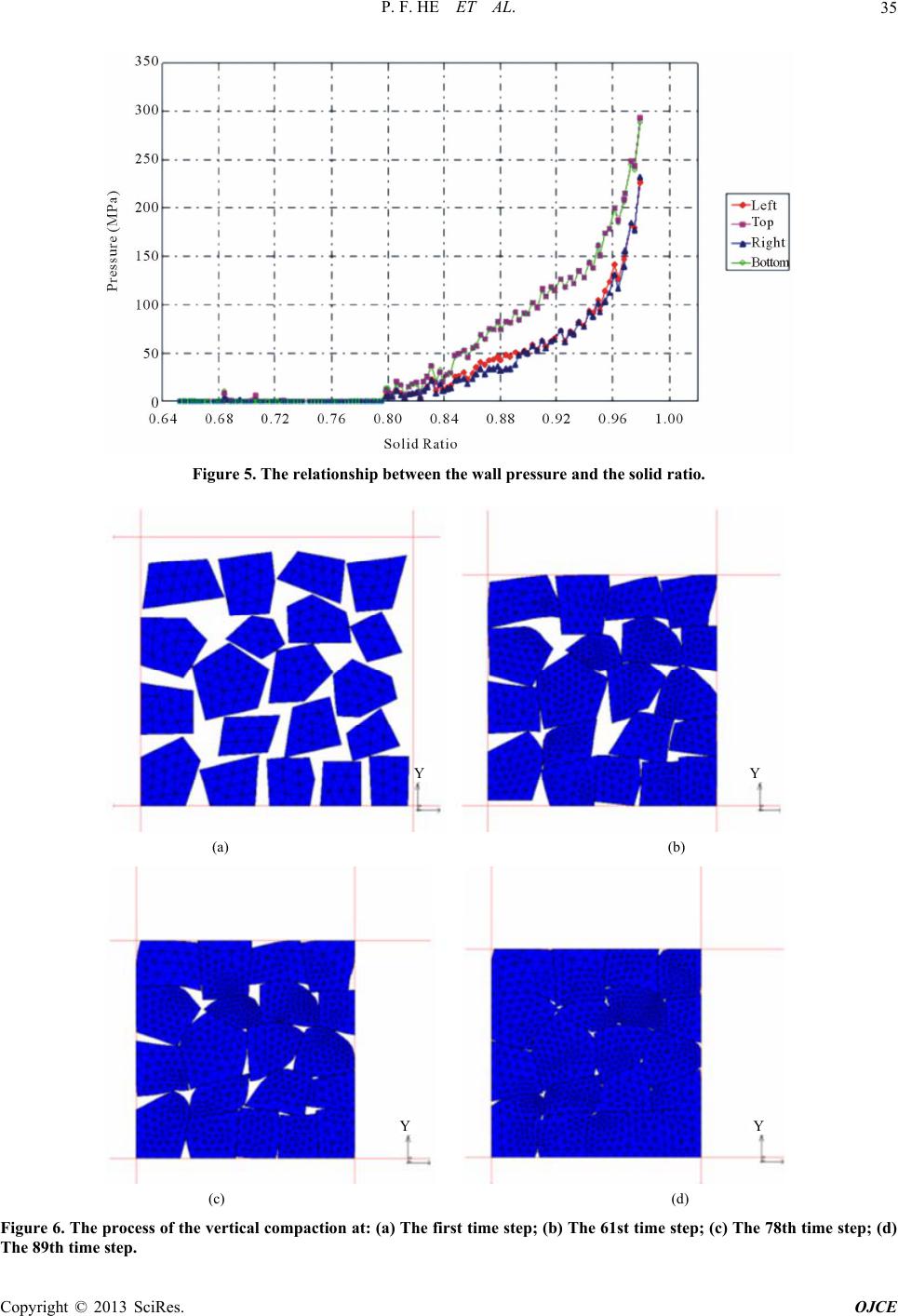

P. F. HE ET AL. 35
Figure 5. The relationship between the wall pressure and the solid ratio.
YY
(a) (b)
YY
(c) (d)
Figure 6. The process of the vertical compaction at: (a) The first time step; (b) The 61st time step; (c) The 78th time step; (d)
The 89th time step.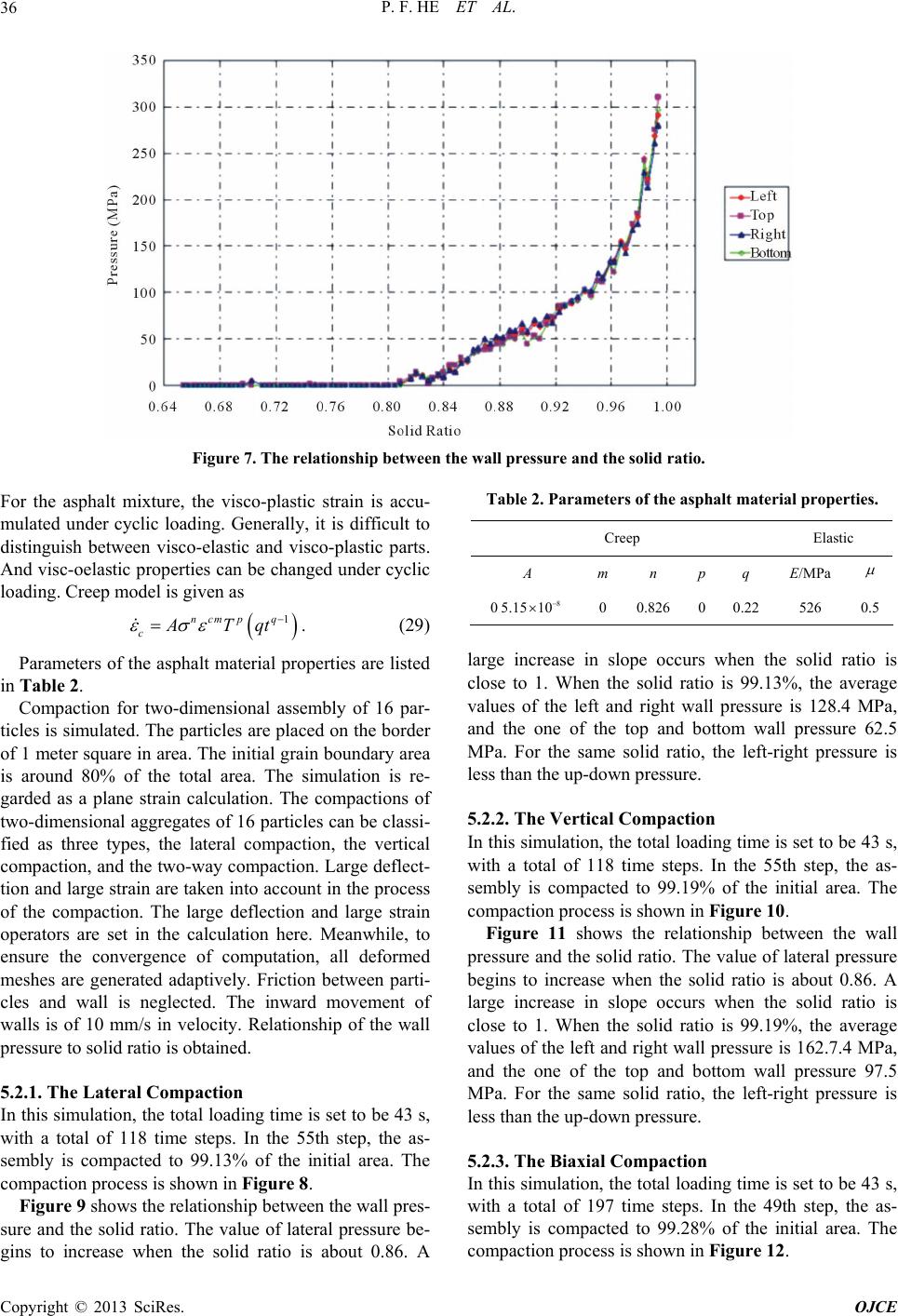

P. F. HE ET AL. 36
Figure 7. The relationship between the wall pressure and the solid ratio.
Table 2. Parameters of the asphalt material properties.
For the asphalt mixture, the visco-plastic strain is accu-
mulated under cyclic loading. Generally, it is difficult to
distinguish between visco-elastic and visco-plastic parts.
And visc-oelastic properties can be changed under cyclic
loading. Creep model is given as
Creep Elastic
A mn p q E/MPa

05.15 8 10

 00.826 0 0.22 526 0.5

1ncmpq
c
A
Tqt 

 
. (29)
large increase in slope occurs when the solid ratio is
close to 1. When the solid ratio is 99.13%, the average
values of the left and right wall pressure is 128.4 MPa,
and the one of the top and bottom wall pressure 62.5
MPa. For the same solid ratio, the left-right pressure is
less than the up-down pressure.
Parameters of the asphalt material properties are listed
in Table 2.
Compaction for two-dimensional assembly of 16 par-
ticles is simulated. The particles are placed on the border
of 1 meter square in area. The initial grain boundary area
is around 80% of the total area. The simulation is re-
garded as a plane strain calculation. The compactions of
two-dimensional aggregates of 16 particles can be classi-
fied as three types, the lateral compaction, the vertical
compaction, and the two-way compaction. Large deflect-
tion and large strain are taken in to account in the process
of the compaction. The large deflection and large strain
operators are set in the calculation here. Meanwhile, to
ensure the convergence of computation, all deformed
meshes are generated adaptively. Friction between parti-
cles and wall is neglected. The inward movement of
walls is of 10 mm/s in velocity. Relationship of the wall
pressure to solid ratio is obtained.
5.2.2. The Vertical Com p action
In this simulation, the total loading time is set to be 43 s,
with a total of 118 time steps. In the 55th step, the as-
sembly is compacted to 99.19% of the initial area. The
compaction process is shown in Figure 10.
Figure 11 shows the relationship between the wall
pressure and the solid ratio. The value of lateral pressure
begins to increase when the solid ratio is about 0.86. A
large increase in slope occurs when the solid ratio is
close to 1. When the solid ratio is 99.19%, the average
values of the left and right wall pressure is 162.7.4 MPa,
and the one of the top and bottom wall pressure 97.5
MPa. For the same solid ratio, the left-right pressure is
less than the up-down pressure.
5.2.1. The Lateral Compaction
In this simulation, the total loading time is set to be 43 s,
with a total of 118 time steps. In the 55th step, the as-
sembly is compacted to 99.13% of the initial area. The
compaction process is shown in Figure 8. 5.2.3. The Biaxial Compaction In this simulation, the total loading time is set to be 43 s,
with a total of 197 time steps. In the 49th step, the as-
sembly is compacted to 99.28% of the initial area. The
ompaction process is shown in Figure 12.
Figure 9 shows the relationship between the wall pres-
sure and the solid ratio. The value of lateral pressure be-
gins to increase when the solid ratio is about 0.86. A c

P. F. HE ET AL. 37
YY
(a) (b)
YY
(c) (d)
Figure 8. The process of the lateral compaction at: (a) The first time step; (b) The 33rd time step; (c) The 45th time step; (d)
The 55th time step.
Figure 9. The relationship between the wall pressure and the solid ratio.

P. F. HE ET AL. 38
YY
(a) (b)
YY
(c) (d)
Figure 10. The process of the vertical compaction at: (a) The first time step; (b) The 32nd time step; (c) The 45th time step; (d)
The 55th time step.
Figure 11. The relationship between the wall pressure and the solid ratio.

P. F. HE ET AL. 39
YY
(a) (b)
YY
(c) (d)
Figure 12. The process of the lateral compaction at: (a) The first time step; (b) The 22nd time step; (c) The 40th time step; (d)
The 49th time step.
high temperature and to provide the basis for error as-
sessment.
Figure 13 shows the relationship between the wall
pressure and the solid ratio. The value of lateral pressure
begins to increase when the solid ratio is about 0.86. A
large increase in slope occurs when the solid ratio is
close to 1. When the solid ratio is 99.28%, the values of
the left wall pressure is 143.1 Mpa, the one of the right
wall pressure is 146.1 MPa, the one of the top wall pres-
sure is 132.9 MPa, and the one of the bottom wall pres-
sure is 142.4 MPa. For the same solid ratio, the left-right
pressure is less than the up-down pressure.
Simulations made for compaction of 4 aggregates of
asphalt have same area but are arranged in different ways
shown in Figure 14. The simulation is regarded as a
plane strain problem. Large deflection and large strain
are taken into account in the process of the compaction.
The large deflection and large strain operators are set in
the calculation here. Meanwhile, to ensure the conver-
gence of computation, all deformed meshes are generated
adaptively. Friction between particles and wall is ne-
glected. The inward movement of walls is of 10 mm/s in
velocity. Relationship of the wall pressure to solid ratio
is obtained.
5.3. The Mixed Visco-Plastic Analysis
In this section, a series of mixed visco-plastic analyses
for assembles of three types of asphalt are made to offer
some reference data for asphalt industry. Three types of
asphalt materials are used for analysis. Parameters of the
material properties are shown in Table 3. Also Poisson
ratio is set as 0.5 to ensure incompressibility of asphalt at
The relationships between pressure and solid ratio of 4
mixed aggregates are shown in Figure 15. It is indicated
tha t, in descending order of required compactio n p re ssu r e,
the sequence is the first combination, the fourth combi-
nation, the third composition and second composition.

P. F. HE ET AL. 40
Figure 13. The relationship between the wall pressure and the solid ratio.
Table 3. Parameters of material properties of the three types of asphalts.
Creep Elastic
Type
A m n p q E/MPa

m1 8 5.15 10  0 0.826 0 0.221 526 0.5
m2 7 1.41 10 
8
6.28 10 
0 1.101 0 0.358 440 0.5
m3 0 1.073 0
0.324 420 0.5
m1
m2
m3
m1
m2
m3
(a) (b)
m1
m2
m3
m1
m2
m3
(c) (d)
Figure 14. Vertical compaction of 4 assemblies of asphalt: their initial and final configurations.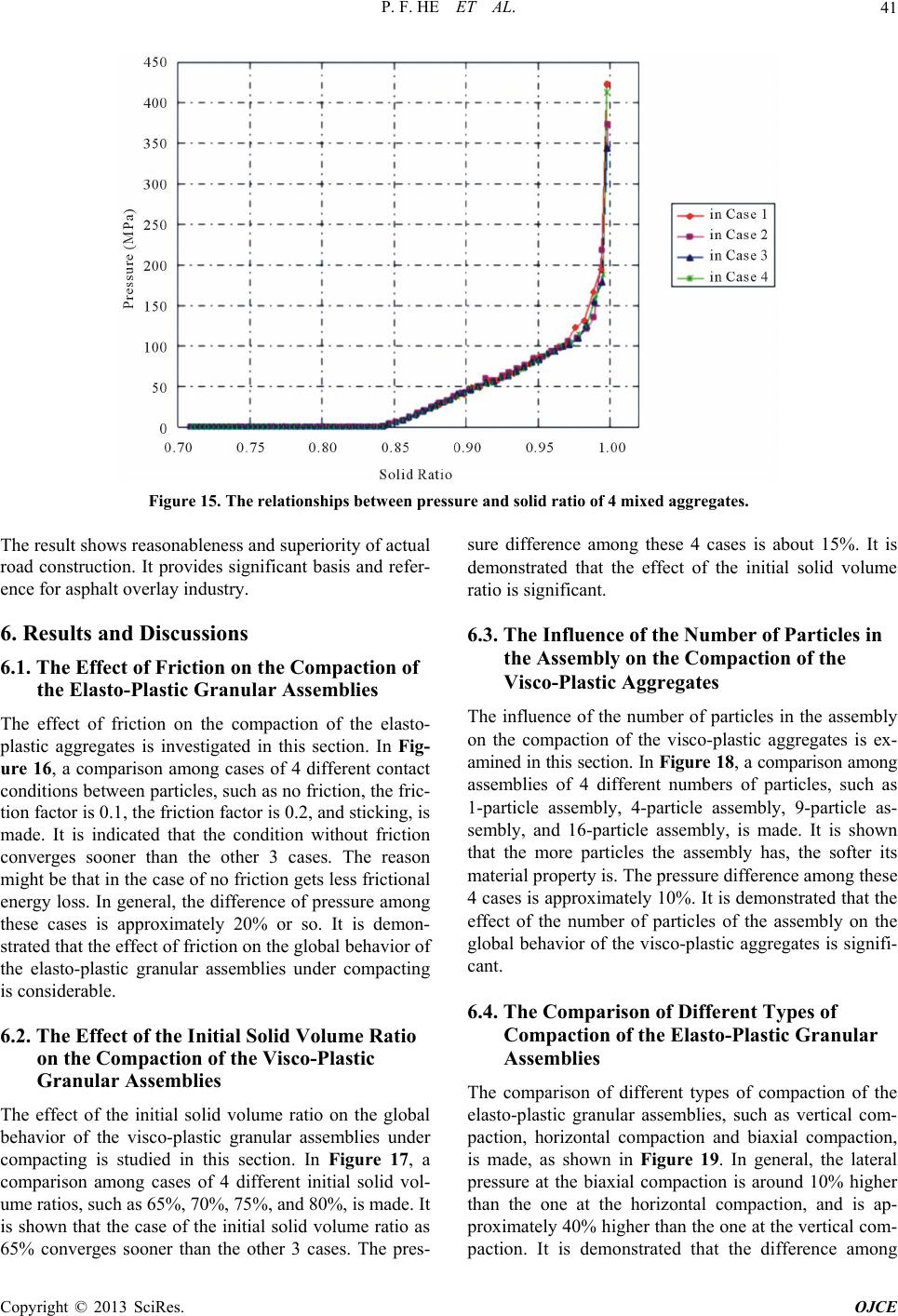

P. F. HE ET AL. 41
Figure 15. The relationships between pressure and solid ratio of 4 mixed aggregates.
The result shows reasonableness and superiority of actual
road construction. It provides significant basis and refer-
ence for asphalt overlay industry.
6. Results and Discussions
6.1. The Effect of Friction on the Compaction of
the Elasto-Plastic Granular Assemblies
The effect of friction on the compaction of the elasto-
plastic aggregates is investigated in this section. In Fig-
ure 16, a comparison among cases of 4 different contact
conditions between particles, such as no friction, the fric-
tion factor is 0.1, the friction factor is 0.2, and sticking, is
made. It is indicated that the condition without friction
converges sooner than the other 3 cases. The reason
might be that in the case of no friction gets less frictional
energy loss. In general, the difference of pressure among
these cases is approximately 20% or so. It is demon-
strated that the effect of friction on the global behavior of
the elasto-plastic granular assemblies under compacting
is considerable.
6.2. The Effect of the Initial Solid Volume Ratio
on the Compaction of the Visco-Plastic
Granular Assemblies
The effect of the initial solid volume ratio on the global
behavior of the visco-plastic granular assemblies under
compacting is studied in this section. In Figure 17, a
comparison among cases of 4 different initial solid vol-
ume ratios, such as 65%, 70%, 75%, and 80%, is made. It
is shown that the case of the initial solid volume ratio as
65% converges sooner than the other 3 cases. The pres-
sure difference among these 4 cases is about 15%. It is
demonstrated that the effect of the initial solid volume
ratio is significant.
6.3. The Influence of the Number of Particles in
the Assembly on the Compaction of the
Visco-Plastic Aggregates
The influence of the number of particles in the assembly
on the compaction of the visco-plastic aggregates is ex-
amined in this sect ion. In Figure 18, a comparison among
assemblies of 4 different numbers of particles, such as
1-particle assembly, 4-particle assembly, 9-particle as-
sembly, and 16-particle assembly, is made. It is shown
that the more particles the assembly has, the softer its
material property is. The pressure difference among these
4 cases is approximately 10%. It is demonstrated that the
effect of the number of particles of the assembly on the
global behavior of the visco-plastic aggregates is signifi-
cant.
6.4. The Comparison of Different Types of
Compaction of the Elasto-Plastic Granular
Assemblies
The comparison of different types of compaction of the
elasto-plastic granular assemblies, such as vertical com-
paction, horizontal compaction and biaxial compaction,
is made, as shown in Figure 19. In general, the lateral
pressure at the biaxial compaction is around 10% higher
than the one at the horizontal compaction, and is ap-
proximately 40% higher than the one at the vertical com-
action. It is demonstrated that the difference among p

P. F. HE ET AL. 42
Figure 16. A comparison among cases of 4 different contact conditions between particles is made.
Figure 17. A comparison among cases of 4 different initial solid volume ratios, such as 65%, 70%, 75%, and 80%, is made.
Figure 18. A comparison among assemblies of 4 different numbers of particles is made.

P. F. HE ET AL. 43
Figure 19. A comparison of different types of compaction, such as vertical compaction, horizontal compaction and biaxial
compaction, is made.
different types of compaction is considerable.
6.5. Error Estimation
Error estimation is made for all simulations of compac-
tions of the granular materials in this section. It is as-
sumed that materials of the granular assemblies are in-
compressible. So one of the methods to estimate error of
analytical results is calculating the ratio of the change of
solid volume to the initial solid volume. In general, the
average of errors in this study is about 0.6%. It is dem-
onstrated that the results of the numerical analyses are
acceptable and satisfactory.
7. Conclusions and Prospect
In this paper, the compactions of elasto-plastic and visco-
plastic polygonal granular materials are simulated using
the finite element method. A couple of numerical experi-
ments are made using the numerical model. Some new
discoveries are presented as follows. First of all, in the
simulation for the compaction of aggregates consising of
particles of a single elasto-plastic incompressible mate-
rial, it is demonstrated that if the initial solid volume
ratios of the assemblies are the same, the more particles
there are, the more oscillated the pressure-density curve
is. But the general trend of the curve almost keeps the
same. When the solid volume ratio is close to 1, stress in
the biaxial compaction is around 15% lower than one in
the uni-axial compaction. The effect of initial solid vol-
ume ratio as well as the effect of friction among particles
on the stress-density relation is considerable. In addition,
in the simulation for the compaction of aggregates con-
sisting of particles of a single viscous incompressible
material, if the initial volumes of the assemblies are the
same, when the solid volume ratio is close to 1, stress in
the biaxial compaction is around 40% lower than one in
the uni-axial compaction . Finally, the numerical model is
extended to simulate the compaction of aggregates con-
sisting of mixed particles of different viscous incom-
pressible materials. It is indicated that, with minor modi-
fication, the method could be used in a variety of pro-
blems that can be represented using granular media, such
as asphalt, polymers, aluminum, snow, food product, etc.
However, the number of particles in the granular as-
semblies presented in this paper is less than 25. To ex-
tend the proposed numerical model to analyze the be-
havior of large-scale granular systems, more studies on
multi-scale methods, statistical random sampling models
and stochastic simulations are necessary.
8. Acknowledgements
This work is spo nso red b y National Natu ral S cien c e Foun-
dation of China under grant 10972162. This support is
gratefully acknowledged.
REFERENCES
[1] H. M. Jaeger and S. R. Nagel, “The Physics of Granular
Materials,” Physics Today, Vol. 49, No. 4, 1996, pp. 32-
38. doi:10.1063/1.881494
[2] S. Luding, “Stress Distribution in Static Two Dimen-
sional Granular Model Media in the Absence of Friction,”
Physical Review E, Vol. 4, No. 55, 1997, pp. 4720-4729.
doi:10.1103/PhysRevE.55.4720
[3] Y. M. Bashir and J. D. Goddard, “A Novel Simulation
Method for the Quasi-Static Mechanics of Granular As-
semblages,” Journal of Rheology, Vol. 5, No. 35, 1991,
pp. 849-885. doi:10.1122/1.550160
[4] M. A. Tzaferopoulos, “On the Numerical Modeli ng of Con-
vex Particle Assemblies with Friction,” Computer Me-
thods in Applied Mechanics and Engineering, Vol. 127,

P. F. HE ET AL. 44
No. 1-4, 1995, pp. 371-386.
doi:10.1016/0045-7825(95)00852-8
[5] S. N. Coppersmith, C. H. Liu and O. Narayan, “Model for
Force Fluctuations in Bead Packs,” Physical Review E,
Vol. 5, No. 53, 1996, pp. 4673-4685.
doi:10.1103/PhysRevE.53.4673
[6] H. G. Matuttis, “Simulations of the Pressure Distribution
under a Two Dimensional Heap of Polygonal Particles,”
Granular Matter, Vol. 2, No. 1, 1998, pp. 83-91.
doi:10.1007/s100350050013
[7] M. Satake, “Tensorial form Definitions of Discrete-Me-
chanical Quantities for Granular Assemblies,” Interna-
tional Journal of Solids and Structures, Vol. 41, No. 21,
2004, pp. 5775-5791. doi:10.1016/j.ijsolstr.2004.05.046
[8] F. Emeriault and C. Claguin, “Statistical Homogenization
for Assemblies of Elliptical Grains: Effect of the Aspect
Ratio and Particle Orientation,” International Journal of
Solids and Structures, Vol. 41, No. 2, 2004, pp. 5837-
5849. doi:10.1016/j.ijsolstr.2004.05.047
[9] S. J. Antony and R. Kuhn, “Influence of Particle Shape
on Granular Contact Signatures and Shear Strength: New
Insights from Simulations,” International Journal of Sol-
ids and Structures, Vol. 41, No. 21, 2004, pp. 5863-5870.
doi:10.1016/j.ijsolstr.2004.05.067
[10] Y. C. Wu, E. G. Thompson, P. R. Heyliger and Z. H. Yao,
“The Compaction of Blended Aggregates of Non-Spheri-
cal Linear Viscous Particles,” Computer Methods in Ap-
plied Mechanics and Engineering, Vol. 193, No. 36-38,
2004, pp. 3871-3890. doi:10.1016/j.cma.2004.02.008
[11] Y. C. Wu, “Automatic Adaptive Mesh Upgrade Schemes
of the Step-by-Step Incremental Simulation for Quasi
Linear Viscoplastic Granular Materials,” Computer Meth-
ods in Applied Mechanics and Engineering, Vol. 197,
2008, pp. 1479-1494. doi:10.1016/j.cma.2007.11.020
[12] Y. Wu, J. Xiao and C. Zhu, “The Compaction of Time-
Dependent Viscous Granular Materials Considering Iner-
tial Forces,” Acta Mechanica Solida Sinica, Vol. 24, No.
6, 2011, pp. 495-505.