 American Journal of Operations Research, 2013, 3, 299-306 http://dx.doi.org/10.4236/ajor.2013.32027 Published Online March 2013 (http://www.scirp.org/journal/ajor) Trapezoidal Approximation of a Fuzzy Number Preserving the Expected Interval and Including the Core B. Asady Department of Mathematics, Islamic Azad University, Arak Branch, Arak, Iran Email: babakmz2002@yahoo.com, b-asadi@iau-arak.ac.ir Received October 11, 2012; revised November 15, 2012; accepted November 28, 2012 ABSTRACT In this paper, we introduce a method to obtain the nearest trapezoidal approximation of fuzzy numbers so that preserv- ing condition s expect interval and include the core of a fuzzy n umber. Keywords: Trapezoidal Approximation; Fuzzy Number; Fuzzy Partition; Fuzzy Approximation; Trapezoidal Fuzzy Numbers 1. Introduction :0,1AR I which satisfies: Trapezoidal fuzzy intervals are often used in practice. An interesting problem is to approximate general fuzzy in- tervals by means of trapezoidal ones, so as to simplify calculations. The investigations in this area were started by Ma et al. [1] that proposed the symmetric triangular approximation. Actually, symmetric triangular approxi- mation is a particular case of the trapezoidal approxima- tion that was discussed by many authors including Abbasbandy, Amirfakhrian [2], Abbasbandy and Asady [3], Coroianu [4], Ban [5-8], Grzegorzewski [9-11], Grzegorzewski and Mrowka [12,13], Grzegorzewski, K. Pasternak-Winiarska [14,15] and Yeh [16-21] and other methods same as [22-27]. Although, there are many scholars who have investigated interval, triangular and trapezoidal approximation of fuzzy numbers, but the re- sult of approximation is not always a fuzzy number, sometimes it is not a fuzzy set. For example Grzegor- zewski and Mrowka proposed in [12] a method to find the nearest (with respect to a well-known metric between fuzzy numbers) trapezoidal approximation operator that preserving the expected interval. Unfortunately, there was a gap in the suggested solution which was later im- proved by Grzegorzewski and Mrowka [13] and finally solved by Ban [7] and Yeh [18]. In this paper, we com- bine the ideas proposed in papers [3,12], so that preserv- ing conditions expect interval and include the core of a fuzzy number. In Section 2, we recall some fundamental results on fuzzy nu mbers. Trap ezo idal app rox imation and examples are in Section 3. 2. Preliminaries Definition 1. (cf. [28]) A fuzzy number is a fuzzy set like 1) A is the strictly quasi-convex, 2) 0Ax outside some interval ,cd cabd , 3) There are real numbers a, b such that and a) x is monotonic increasing on ,ca , b) x is monotonic decreasing on ,bd, 1, xaxb . c) The set of all these fuzzy numbers is denoted by R. The -cut, 20,1 , of a fuzzy number A is a crisp set defined as :AxRAx . Every -cut of a fuzzy number A is a closed interval ,AALAU , where inf :, sup :. ALxRA x AUxRA x The set of all elements that have a nonzero degree of membersh ip in A is called the support of A [27], i.e. supp: 0AxRAx . Definition 2. (complement) The complement of a fuzzy number A is defined as 1. xAx , The pair of functions LAU ,,,aaaa R gives a parametric representation of fuzzy number A (see [29]). Another important type of fuzzy numbers was introduced in [23] as follows. Let 1234 such that A fuzzy number defined as 1234 .aaaa C opyright © 2013 SciRes. AJOR  B. ASADY 300 1 12 23 34 4 f if f if f xa axa axa axa xa ,0,lr ,,, 1 21 4 43 0i 1i 0i l r xa aa Ax ax aa where is denoted by 1234 aaaa 1234 ,,, lr and if by lr aaaa r . Its parametric form is 3 ,, 0,1 LU lr aa aaaa 1lr ,,, . 11 1214 4 ,A AA A popular fuzzy number is the trapezoidal fuzzy num- ber, completely characterized by Equation (1) when , denoted by 1234 aaaa We denoted by R the set of all fuzzy numbers and TR ,LAU the set of all trapezoidal fuzzy numbers. Definition 3. For arbitrary fuzzy numbers A, AA ,LBU BB and B, the quantity 1 0 1 0 ,DAB A 2 2 d d LL UU B AB (2) is the distance between A and B, [3,24,25]. The function , AB is a metric in R and , RD is a complete metric space. The expected interval EIA of a fuzzy number ,AL AUAA 11 00 d Lu A A introduced independently by Dubois and Prade [30] and Heilpern [31]. It is defined by d, , A EI AEAE (3) Grzegorzewski [9] shows that the interval EIA is the nearest interval to the fuzzy number A. Hence in [31] the expected value of a fuzzy number A defined follow- ing as EA AE 1 2 EV A (4) and B. Asady and M. Zendehnam in [32] show that EV A : 1RAx is the best approximation of a fuzzy number A. Finally, let us recall that . coreAx 3. Trapezoidal Approximation of Fuzzy Numbers Suppose we want to approximate a fuzzy number by a trapezoidal fuzzy number. Thus, we use an operator :TFRFTR which transforms fuzzy numbers into family of trapezoidal fuzzy number. Abbasbandy and Asady [3] considered a trapezoidal approximation that includes the -cut superset, i.e., 1core coreTA TA (5) Grzegorzewski and Mrówka [12] said that an operator :TFRFTR TA fulfills the criterion if for any fuzzy number A its output valu e preserves the expected interval, i.e., 2 TEIAEITA (6) In this part, we combine ideas proposed in the papers [3,12] to obtain the nearest trapezoidal fuzzy number respect to the original fuzzy number so that it preserves T1 and T2 conditions. Since, any x belongs to the core A of a fuzzy number A if and only if it does not belong to the complement of A core AxA Therefore, for preserving of these points we consider core core TA. Also, we are going to preserve the expected interv al of the fuzzy number that th is additional requirement by the significant role of the expected inter- val is in many situations an d applications (see, e.g., [5-11, 33]. Additionally, the propose approach can provide de- cision makers with a new alternative to trapezoidal ap- proximation of fuzzy nu mbers. Now, given a fuzzy number B with -cut set ,BL BU, the problem is to find a trapezoidal fuzzy number ,,,TB tttt 1234 which is the nearest to B with respect to metric D and preserves the condi- tions T1 and T2 i.e. we have 12 0 1 12 2 0 min ,d d LL UU DBTBB TB BTB (7) Subject to 23 ,1,1, LU ttB B (8) 11 34 12 00 ,d,d, 22 LU tt tt BB (9) As, in order to minimize ,DBTB it suffices to minimize function Copyright © 2013 SciRes. AJOR  B. ASADY 301 2 12 1 12 0 1 44 0 ,, L U FhhD BTB Btt Bt 2 1 2 3d d , t tt 2 21 1 L tB h 2 32 1 U tB h 12 2d, Lt 43 2d, Ut (10) 112 11 100 11 200 3 1 40 ,0, 4d6d, 2d6 d, 1, 12 d, LL LL U UU hhh tB B tB B tB tB B with respect to h1 and h2. Subject to (11) and (12) and 1 0 tB (13) and 1 0 tB (14) Clearly, with note to Equations (8), (9), we can say the conditions (11)-(14) are suitable for finding the nearest trapezoidal fuzzy number TB coreB to a fuzzy number B with the conditions as the expected interval and are preserved. Theorem 1: Let B with TBcore -cut set ,BUBL 1d 321d, LL B , be a fuzzy number and 1 10 1 0L dB B 1d 321d, UU B (15) 1 20 1 0U dB B 20 0dd (16) Case 1: If 1 and then, optimal solution of problem (10) is 12 0hh 1 0 1 0 d, d LL UU B B and consequently, we have 1 2 3 4 12 1, 1, 12 L U tB tB tB tB 20 0d (17) Case 2: If and d 1 then 10d (18) and d then Case 3: If 20 122 1 10 2 11 300 11 400 0, , 12 d, 1, 2d6d, 4d6 d, LL L UU UU hhd tB B tB tB B tB B 10d20 (19) Case 4: If and d then 112 2 11 100 11 200 11 300 11 400 , 4d6d, 2d6d, 2d6 d, 4d6 d, LL LL UU UU hdhd tB B tB B tB B tB B (20) 12 , Proof: In order to minimize hh it suffices to minimize function 12 12 2, , hh fhh with the par- tial derivatives 12 1 11 2 11 00 12 2 11 2 22 00 41d321d 3 , 41d3 , 21d 3 LL L UU U fhh h hh BBB fhh h hh BBB (21) Copyright © 2013 SciRes. AJOR  B. ASADY Copyright © 2013 SciRes. AJOR 302 212 2 1 212 2 2 212 12 , , , fhh h fhh h fhh hh 2 11 2 22 4 43 4 43 0, hd hd 0hh (22) system (10) is 12 and the point 0,0 mini- mizes the function F in the Equation (10). Because 12 , hh 0d is lower bounded function and has only a critical point. Also, with note to Equations (11)-(14) and optimal solution formula (17) is correct. 12 2) If 1 and 2 d are satisfied then the solu- tions of the system (10) are 0hh 0 1020h Case 1: , , h Case 2: 11 hd20h , Moreover, since 2 2 1 2 2 2 21 2 1 21 2 2 0,0 0,0 ,0 ,0 f h f h fd h fd h 1 2 0, 0, 80, 3 40, 3 d d therefore case 2 such that 11 , 2 minimizes the function F. Because the Hessian matrix for it is posi- tive definite and for case 1 is not positive definite. Also, with note to Equations (11)-(14) and hd 0h 11 hd20h, Formulae (18) are satisfied. 3) Proof is similar with 2) 4) If 1 and 2 are satisfied then the solu- tions of the system (10) are given by 0d0d 1020h 10h Case 1: , ; h Case 2: , 22 hd; Case 3: 11 hd20h, ; Case 4: 11 hd, 22 Because the Hessian matrix for of case 4 is positive definite and for others cases are not positive definite, then the solution of case 4 is minimizer and formulae (20) is correct. 2 Now we compare our method with the other works [3,7,20] in following exa mples. hd. Example 1. [7] Let us consider the fuzzy number 1,2, 3,302A , in the parametric forms, 1,3027,0,1 . LU AA By substitute abov e equations on the (2) and (3) equa- tions, we obtain the expect interval and core of the fuzzy number A same as follows 5,12, core2,3 3 EI AA Also, trapezoidal approximation of it by the other methods and proposed method is shown in Table 1. Clearly, in Table 1, by Ban and Yeh methods, we have EIAEI TA core core. and TA and, by Abbasbandy and Asady method, get EIAEI TA core core. and TA Consequently, with note above results proposed method preserved T1 and T2 conditions (see Figures 1-4). Example 2. Consider the fuzzy number 41 3 10,10,10,14B coreTA that the parametric form of it is as follows Table 1. Comparative results of example 1. EI TA The trapezoidal approximation of fuzzy numbers A Authors 5 3 5,12 3 53,53,53,673 Ban 71 78 , 35 35 5,12 3 4735,7135,7835,72635 Yeh 2,3 33 240 , 20 20 13 10,2,3,219 10 Abbasbandy Asady 2,3 5,12 3 3 4,2,3,21 Proposed method 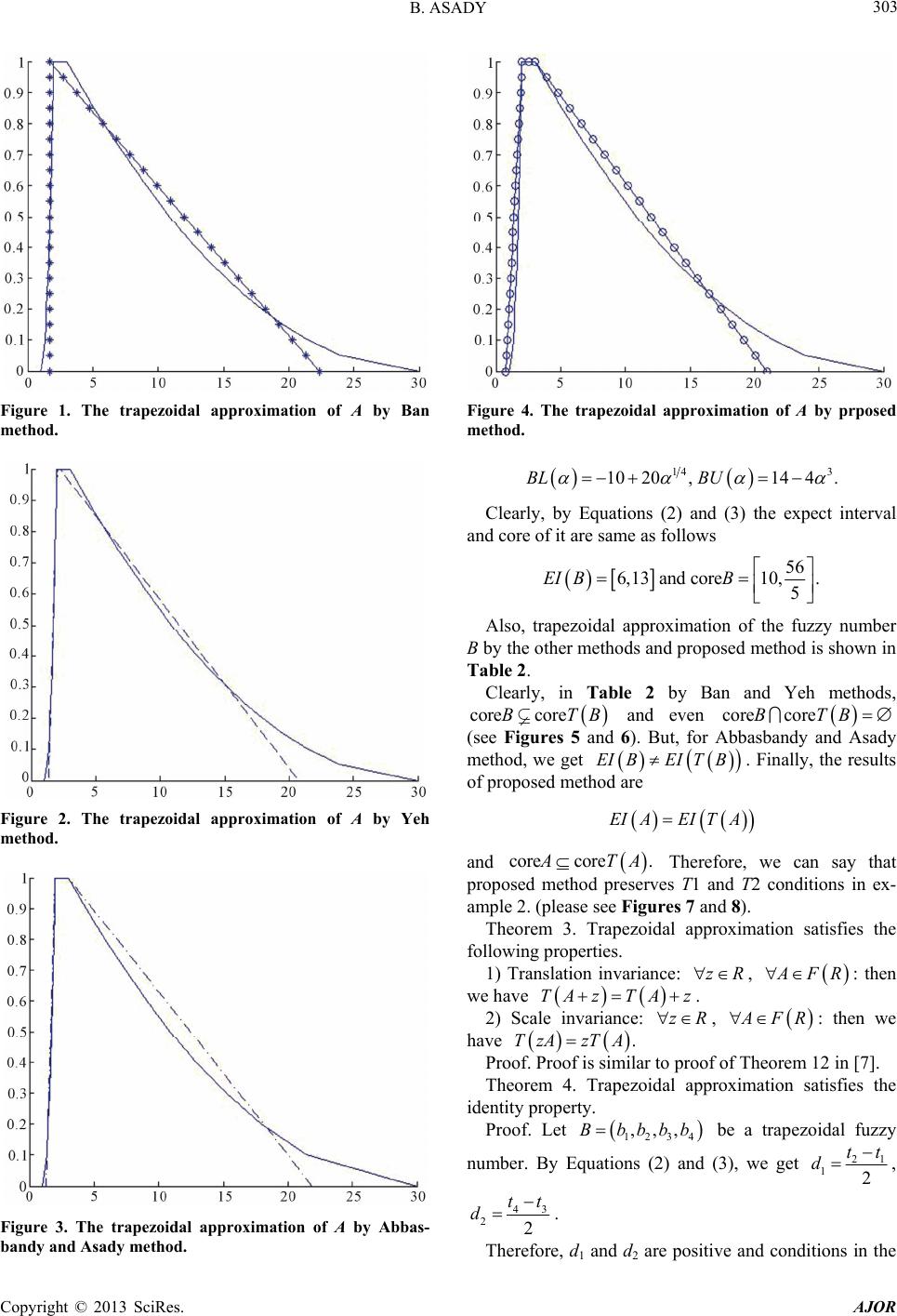 B. ASADY 303 Figure 1. The trapezoidal approximation of A by Ban method. Figure 2. The trapezoidal approximation of A by Yeh method. Figure 3. The trapezoidal approximation of A by Abbas- bandy and Asady method. Figure 4. The trapezoidal approximation of A by prposed method. 14 3 1020, 144BL BU . Clearly, by Equations (2) and (3) the expect interval and core of it are same as follows 6,13and core56 5 10, .EI BB Also, trapezoidal approximation of the fuzzy number B by the other methods and proposed method is shown in Table 2. Clearly, in Table 2 by Ban and Yeh methods, core coreBTB and even core coreBTB (see Figures 5 and 6). But, for Abbasbandy and Asady method, we get EIBEI TB. Finally, the results of proposed method are EIAEI TA core core. and TA zR Therefore, we can say that proposed method preserves T1 and T2 conditions in ex- ample 2. (please see Figures 7 and 8). Theorem 3. Trapezoidal approximation satisfies the following properties. 1) Translation invariance: , FR : then we have TA zTAz zR . , 2) Scale invariance: FR : then we have .TzA zTA Proof. Proof is similar to proof of Theorem 12 in [7]. Theorem 4. Trapezoidal approximation satisfies the identity property. 1234 ,,,Bbbbb be a trapezoidal fuzzy Proof. Let number. By Equations (2) and (3), we get 21 12 tt d , 43 22 tt d . Therefore, d1 and d2 are poitive and conditions in the s Copyright © 2013 SciRes. AJOR 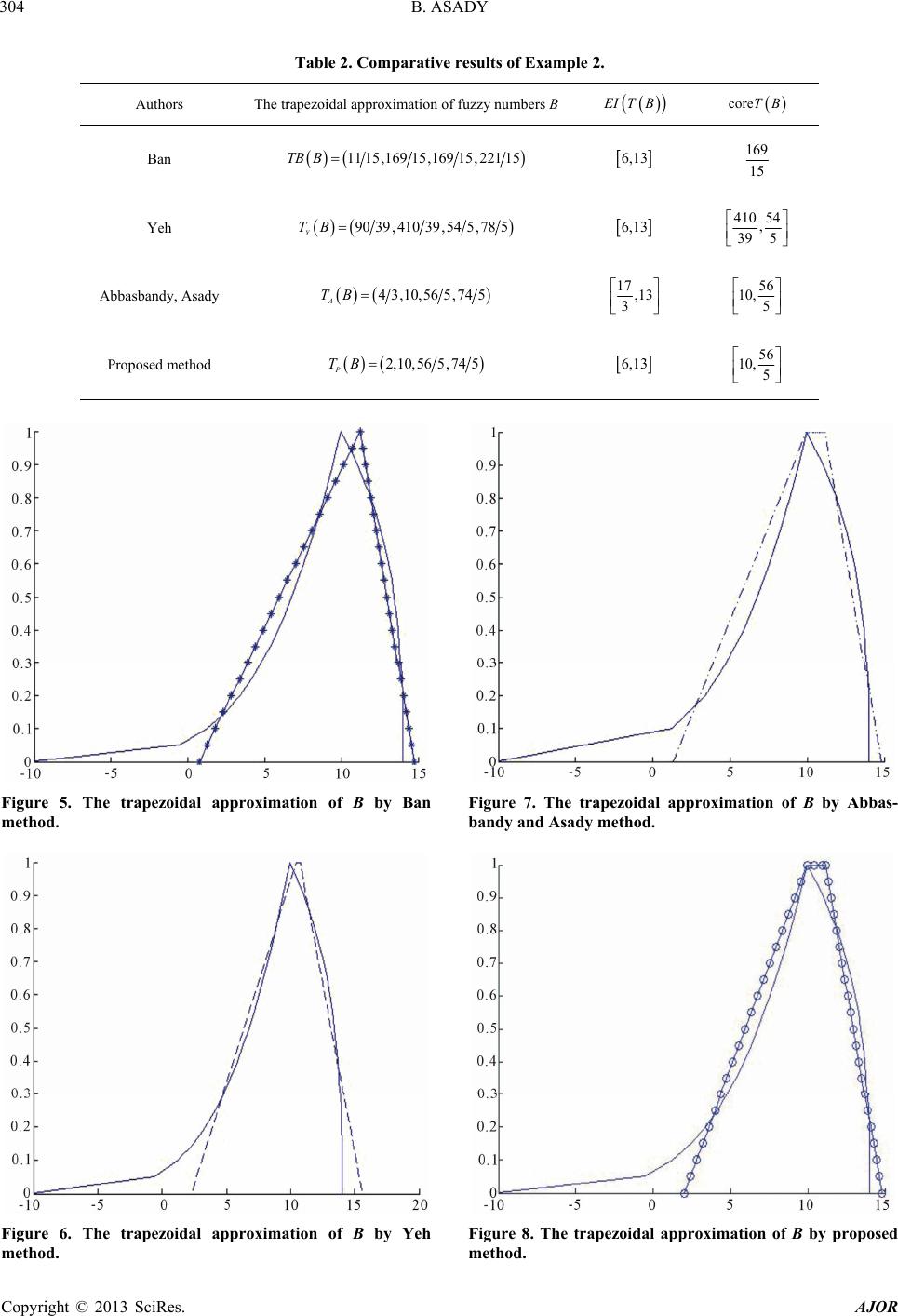 B. ASADY 304 Table 2. Comparative results of Example 2. coreTB EI proximation of fuzzy numbers B TB The trapezoidal apAuthors 169 15 6,13 15 11 15,16915,16915,221TB B Ban 410 54 , 39 5 6,13 5 90 39,410 39,54 5,78 Y TB Yeh 17 ,13 3 56 10, 5 3,10,565,745 A Abbasbandy, Asady 4TB 56 10, 5 6,13 2,10,565,745 P Proposed method TB of B by BaFigure 5. The trapezoidal approximation n Figure 7. The trapezoidal approximation of B by Abbas- bandy and Asady method. method. of B by Ye method. Figure 6. The trapezoidal approximation h Figure 8. The trapezoidal approximation of B by proposed method. Copyright © 2013 SciRes. AJOR  B. ASADY 305 Case 4) are satisfied, Theorem 1 is applicable. 1, 2, 3, 4k. 4. Conclusion In this paper, we have been suggested an interesting ap- proach to trapezoidal approximation of general fuzzy numbers. The proposed method leads to the trapezoidal fuzzy number which is the best one with respect to a tain measure of distance between fuzzy numbers , We obtain kk tb, cer- , uv . REFERENCES [1] Ming Ma, A. Kandel and M. Friedman, “A New Ap- proach for defuzzification,” Fuzzy Sets and Systems 111, No. 3, 2000, pp. 351-356. , Vol. doi:10.1016/S0165-0114(98)00176-6 [2] S. Abbasbandy and M. Amirfakhrian, “The Nearest Ap- ric Form,” athematics and Computation, Vol. 172, No. 1, 3doi:10.1016/j.amc.2005.02.019 proximation of a Fuzzy Quantity in Paramet Applied M 2006, pp. 624-62. and B. Asady, “The Nearest Trapezoidal of a Fuzzy Quantity,” Applied Mathemat- [3] S. Abbasbandy Fuzzy Number ics and Computation, Vol. 156, No. 2, 2004, pp. 381-386. [4] L. Coroianu, “Best Lipschitz Constant of the Trapezoidal Approximation Operator Preserving the Expected Inter- val,” Fuzzy Sets and Systems, Vol. 165, No. 1, 2011, pp. 81-97. doi:10.1016/j.fss.2010.10.004 [5] A. I. Ban, “On the Nearest Parametric Approximation of Fuzzy Number—Revisited,” Fuzzy Sets and Systems, Vol 166, No. 21, 200 doi:10.1016/j. . 9, pp. 3027-3047. fss.2009.05.001 [6] A. I. Ban, “Triangular and Parametric Approximations of a Fuzzy Number—Inadvertences and Corrections,” Fuzzy Sets and Systems, Vol. 160, No. 1, 2009, pp. 3048-3058. doi:10.1016/j.fss.2009.04.003 [7] A. I. Ban, “Approximation of Fuzzy Numbers by Trape- zoidal Fuzzy Numbers Preserving the Expected Interval,” Fuzzy Sets and Systems, Vol. 159, No. 11, 2008, pp. 1327- 1344. doi:10.1016/j.fss.2007.09.008 [8] A. I. Ban, L. Coroianu and P. Grzegorzewski, “Trapezoi- dal Approximation and Aggregation,” Fuzzy Sets and Systems, Vol. 177, No. 1, 2011, pp. 45-59. doi:10.1016/j.fss.2011.02.016 [9] P. Grzegorzewski, “Nearest Interval Approximation of a Fuzzy Number,” Fuzzy Sets and Systems, Vol. 130, No. 3, 2002, pp. 321-330. doi:10.1016/S0165-0114(02)00098-2 [10] P. Grzegorzewski, “Trapezoidal Approximations of Fuzzy Numbers Preserving the Expected Interval—Algorithms and Properties,” Fuzzy Sets and Systems, Vol. 159, No. 11, 2008, pp. 1354-1364. doi:10.1016/j.fss.2007.12.001 , Springer, Berlin, 2010, [11] P. Grzegorzewski, “Algorithms for Trapezoidal Approxi- mations of Fuzzy Numbers Preserving the Expected In- terval, In: B. Bouchon-Meunier, L. Magdalena, M. Ojeda- Aciego, J.-L. Verdegay, R. R. Yager, Eds., Foundations of Reasoning under Uncertainty pp. 85-98. doi:10.1007/978-3-642-10728-3_5 [12] P. Grzegorzewski and E. Mrówka, “Trapezoidal Approxi- mations of Fuzzy Numbers,” Fuzzy Sets and Systems, Vol. 153, No. 1, 2005, pp. 115-135. doi:10.1016/j.fss.2004.02.015 [13] P. Grzegorzewski and E. Mrówka, “Trapezoidal Approxi- mations of Fuzzy Numbers—Revisited,” Fuzzy Sets and Systems, Vol. 158, No. 7, 2007 , pp. 757-768. doi:10.1016/j.fss.2006.11.015 [14] P. Grzegorzewski and K. Pasternak-Winiarska, “Weighted Trapezoidal Approximations of Fuzzy Numbers,” In: J. P. is- 2009, pp. Carvalho, D. Dubois, U. Kaymak, J. M. C. Sousa (Eds.), Proceedings of the Joint 2009 International Fuzzy Sys- tems Association World Congress and 2009 European Society of Fuzzy Logic and Technology Conference, L bon, 2009, pp. 1531-1534. [15] P. Grzegorzewski and K. Pasternak-Winiarska, “Bi-Sym- metrically Weighted Trapezoidal Approximations of Fuzzy Numbers,” In: Proceedings of 9th International Confer- ence on Intelligent Systems Design and Applications ISDA 2009, Pisa, 30 November-2 December 318-323. doi:10.1109/ISDA.2009.138 [16] R. R. Yager and D. P. Filev, “SLIDE: A Simple Adaptive Defuzzification Method,” IEEE Systems, Vol. 1, No. 1, 1993, pTransactions on Fuzzy p. 69-78. doi:10.1109/TFUZZ.1993.390286 [17] C.-T. Yeh, “A Note on Trapezoidal Approximations of Fuzzy Numbers,” Fuzzy Sets and Systems, Vol 7, 2007, pp. 747-754. . 158, No. 16/j.fss.2006.11.017doi:10.10 [18] C.-T. Yeh, “On Improving Trapezoidal and Triangular Approximations of Fuzzy Numbers,” International Jour- nal of Approximate Reasoning, Vol. 48, No. 1, 2008, pp. 297-313. doi:10.1016/j.ijar.2007.09.004 [19] C.-T. Yeh, “Trapezoidal and Triangular Approximations Preserving the Expected Interval,” Fuzzy Sets and Sys- tems, Vol. 159, No. 11, 2008, pp. 1345-1353. doi:10.1016/j.fss.2007.09.010 [20] C.-T. Yeh, “Weighted Trapezoidal and Triangular Ap- proximations of Fuzzy Numbers,” Fuzzy Sets and Systems, Vol. 160, No. 21, 2009, pp. 3059-3079. doi:10.1016/j.fss.2009.05.008 [21] W. Y. Zeng and H. X. Li, “Weighted Triangular Ap- proximation of Fuzzy Numbers,” International Journal of Approximate Reasoning, Vol. 46, No. 1, 2007, pp. 137- 150. doi:10.1016/j.ijar.2006.11.001 [22] T. Allahviranloo and M. A. Firozja, “Note on ‘Trapezoi- dal Approximation of Fuzzy Numbers’,” Fuzzy Sets and Systems, Vol. 158, No. 7, 2007, pp. 755-756. doi:10.1016/j.fss.2006.10.017 [23] S. Bodjanova, “Median Value and Median Interval of a Fuzzy Number,” Information Sciences, Vol. 172, No. 1-2, 2005, pp. 73-89. doi:10.1016/j.ins.2004.07.018 [24] M. Ma, A. Kandel and M. Friedman, “Correction to ‘A New Approach for Defuzzification’,” Fuzzy Sets and Sys- tems, Vol. 128, No. 1, 2002, pp. 133-134. doi:10.1016/S0165-0114(01)00248-2 [25] D. Dubois and H. Prade, “The Mean Value of a Fuzzy Copyright © 2013 SciRes. AJOR  B. ASADY Copyright © 2013 SciRes. AJOR 306 0028-5 Number,” Fuzzy Sets and Systems, Vol. 24, No. 3, 1987, pp. 279-300. doi:10.1016/0165-0114(87)9 On the Nearest Parametric[26] E. N. Nasibov and S. Peker, “ Approximation of a Fuzzy Number,” Fuzzy Sets and Sys- tems, Vol. 159, No. 11, 2008, pp. 1365-1375. doi:10.1016/j.fss.2007.08.005 [27] Y.-R. Syau, L.-F. Sugianto and E. S. Lee, “A Class of Semicontinuous Fuzzy Mappings,” Applied Mathematics Letters, Vol. 21, No. 8, 2008, pp. 824-827. doi:10.1016/j.aml.2007.09.005 [28] D. P. Filev and R. R. Yager, “A Gen eralized Defuzzifi ca- tion Method via Bad Distribution,” International Journal of Intelligent Systems, Vol. 6, No. 7, 1991, pp. 687-697. doi:10.1002/int.4550060702 [29] R. Goetschel and W. Voxman, “Elementary Fuzzy Cal- culus,” Fuzzy Sets and Systems, Vol. 18, No. 1, 1986, pp. 31-43. doi:10.1016/0165-0114(86)90026-6 [30] D. Dubois and H. Prade, “Operations on Fuzzy Num- bers,” International Journal of Systems Scie No. 6, 1978, pp. 613-626. nce, Vol. 9, doi:10.1080/00207727808941724 [31] S. Heilpern, “The Expected Value of a Fuzzy Number,” Fuzzy Sets and Systems, Vol. 47, No. 1, 1992, pp. 81-86. doi:10.1016/0165-0114(92)90062-9 598. -0 [32] B. Asady and A. Zendehnam, “Ranking of Fuzzy Num- bers by Distance Minimization,” Applied Mathematical Modelling, Vol. 31, No. 11, 2007, pp. 2589-2 [33] S. Abbasbandy and B. Asady, “A Note on ‘A New Ap- proach for Defuzzification’,” Fuzzy Sets a nd Systems, Vol. 128, No. 1, 2002, pp. 131-132. doi:10.1016/S0165-0114(01)00247
|