Journal of Electromagnetic Analysis and Applications, 2013, 5, 120-133
http://dx.doi.org/10.4236/jemaa.2013.53020 Published Online March 2013 (http://www.scirp.org/journal/jemaa)
1
The Onset of Ferromagnetic Convection in a Micropolar
Ferromagnetic Fluid Layer Heated from Below
C. E. Nanjundappa1, I. S. Shivakumara2, K. Srikumar3
1Department of Mathematics, Ambedkar Institute of Technology, Bangalore, India; 2UGC-CAS in Fluid Mechanics, Department of
Mathematics, Bangalore University, Bangalore, India; 3Department of Mathematics, East Point College of Engineering for Women,
Bangalore, India.
Received May 13th, 2012; revised June 20th, 2012; accepted July 10th, 2012
ABSTRACT
The onset of ferromagnetic convection in a micropolar ferromagnetic fluid layer heated from below in the presence of a
uniform applied vertical magnetic field has been investigated. The rigid-isothermal boundaries of the fluid layer are
considered to be either paramagnetic or ferromagnetic and the eigenvalue problem is solved numerically using the
Galerkin method. It is noted that the paramagnetic boundaries with large magnetic susceptibility χ delays the onset of
ferromagnetic convection the most when compared to very low magnetic susceptibility as well as ferromagnetic
boundaries. Increase in the value of magnetic parameter M1 and spin diffusion (couple stress) parameter N3 is to hasten,
while increase in the value of coupling parameter N1 and micropolar heat conduction parameter N5 is to delay the onset
of ferromagnetic convection. Further, increase in the value of M1, N1, N5 and χ as well as decrease in N3 is to diminish
the size of convection cells.
Keywords: Micropolar Ferrofluid; Ferromagnetic Convection; Paramagnetic Boundaries; Rigid Boundaries; Magnetic
Susceptibility
1. Introduction
Ferrofluids or magnetic fluids are commercially manu-
factured colloidal liquids usually formed by suspending
mono domain nanoparticles (their diameter is typically 3
- 10 nm) of magnetite in non-conducting liquids like
heptane, kerosene, water etc. and they are also called mag-
netic nanofluids. These fluids get magnetized in the pre-
sence of an external magnetic field and due to their both
liquid and magnetic properties they have emerged as
reliable materials capable of solving complex engineer-
ing problems. An extensive literature pertaining to this
field and also the important applications of these fluids to
many practical problems can be found in the books by
Rosensweig [1], Berkovsky et al. [2] and Hergt et al. [3].
It is also recognized that these fluids have promising po-
tential for heat transfer applications in electronics, micro
and nanoelectromechanical systems (MEMS and NEMS),
and air-conditioning and ventilation
Several theories were used to describe the motion of
ferrofluids and amongst them the continuum description
of the ferrofluids has been in existence since the work of
Neuringer and Rosensweig [4]. Their theory is called
“quasi-stationary theory”. Based on this theory, several
studies on convective instability in a ferrofluid layer have
been undertaken in the past. Finlayson [5] has studied the
convective instability of a magnetic fluid layer heated
from below in the presence of a uniform vertical mag-
netic field. Gotoh and Yamada [6] have carried out the
same study by assuming the fluid to be confined between
two magnetic pole pieces. Stiles et al. [7] have analyzed
linear and weakly nonlinear thermoconvective instability
in a thin layer of ferrofluid subject to a weak uniform
external magnetic field in the vertical direction. Blen-
nerhassett et al. [8] have analyzed the heat transfer char-
acteristics in a strongly magnetized ferrofluids. The
nonlinear stability analysis for a magnetized ferrofluid
layer heated from below has been performed by Sunil
and Mahajan [9] for the case of stress free boundaries.
Whereas, Nanjundappa and Shivakumara [10] have in-
vestigated the effects of variety of velocity and tempera-
ture boundary conditions on the onset of thermomagnetic
convection in an initially quiescent ferrofluid layer in the
presence of a uniform magnetic field. By using quasista-
tionary theory but treating the ferrofluids as binary mix-
tures, Shliomis [11] and Shliomis and Smorodin [12]
have studied convective instability of magnetized ferro-
fluids by considering the influence of concentration gra-
dients and Soret effects. The latter authors have also pre-

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below 121
dicted oscillatory instability in a certain region of mag-
netic field and the fluid temperature. In a review article,
Odenbach [13] has focused on recent developments in
the field of rheological investigations of ferrofluids and
their importance for the general treatment of ferrofluids.
The development of different kinds of ferrofluids ex-
hibiting significant changes in their microstructure has
outlined the need of new description for ferrofluids. It is
believed that quasi-stationary theory is reasonably valid
for colloidal suspensions of Néel particles in which the
particle magnetic moment m rotates inside the particle
and the particle does not rotate itself and hence no mo-
mentum transfer, from the particle to the fluid, occurs
when the applied magnetic field has a changing direction
or magnitude. On the other hand, for Brownian particle
in which the vector m is locked into the crystal axis of
the particle and rotates along with the particle rotation,
with finite magnetic relaxation time, one has to incorpo-
rate the intrinsic rotation of the particle and there is thus
momentum transfer to the carrier fluid in the form of a
viscous friction. Based on these facts, the equations in-
volving rotational or vortex viscosity and the nonequilib-
rium magnetization equation, involving Brownian re-
laxation time, are used to discuss thermoconvective in-
stability of a ferrofluid in a strong external magnetic field
by Stiles and Kagan [14]. However, more appropriate
equations which allow proper consideration of internal
rotation and vortex viscosity have been considered by
Kaloni and Lou [15] to investigate convective instability
problem in the horizontal layer of a magnetic fluid with
Brownian relaxation mechanism. Recently, Paras Ram
and Kushal Sharma [16] have studied the effect of mag-
netic field-dependent viscosity (MFD) along with poros-
ity on the revolving Axi-symmetric steady ferrofluid
flow with rotating disk.
Since the ferrofluids are colloidal suspensions of nano-
particles, as suggested by Rosensweig [1] in his mono-
graph, it is pertinent to consider the effect of microrota-
tion of the particles in the study. Based on this fact, stud-
ies have been undertaken by treating ferrofluids as mi-
cropolar fluids and the theory of micropolar fluid pro-
posed by Eringen [17] has been used in investigating the
problems. Micropolar fluids have been receiving a great
deal of interest and research focus due to their applica-
tions like solidification of liquid crystals, the extrusion of
polymer fluids, cooling of a metallic plate in a bath col-
loidal suspension solutions and exotic lubricants. In the
uniform magnetic field, the magnetization characteristic
depends on particle spin but does not on fluid velocity:
Hence micropolar ferrofluid stability studies have be-
come an important field of research these days. Although
convective instability problems in a micropolar fluid
layer subject to various effects have been studied exten-
sively, the works pertaining to micropolar ferrofluids is
in much-to-be desired state. Many researchers [18-23]
have been rigorously investigated the Rayleigh-Benard
situation in Eringen’s micropolar non-magnetic fluids.
From all these studies, they mainly found that stationary
convection is the preferred mode for heating from below.
Sharma and Kumar [24] and Sharma and Gupta [25] also
gave a good understanding of thermal convection of mi-
cropolar fluids. Zahn and Greer [26] have considered in-
teresting possibilities in a planar micropolar ferromag-
netic fluid flow with an AC magnetic field. They have
examined a simpler case where the applied magnetic
fields along and transverse to the duct axis are spatially
uniform and varying sinusoidally with time. Abraham
[27] has investigated the problem of Rayleigh-Benard
convection in a micropolar ferromagnetic fluid layer per-
meated by a uniform magnetic field for stress-free boun-
daries. Reena and Rana [28,29] have studied the some
convection problems on micropolar fluids saturating a
porous medium. Recently, Thermal instability problem in
a rotating micropolar ferrofluid has also been considered
by Qin and Kaloni [30] and Sunil et al. [31], and refer-
ences therein.
However, the increased importance of ferrofluids in
many heat transfer applications demand the study of the
onset of ferromagnetic convection in a layer of micropo-
lar ferrofluid for more realistic velocity and magnetic
boundary conditions. The aim of the present paper is,
therefore, to investigate the onset of ferromagnetic con-
vection in a micropolar ferrofluid layer heated from be-
low in the presence of a uniform vertical magnetic field
by considering the bounding surfaces as rigid- isothermal
and which are either paramagnetic or ferromagnetic. The
resulting eigenvalue problem is solved numerically using
the Galerkin technique. The critical thermal Rayleigh
number and associated wave number account for the sta-
bility character.
2. Mathematical Formulation
The physical configuration considered is as shown in
Figure 1. We consider an initially quiescent horizontal
incompressible micropolar ferrofluid layer of character-
istic thickness in the presence of an applied uniform
magnetic field 0
d
H
in the vertical direction with the an-
gular momentum . The lower and the upper bounda-
ries are rigid-isothermal which are either paramagnetic or
ferromagnetic. Let 0 and be the tempera-
tures of the lower and upper rigid boundaries, respec-
tively with
ω
T

10
TT



T
01
being the temperature dif-
ference. A Cartesian co-ordinate system
TT


,,
x
yz is
used with the origin at the bottom of the layer and z-axis
is directed vertically upward. Gravity acts in the negative
z-direction, ˆ
g
k

g where is the unit vector in the
z-direction.
ˆ
k

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below
122
Figure 1. Physical configuration.
In the above equations, is the velocity of
the fluid, the pressure,

,,uvwq
The basic equations governing the motion of an in-
compressible Boussinesq micropolar ferromagnetic fluid
for the above model are as follows [1,6,17,30]:
Continuity equation
0. q (1)
Angular momentum equation
 
 
0
22
rr
p
t

 


 



 
qqq gBH
qω

.
(2)
Internal angular momentum equation
 


00
2
22
.
r
It 



  
 



 
ωqωqωMH
ωω

p

the density,

the shear
kinematic viscosity co-efficient, r

the vortex (rota-
tional) viscosity,


123
,,

ω the angular (average
spin) velocity of colloidal particles along z-axis,
I
the
moment of inertia, 0

the reference density, 0

the
free space magnetic permeability,

 the shear spin
viscosity co-efficient, 1 k the thermal conductivity, T
the temperature,

the thermal expansion co-efficient,

the micropolar heat conduction coefficient, ,VH
the specific heat at constant volume and magnetic field,
the magnetic induction field,
C
B
H
the magnetic field,
H
the magnitude of ,
H
0
H
the constant applied
magnetic field,


00
,
H
T the pyromagnetic
co-efficient, the magnetization,
KMT 
M
M
the magnitude
of , M


0
,
0 0
M
MHT the constant mean value of

(3) magnetization,


H
0, 0
T
MH   
Energy equation

0, 00
,,
2
1.
VH
VH VH
DT D
CT
TDt TD
kT T
 



 
 

 

 


 
MM
t
H
ω
H
the magnetic suscep-
tibility,

the magnetic potential and
2222222
x
yz

    is the Laplacian opera-
tor.
(4)
The basic state is quiescent and is given by

 
2
0
00
222
00 0
2
2
121
b
gz
pz pgz
M
KzK z




 


Equation of state


0
1TT  



0
.


(5)
Maxwell’s equation in the magnetostatic limit


0b
Tz Tz


0 
B
, 0 
H
or

H (6a,b)

00
1
bb
TT 






0.
 BMH

(7)
It is considered that the magnetization is aligned with
the magnetic field and is taken as a function of both
magnetic field and temperature in the form
 
0ˆ
1
b
Kz
zH


k










H

,.

M
HT
H
H M (8)
 
0ˆ
1
b
Kz
zM


k










M (10)
The magnetic equation of state is given by where, Td


 is the temperature gradient and the
subscript b denotes the basic state.

00 .

0
M
MHHKTT    (9)

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below 123
To study the stability of the system, the variables are
perturbed in the form
 

,, ,
,
bb
bb
qppzpTTz
z

   
 
qω
HHHMM M
,T 
(11)
where, , q

,

, , pT

, 
H
and

M are the
perturbed quantities whose magnitude is assumed to be
very small.
Substituting Equation (11) in Equation (6a) and using
Equations (8) and (9) and assuming


0
1
K
zH  
as propounded by Finlayson [6], we obtain (after drop-
ping the primes)

00
00
1, 1
1
,
x
xxyy
zz z
MM
y
M
HHMH
HH
MH HKT

 
 
 
 
 
H
(12)
where

,,
x
yz
H
HH and

,,
x
yz
M
MM are the

,,

x
yz components of the magnetic field and mag-
netization respectively.
Using Equation (11) in Equation (2) and linearizing,
we obtain (after dropping primes)


2
01
1
00 0
2
rr
up u
tx
H
MH z




 







(13)


2
0
2
00 0
2
rr
vp v
ty
H
MH z




 






2

(14)



2
03
3
00 00
2
0
03
2
.
1
rr
wp w
tz
H
M
H
z
KT
KH



 


 




 



gT


(15)
Differentiating Equations (13)-(15) partially with re-
spect to x, y and z respectively and adding, we get

22
00 0
22
0
00
2
(1 )
pMH z
KT
gK
zz




 



 







 
 
 
(16)
Eliminating the pressure term from Equation (15),
using Equation (16) we get
p


22 2
00
2
22
0
03
2
1
rh
hr
wK
tz
K
gT



 



 





 




where, 22222
h
x
y

  is the horizontal Lapla-
cian operator.
Substituting Equation (11) into Equation (3) and lin-
earizing, we obtain (after dropping primes)
22 3
03
22 3r Iw
t
 
 
.



 (18)
As before, substituting Equation (11) into Equation (4)
and linearizing, we obtain (after dropping primes)

2
200
00 100
00 3
1
TK
CkT C
t
TK tz




w






 
















(19)
where, 000,0.
VH b
CC K
 


H
Finally Equations (6),
after using Equation (12), yield (after dropping primes)

2
2
0
2
0
11 0
h
MT
K
Hz z




. 
 
 (20)

The principle of exchange of stability is assumed and
the normal mode expansion of the dependent variables is
taken in the form



 



33
,,,, ,,
exp i
wTW zzzz
lx my
 


(21)
where, and mare the wave numbers in the
l
x
and
directions, respectively.
y
Let us non-dimensionalize the variables by setting

,, ,,
x
yz
xyz ddd
 


,
,DDd
,aad 
d
WW

, d



 ,


2
2
1
Kd





,
3
33
,
d



 2
1
I
I
d
 (22)
where, 0



is the kinematic viscosity and
100
kC



is the thermal diffusivity. Equation (21) is
substituted into Equations (17)-(20) and then Equation
(22) is used to obtain the stability equations in the fol-
lowing form:




2
22 2
11
22
13
11
20
t
NDaWaRMD M
ND a
1

  



(23)


22 22
133
22NDaW NDa



(17)
3
0

 
 (24)




22
253
10Da MWN

 (25)
22
30DaMD

 (26)
where ddDz

is the differential operator,

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below
124
2
a2 m is the horizontal wave number,
4
t
Rgd

   is the thermal Rayleigh number,

2
10 0
1
M
Kg

  is the magnetic number,

2
200 0
10
M
TK C    is the magnetic parameter,
 
300
11MMH

 is the non-linearity of mag-
netization, 1r N

  is the coupling parameter,
2
3
Nd



 is the spin diffusion (couple stress) pa-
rameter and 2
500
NC  d is the micropolar heat
conduction parameter. The typical value of 2
M
for
magnetic fluids with different carrier liquids turns out to
be of the order of and hence its effect is neglected
when compared to unity.
6
10
Equations (23)-(26) are solved using the following
boundary conditions:
i) Both boundaries rigid-isothermal and paramagnetic
3
0,0,0at0WDW z ,1 (27a)


1,at0
1,at1
az
Daz


 

 

.
,1
,
z
(27b)
ii) Both boundaries rigid-isothermal and ferromag-
netic
3
0,0,0,0at0WDW z . (27c)
3. Numerical Solution
Equations (23)-(26) together with the boundary condi-
tions (27a,b) or (27c) constitute an eigenvalue problem
with the thermal Rayleigh number t as the eigenvalue.
For the boundary conditions considered, it is not possible
to obtain the solution to the eigenvalue problem in closed
form and hence it is solved numerically using the Galer-
kin-type weighted residuals method. Accordingly, the va-
riables are written in a series of basis functions as
R
 
 
33
11
11
,
,()
NN
iii i
ii
NN
ii ii
ii
WzAWzCz
zDzzE



 


(28)
where, i
A
, i, i and i are the unknown con-
stants to be determined. The basis functions
C DE


i
Wz,
3i, i and i are generally chosen such
that they satisfy the corresponding boundary conditions
but not the differential equations. Substituting Equation
(28) into Equations (23)-(26), multiplying the resulting
momentum equation by

z



z

z



,
j
Wz angular momentum
equation by 3j temperature equation by

,z


jz
and the magnetic potential equation by


z
j; per-
forming the integration by parts with respect to z between
z = 0 and z = 1 and using the boundary conditions (27a,b)
or (27c), we obtain the following system of 4n linear
homogeneous algebraic equations in the 4n unknowns

i
A
, , and ;
i
Ci Di E1, 2,,:in


ji ijii
C ED 0
ji ijii
CA DFE


0
ji i
E
 (29)
ji i
GA H


0
iji i
C KE
(30)
ji i
IA ji J


0.
i
D
(31)
ji ii
LC j P

 (32)
The coefficients
j
iji
CP

involve the inner products
of the basis functions and are given by

22
1
CN
aD
24
1
2
j i
ji ji
DWDW
WDW aWW

 



ji


2
1
1
j
it
Rji Da MW

 
2
1
j
itji
Ea WDRM


2
13
23
jij i
FNDWDaW


 
ji


2
13 3
2
jijiji
GNDDWa W






133
2
33333
4
jij i
ji ji
HN
ND Da

 






2
1
j
iji
I
MW
2
jijij i
JDDa


 


53
j
ij
KN i
j
ij
LD
i



2
3
21
j
iji
a
PDDaM


ji
 
 (33)
where the inner product is defined as

1
0
d.z 

The above set of homogeneous algebraic equations can
have a non-trivial solution if and only if
00 0.
0
00
jiji jiji
ji ji
ji jiji
ji ji
CDEF
GH
IJ K
LP
 (34)
The eigenvalue has to be extracted from the above
characteristic equation. For this, we select the trial func-
tions as follows:
Case i): Rigid-paramagnetic boundaries




432 2
13 1
2
11
2,
,12
iii
iii i
Wz zzTzzT
zzTzT




 
 
,
i
(35)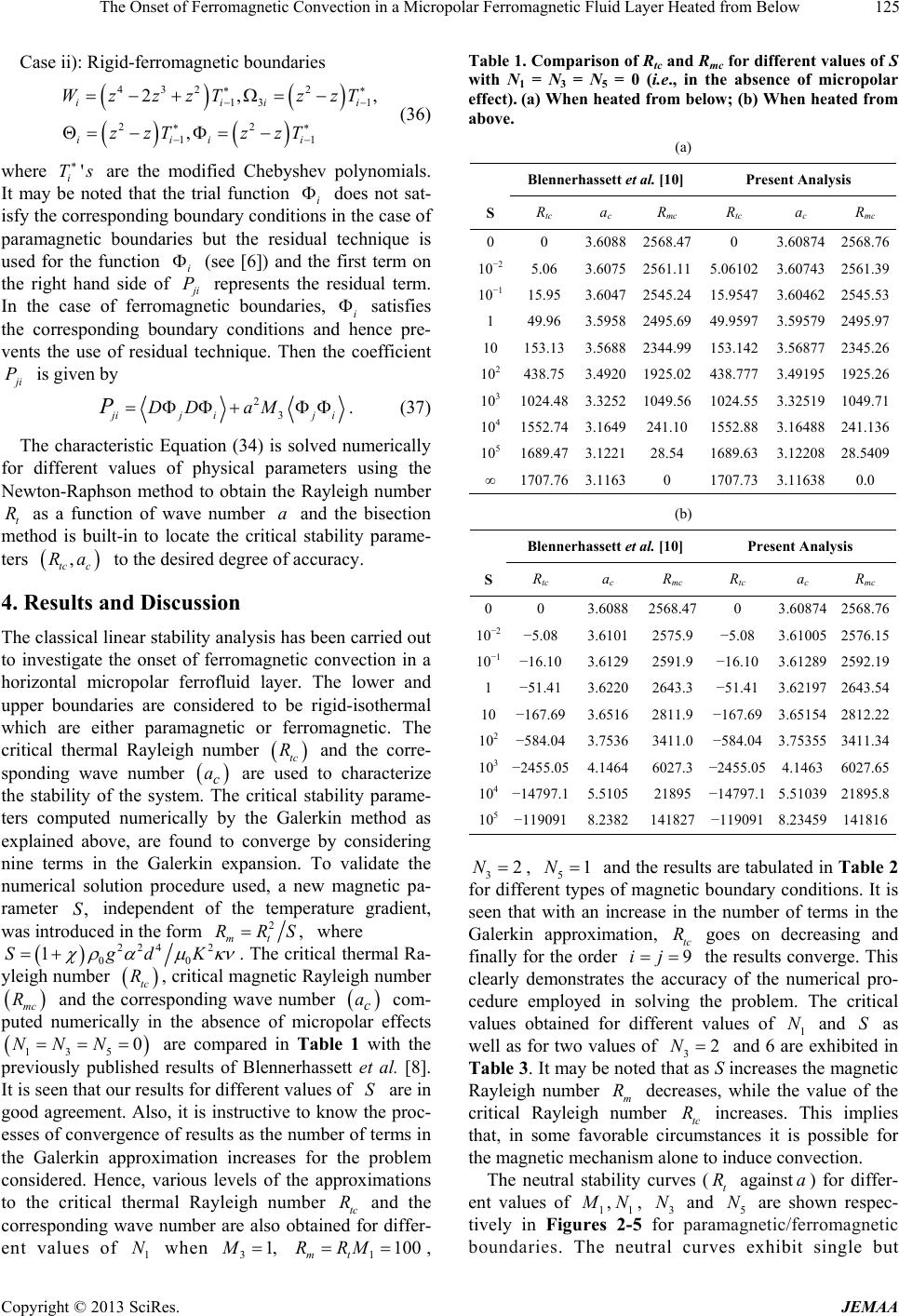

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below 125
Case ii): Rigid-ferromagnetic boundaries

 
432 2
13 1
22
11
2,
,
iii
iiii
Wz zzTzzT
zzT zzT

,
i






 
   (36)
where are the modified Chebyshev polynomials.
It may be noted that the trial function i does not sat-
isfy the corresponding boundary conditions in the case of
paramagnetic boundaries but the residual technique is
used for the function (see [6]) and the first term on
the right hand side of
'
i
Ts


i

j
i represents the residual term.
In the case of ferromagnetic boundaries, i  satisfies
the corresponding boundary conditions and hence pre-
vents the use of residual technique. Then the coefficient
P
j
i
P is given by
2
3
j
iji j
DD aMP 
i


. (37)
The characteristic Equation (34) is solved numerically
for different values of physical parameters using the
Newton-Raphson method to obtain the Rayleigh number
t as a function of wave number and the bisection
method is built-in to locate the critical stability parame-
ters to the desired degree of accuracy.
Ra

,
tc c
Ra
4. Results and Discussion
The classical linear stability analysis has been carried out
to investigate the onset of ferromagnetic convection in a
horizontal micropolar ferrofluid layer. The lower and
upper boundaries are considered to be rigid-isothermal
which are either paramagnetic or ferromagnetic. The
critical thermal Rayleigh number and the corre-
sponding wave number

are used to characterize
the stability of the system. The critical stability parame-
ters computed numerically by the Galerkin method as
explained above, are found to converge by considering
nine terms in the Galerkin expansion. To validate the
numerical solution procedure used, a new magnetic pa-
rameter independent of the temperature gradient,
was introduced in the form

tc
R

c
a
,S
2,
mt
RRS where

224 2
d
00
1SgK

 


  . The critical thermal Ra-
yleigh number , critical magnetic Rayleigh number
and the corresponding wave number com-
puted numerically in the absence of micropolar effects
are compared in Table 1 with the
previously published results of Blennerhassett et al. [8].
It is seen that our results for different values of are in
good agreement. Also, it is instructive to know the proc-
esses of convergence of results as the number of terms in
the Galerkin approximation increases for the problem
considered. Hence, various levels of the approximations
to the critical thermal Rayleigh number tc and the
corresponding wave number are also obtained for differ-
ent values of when ,

tc
R
5
0
1
N

mc
R
NN

c
a
S
R
1mt
M

13
N
31,M100RR
Table 1. Comparison of Rtc and Rmc for different values of S
with N1 = N3 = N5 = 0 (i.e., in the absence of micropolar
effect). (a) When heated from below; (b) When heated from
above.
(a)
Blennerhassett et al. [10] Present Analysis
S Rtc ac Rmc R
tc ac Rmc
0 0 3.60882568.47 0 3.608742568.76
10−25.06 3.60752561.11 5.06102 3.607432561.39
10−115.95 3.60472545.24 15.9547 3.604622545.53
1 49.96 3.59582495.69 49.9597 3.595792495.97
10153.133.56882344.99 153.142 3.568772345.26
102438.753.49201925.02 438.777 3.491951925.26
1031024.483.32521049.56 1024.55 3.325191049.71
1041552.743.1649241.10 1552.88 3.16488241.136
1051689.473.122128.54 1689.63 3.1220828.5409
∞ 1707.763.11630 1707.73 3.116380.0
(b)
Blennerhassett et al. [10] Present Analysis
SRtc ac Rmc Rtc ac Rmc
0 0 3.60882568.47 0 3.608742568.76
10−2−5.08 3.61012575.9 −5.08 3.610052576.15
10−1−16.103.61292591.9 −16.10 3.612892592.19
1 −51.413.62202643.3 −51.41 3.621972643.54
10 −167.693.65162811.9 −167.69 3.651542812.22
102−584.043.75363411.0 −584.04 3.753553411.34
103−2455.054.14646027.3 −2455.05 4.14636027.65
104−14797.15.510521895 −14797.1 5.5103921895.8
105−1190918.2382141827 −119091 8.23459141816
32N

, 51N

and the results are tabulated in Table 2
for different types of magnetic boundary conditions. It is
seen that with an increase in the number of terms in the
Galerkin approximation, goes on decreasing and
finally for the order
tc
R
9ij


N
R
the results converge. This
clearly demonstrates the accuracy of the numerical pro-
cedure employed in solving the problem. The critical
values obtained for different values of 1 and as
well as for two values of 3 and 6 are exhibited in
Table 3. It may be noted that as S increases the magnetic
Rayleigh number m decreases, while the value of the
critical Rayleigh number tc increases. This implies
that, in some favorable circumstances it is possible for
the magnetic mechanism alone to induce convection.
N S
2
R
The neutral stability curves (t againsta) for differ-
ent values of 1
R
M
,1, 3 and 5 are shown respec-
tively in Figures 2-5 for paramagnetic/ferromagnetic
boundaries. The neutral curves exhibit single but
N NN

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below
126
Table 2. Critical values of tc
R
and for different values of when
c
a N13 1,M

100,
m
RN32 and : (a) Para-
magnetic boundaries when
N51
18

; (b) Paramagnetic boundari e s when 0


; (c) Ferromagnetic boundaries.
(a)
i = j = 1 i = j = 3 i = j = 5 i = j = 8 i = j = 9
N1
Rtc ac Rtc ac Rtc ac Rtc ac Rtc ac
0 1692.812 3.14012 1658.586 3.147841658.084 3.147921658.083 3.14792 1658.083 3.14792
0.2 2529.982 3.11900 2495.969 3.131952495.065 3.132042495.064 3.13205 2495.064 3.13205
0.4 3821.487 3.08148 3813.226 3.103183811.682 3.103353811.681 3.10336 3811.681 3.10336
0.6 6049.422 3.00816 6166.736 3.043656164.059 3.043976164.060 3.04397 6164.060 3.04397
0.8 10707.379 2.84549 11477.222 2.8972911472.3092.89794 11472.3172.89794 11472.317 2.89794
(b)
i = j = 1 i = j = 3 i = j = 5 i = j = 8 i = j = 9
N1
Rtc ac Rtc ac Rtc ac Rtc ac Rtc ac
0 1673.024 3.12985 1644.147 3.13635 1643.612 3.13648 1643.611 3.13649 1643.611 3.13649
0.2 2510.090 3.11210 2481.449 3.12425 2480.512 3.12438 2480.511 3.12439 2480.511 3.12439
0.4 3801.401 3.07695 3798.544 3.09814 3796.967 3.09833 3796.966 3.09834 3796.966 3.09834
0.6 6028.949 3.00539 6151.699 3.04056 6148.990 3.04090 6148.991 3.04090 6148.991 3.04090
0.8 10686.048 2.84409 11461.278 2.89572 11456.336 2.89637 11456.344 2.89637 11456.344 2.89637
(c)
1ij 3ij 5ij

 8ij

 9ij
N1
Rtc ac Rtc ac Rtc ac Rtc ac Rtc ac
0 1649.975 3.11652 1628.295 3.12105 1627.728 3.12124 1627.727 3.12124 1627.727 3.12124
0.2 2486.932 3.10307 2465.523 3.11397 2464.554 3.11414 2464.553 3.11415 2464.553 3.11415
0.4 3778.005 3.07093 3782.424 3.09135 3780.815 3.09157 3780.815 3.09157 3780.815 3.09157
0.6 6005.043 3.00158 6135.118 3.03633 6132.378 3.03668 6132.380 3.03668 6132.380 3.03668
0.8 10660.918 2.84198 11443.449 2.89346 11438.477 2.89411 11438.485 2.89411 11438.485 2.89411
Table 3. Critical values of tc
R
and mc
R
for different values of with
N1M31

and .
N51
S = 10−2 S = 102
N3 N1
Rtc ac Rmc Rtc ac Rmc
0 5.06079 3.60743 2561.15669 438.754 3.49195 1925.05399
0.2 5.53993 3.60708 3069.08746 486.25 3.50052 2364.39091
0.4 5.97264 3.60614 3567.24704 529.19448 3.50662 2800.46800
0.6 6.36872 3.60496 4056.06846 568.53897 3.51117 3232.36568
2
0.8 6.73495 3.60373 4535.95975 604.94257 3.51473 3659.55514
0 5.06079 3.60743 2561.15669 438.754 3.49195 1925.05453
0.2 5.54297 3.60738 3072.44943 486.554 3.50085 2367.34421
0.4 5.98366 3.60709 3580.41825 530.297 3.50763 2812.15115
0.6 6.39148 3.60665 4085.10372 570.816 3.51299 3258.31489
6
0.8 6.77241 3.60614 4586.54893 608.691 3.51732 3705.04294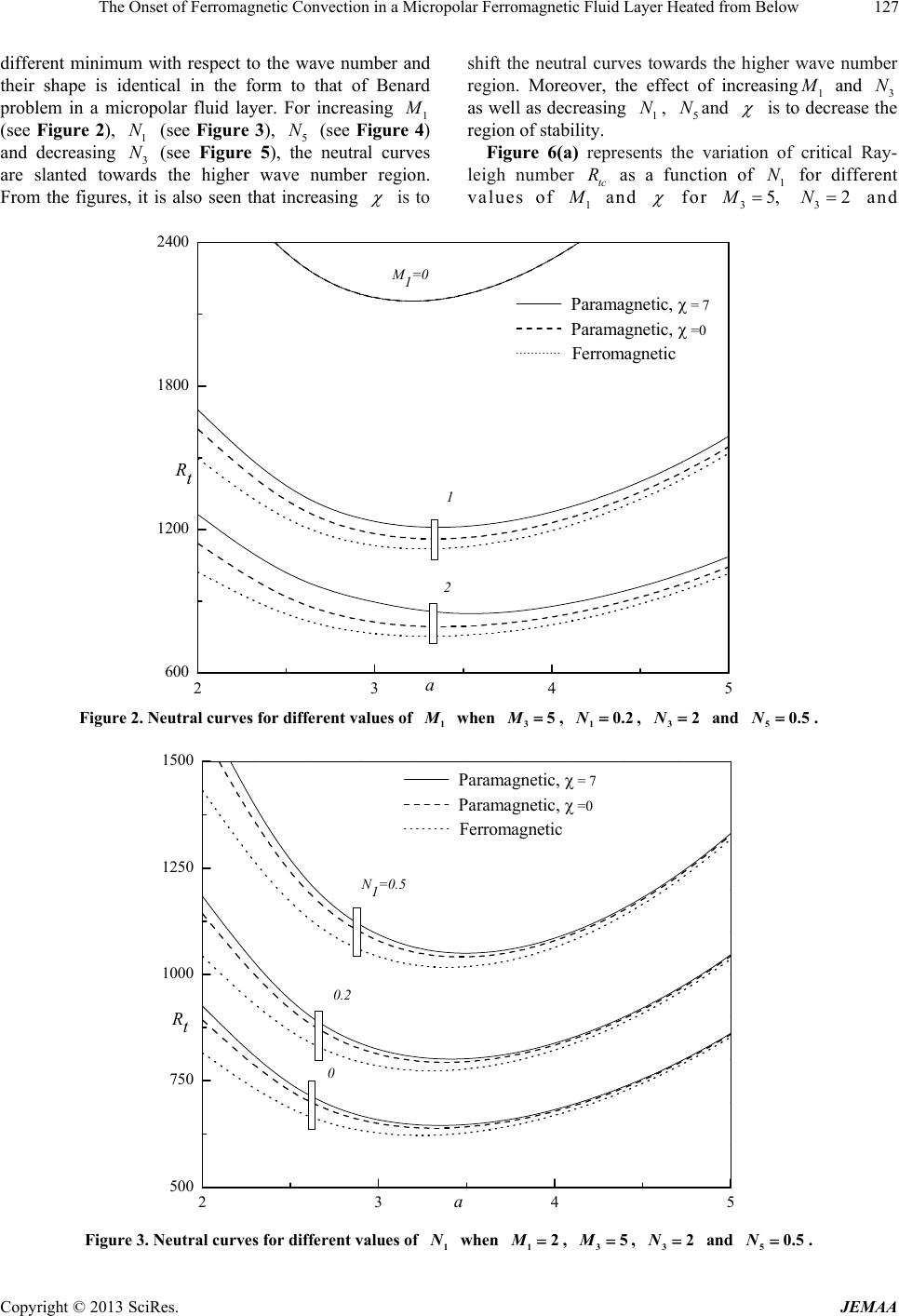

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below 127
different minimum with respect to the wave number and
their shape is identical in the form to that of Benard
problem in a micropolar fluid layer. For increasing 1
M
(see Figure 2), (see Figure 3), 5 (see Figure 4)
and decreasing 3 (see Figure 5), the neutral curves
are slanted towards the higher wave number region.
From the figures, it is also seen that increasing
1
N
N
N

is to
shift the neutral curves towards the higher wave number
region. Moreover, the effect of increasing1
M
and 3
as well as decreasing , and
N
1
N5 N

is to decrease the
region of stability.
Figure 6(a) represents the variation of critical Ray-
leigh number tc as a function of for different
values of
R
1
1
N
M
and

for
35,M3
N2

and
2345
600
1200
1800
2
400
a
Paramagnetic,  = 7
Paramagnetic,  =0
Ferromagnetic
Rt
M1=0
1
2
Figure 2. Neutral curves for different values of when M1M35

, 10.2N

, and .
32N50.5N
2345
500
750
1000
1250
1500 Paramagnetic,  = 7
Paramagnetic,  =0
Ferromagnetic
Rt
N1=0.5
0.2
0
a
Figure 3. Neutral curves for different values of when N11 2M

, 35M

, 32N

and .
50.5N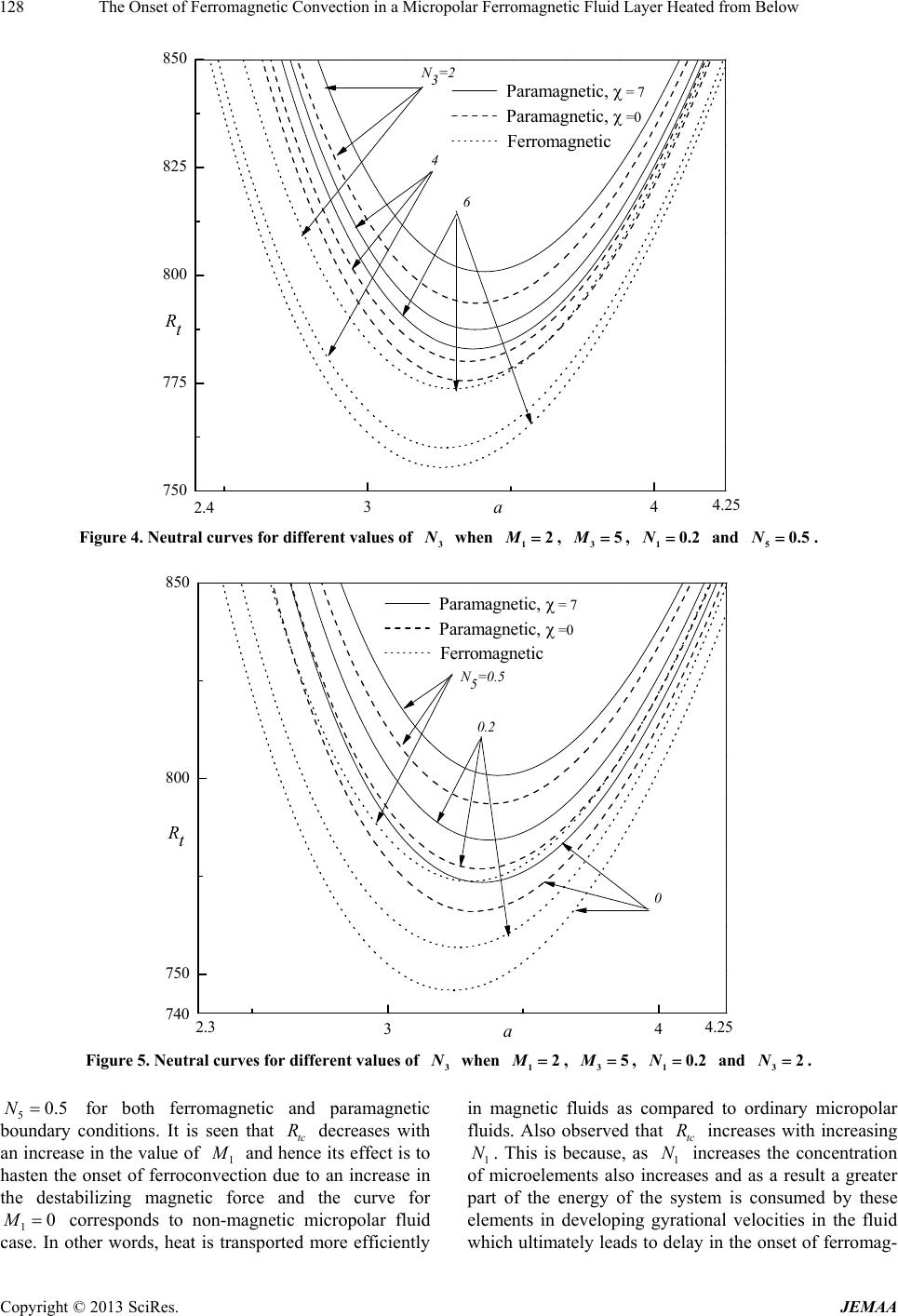

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below
128
34
750
775
800
825
850
4.25
4
6
N3=2
Rt
Paramagnetic,  = 7
Paramagnetic,  =0
Ferromagnetic
a 2.4
Figure 4. Neutral curves for different values of when N31 2M

, 35M

, and .
10.2N50.5N
34
750
800
850
4.252.3
740
0
0.2
N5=0.5
Paramagnetic,  = 7
Paramagnetic,  =0
Ferromagnetic
Rt
a
Figure 5. Neutral curves for different values of when N31 2M

, 35M

, 10.2N

and .
32N
5 for both ferromagnetic and paramagnetic
boundary conditions. It is seen that tc decreases with
an increase in the value of 1
0.5N
R
M
and hence its effect is to
hasten the onset of ferroconvection due to an increase in
the destabilizing magnetic force and the curve for
1 corresponds to non-magnetic micropolar fluid
case. In other words, heat is transported more efficiently
in magnetic fluids as compared to ordinary micropolar
fluids. Also observed that tc increases with increasing
1. This is because, as 1 increases the concentration
of microelements also increases and as a result a greater
part of the energy of the system is consumed by these
elements in developing gyrational velocities in the fluid
which ultimately leads to delay in the onset of ferromag-
0M
R
NN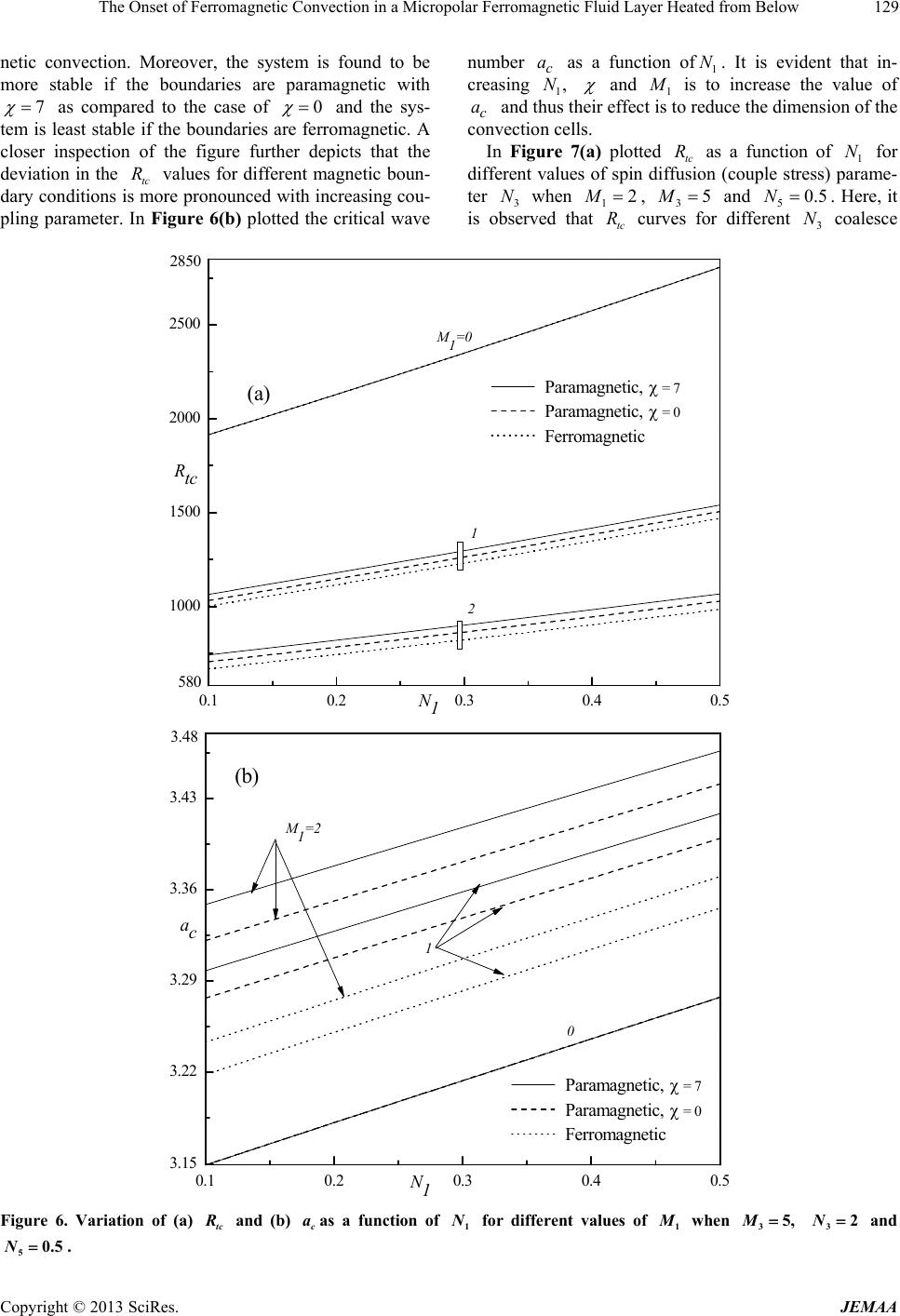

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below 129
netic convection. Moreover, the system is found to be
more stable if the boundaries are paramagnetic with
7

 as compared to the case of 0

 and the sys-
tem is least stable if the boundaries are ferromagnetic. A
closer inspection of the figure further depicts that the
deviation in the tc values for different magnetic boun-
dary conditions is more pronounced with increasing cou-
pling parameter. In Figure 6(b) plotted the critical wave
number as a function of1. It is evident that in-
creasing 1
R
c
a
N
N
,

and 1
M
is to increase the value of
c and thus their effect is to reduce the dimension of the
convection cells.
a
In Figure 7(a) plotted tc as a function of 1 for
different values of spin diffusion (couple stress) parame-
ter 3 when 1
R N
N2M

, 3 and 5. Here, it
is observed that curves for different coalesce
5
0.5
M0.5N
3
N
tc
R
0.1.2 0.
1000
1500
2000
2500
03 0.4
Paramagnetic, = 7
Paramagnetic, = 0
Ferromagnetic
Rtc
N1
2850
(a)
2
1
M1=0
580
0.1 0.2 0.3 0.4 0.5
3.15
3.22
3.29
3.36
3.43
M1=2
1
3.48
0
ac
N1
(b)
Paramagnetic, = 7
Paramagnetic, = 0
Ferromagnetic
Figure 6. Variation of (a) tc
R
and (b) as a function of for different values of when
c
a N1M13 5,M32N

and
.
50.5N

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below
130
when 1 The impact of 3 on the stability char-
acteristics of the system is noticeable clearly with in-
creasing 1 and then it is seen that the critical Rayleigh
number decreases with increasing indicating the spin
diffusion (couple stress) parameter 3 has a destabiliz-
ing effect on the system. This may be attributed to the fact
that as 3 increases, the couple stress of the fluid in-
creases, which leads to a decrease in microrotation and
hence the system becomes more unstable. Figure 7(b)
illustrates that increase in 1 and decrease in 3 for
non-zero values of 1 is to increase c a and hence
their effect is to decrease the size of convection cells.
0.N
N
N
N
3
N
N
N N
N
The variation of critical thermal Rayleigh number
as a function of 1 for different values of 5 for
1
tc
R
NN
2M

, 35M

and 32N

is shown in Figure 8(a).
It is observed that increasing micropolar heat conduction
parameter always has a stabilizing effect for nonzero
values of 1 When 5 increases, the heat induced into
microelements of the fluid is also increased, thus decreas-
ing the heat transfer from the bottom to the top. This de-
crease in heat transfer is responsible for delaying the onset
of ferromagnetic convection. Figure 8(b) illustrates that
increase in 1 and 5 is to increase c and hence
their effect is to decrease the size of convection cells.
5
N
.N
N
tc
R
N
N a
Figure 9 shows the locus of the critical thermal Ray-
leigh number and the critical magnetic Rayleigh
0.1 0.2 0.3 0.4 0.5
700
800
900
1000
1100
6
4
N3=2
650
Rtc
N1
Paramagnetic, = 7
Paramagnetic, = 0
Ferromagnetic
(a)
0.1 0.2 0.3 0.4 0.5
3.24
3.30
3.36
3.42
3.47
6
4
N3=2
Paramagnetic, = 7
Paramagnetic, = 0
Ferromagnetic
ac
N1
(b)
3.22
Figure 7. Variation of (a) tc
R
and (b) as a function of for different values of when
c
a N1N312,M35M

and
.
50.5N

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below 131
0.1 0.2 0.3 0.4 0.5
700
800
900
1000
Paramagnetic, = 7
Paramagnetic, = 0
Ferromagnetic
1050
0
N5=0.5
670
Rtc
(a)
N1
0.1 0.2 0.3 0.4 0.5
3.24
3.30
3.36
3.42
0
3.47
3.20
N5=0.5
ac
(b)
N1
Paramagnetic, = 7
Paramagnetic, = 0
Ferromagnetic
Figure 8. Variation of (a) tc
R
and (b) as a function of for different values of for ,
c
a N1N5M12M35

and
.
32N
mc for 313
and 5 R5, 0.2,2MN N 0.5N

. In
the figure, the regions above and below the curves, corre-
spond, respectively, to unstable and stable ones. It is ob-
served that there is a strong coupling between the critical
thermal Rayleigh and the magnetic Rayleigh numbers
such that an increase in the one decreases the other. Thus,
when the buoyancy force is predominant, the magnetic
force becomes negligible and vice-versa. The stability
curves are slightly convex and in the absence of buoyancy
forces , the instability sets in at higher values of

0
tc R
mc indicating the system is more stable when the mag-
netic forces alone are present. The stability region in-
creases with increasing
R

and also for paramagnetic
boundaries when compared to ferromagnetic boundaries.
5. Conclusions
The linear stability theory is used to investigate the onset
of ferromagnetic convection in a micropolar ferromag-
netic fluid layer hated from below in the presence of a

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below
132
06001200 1800 2400
0
500
1000
1500
2000
2750
Paramagnetic,  = 7
Paramagnetic,  =0
........ Ferromagnetic
Rtc
Rmc
2150
Figure 9. Locus of tc
R
and mc
R
for 35,M

10.2,N32N

and .
50.5N
uniform applied vertical magnetic field for more realistic
rigid boundary conditions which are considered to be
either paramagnetic or ferromagnetic. The resulting ei-
genvalue problem is solved numerically by employing
the Galerkin method.
From the foregoing study, the following conclusions
may be drawn:
i) The neutral stability curves for various values of
physical parameters exhibit that the onset of ferromag-
netic convection retains its unimodal shape with one dis-
tinct minimum which defines the critical thermal Ray-
leigh number and the corresponding wave number.
ii) The system is more stabilizing against the ferro-
magnetic convection if the boundaries are paramagnetic
with high magnetic susceptibility and least stable if the
boundaries are ferromagnetic. It is observed that


00
rigid-ferromagnetic
and and
and
tc ctc c
tc c
Ra Ra
Ra
 

.
iii) The effect of increasing the value of magnetic
number 1
M
is to hasten the onset of ferromagnetic
convection.
iv) The effect of increasing the value of coupling pa-
rameter 1 and micropolar heat conduction parameter
5 is to delay, while increasing the spin diffusion (cou-
ple stress) parameter is to hasten the onset of fer-
romagnetic convection.
N
N
3
N
v) The effect of increasing 1, 5, NN

and 1
M
as
well as decrease in is to increase the critical wave
number.
3
N
vi) The magnetic and buoyancy forces are comple-
mentary with each other and the system is more stabiliz-
ing when the magnetic forces alone are present.
6. Acknowledgements
The work reported in this paper was supported the Man-
agement (Panchajanya Vidya Peetha Welfare Trust) and
Principal of Dr. Ambedkar Institute of Technology and
East Point College of Engineering for Women, Banga-
lore for the encouragement.
REFERENCES
[1] R. E. Rosensweig, “Ferrohydrodynamics,” Cambridge Uni-
versity Press, London, 1985.
[2] B. M. Berkovsky, V. F. Medvedev and M. S. Krakov,
“Magnetic Fluids, Engineering Applications,” Oxford Uni-
versity Press, Oxford, 1993.
[3] R. Hergt, W. Andrä, C. G. Ambly, I. Hilger, U. Richter
and H. G. Schmidt, “Physical Limitations of Hypothermia
Using Magnetite Fine Particles,” IEEE Transictions of
Magnetics, Vol. 34, No. 5, 1998, pp. 3745-3754.
doi:10.1109/20.718537
[4] J. L. Neuringer and R. E. Rosensweig, “Magnetic Fluids,”
Physics of Fluids, Vol. 7, No. 12, 1964, pp. 1927-1937.
doi:10.1063/1.1711103
[5] B. A. Finlayson, “Convective Instability of Ferromagnetic
Fluids,” Journal of Fluid Mechanics, Vol. 40, No. 4, 1970,
pp. 753-767. doi:10.1017/S0022112070000423
[6] K. Gotoh and M. Yamada, “Thermal Convection in a Ho-
rizontal Layer of Magnetic Fluids,” Journal of Physics,
Society of Japan, Vol. 51, 1982, pp. 3042-3048.
doi:10.1143/JPSJ.51.3042

The Onset of Ferromagnetic Convection in a Micropolar Ferromagnetic Fluid Layer Heated from Below 133
[7] P. J. Stiles, F. Lin and P. J. Blennerhassett, “Heat Trans-
fer through Weakly Magnetized Ferrofluids,” Journal of
Colloidal and Interface Science, Vol. 151, No. 1, 1992,
pp. 95-101. doi:10.1016/0021-9797(92)90240-M
[8] P. J. Blennerhassett, F. Lin and P. J. Stiles, “Heat Trans-
fer through Strongly Magnetized Ferrofluids,” Proceed-
ing of Royal Society A: A Mathematical, Physical and En-
gineering Sciences, Vol. 433, 1991, pp. 165-177.
[9] Sunil and A. Mahjan, “A Nonlinear Stability Analysis for
Magnetized Ferrofluid Heated from Below,” Proceeding
of Royal Society of London. A Mathematical, Physical
and Engineering Sciences, Vol. 464, No. 2089, 2008, pp.
83-98. doi:10.1098/rspa.2007.1906
[10] C. E. Nanjundappa and I. S. Shivakumara, “Effect of
Velocity and Temperature Boundary Conditions on Con-
vective Instability in a Ferrofluid Layer,” ASME Journal
of Heat Transfer, Vol. 130, 2008, Article ID: 104502.
[11] M. I. Shliomis, “Convective Instability of Magnetized
Ferrofluids: Influence of Magneto-Phoresis and Soret Ef-
fect,” Thermal Non-Equilibrium Phenomena: Fluid Mix-
tures, Vol. 584, 2002, pp. 355-371.
[12] M. I. Shliomis and B. L. Smorodin, “Convective Instabil-
ity of Magnetized Ferrofluids,” Journal of Magnetism and
Magnetic Materials, Vol. 252, 2002, pp. 197-202.
doi:10.1016/S0304-8853(02)00712-6
[13] S. Odenbach, “Recent Progress in Magnetic Fluid Re-
search,” Journal of Physics: Condensed Matter, Vol. 16,
2004, pp. 1135-1150. doi:10.1088/0953-8984/16/32/R02
[14] P. J. Stiles and M. Kagan, “Thermoconvective Instability
of a Ferrofluid in a Strong Magnetic Field,” Journal Col-
loidal and Interface Science, Vol. 134, 1990, pp. 435-
448.
[15] P. N. Kaloni and J. X. Lou, “Convective Instability of
Magnetic Fluids under Alternating Magnetic Fields,” Phy-
sical Review E, Vol. 71, 2004, Article ID: 066311.
[16] P. Ram and K. Sharma, “Revolving Ferrofluid Flow un-
der the Influence of MFD Viscosity and Porosity with
Rotating Disk,” Journal of Electromagnetic Analysis and
Applications, Vol. 3, 2011, pp. 378-386.
doi:10.4236/jemaa.2011.39060
[17] A. C. Eringen, “Simple Microfluids,” International Jour-
nal of Engineering Sciences, Vol. 2, No. 2, 1964, pp. 205-
217. doi:10.1016/0020-7225(64)90005-9
[18] G. Lebon and C. Perez-Garcia, “Convective Instability of
a Micropolar Fluid Layer by the Method of Energy,” In-
ternational Journal of Engineering Sciences, Vol. 19,
1981, pp. 1321-1329.
[19] L. E. Payne and B. Straughan, “Critical Rayleigh Num-
bers for Oscillatory and Non-Linear Convection in an Iso-
tropic Thermomicropolar Fluid,” International Journal of
Engineering Sciences, Vol. 27, No. 7, 1989, pp. 827-836.
doi:10.1016/0020-7225(89)90048-7
[20] P. G. Siddheshwar and S. Pranesh, “Effect of a Non-Uni-
form Basic Temperature Gradient on Rayleigh-Benard
Convection in a micropolar Fluid,” International Journal
of Engineering Sciences, Vol. 36, No. 11, 1998, pp. 1183-
1196. doi:10.1016/S0020-7225(98)00015-9
[21] R. Idris, H. Othman and I. Hashim, “On Effect of Non-
Uniform Basic Temperature Gradient on Bénard-Maran-
goni Convection in Micropolar Fluid,” International Com-
munications in Heat and Mass Transfer, Vol. 36, No. 3,
2009, pp. 255-258.
doi:10.1016/j.icheatmasstransfer.2008.11.009
[22] M. N. Mahmud, Z. Mustafa and I. Hashim, “Effects of
Control on the Onset of Bénard-Marangoni Convection in
a Micropolar Fluid,” International Communications in
Heat and Mass Transfer, Vol. 37, No. 9, 2010, pp. 1335-
1339. doi:10.1016/j.icheatmasstransfer.2010.08.013
[23] S. Pranesh and R. V. Kiran, “Study of Rayleigh-Bénard
Magneto Convection in a Micropolar Fluid with Max-
well-Cattaneo Law,” Applied Mathematics, Vol. 1, 2010,
pp. 470-480. doi:10.4236/am.2010.16062
[24] R. C. Sharma and P. Kumar, “On Micropolar Fluids Heated
from Below in Hydromagnetics,” Journal of Non-Equi-
librium Thermodynamics, Vol. 20, No. 2, 1995, pp. 150-
159. doi:10.1515/jnet.1995.20.2.150
[25] R. C. Sharma and U. Gupta, “Thermal Convection in Mi-
cropolar Fluids in Porous Medium,” International Jour-
nal of Engineering Sciences, Vol. 33, No. 11, 1995, pp.
1887-1892. doi:10.1016/0020-7225(95)00047-2
[26] M. Zahn and D. R. Greer, “Ferrohydrodynamics Pumping
in Spatially Uniform Sinusoidally Time Varying Magne-
tic Fields,” Journal of Magnetism and Magnetic Materi-
als, Vol. 149, No. 1-2, 1995, pp. 165-173.
doi:10.1016/0304-8853(95)00363-0
[27] A. Abraham, “Rayleigh-Benard Convection in a Micro-
polar Magnetic Fluids,” International Journal of Engi-
neering Sciences, Vol. 40, 2002, pp. 449-460.
[28] Reena and U. S. Rana, “Thermal Convection of Rotating
Micropolar Fluid in Hydromagnetics Saturating a Porous
Media,” International Journal of Engineering. Transac-
tions A: Basics, Vol. 21, No. 4, 2008, pp. 375-396.
[29] Reena and U. S. Rana, “Effect of Dust Particles on a Layer
of Micropolar Ferromagnetic Fluid Heated from Below
Saturating a Porous Medium,” Applied Mathematics and
Computation, Vol. 215, No. 7, 2009, pp. 2591-2607.
doi:10.1016/j.amc.2009.08.063
[30] Y. Qin and P. N. Kaloni, “A Thermal Instability Problem
in a Rotating Micropolar Fluid,” International Journal of
Engineering Sciences, Vol. 30, No. 9, 1992, pp. 1117-
1126. doi:10.1016/0020-7225(92)90061-K
[31] Sunil, P. Chand, P. K. Bharti and A. Mahajan, “Thermal
Convection a Micropolar Ferrofluid in the Presence of
Rotation,” Journal of Magnetism and Magnetic Materials,
Vol. 320, No. 3-4, 2008, pp. 316-324.
doi:10.1016/j.jmmm. 2007.06.006