J. Biomedical Science and Engineering, 2013, 6, 298-307 JBiSE
http://dx.doi.org/10.4236/jbise.2013.63038 Published Online March 2013 (http://www.scirp.org/journal/jbise/)
Segmentation and texture analysis with multimodel
inference for the automatic detection of exudates in early
diabetic retinopathy
Jack Lee, Benny Zee*, Qing Li
Division of Biostatistics, JC School of Public Health and Primary Care, The Chinese University of Hong Kong, Hong Kong, China
Received 10 January 2013; revised 15 February 2013; accepted 2 March 2013
ABSTRACT
Diabet ic retinopathy (DR) is an eye disease caused by
the increase of insulin in blood and may cause blind-
ness if not treated at an early stage. Exudates are the
primary sign of DR. Currently there is no fully auto-
mated method to detect exudates in the literature and
it would be useful in large scale screening if fully
automatic method is available. In this paper we devel-
oped a novel method to detect exudates that based on
interactions between texture analysis and segmen-
tation with mathematical morphological technique by
using multimodel inference. The texture analysis in-
volves three components: they are statistical texture
analysis, high order spectra analysis, and fractal
analysis. The performance of the proposed method is
assessed by the sensitivity, specificity and accuracy
using the public data DIARETDB1. Our results show
that the sensitivity, specificity and accuracy are
95.7%, 97.6% and 98.7% (SE = 0.01), respectively. It
is shown that the proposed method can be run auto-
matically and also improve the accuracy of exudates
detection significantly over most of the previous me-
thods.
Keywords: Texture Analysis; Multimodel Inference;
Morphological Technique; Exudates; Diabetic
Retinopathy
1. INTRODUCTION
Diabetic retinopathy is a severe and common eye disease
which can be regarded as a manifestation of diabetes on
the retina. It is a major public health problem and
diabetic-related eye diseases are the commonest cause of
vision defects and blindness in the world. The appea-
rance of microaneurysms, hemorrhages and exudates
represent to certain extent the degree of severity of the
disease. Exudates are lipid leaks from blood vessels of
abnormal retinas and are one of the most prevalent le-
sions at the early stages of DR [1]. From visual in-
spection, exudates appear to be yellowish or white color
with varying sizes, shape and locations. Automatic exu-
dates detection can assist ophthalmologists in the pre-
vention and allowing the disease to be treated more
efficiently.
Many techniques have been employed to perform
exudates detection. A complete comparative analysis of
the most recent techniques is made on [2]. For these
techniques, contextual information was used with Com-
puter-aided detection systems. The context is based on
the spatial relation with surrounding anatomical land-
marks and similar lesions [3]. Fuzzy C-means clustering
was incorporated with spatial neighbourhood information
[4]. Mathematical morphologic methods have been used
[5,6]. Neural Networks and Support-vector machines
were used in [7]. Split-and-merge techniques, where re-
gion candidates are detected using a combination of
coarse and fine segmentation were used in [8]. An ap-
proach based on Fisher’s linear discriminant analysis
making use of color information was introduced in [9].
Naïve-Bayes and Support Vector Machines classifiers
were employed in [10]. M. U. Akram et al. [11] proposed
a technique that uses filter banks to extract the candidate
regions for possible exudates. It also applied a Bayesian
classifier as a combination of Gaussian functions to de-
tect exudate and non-exudates regions. Among these
techniques, as mentioned in [7], some of methods may
incorrectly detect artifacts as exudates especially those
appear to be like exudates, or only limit to work well in
LUV color space with even illumination image, i.e., the
accuracy is low for the case of uneven illumination
image. Others may produce either high misclassified por-
tion for images that do not contain exudates (low speci-
ficity), or fails to detect faint exudates (low sensitivity).
In order to improve the performance of exudates
detection, we developed a method that based on the
interactions between texture analysis and segmentation
using morphological reconstruction. The texture analysis
*Corresponding author.

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 299
mainly applies on the extracted vessels and enhanced
gray level images. It is used for complementing the
limitation of exudates segmentation with mathematical
morphology approach.
2. MATERIALS AND METHODS
The proposed method is designed to detect exudates
from retinal images under an automatic platform. It
mainly includes four main stages: First, a color retinal
image is given as the input and is preprocessed by local
contrast enhancement and non-uniform background cor-
rection. i.e., the color image is converted to the green
component and is preprocessed to normalize and smooth
the image and then locate the optic disc (OD) (Section
2.1.2). In the second stage, we eliminate the OD and
carry out the exudates detection using mathematical
morphology approach (Section 2.2.1). The segmentation
of exudates is obtained in pixels and their features such
as status of exudates(s), minimal and maximum values
corresponding to the aspect ratios, eccentricity, area in
pixels representing the size of exudates and the ratio of
circularity are also obtained. These features are used to
filter out some spurious exudates candidates. We denoted
this set of features by Ie. The third stage is to generate
another set of features that come from texture analysis
and denoted it by It (Section 2.2.2). In the final stage, we
combined all of the above features to search for signifi-
cant factors that highly associated with exudates (Section
2.2.3). At this stage, dimension reduction and model se-
lection with multi-inference statistical techniques are
applied. Besides, a validation of classifying Exudates/
Non-exudates is given by using both logistic regression
and Multi-layer neural network. The proposed block dia-
gram for exudates detection is given in Appendix (Fig-
ure A1).
2.1. Preprocessing and Optic Disc Localization
The purpose of preprocessing and contrast enhancement
is to remove any false artifacts that occur during retinal
image acquisition process.
2.1.1. Preprocessing and Contrast Enhancement
Since differences in luminosity, contrast, and brightness
among different retinal images contribute to the diffi-
culty to extract useful retinal features to distinguish
exudates from other bright features in the images, shade
correction and noise removal are crucial tasks to pre-
pare the images before processing. To correct uneven
illumination of images, a morphological top-hat ope-
rator with disk-shaped structuring element and fixed
radius of 25 pixels was applied to the green component
of the color image. In general, morphological top-hat
operator can remove background noise efficiently,
which is defined as following.


o
THGGG B 

(1)
where,
G = original image,
B = structuring element
(G◦B) = opening operation to G by B.
To reduce noise, a 3 × 3 (estimated by experimenting)
adaptive median filter is applied to the shade corrected
image. Its purpose is mainly for the removing impulse
noise, smoothing of other noise and reducing distortion,
like excessive thinning or thickening of object boundary.
The detailed algorithm is given in [12,13].
For the further contrast enhancement, we applied a re-
lated operation called “edge enhancement” or “unsharp
masking” (UM) to make edges in an image slightly
sharper and crisper. The idea of unsharp masking is to
subtract a scaled “unsharp” version of the image from the
original. In practice, we can achieve this effect by sub-
tracting a scaled blurred image from the original [14].
Figure 1 illustrates the preprocessing results.
2.1.2. Optic Disc Localization
The optic disc is a component on the fundus photo from
where optic nerves and blood vessels originated. Loca-
lization of an optic disc is a vital step in the automated
retinal image screening system. The optic disc is ex-
emplified by the largest high contrast among circular
shape areas. Referring to the work of U. S. Akram et al.
[15], to locate and segment the OD, we can use image
averaging and Hough transformation, respectively. The
detailed work for OD segmentation is given in [15].
After the OD is localized, we will remove it after we
have segmented all exudates candidates involving the
OD.
2.2. Candidate Region Detection and Features
Extraction
After the preprocessing for contrast enhancement, we
would remove potential artifacts and enhance the con-
trast of bright lesions by suppressing and smoothing out
all dark and red components present in the retinal image.
We then find candidate regions of exudates and gene-
(a) (b) (c)
Figure 1. Result of preprocessing methods. (a) Original image;
(b) Filtered image; (c) Enhanced image.

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 300
rate all possible features related to exudates.
2.2.1. Segmentation and Feature Set 1 Formulation
Exudates detection using mathematical morphology, FCM,
a combination of FCM and mathematical morphology,
naïve Bayesian classifier, SVMs and some other tech-
niques have been used. In this paper we apply the ma-
thematical morphology with three different levels of ada-
pted threshold values (applying 90% confidence interval
for Otsu-approach threshold [16]).
We apply the morphological method to eliminate high
contrast vessels by using a closing operator before a local
variation operator. To ensure that all the neighboring pix-
els are included in the candidate region, a dilation opera-
tor is also applied. Finally the exudates detection areas
are obtained by applying a threshold operator to the dif-
ference between the original image and the reconstructed
image. Finally, the OD is eliminated from the above can-
didate region(s) image. An example can be seen in Fig-
ure 2 (An illustration of the OD localization and removal
of OD region is also given in this figure).
The candidate exudates region detection phase extracts
as many possible regions as it possibly can for potential
exudates. The threshold value is deliberately kept low so
that not a single pixel containing exudates will be missed
at this stage. We removed the spurious pixels or non-
exudates regions in classification stage.
Exudates appear as bright yellow spots with variable
size and shape but they have strong and sharp edges. The
candidate exudates region extraction stage gives all
possible regions that can be considered as potential exu-
dates. If a retinal image I contains k potential candidate
regions, then the set representation for an image I is Ie’ =
{v1, v
2, …, v k}. For an automated system to distinguish
between exudates and non-exudates regions, a feature set
is formed for each candidate region. Each object or can-
didate exudates region is considered as a sample for
classification and represented by a feature vector con-
taining m features; i.e., for a sample candidate region v
from an image I, the feature vector is v = {x1, x2, x3, …,
xm}. The description of features we used for classifi-
cation of exudates and non-exudates regions are as
follows:
(a) (b) (c)
Figure 2. Result of exudates detected methods. (a) Candidates;
(b) OD localized; (c) Exudates.
1) Area (x1) is the number of pixels in candidate exu-
dates region and is defined as sum of all pixels
in candidate region vi.
1
i
v
A
2) Compactness (x2) is the measure of shape defined as


24πACp, where p and A are the perimeter and
area of candidate region, respectively.
3) “Eccentricity” (x3)— Scalar that specifies the eccen-
tricity of the ellipse that has the same second-moments as
the region. The eccentricity is the ratio of the distance
between the foci of the ellipse and its major axis length.
The value is between 0 and 1. (0 and 1 are degenerate
cases; an ellipse whose eccentricity is 0 is actually a
circle, while an ellipse whose eccentricity is 1 is a line
segment.)
4) Aspect ratio (x4) of an image describes the pro-
portional relationship between its width and its height (in
rectangle shape).
For our study, we formulated two subgroup features
sets: features set 1 is generated from exudates segmenta-
tion and features set 2 is generated from texture analysis
(see next section). Here in features set 1 we have four
features from the segmented candidate exudates region
and defined as:




;1,,; 1,,
min;1,,;1, 2,, 4
max;1,,;;1, 2,, 4
ij
minj ij
maxj ij
vxi Kj m
vxiKj
vxiKj
 
 
 



(2)
K is varied but m (=4) is fixed. Therefore, there are 9
variables from the segmented exudates candidates for
each threshold of every image (8 from above features
and one from the status of exudates). Overall, we gene-
rated a total of 27 features from three thresholds of each
image, i.e., Ie = {e1, e2, …, e27}.
Other information of features will be obtained from
the approach of texture analysis. Such approach will
cover information of features from exudates candidate
region such as Mean hue, Mean saturation, Mean value;
Mean gradient magnitude for edge pixels and related
entropy values [11]. Moreover, some complement infor-
mation will also be generated from whole image instead
of extracted exudates candidate regions since we are not
guarantee (surely) to extract all exudates candidates
without missing.
Other features (features set 2) from the texture analy-
sis for each image are given from both segmented blood
vessels and enhanced gray level image.
2.2.2. Texture Analysis and Feature Set 2
Formulation
There are three approaches from texture analysis: 1) Sta-
tistical texture analysis involving gray level co-occur-
rence matrix (GLCM) and run-length matrix; 2) HOS
analysis; and 3) fractal analysis to generate some useful

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 301
features from the enhanced image. There are a total of 75
features generated initially. It includes 50 features com-
ing from HOS analysis and 17 features generated from
statistical texture analysis, and 8 features (three from
mono-spectrum and five from multi-spectrum) from
fractal analysis. The following are discussion of methods
from the approach of statistical texture analysis, HOS
and fractal analysis.
1) Statistical based texture analysis for image pro-
cessing
All related texture features from the statistical-based
texture analysis were generated from each retinal image
that derived from gray level co-occurrence matrix (GLCM)
and run-length matrix [17-25].
For an image of size M × N, the gray level co-occur-
rence matrix (GLCM) is defined as in [19]
 



  
,,,,
,, ,
d
Cijpqpxqy:
I
pqiI pxqyj




,
(3)
where (p,q), and

,,pxqyMNd xy 
 denotes the cardinality of a set. Given a gray level i in
an image, the probability that the gray level of a pixel at
a

,

x
y distance away is j is
 
,,
dd d
PijC ijC ij,
(4)
From each co-occurrence matrix we computed the
following features:
Energy:

2
Angular Second Moment,
d
ij
Pij
Entropy:
 
,ln ,
d
ij
EnPi jPi j

Contrast:
 
2
,,
d
ij
ijP ij

Homogeneity:
 
2
1,
1, d ij
Pij
ij

Energy measures the textural uniformity of the image,
i.e., the repetition of pixel pairs. Basically it is just the
measurement of the denseness or order in the image.
Entropy measures disorder or randomness of the image
and it is an indication of the complexity within an image,
thus, more complex images have higher entropy values.
Contrast is a measure of the local variations present (or
differences in the GLCM) in the image, so higher con-
trast values indicate large local variations. Homogeneity
(also called an inverse difference moment) is inversely
proportional to contrast at constant energy. Similarly at
constant contrast, homogeneity is inversely proportional
to energy (Park, Lawrence, Windham, Chen, & Chao,
2002). It measures how close the distribution of elements
in the GLCM is to the diagonal of GLCM.
Other measurements such as Moments 1 - 4 are
defined as:
 
,
g
g
ij
mijP

,
d
ij
(5)
where g is the integer power exponent that defines the
moment order. Moments are the statistical expectation of
certain power functions of a random variable and are
characterized as follows [19]: moment 1 is the mean
which is the average of pixel values in an image [20];
moment 2 is the standard deviation; moment 3 measures
the degree of asymmetry in the distribution; and moment
4 measures the relative peakedness or flatness of a
distribution and is also known as kurtosis [21].
Other similar approach can also be used: having the
GLCM normalized, we can then derive eight second
order statistic features which are also known as haralick
features [22] for each image, which are: contrast, corre-
lation, energy, entropy, homogeneity, dissimilarity, in-
verse difference momentum, maximum probability. In
addition to these features, we also applied correlation,
dissimilarity, inverse difference momentum and maxi-
mum probability, which is different from above men-
tioned features.
The grey level run-length matrix (RLM) is defined as
the numbers of runs with pixels of gray level i and run
length j for a given direction [23]. RLMs was generated
for each sample image segment having directions (0˚, 45˚,
90˚ & 135˚), then the following five statistical features
were derived: short run emphasis, long run emphasis,
gray level non-uniformity, run length non-uniformity and
run percentage. Basically it allows extraction of higher
order statistical texture features. These five measures
related method from run-length matrixes of θ = 0˚, 45˚,
90˚, and 135˚ were also provided in [25].
2) High order spectra analysis (HOS) for image
processing
Higher order spectra (HOS) are known to have the
ability to detect non-linearity and deviations from
Gaussianity. Motivated by these, a set of HOS based
parameters were proposed as features to differentiate the
exudates, and non-exudates. HOS are spectral represen-
tations of higher moments and they are derived from the
averaged Fourier spectrum signal. The bispectrum


12
,Bf f, of a signal is the Fourier transform (FT) of
the third order correlation of the signal. It is given by



 
12121 2
,*BffEXfXf Xff



 (6)
where X(f) is the FT of the signal x(nT), * represents
complex conjugation and E[.] stands for the expectation
operation. It retains Fourier phase information. The fre-
quency f may be normalized by the Nyquist frequency to
be between 0 and 1. The bispectrum, given by Equation
(6), is a complex-valued function of two frequencies. The
bispectrum which is the product of three Fourier coeffi-
cients exhibits symmetry and need only be computed in a
non-redundant region. Assuming that there is no bispec-

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 302
tral aliasing, the bispectrum of a real-valued signal is
uniquely defined with the triangle 0 ≤ f2 ≤ f1 ≤ f1 + f2 ≤
1. This is termed as Ω, the principal domain or the non-
redundant region (See the triangle region in Figure A2 in
Appendix).
Briefly, HOS based and spectral based features are:
Mean of spectral magnitude for HOS [26]:

12
1,
ave
M
Bf f
L
 (7)
where B(f1, f2) is the bispectrum of the signal.
Other features such as Entropy 1, 2 and 3 are defined
as:
Entropy 1:
1log kk
k
Pp
p
where


12
12
,
,
k
Bf f
pBf f

, and
Entropy 2:
2log ii
i
Pq
q
where


2
12
2
12
,
,
i
Bf f
q
Bf f

 for HOS.
Entropy 3:
2log nn
n
Pr
r
where


3
12
3
12
,
,
n
Bf f
r
Bf f

 for HOS.
And the feature of bispectrum phase entropy (EntPh):
 
log
nn
n
EntPh p

 
where

2π1
2π
ππ,0,1,,1
n
n
nnN
NN





 








and
  


12
Ω
1,,
is indicator function
n
pIbff
L
I
n






: Bispectrum phase angle
L: Number of points within the samples
We used each of these bispectral invariant features for
every 18˚ from 0˚ to 180˚. Therefore we obtained total 50
features of HOS. In the next section we will discuss the
model-based methods such as fractal model approach.
The fractal model is useful for modeling certain natural
textures that have a statistical quality of roughness at
different scales, and also for texture analysis and dis-
crimination.
3) Fractal analysis
Fractal model (analysis) may be considered as the
model-based texture analysis. We can classify it into
mono-fractal and multi-fractal. Since the surface com-
plexity is fundamental to several properties and physical
phenomena of a pattern. The diversified complexity of
fractal may be described with the concept of fractal di-
mension [27], which may easily describe the incom-
pleteness or fragmentation of an entirety. Moreover, re-
cent studies show that such surface complexity of image
may be described not only by its fractal dimension but
also its multifractal spectra, which its mathematical
description of a surface can accurately reflect its features,
and can be compatible with the various theoretical
models which are related to surface structures. Thus we
can apply fractal analysis to determine the surface com-
plexity which is measured on the gray scale and by using
multifractal spectra one can obtain more detailed in-
formation than is possible with the fractal dimension
alone. Recently this kind of technique is widely used in
retinal vessels analysis.
Measuring fractal dimension has previously attempted
to quantify small changes to the human retinal vascula-
ture, not immediately apparent by human observation,
and act as an early marker of disease [28-30]. Mono-
fractal analysis is an indicator of vascular change or
disease has achieved limited success as retinal vessels
may have different properties in different regions and
different characteristics can be found depending on the
location or scale of the measurement considered. Greater
success has been reported by considering the retinal
vascular pattern to be geometrical multi-fractal charac-
terized by a hierarchy of exponents rather than a single
fractal dimension [31].
We first applied box-counting algorithm (with Haus-
dorff dimension) approach to calculate fractal dimension
in binary type of image (segmentation of vessels) and
then the Fourier fractal dimension (FFD) approach,
which have been proposed by [28-30]. FFD has been
used to quantify the grayscale images projected on to
3-D fractal surface [31]. The advantage of FFD is that it
computes the fractal dimension of gray scale images, and
eliminates the need for image segmentation [31]. It has
also been found to be relatively insensitive to noise and it
is believed to work effectively with data having low
signal-to-noise ratio [31,32]. We adapted the similar FFD
approach proposed by Azemin M. and et al. [30]. The
parameters related such as slope and intercept are gene-
rated based on this approach. Finally we applied the
multifractal spectra since it can describe the evolution of
the probability distribution of fractal structures [28,
31-33]. Instead of using simple fractals (or monofractals),
multifractals are characterized by a hierarchy of ex-
ponents, rather than a single fractal dimension. In this
paper the box-counting method was used to characterize
multiple spectra [31].

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 303
Based on the above three approaches, the feature set 2
formulated from the texture analysis is given as

12
,,, ;
tn
I

 
where n is the number of features set 2 for each image.
Total features generated from each image are defined as

128 27
,,,,,, ,,
ten nn
IIIff f ff

 

.
Since n is 75 and so we have a total of 102 features
used for classifying the exudates and non-exudates.
2.2.3. Dimension Reduction and Best Model
Searching
Since there are a total of 102 related variables (factors)
for the analysis, but the number of samples is limited
thus we need to reduce the dimension (filtering out some
not-as-useful factors). This will help us find a more
suitable diagnostic model in order to detect exudates
with more efficiency. The following are the two major
steps.
1) Dimension reduction
We first reduce dimension since most of the features
are correlated or redundant in the model. A penalized
logistic regression method (Pelora) [35] was used to
cluster the datasets from the above procedures combining
all 102 parameters (factors). This is a supervised clu-
stering algorithm that has been used with external infor-
mation about response variables for clustering genes in
genetic study. This algorithm is mainly based on penalize
logistic regression analysis and it combines feature selec-
tion, supervision, feature clustering and sample classi-
fication in a single step. We have adapted this method for
features selection generated from retinal images and then
classified the variables (potential factors) obtained. This
approach will preserve the property of the classified
(identified) groups with complex interactions.
2) Model selection with multimodel inference
After the dimensions have been reduced, we applied
the method of automated model selection and model-
averaging that provides a wrapper for GLM and similar
functions, automatically generating all possible models
with the specified response of exudates(s) and explana-
tory variables, and determine the best models with a
defined criterion (e.g. AIC or AICc). The best model is
mainly based on the bias-variance trade-off.
Statistical models are probability density functions,
where we can maximize the likelihood

ˆ,argmax f


  

 


by minimize the Kullback-Lei-
bler distance from the true model to the approximating
model, i.e.,
 
..
ˆ,,
as argmaxKL gf







Here KL distance is one way to measure the distance
between two densities:
   

,,log d
,
gy
K
Lgf gyy
fy
 

g(y) for the discrepancy is weighted by the probability
observing the data y, and


,
g
y
fy

is the ratio that mea-
sures the discrepancy between the two models for data y.
AIC selects the model closest to the true model on
average. Since the true distribution of g is unknown, so
we replace it with the empirical (observed) distribution.
Thus the estimation of KL distance is introduced and a
bias will also be given. To determine the expected value
of this bias, the so called Takeuchi Information Criterion
(TIC) is used. Finally under the assumption of appro-
ximate model correct, we derived AIC and related crite-
ria.
On the other hands, since AIC selects the model
closest to the true model on average (Atypical datasets
have lower influence than typical ones) to deal with the
model selection uncertainty and usual sampling uncer-
tainty. To do this, we bootstrap the data and produce the
distribution of best models. Then apply the smoothed
model weights and finally determine: 1) the value of the
parameter on average (also its variance) for solving the
model selection uncertainty problem; and 2) the standard
error for a given model that follows a ˆ

distribution
(conditional variance of the estimator), this is to deal
with usual sampling uncertainty. Thus we can combine
the above two variances to form the overall variance for
the estimator ˆ

. Such approach reduces the spurious
estimates (false positive) problem, which standard model
selection techniques often encountered (see Freedman’s
paradox).
Because algorithm convergence for the best model is
not guaranteed and the number of models is large when
involving interactions in model, we used a genetic
algorithm (better when the number of models to explore
is prohibitively large). The model AICc values and com-
plexity are obtained for the selection of the best model.
We then applied GLMULTI, an R package for automated
model selection and multi-model inference with GLM
and related functions. The basic idea of this approach is
that from a list of explanatory variables, GLMULTI
builds all possible models involving these variables and,
optionally, included their pairwise interactions (for the
computing of simplicity and easy interpretation reasons
we will not consider higher order interaction in this
paper). Restrictions can be specified for candidate mod-
els, by excluding specific terms, enforcing marginality,
or controlling model complexity. Detailed information is
referred to [36-39].
The model selection (variable selection in multiple re-
gression framework) framework is given in Figure 3.

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 304
Model SelectionInference
Set of Candidate models Best ModelEstimates/Predictions
Figure 3. Multi-model inference approach diagram.
2.2.4. Classification and Validation
Two different classification methods were investigated to
detect exudates. We first applied logistic regression with
ROC to classify and validate the abnormal of DR with
exudates. Then we applied the approach of Multilayer
perception (MLP), a multilayer feed-forward network
which is an important class of NNs that can represent
non-linear functional mapping between a set of input
variables and a set of output variables [40,41]. A MLP
with enough units in a single hidden layer can approxi-
mate any function, provided the activation function of
the neurons satisfies some general constraints [42,43].
From these considerations, we decide to use a MLP with
one hidden layer, for which the optimum number of hid-
den neurons was experimentally determined. As neuron
activation function in the hidden layer, we chose the hy-
perbolic tangent sigmoid function (tan-sigmoid) an anti-
symmetric function in the interval (−1,1). Tan-sigmoid
satisfies the constraints in [42,43]. Moreover, it improves
the learning speed of MLP [40]. In the output layer, we
used the logistic sigmoid activation function, that also
satisfies the aforementioned constraints and whose out-
puts lie in the range (0,1). This choice was motivated by
the fact of interpreting the outputs of the network as pos-
terior probabilities [41].
The problem of training a NN can be formulated in
terms of the minimization of an error function. The
choice of a suitable error function and minimization al-
gorithm can improve the performance of MLP. It has
been demonstrated [41] that a cross-entropy error func-
tion simplifies the optimization process when the logistic
sigmoid activation function is used in the output layer.
Therefore, we considered this function as an appropriate
choice in our study.
Regarding the minimization algorithm, several choices
are available for MLP. We selected the scaled conjugate
gradients algorithm, for which the error function is
guaranteed not to increase during training [41]. Moreover,
it generally shows faster convergence when compared to
gradient descent-based techniques or even conventional
conjugate gradient algorithms [41].
To avoid overfitting and improve generalization, we
can also employ a weight decay regularizer [41]. The re-
gularization parameter, ν, was experimentally settled. If
the output is above 0.5 for some input vector, the pro-
bability of the image region represented by that input
vector of being an EX is greater than that of being a
non-EX. Therefore, the output threshold was set to 0.5.
3. RESULTS AND DISCUSSION
Many experiments have been performed on normal and
abnormal retinal images based on presenting of exudates.
To test and validate our proposed method, the following
89 images from the DIARETDB1 database of resolution
1500 × 1152 with their clinician marked images [44]
were used to validate our method at the pixel level. 47 of
these images contain exudates while the remaining 42
either contain other type of lesions or are normal. We
used this database to measure the accuracy of the pro-
posed method based on its ability to distinguish between
normal and abnormal images. An example of the classi-
fication with MLP is shown in Table 1 (with AUC =
0.98).
The performance of the proposed approach for exu-
dates detection was assessed quantitatively by comparing
the results of extractions with the ophthalmologist’s
ground-truth images. The comparison for the results of
the proposed approach (classified using logistic regres-
sion and MLP in SPSS) and other previous methods are
shown in Table 2. In classification stage, MLP method is
used and a training set was obtained from approximately
70% of whole dataset randomly. The remaining about
30% will be used for testing. The similar procedure was
repeat used in 50 times. The average of measured cor-
rectness obtained as the final results.
4. CONCLUSION
We propose a novel method to automatically detect exu-
dates from retinal images. The method combined both
exudates segmentation and the analysis using statistical
texture features, higher order spectra related features and
fractal analysis related features. For the segmentation
process, we also generate few (four) segmented region
properties including maximum of Eccentricity, minimum
and maximum of aspect ratio, and also the area of exu-
dates in pixels. For the texture analysis, we generated
some multifractal spectrum related features and also
some related interaction. We may consider fitting gener-
alized linear models with L1(lasso) and/or L2(ridge) pe-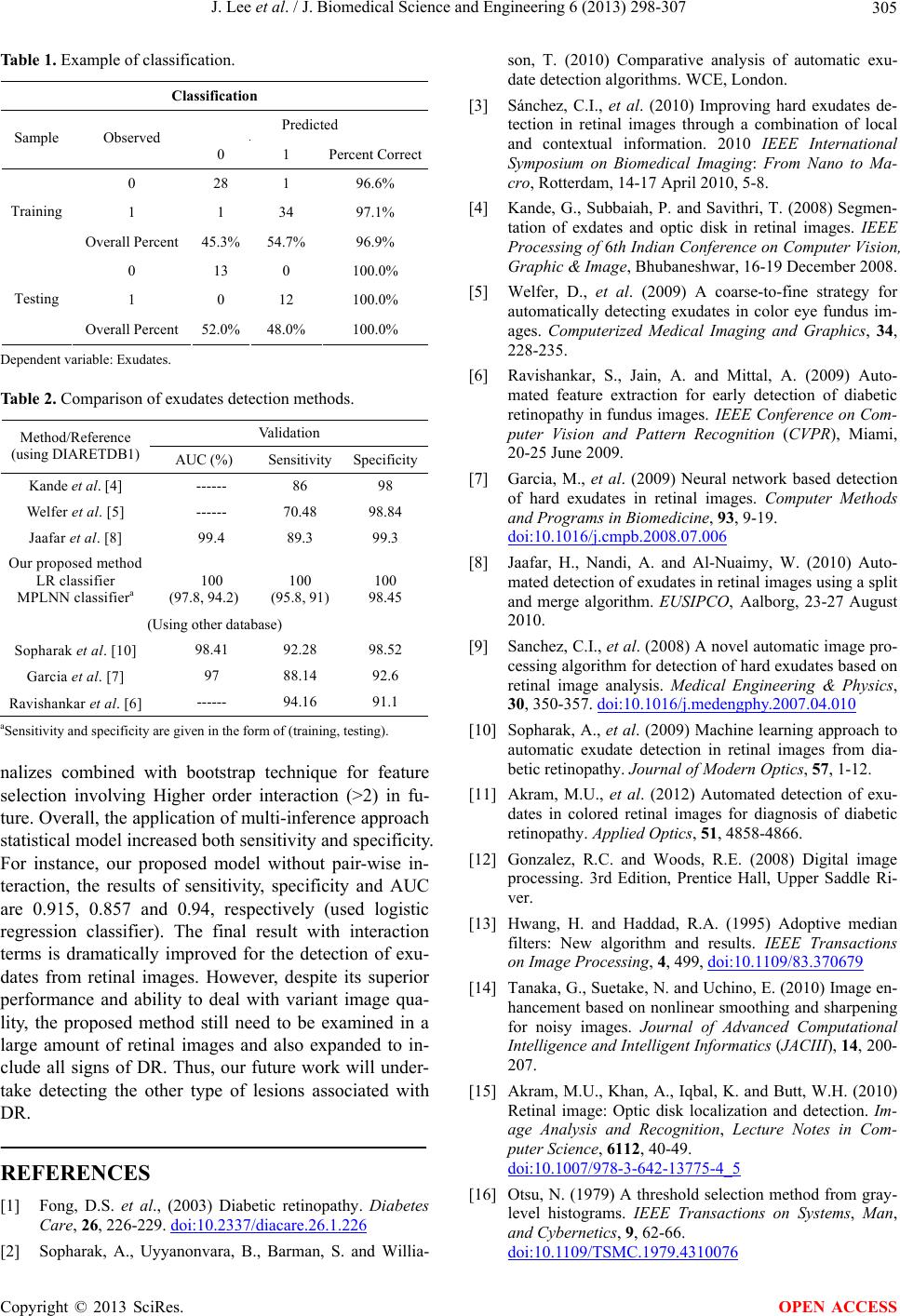

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 305
Table 1. Example of classification.
Classification
Predicted
Sample Observed
0 1 Percent Correct
0 28 1 96.6%
1 1 34 97.1%
Training
Overall Percent 45.3% 54.7% 96.9%
0 13 0 100.0%
1 0 12 100.0%
Testing
Overall Percent 52.0% 48.0% 100.0%
Dependent variable: Exudates.
Table 2. Comparison of exudates detection methods.
Validation
Method/Reference
(using DIARETDB1) AUC (%) Sensitivity Specificity
Kande et al. [4] ------ 86 98
Welfer et al. [5] ------ 70.48 98.84
Jaafar et al. [8] 99.4 89.3 99.3
Our proposed method
LR classifier
MPLNN classifiera
100
(97.8, 94.2)
100
(95.8, 91)
100
98.45
(Using other database)
Sopharak et al. [10] 98.41 92.28 98.52
Garcia et al. [7] 97 88.14 92.6
Ravishankar et al. [6] ------ 94.16 91.1
aSensitivity and specificity are given in the form of (training, testing).
nalizes combined with bootstrap technique for feature
selection involving Higher order interaction (>2) in fu-
ture. Overall, the application of multi-inference approach
statistical model increased both sensitivity and specificity.
For instance, our proposed model without pair-wise in-
teraction, the results of sensitivity, specificity and AUC
are 0.915, 0.857 and 0.94, respectively (used logistic
regression classifier). The final result with interaction
terms is dramatically improved for the detection of exu-
dates from retinal images. However, despite its superior
performance and ability to deal with variant image qua-
lity, the proposed method still need to be examined in a
large amount of retinal images and also expanded to in-
clude all signs of DR. Thus, our future work will under-
take detecting the other type of lesions associated with
DR.
REFERENCES
[1] Fong, D.S. et al., (2003) Diabetic retinopathy. Diabetes
Care, 26, 226-229. doi:10.2337/diacare.26.1.226
[2] Sopharak, A., Uyyanonvara, B., Barman, S. and Willia-
son, T. (2010) Comparative analysis of automatic exu-
date detection algorithms. WCE, London.
[3] Sánchez, C.I., et al. (2010) Improving hard exudates de-
tection in retinal images through a combination of local
and contextual information. 2010 IEEE International
Symposium on Biomedical Imaging: From Nano to Ma-
cro, Rotterdam, 14-17 April 2010, 5-8.
[4] Kande, G., Subbaiah, P. and Savithri, T. (2008) Segmen-
tation of exdates and optic disk in retinal images. IEEE
Processing of 6th Indian Conference on Computer Vision,
Graphic & Image, Bhubaneshwar, 16-19 December 2008.
[5] Welfer, D., et al. (2009) A coarse-to-fine strategy for
automatically detecting exudates in color eye fundus im-
ages. Computerized Medical Imaging and Graphics, 34,
228-235.
[6] Ravishankar, S., Jain, A. and Mittal, A. (2009) Auto-
mated feature extraction for early detection of diabetic
retinopathy in fundus images.IEEE Conference on Com-
puter Vision and Pattern Recognition (CVPR), Miami,
20-25 June 2009.
[7] Garcia, M., et al. (2009) Neural network based detection
of hard exudates in retinal images. Computer Methods
and Programs in Biomedicine, 93, 9-19.
doi:10.1016/j.cmpb.2008.07.006
[8] Jaafar, H., Nandi, A. and Al-Nuaimy, W. (2010) Auto-
mated detection of exudates in retinal images using a split
and merge algorithm. EUSIPCO,Aalborg, 23-27 August
2010.
[9] Sanchez, C.I., et al. (2008) A novel automatic image pro-
cessing algorithm for detection of hard exudates based on
retinal image analysis. Medical Engineering & Physics,
30, 350-357. doi:10.1016/j.medengphy.2007.04.010
[10] Sopharak, A., et al. (2009) Machine learning approach to
automatic exudate detection in retinal images from dia-
betic retinopathy. Journal of Modern Optics, 57, 1-12.
[11] Akram, M.U., et al. (2012) Automated detection of exu-
dates in colored retinal images for diagnosis of diabetic
retinopathy. Applied Optics, 51, 4858-4866.
[12] Gonzalez, R.C. and Woods, R.E. (2008) Digital image
processing. 3rd Edition, Prentice Hall, Upper Saddle Ri-
ver.
[13] Hwang, H. and Haddad, R.A. (1995) Adoptive median
filters: New algorithm and results. IEEE Transactions
on Image Processing, 4, 499, doi:10.1109/83.370679
[14] Tanaka, G., Suetake, N. and Uchino, E. (2010) Image en-
hancement based on nonlinear smoothing and sharpening
for noisy images. Journal of Advanced Computational
Intelligence and Intelligent Informatics (JACIII), 14, 200-
207.
[15] Akram, M.U., Khan, A., Iqbal, K. and Butt, W.H. (2010)
Retinal image: Optic disk localization and detection. Im-
age Analysis and Recognition, Lecture Notes in Com-
puter Science, 6112, 40-49.
doi:10.1007/978-3-642-13775-4_5
[16] Otsu, N. (1979) A threshold selection method from gray-
level histograms. IEEE Transactions on Systems, Man,
and Cybernetics, 9, 62-66.
doi:10.1109/TSMC.1979.4310076

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 306
[17] Tan, J.H., Ng, E.Y.K. and Acharya, U.R. (2009) Study of
normal ocular thermogram using textural parameters. In-
frared Physics & Technology, 53, 120-126.
[18] Bremananth, R., Nithya, B. and Saipriya, R. (2009) Wood
species recognition system using GLCM and correlation.
International Conference on Advances in Recent Tech-
nologies in Communication and Computing (ARTCom’
09), Kottayam, 27-28 October 2009, 615-619.
[19] Bailey, R.R. and Srinath, M.D. (2002) Orthogonal mo-
ment features for use with parametric and non-parametric
classifiers. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 18, 389-399.
[20] Silakari, S., Motwani, M. and Maheshwari, M. (2009)
Color image clustering using block truncation algorithm.
International Journal of Computer Science Issues, 4, 31-
35.
[21] Press, W.H., Flannery, B.P., Teukolsky, S.A. and Vetter-
ling, W.T. (1990) Numerical recipes in C: The art of sci-
entific computing. Cambridge University Press, New York,
1990.
[22] Acharaya, U.R., Ng, E.Y.K., Tan, J.H., Sree, S.V. and Ng,
K.H. (2012) An integrated index for the identification of
diabetic retinopathy stages using texture parameters. Jour-
nal of Medical Systems, 36, 2011-2020.
[23] Tuceryan, M. and Jain, A.K. (1993) Texture analysis. In:
Chen, C.H., Pau, L.F. and Wang, P.S.P., Eds., Handbook
of Pattern Recognition & Computer Vision, World Scien-
tific Pub Co Inc.,Singapore City.
doi:10.1142/9789814343138_0010
[24] Weszka, J.S. and Rosenfield, A. (1976) An application of
texture analysis to material inspection. Pattern Recogni-
tion, 8, 195-200. doi:10.1016/0031-3203(76)90039-X
[25] Galloway, M.M. (1975) Texture classification using gray
level run length. Computer Graphics and Image Process-
ing, 4, 172-179. doi:10.1016/S0146-664X(75)80008-6
[26] Acharya, U.R., Chua, K.C., Ng, E.Y.K., Wei, W. and
Chee, C. (2008) Application of higher order spectra for
the identification of diabetes retinopathy stages. Journal
of Medical Systems, 32, 431-488.
[27] Hubbard, L.D., Brothers, R.J., King, W.N., Clegg, L.X.,
Klein, R., Cooper, L.S., Sharrett, A.R., Davis, M.D. and
Cai, J. (1999) Methods for evaluation of retinal micro-
vascular abnormalities associated with hypertension/
sclerosis in the atherosclerosis risk in communities study.
Ophthalmology, 106, 2269-2280.
doi:10.1016/S0161-6420(99)90525-0
[28] Azemin, M.Z.C., Kumar, D.K., Wong, T.Y., Wang, J.J.,
Kawasaki, R. and Mitchell, P. (2010) Retinal stroke pre-
diction using logistic-based fusion of multiscale fractal
analysis. 2010 IEEE International Conference on Imag-
ing Systems and Techniques (IST), Thessaloniki, 1-2 July
2010, 125-128.
[29] Azemin, M.Z.C., Kumar, D.K., Wong, T.Y., Wang, J.J.,
Kawasaki, R., Mitchell, P. and Arjunan, S.P. (2010) Fu-
sion of multiscale wavelet-based fractal analysis on retina
image for stroke prediction. 2010 Annual International
Conference of the IEEE Engineering in Medicine and Bi-
ology Society (EMBC), Buenos Aires, 31 August 2010-4
September 2010, 4308-4311,
[30] Azemin, M.Z.C., Kumar, D.K., Wong, T.Y., Kawasaki,
R., Mitchell, P. and Wang, J.J. (2011) Robust methodol-
ogy for fractal analysis of the retinal vasculature. IEEE
Transactions on Medical Imaging, 30.
[31] Stosic, T. and Stosic, B.D. (2006) Multifractal analysis of
human retinal vessels. IEEE Transactions on Medical
Imaging, 25, 1101-1107. doi:10.1109/TMI.2006.879316
[32] MacGillivary, T.J., Patton, N., Doubal, F.N., Graham, C.
and Wardlaw, J.M. (2007) Fractal analysis of the retinal
vascular network in fundus images. Proceedings of the
29th Annual International Conference of the IEEE EMBS,
Lyon, 23-26 August 2007
[33] Andjelkovic, J., Zivic, N., Reljin, B., Celebic, V. and Sa-
lom I. (2008) Application of multifractal analysis on me-
dical images. Wseas Transactions on Information Science
and Applications, 5.
[34] Faust, O., Acharya, R., Ng, E.Y.K., Ng, K.H. and Suri,
J.S. (2012) Algorithm for the automated detection of dia-
betic retinopathy using digital fundus images: A review.
Journal of Medical Systems, 36, 145-157.
[35] Marcel, D. and Peter, B. (2003) Supervised gene cluster-
ing with penalized logistic regression. Research Report
No.115, Switzerland, 2003
[36] Anderson, D.R. (2008) Model based inference in the life
sciences. Springer-Verlag, New York.
doi:10.1007/978-0-387-74075-1
[37] Barton, K. (2009) MuMIn: Multi-model inference. R Pac-
kage Version 0.12.2/r18.
http://R-Forge.R-project.org/projects/mumin/
[38] Buckland, S.T., Burnham, K.P. and Augustin, N.H. (1997)
Model selection: An integral part of inference. Biometrics,
53, 603-618. doi:10.2307/2533961
[39] Burnham, K.P. and Anderson, D.R. (2002) Model selec-
tion and multimodel inference. Springer-Verlag, New York.
[40] Haykin, S. (1999) Neural networks: A comprehensive
foundation. Prentice-Hall International, New Jersey.
[41] Bishop, C.M. (2004) Neural networks for pattern recog-
nition. Oxford University Press, New York.
[42] Hornik, K. (1991) Approximation capabilities of multi-
layer feedforward networks. Neural Networks, 4, 251-257.
doi:10.1016/0893-6080(91)90009-T
[43] Huang, G.B., Chen, Y.Q. and Babri, H.A.(2000) Classi-
fication ability of single hidden layer feedforward neural
networks. IEEE Transactions on Neural Networks, 11,
799-801. doi:10.1109/72.846750
[44] DIARETDB1 database (2007).
http://www2.it.lut.fi/project/imageret/diaretdb1/index.htm
l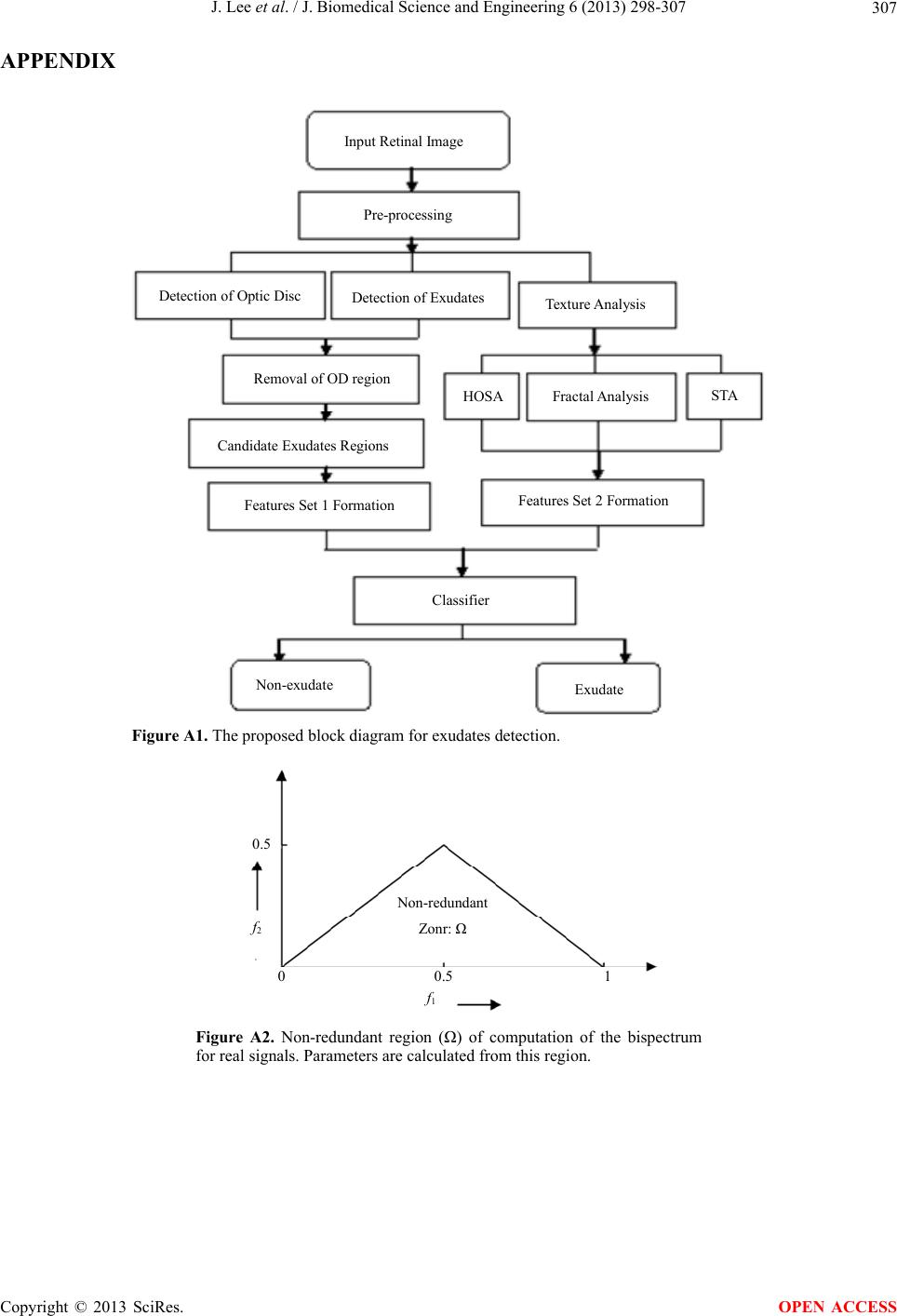

J. Lee et al. / J. Biomedical Science and Engineering 6 (2013) 298-307 307
APPENDIX
Input Retinal Image
Pre-processing
Detection of Optic Disc Detection of ExudatesTexture Analysis
Removal of OD region
Candidate Exudates Regions
Features Set 1 Formation Features Set 2 Formation
HOSA Fractal Analysis STA
Classifier
Non-exudate Exudate
Figure A1. The proposed block diagram for exudates detection.
0.5
f
2
f
1
0 0.5 1
Non-redundant
Zonr: Ω
Figure A2. Non-redundant region (Ω) of computation of the bispectrum
for real signals. Parameters are calculated from this region.