Applied Mathematics, 2010, 1, 312-315
doi:10.4236/am.2010.14041 Published Online October 2010 (http://www.SciRP.org/journal/am)
Some Notes on the Distribution of Mersenne Primes
Sibao Zhang1, Xiaocheng Ma1, Lihang Zhou2
1Department of Mat hem ati c s, Kash g ar Teachers College, Kashgar, China
2Department of Computer Science, Guangdong Technical College of Water Resources and Electric Engineering,
Guangzhou, China
Received July 13, 2010; revised August 19, 2010; accepted August 21, 2010
Abstract
Mersenne primes are a special kind of primes, which are always an important content in number theory. The
study of Mersenne primes becomes one of hot topics of the nowadays science. It has not settled that whether
there exist infinite Mersenne primes. And several of conjectures on the distribution of it provided by scholars.
Starting from the Mersenne primes known about, in this paper we study the distribution of Mersenne primes
and argued against some suppositions by data analyzing.
Keywords: Mersenne Primes, Distribution, Zhou Conjecture, Number Theory
1. Introduction
In 300 B.C , Euclid, famed ancient Greek mathematician
proved that there are infinitude prime numbers by con-
tradiction, and raised that a small amount of prime num-
bers could be expressed in the formulation of 21
p

(p
is a prime number). After that, many famous mathemati-
cians including mathematical masters like Fermat, Des-
cartes, Leibniz, Goldbach, Euler, Gauss all researched
into the prime numbers of this kinds of special formula-
tion. But M. Mersenne, the French mathematician in 17th
century and founder of Institute of France, was the first
one to research into the prime number of 21
p formu-
lation deeply and systematically. These kinds of formu-
lation like 21
p is named as “Mersenne number” and
expressed as Mp to commemorate him. If a Mersenne
number is a prime number, then is named as “Mersenne
prime”. The Mersenne prime seems like very simple, but
the calculation of it is very complex. As the increase of
index p, the calculation increases more complex. It not
only need advanced theory and practiced skills, but ar-
duous calculation is needed to validate whether a
Mersenne number is prime or not. People have only dis-
covered 47 Mersenne primes in the past 2300 years [1].
It should be noted that we have only settled the se-
quence of first 39 primes, while the last 8 primes left.
That is, there is no other prime number p which makes
21
p to be a prime number in the range of 2 ≤ p ≤ 13
466 917. And we still cant assure that whether exists
other prime number p which makes 21
p to be prime
number in the range of 20 996 011 ≤ p ≤ 43 112 609.
Though we have not discovered other prime p which
makes 21
p

to be a prime number by checked the
range at least once, but twice could confirm the seating
arrangement [2].
It is not known whether the set of Mersenne primes is
infinite. But researching on the attribution of Mersenne
Primes is very important for the seeking of new Mersenne
primes and exploring whether exist infinitude Mersenne
primes. From the known Mersenne primes, the distribu-
tion of these special kinds of prime number is either
sparse or dense in the positive integer, so very anoma-
lous. In the long-term exploring, mathematicians have
advanced some kind of suppositions. For example,
mathematicians like Shanks from England, Bertrand
from France, Ramanujan from India, Gilles from Amer-
ica and Brillhart from Germany have all supposed the
distribution of Mersenne primes. The common point of
their supposition is that they all presented as asymptotic
expression.
In 1992, Haizhong Zhou [3], famed Chinese mathe-
matician and linguist advanced the precise formulation of
the Mersenne prime distribution: If 1
22
22
nn
p

 (n =
0, 1, 2, 3,…), then the amount of Mersenne primes is
1
21
n

. The accurate and beautiful expression is made
by him. Zhou conjecture has not been proved or dis-
proved, and becomes a well-known mathematical prob-
lem [4].
Some researchers have raised the suppositions for the
distribution of Mersenne primes. In this article we would

S. B. ZHANG ET AL. 313
argue against the deduction and raise different views by
data analyzing for several suppositions.
2. Questions and View Points
2.1. Questions
In 1995, based on Zhou conjecture, Suwen Chen tried to
make a further discussion on the distribution of Mersenne
primes [5]. In the paper he defined that: Sequence R
consists of primes p which makes 21
p to be prime
and numbers like 2
2k (k = 0, 1, 2, …) in ascending, and
the item No. n marked R(n); P is the sequence consists of
primes p which makes 21
p

primes in ascending,
while the item No. n marked P(n); Q is the sequence
consists of numbers like 2
() 2
n
nQ (n = 0, 1, 2, 3, …).
By analyzing the first 35 items settled by R (n), conjec-
tures proposed like this:
CONJECTURE 1
1) 12
(2)( )2
nn
n
RQ ;
2) 2
21 log()21nnn R;
3) 2
log( )1
lim 2
n
n
n
 
R
Then, raise doubts on item 2). we shall list the related
data as following for convenience.
Attention to this data:
WHEN n = 20 and R(n) = 2 203, GET log2R(n) =
11.10525, n/2 = 10.00000, n/2 + 1 = 11.00000;
WHEN n = 37 and R(n) = 756 839, GET log2R(n) =
19.52963, n/2 = 18.50000, n/2 + 1 = 19.50000;
WHEN n = 41, R(n) = 2 976 221, GET log2R(n) =
21.50505, n/2 = 20.50000, n/2 + 1 = 21.50000;
WHEN n = 43, R(n) = 6 972 593, GET log2R(n) =
22.73326, n/2 = 21.50000, n/2 + 1 = 22.50000;
WHEN n = 44, R(n) = 13 466 917, GET log2R(n) =
23.68292, n/2 = 22.00000, n/2 + 1 = 23.00000
The location of Mersenne primes ignored for they
have not been settled when 20 996 011 ≤ p ≤43 112 609.
The data listed above satisfied the formula log2R(n) >
n/2 + 1, and item 2) in the conjecture follows the formula
log2R(n) < n/2 + 1 which contradicts the result log2R(n) >
n/2 + 1, so it concludes that the formula log2R(n) < n/2 +
1 in conjecture n/2 − 1 < log2R(n) < n/2 + 1 is wrong.
In Chen’s paper, the author presupposed that
3
2
2
n

<
P(n) <
7
2
2
n
, while P(31) ≤ P(n) ≤ P(58) according to
conjecture n/2 − 1 < log2R(n) < n/2 + 1. According to
Chen’s deduction, a great difference occurred on some
numbers. It will be subscribed by the location-settled
Mersenne primes as following.
WHEN R(32) = 756839, 19.5 2 741456, GET 756
839 < 741 456, impossible;
WHEN R(36) = 2976221, 21.5 2 2965821, GET 2
976221 < 2 965 821, impossible;
WHEN R(38) = 6 972 593, 22.5 2 5931642, GET 6
972 593 < 5 931 642, impossible;
2.2. Different Views
Scholars proposed many conjectures on how to confirm
the quantity of Mersenne primes in certain range. In
1980, Lenstra and Pomerance [6] independently presup-
posed the quantity of Mersenne primes while less than x,
which would be (/log2) loglogex

, as 0.5772

 is
the Euler’s constant. Based on that, Wagstaff presup-
posed a conjecture in 1983, as following:
CONJECTURE 2 [7]
1) IF the quantity of Mersenne primes which less than
x is ()
M
x
p, Then
()log log(2.5695) ln ln
ln 2
Me
x
xx
g
p»=,
As g is the Euler’s constant;
2) the expect value of Mersenne primes q
M
is about
1.7806eg=, while 2
x
qx<< ;
3) the probability of q
M
is a prime number is about
ln ln
(2.5695 )
ln 2ln 2
eaq aq
q
g
⋅= ,
as 23(mod4)
61(mod4)
q
aq
ìº
ï
ï
=í
ïº
ï î
.
This conjecture explains the probability of q
M
is a
Mersenne prime in the precondition of q, and also
pointed the quantity of Mersenne primes in certain range.
It has been confirmed that there are 39 Mersenne primes
when 13466917p£. However, the number
()log log13466917
ln 2
(2.5695) ln ln134669177.190360
Me
xg p»
=»
,
quite differs from the actual situation which could be
thought that the conjecture 1) is not advisable. Based on
conjecture 3), take 521q= and 257q= in Mersenne
conjecture as an example, for 521*257 l(mod4), while
6a=, then we get
lnln(6 521)
(2.5695 )(2.5695 )0.039691
521
aq
q
⋅
=»
lnln(6 257)
(2.5695 )(2.5695 )0.073397
257
aq
q
⋅
=»
It’s well known that 521
M
is a Mersenne prime, but
257
M. It could meet a big mistake to some extent if we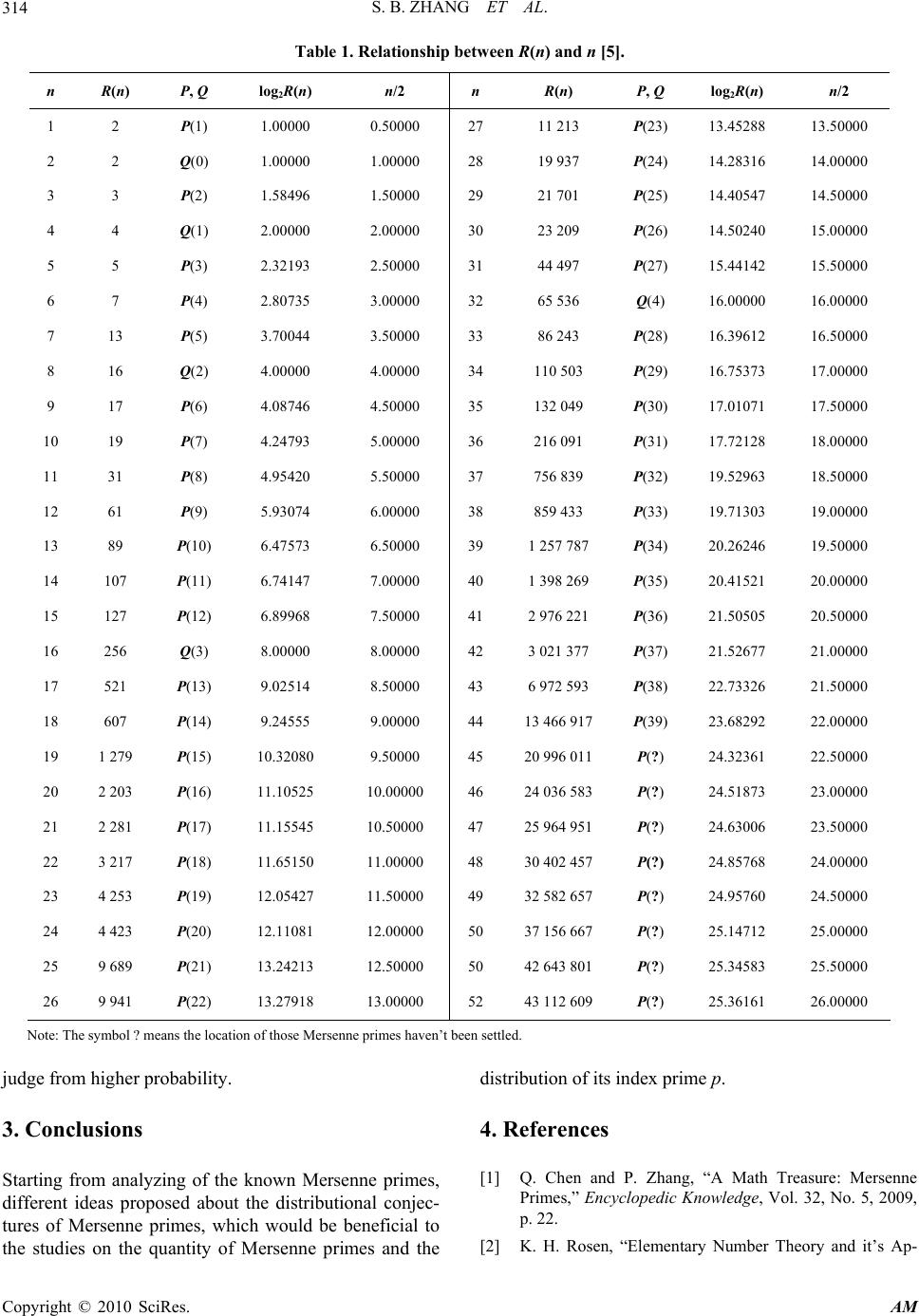

S. B. ZHANG ET AL. 314
Table 1. Relationship betwee n R(n) and n [5].
n R(n) P, Q log2R(n) n/2 n R(n) P, Q log2R(n) n/2
1 2 P(1) 1.00000 0.50000 27 11 213 P(23) 13.45288 13.50000
2 2 Q(0) 1.00000 1.00000 28 19 937 P(24) 14.28316 14.00000
3 3 P(2) 1.58496 1.50000 29 21 701 P(25) 14.40547 14.50000
4 4 Q(1) 2.00000 2.00000 30 23 209 P(26) 14.50240 15.00000
5 5 P(3) 2.32193 2.50000 31 44 497 P(27) 15.44142 15.50000
6 7 P(4) 2.80735 3.00000 32 65 536 Q(4) 16.00000 16.00000
7 13 P(5) 3.70044 3.50000 33 86 243 P(28) 16.39612 16.50000
8 16 Q(2) 4.00000 4.00000 34 110 503 P(29) 16.75373 17.00000
9 17 P(6) 4.08746 4.50000 35 132 049 P(30) 17.01071 17.50000
10 19 P(7) 4.24793 5.00000 36 216 091 P(31) 17.72128 18.00000
11 31 P(8) 4.95420 5.50000 37 756 839 P(32) 19.52963 18.50000
12 61 P(9) 5.93074 6.00000 38 859 433 P(33) 19.71303 19.00000
13 89 P(10) 6.47573 6.50000 39 1 257 787 P(34) 20.26246 19.50000
14 107 P(11) 6.74147 7.00000 40 1 398 269 P(35) 20.41521 20.00000
15 127 P(12) 6.89968 7.50000 41 2 976 221 P(36) 21.50505 20.50000
16 256 Q(3) 8.00000 8.00000 42 3 021 377 P(37) 21.52677 21.00000
17 521 P(13) 9.02514 8.50000 43 6 972 593 P(38) 22.73326 21.50000
18 607 P(14) 9.24555 9.00000 44 13 466 917 P(39) 23.68292 22.00000
19 1 279 P(15) 10.32080 9.50000 45 20 996 011 P(?) 24.32361 22.50000
20 2 203 P(16) 11.10525 10.00000 46 24 036 583 P(?) 24.51873 23.00000
21 2 281 P(17) 11.15545 10.50000 47 25 964 951 P(?) 24.63006 23.50000
22 3 217 P(18) 11.65150 11.00000 48 30 402 457 P(?) 24.85768 24.00000
23 4 253 P(19) 12.05427 11.50000 49 32 582 657 P(?) 24.95760 24.50000
24 4 423 P(20) 12.11081 12.00000 50 37 156 667 P(?) 25.14712 25.00000
25 9 689 P(21) 13.24213 12.50000 50 42 643 801 P(?) 25.34583 25.50000
26 9 941 P(22) 13.27918 13.00000 52 43 112 609 P(?) 25.36161 26.00000
Note: The symbol ? means the location of those Mersenne primes haven’t been settled.
judge from higher probability.
3. Conclusions
Starting from analyzing of the known Mersenne primes,
different ideas proposed about the distributional conjec-
tures of Mersenne primes, which would be beneficial to
the studies on the quantity of Mersenne primes and the
distribution of its index prime p.
4. References
[1] Q. Chen and P. Zhang, “A Math Treasure: Mersenne
Primes,” Encyclopedic Knowledge, Vol. 32, No. 5, 2009,
p. 22.
[2] K. H. Rosen, “Elementary Number Theory and it’s Ap-

S. B. ZHANG ET AL. 315
plications,” Published by arrangement with the original
publisher, Pearson Education, Inc., publishing as Ad-
dision-Wesley, 2005.
[3] H. Z. Zhou, “The Distribution of Mersenne Primes,” Acta
Scientiarum Naturalium Universitatis Sunyatseni, Vol. 31,
No. 4, 1992, pp. 121-122.
[4] J. Z. Zhang, “Zhou Conjecture Reveals the Beauty of
Mathematics,” In: J. Z. Zhang, et al., Ed., 100 Cases of
Scientific and Technological Achievements in Three Dec-
ades: 1978-2008, Children’s Press, Wuhan: Hubei, 2008,
pp. 8-9.
[5] S. W. Chen, “Conjecture on Distribution of Mersenne
Primes,” Huanghuai Journal, Vol. 11, No. 4, 1995, pp.
44-46.
[6] C. Pomerance, “Recent Developments in Primality Test-
ing,” Mathematical Intelligencer, Vol. 3, No. 3, 1980, pp.
97-105.
[7] S. Wagstaff, “Divisors of Mersenne Numbers,” Mathe-
matics and Computation, Vol. 40, No. 38, 1983, pp. 385
-397.