Int. J. Communications, Network and System Sciences, 2013, 6, 134-138
http://dx.doi.org/10.4236/ijcns.2013.63016 Published Online March 2013 (http://www.scirp.org/journal/ijcns)
Fractal Parametric Oscillator as a Model of a Nonlinear
Oscillation System in Natural Mediums
Roman I. Parovik1,2
1Institute of Space Physics Research and Radio Wave Propagation, Far East Branch Kamchatskiy kray, Paratunka, Russia
2Branch of Far Eastern Federal University, Petropavlovsk-Kamchatsky, Russia
Received October 16, 2012; revised December 5, 2012; accepted February 1, 2013
ABSTRACT
The paper presents a model of fractal parametric oscillator. Showing that the solution of such a model exists and is
unique. A study of the solution with the aid of diagrams Stratton-Ince. The regions of instability, which can occur pa-
rametric resonance. It is suggested that this solution can be any signal, including acoustic.
Keywords: Parametric Resonance; Fractal Analysis; Strutt-Ince Diagram; Plastic Deformation; Fractal Oscillator
1. Introduction
It is known that the natural medium (geological medium)
may have fractal properties. These properties charac-
terize the spatial-temporal nonlocality or “memory” of
the medium, which in turn is determined by the power
laws.
Usually geological medium with fractal properties de-
scribed in terms of fractional calculus [1] by equations
with fractional parameters, which depend on the fractal
dimension of the geomedium. This fact allows us to
make extensive use of mathematical constructions of
fractional calculus in a variety of fields, such as the de-
velopment of new methods of vector-phase acoustic di-
agnostic of plasticity geological medium [2].
In this paper the nonlinear parametric oscillatory pro-
cess in the geological medium with fractal properties.
Feature of this process is that the displacement of the
points geomedium a result of its stress-strain of the state
of can occur with increasing amplitude due to changes in
the parameters of the medium itself.
Through this process may be described cracks in the
avalanche geomedium, which in most cases is preceded
by seismic activity in the region (Kamchatka), which can
be used in prediction of strong earthquakes.
2. Statement of the Problem
The geomedium formed loose deposits of rocks. Assume
that this medium has fractal properties. Then the problem
of displacement geomedium points in time can be
stated as follows:
0t
 
0cos 0, txtxt 
    


(1)
with the initial conditions of the problem


12
0,0.Cx C


x
(2)


-
x
Here t
 



shift function geomedium;
0
1
cos 1
kk
k
t
tE tk




 



 
—the general-
ized cosine with

parameter 12

 2. Taking


get the usual cosine, i.e.,
 
2
cos costt

 
 
[3],



01
0
1d
2
t
t
x
x
t









 

12
—the fractional differ-


,

and ential order

-parameters of medium.
Assume,

and

parameters of geomedium, as they
are depend on its fractal dimension.
The Equation (1) is a generalization of parametric
resonance the classical Mathieu’s equation in a case
2
2,, 0


.



Note if put


 
0
d.
t
, then Equation (1) is
known as equation of fractional oscillator, which is in-
vestigated in study [4].
Since Equation (1) is considered first, then call it a
fractal equation parametric oscillator.
3. Solution
In study [5] have shown that the solution of equation
Cauchy problems (1) and (2) can be represented in the
form the Volterra integral equation of the second kind:
tKtx gt   

x
(3)
The kernel of the Equation (3)
C
opyright © 2013 SciRes. IJCNS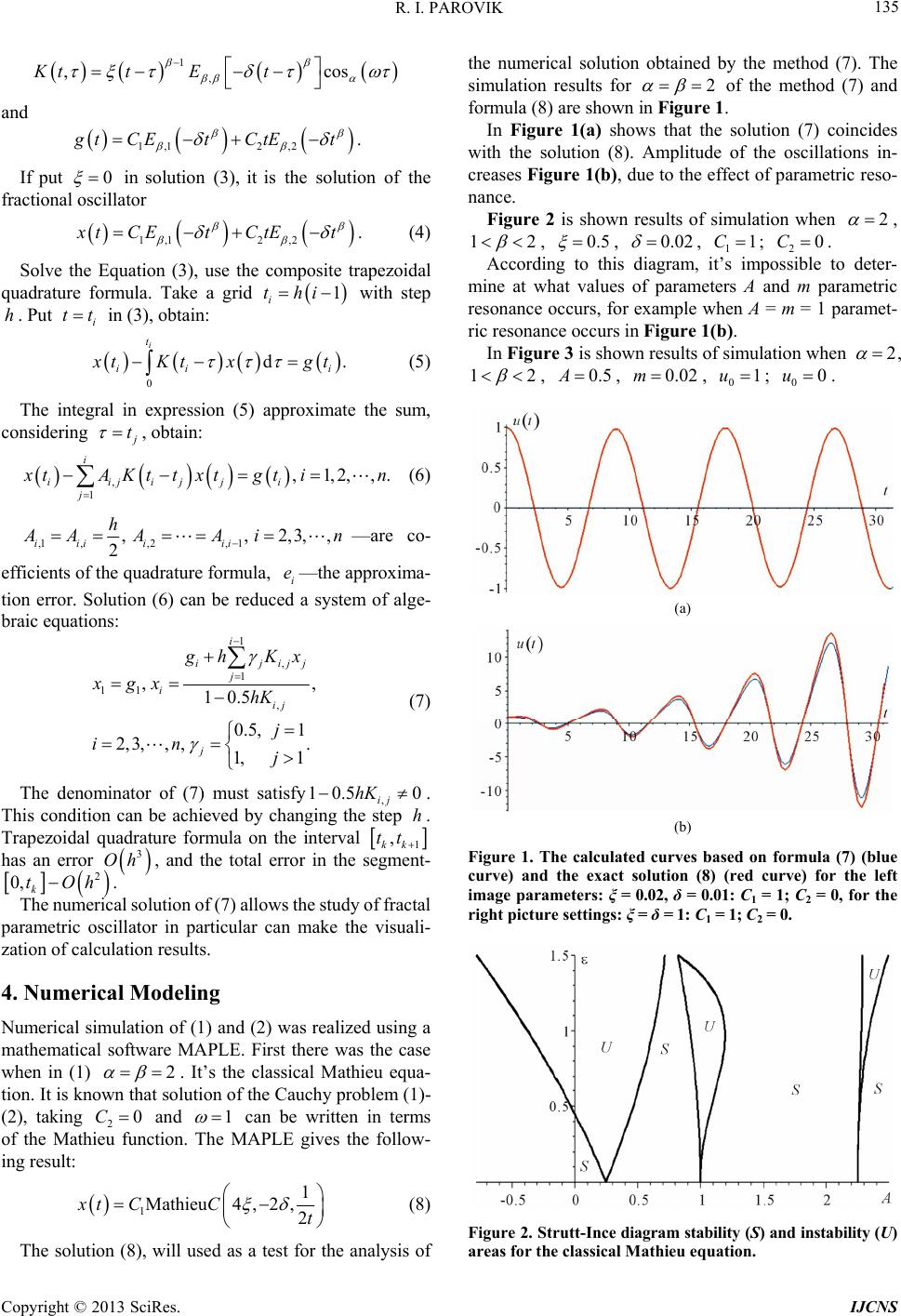

R. I. PAROVIK 135
 
1
,
,Ktt Et


cos



 

   



2 ,2
and


1,1
g
tCEt CtEt



  
0
 .
If put



2 ,2
in solution (3), it is the solution of the
fractional oscillator


1,1
x
tCEt CtEt



  

1
ii
hi tt


d
i

 . (4)
Solve the Equation (3), use the composite trapezoidal
quadrature formula. Take a grid th with step
. Put in (3), obtain:
 
0
t
ii .
i
x
tKt  
x gt
  (5)
The integral in expression (5) approximate the sum,
considering
j
t


,1,2,,.
i
, obtain:
  
,
1
i
iijijj
j
x
tAKttxtg


ti n (6)
,1,,2, 1
,
2
iiiii
h,2,3,,
i
A
AA A

i n
i
e
—are co-
efficients of the quadrature formula, —the approxima-
tion error. Solution (6) can be reduced a system of alge-
braic equations:
1
,
1
,
,,
10.5
0.5, 1.
1, 1
i
ijijj
j
ij
11
2,3,,,
i
j
g
hKx
hK
j
j








.5 0hK
h
xg
x
in





(7)
The denominator of (7) must satisfy,
10 ij .
This condition can be achieved by changing the step .
Trapezoidal quadrature formula on the interval


1kk
has an error , and the total error in the segment-
,tt

3
Oh



2
tOh
2
0, k.
The numerical solution of (7) allows the study of fractal
parametric oscillator in particular can make the visuali-
zation of calculation results.
4. Numerical Modeling
Numerical simulation of (1) and (2) was realized using a
mathematical software MAPLE. First there was the case
when in (1)

 
0 1
. It’s the classical Mathieu equa-
tion. It is known that solution of the Cauchy problem (1)-
(2), taking 2 and C

 can be written in terms
of the Mathieu function. The MAPLE gives the follow-
ing result:

1Mathieuxt CC1
4,2, 2t 




2
(8)
The solution (8), will used as a test for the analysis of
the numerical solution obtained by the method (7). The
simulation results for


 
2
of the method (7) and
formula (8) are shown in Figure 1.
In Figure 1(a) shows that the solution (7) coincides
with the solution (8). Amplitude of the oscillations in-
creases Figure 1(b), due to the effect of parametric reso-
nance.
Figure 2 is shown results of simulation when


,
12


0.5,


, 0.02

, ; .

1 2
According to this diagram, it’s impossible to deter-
mine at what values of parameters A and m parametric
resonance occurs, for example when A = m = 1 paramet-
ric resonance occurs in Figure 1(b).
1С0С
2 In Figure 3 is shown results of simulation when


,
120.5A, 0.02m



,

, ; .
01u00u
(a)
(b)
Figure 1. The calculated curves based on formula (7) (blue
curve) and the exact solution (8) (red curve) for the left
image parameters: ξ = 0.02, δ = 0.01: C1 = 1; C2 = 0, for the
right picture settings: ξ = δ = 1: C1 = 1; C2 = 0.
Figure 2. Strutt-Ince diagram stability (S) and instability (U)
areas for the classical Mathieu equation.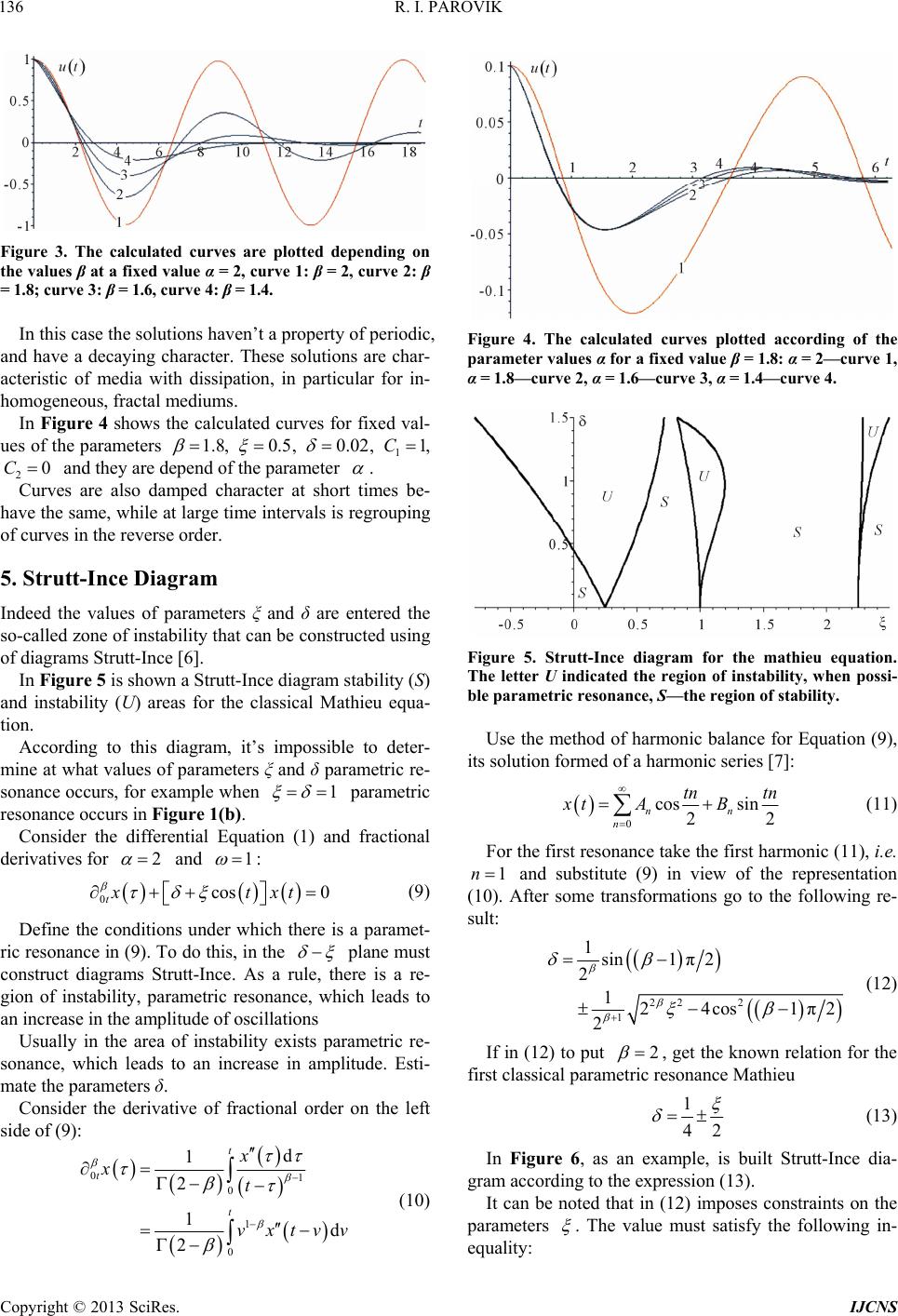

R. I. PAROVIK
136
Figure 3. The calculated curves are plotted depending on
the values β at a fixed value α = 2, curve 1: β = 2, curve 2: β
= 1.8; curve 3: β = 1.6, curve 4: β = 1.4.
In this case the solutions haven’t a property of periodic,
and have a decaying character. These solutions are char-
acteristic of media with dissipation, in particular for in-
homogeneous, fractal mediums.
In Figure 4 shows the calculated curves for fixed val-
ues of the parameters 1.8

, 0.5

, 0.02

11C,

,
and they are depend of the parameter
20C

.
Curves are also damped character at short times be-
have the same, while at large time intervals is regrouping
of curves in the reverse order.
5. Strutt-Ince Diagram
Indeed the values of parameters ξ and δ are entered the
so-called zone of instability that can be constructed using
of diagrams Strutt-Ince [6].
In Figure 5 is shown a Strutt-Ince diagram stability (S)
and instability (U) areas for the classical Mathieu equa-
tion.
According to this diagram, it’s impossible to deter-
mine at what values of parameters ξ and δ parametric re-
sonance occurs, for example when 1

 
2
parametric
resonance occurs in Figure 1(b).
Consider the differential Equation (1) and fractional
derivatives for

 and 1


:
 
0cos tx



 
0txt

(9)
Define the conditions under which there is a paramet-
ric resonance in (9). To do this, in the

  plane must
construct diagrams Strutt-Ince. As a rule, there is a re-
gion of instability, parametric resonance, which leads to
an increase in the amplitude of oscillations
Usually in the area of instability exists parametric re-
sonance, which leads to an increase in amplitude. Esti-
mate the parameters δ.
Consider the derivative of fractional order on the left
side of (9):
 
Figure 4. The calculated curves plotted according of the
parameter values α for a fixed value β = 1.8: α = 2—curve 1,
α = 1.8—curve 2, α = 1.6—curve 3, α = 1.4—curve 4.
Figure 5. Strutt-Ince diagram for the mathieu equation.
The letter U indicated the region of instability, when possi-
ble parametric resonance, S—the region of stability.
Use the method of harmonic balance for Equation (9),
its solution formed of a harmonic series [7]:



 
1
d
dvxtvv









0
0
1
0
1
2
1
2
t
t
t
x
x
t









(10)
0
cos sin
22
nn
n
tn tn
xt AB




1n
(11)
For the first resonance take the first harmonic (11), i.e.

and substitute (9) in view of the representation
(10). After some transformations go to the following re-
sult:
 
 
22 2
1
1sin1 π2
2
124cos1π2
2








2
(12)
If in (12) to put


, get the known relation for the
first classical parametric resonance Mathieu
1
42

(13) 


In Figure 6, as an example, is built Strutt-Ince dia-
gram according to the expression (13).
It can be noted that in (12) imposes constraints on the
parameters

. The value must satisfy the following in-
equality: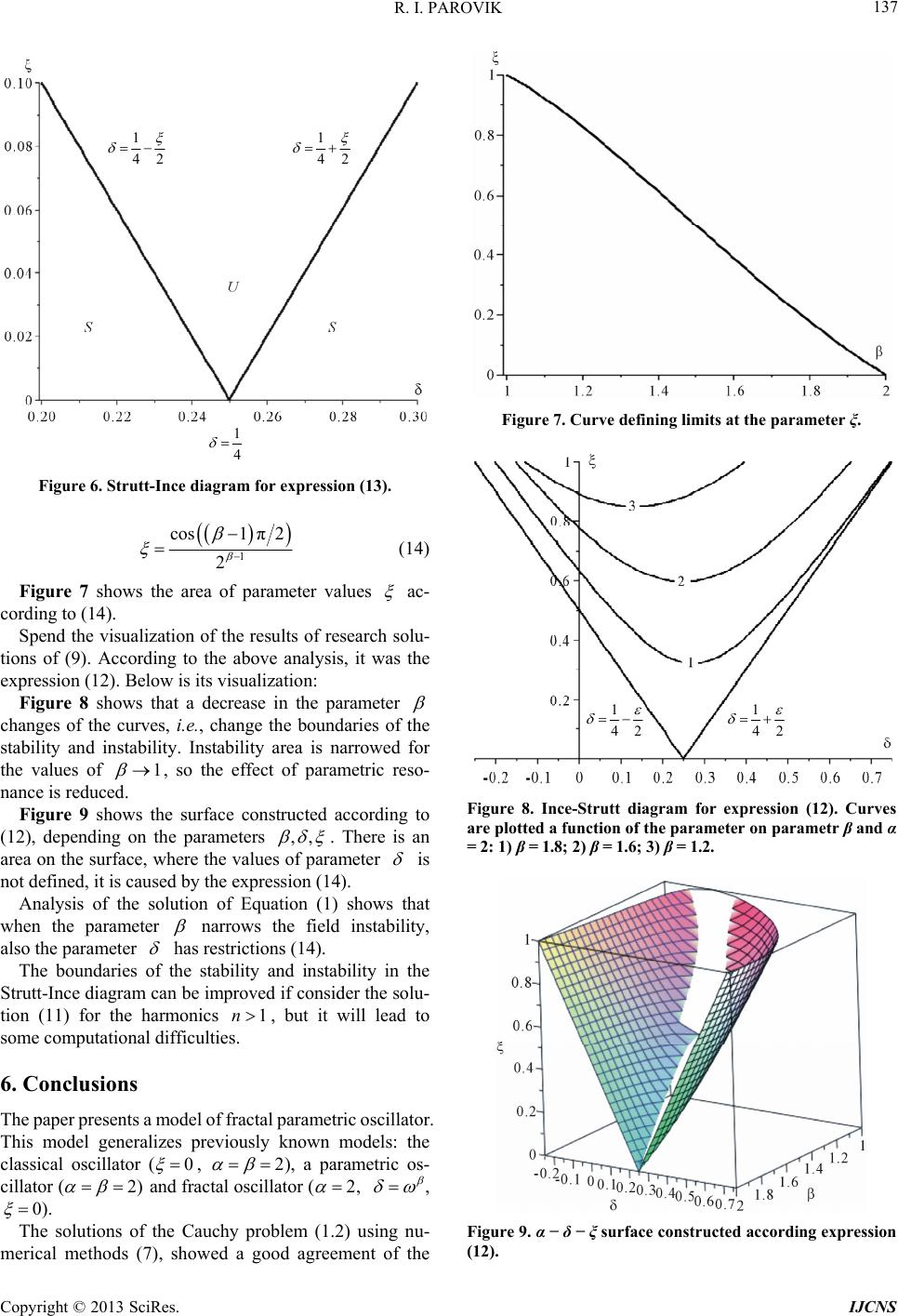

R. I. PAROVIK 137
1
42

  1
42

 
1
4


Figure 6. Strutt-Ince diagram for expression (13).


1
1π2
2



cos

 (14)
Figure 7 shows the area of parameter values

ac-
cording to (14).
Spend the visualization of the results of research solu-
tions of (9). According to the above analysis, it was the
expression (12). Below is its visualization:
Figure 8 shows that a decrease in the parameter

changes of the curves, i.e., change the boundaries of the
stability and instability. Instability area is narrowed for
the values of 1


,,
, so the effect of parametric reso-
nance is reduced.
Figure 9 shows the surface constructed according to
(12), depending on the parameters

 . There is an
area on the surface, where the values of parameter

is
not defined, it is caused by the expression (14).
Analysis of the solution of Equation (1) shows that
when the parameter

narrows the field instability,
also the parameter

has restrictions (14).
The boundaries of the stability and instability in the
Strutt-Ince diagram can be improved if consider the solu-
tion (11) for the harmonics , but it will lead to
some computational difficulties.
1n
0
6. Conclusions
The paper presents a model of fractal parametric oscillator.
This model generalizes previously known models: the
classical oscillator (

, 2



), a parametric os-
cillator (2

  2) and fractal oscillator (

,




,
0

).
The solutions of the Cauchy problem (1.2) using nu-
merical methods (7), showed a good agreement of the
Figure 7. Curve defining limits at the parameter ξ.
1
42



1
42

 
Figure 8. Ince-Strutt diagram for expression (12). Curves
are plotted a function of the parameter on parametr β and α
= 2: 1) β = 1.8; 2) β = 1.6; 3) β = 1.2.
Figure 9. α − δ − ξ surface constructed according expression
(12).

R. I. PAROVIK
138
1
REFERENCES numerical solution of (7) with the exact solution (8).
Explore the first parametric resonance for Equation (9)
with the harmonic balance method (11). With Strutt-Ince
diagrams identify areas of instability, the existence of
parametric resonance. It is shown that the values
[1] A. M. Nakhushev, “Fractional Calculus and Its Applica-
tion,” Fizmatlit, Moscow, 2003, p. 272.
[2] V. A. Gordeenko, “Vector-Phase Methods in Acoustics,”
Fizmatlit, Moscow, 2007, p. 480.


of these areas are narrow. Therefore the probability that
the parameters [3] V. A. Nakhusheva, “Differential Equations of Mathe-
matical Models of Non-Local Processes,” Nauka, Mos-
cow, 2006, p. 173.

and

in such areas is reduced.
Further interest is the study of the Equation (9)—calcu-
lation of the second or the third resonance, as well as the
more general Equation (1). There is interest in the study of
the phase trajectories for the solution (3).
[4] R. P. Meilanov and M. S. Yanpolov, “Features of the
Phase Trajectory of a Fractal Oscillator,” Technical Phy-
sics Letters, Vol. 28, No. 1, 2002, pp. 67-73.
doi:10.1134/1.1448634
There is interest in the equation with the right side. It
should be noted that in study [8], the authors considered
the equation of the fractional oscillator with an external
stabilizing inertial effects. It would be interesting to con-
sider the Equation (1) subject to an external force, ac-
cording to this work, and then proceed to the considera-
tion of (1) with a random external force.
[5] R. I. Parovik, “Cauchy Problem for Non Local Mathieu
Equation,” Doklady AMAN, Vol. 13, No. 2, 2011, pp.
90-98.
[6] F. Van de Pol and M. J. Strutt, “On the Stability of the
Solutions of Mathieu’s Equation,” Philosophical Maga-
zine, Vol. 5, 1928, pp. 18-38.
[7] R. H. Rand, S. M. Sah and M. K. Suchrsky, “Fractional
Mathieu Equation,” Communications in Nonlinear Sci-
ence and Numerical Simulation, Vol. 15, 2010, pp. 3254-
3262.
7. Acknowledgements
The work was performed as part of the program DPS RAS
IV.10 “Fundamentals of acoustic diagnostics of artificial
and natural environments” and is supported by RFBR
(grant no. 11-01-90715).
[8] V. V. Afanas’ev and M. J. E. Daniel, “Polish Stabilization
of the Inertial Effects of the Fractal Oscillator,” Technical
Physics Letters, Vol. 36, No. 7, 2010, pp. 1-6.