Applied Mathematics, 2010, 1, 260-264
doi:10.4236/am.2010.14032 Published Online October 2010 (http://www.SciRP.org/journal/am)
Transformation of Nonlinear Surface Gravity Waves
under Shallow-Water Conditions
Iftikhar B. Abbasov
Taganrog Technological Institute, Southern Federal University, Taganrog, Russia
Received April 30, 2010; revised June 18, 2010; accepted June 21, 2010
Abstract
This article describes transformation of nonlinear surface gravity waves under shallow-water conditions with
the aid of the suggested semigraphical method. There are given profiles of surface gravity waves on the
crests steepening stages, their leading edges steepening. There are discussed the spectral component influ-
ence on the transformation of surface wave profile.
Keywords: Nonlinear Surface Gravity Waves, Shallow-Water, Semigraphical Method, Transformation of
Surface Wave Profile
1. Introduction
Surface gravity waves under shallow-water conditions
were of great interest for many researchers many years
ago. In spite of their magnetic view, they are rather hard to
describe. The research problems of surface waves in the
near-shore region within shallow-water model are dis-
cussed in [1,2]. [3] is concerned with nonlinear waves in
strongly dispersive media. Transformation of surface
waves in the near-shore region is discussed in [4]. The
nonlinear dynamics of surface gravity waves in long-
wave approximation is described in [5,6]. [6] analysed the
process of surface wave deformation under shallow-water
conditions, estimated spectral amplitude of nonlinear wave
with its steepness.
In works [7,8] give mathematic simulation of gravity
waves in approximation of shallow water. [8] is con-
cerned with numerical simulation of water waves within
nonlinear-dispersive model of shallow water taking ac-
count of bed topography. Experimental data on influence
of the dispersion effects on the propagation of nonlinear
surface waves in inshore area are given in [9].
2. Statement of the Problem
In work [10] discussed the problem of nonlinear surface
waves propagation under shallow-water conditions. Shal-
low-water equation taking account of quadratic nonlin-
earity was solved by the method of successive approxi-
mations.
Either the shallow-water equation or the method of
successive approximations is the basis of nonlinear wave
research. In the middle of the 19th century G. Airy described
tide waves and G. Stokes described waves of finite am-
plitude with this equation and this method [11]. However,
the generating process of higher harmonics, resulting in
wave crest sharpening, did not always meet energy con-
servation law. When higher harmonics are growing, the
decrease of principal wave energy is ignored. The exact
solution of shallow-water equation without dispersion
and damping appears to be Riemannian invariants, based
on different propagation velocity of wave crests and
troughs [12,13]. In addition, shallow-water equation ig-
nores dispersion effect because of its weakening on shallow
water.
Surface gravity waves on shallow water in approxima-
tion of small nonlinearity and small dispersion are de-
scribed by well known Cortvega and De Vries equation
[11,12]. In the equation small nonlinearity, resulting in
wave steepening, and small dispersion, resulting in wave
diffusion, compensate each other. Thereat, stationary nonlinear
wave (named as a cnoidal wave) occurs, which propa-
gates without form change at a constant velocity. How-
ever, form stability of cnoidal waves doesn’t allow re-
tracing the dynamics of nonlinear surface gravity waves
with the propagation on the shallow water.
In the development of earlier studies this work de-
scribes the transformation process of surface wave profile
with the propagation on the shallow water. There was an
attempt to describe not only the initial wave crest sharp-

I. B. ABBASOV 261
ening but further steepening of its leading edge. One uses
rather understandable and vivid semigraphical method
based on energy conservation law given in [10].
3. Research Method
Method of successive approximations is the straightest
way of the solution of nonlinear Equations [14]. Here, the
small parameter expansion


1   is used, restricting
to the first two terms under the restriction (1) ()nn uu
.
The equation taking account of quadratic nonlinearity
takes the form [12,13]:
uu u
cu
tx x

 

 
(1)
where
x
u

— the horizontal component of medium
particle velocity, nonlinearity —xa
cH

 , the propa-
gation velocity of gravity waves cgH, a — the
amplitude of the vertical shift of the free surface, H — the
fluid depth.
With the propagation of the initial harmonic wave on
shallow water as a consequence of nonlinear effects, the
second harmonic appears. With the growth of the second
harmonic its interaction with first harmonic will get
stronger. This interaction will lead to the exciting of the
third, fourth, and so on, harmonics.
In the first approximation, solution of Equation (1)
consists of primary waves and takes the form [10]:
 
(1)(1)2 (2)
.
22
00
(,) (,)(,)
expexp2. .
prim
uxtuxt uxt
UikxiktUikxcс


 
 
(2)
In the second approximation the non-homogeneous
linear equation is solved
2
(1)
(2) (2)
.
sec. sec.
2
p
rim
u
uu
c
tx x



 
. (3)
After squaring and solution differentiation in the first
approximation (2) we obtain the expression in the second
approximation:








(2)2 2
sec.0 22
23 44
044
23 3
03 3
23 3
01 1
(,)2 exp
2exp
exp
exp(..)
uxt tUikikx
kt Uikikx
iktUikik x
iktUikikxc с





 

 
 

 

(4)
where , 1,2,3,4
n
knkn — harmonic number.
As a consequence of interaction between principal
wave k and second 2k secondary waves with double val-
ues 2k, 4k, and complex waves k and 3k will occur. With
time, higher harmonics in the spectrum lead to the distor-
tion of wave profile.
The solution of shallow-water Equation (1) in two ap-
proximations for horizontal velocity of medium particles
will take the form
 
  



(1)2( 2)
sec.. sec.
232
00
25 342
01 1022
25 3
03 3
23 64
044
(,)(,) (,)
expexp2
exp2 exp
exp
2exp (..)
prim
uxtu xtuxt
UikxiktUikx
ktUkik xtUikikx
ktUkik x
kt Uikikxcс







 



 

 

 

(5)
4. Simulation within the Gulf
To check the results obtained we will use hydrologic
conditions of the Gulf of Taganrog of the Azov Sea. The
mean depth of the gulf does not exceed 5 m, therefore, the
shallow-water conditions will be satisfied with gravity
waves with their lengths are not longer than 30 m, the gulf
bed is flat, surface tension is absent, the effect of wind is
not taken into account.
Before calculation one should mark some physical fea-
tures of existent wave processes. In formula (5) all har-
monic amplitudes are always growing because of secular
terms. However, according to the formula, the first har-
monic amplitude remains constant at that. Though, higher
harmonics are fared energetically from the first harmonic.
It follows that the primary waves amplitude in formula
(5) (1)
.(,)
prim
uxt should be getting decreased. That is why
to research profile dispersions of a gravity wave it is nec-
essary to consider these physical features of wave proc-
esses otherwise it will break the energy conservation law.
In the absence of dissipation, energies of primary and
secondary waves should satisfy должны отвечать the
energy conservation law
(1)(1) (2)(2)(2)(2)
12123 4
()()() () () ()ExExExExExEx
(6)
where (1) ()
n
Ex, (2) ()
n
Ex— energies of primary and sec-
ondary waves.
Let us follow variations the profile change of the grav-
ity wave after coming into the gulf with the initial pa-
rameters: frequency f = 0.09 Hz; length  = 77.8 m; ini-
tial steepness – 2a/  = 0.014; a = 0.537 m; kH = 0.4.
According to Figure 1(а) for this wave instability appears
at the distance: (2)
.inst
x
 10 km (i.e. in (2)
.inst
t  24 min.).
Though our model is correct only within
x
 6 km, i.e.
till, while the primary limitation (1) ()nn
uu
 is fulfilled,

I. B. ABBASOV 262
(a)
(b)
(c)
(d)
Figure 1. Primary and secondary wave velocities (а) and
profiles (b, c, d) of the surface gravity wave: f = 0.09 Hz;

= 77.8 m; wave parameter – kH = 0.4; initial steepness –
2a/
 = 0.014; nonlinear parameter – ε = 0.107.
when the value for the second approximation is by an
order less than the value for the initial approximation.
Because of Figure 1(а) analysis, it is possible point out
that the amplitude of primary waves and first harmonic
falls with the growth of secondary waves summary am-
plitude. The amplitude of the second harmonic grows
slowly, and to the moment of instability it falls down as
there is a complete energy transfer from primary waves
(principal wave and the second harmonic) to secondary
waves.
With the growth of initial steepness the instability dis-
tance decreases, with the growth of the wave amplitude
(with the constant steepness) this distance lengthens, as
nonlinear parameter value decreases.
Let us follow the profile change of the initial gravity
wave within distance
x
 6 km. Figures 1(b), 1(c) and
1(d) describe dependences of horizontal velocity change
(,)uxt on the distance run taking account of the formula
(5) (expanded vertical scale). The wave with an initially
cosinusoidal profile is gradually distorted in a run dis-
tance time, the crests steepen Figure 1(c), and the wave
troughs flatten. Thereafter there is a steepening of the
wave leading edge Figure 1(d). This is the result of the
increasing influence of high frequency harmonics. The
increasing of particle velocity on the crest leads to the
further steepening of the wave leading edge. The breaking
of such a wave in shallow water happens as a plunging or
spilling breaker [15,16]. The breaking cause in our case is
naturally liquid depth.
An additional point to emphasize is that the shal-
low-water condition could not be observed for the higher
harmonics appear. It could lead to the propagation veloc-
ity dispersion that could cause braking of nonlinear
process. But approaching the coast as the depth lessens,
the shallow-water condition will be met better, therefore
the wave breaks.
To analyse the secondary waves influence Figure 2
gives graphs showing the growth of velocity amplitude of
the secondary waves because of the distance. It clearly
enough shows the relation between harmonics. Within the
secondary waves, velocity amplitude of the fourth har-
monic increases faster (because of the greatest degree of a
secular term in the formula (5)), then there comes the third
one, the first one and the second one. This conformity is
observed for the gravity waves with other initial data as
well.
5. Analysis and the Result Comparison
Analysing the constructed profiles of the surface gravity
waves it is necessary to note their following features.
From the field studies it is known that the profile of real
surface waves is asymmetrical: the crests are steep and
short, sharpened, and troughs are flattened and broad [11].
Undulations are asymmetrical as well: particles velocity
below the crests is lower than below the troughs. Theses
peculiarities are explained by Stokes theory and the ap-
Figure 2. The increase of velocity amplitudes of secondary
waves from the distance with: f = 0.09 Hz;
 = 77.8 m; kH =
0.4; 2a/  = 0.014; ε = 0.107.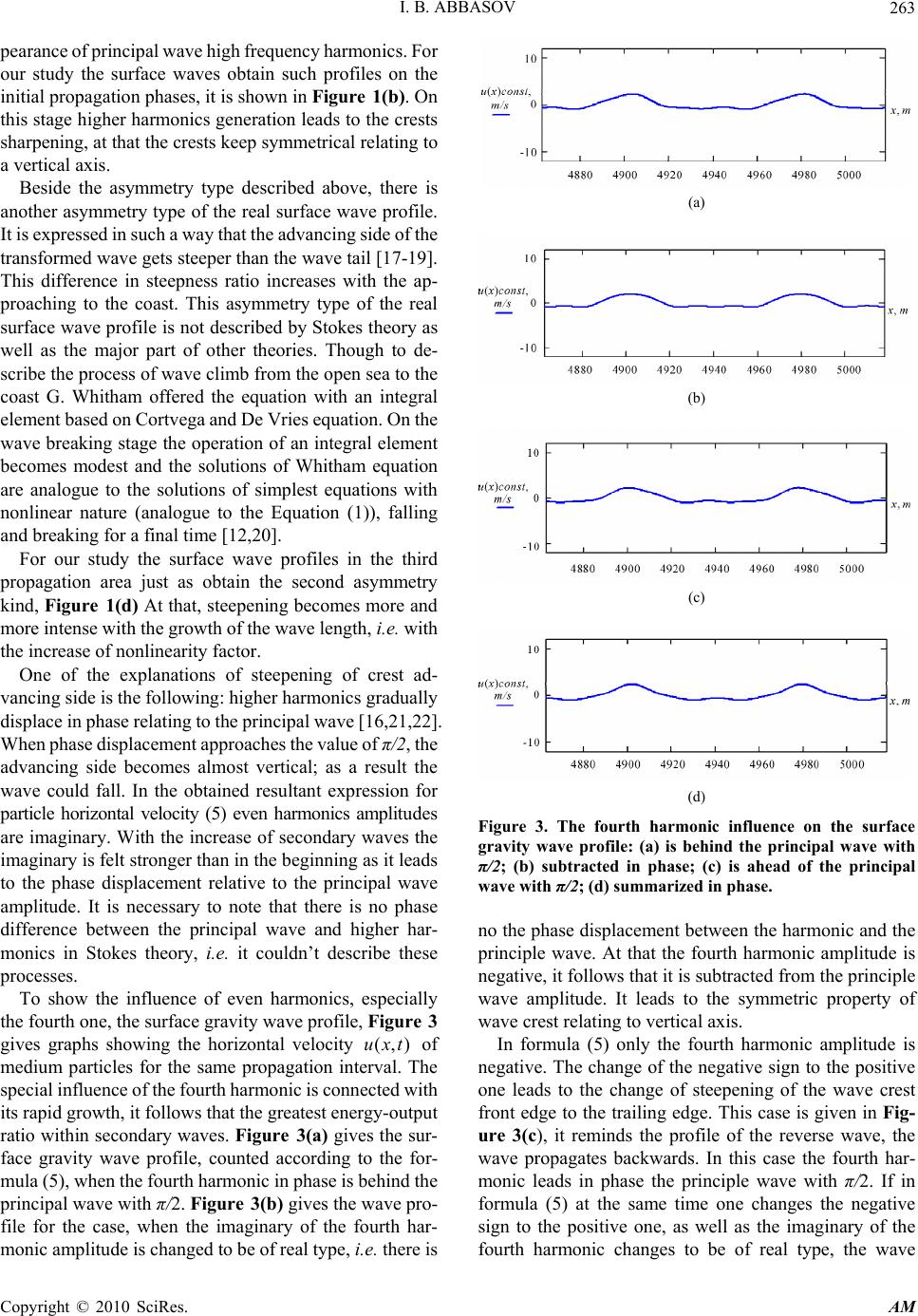

I. B. ABBASOV 263
pearance of principal wave high frequency harmonics. For
our study the surface waves obtain such profiles on the
initial propagation phases, it is shown in Figure 1(b). On
this stage higher harmonics generation leads to the crests
sharpening, at that the crests keep symmetrical relating to
a vertical axis.
Beside the asymmetry type described above, there is
another asymmetry type of the real surface wave profile.
It is expressed in such a way that the advancing side of the
transformed wave gets steeper than the wave tail [17-19].
This difference in steepness ratio increases with the ap-
proaching to the coast. This asymmetry type of the real
surface wave profile is not described by Stokes theory as
well as the major part of other theories. Though to de-
scribe the process of wave climb from the open sea to the
coast G. Whitham offered the equation with an integral
element based on Cortvega and De Vries equation. On the
wave breaking stage the operation of an integral element
becomes modest and the solutions of Whitham equation
are analogue to the solutions of simplest equations with
nonlinear nature (analogue to the Equation (1)), falling
and breaking for a final time [12,20].
For our study the surface wave profiles in the third
propagation area just as obtain the second asymmetry
kind, Figure 1(d) At that, steepening becomes more and
more intense with the growth of the wave length, i.е. with
the increase of nonlinearity factor.
One of the explanations of steepening of crest ad-
vancing side is the following: higher harmonics gradually
displace in phase relating to the principal wave [16,21,22].
When phase displacement approaches the value of π/2, the
advancing side becomes almost vertical; as a result the
wave could fall. In the obtained resultant expression for
particle horizontal velocity (5) even harmonics amplitudes
are imaginary. With the increase of secondary waves the
imaginary is felt stronger than in the beginning as it leads
to the phase displacement relative to the principal wave
amplitude. It is necessary to note that there is no phase
difference between the principal wave and higher har-
monics in Stokes theory, i.e. it couldn’t describe these
processes.
To show the influence of even harmonics, especially
the fourth one, the surface gravity wave profile, Figure 3
gives graphs showing the horizontal velocity (,)uxt of
medium particles for the same propagation interval. The
special influence of the fourth harmonic is connected with
its rapid growth, it follows that the greatest energy-output
ratio within secondary waves. Figure 3(а) gives the sur-
face gravity wave profile, counted according to the for-
mula (5), when the fourth harmonic in phase is behind the
principal wave with π/2. Figure 3(b) gives the wave pro-
file for the case, when the imaginary of the fourth har-
monic amplitude is changed to be of real type, i.e. there is
(a)
(b)
(c)
(d)
Figure 3. The fourth harmonic influence on the surface
gravity wave profile: (а) is behind the principal wave with
π/2; (b) subtracted in phase; (c) is ahead of the principal
wave with π/2; (d) summarized in phase.
no the phase displacement between the harmonic and the
principle wave. At that the fourth harmonic amplitude is
negative, it follows that it is subtracted from the principle
wave amplitude. It leads to the symmetric property of
wave crest relating to vertical axis.
In formula (5) only the fourth harmonic amplitude is
negative. The change of the negative sign to the positive
one leads to the change of steepening of the wave crest
front edge to the trailing edge. This case is given in Fig-
ure 3(c), it reminds the profile of the reverse wave, the
wave propagates backwards. In this case the fourth har-
monic leads in phase the principle wave with π/2. If in
formula (5) at the same time one changes the negative
sign to the positive one, as well as the imaginary of the
fourth harmonic changes to be of real type, the wave

I. B. ABBASOV 264
profile takes the form as in Figure 3(d).
In this case the fourth harmonic amplitude is summa-
rized in phase with the principle wave amplitude, inten-
sifying the wave crest. The given profile resembles Stokes
waves of finite amplitude on the deep water (or trochoidal
wave).
It is important to pay attention to the appearance of the
local projection in the trough between the crests. This
projection is also connected with the fourth harmonic, and
it changes its location depending on the phase. Experi-
mental observations with the trough between the principal
wave crests in nearshore zone are given in [9,21,23].
6. Conclusions
As a consequence of the researches made, one could note
that the suggested semigraphical method allows to de-
scribe not only the process of the initial sharpening of the
surface waves during the propagation under shallow wa-
ter conditions, and further steepening of their front edge.
In our study we described the influence of the first four
harmonics of the principle wave on profile transforma-
tion but the real wave spectrum is constant, and for more
reasonable study it is necessary to record at least first
eight harmonics. The record of higher harmonics will
lead to more intense sharpening of wave crests and steep-
ness growing of the wave leading edge.
7. References
[1] D. H. Peregrine, “Long Waves on a Beach,” Journal of
Fluid Mechanics, Vol. 27, No. 0404, 1967, pp. 815-827.
[2] N. Е. Voltsinger, К. А. Klevanniy and Е. Н. Pelinovskiy,
“Long-Wave Dynamics of Coastal Zone,” Gidrometeo-
izdat, 1989, p. 272.
[3] P. I. Naumkin and I. А. Shishmarev, “On the Existence
and Breaking the Waves Described by the Whitham
Equation,” Soviet Physics-Doklady, Vol. 384, No. 31, 1986,
pp. 90-95.
[4] V. G. Galenin and V. V. Kuznetsov, “Simulation of
Wave Transformation in Coastal Zone,” Water Resources,
Vol. 7, No. 1, 1980, pp. 156-165.
[5] U. Kanoglu, “Nonlinear Evolution and Run Up-Run
Down of Long Waves over a Sloping Beach,” Journal of
Fluid Mechanics, Vol. 513, 2004, pp. 363-372.
[6] I. I. Didenkulova, N. Zaibo, А. А. Kurkin and Е. N. Peli-
novskiy, “Steepness and Spectrum of Nonlinear Deformed
Wave under Water Conditions,” Izvestiya RAN Atmos-
pheric and Oceanic Physics, Vol. 42, No. 6, 2006, pp.
839-842.
[7] N. А. Kudryashov, Yu. I. Sytsko and S. А. Chesnokov,
“Mathematic Simulation of Gravity Waves in the Ocean
in ‘Shallow Water’ Approximation,” Pisma v ZhETF, Vol.
77, No. 10, 2003, p. 649.
[8] А. А. Litvinenko and G. А. Khabakhpashev, “Computer
Simulation of Nonlinear Considerably Long Two-di-
mensional Waves under Water Conditions in Basins with
Sloping Floor,” Computer technologies, Vol. 4, No. 3,
1999, pp. 95-105.
[9] S. Yu. Kuznetsov and Ya. V. Saprykina, “Experimental
Researches of Wave Group Evolution in the Coastal Sea
Zone,” Oceanology, Vol. 42, No. 3, 2002, p. 356-363.
[10] I. B. Abbasov, “Study and Simulation of Nonlinear Sur-
face Waves under Shallow-Water Conditions,” Izvestiya
RAN Atmospheric and Oceanic Physics, Vol. 39, No. 4,
2003, pp. 506-511.
[11] H. Lamb, “Hydrodynamics,” Dover, New York, 1930, p.
524.
[12] G. Whitham, “Linear and Nonlinear Waves,” Wiley, New
York, 1974, p. 622.
[13] L. М. Brekhovskikh and V. V. Goncharov, “Introduction
to the Mechanics of Continuous Media,” Nauka, 1982, p.
325.
[14] М. B. Vinogradova, О. V. Rudenko and А. P. Sukhoru-
kov, “Wave Theory,” Nauka, 1979, p. 383.
[15] А. K. Monin and V. P. Krasitskiy, “Phenomena at the
Ocean Surface,” L. Gidrometeoizdat, 1985, p. 375.
[16] I. О. Leontiev, “Coastal Dynamics: Waves, Streams, Burden
Streams,” M.: GEOS, 2001, p. 272.
[17] R. E. Flick, R. T. Guza and D. L. Inman, “Elevation and
Velocity Measurements of Laboratory Shoaling Waves,”
Journal of Geophysical Research, Vol. 86, No. 5, 1981,
pp. 4149-4160.
[18] M. S. Lonquet-Higgins, “Grest Instabilities of Gravity
Waves, Part 1,” Journal of Fluid Mechanics, Vol. 258,
No. 1, 1994, pp. 115-129.
[19] V. Zaharov, “Weakly Non-Linear Waves on the Surface
of an Ideal Finite Depth Fluid,” American Mathematical
Society Transactions, Series 2, Vol. 182, 1998, pp. 167-
197.
[20] S. А. Gabov, “Introduction to the Theory on Nonlinear
Waves,” Moscow State Unversity, 1988, p.176.
[21] Y. Goda and K. Morinobu, “Breaking Wave Heights on
Horizontal Bed Affected by Approach Slope,” Coastal
Engineering Journal, Vol. 40, No. 4, 1998, pp. 307-326.
[22] Ya. V. Saprykina, S. Yu. Kuznetsov, Zh. Tcherneva and
N. Andreeva, “Space-Time Unsteadiness of the Ampli-
tude-Phase Structure of Storm Waves in the Coastal Sea
Zone,” Oceanology, Vol. 49, No. 2, 2009, pp. 198-208.
[23] K. Kawasaki, “Numerical Simulation of Breaking and
Post-Breaking Wave Deformation Process around a Sub-
merged Breakwater,” Coastal Engineering Journal, Vol.
41, No. 3-4, 1999, pp. 201-223.