Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23139,14 pages DOI:10.4236/jmp.2012.329172
Geometrization of Radial Particles in Non-Empty Space Complies with Tests of General Relativity
Moscow Institute of Physics and Technology, Moscow, Russia
Email: inter@mipt.ru
Received June 25, 2012; revised July 25, 2012; accepted August 2, 2012
Keywords: Euclidean Material Space; Metric Four-Potentials; Radial Masses; Energy-to-Energy Gravitation; Nonlocal Universe
ABSTRACT
Curved space-time 4-interval of any probe particle does not contradict to flat non-empty 3-space which, in turn, assumes the global material overlap of elementary continuous particles or the nonlocal Universe with universal Euclidean geometry. Relativistic particle’s time is the chain function of particles speed and this time differs from the proper time of a motionless local observer. Equal passive and active relativistic energy-charges are employed to match the universal free fall and the Principle of Equivalence in non-empty (material) space, where continuous radial densities of elementary energy-charges obey local superpositions and mutual penetrations. The known planetary perihelion precession, the radar echo delay, and the gravitational light bending can be explained quantitatively by the singularity-free metric without departure from Euclidean spatial geometry. The flatspace precession of non-point orbiting gyroscopes is non-Newtonian one due to the Einstein dilation of local time within the Earth’s radial energy-charge rather than due to unphysical warping of Euclidean space.
1. Introduction
The ideal penetration of a static superfluid medium through a rotating drag one was observed in He3-He4 experiments well before the distributed Cooper pair explained the nonlocal nature of superconductivity. But does spatial distribution of paired superelectrons mean that two nonlocal carriers move one through another as overlapping continuous distributions of mass-densities or do these densities bypass each other separately without mutual penetrations? Is there a principle difference between the superfluid motion of two paired electrons and the free, geodesic motion of any normal electron between drag collisions with energy exchanges?
During the last fifty years the celebrated AharonovBohm effect is trying to dismiss doubts regarding the nonlocal nature of the electron, while the Classical Theory of Fields is persisting to accept a self-coherent analytical distribution of the charged elementary density (instead of the point particle approximation for the electron). Fermions take different energies and, therefore, cannot exhibit one net phase even under the ideal (without dissipation) motion. At the same time, each distributed electron may have a self-coherent state of its own matter. Particles motion with drag collisions and heat release represents much more complicated physics than the superfluid motion with a self-coherent state of distributed elementary mass. Such a nonlocal superfluid state is free from energy and information exchanges. Charged densities of drag and superconducting electrons in the same spatial point can move even in opposite directions, for example under thermoelectric phenomena where nonequilibrium superconductors exhibit up to five [1] different ways for heat release/absorption. Such a steady countermotion of drag and superfluid densities of electrons may be a laboratory guiding for theories toward the global counterbalance of all material flows in the nonlocal Universe with local energy dissipation. However, if there is a mutual penetration of extended bodies (with or without dissipation), then how can General Relativity (GR) address the laboratory nonlocality of each electron in order to incorporate the material spatial overlap of distributed carriers of mass-energy? Below we accept the ideal global overlap of all elementary energy flows in all points of their joint 3D space, which is associated with the superposition of flat material 3-sections of curved elementary 4D manifolds. We shall rely on superfluid, self-coherent states of extended elementary particle (called the astroparticle due to its infinite spatial distribution [2]) between drag collisions and dissipation events. At the same time, 3D overlap of such self-coherent radial distributions can rarely exhibit, due to drag collisions, summary superfluid states of identical bosons, while 3D energy ensembles of extended fermions can exhibit only ideal summary flows without joint coherent properties.
It is important to emphasize that strict spatial flatness is principal for reasonable Quantum Mechanics, say for the Bohr-Sommerfeld quantization, and for reasonable Electrodynamics, which is based on constant Gauss flux through any closed surface. The author does not see clear experimental reasons why one should redesign Classical Electrodynamics for a curved-space laboratory in question. On the contrary, due to well established measurements of magnetic flux quantization in superconducting rings, one may insist that would gravity contribute to length of superconducting contours, then SQUIDs could not be explained satisfactorily, for example [3]. Indeed, would spatial intervals depend on gravity or acceleration, working SQUID accelerometers were already created. In such a view, Einsteins metric gravitation, which started from the very beneficial 1913 idea of 4D geometrization of fields, should double-check its wide opportunities and overcome the current phase with unphysical metric singularities. There are no sharp material densities in reality like Dirac operator delta-densities and relativistic physics should try continuous particles prior to declare singularities and black holes in physical space. One may expect that advanced metric gravitation should be a self-cotained theory of continuous energy flows which ought to derive analytical components of the metric tensor  for space-time dynamics of distributed astroparticles without references on the point matter paradigm in question and the Newtonian limit for point masses. Advanced GR solutions for mass-energy densities of moving material space should provide Lorentz force analogs even in the non-relativistic limit. Newtons gravitation cannot satisfactorily describe this limit for moving sources and, therefore, should not be used for relevant gravitational references for a rotating galaxy (that raised the dark matter problem).
for space-time dynamics of distributed astroparticles without references on the point matter paradigm in question and the Newtonian limit for point masses. Advanced GR solutions for mass-energy densities of moving material space should provide Lorentz force analogs even in the non-relativistic limit. Newtons gravitation cannot satisfactorily describe this limit for moving sources and, therefore, should not be used for relevant gravitational references for a rotating galaxy (that raised the dark matter problem).
Recall that in 1913 Einstein and Grossmann published their Entwurf metric formalism for the geodesic motion of a passive material point in a gravitational field [4]. In October 1915, Einstein’s field equation [5] and the Hilbert variational approach to independent field and particle densities [6] were proposed in Berlin and Gottingen, respectively, for geometrization of gravitational fields “generated” by the energy-momentum density of Mies continuous matter [7], which later failed to replace point masses of the pre-quantum Universe. This metric theory of gravitational fields around still localized particles, known today as General Relativity, can operate fluently with curved spatial displacement 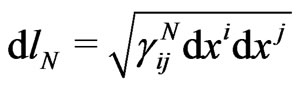 of a point mass
of a point mass 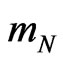 by accepting the Schwarzschild or Droste empty-space solutions [8] without specific restrictions on the space metric tensor
by accepting the Schwarzschild or Droste empty-space solutions [8] without specific restrictions on the space metric tensor
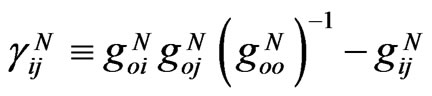 .
.
GR solutions for dynamics of the considered probe particle N are related to its space-time interval,
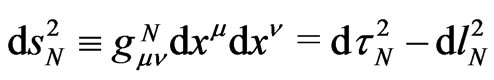 where the time element
where the time element 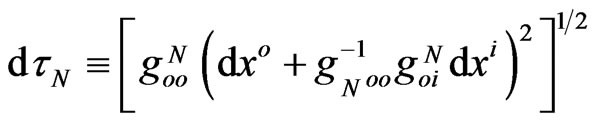
depends on the local pseudo-Riemannian metric tensor 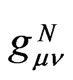 and, consequently, on local gravitational fields. Hereinafter,
and, consequently, on local gravitational fields. Hereinafter, 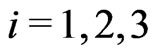 ,
, 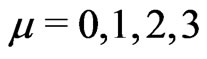 , and the speed of light c = 1 in the most of equations.
, and the speed of light c = 1 in the most of equations.
The author intends to revisit time, 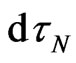 , and space,
, and space, , elements within the conventional GR four-interval
, elements within the conventional GR four-interval 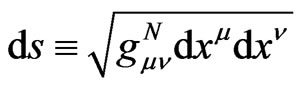 in order to prove that the time element of the freely moving mass
in order to prove that the time element of the freely moving mass 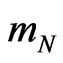 depends not only on the world time differential
depends not only on the world time differential 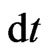 (with
(with 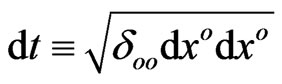 =
=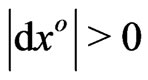 ) and gravitation, but also on space differentials or matter displacements
) and gravitation, but also on space differentials or matter displacements  in gravitational fields. Then the ratio
in gravitational fields. Then the ratio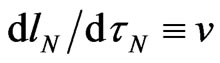 , called the physical speed in Special Relativity (SR), should non-linearly depend on spatial displacement
, called the physical speed in Special Relativity (SR), should non-linearly depend on spatial displacement 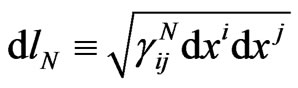 , called the space interval in SR. Nonlinear field contributions to such an anisotropic (Finslertype) time element
, called the space interval in SR. Nonlinear field contributions to such an anisotropic (Finslertype) time element 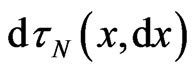 within the four-interval
within the four-interval 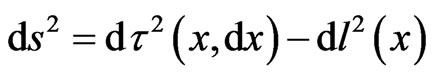 of Einstein’s Relativity may modify Schwarzschild-type metric solutions based on curved three-space around non-physical point singularities for GR energy-sources [2]. Moreover, the calculated ratio
of Einstein’s Relativity may modify Schwarzschild-type metric solutions based on curved three-space around non-physical point singularities for GR energy-sources [2]. Moreover, the calculated ratio  may differ from a real speed
may differ from a real speed 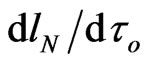 measured by a motionless observer with local proper-time
measured by a motionless observer with local proper-time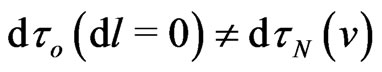 . This metric-type anisotropy of measured time rate was already confirmed by observations of the gravitational Sagnac effect when
. This metric-type anisotropy of measured time rate was already confirmed by observations of the gravitational Sagnac effect when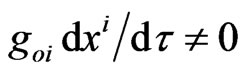 . Rigorous consideration of anisotropic physical time
. Rigorous consideration of anisotropic physical time 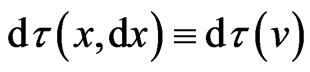 of each moving particle may preserve universal flatness of its 3-space element
of each moving particle may preserve universal flatness of its 3-space element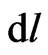 . We shall start from the 1913 Entwurf metric formalism for the geodesic motion of passive masses. Then, we shall employ the tetrad approach and analyze nonlinear relations in the anisotropic relativistic time for a passive mass under the geodesic motion. This will suggest to keep for physical reality Euclidean 3D sub-intervals in curved 4D intervals of moving probe particles.
. We shall start from the 1913 Entwurf metric formalism for the geodesic motion of passive masses. Then, we shall employ the tetrad approach and analyze nonlinear relations in the anisotropic relativistic time for a passive mass under the geodesic motion. This will suggest to keep for physical reality Euclidean 3D sub-intervals in curved 4D intervals of moving probe particles.
The first attempt to interpret GR in parallel terms of curved and flat spaces was made by Rosen [9], Einstein’s co-author of the unpublished 1936 paper about the nonexistence of plane metric waves from line singularities of cylindrical sources. Later, Sommerfeld, Schwinger, Brillouin and many other theorists tried to justify Euclidean space for better modern physics. Moreover, the original proposal of Grossmann (to use 4D Riemannian geometry for geometrization of gravitational fields in the 1913 Entwurf version of GR) relied exclusively on 3D Euclidean sub-space. Grossmann did not join further GR metric developments with curved 3D intervals. In 1913 Einstein clearly underlined that space cannot exist without matter in the Entwurf geometrization of fields. However, at that pre-quantum time there were not many options for geometrization of particles, because all (but Mie) considered them localized entities for local events. This might be the reason why in January 1916 Einstein promptly accepted Schwarzschild’s warping of 3D space around the point particle. Nonetheless, in 1939 Einstein finally rejected Schwarzschild metric singularities for physical reality. The well derived Schwarzschild’s solution has no mathematical errors in the empty-space paradigm. However, we tend to use the non-empty-space paradigm for the global superfluid overlap of self-coherent elementary particles, when each continuous particle is distributed over the entire Universe together with the elementary field. This nonlocal approach to matter can avoid difficulties of the Entwurf geometrization of fields, proposed in 1913 without geometrization of particles, and, ultimately, can avoid non-physical warping of the universal spatial ruler, which becomes the same for all local observers in the flat Universe.
Contrary to non-metric approaches to gravitation with spatial flatness, for example [10], we shall comply with the Einstein-Grossmann extension of Special Relativity (SR) to gravitation through warped space-time with nonEuclidean pseudo-geometry, founded by Lobachevsky, Bolyai and Riemann [11]. Inertia and gravitation keep the same metric nature in our reiteration of the EinsteinGrossmann approach. The proposed 4D geometrization of matter together with fields will be made under six metric bounds for  (called sometime intrinsic metric symmetries) in the GR tensor formalism for every physical object. In other words, the author is planning to revise neither Einstein’s Principle of Relativity nor the GR geometrization concept. On the contrary, I am planning further GR geometrization of continuous particles together with the already available geometrization of gravitational fields. Local nullification of the Einstein tensor curvature for paired densities of the distributed astroparticle and its field will be requested in their rest frame of references. I intend to prove, for example, that Schwarzschild’s solution for a central field is not “the only rotationally invariant GR metric extension of the SR interval”. One should admit non-empty (material) space or Newtonian stresses of the material medium-aether associated with continuous very low dense distributions of non-local gravitation/inertial mass-energies. Then bound ensembles of elementary radial energies form so called “macroscopic” bodies with sharp visual boundaries (observed exclusively due to experimental restrictions to measure fine energy densities).
(called sometime intrinsic metric symmetries) in the GR tensor formalism for every physical object. In other words, the author is planning to revise neither Einstein’s Principle of Relativity nor the GR geometrization concept. On the contrary, I am planning further GR geometrization of continuous particles together with the already available geometrization of gravitational fields. Local nullification of the Einstein tensor curvature for paired densities of the distributed astroparticle and its field will be requested in their rest frame of references. I intend to prove, for example, that Schwarzschild’s solution for a central field is not “the only rotationally invariant GR metric extension of the SR interval”. One should admit non-empty (material) space or Newtonian stresses of the material medium-aether associated with continuous very low dense distributions of non-local gravitation/inertial mass-energies. Then bound ensembles of elementary radial energies form so called “macroscopic” bodies with sharp visual boundaries (observed exclusively due to experimental restrictions to measure fine energy densities).
First, we discuss a local time element, 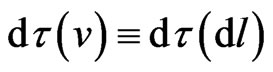 , which should be considered as a chain function of speed
, which should be considered as a chain function of speed 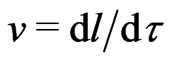 or spatial displacement
or spatial displacement 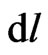 of a passive material point in external gravitational field. Then, we discuss the electric Weber-type potential energy
of a passive material point in external gravitational field. Then, we discuss the electric Weber-type potential energy

for a point planet with mass 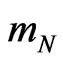 and relativistic energy
and relativistic energy 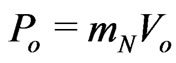 in the Sun’s static field generated by the active energy-charge
in the Sun’s static field generated by the active energy-charge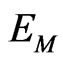 . Ultimately, this paper presents the self-contained GR scheme with the energy-to-energy interaction potential
. Ultimately, this paper presents the self-contained GR scheme with the energy-to-energy interaction potential 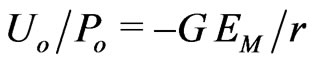 for Machian mechanics of nonlocal astroparticles with an analytical radial density
for Machian mechanics of nonlocal astroparticles with an analytical radial density 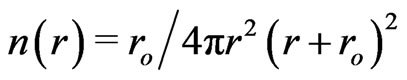 instead of the Dirac delta density
instead of the Dirac delta density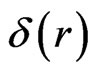 . One should see arguments for the singularity-free gravitational contribution
. One should see arguments for the singularity-free gravitational contribution 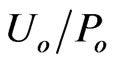 to the smooth metric tensor component
to the smooth metric tensor component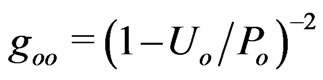 . The main challenge here was to keep the free fall universality and the GR Principle of Equivalence for all carriers of probe (passive, inertial) energies
. The main challenge here was to keep the free fall universality and the GR Principle of Equivalence for all carriers of probe (passive, inertial) energies 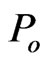 in radial fields of the Sun’s gravitational (active) energy
in radial fields of the Sun’s gravitational (active) energy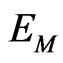 .
.
In the speed-dependent time approach, the warped GR four-interval  cannot be approximated in weak fields by pure time and pure space subintervals, like in Schwarzschild-type solutions [8] with their formal time and space metric split without chain relations. In order to justify the indivisible non-linear involvement of space displacements into physical time
cannot be approximated in weak fields by pure time and pure space subintervals, like in Schwarzschild-type solutions [8] with their formal time and space metric split without chain relations. In order to justify the indivisible non-linear involvement of space displacements into physical time 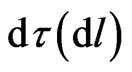 of a probe particle under the the geodesic motion, one should clarify how the already known gravitational tests of GR can be explained quantitatively without departure from spatial flatness. Then we discuss our energy-to-energy attraction under the Einstein-Grossmann geodesic motion in metric fields with flat 3-section (i.e. without Schwarzschild singularities). The author also accepts the Einstein-Infeld-Hoffmann approach (but under flat 3-space) to non-point slow-moving gyroscopes in order to describe the Gravity Probe B quantitatively.
of a probe particle under the the geodesic motion, one should clarify how the already known gravitational tests of GR can be explained quantitatively without departure from spatial flatness. Then we discuss our energy-to-energy attraction under the Einstein-Grossmann geodesic motion in metric fields with flat 3-section (i.e. without Schwarzschild singularities). The author also accepts the Einstein-Infeld-Hoffmann approach (but under flat 3-space) to non-point slow-moving gyroscopes in order to describe the Gravity Probe B quantitatively.
In 1913, Einstein and Grossmann put weak Newtonian field only into the temporal part of the Entwurf 4D interval. Today, one tends to justify that strong-field GR metric may also admit for reality six metric bounds 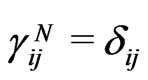 which preserve universal 3D interval in specifically curved space-time for any elementary particle N. Then the metric tensor
which preserve universal 3D interval in specifically curved space-time for any elementary particle N. Then the metric tensor 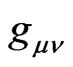 for curved 4D with flat 3- section depends on four gravitational potentials
for curved 4D with flat 3- section depends on four gravitational potentials 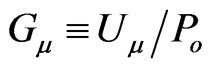 for the particle energy-charge
for the particle energy-charge
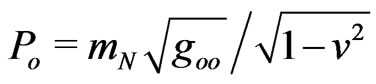 .
.
This finding matches 6 metric bounds for spatial flatness under any gravitational fields and their gauges. Since 2000, this post-Entwurf metric scheme with warped space-time, but strictly flat three-space, became consistent with the observed Universe’s large-scale flatness, confirmed at first by balloon measurements of the Cosmic Microwave Background and then by all ongoing Wilkinson Microwave Anisotropy Probe (WMAP) Observations of the flat Universe [12]. This new reading of curved 4D geometry with non-linearly dilated anisotropic time and flat non-empty space, explains quantitatively all GR tests, the known planet perihelion precession, the radar echo delay, and the gravitational light bending, for example [13].
Speed-dependent time corrections to post-Newtonian dynamics in Sun’s flat material space lead to computation results similar to numerical computations of other authors who traditionally correct Newton in empty, but curved 3-space. Observable dynamics of matter in moderate and strong static fields provides, in principle, an opportunity to distinguish our metric solutions with isotropic flat space and speed-dependent time from Schwarzschild’s solutions, based on curved 3-space and dilated time. Alternative empty-space and non-empty space paradigms can also be distinguished through different probe body dynamics in stationary fields of rotating astrophysical objects.
2. Warped Four-Space with Intrinsic Metric Symmetries for Flat Three-Space
To begin, we employ the GR tetrad formalism, for example [14,15], in covariant expressions for an elementary rest-mass 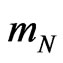 in order to justify the mathematical opportunity to keep a flat 3D subspace
in order to justify the mathematical opportunity to keep a flat 3D subspace 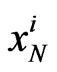 in curved fourspace
in curved fourspace 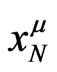 with a pseudo-Riemannian metric tensor
with a pseudo-Riemannian metric tensor 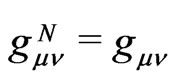 (for short). First, we rewrite the curved fourinterval,
(for short). First, we rewrite the curved fourinterval,
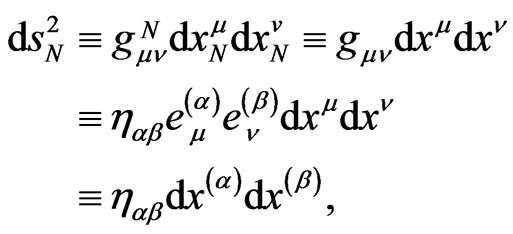
in plane coordinates 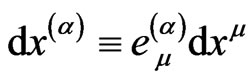 and
and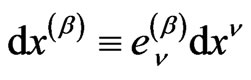 , with
, with
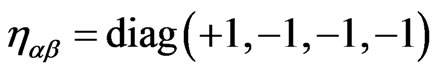 .
.
One can find 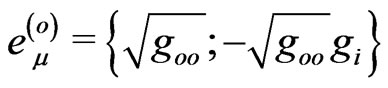 and
and 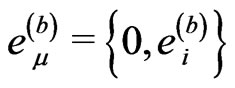 from the equality
from the equality
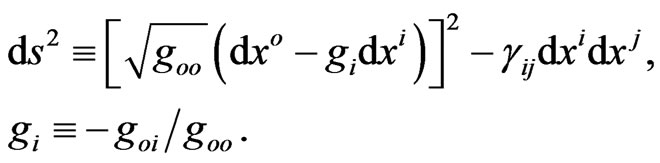
At first glance, the spatial triad 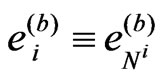 (a, b = 1,2,3 and
(a, b = 1,2,3 and 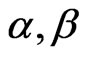 = 0,1,2,3) should always depend essentially on the gravitational fields of other particles because this triad is related to components of
= 0,1,2,3) should always depend essentially on the gravitational fields of other particles because this triad is related to components of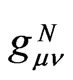 . However, this might not be the case when there are internal metric relations or bounds in the general pseudo-Riemannian metric with the warped tensor
. However, this might not be the case when there are internal metric relations or bounds in the general pseudo-Riemannian metric with the warped tensor . Shortly, a curved mathematical 4D manifold does not necessarily mean a curved 3D section for real matter (warped 2D paper in 3D trash, for example, keeps parallel Euclidean lines due to steady metric relations between neighboring points of paper).
. Shortly, a curved mathematical 4D manifold does not necessarily mean a curved 3D section for real matter (warped 2D paper in 3D trash, for example, keeps parallel Euclidean lines due to steady metric relations between neighboring points of paper).
It is not obvious that physical restrictions for four-velocities of real matter, like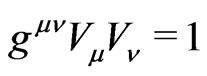 , might require to keep flat 3D sections of curved pseudo-Riemannian 4D manifolds. Therefore, let us look at three spatial components
, might require to keep flat 3D sections of curved pseudo-Riemannian 4D manifolds. Therefore, let us look at three spatial components 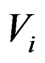 of the four-vector
of the four-vector 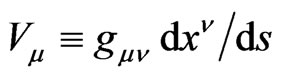 by using the conventional tetrad formalism,
by using the conventional tetrad formalism,

Here, we used 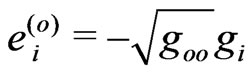 and
and
 .
.
Now one can trace that the considered equalities 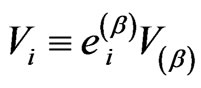 admit trivial relations
admit trivial relations 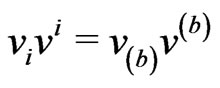 and
and
 between the curved velocities,
between the curved velocities,
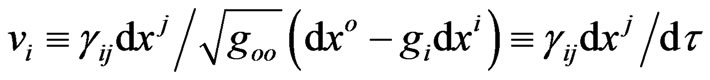 and the plane velocities,
and the plane velocities,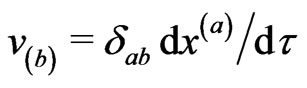 . All spatial triads for these “trivial” relations may be considered as universal Kronecker delta symbols,
. All spatial triads for these “trivial” relations may be considered as universal Kronecker delta symbols, 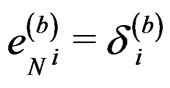 , and, consequently, the three-space metric tensor is irrelevant to gravitation fields, i.e.
, and, consequently, the three-space metric tensor is irrelevant to gravitation fields, i.e.
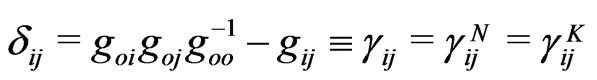 .
.
All components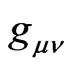 , involved in these six relations, may depend on gravitations fields or system accelerations but their combination should always keep spatial flatness under admissible coordinate transformations. One could, surely, ignore flat 3-space option within curved 4D manifold, as was suggested by the above tetrad analysis, by trying curved 3D solutions in
, involved in these six relations, may depend on gravitations fields or system accelerations but their combination should always keep spatial flatness under admissible coordinate transformations. One could, surely, ignore flat 3-space option within curved 4D manifold, as was suggested by the above tetrad analysis, by trying curved 3D solutions in 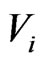 when
when . But we do not see much physical sense in such complications and, therefore, restrict GR geometrical constructions by a partial case with six metric relations
. But we do not see much physical sense in such complications and, therefore, restrict GR geometrical constructions by a partial case with six metric relations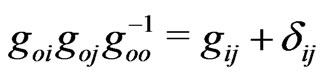 . Applications of pseudoRiemannian space-time with flat 3-sections will quantitatively describe all known gravitational experiments plus magnetic flux quantization. The latter and the Aharonov-Bohm effect require only flat 3-space for satisfactory interpretations.
. Applications of pseudoRiemannian space-time with flat 3-sections will quantitatively describe all known gravitational experiments plus magnetic flux quantization. The latter and the Aharonov-Bohm effect require only flat 3-space for satisfactory interpretations.
Again, we shall read 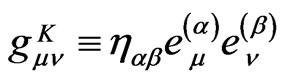 though
though
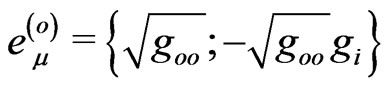
and

for all physical cases we are interested in describing. This means for our consideration that
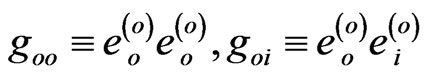 and
and
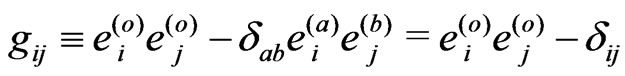 .
.
And Euclidean spatial geometry,
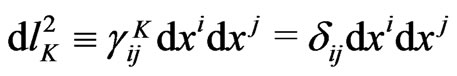 will be applied to pseudo-Riemannian 4-intervals of all particles (due to intrinsic metric relations
will be applied to pseudo-Riemannian 4-intervals of all particles (due to intrinsic metric relations
 ).
).
Contrary to universal spatial displacements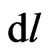 , invariant four-intervals have differently warped metrics for particles K and N, because
, invariant four-intervals have differently warped metrics for particles K and N, because 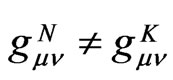 and
and 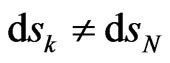 in different external fields (for example, in the two-body problem). The GR four-interval for a selected massenergy carrier,
in different external fields (for example, in the two-body problem). The GR four-interval for a selected massenergy carrier,
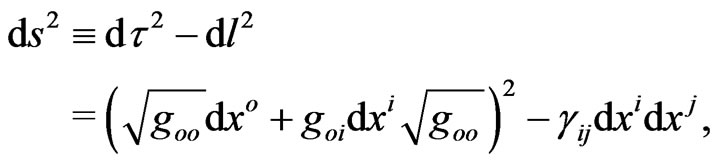 (1)
(1)
is defined for only one selected probe mass  despite notifications
despite notifications 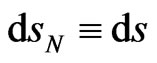 and
and 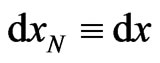 are regularly used for brevity. This geometrical 4-interval should be physically commented in terms of time
are regularly used for brevity. This geometrical 4-interval should be physically commented in terms of time 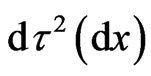 and space
and space  elements, albeit 3-space differentials
elements, albeit 3-space differentials 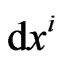 contribute to particle’s physical time
contribute to particle’s physical time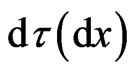 . We prove below that particles proper time
. We prove below that particles proper time 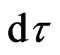 depends on
depends on 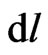 even in constant gravitational fields (where there is a first integral of motion
even in constant gravitational fields (where there is a first integral of motion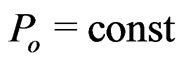 ). Such an anisotropic time element
). Such an anisotropic time element

of the moving mass  always counts its spatial displacement
always counts its spatial displacement  in a oriented gravitational field, despite the fact that it is not immediately obvious from the physical time definition for metrics with
in a oriented gravitational field, despite the fact that it is not immediately obvious from the physical time definition for metrics with . This postNewtonian phenomenon, related to the energy nature of anisotropic time, appears in nonlinear gravitational equations through the energy(velocity)-dependent potentials. Our interpretation of the warped four-interval (1), based on warped anisotropic time in isotropic non-empty flatspace rather than in empty warped space, may be considered as a prospective way for further developments of the 1913 metric gravitation through joint geometrization of distributed fields and distributed elementary particles.
. This postNewtonian phenomenon, related to the energy nature of anisotropic time, appears in nonlinear gravitational equations through the energy(velocity)-dependent potentials. Our interpretation of the warped four-interval (1), based on warped anisotropic time in isotropic non-empty flatspace rather than in empty warped space, may be considered as a prospective way for further developments of the 1913 metric gravitation through joint geometrization of distributed fields and distributed elementary particles.
Now we return to components of the four-vector 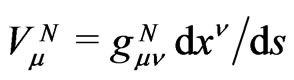 . Notice that
. Notice that

with the four-velocity
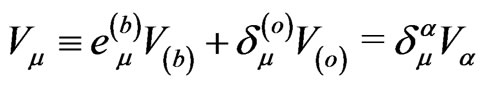 because
because 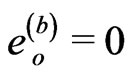 and
and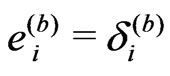 . Flat three-space geometry is a promising way to introduce gauge invariant gravitational potentials,
. Flat three-space geometry is a promising way to introduce gauge invariant gravitational potentials,
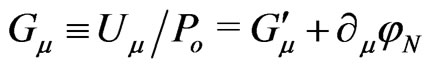
with
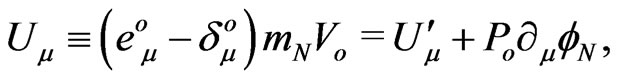
for the passive (probe) mass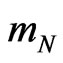 , in close analogy to four-component electromagnetic potentials for the classical electric charge. The point is that a four-momentum
, in close analogy to four-component electromagnetic potentials for the classical electric charge. The point is that a four-momentum 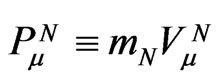 of the selected scalar mass
of the selected scalar mass 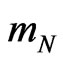 (without rotation) can be rigorously decomposed into mechanical,
(without rotation) can be rigorously decomposed into mechanical,  , and gravitational,
, and gravitational,  , parts only under strict spatial flatness,
, parts only under strict spatial flatness,
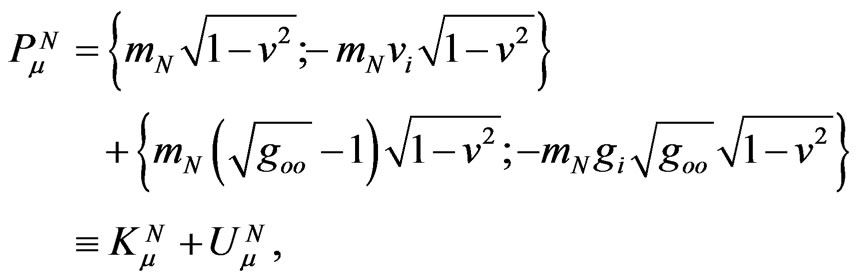 (2)
(2)
where
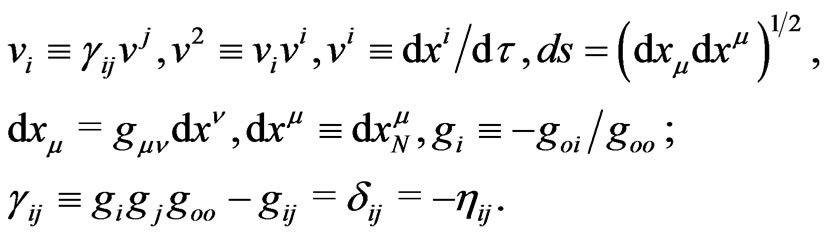
Again, we use a time-like worldline with 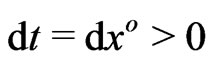 and
and 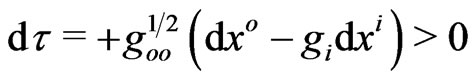 for the passive-inertial
for the passive-inertial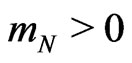 . The gravitational energy-momentum part
. The gravitational energy-momentum part  is defined in (2) for a selected mass
is defined in (2) for a selected mass 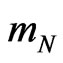 and its positively defined passive energy
and its positively defined passive energy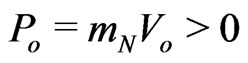 , associated with the global distribution of all other masses
, associated with the global distribution of all other masses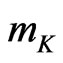 . This gravitational part,
. This gravitational part, 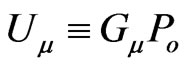 , is not a full four-vector in pseudo-Riemannian space-time, like
, is not a full four-vector in pseudo-Riemannian space-time, like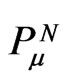 , nor is the mechanical summand
, nor is the mechanical summand .
.
Because 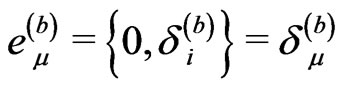 and
and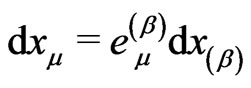 the tetrad with the zero (i.e. time) label takes the following components from (2):
the tetrad with the zero (i.e. time) label takes the following components from (2):
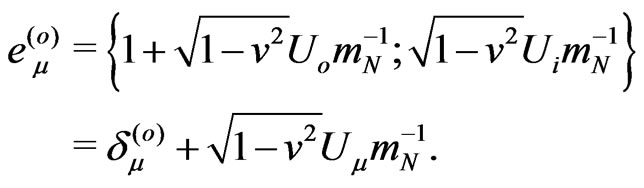
Ultimately, the tetrad 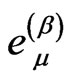 for the selected particle
for the selected particle 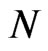 and the metric tensor
and the metric tensor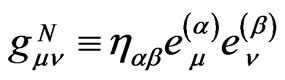 , with
, with 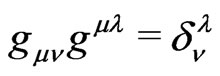 , depends in Cartesian coordinates only on the gravitational four-potential
, depends in Cartesian coordinates only on the gravitational four-potential 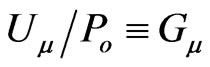 (introduced for the relativistic energy-charge
(introduced for the relativistic energy-charge 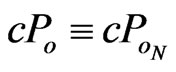 [16]),
[16]),
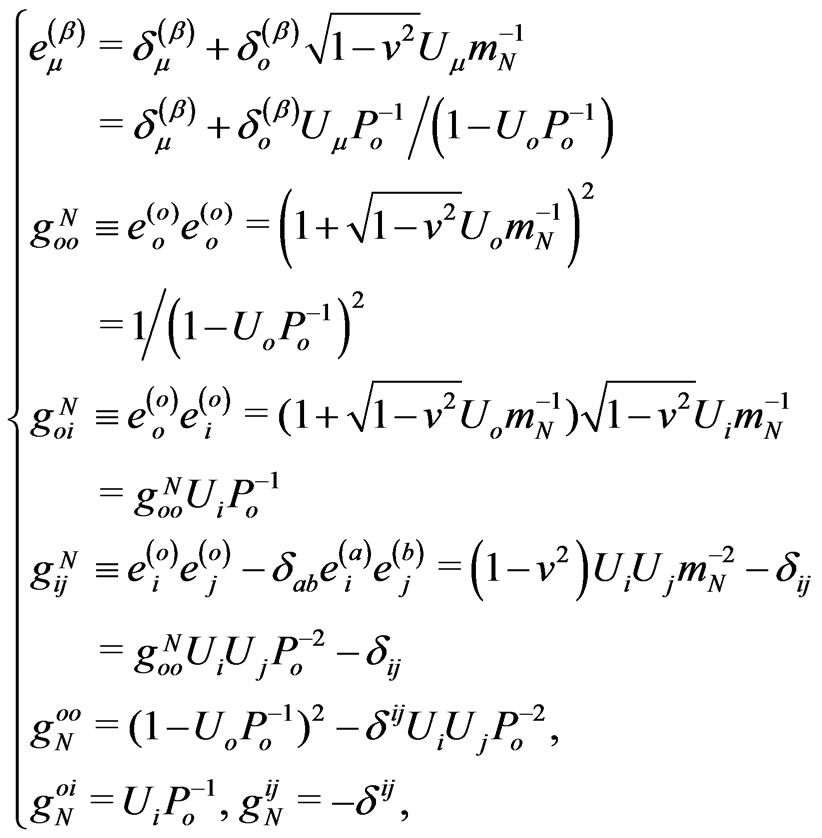 (3)
(3)
where we used 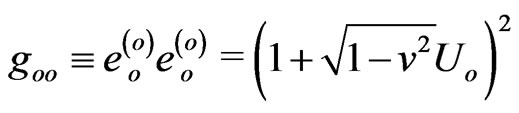 and
and 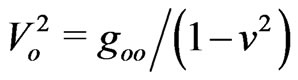 to prove that
to prove that
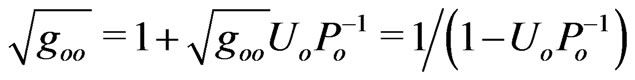 .
.
Therefore, the passive-inertial GR energy,

takes a linear superposition of kinetic and potential energies in all points of pseudo-Riemannian space-time warped by strong external fields. Note that we did not assign spin  or internal angular mechanical momentum to the Einstein-Grossmann “material point” or the probe mass
or internal angular mechanical momentum to the Einstein-Grossmann “material point” or the probe mass  with the energy-momentum (2). The affine connections for the metric tensor (3) depend only on four gravitational potentials
with the energy-momentum (2). The affine connections for the metric tensor (3) depend only on four gravitational potentials  in our space-time geometry, which is not relevant to warped manifolds with asymmetrical connections and torsion fields, for example [17].
in our space-time geometry, which is not relevant to warped manifolds with asymmetrical connections and torsion fields, for example [17].
Every component of the metric tensor in (3) depends on the gravitational part  of the probe carrier energy-momentum
of the probe carrier energy-momentum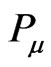 . At the same time, all the components of the three-space metric tensor,
. At the same time, all the components of the three-space metric tensor, 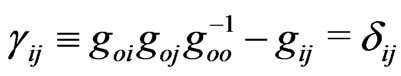 , are always independent from the gravitational potential
, are always independent from the gravitational potential 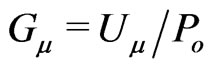 or its gauge. Such inherent metric symmetries for 3D subspace may be verified directly from (3). In fact, our tetrad, and the metric tensor, depends formally on the inharmonic Webertype potentials,
or its gauge. Such inherent metric symmetries for 3D subspace may be verified directly from (3). In fact, our tetrad, and the metric tensor, depends formally on the inharmonic Webertype potentials,
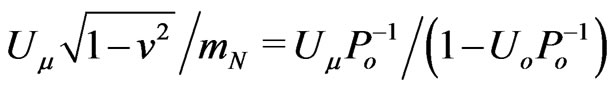 associated with the particle speed
associated with the particle speed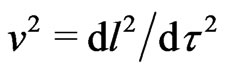 . In 1848 Weber introduced [18] the non-Coulomb potential
. In 1848 Weber introduced [18] the non-Coulomb potential 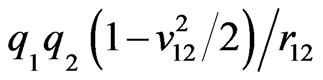 based on lab measurements of accelerating forces between moving charges
based on lab measurements of accelerating forces between moving charges 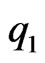 and
and 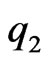 with the relative radial velocity
with the relative radial velocity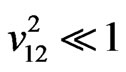 . This might was the first experimental finding that mechanical inertia and acceleration depend on the kinetic energy or speed of interacting bodies.
. This might was the first experimental finding that mechanical inertia and acceleration depend on the kinetic energy or speed of interacting bodies.
By substituting the metric tensor (3) into the interval , one can rewrite (1) and submit the chain relation for the proper time
, one can rewrite (1) and submit the chain relation for the proper time 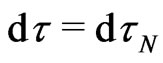 of the probe mass-energy carrier N in external gravitational fields,
of the probe mass-energy carrier N in external gravitational fields,
 (4)
(4)
Notice that the proper-time differential,
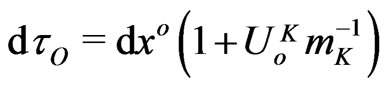 of the local observer
of the local observer , with
, with 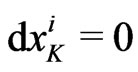 and
and , differs from the time element (4) of the moving mass
, differs from the time element (4) of the moving mass  with the GR energy-charge
with the GR energy-charge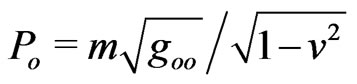 . The proper interval
. The proper interval 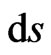 of the moving mass and its proper time element (4) depends, in general, on all four components of
of the moving mass and its proper time element (4) depends, in general, on all four components of . Therefore, the observable three-speed
. Therefore, the observable three-speed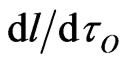 , of a moving particle always differs in relativistic gravito-mechanics from the non-linear ratio
, of a moving particle always differs in relativistic gravito-mechanics from the non-linear ratio 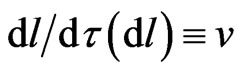 , called the particle’s physical speed (1). The chain relation
, called the particle’s physical speed (1). The chain relation  in the physical time (4) of a moving particle changes the GR interpretation of the geodesic motion and allows to apply flat 3D space for gravitational tests.
in the physical time (4) of a moving particle changes the GR interpretation of the geodesic motion and allows to apply flat 3D space for gravitational tests.
The metric tensor (3), the interval (1), and the local time element (4) are associated with warped space-time specified by external fields for one selected mass 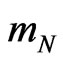 or, to be precise, for the passive energy-charge
or, to be precise, for the passive energy-charge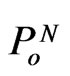 . We may employ common three-space for all elementary particles (due to universal Euclidean geometry for their spatial displacements), but we should specify warped spacetimes with differently dilated times for the mutual motion of gravitational partners. The particle’s time element
. We may employ common three-space for all elementary particles (due to universal Euclidean geometry for their spatial displacements), but we should specify warped spacetimes with differently dilated times for the mutual motion of gravitational partners. The particle’s time element 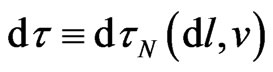 in (4) may depend on the particles velocity or displacement. Ultimately, a non-linear time rate
in (4) may depend on the particles velocity or displacement. Ultimately, a non-linear time rate 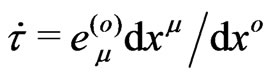 (hereinafter
(hereinafter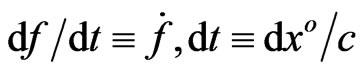 ) of moving material objects in (4) depends on the ratio
) of moving material objects in (4) depends on the ratio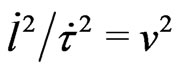 . This non-linear chain relation can be simplified in several subsequent steps through the following equalities to (4):
. This non-linear chain relation can be simplified in several subsequent steps through the following equalities to (4):
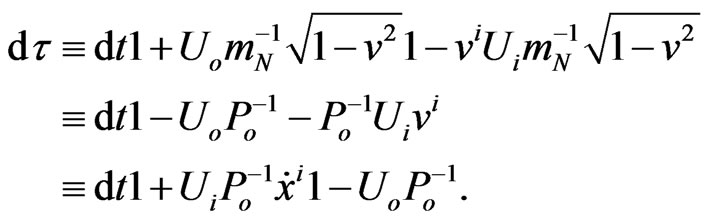 (5)
(5)
Such anisotropic time dilatation in (5) by the external four-potential 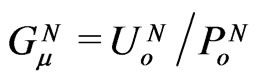 results in the gravitational Sagnac effect when an observer compares the dynamics of different elementary energy-charges
results in the gravitational Sagnac effect when an observer compares the dynamics of different elementary energy-charges  in fields with
in fields with .
.
Now, one may conclude that the anisotropic time element  in the metric interval (1) and, consequently, in the physical speed
in the metric interval (1) and, consequently, in the physical speed 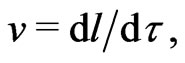 depends only on universal four potentials
depends only on universal four potentials 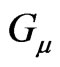 for positive probe charges
for positive probe charges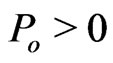 . The potential energy part
. The potential energy part 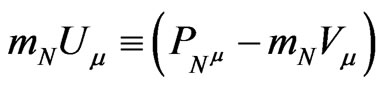 contributes to GR energy-momentum of the probe body and, therefore, to its passive energy-charge,
contributes to GR energy-momentum of the probe body and, therefore, to its passive energy-charge,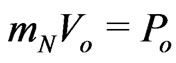 . The universal ratio
. The universal ratio 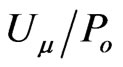 should be tried in Einstein’s gravitation as a metric field four-potential (which is not a covariant four-vector) of active gravitational charges for passive energy-charges. Contrary to Newton’s gravitation for masses, Einstein’s gravitation is the metric theory for interacting energies. The static Sun, with the active energy-charge
should be tried in Einstein’s gravitation as a metric field four-potential (which is not a covariant four-vector) of active gravitational charges for passive energy-charges. Contrary to Newton’s gravitation for masses, Einstein’s gravitation is the metric theory for interacting energies. The static Sun, with the active energy-charge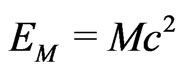 , keeps the universal potential
, keeps the universal potential 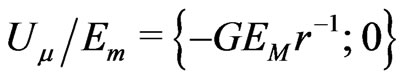 in the Sun’s frame of reference for the passive, inertial energy content
in the Sun’s frame of reference for the passive, inertial energy content  of the probe mass
of the probe mass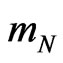 . Below, we employ the universality of the Sun’s potential,
. Below, we employ the universality of the Sun’s potential,  , for all planets in our computations for gravitational tests of General Relativity with dilated time (4)-(5) and flat material space filled everywhere by
, for all planets in our computations for gravitational tests of General Relativity with dilated time (4)-(5) and flat material space filled everywhere by  gravitational fields and the
gravitational fields and the  extended masses.
extended masses.
3. Flatspace for the Planetary Perihelion Precession
Now we consider the metric tensor (3) for a central gravitational field with a static four-potential, 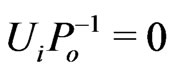 ,
, 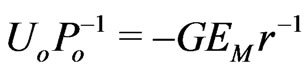 , where
, where 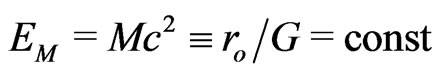 is the active gravitational energy of the ‘motionless’ Sun (in the moving Solar system). We use Euclidean geometry for the radial distance
is the active gravitational energy of the ‘motionless’ Sun (in the moving Solar system). We use Euclidean geometry for the radial distance  from the Sun’s center of spherical symmetry in agreement with spatial flatness maintained by (3) for any gravitational fourpotential
from the Sun’s center of spherical symmetry in agreement with spatial flatness maintained by (3) for any gravitational fourpotential 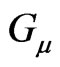 and its gauge
and its gauge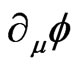 . Let us denote the energy content of a probe mass
. Let us denote the energy content of a probe mass 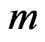 in the static central field as a passive energy-charge
in the static central field as a passive energy-charge
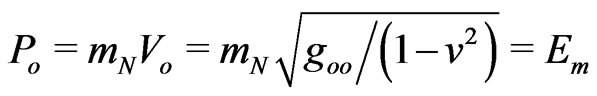 .
.
Then, the interval (1) for the passive energy carrier in a central field with 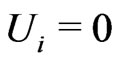 takes two equivalent presentations due to (4) and (5),
takes two equivalent presentations due to (4) and (5),
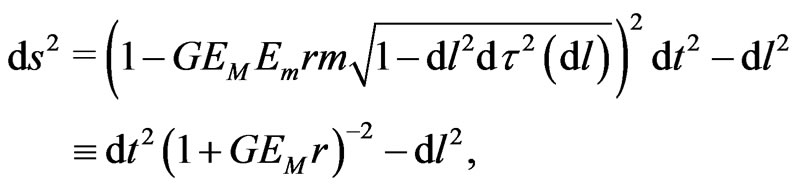 (6)
(6)
where iterations

over the chain function 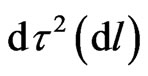 in the Lorentz factor result in
in the Lorentz factor result in  for the Sun-Mercury potential energy
for the Sun-Mercury potential energy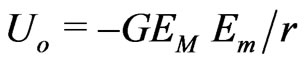 . In other words, the specific, Weber velocity-dependent potentials exhibit after chain iterations common for all probe particles local time,
. In other words, the specific, Weber velocity-dependent potentials exhibit after chain iterations common for all probe particles local time, 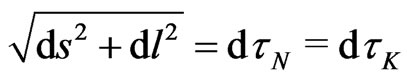 , in static fields. Spherical coordinates can be equally used in (6) for the Euclidean element
, in static fields. Spherical coordinates can be equally used in (6) for the Euclidean element in flat laboratory space.
in flat laboratory space.
The static metric solution (6) for probe elementary energy-charges in non-empty space of the radial energycharge does not coincide with the Schwarzschild metric [8] in empty space. Therefore, the Schwarzschild extension of the SR interval is not the only rotationally invariant solution which GR’s tensor formalism can propose for tests of space-time-energy self-organizations. Ultrarelativistic velocities, 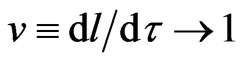 and
and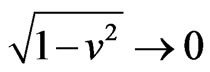 , in the Weber-type energy-to-energy interaction in (6) revise the Schwarzschild singularity. The latter is not expected at the finite radius in the energy-charge formalism of Einstein’s gravitation. Einstein, “the reluctant father of black holes”, very strictly expressed his final opinion regarding the Schwarzschild solution: ‘The essential result of this investigation is a clear understanding as to why Schwarzschild singularities do not exist in physical reality’ [19]. In authors view, Schwarzschild’s metric solution, and all Birkhoff class solutions for the empty space dogma, originates with ad hoc modeling of matter in the 1915 Einstein equation in terms of point particles. However, Einstein anticipated extended sources for his equation and for physical reality. Below, we prove that the static metric (6) corresponds to the
, in the Weber-type energy-to-energy interaction in (6) revise the Schwarzschild singularity. The latter is not expected at the finite radius in the energy-charge formalism of Einstein’s gravitation. Einstein, “the reluctant father of black holes”, very strictly expressed his final opinion regarding the Schwarzschild solution: ‘The essential result of this investigation is a clear understanding as to why Schwarzschild singularities do not exist in physical reality’ [19]. In authors view, Schwarzschild’s metric solution, and all Birkhoff class solutions for the empty space dogma, originates with ad hoc modeling of matter in the 1915 Einstein equation in terms of point particles. However, Einstein anticipated extended sources for his equation and for physical reality. Below, we prove that the static metric (6) corresponds to the  radial energycharge or the extended source of gravity. Therefore, our analysis denies the empty space paradigm. Non-empty material space is in full agreement with Einstein’s idea of continuous sources and Newton’s “absurd” interpretation of distant attractions through stresses in an invisible material ether (called in 1686 as “God’s sensorium”).
radial energycharge or the extended source of gravity. Therefore, our analysis denies the empty space paradigm. Non-empty material space is in full agreement with Einstein’s idea of continuous sources and Newton’s “absurd” interpretation of distant attractions through stresses in an invisible material ether (called in 1686 as “God’s sensorium”).
Our next task is to derive integrals of motion for the passive (probe) mass-energy in a strong central field from the geodesic equations
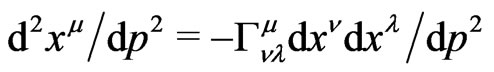 .
.
Nonzero affine connections 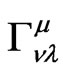 for the metric (6) take the following components:
for the metric (6) take the following components:


and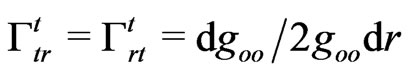 , where
, where 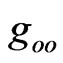 is the function next to
is the function next to 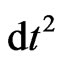 in the interval (6),
in the interval (6), .
.
By following the verified approach with 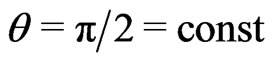 for the isotropic central field, for example [15], and by substituting flatspace connections
for the isotropic central field, for example [15], and by substituting flatspace connections 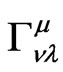 into GR’s geodesic equations, one can define the parametric differential
into GR’s geodesic equations, one can define the parametric differential 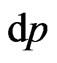 and write the following gravitational relations,
and write the following gravitational relations,
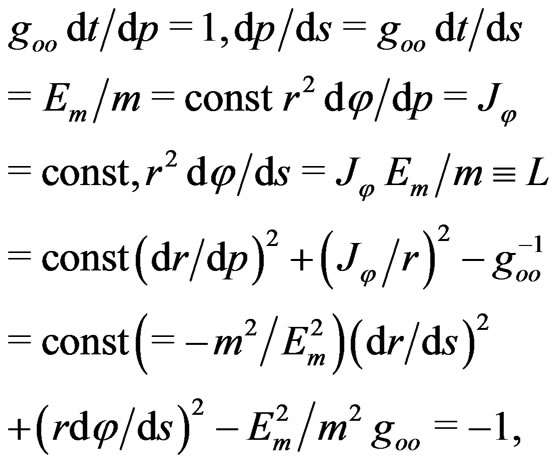 (7)
(7)
with the first integrals  and
and 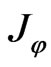 of the relativistic motion in strong static fields.
of the relativistic motion in strong static fields.
The last line in (7) is the interval equation 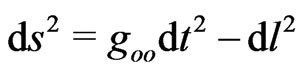 with two integrals of motion
with two integrals of motion 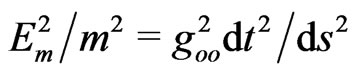 and
and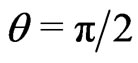 . Therefore, the scalar invariant (6) is actually the equation of motion for the constant energy charge
. Therefore, the scalar invariant (6) is actually the equation of motion for the constant energy charge 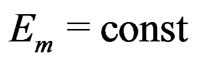 in a central field with the static Weber-type potential
in a central field with the static Weber-type potential
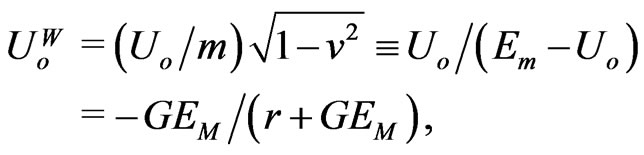
which is inharmonic for the Laplacian, . Recall that Schwarzschild’s curved 3D solution not only differs from (6), but results in conceptual inconsistencies [20] for the Einstein equation. We can use (6) and (7) for relativistic motion in strong central fields in order to reinforce the ignored statement of Einstein that Schwarzschild singularities do not exist in physical reality. There are no grounds for metric singularities either in the interval (6), or in the radial potential
. Recall that Schwarzschild’s curved 3D solution not only differs from (6), but results in conceptual inconsistencies [20] for the Einstein equation. We can use (6) and (7) for relativistic motion in strong central fields in order to reinforce the ignored statement of Einstein that Schwarzschild singularities do not exist in physical reality. There are no grounds for metric singularities either in the interval (6), or in the radial potential 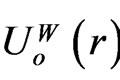 for
for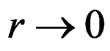 , because
, because 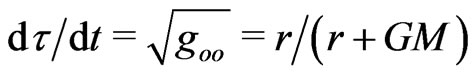 is a smooth function. One can verify that the non-empty space metric tensor (3), as well as
is a smooth function. One can verify that the non-empty space metric tensor (3), as well as , does correspond to the continuous energy-source in the 1915 Einstein equation.
, does correspond to the continuous energy-source in the 1915 Einstein equation.
The strong field relations (6) and (7) can be used, for example, for computations of planetary perihelion precession in the solar system. The planet’s gravitational energy for the GR energy-to-energy attraction, 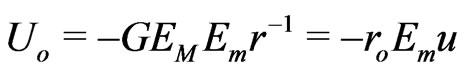 , where
, where 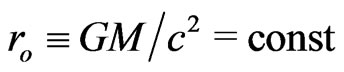 and
and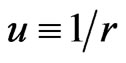 , is small compared to the planet’s energy,
, is small compared to the planet’s energy,  , that corresponds to the non-relativistic motion of a planet N (with
, that corresponds to the non-relativistic motion of a planet N (with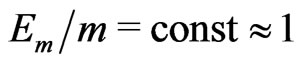 ,
, 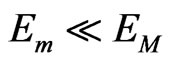 , and
, and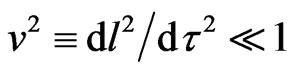 ) in the Sun’s rest frame, with
) in the Sun’s rest frame, with . The GR time element for the planet reads from (6) or (7) as
. The GR time element for the planet reads from (6) or (7) as
 (8)
(8)
where we set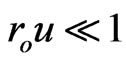 ,
, 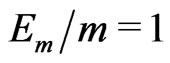 ,
, 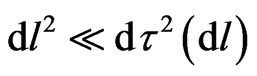 , and
, and .
.
The field term with spatial displacement  on the right hand side of (8) belongs to the physical time element within the invariant
on the right hand side of (8) belongs to the physical time element within the invariant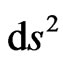 . This displacement corresponds to the non-linear chain nature of anisotropic time
. This displacement corresponds to the non-linear chain nature of anisotropic time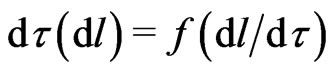 , originating from the Webertype energy potential
, originating from the Webertype energy potential 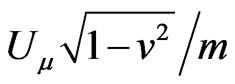 in (3). There is no departure from Euclidean space geometry with the flat metric
in (3). There is no departure from Euclidean space geometry with the flat metric
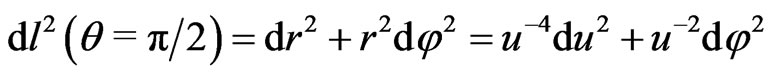
in the chain reading of geometrical intervals (6) or (8). Again, a particle’s non-linear time with chain spatial displacement  differs in (8) from the proper-time
differs in (8) from the proper-time 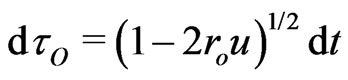 of the local (motionless) observer. Displacement corrections,
of the local (motionless) observer. Displacement corrections, 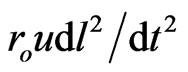 , for the non-relativistic limit are very small compared to the main gravitational corrections,
, for the non-relativistic limit are very small compared to the main gravitational corrections,  , to Newtonian time rate
, to Newtonian time rate . However, the chain dependence of a particle’s time element
. However, the chain dependence of a particle’s time element  from spatial displacement
from spatial displacement 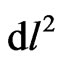 accounts for the reverse value of this time element,
accounts for the reverse value of this time element, 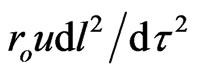 , that is ultimately a way to restore strict spatial flatness at all orders of Einstein’s metric gravitation. Here there is some kind of analogy with electrodynamics where small contributions of Maxwell’s displacement currents restore the strict charge conservation in Ampere’s quasi-stationary magnetic law.
, that is ultimately a way to restore strict spatial flatness at all orders of Einstein’s metric gravitation. Here there is some kind of analogy with electrodynamics where small contributions of Maxwell’s displacement currents restore the strict charge conservation in Ampere’s quasi-stationary magnetic law.
Two integrals of motion 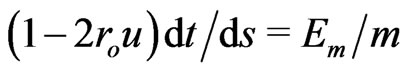 and
and 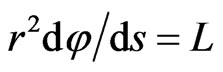 result from (7) and (8) for weak fields in a rosette motion of planets,
result from (7) and (8) for weak fields in a rosette motion of planets,
 (9)
(9)
where 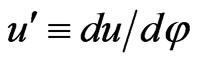 and
and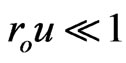 . Indeed, (9) may be differentiated with respect to the polar angle
. Indeed, (9) may be differentiated with respect to the polar angle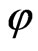 ,
,
 (10)
(10)
by keeping only the largest gravitational terms. This equation may be solved in two steps when a noncorrected Newtonian solution, 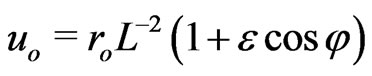 , is substituted into the GR correction terms at the right hand side of (10).
, is substituted into the GR correction terms at the right hand side of (10).
The most important correction (which is summed over century rotations of the planets) is related to the “resonance” (proportional to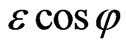 ) GR terms. Therefore, one may ignore in (10) all corrections apart from
) GR terms. Therefore, one may ignore in (10) all corrections apart from 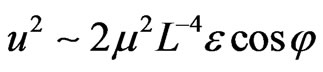 and
and . Then the approximate equation for the rosette motion,
. Then the approximate equation for the rosette motion, 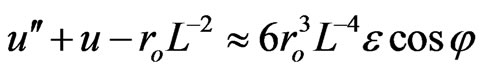 , leads to the well known perihelion precession
, leads to the well known perihelion precession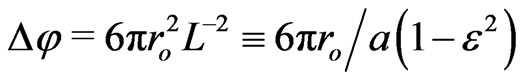 , which may also be derived through Schwarzschild’s metric approximations with warped three-space, as in [13-15].
, which may also be derived through Schwarzschild’s metric approximations with warped three-space, as in [13-15].
It is important to emphasize that the observed result for a planet perihelion precession 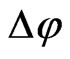 (in the Solar nonempty flatspace with dilated time by Sun’s energy densities) has been derived here from the invariant fourinterval (1) under flat three-space,
(in the Solar nonempty flatspace with dilated time by Sun’s energy densities) has been derived here from the invariant fourinterval (1) under flat three-space, 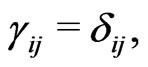 rather than under empty but curved three-space.
rather than under empty but curved three-space.
4. The Radar Echo Delay in Flatspace
The gravitational redshift of light frequency  can be considered a direct confirmation that gravity couples to the energy content of matter, including the massless photon’s energy
can be considered a direct confirmation that gravity couples to the energy content of matter, including the massless photon’s energy , rather than to the scalar mass of the particle. Indeed, Einstein’s direct statement
, rather than to the scalar mass of the particle. Indeed, Einstein’s direct statement 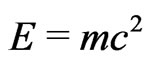 for all rest-mass particles is well proved, but the inverse reading,
for all rest-mass particles is well proved, but the inverse reading, 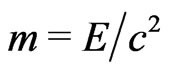 , does not work for electromagnetic waves (with
, does not work for electromagnetic waves (with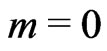 ) and requires a new notion, the wave energy-charge
) and requires a new notion, the wave energy-charge 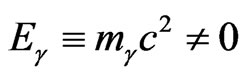 or the relativistic mass
or the relativistic mass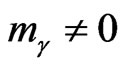 .
.
In 1907, Einstein introduced the Principle of Equivalence for a uniformly accelerated body and concluded that its potential energy depends on the gravitationally passive (“heavy”) mass associated with the inertial mass [21]. This correct conclusion of Einstein was generalized in a wrong way that any energy, including light, has a “relativistic mass” (the gravitational energy-charge in our terminology) for Newtons mechanics. Proponents of this generalization in question proposed that photon’s “relativistic mass” is attracted by the Sun’s mass M in agreement with the measured redshift
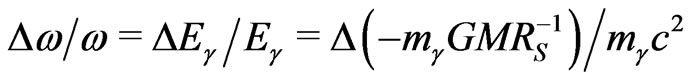 .
.
Nonetheless, the coherent application (in the absence of the correct EM wave equations in gravitational fields) of the “relativistic mass” to zero-mass waves promptly resulted in the underestimated light deflection, 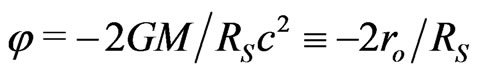 , for the “mechanical free fall” of photons in the Sun’s gravitational field [22]. In 1917, when Schwarzschild’s option [8] for spatial curvature had been tried for all GR solutions, the new nonNewtonian light deflection,
, for the “mechanical free fall” of photons in the Sun’s gravitational field [22]. In 1917, when Schwarzschild’s option [8] for spatial curvature had been tried for all GR solutions, the new nonNewtonian light deflection, 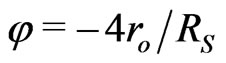 , had been predicted due to additional contributions from the supposed spatial curvature in question. Later, all measurements supported this curve-space modification for the “relativistic mass” deflection by the Sun that provided false “experimental evidences” of non-Euclidean three-space in contemporary developments of metric gravitation.
, had been predicted due to additional contributions from the supposed spatial curvature in question. Later, all measurements supported this curve-space modification for the “relativistic mass” deflection by the Sun that provided false “experimental evidences” of non-Euclidean three-space in contemporary developments of metric gravitation.
Below, we prove that Einstein’s GR for the Maxwell wave equation firmly maintains the flatspace concept for interpretation of light phenomena in gravitational fields if one coherently couples the Sun’s rest energy to the photon’s wave energy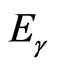 . We consider both the radar echo delay and the gravitational deflection of light by coupling its energy-charge with local gravitational potentials. Our purpose is to verify that Euclidean space can match the known measurements [13,23,24] of light phenomena in the Solar system. Let us consider a static gravitational field (
. We consider both the radar echo delay and the gravitational deflection of light by coupling its energy-charge with local gravitational potentials. Our purpose is to verify that Euclidean space can match the known measurements [13,23,24] of light phenomena in the Solar system. Let us consider a static gravitational field ( , for simplicity), where the physical slowness of photons,
, for simplicity), where the physical slowness of photons, 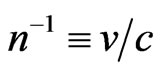 , can be derived directly from the covariant Maxwell equations [14],
, can be derived directly from the covariant Maxwell equations [14],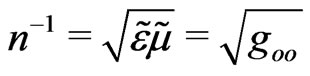 . Recall that a motionless local observer associates
. Recall that a motionless local observer associates 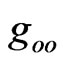 with the gravitational potential
with the gravitational potential 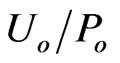 at a given point. The light velocity
at a given point. The light velocity , measured by this observer, as well as the observed light frequency
, measured by this observer, as well as the observed light frequency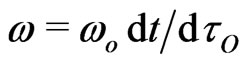 , is to be specified with respect to the observer’s time rate
, is to be specified with respect to the observer’s time rate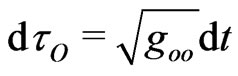 . This consideration complies with Einsteins approach, where the light’s redshift is associated with different clock rates (of local observers) in the Sun’s gravitational potential [21].
. This consideration complies with Einsteins approach, where the light’s redshift is associated with different clock rates (of local observers) in the Sun’s gravitational potential [21].
Compared to the physical speed of light, 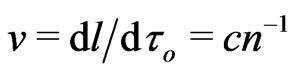 , its coordinate speed
, its coordinate speed
 (11)
(11)
is double-shifted by the gravitational potential 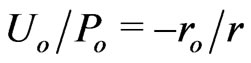 , where
, where 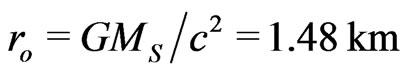 and
and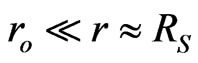 . Notice that both the local physical slowness
. Notice that both the local physical slowness
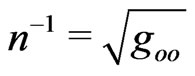 and the observer time dilation
and the observer time dilation
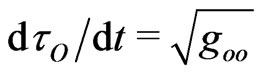 are responsible for the double slowness of the coordinate velocity (11), which is relevant to observations of light coordinates or rays under gravitational tests.
are responsible for the double slowness of the coordinate velocity (11), which is relevant to observations of light coordinates or rays under gravitational tests.
A world time delay of Mercury’s radar echo reads through relation (11) as
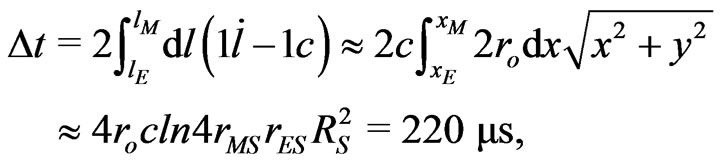 (12)
(12)
where 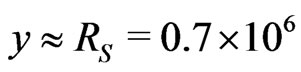 km is the radius of the Sun, while
km is the radius of the Sun, while  km and
km and 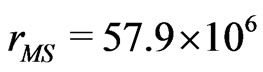 km are the Earth-Sun and Mercury-Sun distances, respectively. Notice that in flat space we use the Euclidean metric for spatial distance,
km are the Earth-Sun and Mercury-Sun distances, respectively. Notice that in flat space we use the Euclidean metric for spatial distance, 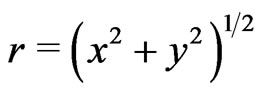 , between the Sun’s center (0,0) and any point (x, y) on the photonic ray. One can measure in the Earth’s laboratory only the physical time delay
, between the Sun’s center (0,0) and any point (x, y) on the photonic ray. One can measure in the Earth’s laboratory only the physical time delay , which practically coincides with the world time delay
, which practically coincides with the world time delay 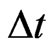 in the Earth’s weak field, i.e.
in the Earth’s weak field, i.e.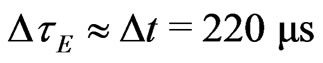 . From here, the known experimental results [13,24] correspond to the radar echo delay (12), based on strictly flat three-space and dilated time as in 1913 Entwurf metric scheme.
. From here, the known experimental results [13,24] correspond to the radar echo delay (12), based on strictly flat three-space and dilated time as in 1913 Entwurf metric scheme.
5. Gravitational Light Bending in Non-Empty Flatspace
A coordinate angular deflection 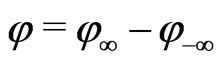 of a light wave front in the Sun’s gravitational field can be promptly derived in flat space geometry by using the coordinate velocity (11) for observations,
of a light wave front in the Sun’s gravitational field can be promptly derived in flat space geometry by using the coordinate velocity (11) for observations,
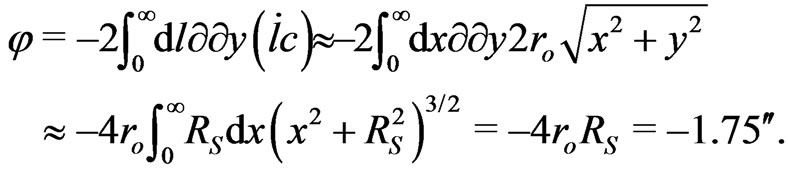 (13)
(13)
The most rigorous classical procedure to derive the ray deflection (13) is to apply the verified Fermat principle to light waves. This basic principle of physics should also justify spatial flatness under suitable applications [25].
In agreement with Einstein’s original consideration [21], one may relate the vector component 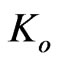 in the scalar wave equation
in the scalar wave equation 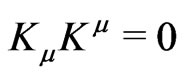 to the measured (physical) energy-frequency
to the measured (physical) energy-frequency 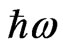 of the photon
of the photon 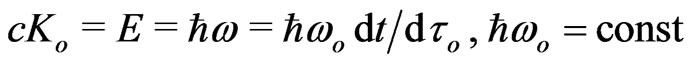 ). Recall that
). Recall that 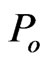 is also the measured particle’s energy in the similar equation,
is also the measured particle’s energy in the similar equation, 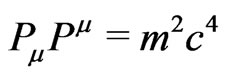 , for a rest-mass particle. The scalar wave equation
, for a rest-mass particle. The scalar wave equation  has the following solution for the electromagnetic wave,
has the following solution for the electromagnetic wave,
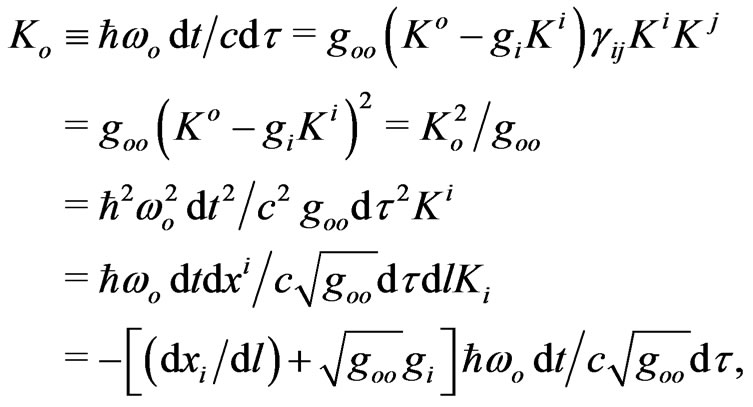 (14)
(14)
with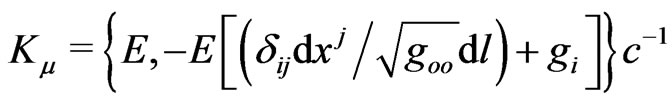 .
.
The Fermat-type variations with respect to 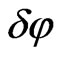 and
and 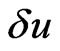 (
(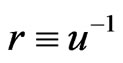 ,
,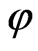 , and
, and  are the spherical coordinates) for photons in a static gravitational field are
are the spherical coordinates) for photons in a static gravitational field are
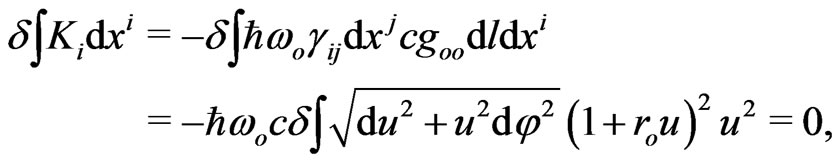 (15)
(15)
(where ,
, 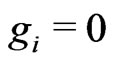 ,
, 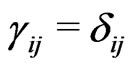 ,
, 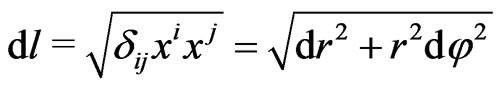 ) resulting in a couple of light ray equations for
) resulting in a couple of light ray equations for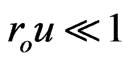 ,
,
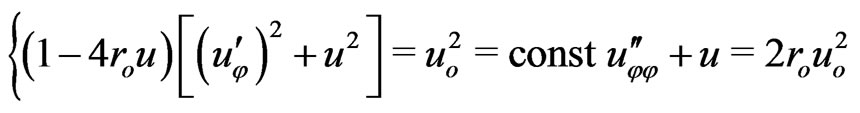 (16)
(16)
Solutions of (16),
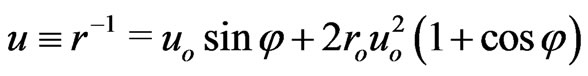
and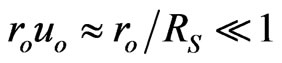 , may be used for the Sun’s weak field. The propagation of light from
, may be used for the Sun’s weak field. The propagation of light from
 to
to 
corresponds to the angular deflection
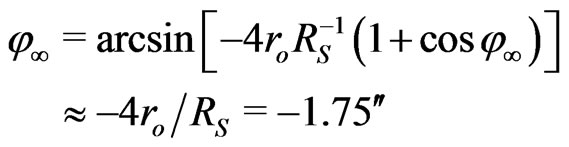
from the light’s initial direction. This deflection coincides with (13) and is in agreement with the known measurements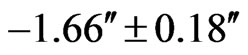 , for example [13].
, for example [13].
We may conclude that there is no need to warp Euclidean three-space for the explanation of the “non-Newtonian” light deflections if one strictly follows Einstein’s original approach to light in gravitational fields [21]. In fact, the massless electromagnetic energy exhibits an inhomogeneous slowness of its physical velocity, 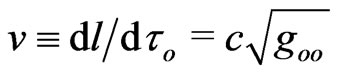 , and, therefore, a double slowness of the coordinate velocity,
, and, therefore, a double slowness of the coordinate velocity,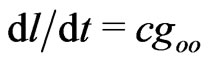 . This coordinate velocity slowness is related to the coordinate bending of light measured by observers. In closing, the variational Fermat’s principle supports Entwurf physics of Einstein and Grossmann with dilated time and strict spatial flatness for light in the Solar system.
. This coordinate velocity slowness is related to the coordinate bending of light measured by observers. In closing, the variational Fermat’s principle supports Entwurf physics of Einstein and Grossmann with dilated time and strict spatial flatness for light in the Solar system.
6. Geodetic and Frame-Dragging Precessions of Orbiting Gyroscopes
Precession of the orbiting gyroscopes in the Gravity Probe B Experiment [26] has been compared only with Schiffs formula [27] based on the Schwarzschild-type metric for curved and empty 3D space. Here the author plans to criticize the point spin model for GP-B computations in favor of the regular Einstein-Infeld-Hoffman approach to slowly rotating distributions of masses. This original GR approach practically coincides in the weak Earths field with our flatspace reading of Einstein’s physics. Recall that our Entwurf-type space interval is strictly flat due to the intrinsic metric bounds in the GR four-interval (1) with the metric tensor (3). However, the GR tensor formalism can be universally applied to any warped space-time manifold with or without intrinsic metric bounds.
By following Schiff and many other point particle proponents in gravitation, one has to assume for a moment that the vector geodesic equation,
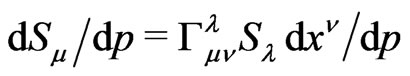 in pseudo-Riemannian fourspace with only symmetrical connections,
in pseudo-Riemannian fourspace with only symmetrical connections, 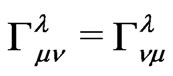 , may be applied to the point spin “four-vector”
, may be applied to the point spin “four-vector”  with “invariant” bounds
with “invariant” bounds 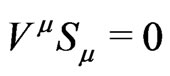 or
or 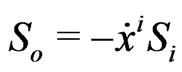 for orthonormal four-vectors,
for orthonormal four-vectors,
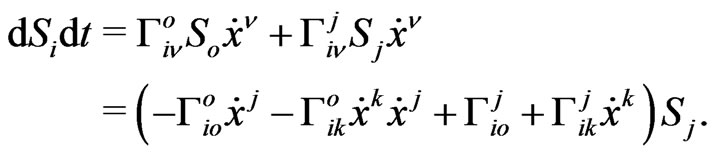 (17)
(17)
Our flat-space for a strong static field with (3) and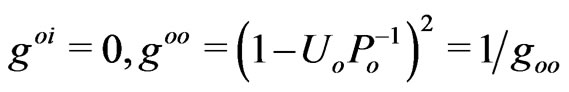 , and
, and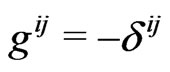 , would formally maintain an inertial conservation,
, would formally maintain an inertial conservation,
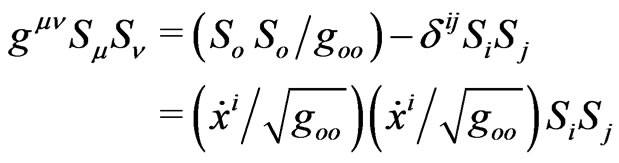
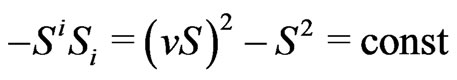 in agreement with Einstein’s teaching for a free-falling body. At the same time, Schwarzschild’s metric option (curved space) tends to suggest [15,27] the non-compensated Newtonian potential
in agreement with Einstein’s teaching for a free-falling body. At the same time, Schwarzschild’s metric option (curved space) tends to suggest [15,27] the non-compensated Newtonian potential 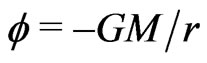 even in the “free fall” equation,
even in the “free fall” equation,
 .
.
Therefore, formal applications of the Einstein-Grossmann geodesic relations (derived for spatial translations of material points) to localized spins 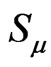 (which are not four-vectors in 4D manifolds with symmetrical affine connections) contradict the spirit of GR inertial motion and, ultimately, the Principle of Equivalence.
(which are not four-vectors in 4D manifolds with symmetrical affine connections) contradict the spirit of GR inertial motion and, ultimately, the Principle of Equivalence.
Our affine connections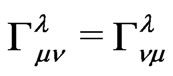 , related to the metric tensor (3), depend only on four field potentials
, related to the metric tensor (3), depend only on four field potentials 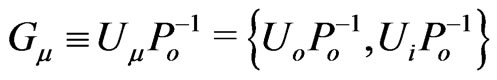 . This post-Entwurf metric tensor has been introduced for the local energy-momentum (2) without any rotational or spin components. Moreover, neither the mechanical part,
. This post-Entwurf metric tensor has been introduced for the local energy-momentum (2) without any rotational or spin components. Moreover, neither the mechanical part,  , nor the gravitational part,
, nor the gravitational part,  , in (2) are separately covariant four-vectors in warped space-time with the metric tensor (3). Therefore, there are no optimistic grounds to believe that four spin components
, in (2) are separately covariant four-vectors in warped space-time with the metric tensor (3). Therefore, there are no optimistic grounds to believe that four spin components 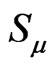 might accidentally form a covariant four vector in space-time with symmetrical connections for translation of the energy-momentum fourvector,
might accidentally form a covariant four vector in space-time with symmetrical connections for translation of the energy-momentum fourvector,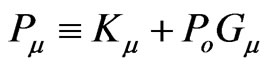 . Nonetheless, we try by chance these symmetrical connections for the point spin avenue (17) in question in constant fields (when
. Nonetheless, we try by chance these symmetrical connections for the point spin avenue (17) in question in constant fields (when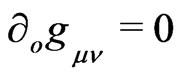 , for simplicity),
, for simplicity),
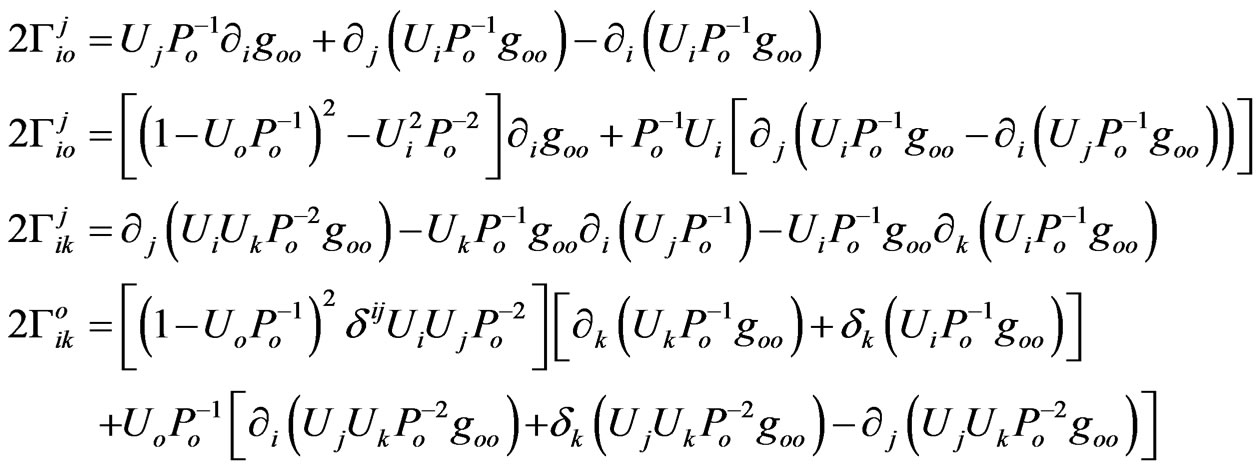 (18)
(18)
One could start with 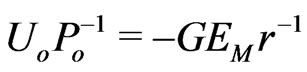 and
and 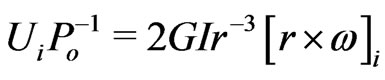 for the homogeneous spherical mass M rotating with low angular velocity, i.e.
for the homogeneous spherical mass M rotating with low angular velocity, i.e.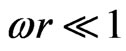 ,
, 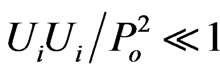 ,
, 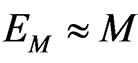 , and
, and 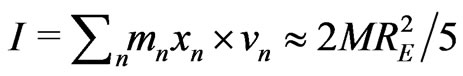 for
for 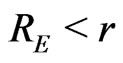 [14]. Then, by keeping only linear terms with respect to
[14]. Then, by keeping only linear terms with respect to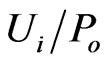 , one can rewrite (17) for a slowly rotating gravitational field:
, one can rewrite (17) for a slowly rotating gravitational field:
 (19)
(19)
The last three terms on the right-hand side of (19) are responsible for frame rotation and frame dragging, which vanish for non-rotating centers when 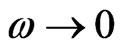 and
and 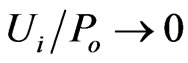 . Precessions of the constant magnitude vector
. Precessions of the constant magnitude vector , obtained for the weakfield limit of
, obtained for the weakfield limit of
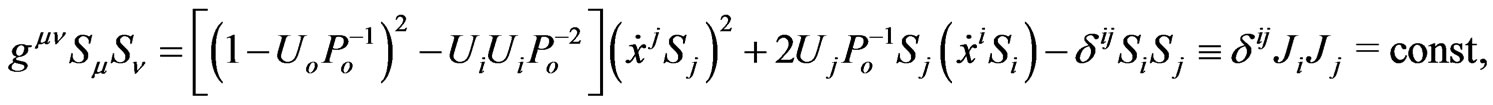
when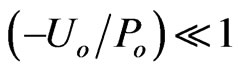 ,
,  , and
, and  in (19),
in (19),
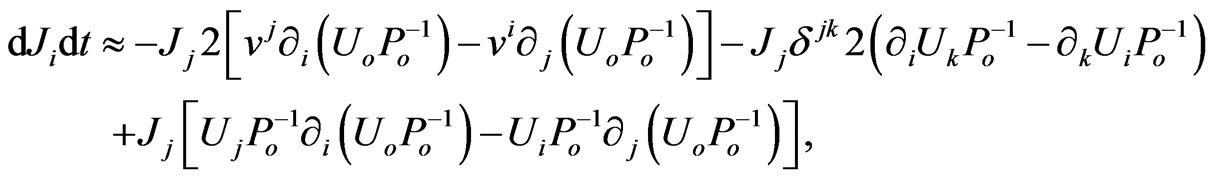 (20)
(20)
may be compared with Schiff’s non-relativistic prediction 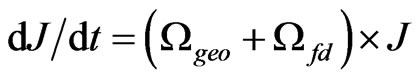 for Gravity Probe B.
for Gravity Probe B.
The second summand at the right hand side of (20), ![]() , takes exactly Schiff’s answer [27] for the frame-dragging precession,
, takes exactly Schiff’s answer [27] for the frame-dragging precession,
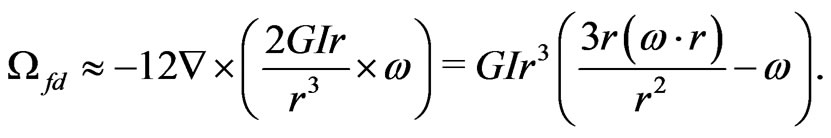 (21)
(21)
The first and third precession terms in (20) depend on the Earth’s radial field  and they count together geodetic and frame phenomena. These terms provide
and they count together geodetic and frame phenomena. These terms provide
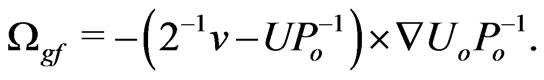 Such a precession for a point spin model, formally borrowed from the Einstein-Grossmann theory for the probe mass without rotation, fails to reiterate the already well verified de Sitter geodetic precession,
Such a precession for a point spin model, formally borrowed from the Einstein-Grossmann theory for the probe mass without rotation, fails to reiterate the already well verified de Sitter geodetic precession, 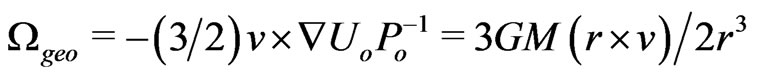 of the Earth-Moon gyroscope in the Sun’s field, where
of the Earth-Moon gyroscope in the Sun’s field, where . Why does the Einstein-Grossmann geodesic point mass fail for physics of spins and mass rotations?
. Why does the Einstein-Grossmann geodesic point mass fail for physics of spins and mass rotations?
First of all, there is a clear mathematical reason to reject point spins from the Einstein-Grossman metric formalism. The point spin approach to GR matter cannot justify that 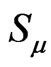 is a covariant four-vector in pseudo-Riemannian space-time where the metric tensor is defined exclusively for matter without self-rotations or for the four-momentum of a probe particle without spin. Therefore, one cannot place
is a covariant four-vector in pseudo-Riemannian space-time where the metric tensor is defined exclusively for matter without self-rotations or for the four-momentum of a probe particle without spin. Therefore, one cannot place  into the Einstein-Grossmann geodesic equation with symmetrical connections. RiemannCartan geometries with the affine torsion and asymmerical connection [17] are still under discussions for proper applications.
into the Einstein-Grossmann geodesic equation with symmetrical connections. RiemannCartan geometries with the affine torsion and asymmerical connection [17] are still under discussions for proper applications.
In 1938 Einstein already answered the point spin question by developing with Infeld and Hoffmann relativistic dynamics of slowly moving distributions of active and passive masses. It is well known (Weyl in 1923 and Einstein-Infeld-Hoffmann in 1938 for example [14]) that the inhomogeneous GR time dilation (or inhomogeneous 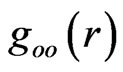 for mass elements rotating over a joint axis) defines a relativistic Lagrangian for the classical nonpoint gyroscope. Therefore, Einstein’s relativity quantitatively explains the de Sitter precession through local non-Newtonian time rates for distributed rotating systems. The non-Newtonian (three-times enhanced) precession originates exclusively from different GR time rates in neighboring material points, rather than from a local space curvature in question for the ill-defined GR spin of a point mass. The author does not understand Schiffs reasons to ignore Einstein-Infeld-Hoffmann physics and Weyl results for relativistic gyroscopes prior to testing General Relativity through rotation of masses.
for mass elements rotating over a joint axis) defines a relativistic Lagrangian for the classical nonpoint gyroscope. Therefore, Einstein’s relativity quantitatively explains the de Sitter precession through local non-Newtonian time rates for distributed rotating systems. The non-Newtonian (three-times enhanced) precession originates exclusively from different GR time rates in neighboring material points, rather than from a local space curvature in question for the ill-defined GR spin of a point mass. The author does not understand Schiffs reasons to ignore Einstein-Infeld-Hoffmann physics and Weyl results for relativistic gyroscopes prior to testing General Relativity through rotation of masses.
The Einstein-Hilbert tensor formalism for energy densities of a gravitational source (rather than for a point source) requires non-Schwarzschildian interpretation of all gravitational tests, including Lunar-Laser-Ranging and Gravity Probe B data. In authors view, the 1913 Einstein-Grossmann geodesic motion in pseudo-Riemannian space-time with flat space can provide a physical basis for translational dynamics of only point particles, but not for self-rotations of distributed relativistic matter. Point spin models for geodetic and frame-dragging angular drifts of free-falling gyroscopes cannot be reasonable for GR physics even under formal success of pointspin approximations for the observable geodetic precession. Possible speculations that the de Sitter geodetic precession of the Earth-Moon gyroscope or that the Mercury perihelion precession have already confirmed nonEuclidean space geometry are against proper applications of the well-tested GR time dilation by gravitational fields, and, therefore, against Einstein-Infeld-Hoffmann’s physics of slowly rotating systems having finite active/ passive masses at finite dimensions. In fact, the available GP-B releases (einstein.stanford.edu) of the processed geodetic precession data perfectly confirmed time dilatation for Einstein-Infeld-Hoffmann rotating distributions of masses. Lunar laser ranging of the Earth-Moon gyroscope and the GP-B geodetic precession are irrelevant, in fact, to experimental proofs of space warping by the missing inch. These tests are equally irrelevant to experimental proves of black holes existence. On the contrary, all known precision measurements in gravitation confirms the strong-field metric (3) with time dilation and continuous gravitational masses in nonempty Euclidean 3-space.
7. Conclusions
There are a lot of disputes in modern gravitation and astroparticle physics. Our main goal was to reinforce spatial flatness for real, non-point matter in a line of the original Entwurf geometrization of fields, rather than to discuss other consequences of the selfcontained SR-GR metric scheme [2,16]. In order to achieve this main goal, we derived quantitative geodesic predictions for Mercury’s perihelion precession, Mercury’s radar echo delay, and the gravitational light deflection by the Sun in strictly flat three-space without references on the 1915 GR equations at all. The numerical results are well known from the Schwarzschild empty-space approximation of reality. Recall that the conventional interpretation of post-Newtonian corrections relies on space warping around the localized gravitational source (including the ‘point’ Sun). On the contrary, our chain analysis of particles physical time allows us to infer that curved 4-interval can keep strict spatial flatness and the Entwurf metric scheme for strong-field gravitation. The GR displacement  may be referred as a space interval (like in Special Relativity) in flatspace relativity of nonlocal superfluid masses with mutual spatial penetrations. Consequently, the integral
may be referred as a space interval (like in Special Relativity) in flatspace relativity of nonlocal superfluid masses with mutual spatial penetrations. Consequently, the integral  along a space curve does not depend anymore on gravitational fields and takes a well-defined meaning. Such a Machian-type nonlocality of superfluid astroparticles reconciles 3D space properties with the relativistic Sommerfield quantization along a line contour. Indeed, these are no reasonable explanations for quantized magnetic flux in laboratory SQUIDs, unless one accepts 3D spatial flatness for any 2D surface [3].
along a space curve does not depend anymore on gravitational fields and takes a well-defined meaning. Such a Machian-type nonlocality of superfluid astroparticles reconciles 3D space properties with the relativistic Sommerfield quantization along a line contour. Indeed, these are no reasonable explanations for quantized magnetic flux in laboratory SQUIDs, unless one accepts 3D spatial flatness for any 2D surface [3].
GR physics may attach all field corrections within the GR invariant  to the time element
to the time element 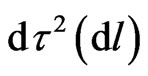 with chain relations. Gravity indeed curves elementary spacetime intervals (therefore
with chain relations. Gravity indeed curves elementary spacetime intervals (therefore  and
and 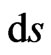 are specific for each moving particle), but their space sub-intervals
are specific for each moving particle), but their space sub-intervals 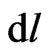 are always flat or universal for all particles and observers. It is not surprising that our approach to relativistic corrections, based on the strong-field equations (7), resulted in Schwarzschild-type estimations, which are based on very close integrals of motion in the Sun’s weak field. However, strong fields in (7) will not lead to further coincidences with empty-space Schwarzschild-type solutions for dynamics of probe particles.
are always flat or universal for all particles and observers. It is not surprising that our approach to relativistic corrections, based on the strong-field equations (7), resulted in Schwarzschild-type estimations, which are based on very close integrals of motion in the Sun’s weak field. However, strong fields in (7) will not lead to further coincidences with empty-space Schwarzschild-type solutions for dynamics of probe particles.
Both the Euclidean space interval 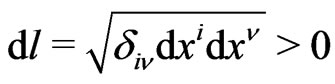 and the Newtonian time interval
and the Newtonian time interval  are independent from local fields and proper parameters of elementary particles. This absolute universality of world space and time rulers is a mandatory requirement for these notions in their applications to different particles and their ensembles. Otherwise, there would be no way to introduce for different observers one universal ruler to measure three-intervals and to compare dynamics of particles in common 3-space under the common time parameter. For example, it is impossible to measure or to compare differently warped four-intervals
are independent from local fields and proper parameters of elementary particles. This absolute universality of world space and time rulers is a mandatory requirement for these notions in their applications to different particles and their ensembles. Otherwise, there would be no way to introduce for different observers one universal ruler to measure three-intervals and to compare dynamics of particles in common 3-space under the common time parameter. For example, it is impossible to measure or to compare differently warped four-intervals 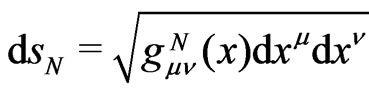 of different particles. In other words, there is no universal, non-specific pseudo-Riemannian geometry for all world matter. Therefore, joint evolution of energy carriers can be observed only in common sub-spaces when they maintain universal (for all matter) sub-metrics.
of different particles. In other words, there is no universal, non-specific pseudo-Riemannian geometry for all world matter. Therefore, joint evolution of energy carriers can be observed only in common sub-spaces when they maintain universal (for all matter) sub-metrics.
Space-time-energy self-organization of extended matter can be well described without 3D metric ripples, which have no much sense in strictly flat material space. Laboratory search of observable chiral phenomena for paired vector interactions in flat material space is worth to be performed before expansive projects to find 3D metric ripples in cosmic space. Record measurements of flat material space beyond the present limit  might not be required for confirmation of the residual EM nature of elementary masses under their Einsteintype geometrization. Once chiral symmetry for hadrons was violated at
might not be required for confirmation of the residual EM nature of elementary masses under their Einsteintype geometrization. Once chiral symmetry for hadrons was violated at , then this mass-forming symmetry was equally violated in the entire nonlocal structure of the superfluid astroparticle [2] or in its infinite material space. Non-empty Euclidean 3-space does match curved 4D space-time in metric gravitation. Such a matching allows the extended radial electron to move (both in theory and in practice) without spatial splits of mass and electric charge densities. Strict spatial flatness is a real way for quantization of elementary fields and for unified geometrization of extended gravitational and electric charges.
, then this mass-forming symmetry was equally violated in the entire nonlocal structure of the superfluid astroparticle [2] or in its infinite material space. Non-empty Euclidean 3-space does match curved 4D space-time in metric gravitation. Such a matching allows the extended radial electron to move (both in theory and in practice) without spatial splits of mass and electric charge densities. Strict spatial flatness is a real way for quantization of elementary fields and for unified geometrization of extended gravitational and electric charges.
8. Acknowledgements
I acknowledge useful discussions with Yu. S. Vladimirov regarding relation nature for binary interactions of elementary matter and for the non-empty space concept.
REFERENCES
- I. E. Bulyzhenkov, “Thermoelectric Flux in Superconducting Hollow Cylinders,” Physical Review B, Vol. 51, No. 2, 1995, pp. 1137-1139. doi:10.1103/PhysRevB.51.1137
- I. E. Bulyzhenkov, “Superfluid Mass-Energy Densities of Nonlocal Particle and Gravitational Field,” Journal of Superconductivity and Novel Magnetism, Vol. 22, No. 8, 2009, pp. 723-727. doi:10.1007/s10948-009-0583-5
- I. E. Bulyzhenkov, “Relativistic Quantization of Cooper Pairs and Distributed Electrons in Rotating Superconductors,” Journal of Superconductivity and Novel Magnetism, Vol. 22, No. 7, 2009, pp. 627-629. doi:10.1007/s10948-009-0510-9
- A. Einstein and M. Grossmann, “Entwurf Einer Verallgemeinerten Relativitatstheorie und Einer,” Zeitschrift für Mathematik und Physik, Vol. 62, 1913, pp. 225-261.
- A. Einstein, “Sitzungsber. Preuss. Akad. Wiss. Berlin,” Mathematical Physics, 1915, pp. 778, 799, 831, 844.
- A. Einstein, “Die Grundlage der Allgemeinen Relativitätstheorie,” Annalen der Physik, Vol. 354, No. 7, 1916, pp. 769-822. doi:10.1002/andp.19163540702
- D. Hilbert, “Die Grundlagen der Physik,” Nachrichten K. Gesellschaft Wiss. Gøttingen, Math-Phys. Klasse, Heft 3, 1915, S. 395.
- G. Mie, “Grundlagen einer Theorie der Materie,” Annalen der Physik, Vol. 344, No. 11, 1912, pp. 1-40. doi:10.1002/andp.19123441102
- K. Schwarzschild, “Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie,” Sitzungsberichte der Königlich-Preussischen Akademie der Wissenschaften, Vol. 3, 1916, pp. 189-196.
- J. Droste, “The Field of a Single Centre in ElNSTEIN’s Theory of Gravitation,” Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, Vol. 19, 1916, p. 197.
- N. Rosen, “General Relativity and Flat Space. I,” Physical Review, Vol. 57, No. 2, 1940, pp. 147-150. doi:10.1103/PhysRev.57.147
- A. A. Logunov, “The Theory of Gravitational Field,” Nauka, Moscow, 2001.
- W. Petry, “Gravitation in Flat Space-Time,” General Relativity and Gravitation, Vol. 13, No. 9, 1981, p. 865.
- N. I. Lobachevsky, “A Concise Outline of the Foundations of Geometry,” University of Kazan Messenger, Kazan, 1829.
- J. Bolyai, “Appendix Explaining the Absolutely True Science of Space,” In: F. Bolyai, Ed., Tentamen, Transylvania, 1832.
- B. Riemann, “On the Hypotheses That Form the Foundations of Geometry,” 1854 Lecture (Nachrichten K. Gesellschaft Wiss, Gottingen, 1868.
- P. De Bernardis, et al., “A Flat Universe from High-Resolution Maps of the Cosmic Microwave Background Radiation,” Nature, Vol. 404, No. 6781, 2000, pp. 955- 959. doi:10.1038/35010035
- A. Lange, et al., “Cosmological Parameters from the First Results of Boomerang,” Physical Review D, Vol. 63, No. 4, 2001, Article ID: 042001. doi:10.1103/PhysRevD.63.042001
- S. Hanany, et al., “MAXIMA-1: A Measurement of the Cosmic Microwave Background Anisotropy on Angular Scales of 10' - 5°,” The Astrophysical Journal Letters, Vol. 545, No. 1, 2001, pp. L5-L9. doi:10.1086/317322
- E. Komatsu, et al., “Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation,” The Astrophysical Journal Supplement Series, Vol. 180, No. 2, 2009, pp. 330-376. doi:10.1088/0067-0049/180/2/330
- C. W. Misner, K. S. Thorne and J. A. Wheeler, “Gravitation,” Freeman, San Francisco, 1973.
- R. Wald, “General Relativity,” University of Chicago Press, Chicago, 1984.
- C. M. Will, “Theory and Experiment in Gravitational Physics,” Cambridge University Press, Cambridge, 1981.
- L. D. Landau and E. M. Lifshitz, “The Classical Theory of Fields,” Pergamon, Oxford, 1971.
- S. Weinberg, “Gravitation and Cosmology,” John Wiley and Sons, New York, 1972.
- I. E. Bulyzhenkov, “Einstein’s Gravitation for Machian Relativism of Nonlocal Energy-Charges,” International Journal of Theoretical Physics, Vol. 47, No. 5, 2008, pp. 1261-1269. doi:10.1007/s10773-007-9559-z
- R. Weitzenbock, “Invariantentheorie,” Noordhoff, Groningen, 1923.
- G. Vitali, Atti Soc. Ligust. Sci. Lett., Vol. 11, 1924, p. 248.
- E. Cartan and J. Schouten, “On Riemannian Geometries admitting an Absolute Parallelism,” Proceedings Knkl. Neder. Akad. Vol. 28, 1926, p. 400.
- W. Weber, “On the Electromagnetic and Electrostatic Units of Current and the Meaning of the Absolute System of Units,” Annalen der Physik, Vol. 73, 1848, p. 193.
- A. Einstein, “On a Stationary System with Spherical Symmetry Consisting of Many Gravitating Masses,” Annals of Mathematics, Vol. 40, No. 4, 1939, pp. 922-936. doi:10.2307/1968902
- J. V. Narlikar, “A Random Walk in General Relativity and Cosmology,” Wiley Eastern, New Delhy 1985, p. 171.
- J. V. Narlikar and T. Padmanabhan, “The Schwarzschild Solution: Some Conceptual Difficulties,” Foundation of Physics, Vol. 18, No. 6, 1988, pp. 659-668.
- A. Einstein, “Über das Relativitätsprinzip und die aus Demselben Gezogenen Folgerungen,” Jahrbuch der Radioaktivitaet und Elektronik, Vol. 4, 1907, p. 411.
- A. Einstein, “Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes,” Annalen der Physik, Vol. 340, No. 10, 1911, pp. 898-908. doi:10.1002/andp.19113401005
- R. V. Pound and G. A. Rebka, “Apparent Weight of Photons,” Physical Review Letters, Vol. 4, No. 7, 1960, pp. 337-341. doi:10.1103/PhysRevLett.4.337
- I. I. Shapiro, “Fourth Test of General Relativity,” Physical Review Letters, Vol. 13, No. 26, 1964, pp. 789-791. doi:10.1103/PhysRevLett.13.789
- R. d’E. Atkinson, “General relativity in Euclidean Terms,” Proceedings of the Royal Society A, Vol. 272, No. 1348, 1963, pp. 60-78.
- F. H. J. Cornish, “General Relativity in Terms of a Background Space,” Proceedings of the Royal Society A, Vol. 376, No. 1366, 1963, pp. 413-417. doi:10.1098/rspa.1963.0214
- C. Møller, “The Theory of Relativity,” Oxford University Press, Oxford, 1952, p. 308.
- C. W. F. Everitt, “The Stanford Relativity Gyroscope Experiment: History and Overview,” In: J. D. Fairbank, et al., Eds., Near Zero: New Frontiers of Physics, Freeman and Co., New York, 1988, p. 587.
- L. I. Schiff, “Motion of a Gyroscope According to Einstein’s Theory of Gravitation,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 46, No. 6, 1960, pp. 871-882. doi:10.1073/pnas.46.6.871
- L. I. Schiff, “Possible New Experimental Test of General Relativity Theory,” Physical Review Letters, Vol. 4, No. 5, 1960, pp. 215-217. doi:10.1103/PhysRevLett.4.215

