Applied Mathematics
Vol.3 No.10A(2012), Article ID:24145,8 pages DOI:10.4236/am.2012.330205
Efficient Numerical Optimization Algorithm Based on New Real-Coded Genetic Algorithm, AREX + JGG, and Application to the Inverse Problem in Systems Biology
1Department of Bioinformatics, Graduate School of Systems Life Sciences, Kyushu University, Fukuoka, Japan
2Faculty of Inernational Communications, Fukuoka International University, Fukuoka, Japan
3Synthetic Systems Biology Research Center, Kyushu University, Fukuoka, Japan
4Department of Systems Bioscience for Drug Discovery, Graduate School of Pharmaceutical Sciences, Kyoto University, Kyoto, Japan
5Graduate School of Computational Intelligence and Systems Science, Tokyo Institute of Technology, Tokyo, Japan
Email: *okahon@brs.kyushu-u.ac.jp
Received July 10, 2012; revised August 10, 2012; accepted August 17, 2012
Keywords: Inverse Problem; S-System Formalism; Gene Regulatory Network; System Identification; Real-Coded Genetic Algorithm
ABSTRACT
In Systems Biology, system identification, which infers regulatory network in genetic system and metabolic pathways using experimentally observed time-course data, is one of the hottest issues. The efficient numerical optimization algorithm to estimate more than 100 real-coded parameters should be developed for this purpose. New real-coded genetic algorithm (RCGA), the combination of AREX (adaptive real-coded ensemble crossover) with JGG (just generation gap), have applied to the inference of genetic interactions involving more than 100 parameters related to the interactions with using experimentally observed time-course data. Compared with conventional RCGA, the combination of UNDX (unimodal normal distribution crossover) with MGG (minimal generation gap), new algorithm has shown the superiority with improving early convergence in the first stage of search and suppressing evolutionary stagnation in the last stage of search.
1. Introduction
A system is not just an assembly of more than two components which have unique function and show timevariant behavior. Since there are principles that govern at the system-level, mere collection of database of components does not lead to the understanding of system’s functional property. The aim of systems biology is to understand how functional properties and behavior of living organisms are brought about by the interactions of their constituents such as genes, proteins, metabolites and so on. The research strategies of systems biology can be divided into the following four fields: 1) System identification: inference of interaction between system components, 2) System analysis: dynamics of time-variant components, 3) System control: control toward the desirable condition of the system, 4) System design: design the system which realizes a certain dynamic or timevariant behavior, which expands to the research field, “Synthetic Biology”. These research developments are strongly supported by mathematical and computational methodologies, such as inference algorithm, statistical analysis, numerical calculation, nonlinear optimization, computer simulation and so on. Especially at the research field of systems identification, in order to infer the interaction among systems components, we have to develop the powerful inferring engine, in which large numbers of real-coded parameter values related to the interactions can be estimated efficiently using experimentally observed time-course data; algorithm of powerful numerical optimization for inverse problem involving more than 100 numbers of numerical parameters.
Organizationally complex systems such as gene regulatory networks and metabolic pathways are composed of many interacting components. In the many cases, the details of the molecular mechanism that govern interactions among system components are not well known, however, how do we represent mathematical model of such complex processes? most of theses processes are nonlinear. Description of these processes requires a representation that is general enough to capture the essence of the experimentally observed response. One of the best approaches that satisfy this requirement is the “S-system [1]” which is a type of power-law formalism because it is based on a particular type of ordinary differential equation in which the component processes are characterized by power-law functions (see Section 2). The S-system is suitable for conceptual modeling and describing organizationally complex systems including loop or cyclicstructure between system components. However, S-system formalism has a major disadvantage; this formalism includes large number of parameters must be estimated. This number is 2n (n + 1), where n is the number of system components.
Tominaga et al. have developed the numerical optimization method based on the simple genetic algorithm (SGA) in S-system formalism [2]. However, the SGA has two problems that early convergence in the fast stage of search and evolutionary stagnation in the last stage of search. Then, real-coded genetic algorithms (RCGAs) [3] have attracted attention as alternative numerical optimization methods to the SGA. One of the crossover operators for RCGA, known as the unimodal normal distribution crossover (UNDX) [4,5], has shown good performance in optimizing various functions including multimodal ones and benchmark functions with epistasis among the parameters. Sato et al. have proposed a new generation-alternation model called the minimal generation gap (MGG) [6,7], to improve early convergence in the first stage of search and to suppress evolutionary stagnation in the last stage of search. So far, we have developed efficient numerical optimization method using S-system modeling and RCGAs, with a combination of the UNDX and the MGG. This method can be applied to not only the estimation of gene networks but also the estimation of metabolic regulatory network. Shikata et al. have applied this method to the estimation of the amino acid network [8]. However, this method has not been able to estimate 20 amino acids’ network (n = 20), because this method converges slowly in the early stage of search, followed by the stagnation of optimization.
Therefore, in order to achieve the estimation of the larger network involving more than 100 real-coded parameters, we have developed a new estimation method using RCGA. The research group of Kobayashi has proposed just generation gap (JGG) [9,10], modified MGG. Akimoto et al. have reported that a combination of the adaptive real-coded ensemble crossover (AREX) with JGG showed the superiority in most of the benchmark functions [11]. In this study, we have applied new RCGA, AREX + JGG, to the inverse problem in Systems Biology, that is inference of regulatory network in genetic system and metabolic pathways for realizing experimentally observed time-course data of system components, and have compared with conventional RCGA, UNDX + MGG.
2. Method
2.1. S-System Formalism
The S-system [1] is a type of power-law formalism because it is based on a particular type of ordinary differential equation in which the component processes are characterized by power-law functions:
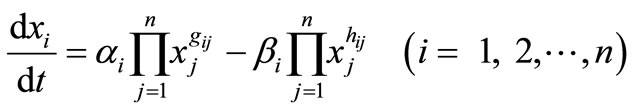 (1)
(1)
where n is the total number of state variables or reactants (xi), i, j (1 ≤ i, j ≤ n) are suffixes of state variables. The terms gij and hij are interactive effectivity of xj to xi. The first term represents all influences that increase xi, whereas these cond term represents all influences that decrease xi. In a genetic network context, the non-negative parameters αi and βi are called relative inflow and outflow of gene xi, respectively, and real-valued exponents gij and hij are referred to the interrelated coefficients between genes xj and xi. Given the experimentally observed time-course data of xi, the task is to estimate the values of interrelated coefficients gij, hij and non-negative constant αi and βi, which can be realized experimentally observed time-course of xi. The S-system formalism has a major disadvantage in that this formalism includes large number of parameters that must be estimated (αi, βi, gij, hij); the number of estimated parameters in S-system formalism is 2n (n + 1), where n is the number of state variables (xi); the number of estimated parameters increases with the second power of the number of system component (n).
2.2. Optimization Procedure
Because the S-system is a formalism of ordinary nonlinear differential equations, the system can easily be solved numerically by using a numerical calculation program to be customized specifically for this structure. However, when an adequate time-course of relevant state variables is given, the set of parameter values αi, βi, gij and hij, in many cases, will not be uniquely determined, as it is highly possible that other sets of parameter values will also show a similar time-course. Therefore, even if one set of parameter values that explains the observed time-course is obtained, this set is still one of the best candidates to explain the observed time-courses. Our strategy is to explore and exploit these candidates within the immense searching space of parameter values.
In this problem, each set of parameter values to be estimated is evaluated using the following procedure:
Suppose that 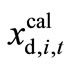 is the numerically calculated timecourse at time t of state variable xi in the d-th. Data set and that
is the numerically calculated timecourse at time t of state variable xi in the d-th. Data set and that 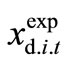 represents the experimentally observed time-course at time t of xi in the d-th. Data set. The sum of the square values of the relative error between
represents the experimentally observed time-course at time t of xi in the d-th. Data set. The sum of the square values of the relative error between  and
and 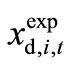 gives the total relative error E;
gives the total relative error E;
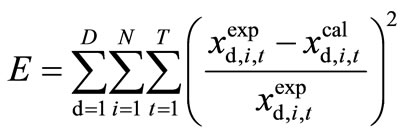 (2)
(2)
where D is the total number of data sets observed under different experimental conditions, such as gene disruption and over expression, N is the number of experimentally observable state variables, and T is the number of sampling points over time in one experimental condition. The computational task is to determine the set of parameter values that minimizes the objective function E.
2.3. Real-Coded Genetic Algorithms (RCGAs)
The genetic algorithm (GA) is stochastic search and optimization technique based on the mechanism of biological evolution, such as natural selection and natural genetics. The GA can seek out the “best” solution which will be found in regions of the search space containing a relatively high proportion of “good” solutions, that is, the GA can escape from trapping in local minima. The GAs employing real-valued vectors for representation of the chromosomes is called RCGAs [3]. The RCGAs are one of promising evolutional algorithms and are applied to several real world problems and have shown good results [12,13]. We have developed an efficient computational technique based on the RCGA called UNDX + MGG [14-16] and have applied to the inference of genetic interaction. In this study, we propose a new method using the RCGA, the combination of AREX (adaptive real-coded ensemble crossover) with JGG (just generation gap).
2.3.1. UNDX
The UNDX [4,5], unimodal normal distribution crossover, generates offspring using the normal distribution defined by three parents, as shown in Figure 1. Offsprings are generated around the line segment, which is connecting two parents, P1 and P2. The third parent, P3,
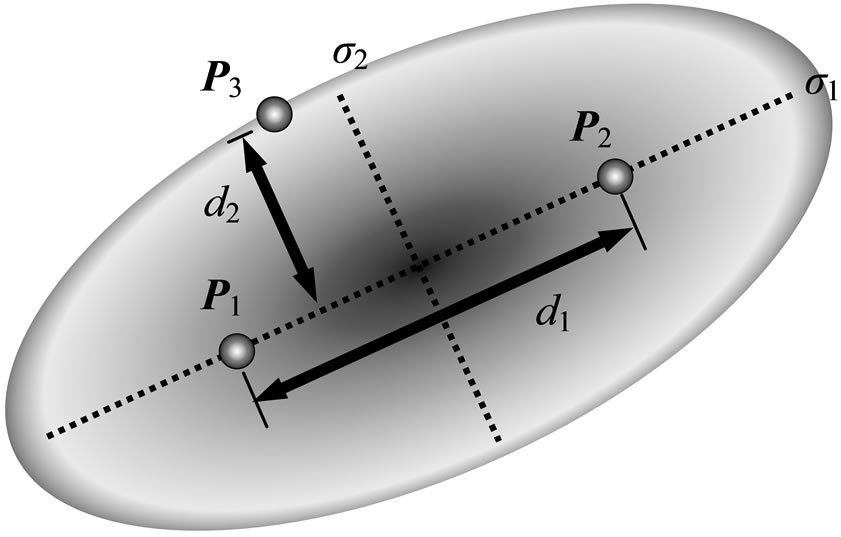
Figure 1. UNDX for parameter search.
is used to determine the standard deviation of the normal distribution. The standard deviation, which corresponds to the coordinate axis along the line segment, is proportional to the distance between P1 and P2. The others are proportional to the distance of P3 from the line segment and multiplied by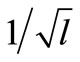 , where l is the number of parameters must be estimated; 2n (n + 1) for S-system. The effect of
, where l is the number of parameters must be estimated; 2n (n + 1) for S-system. The effect of 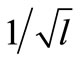 is to keep the distribution of offspring around line segment against increasing the number of parameters must be estimated. The mathematical representation of
is to keep the distribution of offspring around line segment against increasing the number of parameters must be estimated. The mathematical representation of
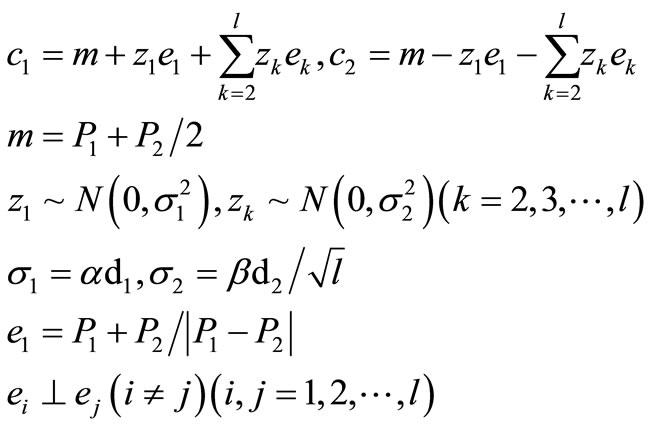 (3)
(3)
UNDX is as follows:
where c1 and c2 are offspring vector, P1 and P2 are parent vectors, m is the middle point of P1 and P2, d1 is the distance between P1 and P2, d2 is the distance of the third parent, P3, from the line connecting P1 to P2. α and β are constants given by the user, and α = 0.5 and β = 0.35 are recommended. The e1 is the basis vector in a direction parallel to the coordinate axis along the line segment, and vectors ei (i = 2, 3, ···, l), which are linearly independent basis vectors perpendicular to the vector e1, are defined by Gram-Schmidt procedure for finding orthogonal vectors.
2.3.2. MGG
The MGG [6,7] is the generation-alternation model. Figure 2 shows the conceptual figure of the MGG the procedure of which can be summarized as follows:
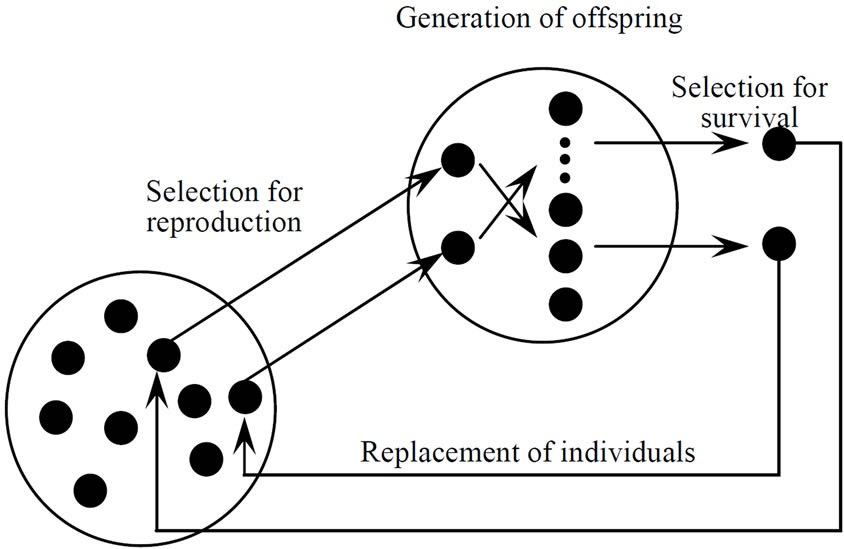
Figure 2. Conceptual figure of minimal generation gap (MGG).
1) Generation of initial population Make an initial population that is composed of random real number vectors.
2) Selection for reproduction Select a pair of individuals by random sampling without there placement from the population. The selected pair of individuals becomes the parents of offspring.
3) Generation of offspring Generate offspring by applying crossover to the parents and evaluate the offspring.
4) Selection for survival Select two individuals from the family containing the parents and their offspring; one is the best individual and the other is chosen using a roulette-wheel selection. Replace the parents chosen in step 2 in the population with the two selected individuals.
5) Repeat the above procedures from step 2 to step 4 until a certain stop condition is satisfied.
2.3.3. AREX
The AREX [11], adaptive real-coded crossover, is a crossover has been developed to improve the premature convergence in early stage. Akimoto et al. has proposed the AREX based on the REX [10,17], real-coded ensemble crossover, which is the generalization of UNDX-m [18]. The AREX generates λ candidate points ci (1 ≤ i ≤ μ; μ is the number of parents) around the center 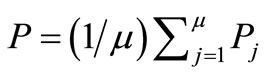 of μ parents Pj (1 ≤ i ≤ μ), as shown in Figure 3. And the mathematical representation of the REX is as follows:
of μ parents Pj (1 ≤ i ≤ μ), as shown in Figure 3. And the mathematical representation of the REX is as follows:
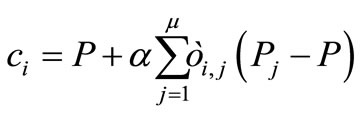 (4)
(4)
where α is the expansion rate, all 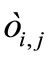 are independently and identically distributed (i.i.d.) random numbers with the average 0 and the variance
are independently and identically distributed (i.i.d.) random numbers with the average 0 and the variance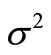 . There is arbitrariness in choice of the probability density function (p.d.f.) of
. There is arbitrariness in choice of the probability density function (p.d.f.) of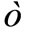 . For example, if
. For example, if 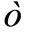 obeys normal distribution
obeys normal distribution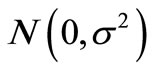 , the candidate solution generated by Equation (4) obeys
, the candidate solution generated by Equation (4) obeys
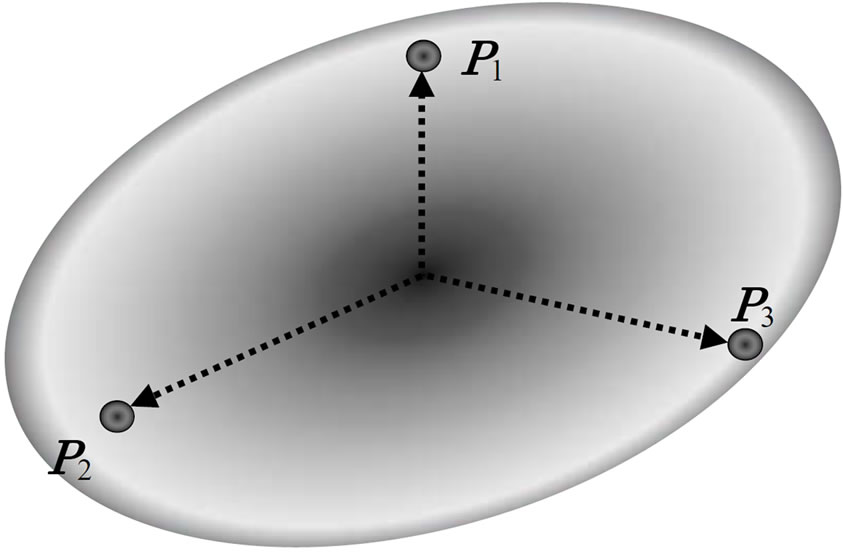
Figure 3. REX using normal distribution.
the normal distribution 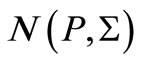 with mean vector 0 and covariance matrix Equation (5).
with mean vector 0 and covariance matrix Equation (5).
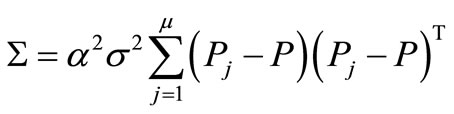 (5)
(5)
The REX shows the good performance in ill-conditioned and variable dependent problems because of the invariance against scale transformations and rotation transformations. However, Akimoto et al. have reported that there are the situations where the REX is likely to cause early convergence [11]. Furthermore, being combined the adaption of expansion rate (AER) technique and the crossover mean descent (CMD) technique with the REX, they have proposed the AREX to solve the early convergence.
The AER is the expansion rate which is controlled in the middle of the ongoing search process in AREX [11,17]. The CMD is a technique to shifts the center of the crossover to promising offspring point. The offspring are generated around the weighted average based on the ranking of evaluation values in parents. The CMD, m, is as follows:
 (6)
(6)
where 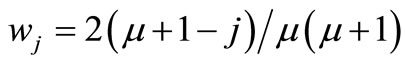 is the weight coefficient under the condition of
is the weight coefficient under the condition of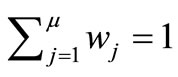 .
.
The AREX is the crossover applying the CMD and the AER to the REX. The mathematical representation of the AREX is as follows:
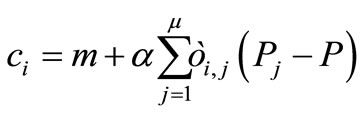 (7)
(7)
2.3.4. JGG
The JGG was proposed for multi-parental crossovers [9,10], and it is a modification model of MGG in two major points. First, the JGG does not employ elitist selection in evolution strategies. This modification makes a good effect on multimodal problems. Second, the JGG replaces parents with children completely in every generation. Figure 4 shows the conceptual figure of the JGG, and the procedure of the JGG can be summarized as follows:
1) Generation of initial population Make an initial population that is composed frandom real number vectors.
2) Selection for reproduction Select randomly μ parents from the population. The selected μ of individuals becomes the parents of offspring and μ = l + 1 is recommended [9,10], where l is the number of parameters must be estimated.
3) Generation of offspring
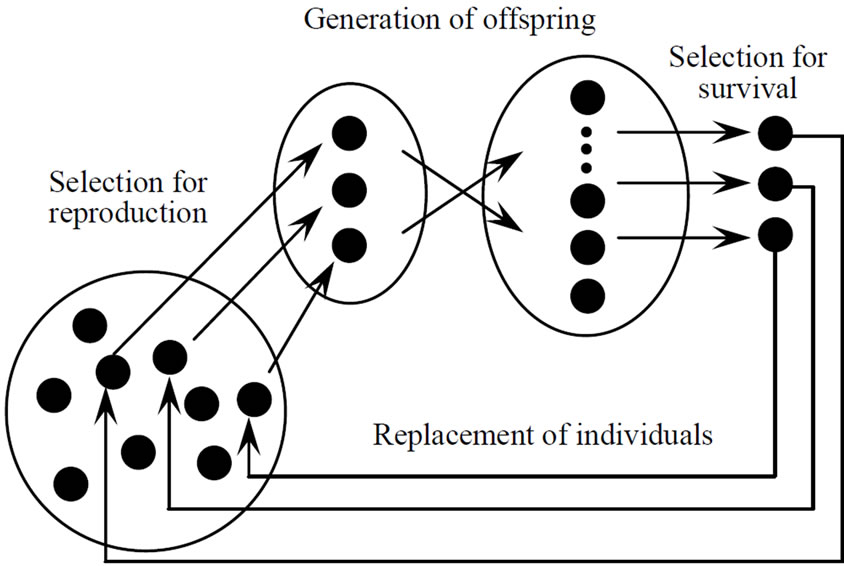
Figure 4.Conceptual figure of just generation gap (JGG).
Generate offspring by applying crossover to the parents and evaluate the offspring.
4) Selection for survival Select the top ranked μ individuals with respect to the fitness value from the offspring. And replace the parents chosen in step 2 in the population with the μ selected individuals.
5) Repeat the above procedures from step 2 to step4 until a certain stop condition is satisfied.
3. Results
We prepared an S-system network models composed of six genes, as shown in Figure 5, and of seven genes, as shown in Figure 6. In these figures, the arrow and T bar represent active and inhibitory interactions, respectively, and the numerals show the value of gij in S-system formalism. The S-system representation of Figures 5 and 6 are shown in Table 1. We applied the conventional RCGA method (UNDX + MGG) and the proposed method (AREX + JGG) for inferring gene expression network candidates to these artificial gene regulatory network models. We prepared 7 types of time-course data (one a “wild-type” and six “one gene-disrupted strain”) for six genes network model (Figure 5) and 8 types of time-course data (one a “wild-type” and seven “one gene-disrupted strain”) for seven genes network model (Figure 6), respectively. The number of sampling points in each time-course data set was 70. We calculated time-course data sets for the “one gene-disrupted strain” with the rate constant for the synthetic process of disrupted gene i(αi) set to 0.
Using these networks, we prepared 4 case studies to compare the performance of UNDX + MGG and AREX + JGG. The case studies 1 to 3 are for the estimation of the parameters of six genes network model, and case study 4 is for the estimation of the parameters of seven genes network model. In each case, the parameters must be estimate dare shown in Table 1.
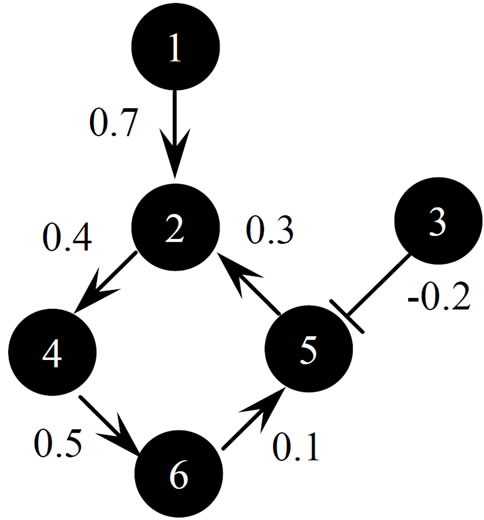
Figure 5. Six-genes network model.
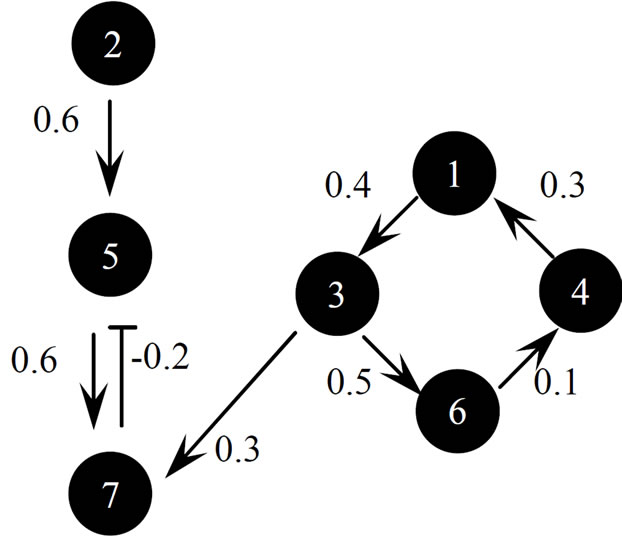
Figure 6. Seven-genes network model.
3.1. Case Study 1
First, in order to compare the convergence speed of two RCGA methods (UNDX + MGG, AREX + JGG), we performed the estimation of parameters in case study 1. In this experiment, we used the recommended default parameter [11,17] of RCGAs as follows: in UNDX + MGG, population size npop was set to 300, the number of offspring nc was set to 100, the number of parents np was set to 2, and in AREX + JGG, npop was set to 200, nc was set to 80, np was set to 21. We regarded the optimization terminated successfully when the total relation error E in Equation (2) is less than 0.1. We performed 50 trials, in each RCGA, and evaluated the performances with the average of 50 trials. Figure 7 shows the average of 50 trials in E of each generation. As shown in Figure 7, it is obvious that the convergence speed of AREX + JGG is faster than UNDX + MGG. In all trials, both methods can be estimated the correct values of parameters shown in Figure 5. Comparing the CPU time (CPU: XeonE5540 2.53 GHz, Memory: 8.0 GB), AREX + JGG was approximately 20-times faster than UNDX + MGG; the CPU time for AREX + JGG was 38.6 sec and that for UNDX + MGG was 765.0 sec. This experiment shows that AREX + JGG is remarkably better than UNDX + MGG in the convergence speed.

Table 1. Default parameters setting for UNDX + MGG and AREX + JGG.

Figure 7. Convergence profile for AREX + JGG and UNDX + MGG.
3.2. Case Study 2, 3, 4
Next, in order to evaluate the scalability of optimization, the number of parameters to be estimated increased in case studies 2 to 4. The default parameter of nc and np were set to the recommended values [11] for AREX + JGG. In case studies 2 to 3, in order to find an adequate the default parameter of npop for AREX + JGG, npop was scanned between 20l and 50l (l is the number of estimated parameters). In all runs, the maximum number of generation was set to 100,000. We regarded the optimization terminated successfully when the total relation error E in Equation (2) is less than 0.5. Table 2 shows the result of convergence speed in UNDX + MGG and AREX + JGG. As shown in Table 2, UNDX + MGG could not estimate 54 and 84 parameters within the maximum limit of generation (100,000). On the other hand, AREX + JGG succeeded the estimation of all parameters except when npop was set to 20l. Especially, AREX + JGG showed the best performance when npop was set to 30l.
4. Discussion
In this study, we proposed new inferred engine for estimating the gene regulatory network using time-courses of gene expression data using real-coded genetic algorithm (RCGA) with combination of the adaptive realcoded ensemble crossover (AREX) and the just generation gap (JGG). The combination of unimodal normal distribution crossover (UNDX) with the minimal generation gap MGG has disadvantage in convergence and can estimate only a few parameters. The AREX works well in ill-conditioned and variable dependent problems, because the AREX has the invariance against scale transformations and rotation transformations [11]. The JGG is suited for multi-parental crossovers. The JGG is a modification of the MGG in the points that replaces parents with offspring completely every generation and does not employ elitist selection. Akimoto et al. reported the AREX + JGG outperforms the existing RCGAs in a number of function evaluations on various functions including functions whose landscape forms ridge structure or multi-peak structure. In this study, AREX + JGG showed remarkably better performance (convergence speed) than UNDX + MGG in all experiments. Table 2 shows that AREX + JGG could solve the problems in which UNDX + MGG could not do that, and suggests that the adequate default parameter of the population size for AREX + JGG is 30l, where l is the total number of parameters. By employing AREX + JGG, we succeeded in improving the performances in the point of the convergence speed and the scalability in the number of estimated parameters; compared with UNDX + MGG, the
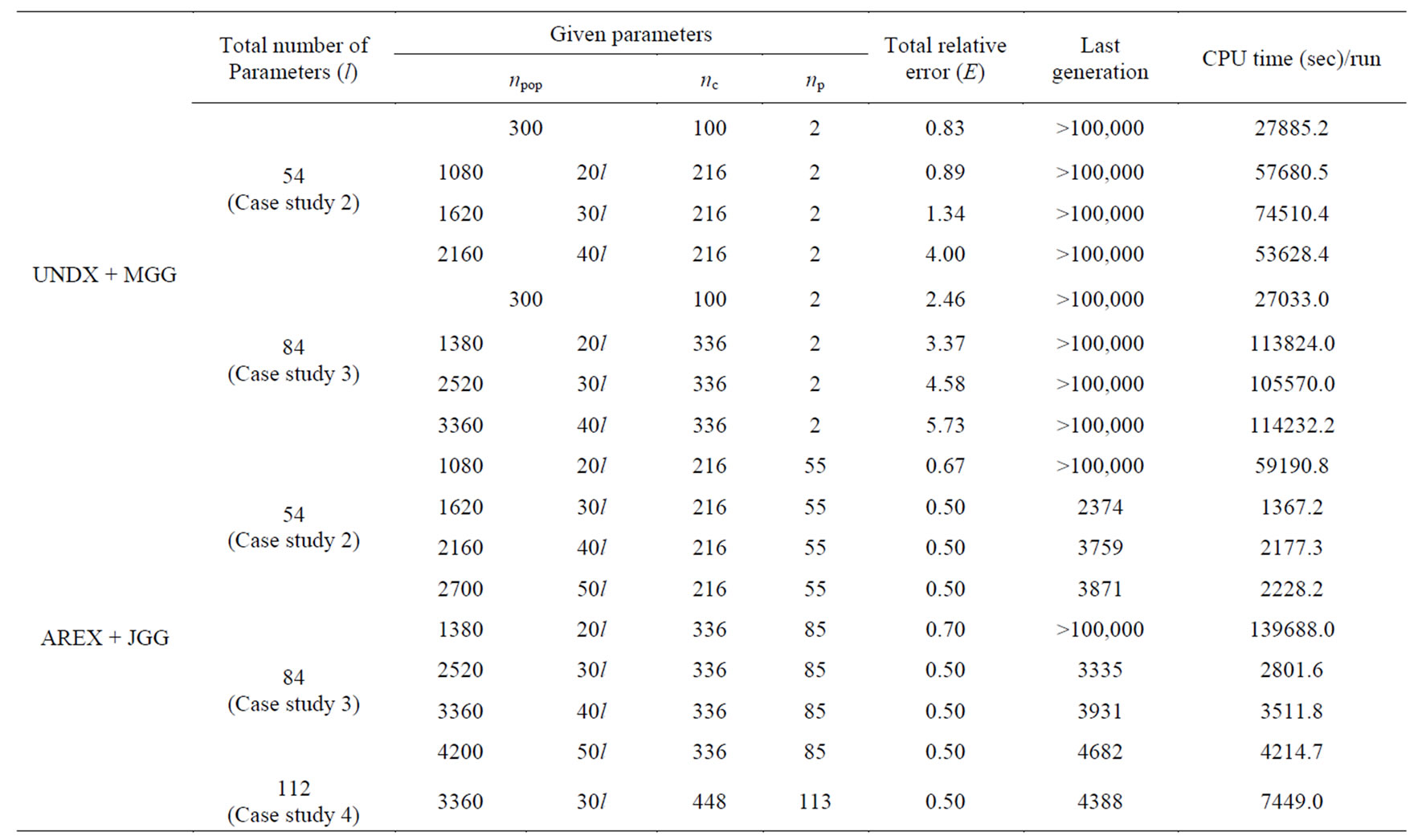
Table 2. Results of convergence speed in UNDX + MGG and AREX + JGG.
convergence speed and the scalability made rapid progress to approximately 5-foldand 20-fold, respectively.
As described already, in S-system formalism, the number of parameters to be estimated is proportion to the second power of the number of system components (n). In this study, AREX + JGG could estimate maximum 112 parameters, which corresponds to n = 7. Suppose we apply this method to the inference of regulatory network of all amino acids, we have to estimated 840 parameters because the total number of amino acids is 20 (n = 20). For the larger network estimation, we should further improve the proposed method. Substantially the GA can find the solution within a comparatively large searching range, but it is stepwise convergence, because the GA does not have an efficient local searching function. One of the methods having a local searching function is the modified Powell method. The modified Powell method is well known to have an ultimate fast convergence among the various direct-search methods without calculating the derivative of the objective function, especially where the objective function is well approximated by a quadratic form of parameters to be estimated. The modified Powell method can find the solution very quickly only when the initial guess is very near the solution; this method has no way to escape from a local minimum. The hybrid method, the RCGA and the modified Powell method, is expected to offer all advantages of both optimization techniques. We are now on going the development of the hybrid method by incorporation the modified Powell method into AREX + JGG, which is expected to become a more powerful optimization method for the larger network estimation.
5. Acknowledgements
This study was supposed by Gant-in-Aid for Scientific Research on Innovative Areas (Research in a proposed area), “Synthetic Biology for the Comprehension of Biomolecular Networks” from the Ministry of Education, Culture, Sports, Science and Technology, Japan (No. 23119001 (M. Okamoto)).
REFERENCES
- M. A. Savageau, “Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology,” Addison-Wesley, Reading, Boston, 1976.
- D. Tominaga, N. Koga and M. Okamoto, “Efficient Numerical Optimization Algorithm Based on Genetic Algorithm for Inverse Problem,” Proceedings of the Genetic and Evolutionary Computation Conference, Las Vegas, 8-12 July 2000, p. 251.
- L. J. Eshleman and J. D. Schaffer, “Real-Coded Genetic Algorithms and Interval-Schemata,” Foundations of Genetic Algorithms, Vol. 2, 1993, pp. 187-202.
- I. Ono and S. Kobayashi, “A Real-Coded Genetic Algorithm for Function Optimization Using Unimodal Normal Distribution Crossover,” Journal of Japanese Society for Artificial Intelligence, Vol. 14, No. 6, 1999, pp. 1146- 1155.
- I. Ono, S. Kobayashi and K. Yoshida, “Global and Multi-Objective Optimization for Lens Design by RealCoded Genetic Algorithms,” International Optical Design Conference Proceedings of SPIE, Vol. 3482, 1998, pp. 110-121.
- H. Sato, I. Ono and S. Kobayashi, “A New Generation Alternation Model of Genetic Algorithms and Its Assessment,” Journal of Japanese Society for Artificial Intelligence, Vol. 12, No. 5, 1997, pp. 734-744.
- H. Satoh, M. Yamamura and S. Kobayashi, “Minimal Generation Gap Model for GAs Considering Both Exploration and Exploitation,” Proceedings of 4th International Conference on Soft Computing, Iizuka, 30 September-5 October 1996, pp. 494-497.
- N. Shikata, Y. Maki, M. Nakatsui, M. Mori, Y. Noguchi, S. Yoshida, M. Takahashi, N. Kondo and M. Okamoto, “Determining Important Regulatory Relations of Amino Acids from Dynamic Network Analysis of Plasma Amino Acids,” Amino Acids, Vol. 38, No. 1, 2009, pp. 179-187. doi:10.1007/s00726-008-0226-3
- Y. Akimoto, R. Hasada, J. Sakuma, I. Ono and S. Kobayashi, “Generation Alternation Model for Real-Coded GA Using Multi-parent: Proposal and Evaluation of Just Generation Gap (JGG),” Proceedings of the 19th SICE Symposium on Decentralized Autonomous Systems, Tokyo, 29-30 January 2007, pp. 341-346.
- S. Kobayashi, “The Frontiers of Real-Coded Genetic Algorithms,” Journal of Japanese Society for Artificial Intelligence, Vol. 24, No. 1, 2009, pp. 147-162.
- Y. Akimoto, Y. Nagata, J. Sakuma, I. Ono and S. Kobayashi, “Proposal and Evaluation of Adaptive Real-Coded Crossover AREX,” Journal of Japanese Society for Artificial Intelligence, Vol. 24, No. 6, 2009, pp. 446-458.
- J. Sakuma and S. Kobayashi, “Latent Variable Crossover Fork-Tablet Structures and Its Application to Lens Design Problems,” Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2005), Washington DC, 2005, pp. 1347-1353.
- I. Ono, H. Kita and S. Kobayashi, “A Robust Real-Coded Genetic Algorithm Using Unimodal Normal Distribution Crossover Augmented by Uniform Crossover: Effects of Self-Adaptation of Crossover Probabilities,” Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-1999), Orlando, 1999, pp. 496-503.
- T. Ueda, N. Koga, I. Ono and M. Okamoto, “EfficientNumerical Optimization Technique Based on Real-Coded Genetic Algorithmfor Inverse Problem,” Proceedings of 7th International Symposium on Artificial Life and Robotics, Beppu, Oita, 16-18 January 2002, pp. 290-293.
- T. Ueda, N. Koga, I. Ono and M. Okamoto, “Development of Efficient Numerical Optimization Method Based on Real-Coded Genetic Algorithm: Application to the Estimation of Large Number of Real-Valued Parameters,” Proceedings of the 7th International Symposium for Biochemical Systems Theory: From Phenotype to Genotype and Back, Averoy, More og Romsdal, 17-20 June 2002, pp. 43-44.
- M. Nakatsui, T. Ueda, Y. Maki, I. Ono and M. Okamoto, “Method for Inferring and Extracting Reliable Genetic Interactions from Time-Series Profile of Gene Expression,” Mathematical Biosciences, Vol. 215, No. 1, 2008, pp. 105-114. doi:10.1016/j.mbs.2008.06.007
- Y. Akimoto, J. Sakuma, I. Ono and S. Kobayashi, “Adaptation of Expansion Rate for Real-Coded Crossovers,” Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2009), Montreal, 8-12 July 2009, pp. 739-746.
- H. Kita, I. Ono and S. Kobayashi, “Multi-Parental Extension of the Unimodal Normal Distribution Crossover for Real-Coded Genetic Algorithms,” Proceedings of the IEEE Congress on Evolutionary Computation, Washington DC, 6-9 July 1999, pp. 1581-1587.
NOTES
*Corresponding author.

