Creative Education
2013. Vol.4, No.3, 205-216
Published Online March 2013 in SciRes (http://www.scirp.org/journal/ce) DOI:10.4236/ce.2013.43031
Students’ Self-Diagnosis Using Worked-Out Examples
Rafi’ Safadi1,2, Edit Yerushalmi2
1Department of Research and Evaluation, Academic Arab College for Education in Israel, Haifa, Israel
2Department of Science Teaching, Weizmann Institute of Science, Rehovot, Israel
Received December 30th, 2012; revised January 30th, 2013; accepted February 14th, 2013
Students in physics classrooms are often asked to review their solution to a problem by comparing it to a
textbook or worked-out example. Learning in this setting depends to a great extent on students’ inclina-
tion for self-repair; i.e., their willingness and ability to recognize and resolve conflicts between their
mental model and the scientifically acceptable model. This study examined the extent to which self-repair
can be identified and assessed in students’ written responses on a self-diagnosis task in which they are
given time and credit for identifying and explaining the nature of their mistakes assisted by a worked-out
example. Analysis of 180 10th and 11th grade physics students in private and public schools in the Arab
sector in Israel showed that although most students were able to identify differences between their solu-
tion and the worked-out example that significantly affected the way they approached the problem many
did not acknowledge the underlying conflicts between their interpretation and a scientifically acceptable
interpretation of the concepts and principles involved. Rather, students related to the worked-out example
as an ultimate template and simply considered their deviations from it as mistakes. These findings were
consistent in all the classes and across all the teachers, irrespective of grade level or school affiliation.
However, younger students in some classrooms also perceived the task as a communication channel to
provide feedback to their teachers on their learning and the instructional materials used in the task. Taken
together, the findings suggest that instructional intervention is needed to develop students’ ability to
self-diagnose their work so that they can learn from this type of task.
Keywords: Problem Solving; Worked-Out Example; Self-Diagnosis; Self-Repair
Introduction
Students in physics classrooms are often given worked-out
examples1 of homework problems to enable them to analyze
their mistakes, or as models to introduce new material in class.
However, research has shown that students differ in terms of
how well they are able to explain the worked-out examples to
themselves, and how well they perform on subsequent transfer
problems. Specifically, successful problem solvers provide
more self-explanations—defined as content-relevant articula-
tions formulated after reading a line of text that state something
beyond what the sentence explicitly said (Chi et al., 1989).
Moreover, there are qualitative differences in the self-expla-
nations generated by successful and non-successful problem
solvers. For example, in the context of studying a worked-out
example, self-explanations produced by successful problem
solvers are characterized by relating solution steps to domain
principles or elaborating the application conditions of physics
principles (Chi & Vanlehn, 1991). Certain researchers have
argued (Chi, 2000) that to explain how self-explanations facili-
tate learning, self-explanation has, in part, to involve a process
of self-repair; i.e., a process of recognizing and acknowledging
that a conflict exists between the scientific model conveyed by
a worked-out example and the student’s possibly flawed mental
model, and attempting to resolve this conflict.
A variety of interventions aimed at enhancing the capacity of
self-explanations within the context of studying worked-out
examples have been proposed and shown to foster learning
outcomes (Atkinson et al., 2003; Chi et al., 1994; Renkl et al.,
1998). Enhancing the capacity of self-explanations can also
take place within the context of solving problems. Curriculum
developers have produced instructional interventions that pre-
sent students with problem situations designed to elicit intuitive
ideas and encourage peer discussions in which students work in
groups, suggest various approaches to solve the problem at
hand, reflect on their and their peers’ approaches and explain
their ideas (Mazur, 1997; McDermott et al., 1998; Sokoloff &
Thornton, 2001). Such discussions can induce students to pro-
vide self-explanations. By explaining their approach to a prob-
lem out loud, and comparing it to their peers’ solutions, stu-
dents are encouraged to engage in self-repair through recogniz-
ing and resolving conflicts between their and their peers’ men-
tal models.
Researchers have also developed “self-diagnosis tasks”
(Henderson & Harper, 2009; Etkina et al., 2006; Yerushalmi,
Singh et al., 2007) that exploit a frequent activity in physics
classrooms where students are provided with worked-out ex-
amples after having done some task on their own as part of their
homework, or on a quiz or exam. Instructors provide worked-
out examples to help their students self-diagnose their solutions
by comparing their solution to the worked-out example to im-
prove it or learn from their mistakes. However, many instruct-
tors worry that only a few of their students indeed engage in
this reflective activity (Yerushalmi, Henderson et al., 2007).
They suspect that most students merely skim over the worked-
1In this paper, we use the term “worked-out examples” to refer to
p
roblem solutions that the instructor distributes to students demon-
strating step-by-step how to solve a problem (Clark et al., 2006:p.
190).
Copyright © 2013 SciRe s . 205

R. SAFADI, E. YERUSHALMI
out example rather than carefully comparing it to their own
solution to learn from it. Self-diagnosis tasks modify this com-
mon classroom practice to make certain that students will re-
flect on their solution by providing them with time and credit
for writing “self-diagnoses”.
As in the case of interventions prompting students to provide
self-explanations when studying worked-out examples, inter-
ventions where students review and correct their own solutions
using a worked-out example are designed to generate self-ex-
planations involving self-repair leading to changes in mental
models. However research has shown that students’ self-diag-
nosis performance is not correlated with their performance on
transfer problems when they are supplied with worked-out ex-
amples (Yerushalmi et al., 2009; Mason et al., 2009). These
researchers hypothesized that when students receive a worked-
out example they interpret the task as a comparison of the sur-
face features of their solution to the worked-out example. Thus
in their diagnosis they merely “copy paste” the procedures in
the worked-out example that differ from their own solution
without actually self-repairing their mental model. In this arti-
cle we examine how students perceive the function of self-
diagnosis tasks, and the extent to which students involved in
self-diagnosis on worked out-examples engage in self-repair.
Scientific Background
Worked-out examples in textbooks or by instructors are
among the main learning and teaching resources in problem
solving in physics (Maloney, 2011) (as in other subjects). They
are used in different ways: a) in the first stages of skill acquisi-
tion or learning a new topic, instructors usually use worked-out
examples to demonstrate how to apply principles and concepts;
b) students rely on worked-out examples as aids in solving new
problems throughout a course (Eylon & Helfman, 1982; Gick &
Holyack, 1983); and c) after homework and/or tests, instruc-
tors commonly provide their students with worked-out exam-
ples as feedback on problems they were asked to solve
(Yerushalmi et al., 2007). This paper deals with self-diagnostic
tasks that relate to the latter case. In this context, students in-
teract with two artifacts: a possibly deficient textual artifact
which is the outcome of processes that they themselves carried
out, and the worked-out example which is the product of a
process that has been carried out by somebody else. To better
explore self-repair that take place in this context, we first re-
view research on learning through interaction with worked-out
examples, and studies on learning through interaction with
deficient solutions.
Learning through Interaction with Worked- Out
Examples
In self-explaining a worked out example, the learner reads an
artifact created by someone else (i.e., an expert). Thus, the text
acts as a mediator between the expert’s mental model and that
of the learner. Chi et al. (1989) analyzed worked-out examples
in standard textbooks and showed that they frequently omit
information justifying the solution steps. This is important be-
cause research has documented differences between students
with respect to the amount and the nature of self-explanations
they generate (Chi et al., 1989; Renkl, 1997) when explaining
solution steps to themselves. These studies found that students
who self-explain more learn more (Chi et al., 1989), and more-
over that successful learners tend to generate principle-based
self-explanations (Renkl, 1997).
A variety of instructional interventions have been shown to
be effective in both increasing the amount as well as the nature
of self-explanations. These interventions are based on “pro-
mpting”; i.e., providing students with explicit verbal reminders
to engage in the process of self-explaining (Chi et al., 1994).
This can take many forms such as prompting via computer
tutors (Aleven & Koedinger, 2002; Crippen & Earl, 2005;
Hausmann & Chi, 2002), or by embedding the reminders in the
learning materials (Hausmann & VanLehn, 2007). Principle-
based prompts have been shown to be effective in inducing
principle-based self-explanations (Atkinson et al., 2003).
Research has also shown that the effectiveness of students’
learning from examples is affected by their design (Ward &
Sweller, 1990; Chandler & Sweller, 1991; Chandler & Sweller,
1992). The critical factors are whether they can direct the
learner’s attention appropriately and reduce cognitive load. For
example, worked-out examples that include diagrams that are
separate from related formulas require students to split their
attention and were found to be less effective than examples that
integrate these elements. Labeling the solution steps into
“sub-goal” categories encourages students to generate self-ex-
planations explicating the sub-goals related to these categories
(Catrambone, 1998).
Last but not least, research has indicated that learning from
worked-out examples is more effective than problem solving at
the initial stages of skill acquisition (Atkinson et al., 2000;
Sweller et al., 1998). Process-oriented solutions (presenting the
rationale behind solution steps) are appropriate at this stage
(Van Gog et al., 2008). When learners acquire more expertise,
worked-out examples per se are less effective (the expertise-
reversal effect, Kalyuga et al., 2003). At this stage students
benefit more from learning from practice problems on their
own followed by isomorphic examples (Reisslein et al., 2006).
Learning through Interactions with Deficient
Solutions
Research has focused on two types of deficient solutions: a)
“teacher-made’, and b) “student-made”.
a) “Teacher-made” deficient solutions. Studying “teacher-
made” mistaken solutions was found to be advantageous for
learners with a high level of knowledge. By contrast, learners
with poor prior knowledge benefit to some extent only if the
errors in the mistaken solution are highlighted (Große & Renkl,
2007). Activities in which students were asked to diagnose
mistaken statements (i.e., explain the nature of the mistake,
note what they should pay attention to in order to avoid similar
mistakes in the future, and formulate a correct statement) were
shown to significantly improve students’ understanding of the
topics addressed (Labudde et al., 1988). Another example is the
PAL computer coach that employs a reciprocal-teaching strate-
gy (Reif & Scott, 1999) in which computers and students alter-
nately coach each other. PAL deliberately makes mistakes
mimicking common student errors and asks to be told if the
student catches any mistakes.
b) “Student-made” incorrect solutions. Research on learning
from student-made incorrect solutions has focused on students’
performance in “self-diagnosis” (Henderson & Harper, 2009) or
“self-assessment” tasks (Etkina et al., 2006). Self-diagnosis
tasks explicitly require students to self-diagnose their own solu-
tions when given some feedback on the solution, for example in
Copyright © 2013 SciR es . 206

R. SAFADI, E. YERUSHALMI
the form of a worked-out example.
Researchers (Cohen et al., 2008) studied students’ perform-
ance in self-diagnosis tasks in the context of an algebra-based
introductory course in a US college. Students were first in-
volved in a short training session about self-diagnosis. The
students then had to solve context-rich problems as part of a
quiz. The following week they were each given a photocopy of
their quiz solution and were asked to diagnose it with alterna-
tive external supports, one of which was a worked-out example.
The results showed that students’ self-diagnosis performance
was better with a worked-out example than without it, but
self-diagnosis performance correlated with their performance
on transfer problems only when they were not supplied with
worked-out examples. The authors suggested that the students
compared their solution to the worked-out example in a super-
ficial manner that did not allow them to generalize the analysis
of their mistakes beyond the specific problem (Yerushalmi et
al., 2009; Mason et al., 2009).
Methodology
As mentioned earlier, the process of self-repair was origin-
nally suggested (Chi, 2000) to explain how self-explanations
facilitate learning when reading a worked-out example. How-
ever, self-repair in the context of a self diagnosis task using a
worked-out example differs from self-repair in the context of
studying a worked-out example per se, as self diagnosis in-
volves two written texts; i.e., the student’s solution as well as
the worked-out example, rather than merely the latter. Accord-
ingly, in the self diagnosis context students are asked to identify
differences between the two written texts that are related to dif-
ferences between their own mental model and the scientific
model underlying the worked out example.
To assess self-repair in students’ written responses on a
self-diagnosis task when using a worked-out example we pos-
ited that for self-repair to take place in this context students
must a) identify differences between their solution and the
worked-out example that are crucial to finding the correct solu-
tion to the problem. We term these “significant differences”; b)
acknowledge that there is a conflict between their (possibly
flawed) mental model and the scientific model conveyed by the
worked-out example (i.e., conflicts underlying the identified
differences); and c) try to resolve the conflict. In view of that,
we examined:
1) To what extent students identify significant differences
between their own solutions and the worked-out example?
2) To what extent students acknowledge and try to resolve
conflicts between their mental model and the scientific model
underlying the worked-out example?
To understand how students perceive the function of the self-
diagnosis task we drew on the concept of action pattern
(Wertsch, 1984). When individuals carry out a specific task
they operate according to a mental representation of the task
involving both object representation—the way in which objects
that pertain to the task setting are represented, and action pat-
terns—the way in which the operator of the task perceives what
is required. In the context of a self-diagnosis task, object repre-
sentation refers to the representation of the problem situation in
terms of physics concepts and principles, whereas action pat-
tern refers to perceiving the interaction with a worked-out ex-
ample as a process of identifying, clarifying and bridging dif-
ferences between the instructor’s and the student’s representa-
tion of the problem situation. Another possible action pattern is
tracking visual difference between the worked-out example and
the student’s solution to satisfy the instructor’s perceived re-
quirements. In the present study, we looked for manifestations
of such action patterns/perceptions in the way students carried
out the self-diagnosis task.
Students primarily form their perceptions of physics learning
in the classroom, and their perceptions of a self diagnosis task
are likely to vary as a function of their specific classroom cul-
ture, which depends on various factors such as grade level,
school culture, the agenda of a specific teacher, etc. For ex-
ample, studies of school culture in the Arab sector in Israel
portray it as highly authoritative and formal, and shaped by
strong family traditions that stress values such as honor and
respect for elders (Dkeidek et al., 2011; Eilam, 2002; Tamir &
Caridin, 1993). To determine whether such a group effect took
place, we examined how students’ perceptions of the self-di-
agnosis task differ across classrooms.
Participants
We examined the above questions in a group of high school
students from nine schools in the Arab sector in Israel, for
whom this was their first exposure to a self-diagnosis task. The
classroom teachers had attended a year-long in-service profess-
sional development workshop for high-school physics teachers
from the Arab sector in Israel. The aim of the workshop was to
promote teaching methods to develop students’ learning skills
in the context of problem-solving, in particular formative as-
sessment tasks. As part of the workshop, a self-diagnosis task
was administered by the teachers. No training took place prior
to the administration of the task.
One hundred and eighty high school students taking ad-
vanced physics participated in the study. Students were drawn
from classrooms differing in grade level and school affiliation.
Three classes (two 10th grade (N = 39) and one 11th grade (N =
26)) were drawn from private schools operated by the Christian
church in Israel. These pluralistic schools, where Christian and
Muslim students study together, target students from urban
middle class families. The other classes (one 10th grade (N = 26)
and five 11th grade (N = 89)) were from state (governmental)
and private schools that target a more rural and traditional
population. All students had already completed or were in the
final stage of studying t he topic of k inematics.
Data Collection
The data for this study consisted of students’ answers on this
self-diagnosis task; i.e., students’ problem solutions and their
written self-diagnoses.
In the self-diagnosis task, students were first asked to solve a
problem based on kinematics concepts as part of a quiz (see
Figure 1).
This was to some extent a “context-rich” problem (Heller &
Hollbaugh, 1992) presented in a real-life context, not broken
down into parts, and without any accompanying diagram. Stu-
dents were provided with presentation guidelines (see Figure 1)
for the problem solution to help them unravel the intertwined
requirements posed by a context-rich problem. The classroom
teachers confirmed that the problem was suitable for high
school physics students in terms of its content and level of dif-
ficulty. The participating students, however, had only had little
Copyright © 2013 SciRe s . 207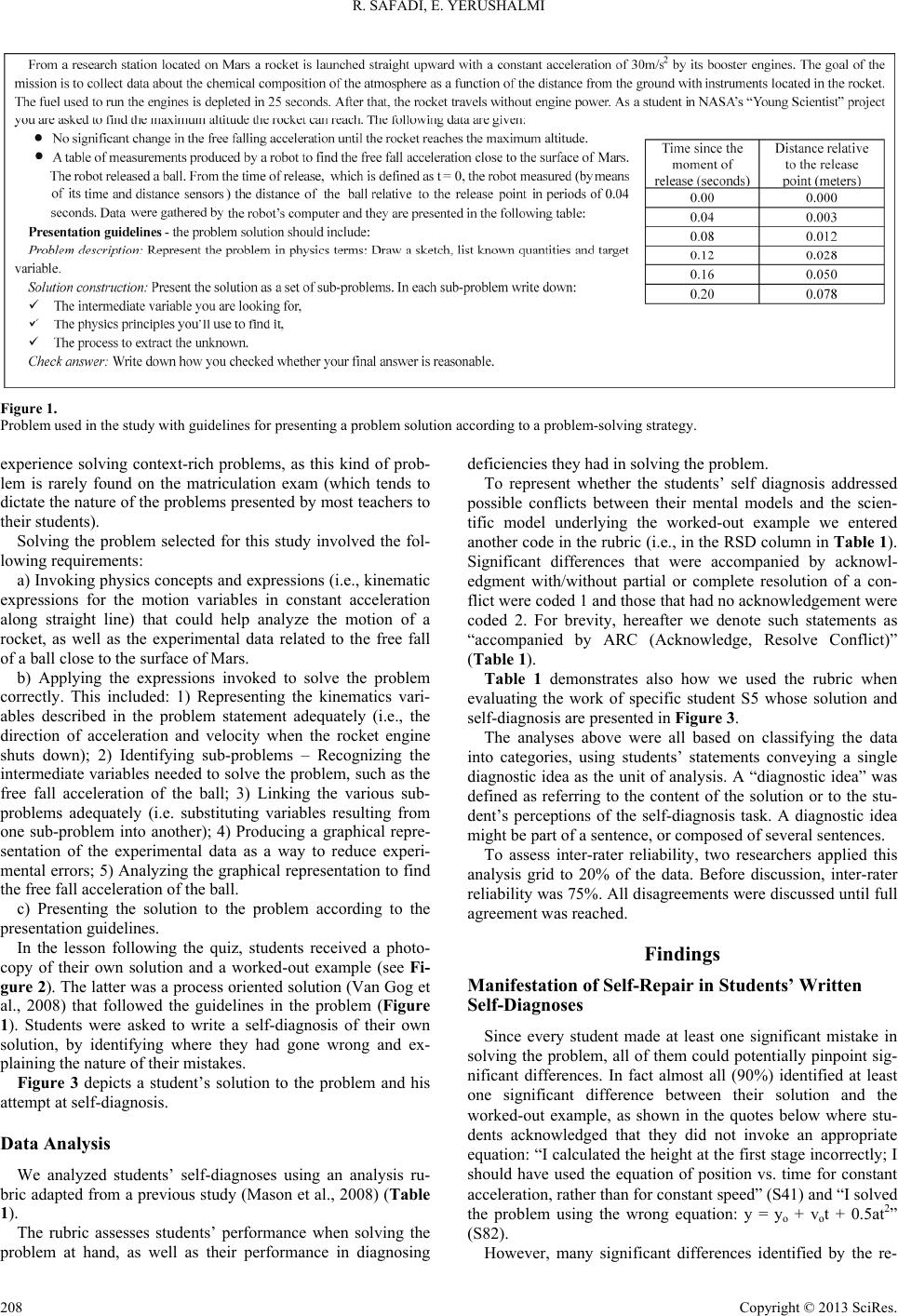

R. SAFADI, E. YERUSHALMI
Copyright © 2013 SciRe s . 208
Figure 1.
Problem used in the study with guidelines for presenting a problem solution according to a problem-solving strategy.
experience solving context-rich problems, as this kind of prob-
lem is rarely found on the matriculation exam (which tends to
dictate the nature of the problems presented by most teachers to
their students).
Solving the problem selected for this study involved the fol-
lowing requirements:
a) Invoking physics concepts and expressions (i.e., kinematic
expressions for the motion variables in constant acceleration
along straight line) that could help analyze the motion of a
rocket, as well as the experimental data related to the free fall
of a ball close to the surface of Mars.
b) Applying the expressions invoked to solve the problem
correctly. This included: 1) Representing the kinematics vari-
ables described in the problem statement adequately (i.e., the
direction of acceleration and velocity when the rocket engine
shuts down); 2) Identifying sub-problems – Recognizing the
intermediate variables needed to solve the problem, such as the
free fall acceleration of the ball; 3) Linking the various sub-
problems adequately (i.e. substituting variables resulting from
one sub-problem into another); 4) Producing a graphical repre-
sentation of the experimental data as a way to reduce experi-
mental errors; 5) Analyzing the graphical representation to find
the free fall acceleration of the ball.
c) Presenting the solution to the problem according to the
presentation guidelines.
In the lesson following the quiz, students received a photo-
copy of their own solution and a worked-out example (see Fi-
gure 2). The latter was a process oriented solution (Van Gog et
al., 2008) that followed the guidelines in the problem (Figure
1). Students were asked to write a self-diagnosis of their own
solution, by identifying where they had gone wrong and ex-
plaining the nature of their mistakes.
Figure 3 depicts a student’s solution to the problem and his
attempt at self-diagnosis.
Data Analysis
We analyzed students’ self-diagnoses using an analysis ru-
bric adapted from a previous study (Mason et al., 2008) (Table
1).
The rubric assesses students’ performance when solving the
problem at hand, as well as their performance in diagnosing
deficiencies they had in solving the problem.
To represent whether the students’ self diagnosis addressed
possible conflicts between their mental models and the scien-
tific model underlying the worked-out example we entered
another code in the rubric (i.e., in the RSD column in Table 1).
Significant differences that were accompanied by acknowl-
edgment with/without partial or complete resolution of a con-
flict were coded 1 and those that had no acknowledgement were
coded 2. For brevity, hereafter we denote such statements as
“accompanied by ARC (Acknowledge, Resolve Conflict)”
(Table 1).
Table 1 demonstrates also how we used the rubric when
evaluating the work of specific student S5 whose solution and
self-diagnosis are presented in Figure 3.
The analyses above were all based on classifying the data
into categories, using students’ statements conveying a single
diagnostic idea as the unit of analysis. A “diagnostic idea” was
defined as referring to the content of the solution or to the stu-
dent’s perceptions of the self-diagnosis task. A diagnostic idea
might be part of a sentence, or composed of several sentences.
To assess inter-rater reliability, two researchers applied this
analysis grid to 20% of the data. Before discussion, inter-rater
reliability was 75%. All disagreements were discussed until full
agreement was reached.
Findings
Manifestation of Self-Repair in Students’ Written
Self-Diagnoses
Since every student made at least one significant mistake in
solving the problem, all of them could potentially pinpoint sig-
nificant differences. In fact almost all (90%) identified at least
one significant difference between their solution and the
worked-out example, as shown in the quotes below where stu-
dents acknowledged that they did not invoke an appropriate
equation: “I calculated the height at the first stage incorrectly; I
should have used the equation of position vs. time for constant
acceleration, rather than for constant speed” (S41) and “I solved
the problem using the wrong equation: y = yo + vot + 0.5at2”
(S82).
However, many significant differences identified by the re-

R. SAFADI, E. YERUSHALMI
Figure 2.
The instructo r’s solution used in the study, aligned with guideline s.
searchers were missing from students self-diagnoses (e.g. only
one-third of the students identified more than half of the diffe-
rences that the researchers labeled as significant). Worse, many
students (40%) mentioned differences that had no bearing on
finding the solution to the problem such as superficial diffe-
rences between their solution and the worked-out example such
as: “I did not provide a detailed verbal description throughout
the solution” (S92).
Moreover, most students did not accompany their self-diag-
noses with ARCs—Acknowledgment, and in the best case
Resolution of Conflict; hence their self-diagnosis did not indi-
cate engagement in self-repair. The citations above are good
examples in that they do not include further discussion as to
why the equations invoked were not appropriate (i.e., student
S82 could have explained that as time was not one of the
knowns in the problem statement, the equation she used was
not useful). An example of a statement that does reflect ARC is
the following: “I made a mistake in calculating the acceleration
due to the gravity on Mars. I used only 1 point from the table
and this resulted in a larger inaccuracy. I should have plotted
position vs. time, namely y(t2)” (S153). This student, as well as
realizing what was wrong (using only one empirical data point
to calculate acceleration), also explained why it was wrong (it
increases the inaccuracy). In total, 15 (8%) students provided
ARCs.
We next examined whether there were differences between
the various sub-categories described in Table 1 with respect to
the students’ ability to identify significant differences and pro-
vide ARCs. The results are presented in Table 2.
The problem did not challenge students in terms of the “In
Copyright © 2013 SciRe s . 209

R. SAFADI, E. YERUSHALMI
Table 1.
The analysis rubric. The rubric is applied to the work of specific student S5 (shown in Figure 3) that had no mistakes in the “Invoking” category
(RDS = “+”; SDS= “×”; “RSD” = “NA”). In the “ Applying” category, this student mistakenly (see mistake 3 in Figure 3) identified the direction of
the acceleration when the rocket engine shuts down and identified this mistake in his self-diagnosis (note d). Even though the student did not clearly
articulate the nature of his misunderstanding, we believe that he acknowledged it, thus providing a partial ARC (RDS = “–”; SDS = “–”; “RSD” = “1.
+”).
Sub-categories RDS SDS RSD
Kinematic equations for con s t ant acceleration in straight line motion r equired to analyze the moti o n o f t h e rocket + × 1. NA
2. NA
Invoking
Kinematic equations for con s t ant acceleration in straight line motion r equired to analyze the free fall of a ball near the
surface of Mars + ×
1. NA
2. NA
Represent in g kinemati c variables described in the p roblem statement adequa t ely – – 1. +
2.
Identifying the entire set of required sub-prob lems + × 1. NA
2. NA
Kinematic equations for constant
acceleration in straight line
motion required to find the rocket’s
motion variables Adequately linking data acquired in o ne sub-problem to another sub-problem + × 1. NA
2. NA
Represent in g the experimental data graphically – × 1. –
2. –
Applying
Kinematic equations for finding
constant acceleration given
experime ntal data Calculating the acceleration based on the graphical representation – × 1. –
2. –
Legend: The sub-categories column reflects the specific principles and concepts required to be invoked and applied to solve the probl em. Students’ work is evaluated in
three ways: RDS column—th e rese archer’s diagno sis o f the stud ent ’s qu iz solut ion (we assi gn “+” if a stud en t carries out so me sub catego ry correctly an d “–” if i t is incor-
rect). SDS column—the student’s self-diagnosis of his/her solution interpreted in terms of the analysis rubric (if a student diagnoses a mistake we assign “–” to reflect how
the student assessed his/her solution. If a student does not refer to some category we assign “×”). RSD column—researcher’s judgment of this student’s self-diagnosis
based on comparison of the researchers’ and the student’s diagnosis of the stud ent’s solution (we assign “+” if a student correctly identifies a mistake; “–” if the student
fails to identi fy a mist ake or identifies it i nco rrectl y; an d “NA” if it is reasonabl e not to address so me su bcat ego r y (i.e., if the student did no t make a mist ak e in th e sol ution
(RDS marked “+”) and did not refer to it in his/her self-diagnosis (SDS marked “×”)); “1” = significant differences accompanied by ARC (Acknowledge, Resolve Conflict);
“2” = significant differences no t a ccompanied by ARC; NA = not applicable.
Table 2.
Students’ distribution i nto sub-categories of significant differences, with and without ARC.
Sub-categories Having deficiencies
% out of total; # of students
Realizing deficiencies
% out of those having defi-
ciencie s; # of students
1. 40%; 2
Kinematic equations for constant acceleration in straight line motion required toanalyze the
motion of the rocket 3%; 5 2. 60%; 3
1. 25%; 1
Invoking
Kinematic equations for constant acceleration in straight line motion required to analyze the
free fall of a ball near the surface of Mars 2%; 4 2. 75%; 3
1. 3%; 2
Representing kinematic variables described in the
problem statement adequately 24%; 43 2. 30%; 12
1. NA
Identifying the entire set of required sub-problems 43%; 77 2. 33%; 26
1. NA
Kinematic equations for
constant acceleration in straight
line motion required to find the
rocket’s motion variables
Adequately linking data acquired in one sub-
p
roblem to
another sub-problem 40%; 72 2. 50%; 36
1. 7%; 10
Representing the experimental data graphical ly 82%; 148 2. 46%; 68
1. -
Applying
Kinematic equations for
finding constant acceleration
given experimental data Calculating the acceleration based on the graphical
representation 18%; 32 2. 57%; 18
Legend: “1” = significant differences accompanied by ARC (Acknowledge, Resolve Conflict); “2” = significant differences not accompanied by ARC; NA = not applica-
ble.
Copyright © 2013 SciR es . 210

R. SAFADI, E. YERUSHALMI
Student’s solution: student’s self-diagnosis:
Student’s mistakes are labeled by the circled numbers 1, 2, 3 and 4 in the student’s solution. 1) the figures on the graph reveals that the student related the
velocity calculated via 21
21
xx
v(t) tt

 to rather than
2
tt 


21
ttt2 . 2) The slope was calculated using one experimental data point rather than
two points that lie exactly on the straight line. 3) The positive direction of the y axis was set as pointing upwards. Yet, when calculating the maximum alti-
tude, the student substituted a positive value for the acceleration of gravity pointing downwards, 4) a minus sign was arbitrarily inserted before 7502. Re-
garding presentation: the student did not draw a sketch, and did not write down the relevant knowns or the target quantity. He did not make explicit the in-
termediate variables and principles used in the various sub-prob lems, and did not check his answer.
Student’s self-diagnosis: the student did not id entify mis takes 1 and 2. He id entified a d ifferen ce between h is appr oach to fi nd the accel eratio n (of gr avity)
and the worked-out example (see note c). However this is a non-significant difference because the student’s approach is legitimate even though it differs
from the ap proach in the worked out exampl e. Note d in dicates th at the st udent iden tified mist ake 3 – th e word “cont inued” implies that he realized that he
dismissed the fact that t he rocket eng ines shut down. He t hen writes th at “I consider ed the positive d irection as p ointing upwards rather than downwards”.
We believe he is ref erring to t he accel erat ion and r ecogni zes th at he er ron eously alig ned t he di rectio n of acceler atio n with that of the velocity. We conclude
that he acknowledged a conflict between his understanding and the scientific one, thus providing partial ARC. Although he mentioned that he substituted a
negative value for the initial velocity (note d, ) he did not fully recognize mistake 4. Concerning the presentation, the student identified only some of
00v
his deficiencies related to the problem description (notes a and b in the student’s self-diagnosis) a n d his failure to check his answer (see note e).
Figure 3.
A sample solution and self-diagnosis provided by one of the students (S5).
voking” category. Only nine students (see Table 2) had diffi-
culties and all of them realized their mistakes. As the worked-
out example makes clear, it was reasonable to expect that given
the explicit manner in which principles were referred to in the
various sub-problems, students would recognize the principles
missing in their own solution. However, only three of the stu-
dents (one-third of the group) provided ARCs (i.e., most stu-
dents did not try to explain why the equations invoked were not
appropriate).
The situation was different regarding “Applying”: all the
students made at least one mistake in their applications; only
about half of them identified their mistakes and very few of
these generated ARCs.
In the “Applying” category students stumbled into two
widespread difficulties. The first relates to the representation of
kinematics variables described in the problem statement. Once
the rocket engine shuts down, the only force acting upon the
rocket is the force of gravity; hence, the acceleration should
point downwards. Yet about a quarter of the students identified
the direction of acceleration as pointing upward, possibly be-
cause when the rocket engine shuts down the velocity is still
pointing upwards. It is well known that students expect that an
object should move in the same direction as the force acting
upon it (Viennot, 1979; Halloun & Hestenes, 1985) and that the
velocity and the acceleration should thus be in the same direc-
tion. The following quote captures a diagnosis that indicates the
student is aware of having misinterpreted the situation: “In the
second stage of the motion, I did not substitute a negative value
Copyright © 2013 SciRe s . 211

R. SAFADI, E. YERUSHALMI
for the acceleration of gravity” (S109). This student recognized
her mistake in substituting a positive value for the acceleration
of gravity rather than a negative one. However, the student did
not articulate an ARC (for example, by explaining what made
her choose the direction of acceleration the way she did, possi-
bly aiming to align the direction of acceleration with that of the
velocity), either because she did not realize that she was re-
quired to do so, or because it was beyond her ability. In fact,
only a third of the students who made this kind of mistake rec-
ognized it in their self-diagnosis and only two students pro-
vided partial ARCs (see Table 2).
The second difficulty relates to representing experimental
data graphically and analyzing the graph to find the free fall
acceleration. Most of the students failed to recognize the utility
of representing the experimental data graphically to improve
the precision of their results. Some students refrained from
producing a graphical representation altogether. Instead, they
relied on one or two empirical data points to calculate the ac-
celeration (50%); others produced an inadequate graphical rep-
resentation (32%)—these students plotted the distance y against
the time t and got a parabola, dismissing the fact that plotting y
as function of t2 would result in a straight line, and would have
enabled them to find the acceleration from the slope of this
graph that equals g/2. Of those students who did provide an
adequate graph, none were able to analyze it appropriately
(18%). Similar to their peers who did not come up at all with a
graph, these students’ most frequent mistake was relying on one
or two empirical data points to calculate the acceleration rather
than from the slope of the graph.
Since the graph was a dominant visual element in the
worked-out example, it would seem that self diagnosing a
missing or inadequate graph would be straightforward. The
students did better in recognizing their mistakes in this area
than in others but they did not do well in providing ARCs. About
half of the students who did not provide a graph or provided an
inadequate one realized their mistakes, and only ten students
(7%) provided diagnoses with ARCs. Similarly, a little more
than half of the students (57%) noticed that they used empirical
data points rather than their graph to calculate the acceleration
of gravity, but none of them provided ARCs.
The following quote: “I did not plot a graph at all” (S136)
represents a frequent diagnosis of this kind. The student merely
mentioned the omission, but offered no explanation indicating
he understood why he should have used a graph rather than one
or two experimental data points. The following quote illustrates
a diagnosis involving an ARC: “My mistake was that I used a
graph of position vs. time, in which one cannot find the exact
acceleration as it is a parabola. I should have used position vs.
time squared as it results in a linear function that can be used to
find the slope accurately… To find the acceleration you have to
plot the slope in between the points (averaging the points) and
check all the data in the table” (S30).
The other aspects of applying the kinematic equations to find
the rocket’s motion variables involved a) identifying the sub-
problems required to get the correct solution and b) adequately
linking data from one sub-problem to another sub-problem.
These aspects do not involve conflicts between students’ con-
ceptual understanding and the scientific model. One would
expect that most students would be able to self-diagnose these
two components, as the worked-out example made a visual
distinction between the various sub-problems to prompt stu-
dents to notice these kinds of differences between the two solu-
tions. For example, a student wrote “Sub-problems d’ and e’ are
missing” (S14). Unfortunately, only half of the students who
made errors realized they had made mistakes (see Table 2).
To summarize, students did better in noticing significant dif-
ferences related to Invoking as compared to Applying; although
all the students who had deficiencies in invoking some prince-
ples identified that their solution was missing in this respect,
only one third to one half did so in terms of application. Here,
they did better in recognizing significant differences related to
visually prominent features in the worked-out example. In gen-
eral the generation of ARCs was poor, but it was better in terms
of Invoking. Furthermore, more students provided ARCs that
were related to visually prominent features.
Students’ Perceptions of the Function of the
Self-Diagnosis Task
The simplest explanation why most students did not provide
ARCs is that they were not able to articulate the fundamental
nature of their mistakes. Alternatively, students may not have
understood that the function of the self-diagnosis task is to
identify, clarify and bridge differences between the instructor’s
and the student’s understanding of physics concepts and princi-
ples, and that they were required to provide ARCs. This inter-
pretation is supported by other statements students made that
could not be categorized as “significant differences” (with or
without ARCs). These statements focused on non-significant
differences, such as the order of sub-problems in the student’s
example compared to the worked-out example or reflected stu-
dents’ opinions about the artifacts used in the self-diagnosis
task or the requirements posed by the problem.
These kinds of statements provide a resource for identifying
“action patterns” (Wertsch 1984); i.e., students’ perceptions of
what they are required to do in the self-diagnosis task. Here we
employed a bottom-up approach by reading and identifying
common themes in the students’ statements. The emerging
categories and the distribution of students’ statements in these
categories are shown in Table 3.
First we looked at the group of 72 students (40%) who re-
ferred to differences that the researchers did not categorize as
significant to finding the correct solution to the problem. Half
of these students referred to deficiencies in their solution in a
Table 3.
Students’ distribu tion into categories related to perceptions of the task.
Major
categories Sub-categories (% of group identified in the major cate- gories; # of students)
Vaguely de fined deficiencies (50%; 36)
Focused on amount of detail (25%; 18)
Non-significant
differences
(72 students)Differences in the solution orde r/ arrangement
(75%; 54)
Progress in t he solution proc ess (60%; 55)
Time management (40%; 36)
Solution
process
(90%; 80)Interaction with teacher (20%; 18)
Problem characteristics: w o rding, breaki n g
down into parts, etc. (40%; 36)
Reflection o n the
experience
(90 students)Artifacts
(40%; 36)Characteristics of the worked-out example
(20%; 18)
Copyright © 2013 SciR es . 212

R. SAFADI, E. YERUSHALMI
vague, nonspecific manner, such as: “All the answers were
wrong. I just knew the value of gravity” (S42). Most of these
students related to the worked-out example as the ultimate tem-
plate by identifying external deviations from it as flaws or
weaknesses in their solutions. Eighteen students referred to the
extent to which their solution was detailed relative to that of the
worked-out example: “I did not provide a detailed verbal de-
scription throughout the solution” (S92); and fifty four of them
referred to the order of sub-problems tackled in the student’s
solution relative to that in the worked-out example: “I found the
final velocity of the first stage only in a later step” (S82).
Half of the students reflected on their experience in carrying
out the task rather than focusing on the content of the solution,
making use of the task of self-diagnosis as an outlet, a way in
which the students could share their experiences with the in-
structor (see “Reflection on the experience” category in Table
3). Almost all of them attended to the solution process. Some,
for example, reflected on their progress in this process: “It be-
came clear to me that my solution up to the stage I got to was
right. However, I couldn’t continue the quiz” (S43). Others
addressed time management difficulties: “I spent a lot of time
describing the problem” (S43) or reflected on the interaction
with their teachers in the course of solving the problem: “Con-
cerning the unfortunate graph that I drew, it was just to provi-
de a graph as the teacher emphasized the need for a graph”
(S166).
Almost half (40%) of the students who reflected on their ex-
perience also expressed opinions regarding the artifacts used in
the task, either by commenting on the challenging requirements
of the target problem: “The problem is not broken down into
parts. This means you have to understand a lot of things at once.
Also, we are not familiar with this kind of problem” (S166) or
expressing their opinion regarding the longer and detailed na-
ture of the worked-out example: “To some extent the sample
solution is long” (S174) and “The instructor’s solution is very
complicated, and I did not understand it” (S164). “Context-
rich” problems are indeed not commonplace in physics text-
books used in Israeli high schools, since these types of prob-
lems are only rarely found on the matriculation exam.
Last, we examined how students’ perceptions of the self-di-
agnosis task differed across classrooms.
Table 4 presents the students’ distributions into the catego-
ries: 1) “Provided ARCs”, 2) “Addressed non-significant dif-
ferences”, and 3) “Reflection on the experience” for each of the
nine classes involved in the study.
Only a small number of students provided ARCs in each
class (maximum three students) irrespective of grade level or
school affiliation. While the classrooms varied significantly in
the percentage of students who addressed non-significant dif-
ferences (from 27% to 75%) the disparities could not be attrib-
uted to grade level or school affiliation. On the other hand,
students’ answers in the “Reflection on the experience” cate-
gory varied as a function of grade level and school affiliation.
In particular, in 10th grade classrooms affiliated with plural-
istic schools, the self-diagnosis task served as a communication
channel between students and their teachers to provide feed-
back on their learning and on the instructional materials used in
the task, rather than only as a tool for self-repairing students’
misinterpretations related to the problem at hand. Possibly
teachers working with younger students in these schools, are
more open to such communication.
Table 4.
Students’ distribution into main categories for each class.
School affiliation
Grade
level Class Provided ARCs
Addressed
non-significant
differen ces
Reflection o n
the
experien ce
A (N = 16)6% 50% 88%
10th
grade B (N = 23)9% 39% 100%
Heterogeneous
schools
11th
grade C (N = 26)8% 31% 50%
10th
grade D (N = 26)8% 27% 65%
E (N = 12)9% 75% 50%
F (N = 15)- 53% 40%
G (N = 20)15% 35% 35%
H (N = 11)10% 73% 18%
Homogenou s schools
11th
grade
I (N = 31)9% 52% 16%
Summary and Discussion
It is common practice in physics classrooms to provide stu-
dents with worked-out examples after they have attempted to
solve a problem on their own (i.e., homework, quiz or exam) to
encourage them to compare their solutions to the worked-out
example and self-diagnose their mistakes—i.e. identify where
they went wrong, explain their mistakes and learn from them.
In this study we examined how students self-diagnose their
solutions when given time and credit for writing “self-diagno-
ses”, aided by worked-out examples. In particular we studied a)
the extent to which students’ self-diagnosis when they are aided
with worked-out examples indicates engagement in self-repair,
and b) students’ perceptions of what they are expected to do in
such a self-diagnosis task. Following Chi (2000), we differenti-
ated between two stages of self-repair. This involved a first
stage in which students identified significant differences (i.e.,
differences between their solutions and the worked-out example
that were judged by the researchers as significant to get the
correct solution), and a second stage in which students ac-
knowledged a conflict between their understanding and the
scientific model, and in the best case, were able to partially or
completely resolve this conflict (i.e., provided ARCs).
We found that almost all of the students identified at least
one significant difference. However, most of the students did
not provide ARCs. Specifically the first stage of self-repair took
place, but the second stage did not occur, or at least was not
articulated. Moreover, when students self-diagnosed the various
aspects of the “Applying” category, where they made the vast
majority of their mistakes, at best half of those who had defi-
ciencies identified their significant differences. This result
might suggest that the self-diagnosis task did not provide an
opportunity to self-repair deficiencies in the students’ under-
standing of related concepts and principles. Furthermore, we
found that at least half of the significant differences that stu-
dents identified were related to visually prominent elements in
the worked-out example (such as the graph). It is possible that
students merely skimmed over the worked-out example and
simply pinpointed obvious elements. Also, almost half of the
students focused on non-significant differences by relating to
Copyright © 2013 SciRe s . 213

R. SAFADI, E. YERUSHALMI
the worked-out example as an ultimate template and simply
considering their deviations from it as mistakes. These findings
were consistent in all the classes and with all the teachers who
participated in the study, irrespective of grade level or school
affiliation. Thus we conjecture that the majority of the students
did not experience self-repair processes when they engaged in
self-diagnosis via the worked-out example. This conclusion is
consistent with previous research findings that students’ self-
diagnosis performance did not correlate with their performance
on transfer problems when they were aided in a self-diagnosis
task by a worked-out example (Yerushalmi et al., 2009; Mason
et al., 2009). This is because the students’ process of diagnos-
ing their solution did not incorporate acknowledging and re-
solving conflicts (ARCs), and hence did not result in self-repair
and transfer.
One possible explanation for these results is that the students
did not realize that the function of the self-diagnosis task was to
identify, clarify and bridge differences between the instructor’s
and their understanding of physics concepts and principles, and
that they were required to provide ARCs. Bereiter & Scar-
damalia (1989) use the term “intentional learning” to refer to
“processes that have learning as a goal rather than an incidental
outcome” (p. 363). For self-repair to take place in the context of
a self-diagnosis task, students should perceive learning as the
goal of this experience and deliberately reflect on their inter-
pretation of concepts and the principles involved in the solution.
Our results suggest that students did not approach the task in an
intentional manner. The dominant listing of non-significant
differences suggests that many students did not make the dis-
tinction between significant vs. non-significant differences as
regards learning when self-diagnosing their work. The limited
occurrences of ARCs suggest that students perceived learning
from the worked example merely as a comparison and identifi-
cation of differences between the worked-out example and their
own solution, and not as an artifact enabling reflection and
refinement of ideas.
It might be claimed that these perceptions are the outcome of
an authoritative classroom culture as is known to be the case in
Arab society in Israel (Tamir & Caridin, 1993; Dkeidek et al.,
2011; Eilam, 2002). In an authoritative classroom culture one
would expect a dominance of epistemological beliefs including
notions that knowledge in physics should come from a teacher
or authority figure rather than be independently constructed by
the learner. Such an outlook would foster students’ tendencies
to refer to anything the teacher produces, such as a worked-out
example, as the ultimate template and hence devote their un-
productive attention to non-significant differences. However,
similar beliefs have been documented to be widespread in other
cultural contexts as well. For example, in the Maryland Physics
Expectations (MPEX) survey of epistemological beliefs (Re-
dish et al., 1998) that involved 1500 students in introductory
calculus-based physics courses from six colleges and universi-
ties in the US, 40% - 60% of the students in each institution
expressed the epistemological belief that knowledge in physics
should come from an authoritative source such as an instructor
or a text rather than be independently constructed by the
learner.
Our findings indicate that providing time, credit and suppor-
tive resources for self-diagnosis in the form of a worked-out
example does not guarantee learning in this context. Teachers
need to help students realize that identifying significant differ-
ences between the worked-out example and their own solution
serves as groundwork for subsequent learning process, and aids
in acknowledging and resolving the underlying conflicts be-
tween their interpretations and a scientifically acceptable inter-
pretation of the concepts and principles involved. To do so,
teachers need to address the following key facets: a) developing
in students a perception of problem solving as an intentional
learning experience; b) developing students’ ability to recog-
nize the deep structure of worked-out examples; c) developing
in students diagnostic skills.
a) Developing in students a perception of problem solving as
an intentional learning experience. Elby (2001) developed an
epistemology-focused course that was found to help students
develop more positive attitudes toward the meaningfulness of
mathematical equations and the constructive nature of learning.
Our findings suggest that incorporating instructional practices
and curricular elements from an introductory physics course
could improve students’ learning in the context of self-diagno-
sis tasks.
b) Developing students’ ability to recognize the deep struc-
ture of worked-out examples: As mentioned earlier, studies
have shown that students can be encouraged to provide more
self-explanations when reading worked-out examples by en-
gaging them in activities where they are “prompted” to self-
explain (Chi et al., 1994) by computerized training systems
(Aleven & Koedinger, 2002; Crippen & Earl, 2005; Hausmann
& Chi, 2002), or by prompts embedded in the learning materi-
als (Hausmann & VanLehn, 2007). Atkinson, Renkl and Merrill
(2003) showed that principle-based prompts are effective in
inducing the principle based self-explanations characteristic of
successful learners Renkl (1997). Future research could exam-
ine the effect of training providing principle-based self-expla-
nations on students’ performance in self-diagnosis tasks.
c) Developing diagnostic skills: It has been shown (Schwartz
& Martin, 2004) that contrasting cases can help learners de-
velop more differentiated knowledge, which can guide their
subsequent interpretation and learning from other learning re-
sources, for example, as in the case cited, from a lecture. By
analogy, activities that present students with incorrect solutions,
and require them to explain the error with reference to princi-
ples requires students to distinguish scientifically acceptable
interpretations of concepts from the lay interpretation, thereby
prompting them to focus on those features of a concept needed
to interpret it accurately. Awareness of such features could in
turn support learning from other resources, for example, a
worked-out example. Curriculum developers have created in-
ventories of troubleshooting tasks that present students with
incorrect solutions and require them to detect, explain and cor-
rect the error (Hieggelke et al., 2006). Yerushalmi et al. (2012)
studied pairs of students engaged in a troubleshooting online
activity. In the first stage of the activity students were asked to
identify the misused concept or principle and explain how it
conflicted with the scientifically acceptable view. In the second
stage students were asked to compare their own diagnosis with
an expert diagnosis provided by the online system to ascertain
whether they had recognized the misused concept and clarified
how the mistaken solution conflicted with the correct one. The
findings indicated that pairs of students working on these ac-
tivities engaged in discussions regarding the distinction be-
tween scientifically acceptable interpretations of concepts and
their own interpretations, and were able to identify features of
Copyright © 2013 SciR es . 214

R. SAFADI, E. YERUSHALMI
the concept needed to interpret it accurately. In other words,
these activities focus students’ attention on criteria for evaluat-
ing conflicting interpretations. Such activities can thus also
develop diagnostic learning skills that can lead students to gen-
erate ARCs when engaged in subsequent self diagnosis tasks.
Future research could examine the effect of such activities on
students’ tendencies and skills to engage in self-repair when
self-diagnosing their solutions.
Acknowledgements
We wish to thank the high school physics teachers who gave
their valuable time to participate in this study. We appreciate
the support of the Weizmann Institute of Science, Department
of Science Teaching, and The Academic Arab College for
Education in Israel.
REFERENCES
Aleven, V. A. W. M. M., & Koedinger, K. R. (2002). An effective
metacognitive strategy: Learning by doing and explain with a com-
puter-based Cognitive Tutor. Cognitive Science, 26, 147-179.
doi:10.1207/s15516709cog2602_1
Atkinson, R. K, Derry, S. J., Renkl, A., & Wortham, D. W. (2000).
Learning from examples: Instructional principles from the worked
examples research. Review of Educational Research, 70, 181-214.
Atkinson, R. K., Renkl, A., & Merrill, M. M. (2003). Transitioning
from studying examples to solving problems: Effects of self-exp-
lanation prompts and fading worked-out examples. Journal of Edu-
cational Psychology, 95, 774-783. doi:10.1037/0022-0663.95.4.774
Bereiter, C., & Scardamalia, M. (1989). Intentional learning as a goal of
instruction. In L. B. Resnick (Ed.), Knowing, learning, and instruct-
tion: Essays in honor of Robert Glaser (p. 361). Hillsdale, NJ: Law-
rence Erlbaum Associates.
Catrambone, R. (1998). The subgoal learning model: Creating better
examples so that students can solve novel problems. Journal of Ex-
perimental Psychology: General, 127, 355-376.
doi:10.1037/0096-3445.127.4.355
Chandler, P., & Sweller, J. (1991). Cognitive load theory and the for-
mat of instruction. Cognition and Instructio n , 8, 293-332.
doi:10.1207/s1532690xci0804_2
Chandler, P., & Sweller, J. (1992). The split-attention effect as a factor
in the design of instruction. British Journal of Educational Psycholo-
gy, 62, 233-246. doi:10.1111/j.2044-8279.1992.tb01017.x
Chi, M. T. H. (2000). Self-explaining expository texts: The dual pro-
cesses of generating inferences and repairing mental models. In R.
Glaser (Ed.), Advances in Instructional Psychology (pp. 161-238).
Mahwah, NJ: Lawrence Erlbaum Associates.
Chi, M. T. H., Bassok, M., Lewis, M. H., Reimann, P., & Glaser, R.
(1989). Self-explanations: How students study and use examples in
learning to solve problems. Cognitive Science, 13, 145-182.
doi:10.1207/s15516709cog1302_1
Chi, M. T. H., de Leeuw, N., Chiu, M. H., & LaVancher, C. (1994).
Eliciting self-explanations improves understanding. Cognitive Sci-
ence, 18, 439-477.
Chi, M. T. H., & VanLehn, K. A. (1991). The content of physics
self-explanations. The Journal of the Le arning Sciences, 1, 69- 105.
doi:10.1207/s15327809jls0101_4
Clark, R. C., Nguyen, F., & Sweller, J. (2006). Efficiency in learning:
Evidence-based guidelines to manage cognitive load. San Francisco:
Pfeiffer.
Cohen, E., Mason, A., Singh, C., & Yerushalmi, E. (2008). Identifying
differences in diagnostic skills of physics students: Students’
self-diagnostic performance given alternative scaffolding. 2008 Pro-
ceedings of the Physics Education Research Conference (pp. 99-102).
Edmonton: AIP.
Crippen, K. J., & Earl, B. L. (2005). The impact of web-based worked
examples and self-explanation on performance, problem solving, and
self-efficacy. Computers & Education, 49, 809-821.
doi:10.1016/j.compedu.2005.11.018
Dkeidek, I., Hofstien, A., & Mamlouk, R. (2011). Effect of culture on
high-school students’ question-asking ability resulting from an in-
quiry-oriented chemistry laboratory. International Journal of Science
and Mathematics Educat i o n , 9, 1305-1331.
doi:10.1007/s10763-010-9261-0
Eilam, B. (2002). Passing through a western-democratic teacher educa-
tion: The case of Israeli-Arab teachers. Teacher College Record, 104,
1656-1701. doi:10.1111/1467-9620.00216
Elby, A. (2001). Helping physics students learn how to learn. American
Journal of Physics, Physics Education Research Supplement, 69,
S54-S64.
Etkina, E., Van Heuvelen, A., White-Brahmia, S., Brookes, D. T., Gen-
tile, M., Murthy, S., Rosengrant, D., & Warren, A. (2006). Develop-
ing and assessing student scientific abilities. Physical Review. Spe-
cial Topics, Physics E d u cation Research, 2, 020103.
doi:10.1103/PhysRevSTPER.2.020103
Eylon, B., & Helfman, J. (1982). Deductive and analogical problem-
solving processes in physics. New York: American Educational Re-
search Association (AERA).
Gick, M. L., & Holyack, K. J. (1983). Schemainduction and analogical
transfer. Cognitive Psychology, 1 5, 1-38.
doi:10.1016/0010-0285(83)90002-6
Große, C. S., & Renkl, A. (2007). Finding and fixing errors in worked
examples: Can this foster learning outcomes? Learning and Instruc-
tion, 17, 612-634. doi:10.1016/j.learninstruc.2007.09.008
Halloun, I. A., & Hestenes, D. (1985). Common sense concepts about
motion. American Journal of Physics, 53, 1056-1065.
doi:10.1119/1.14031
Hausmann, R. G. M., & Chi, M. T. H. (2002). Can a computer interface
support self-explaining? Cognitive Technology, 7, 4-14.
Hausmann, R. G. M., & VanLehn, K. (2007). Explaining self-explain-
ing: A contrast between content and generation. In R. Luckin, K. R.
Koedinger, & J. Greer (Eds.), Artificial intelligence in education:
Building technology rich learning contexts that work (Vol. 158, pp.
417-424). Amsterdam: IOS Press.
Heller, P., & Hollbaugh, M. (1992). Teaching problem solving through
cooperative grouping. Part 2: Designing problems and structuring
groups. Ameri c a n J o u r nal of Physics, 60, 637-645.
doi:10.1119/1.17118
Henderson, C., & Harper, K. A. (2009). Quiz corrections: Improving
learning by encouraging students to reflect on their mistakes. The
Physics Teacher, 47, 581-586. doi:10.1119/1.3264589
Hieggelke, C. J., Maloney, D. P., O’Kuma, T. L., & Kanim, S. (2006).
E&M TIPERs: Electricity & magnetism tasks. Boston, MA: Addison
Wesley.
Kalyuga, S., Ayres, P., Chandler, P., & Sweller, J. (2003). The exper-
tise reversal effect. Educational Psychologist, 38, 23-31.
doi:10.1207/S15326985EP3801_4
Labudde, P., Reif, F., & Quinn, L. (1988). Facilitation of scientific
concept learning by interpretation procedures and diagnosis. Interna-
tional Journal of Science Education, 10, 81-98.
doi:10.1080/0950069880100108
Maloney, D. (2011). An overview of physics education research on
problem solving. Getting Started in PER (Vol. 2). URL (last checked
1 May 2012).
http://www.compadre.org/Repository/document/ServeFile.cfm?ID=1
1457&DocID=2427
Mason, A., Cohen, E., Singh, C., & Yerushalmi, E. (2009). Self-diag-
nosis, scaffolding and transfer: A tale of two problems. In M. Sabella,
C. Henderson, & C. Singh (Eds.), 2009 Physics Education Research
Conference (pp. 2 7-30). Ann Arbor, MI: AIP.
Mason, A., Cohen, E., Yerushalmi, E., & Singh, C. (2008). Identifying
differences in diagnostic skills between physics students: Developing
a rubric. In L. Hsu, C. Henderson, & M. Sabella (Eds.), 2008 Pro-
ceedings of the Physics Education Research Conference (pp. 147-
150). Edmonton: AIP.
Mazur, E. (1997). Peer instruction: A user’s manual. Upper Saddle Ri-
ver, NJ: Prentice Hall.
Copyright © 2013 SciRe s . 215

R. SAFADI, E. YERUSHALMI
Copyright © 2013 SciRe s . 216
McDermott, L. C., Shaffer, P. S., & The Physics Education Group at
the University of Washington (1998). Tutorials in introductory
physics (Preliminary Ed.). Upper Saddle River, NJ: Pr entice Hall.
Redish, E., Saul, J., & Steinberg, R. (1998). Student expectations in
introductory physics. American Journal of Physics, 66, 212-224.
doi:10.1119/1.18847
Reif, F., & Scott, L. (1999). Teaching scientific thinking skills: Stu-
dents and computers coaching each other. American Journal of Phy-
sics, 67, 819-831. doi:10.1119/1.19130
Renkl, A. (1997). Learning from worked-out examples: A study on
individual differences. Cognitive Scien c e, 21, 1-29.
doi:10.1207/s15516709cog2101_1
Renkl, A., Stark, R., Gruber, H., & Mandl, H. (1998). Learning from
worked-out examples: The effects of example variability and elicited
self-explanations. Contemporary Educational Psychology, 23, 90-108.
doi:10.1006/ceps.1997.0959
Reisslein, J., Atkinson, R. K., Seeling, P., & Reisslein, M. (2006).
Encountering the expertise reversal effect with a computer-based en-
vironment on electrical circuit analysis. Learning and Instruction, 16,
92-103. doi:10.1016/j.learninstruc.2006.02.008
Schwartz, D. L., & Martin, T. (2004). Inventing to prepare for learning:
The hidden efficiency of original student production in statistics in-
struction. Cognition & Instruction, 22, 129-184.
doi:10.1207/s1532690xci2202_1
Sokoloff, D. R., & Thornton, R. K. (2001). Interactive lecture demon-
strations. New York, NY: Wiley.
Sweller, J., van Merriënboer, J. J. G., & Paas, F. G. (1998). Cognitive
architecture and instructional design. Educational Psychology Re-
view, 10, 251-296. doi:10.1023/A:1022193728205
Tamir, P., & Caridin, H. (1993). Characteristics of the learning envi-
ronment in biology and chemistry classes as perceived by Jewish and
Arab high school students in Israel. Research in Science and Tech-
nological Education, 11, 5-14. doi:10.1080/0263514930110102
Van Gog, T., Paas, F., & van Merriënboer, J. J. G. (2008). Effects of
studying sequences of process-oriented and product-oriented worked
examples on troubleshooting transfer efficiency. Learning and In-
struction, 18, 211-222. doi:10.1016/j.learninstruc.2007.03.003
Viennot, L. (1979). Spontaneous reasoning in elementary dynamics.
European Journal of Science Education, 1, 205-221.
doi:10.1080/0140528790010209
Ward, M., & Sweller, J. (1990). Structuring effective worked examples.
Cognition and Instruction, 7, 1-39.
doi:10.1207/s1532690xci0701_1
Wertsch, J. V. (1984). The zone of proximal development & some
conceptual issues. In B. Rogoff & J. V. Wertsch (Eds.), Children’s
learning in the “zone of proximal development”—New directions for
child development (pp. 7-18). San Francisco: Jossey-Bass.
Yerushalmi, E., Henderson, C., Heller, K., Heller, P., & Kuo, V. (2007).
Physics faculty beliefs and values about the teaching and learning of
problem solving part 1: Mapping the common core. Physical Review
Special Topics—Physics Education Research, 3 , 020109.
doi:10.1103/PhysRevSTPER.3.020109
Yerushalmi, E., Mason, A., Cohen, E., & Singh, C. (2009).
Self-diagnosis, scaffolding and transfer in a more conventional in-
troductory physics problem. In M. Sabella, C. Henderson, & C. Singh
(Eds.), 2009 Physics Education Research Conference (pp. 23-27).
Ann Arbor, MI: AIP.
Yerushalmi, E., Puterkovski, M., & Bagno, E., (2012). Knowledge
integration while interacting with an online troubleshooting activity,
Journal of Science Education and Technology.
doi:10.1007/s10956-012-9406-8
Yerushalmi, E., Singh, C., & Eylon, B. (2007). Physics learning in the
context of scaffolded diagnostic tasks (1): The experimental setup. In
L. McCullough, L. Hsu, & C. Henderson (Eds.), Proceedings of the
Physics Education Research Conference (pp. 27-30). Greensboro,
NC: AIP.