Paper Menu >>
Journal Menu >>
 J. Biomedical Science and Engineering, 2010, 3, 1001-1005 JBiSE doi:10.4236/jbise.2010.310130 Published Online October 2010 (http://www.SciRP.org/journal/jbise/). Published Online October 20 10 in SciRes. http://www.scirp.org/journal/jbise Different initial conditions in fuzzy Tumor model Somayeh Saraf Esmaili1, Ali Motie Nasrabadi2 1Department Biomedical engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran; 2Department Biomedical engineering, Engineering Faculty, Shahed University, Tehran, Iran. Email: Somayeh_saraf83@yahoo.com; nasrabadi@shahed.ac.ir Received 26 July 2010; revised 18 August 2010; accepted 25 August 2010. ABSTRACT One of the best ways for better understanding of biological experiments is mathematical modeling. Modeling cancer is one of the complicated biologi- cal modeling that has uncertainty. Therefore, fuzzy models have studied because of their application in achievement uncertainty in modeling. Overall, the main purpose of this modeling is creating a new view of complex phenomena. In this paper, fuzzy differential equation model consisting of tumor, the immune system and normal cells has been studied. Model derived from a classical model DePillis in 2003, which some parameters from a clinical point of view can be described in the region. In this model, by considering fuzzy parameters from clinical point of view, the three-dimensional fuzzy tumor cells in terms of time and membership function are pic- tured and region of uncertainties are determined. To access the uncertainty area we use fuzzy differ- ential inclusion method that is one of the including methods of solving differential equations. Also, dif- ferent initial conditions on the model are inserted and the results of them are analyzed because tumor has different treatment in different initial condi- tions. Results show that fuzzy models in the best way justify what happens in the reality. Keywords: Tumor Cells; Mathematical Modeling; Fuzzy Parameters; Fuzzy Differential Equation 1. INTRODUCTION R Using mathematical models is one of the techniques stricken with cancer for finding appropriate treatment and low risk of it. In this way, models of diversity in to different factors such as competition in tumor cells with normal cells over food sources and effects of the im- mune system on the growth of tumor cells and in some cases different ways of treatment such as chemotherapy have been presented [1-6]. These models often based on biological principles and by using the parameters as ob- tained from experiment or estimated investment are ori- ginated. Thus always to determine these parameters, there are some uncertainties [7,8]. Therefore, because of uncertainty in the parameters of models, using of differential equations and definite ten- dency in some of artificial systems don’t have efficiency to analyze the behavior of living systems, and all the reality not be said by these models. More generally, there are two major reasons for using fuzzy systems in modeling uncertainties. The first reason is being fuzzy measurements. Modeling phenomena are always come from observations and measurements, and these meas- urements are always exposed to errors and errors from the physical and biological processes with uncertainty are natural. Any numeric measurements that can be ex- tracted also affected by measurement tools and are also influenced by the observer to understand. The second reason is due to be qualitative model. Each of the ma- thematical variables of model is a sign and the desired quantity, which in turn is a matter of quality. Characters and relationships in the analysis of phenomena common to the process (recognition condition), all those answers are generating subsets acceptable answers and because of that they are accepted in daily applications [9]. There are many different viewpoints for modeling uncertainty. Use of fuzzy differential equations is one of these view- points. When these uncertainties in the modeling are combined with differential equation, they are caused fuzzy differential equations in the modeling that can be kept ambiguity in the phenomena. Recent years, fuzzy differential equations have been proposed as a tool for modeling in non-deterministic systems. The main goal of a fuzzy differential equation estimates further confor- mity with reality in comparison with ordinary differen- tial equations. There have been many different methods for solving fuzzy differential equations that across them fuzzy differential inclusion (FDI) because having the ability to prevent and eliminate the production and dis- semination of uncertainty in the problem solving process to occur, is suitable for all types of equations including  S. S. Esmaili et al. / J. Biomedical Science and Engineering 3 (2010) 1001-1005 Copyright © 2010 SciRes. JBiSE 1002 Responsiveness is the linear and nonlinear [10-12]. For the first time in 2004, K. Kumar Majumdar and D. Dutta Majumder in one grade differential equation tumor model proposed the idea of using fuzzy differential equ- ations and the advantages of its use in modeling [10,11,13]. In 2009, we simulated and analyzed that model by using fuzzy differential inclusion method [14]. In this paper, a model of third degree consists of tu- mor cells, immune system cells and normal cells are used and method of solving fuzzy differential inclusion are expressed and all areas of response three-dimen- sional figures using the above method are determined. The purpose of this article is entering uncertainty into tumor model by considering fuzzy model parameters. Fuzzy parameters change crisp system into fuzzy system. Areas of uncertainty for the number of tumor cells in terms of membership function and time are determined. Also in this model, different initial conditions are evalu- ated by their results of simulation. The main purpose of this article is creation a new view of cancer noted that simulation could be stomata for complex phenomena to determine the uncertainty area. This paper is organized as follows. In Section 2, the model from Depillis in 2003 and its mathematical equations are presented. In Sections 3 and 4 the fuzzy model-based and the method reached the fuzzy surfaces is described, and then simulation re- sults of the different initial conditions are evaluated. Section 5 presents some conclusions. 2. TUMOR MODEL AND ITS MATEMATICAL EQUATIONS Mathematical model presented in this paper based on the Depillis model [15]. Since the clinical observations, some parameters of the model with uncertainty and range are acceptable, so in this paper these parameters based on clinical observations and based on the possibil- ity of its occurrence are considered fuzzy. In this paper, for the first time, the uncertainty range of tumor cells in terms of time and membership function is drawn and behavior in terms of its possible occurrence is deter- mined. In this model, Tis the population of tumor cells,Nis the total population of healthy cells and I the total popu- lation of immune cells. The dynamic model of three populations as well as the drug concentration in the blood has been written. Equations of model are presented as follow: 2243 11232 111 2 (1)(1 ) (1 )(1 ) (1 ) () u u u NrNbN cTNaeN TrTbT cTIcTNaeT IT I scTIdIaeI T uvtdu (1) Range of parameters was introduced as follows [15] (see Table 1): 1 a, 2 aand 3 a are fraction cell kill with 312 aaa and high bandwidth is not more than 0.5. 11 12 1bb are carrying capacities. 4312 ,,,cccc are completion terms. s is immune source rate; in our experi- ments 00.5s . 1 d and2 dare death rate of immune cells and death rate of drug, respectively. α is immune threshold rate. is immune response rate; a clinical range of is the interval (0, 2.5). 3. CONSIDERING FUZZY PARAMETERS According to the parameters described in the previous section, can be concluded that some model parameters such as s ,1 a,2 a,3 aand are non-deterministic and uncertain in model. Thus, for entering the uncertainty in model, these parameters are considered fuzzy. Trapezoi- dal fuzzy number is written as a/b/c/d, where [a d] de- fines the support and [b c] is the vertex (or core) that is used in the model. The parameters in the peril immune system disease, are in the area with membership function is equaled one (vertex) and minimum and maximum value of described parameters are on the base and their membership functions are zero (trapezoid fuzzy number). Values of parameters are in Table 1. Functions of fuzzy parameters such as s ,1 a,2 a,3 aand in term of () x are located in Table 2. Figures of membership functions of() s x ,1() a x ,2() a x ,3() a x and () x are shown in Figure 1. 4. SIMULATION OF TUMOR MODEL USING FDI Fuzzy differential inclusion (FDI) is one of the new solving methods. Five parameters are fuzzy parameters and other parameters have precise amount. For modeling the system using FDI method in MATLAB command Table 1. Fuzzy functions of rigght and left supports of parameters. parameter Crisp value parameter Crisp and fuzzy value 1 d 0.2 0/0.009/0.011/2.5 2 d 1 s 0/0.32/0.34/0.5 1 r 1.5 1 a 0/0.19/0.21/0.5 2 r 1 2 a 0/0.29/0.31/0.5 431 ccc 1 3 a 0/0.09/0.11/0.5 2 c 0.5 2 a 1 α 0.5 1 a 1  S. S. Esmaili et al. / J. Biomedical Science and Engineering 3 (2010) 1001-1005 Copyright © 2010 SciRes. JBiSE 1003 Table 2. Fuzzy and crisp value parameters. Description Fuzzy function Left supprot of (s) parameter 0.32( ) x Right supprot of (s) parameter 0.16( )0.5x Left supprot of (1 a) parameter 0.19( ) x Right supprot of (1 a) parameter 0.29( )0.5x Left supprot of (2 a) parameter 0.29( ) x Right supprot of (2 a) parameter 0.19( )0.5x Left supprot of (3 a) parameter 0.09( ) x Right supprot of (3 a) parameter 0.39( )0.5x Left supprot of ( ) parameter 0.0099( ) x Right supprot of ( ) parameter 2.489()2.5x 00.33 0.5 0 0.5 1 s m embership function 0 24 0 0.5 1 ro 00.2 0.5 0 0.5 1 a1 00.1 0.5 0 0.5 1 a3 m embership function 00.3 0.5 0 0.5 1 a2 Figure 1. Trapezoidal fuzzy numbers of s , 1 a, 2 a, 3 aand parameters. file, the five parameters with regard to fuzzy member- ship functions are written (analysis with fuzzy numbers is based on using intervals after taking α-cuts), then low and high and middle support of each of the five parame- ters are considered by low and high and middle support of other five parameters. The figures have been specially created which are computed from all left and right sup- ports of parameters with left and right supports of other parameters, and left and right supports of other parame- ters with middle supports of other parameters. There are 32 (25 = 32) figures for upper and lower supports of each parameter with other parameters and 80 (5×25-1=80) figures for each parameter bound middle with upper and lower support of other parameters (In total there are 112 figures). The fuzzy differential equa- tion solutions by the program per membership function from zero to one are found. A total 112 figures per level from zero to one membership function is created. Max- imum and minimum of three dimensional fuzzy figures, respectively as the upper bound and lower bound of the final model are considered. The general uncertainties by using fuzzy parameters are into the model. Fuzzy pa- rameters change crisp system to fuzzy system. Upper and lower supports of model are come from maximum and minimum of 112 figures. Thereby uncertainty in the system can be modeled (high and low figures of three dimensional fuzzy figures). Two different initial conditions of tumor size will in- sert in the model because the size of recognition of tu- mor by immune system is a serious element in early disappearance of tumor or in tumor regression. 4.1. Results of Simulation in Large Initial Conditions of Tumor First, assume that tumor is identified in large size; i.e. the initial condition is as follow: (0) 1N, (0) 0.15I and (0) 0.25T , (this corresponds to a tumor with 0.25×1011 cells and (0) 0.25Tis normalized value) and in no treatment conditions we found the area of the tumor cells response. Early recognition of tumor by im- mune system is a serious element in early disappearance of tumor as the tumor obviation will occur if the immune cells can identify the tumor in small size. The clinical detection threshold for a tumor is generally 107 cells [16], so the initial tumor volume of 0.25 normalized units is above clinical detection levels and we will expect growth on tumor. The number of tumor cells based on time and member- ship function is shown in Figure 2. Considering Figures 2 and 3, in the case without treatment, the number of cells will increase in the high possibility (membership function = 1). The number of tumor cells will be in the normalized range of 0.53 to 0.59. As shown in the Figure 2 where the membership function is equaled to zero, number of cancer cells is near zero in on a lower bound and it is one in up- per bound, this means that the event can reach tumor cells to zero is zero or on a very low possibility. Figure 2 is good confirming by the reality. In the reality, due to im- mune cells, the possibility that the number of cells reaches its maximum value on the whole body is very low, and in this status the possibility that the number of tumor cells to zero, is also very low. It is confirming the fact that de- creasing the number of normal cells due to increasing of tumor cells is possible. Since the figures created are oc- curred by combining uncertainty of all the fuzzy parame- ters together, so all shapes have as well as confirmation of what happens in the real world. 4.2. Results of Simulation in Small Initial Conditions of Tumor In different initial condition, assume that tumor is identi- fied in small size; i.e. the initial condition is as follow: (0) 1N ,(0) 0.15I and 5 (0) 10T , (relatively very small tumor volume in normalized value). Again by us- ing the above method, uncertainty region of tumor 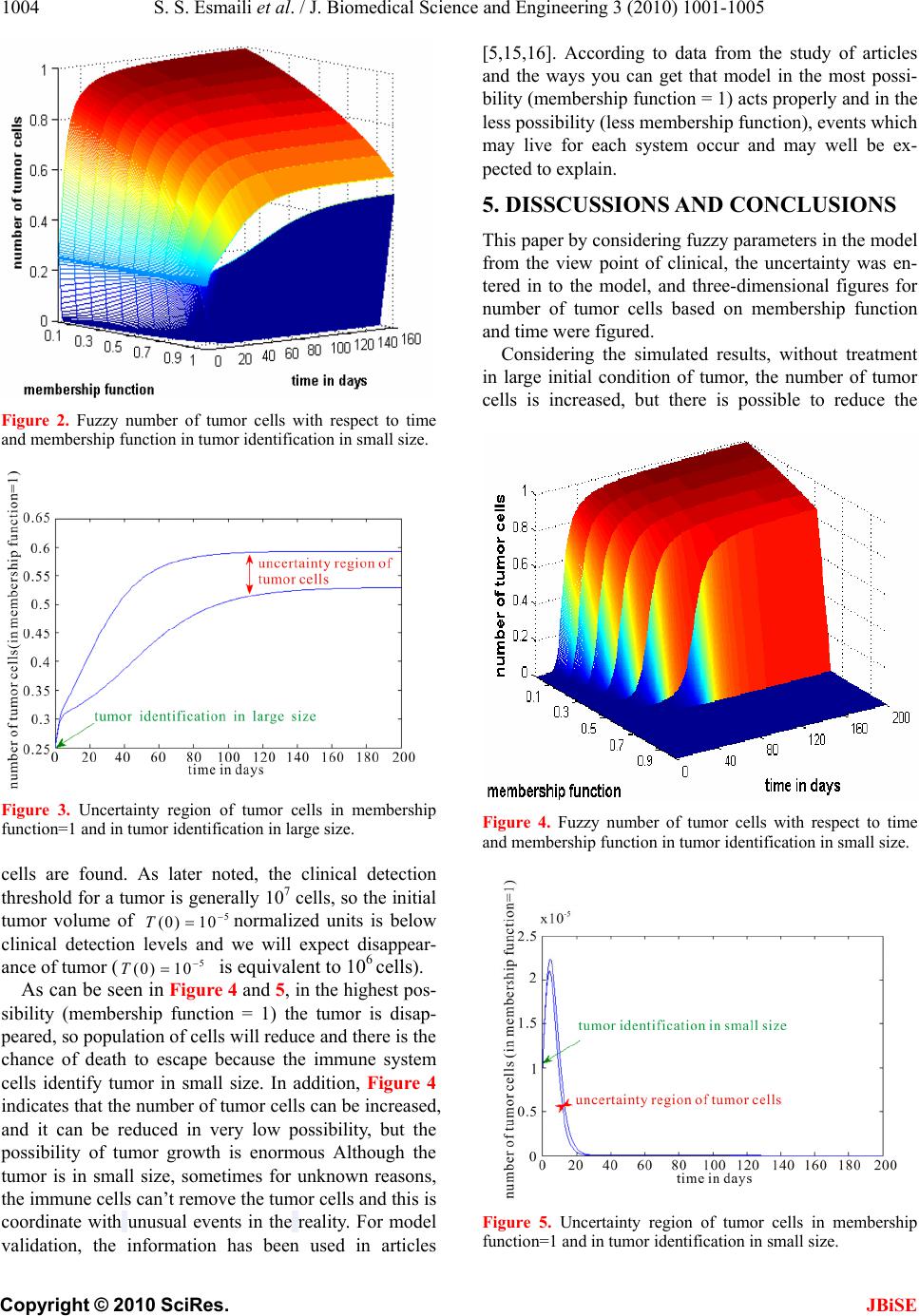 S. S. Esmaili et al. / J. Biomedical Science and Engineering 3 (2010) 1001-1005 Copyright © 2010 SciRes. JBiSE 1004 Figure 2. Fuzzy number of tumor cells with respect to time and membership function in tumor identification in small size. Figure 3. Uncertainty region of tumor cells in membership function=1 and in tumor identification in large size. cells are found. As later noted, the clinical detection threshold for a tumor is generally 107 cells, so the initial tumor volume of 5 (0) 10T normalized units is below clinical detection levels and we will expect disappear- ance of tumor (5 (0) 10T is equivalent to 106 cells). As can be seen in Figure 4 and 5, in the highest pos- sibility (membership function = 1) the tumor is disap- peared, so population of cells will reduce and there is the chance of death to escape because the immune system cells identify tumor in small size. In addition, Figure 4 indicates that the number of tumor cells can be increased, and it can be reduced in very low possibility, but the possibility of tumor growth is enormous Although the tumor is in small size, sometimes for unknown reasons, the immune cells can’t remove the tumor cells and this is coordinate with unusual events in the reality. For model validation, the information has been used in articles [5,15,16]. According to data from the study of articles and the ways you can get that model in the most possi- bility (membership function = 1) acts properly and in the less possibility (less membership function), events which may live for each system occur and may well be ex- pected to explain. 5. DISSCUSSIONS AND CONCLUSIONS This paper by considering fuzzy parameters in the model from the view point of clinical, the uncertainty was en- tered in to the model, and three-dimensional figures for number of tumor cells based on membership function and time were figured. Considering the simulated results, without treatment in large initial condition of tumor, the number of tumor cells is increased, but there is possible to reduce the Figure 4. Fuzzy number of tumor cells with respect to time and membership function in tumor identification in small size. Figure 5. Uncertainty region of tumor cells in membership function=1 and in tumor identification in small size.  S. S. Esmaili et al. / J. Biomedical Science and Engineering 3 (2010) 1001-1005 Copyright © 2010 SciRes. JBiSE 1005 number of tumor cells in the presence of the immune system, and this possibility with regard to its member- ship function is very low. The simulations show that in small initial condition of tumor, in regions of possible high, the number of tumor cells is reduced to zero. In areas, that the possible occurrence is low, even in small size of tumor, reduce the number of tumor cells is not possible, and immune system cells can’t remove the tu- mor that this is by considering the complex system of the body being very close to reality. This case may be oc- curred sometimes for unknown reasons due to different patient conditions, including the power of being different immune system, its ability to be different in the devel- opment of tumor cells, and etc. Therefore from the ob- servations obtained that the models based on fuzzy dif- ferential equations in three dimensions in term of time and number of cells are appropriate model because of considering the uncertainty in model parameters. It should be noted in the modeling using fuzzy differential equations; the figures created are occurred by combining uncertainty of all the fuzzy parameters together, so all shapes have as well as confirmation of what happens in the real world. Consequently, the theory of fuzzy differential equa- tions is considered as suitable tool for modeling complex phenomena. By using fuzzy differential equations, the ambiguity in the phenomena can be kept and also be- haviors of tumors without the experiment can be pre- dicted. REFERENCES [1] Kirschner, D. and Panetta, J. C. (1998) Modeling immu- notherapy of the tumor–immune interaction. Journal of Mathematical Biology, 37(3), 235-252. [2] Pillis, L.G., Gua, W. and Radunskaya, A.E, (2006) Mixed immunotherapy and chemotherapy of tumors: modeling, applications and biological interpretations. Journal of Theoretical Biology, 238(4), 841-862. [3] Onofrio, A. (2006) Tumor–immune system interaction: Modeling the tumor-stimulated proliferation of effectors and immunotherapy. Mathematical Models and Methods in Applied Sciences, 16(8), 1375-1401. [4] De Pillis, L.G. and Radunskaya, A.E. (2003) Immune response to tumor invasion. In: Bathe, K., Ed., Computa- tional Fluid and Solid Mechanics, 2. MIT Press, Cam- bridge, MA, 1661-1668. [5] De Pillis, L.G. and Radunskaya, A.E. (2001) A mathe- matical tumor model with immune resistance and drug therapy: an optimal control approach. Journal of Theo- retical Medicine, 3(2), 79–100. [6] Derbel, L. (2004) Analysis of a new model for tu- mor–immune system competition including long time scale effects. Math. Mod. Meth. Appl. S. 14(11), 1657-1681. [7] Jowers, L.J., Buckley, J.J. and Reilly, K.D. (2008) Simu- lating continuous fuzzy systems for fuzzy solution sur- faces. Soft Computer, 12(3), 235-241. [8] Jowers, L.J., Buckley, J.J. and Reilly, K.D. (2007) Simu- lating continuous fuzzy systems. Information Sciences, 177(2), 436-448. [9] Bezdek, J.C. (1993) Fuzzy models, what are they and why? Transcation of Fuzzy Set and Systems, 1(1). [10] Majumdar, K.K. (2002/2003) One dimensional fuzzy differential inclusions. Journal of Intelligent & Fuzzy Systems, 13(1), 1-5. [11] http://www.cancer.org/Research/CancerFactsFigures/can cer-facts-figures-2006 [12] Zuchowski, T.R. and Wasowski1, J. (2001) Differential equations with fuzzy parameters via differential inclusions. Journal of Mathematical Analysis and Applications, 255(1), 177-194. [13] Majumdar, K.K. and Majumder, D.D. (2004) Fuzzy differential inclusions in atmospheric and medical cybernetics. IEEE Transaction on Systems, MAN, and Cybernetics, 34(2). [14] Esmaili, S.S. and Nasrabadi, A.M. (2009) Uncertainty analysis in tumor model with fuzzy parameter. Proceedings of the CiSENG Conference, China. [15] Pillis, L.G. and Radunskaya, A.E. (2003) The Dynamics of an optimally controlled tumor model. A Case Study, Mathemaics and Computer Modeling, 37(1), 1221-1244. [16] Pillis, L.G., Gua, W. and Radunskaya, A.E., (2006) Mixed immunotherapy and chemotherapy of tumors: modeling, applications and biological interpretations. Journal of Theoretical Biology, 238(4), 841-862. [17] Majumdar, K.K. and Majumder, D.D. (2004) Some stud- ies on uncertainty management in dynamical systems using cybernetic approaches and fuzzy techniques with applications. International Journal of Systems Science, 35(15), 889-901. |

