J. Biomedical Science and Engineering, 2010, 3, 986-1000 JBiSE
doi:10.4236/jbise.2010.310129 Published Online October 2010 (http://www.SciRP.org/journal/jbise/).
Published Online October 20 10 in SciRes. http://www.scirp.org/journal/jbise
Extending cell cycle synchrony and deconvolving population
effects in budding yeast through an analysis of volume growth
with a structured Leslie model
Chris C. Stowers1, Erik M. Boczko2
1Bioprocess R&D Division, Dow AgroSciences LLC, Indianapolis, USA;
2Department of Biomedical Informatics, Vanderbilt University, Nashville, USA.
Received 22 June 2010; 12 July 2010; 26 July 2010.
ABSTRACT
Budding yeast are a fundamental organism at the
center of systems biology research. Understanding
the physiology and kinetics of their growth and di-
vision is fundamental to the design of models of
gene regulation and the interpretation of experi-
mental measurements. We have developed a Leslie
model with structured volume and age classes to
understand population growth and cell cycle syn-
chrony in budding yeast. The model exhibits broad
agreement with a variety of experimental data. The
model is easily annotated with volume milestones
and cell cycle phases and at least three distinct
goals are realizable: 1) One can investigate how any
single cell property manifests itself at the popula-
tion level. 2) One can deconvolve observed popula-
tion averages into individual cell signals structured
by volume and age. 3) One can investigate control-
lability of the population dynamics. We focus on the
latter question. Our model was initially designed to
answer the question: Can continuous volume filtra-
tion extend synchrony? To date, most general ex-
perimental methods can produce an initially syn-
chronous population whose synchrony decays rap-
idly over three or four cell cycles. Our model pre-
dicts that continuous volume filtration can extend
this maintenance of synchrony by an order of mag-
nitude. Our data inform the development of simple
fluidic devices to extend synchrony in continuous
culture at all scales from nanophysiometers to bio-
reactors.
Keywords: Quantitative Biology, Systems Biology,
Volume Filtration, Cell Cycle
1. INTRODUCTION
Unlike the simple volume symmetric division of E. Coli
[1], an initially synchronous culture of budding yeast
become asynchronous and stationary very rapidly. While
stable, synchronous, autonomous oscillations have been
observed and are of enormous interest, they do not occur
generically and are far from understood [2-5]. Popu-
lation synchrony is often monitored by tracking the
percent of a culture that is budded as a function of time.
The physiological factors influencing the rapid decay of
cell cycle synchrony in budding yeast were investigated
three decades ago. It was found that new daughter cells
take longer to traverse the mitotic cycle than their
mothers because of a volume asymmetry at division.
That is, daughter cells at the time of division, are smaller
in volume than their mothers. Furthermore as mothers
age they give rise to progressively smaller daughters on
average [6], compounding the problem. Currently there
is renewed interest in the physiology of replication in
relation to aging and the asymmetric partitioning of
biomolecules between mother and daughter [1,7,8].
As yeast are now routinely the subject of expression
analysis, synchronous growth and division has important
and largely unexplored implications for attaching mean-
ing to commonly measured population signals [5,9]. Our
interest in developing a model for the volume growth and
population synchrony of budding yeast stems from our
previous work on an ostensibly simple gene regulatory
circuit involved in nitrogen catabolite repression (NCR).
An analysis of a minimal model of the NCR-circuit
indicates that the components of the system oscillate in
phase with the cell cycle [10,11]. In order to understand
how a cellular oscillation is observable at the population
level, and further, how one could engineer an experiment
to convincingly demonstrate periodic oscillation at the
cellular level from a population measurement, we under-
took the development of a structured population model of
yeast growth and division to be described.
The central observations of this study are theoretical

C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000 987
in nature and can be summarized as follows. Theore-
tically, volume symmetric division leads to persistent
synchrony. Each strain of budding yeast has a charac-
teristic mean daughter—mother division volume asym-
metry, some more and some less pronounced. Paren-
thetically, this asymmetry is a function of growth rate
and has been shown to be inversely proportional to it
[12]. As the asymmetry between mother and daughter
division volume increases, synchrony decays in a predic-
table way. For a given strain of yeast, growing exponen-
tially in a bioreactor, our model predicts that continuously
filtering out the smallest and largest cells extends the
synchrony of the system. Our model predicts that with
judicious choices of filtration cutoff volumes, synchrony
can be extended by an order of magnitude. Given strain
specific measurements our model can be used to predict
design parameters such as the filtration cutoff volumes.
The filtration process can be conceived of, in a way that
we shall make precise, as a means to restore partial
symmetry. While it is true that continuous filtration will
skew the population of cells under observation, it can be
accomplished without inducing a generic stress response
within the yeast. This trade off may for certain experi-
ments be useful.
The cell cycle synchrony of a population of yeast, its
persistence, decay and control are essentially an ontolo-
gically dynamical systems phenomena. There is a long
and fruitful history associated with the modeling of
population growth. Budding yeast and their mitotic cell
cycle continue to be an interesting and important area of
mathematical cell biology. We make no formal attempt
to review this enormous literature but restrict our
attention to those models of which we are aware have
dealt with volume growth and the effects of a mixed
population of cells growing with potentially different
growth rates. The mixed mother-daughter model [13]
was developed based on the mathematical results of
branching processes [14,15] to explain the variations in
the 1 G phase of the cell cycle. This model was used to
derive a stationary distribution of mothers and daughters
as a function of the cell cycle. A model developed in [16]
and expanded on by [12] considered the properties of an
asynchronous population growing exponentially. A
central result of their pioneering work was to derive a
formula for the replicative age distribution at stationarity
that depends on only two parameters, the culture growth
rate and the parental doubling time. The formulas and
analysis derived by Lord and Wheals have continued to
underpin current models of cell cycle dynamics and
division [17, see for instance the reset rule at the bottom
of Table 1]. An admitted limitation of their work
however is that it explicitly assumes that the growth
rates among the age classes are the same. Their paper
presented compelling evidence to support this claim.
There is also a wealth of evidence to the contrary [6,18],
and evidence that older mothers grow larger with each
division. Age structured models that take into account
this finer but important level of detail were proposed and
utilized to analyze population signals of a critical protein
[19], in search of the still elusive link between size
control and division [20].
Population balance models that extend that of
Hartwell and Unger have been proposed to explore the
links between metabolism and the cell cycle during
asynchronous as well as synchronous growth. These
models are extensively reviewed in [2]. Recently,
sophisticated population balance models have been cons-
tructed that take into account the mass changes that
accompany growth and division and that can vary among
distinct age classes [21]. The Leslie model that we
present is a discrete version of the continuous population
balance model, although our focus is explicitly on
volume as opposed to mass. The obvious advantage of
this class of model is that it naturally allows one to
describe any variation among age classes since they are
explicitly represented. An important reason for utilizing
and exploring a volume and age structured model is that
it captures the effects that influence synchrony and,
because it is a dynamical systems model, it can directly
be used to examine the dynamical phenomena of
synchrony and the effects of filtration as a control
mechanism. That is the goal of this paper.
There is a long history of elutriation as a means of
preparing and examining yeast sub-populations in the
biological literature [22]. There is also a long history in
the chemical engineering literature of filtration and
sedimentation as a means to separate and control the
growth of micro-organisms [23-25]. These two literatures
are now converging as systems biology has hit its stride
and seeks to leverage every available technology to
Table 1. A glossary of milestones and their meaning.
Symbol Definition
k Denotes replicative age.
k
V The minimal volume of yeast cell of age k.
k
V The maximal volume of yeast cell of age k.
k

The exponential growth rate of a yeast cell of age k.
k--MDV The expected volume at which a yeast cell of age k
will divide.
k--MEDV The expected volume of a daughter born from a
division in age class k.
k--MEPV The expected volume of a mother immediately after a
division event in age class k.
k--BE The expected volume at which a cell of age k begins
to bud.

988 C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000
examine and understand the physiology of networks. As
described in this paper, the main result of our modeling
work suggests that continuous volume filtration can
maintain the synchrony of an initially synchronous
population for 20 to 30 cycles: An order of magnitude
improvement. This theoretical result can be put into
practice utilizing current microfluidic techniques at every
population scale of investigation from the nanophysio-
meter up to the bioreactor.
2. THE LESLIE MODEL
In a culture of budding yeast, the mitotic cell cycles of
distinct cells need not be in phase with each other. We
want to model the dynamics of the mitotic cell cycles of
a population of budding yeast growing in a bioreactor. A
description of the dynamics requires a model describing
the rate at which single cells progress through the mito-
tic cell cycle. The vital rates correspond to growth, divi-
sion, aging and death. We describe the vital rates through
a consideration of two variables, cell volume and
replicative age, with the aid of a Leslie matrix. Leslie
models are an important and well studied class of
structured population models. Structured population
models are commonly used to describe the life cycle of
an organism or process. A comprehensive review of their
mathematical properties can be found in [26]. While we
wish to highlight certain aspects of the model for its
utility we in no way want to obscure or jeopardize the
biological punchline: Continuous volume filtration can
extend cell cycle synchrony. A heuristic understanding of
our model can be obtained without recourse to equations
through the process flow diagram in Figure 1. Figure 1
is analogous, but not identical, to those described in [19,
Figure 5] and [21, Figure 3].
2.1. Variables
The model is organized around two variables:
1) Replicative cell age. As a yeast cell buds during the
mitotic cell cycle, a chitinous bud scar is permanently
formed on the mother cell. The bud scars can be
visualized with calcoflour white staining [27], and like the
rings of a tree, can be used to determine a replicative age.
Each generation can be quantitatively identified with the
equivalence class of those yeast that carry precisely the
same number of bud scars. Traditionally generations, or
bud scar equivalence classes, have been denoted by
012
,, , ,
kn
PPP P P . Replicative age has been identified
as a variable that directly impacts synchrony [6].
Replicative age is properly a discrete variable that we will
index by k, the number of bud scars.
2) The volume of an individual yeast cell. Cell volume
has been observed to increases monotonically with time
until division, within a given age class, and thus is often
used as a proxy for progression through the mitotic cell
cycle. The volume of a budded cell is taken as the total
volume of both the mother cell and the bud, until divi-
sion at which point they become distinct. The results of
this paper confirm that volume is intimately connected
with synchrony. Volume is consistently expressed in units
of cubic microns throughout.
Figure 1. The Leslie model. volume intervals are open circles. Arrows indicate growth or division.

C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000 989
2.2. Volume Intervals and Time
Yeast cells of a given replicative age k, are observed to
grow in volume between well defined limits. The
minimum and maximum cell volumes observed from
experiment are random variables that naturally delimit
and define intervals, ():=[ ,] k
k
kVV. We consider the
temporal evolution of the system at a sequence of
equally spaced times, :=
so
ttst . The volume
intervals, ()k, are partitioned into subintervals

(, ):=(, ),(1,)()
I
ikVik Vikk, with
()= (,)
i
kIik, = 0,1,...k in, where (0,):=k Vk V,
and (1,):= k
k
Vnk V. The partitions are chosen
according to the growth law, within each age class, such
that any cell with volume in the interval (, )
I
ik now,
would have a volume in (1,)
I
ik

, precisely t

later.
The unit of time is minutes and we have taken =1t

throughout. The choice of the time step was chosen
based on experimental time series observations of yeast
growth and model stability. The number of time intervals
k
n is determined from the choice of time step and the
experimental values of the volume limits and the growth
rate equation relating them. The state of the yeast
population at time s t is described by a vector,
(, )( ):
=
(, ).
s
ik t
numberofcells ofgenerationkwithvolume
vIik


Each of the (, )( )
s
ik t

cells living in (, )
I
ik at time
s
t are faced with the following possibilities:
1) The cell dies
2) The volume of the cell increases
3) The cell divides
Each individual yeast does not die or divide at exactly
the same volume and age. The population distributions
governing each of these possibilities are functions of our
independent variables namely volume and age, and are
indexed by i and k. We describe the relevant details of
these events and their distributions in the following
sections.
2.3. Cell Death
The probability that cell death occurs is denoted by
,ik
d. Mortality curves have been measured for several
strains of yeast under a variety of conditions
[18,28,29](In particular see Ta ble 1 of the latter). These
data can be used to determine an age class specific death
rate. In [12] the authors observe that the death rate on
average amounts to 10 10/()cell generation
.
2.4. Volume Gr owth
The probability that growth occurs is denoted by ki g,,
and the fraction of cells that survive and grow is
)(1:= ,,, kikiki dg


. Volume growth has been measured
and is generally considered to increase exponentially
with time. For all of the experiments and analysis in this
paper we have considered exponential volume growth.
Let k

denote the age class specific growth rate. Then,
the volume intervals are conveniently described by



(0, )=,
(, )=(, ),(, )
(,)=(,),
t
k
kk
t
k
k
kk
Ik VVe
IikVikVike
In kVn kV












2.5. Cell Division
All cells do not divide precisely at the same volume. The
probability that a division occurs, at a given volume
indexed by i, within a given age class indexed by k, is
denoted ,, := 1
ik ik
c


. The importance of including
sloppy size control in models of growth and division is
discussed in [30]. We have implemented a variety of
distributions. Two of the most natural are a Poisson
process [31] to model division as time to failure, and
second a Brownian process using a normal distribution.
As will be described in the results section, qualitatively
this choice makes little or no difference. The conditional
mean volume at which a division happens, with respect
to the distribution ki c, for fixed k(age), is referred to as
the k--mean division volume and denoted as k--MDV.
We assume that the division of a cell of volume v in
age class k P results in a cell of age class 0 P with
volume v

and a cell of age class 1k P with volume
v

. Furthermore, =vvv



. We sometimes denote the
division process as 1kk PP

. It has been
experimentally observed [6] that after a cell has budded,
the ensuing volume growth is concentrated almost
entirely in the bud. This implies that there is a
conditional probability distribution for v that depends
on the size and age of the mother. Let ,,ijk

be the
probability that after a cell division, 1kk PP

, we get a
cell of age class 0 P with volume in (,0)
I
i from a
dividing cell in (,)
I
jk . The conditional expected
volume, conditioned on a fixed k, with respect to the
distribution ,,ijk

is referred to as the mean emergent
daughter volume and denoted k--MEDV. Let, ,,ijk

represent the probability that a parent cell of volume
(, 1)Ijk

emerges from a division event in (, )
I
ik .
The conditional expected volume of the parent after
division is denoted k--MEPV. Generally, the distribution
of division volumes has been observed to be normal
[32,33].
Given these definitions we can present the projection

990 C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000
formula that updates the population in time.
11,0 ,,,
,
(,0)()=(1,0)()(,)()
s
lslikiks
ki
ltltc ikt  


 (1)
1
1,, ,1,1
(, )()
=(1,)( )(,1)( );
>0
s
l mslimims
i
lm t
lmtcimt
m

 


 
 (2)
),(=))(,( 00 mltml


(3)
The first summand in each equation represents the
volume growth contribution while the second summation
term represents the density coming from division. The
term ,(,)( )
ik s
cikt

represents the fraction of dividing
cells in volume interval (, )
I
ik and ,, ,(, )()
lik iks
cikt

is the fraction of those that end up in the volume interval
,0)(lI . The first equation represents daughters and is
distinguished because every division results in a
daughter. In the higher age classes, >0m, density from
division arrives from only one source, namely the age
class 1m P.
2.6. Milestones
The parameters of the model that we have described in
the previous three subsections such as k V, k

,
,ik
d,,ik
g
, k--MDV, k--MEDV, and k--MEPV are
experimentally measurable quantities associated to a
particular strain of yeast that often depend on growth
conditions. We refer to these parameters as general
volume milestones. For convenience a glossary is
provided in Table 1.
An experimentally important measure of cell cycle
synchrony is the percent of cells in the culture that are
budded, also known as the bud index. This quantity can
be computed from ))(,( s tki

, given an age class
dependent, bud emergence cumulative distribution
function, ,ik B. That is, , 01
ik
B, is a monotonically
increasing function of i, for each k, and describes the
probability that the cells in (, )
I
ik are budded. The
function is monotone because once a cell has budded it
remains that way until it divides. The mean of the bud
emergence distribution, for fixed k, is denoted as
k--BE. The bud index at time s t is the normalized inner
product:
,
,
,
(, )( )
():= (, )( )
s
ik
ik
ss
ik
ik tB
BI tik t




Careful measurements of bud emergence have been
made [45] and reveal that the cumulative distribution
function of the fraction budded cells relative to volume
derives from an underlying normal distribution.
Bud emergence is also a hallmark at the end of the
1
G phase and the beginning of the S-phase of the cell
cycle. Likewise, other cell cycle phases can be demar-
cated within each age class. This annotation enhances
the power and utility of the Leslie model. As discussed
above the general outline of the process flow in the
Leslie model is similar to that outlined in [19,21]
although there are some qualitative differences. In their
process it is tacitly assumed that the k--MEDV form a
monotone increasing series as a function of k. We make
no such assumptions. The model can be implemented
with measured or arbitrary values. In fact the data
described in [6] indicate that in fact the k--MEDV form
a monotone decreasing series as a function of age class k.
We have utilized the volume milestones of two strains
in this work. To the best of our knowledge the most
comprehensive set of milestones have been measured in
the diploid strain X2180. For this strain the model was
parameterized with yeast physiology data derived from
experiments performed over the past four decades [6,
13,16,33-38]. Among these the data of Woldringh et al.
[6] are particularly comprehensive, and well suited for
our modeling. A list of the volume milestones and their
description are summarized in Table 2.
Additionally we have utilized the haploid,

-factor
sensitive strain LHY3865, which is much larger than
X2180, and for which we have measured many, but not
all, of the volume milestones, see Table 3.
The behavior of the model can be investigated with
arbitrary parameters. For instance we were interested to
examine how the mother daughter volume asymmetry
impacts synchrony, all other factors being equal. For this
part of the study we used a data set that has no analog in
nature that we are aware of, but was constructed to
coincide with realistic volume values and exponential
growth rates, see Table 4.
2.7. Initial Conditions
In order to compare the dynamics of our model with data
we considered several natural initial conditions for our
computational work. For instance, most experiments that
follow the bud index oscillations are performed starting
from an initially synchronized population of cells.
Historically, several different experimental methods
have been used to synchronize yeast. These include
metabolic starvation, elutriation, and pheromone blocks.
These are described in [22]. Perhaps the most common
of these is the use of mating pheromones like

-factor,
that arrests cells in 1 G prior to the cdc28 delimited start.
Computationally we created an initial condition to
mimic this population of cells by pruning the time
invariant population density of each class such that no
cells exist outside of the terminal 20% of the 1 G
volume intervals prior to the mean bud emergence. The
pruned population density was then renormalized.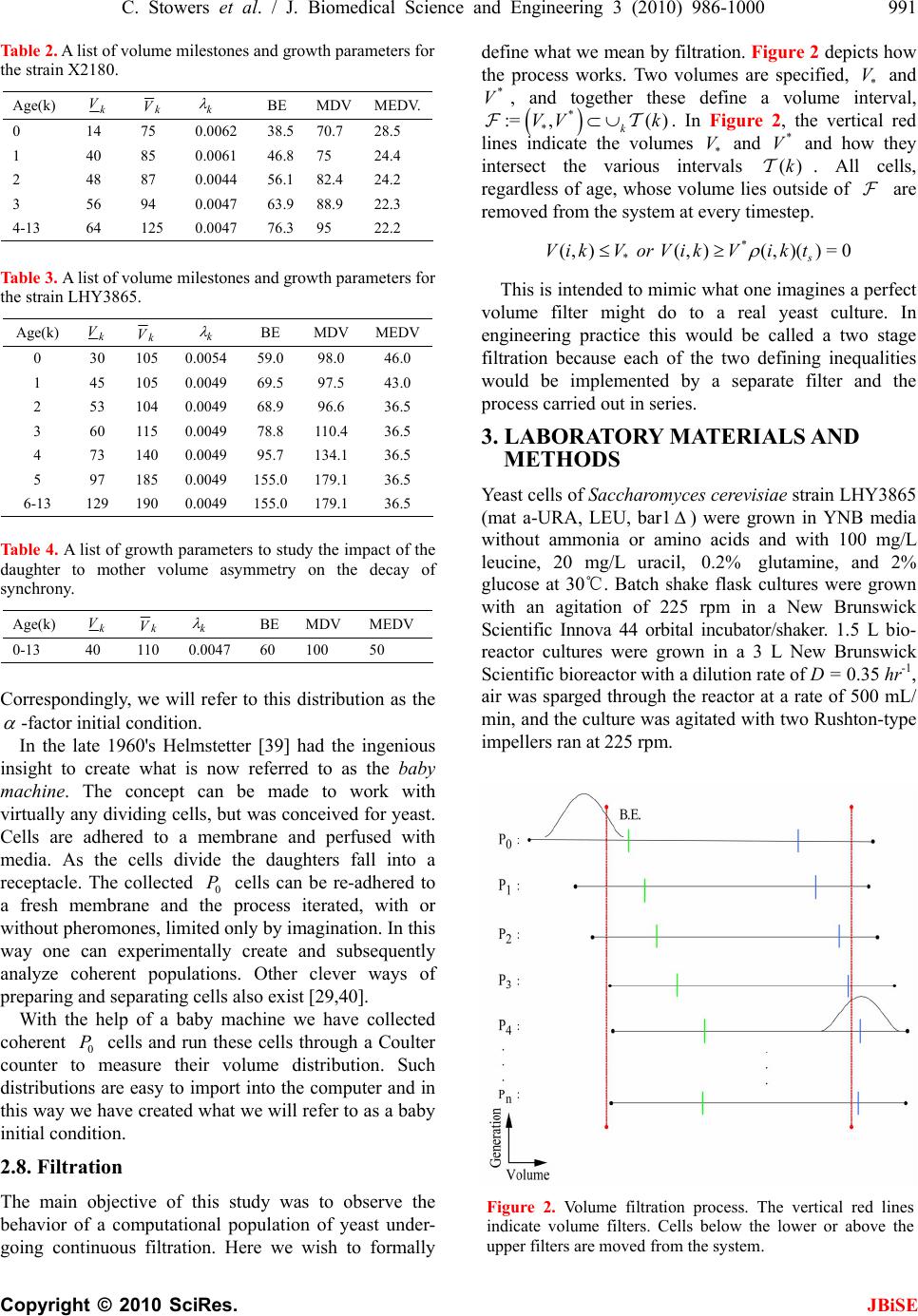

C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000 991
Table 2. A list of volume milestones and growth parameters for
the strain X2180.
Age(k) k
V k
V k

BE MDV MEDV.
0 14 75 0.0062 38.5 70.7 28.5
1 40 85 0.0061 46.8 75 24.4
2 48 87 0.0044 56.1 82.4 24.2
3 56 94 0.0047 63.9 88.9 22.3
4-13 64 125 0.0047 76.3 95 22.2
Table 3. A list of volume milestones and growth parameters for
the strain LHY3865.
Age(k) k
V k
V k

BE MDV MEDV
0 30 105 0.005459.0 98.0 46.0
1 45 105 0.004969.5 97.5 43.0
2 53 104 0.004968.9 96.6 36.5
3 60 115 0.004978.8 110.4 36.5
4 73 140 0.004995.7 134.1 36.5
5 97 185 0.0049155.0 179.1 36.5
6-13 129 190 0.0049155.0 179.1 36.5
Tabl e 4. A list of growth parameters to study the impact of the
daughter to mother volume asymmetry on the decay of
synchrony.
Age(k) k
V k
V k

BE MDV MEDV
0-13 40 110 0.0047 60 100 50
Correspondingly, we will refer to this distribution as the

-factor initial condition.
In the late 1960's Helmstetter [39] had the ingenious
insight to create what is now referred to as the baby
machine. The concept can be made to work with
virtually any dividing cells, but was conceived for yeast.
Cells are adhered to a membrane and perfused with
media. As the cells divide the daughters fall into a
receptacle. The collected 0
P cells can be re-adhered to
a fresh membrane and the process iterated, with or
without pheromones, limited only by imagination. In this
way one can experimentally create and subsequently
analyze coherent populations. Other clever ways of
preparing and separating cells also exist [29,40].
With the help of a baby machine we have collected
coherent 0 P cells and run these cells through a Coulter
counter to measure their volume distribution. Such
distributions are easy to import into the computer and in
this way we have created what we will refer to as a baby
initial condition.
2.8. Filtration
The main objective of this study was to observe the
behavior of a computational population of yeast under-
going continuous filtration. Here we wish to formally
define what we mean by filtration. Figure 2 depicts how
the process works. Two volumes are specified, *
V and
*
V, and together these define a volume interval,


*
*
:=,( )
k
VV k. In Figure 2, the vertical red
lines indicate the volumes * V and * V and how they
intersect the various intervals ()k. All cells,
regardless of age, whose volume lies outside of  are
removed from the system at every timestep.
*
*
(, )(, )(, )( )=0
s
VikV orVikVikt  
This is intended to mimic what one imagines a perfect
volume filter might do to a real yeast culture. In
engineering practice this would be called a two stage
filtration because each of the two defining inequalities
would be implemented by a separate filter and the
process carried out in series.
3. LABORATORY MATERIALS AND
METHODS
Yeast cells of Saccharomyces cerevisiae strain LHY3865
(mat a-URA, LEU, bar1

) were grown in YNB media
without ammonia or amino acids and with 100 mg/L
leucine, 20 mg/L uracil, 0.2% glutamine, and 2%
glucose at 30℃. Batch shake flask cultures were grown
with an agitation of 225 rpm in a New Brunswick
Scientific Innova 44 orbital incubator/shaker. 1.5 L bio-
reactor cultures were grown in a 3 L New Brunswick
Scientific bioreactor with a dilution rate of D = 0.35 hr-1,
air was sparged through the reactor at a rate of 500 mL/
min, and the culture was agitated with two Rushton-type
impellers ran at 225 rpm.
Figure 2. Volume filtration process. The vertical red lines
indicate volume filters. Cells below the lower or above the
upper filters are moved from the system.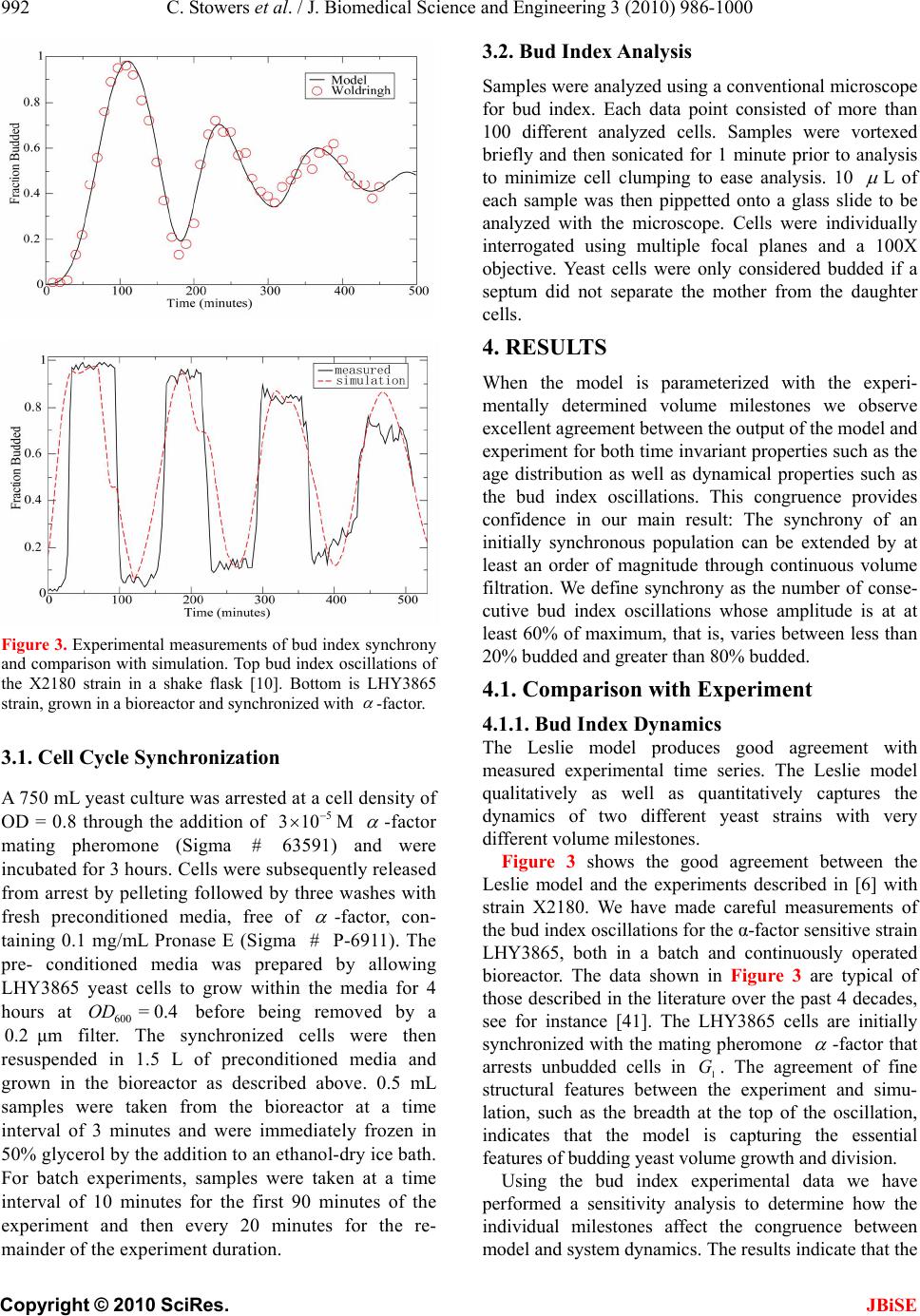

992 C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000
Figure 3. Experimental measurements of bud index synchrony
and comparison with simulation. Top bud index oscillations of
the X2180 strain in a shake flask [10]. Bottom is LHY3865
strain, grown in a bioreactor and synchronized with

-factor.
3.1. Cell Cycle Synchronization
A 750 mL yeast culture was arrested at a cell density of
OD = 0.8 through the addition of 5 310

M

-factor
mating pheromone (Sigma # 63591) and were
incubated for 3 hours. Cells were subsequently released
from arrest by pelleting followed by three washes with
fresh preconditioned media, free of

-factor, con-
taining 0.1 mg/mL Pronase E (Sigma # P-6911). The
pre- conditioned media was prepared by allowing
LHY3865 yeast cells to grow within the media for 4
hours at 600 =0.4OD before being removed by a
0.2 μm filter. The synchronized cells were then
resuspended in 1.5 L of preconditioned media and
grown in the bioreactor as described above. 0.5 mL
samples were taken from the bioreactor at a time
interval of 3 minutes and were immediately frozen in
50% glycerol by the addition to an ethanol-dry ice bath.
For batch experiments, samples were taken at a time
interval of 10 minutes for the first 90 minutes of the
experiment and then every 20 minutes for the re-
mainder of the experiment duration.
3.2. Bud Index Analysis
Samples were analyzed using a conventional microscope
for bud index. Each data point consisted of more than
100 different analyzed cells. Samples were vortexed
briefly and then sonicated for 1 minute prior to analysis
to minimize cell clumping to ease analysis. 10

L of
each sample was then pippetted onto a glass slide to be
analyzed with the microscope. Cells were individually
interrogated using multiple focal planes and a 100X
objective. Yeast cells were only considered budded if a
septum did not separate the mother from the daughter
cells.
4. RESULTS
When the model is parameterized with the experi-
mentally determined volume milestones we observe
excellent agreement between the output of the model and
experiment for both time invariant properties such as the
age distribution as well as dynamical properties such as
the bud index oscillations. This congruence provides
confidence in our main result: The synchrony of an
initially synchronous population can be extended by at
least an order of magnitude through continuous volume
filtration. We define synchrony as the number of conse-
cutive bud index oscillations whose amplitude is at at
least 60% of maximum, that is, varies between less than
20% budded and greater than 80% budded.
4.1. Comparison with Experiment
4.1.1. Bud Index Dynamics
The Leslie model produces good agreement with
measured experimental time series. The Leslie model
qualitatively as well as quantitatively captures the
dynamics of two different yeast strains with very
different volume milestones.
Figure 3 shows the good agreement between the
Leslie model and the experiments described in [6] with
strain X2180. We have made careful measurements of
the bud index oscillations for the α-factor sensitive strain
LHY3865, both in a batch and continuously operated
bioreactor. The data shown in Figure 3 are typical of
those described in the literature over the past 4 decades,
see for instance [41]. The LHY3865 cells are initially
synchronized with the mating pheromone

-factor that
arrests unbudded cells in 1
G. The agreement of fine
structural features between the experiment and simu-
lation, such as the breadth at the top of the oscillation,
indicates that the model is capturing the essential
features of budding yeast volume growth and division.
Using the bud index experimental data we have
performed a sensitivity analysis to determine how the
individual milestones affect the congruence between
model and system dynamics. The results indicate that the

C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000 993
milestones of the daughter generation are the most
sensitive and the sensitivity decays monotonically with
age. How well the model dynamics fit the data is most
sensitive to the mean division volume of the daughter
generation, followed by the mean bud emergence
milestone. In general a 10% change in the milestones
produced less than a 10% change in the overall fit
between model dynamics and experimental time series.
This indicates that the basic processes of the model
robustly capture the dynamical phenomena associated
with bud index oscillations.
4.1.2. Stationary Properties
The model parameterized with the X2180 milestones
reproduces the measured stationary values within the
measured deviations where available, see Table 5. The
measured quantities were the fractions(F) of daughters
(D), parents(P), budded(B) and unbudded(U). It was
observed in [13] that a quantitative relationship exists of
the form 1
(1( ))=
D
PG k

, where 1 ()PG is the
percentage of cells in the 1
G phase,
D

is the observed
population doubling time and k is a constant. This
would be unremarkable save for the fact that =1.1k
hrs was observed over a wide range of growth rates,
suggesting some universality. The observed population
doubling time is in reality a population weighted average
over all the generations and we have computed this
quantity from the model using two natural ensemble
averages that produce the same value of =1.2k hrs
that is in close agreement with the experimental value
for which no standard deviation was reported.
4.2. Decay of Synchrony with Division
Asymmetry
As described in the introduction, it has been well known
that the volume asymmetry between mothers and
daughters has a profound effect on the decay of syn-
chrony of initially synchronized populations of budding
yeast. Since budding yeast display a bewildering array of
strain variation we felt it legitimate and interesting to ask
how the amplitude of the bud index oscillation decays as
a function of inherent volume asymmetry between mo-
thers and daughters at division. This volume asymmetry
has a constant mean value for each strain of yeast.
Essentially this value is
M
EPV MEDV, when it does
not vary with k. From the bud index curve we have
computed the envelope of the oscillation and fit the
amplitude decay. As expected from the theory, see for
instance [26] (Subsection 4.7), the decay is exponential.
The initial rates of decay are described in the top panel
of Figure 4, while the number of corresponding syn-
chronous cycles are shown in the bottom panel. The
computational results show that as expected the number
of cycles of synchrony declines dramatically with
volume asymmetry. When the daughter to mother
volume ratio is 80% the number of synchronous cycles
has decayed from infinity to one for the X2180
milestones.
4.3. Volume Filtration
We have examined two filtration strategies computa-
tionally. Figure 2 describes the general filtering scheme.
In a two stage filtration we impose both an upper and a
lower volume limit. All cells whose volume lies in
between are retained in the system, a bioreactor, and the
rest are continuously removed. In a single stage filtration
there is only a lower volume limit, and all cells smaller
than this are removed, those that are larger remain.
The main two stage filtration results of this paper are
presented in Figures 5 and 6. After inspecting the
volume-time diagram constructed in [6], we conjectured
that it would be possible to emulate the symmetry of
near equal volume division by filtering out cells that
were too small or too large. We reasoned that this would
have the abstract effect of making all the age class grids
nearly the same. In large part this hypothesis was born
out as the data show that by a judicious choice of
filtration parameters we can extend the synchrony from
1 cycle to close to 20 cell cycles in the X2180 strain and
from 3 to 30 in the LHY3865 strain. Figure 7 shows the
bud index profiles associated with several of the
filtration parameters that describe the range from no
filtering to the best that we have been able to observe at
17 cycles for the X2180 milestones.
Equivalently Figure 8 shows the bud index osci-
llations of the LHY3865 milestones subject to single and
double stage filtration. The upper panels show the results
of single stage filtration. Figure 9 codifies the behavior
of the single stage filtration of the LHY3865 milestones.
This figure is annotated with the k-mean daughter
Table 5. Comparison of stationary properties of the model with
experiment for the X2180 strain. The experimental data are
reproduced from table 1 of [47] with the exception of the last
two entries that are taken from [36]. F(D),F(P),F(B),F(U) are
the fractions of daughters, parents, budded and unbudded
respectively.
Property Model prediction Experiment
F(D) 61.0
60.3 1.8

F(P) 39.0
39.7 1.7

F(B) 63.0
66.9 4.0

F(U) 37.0 33.1
F(B)


 1.2 1.1
()FB


 1.2 1.1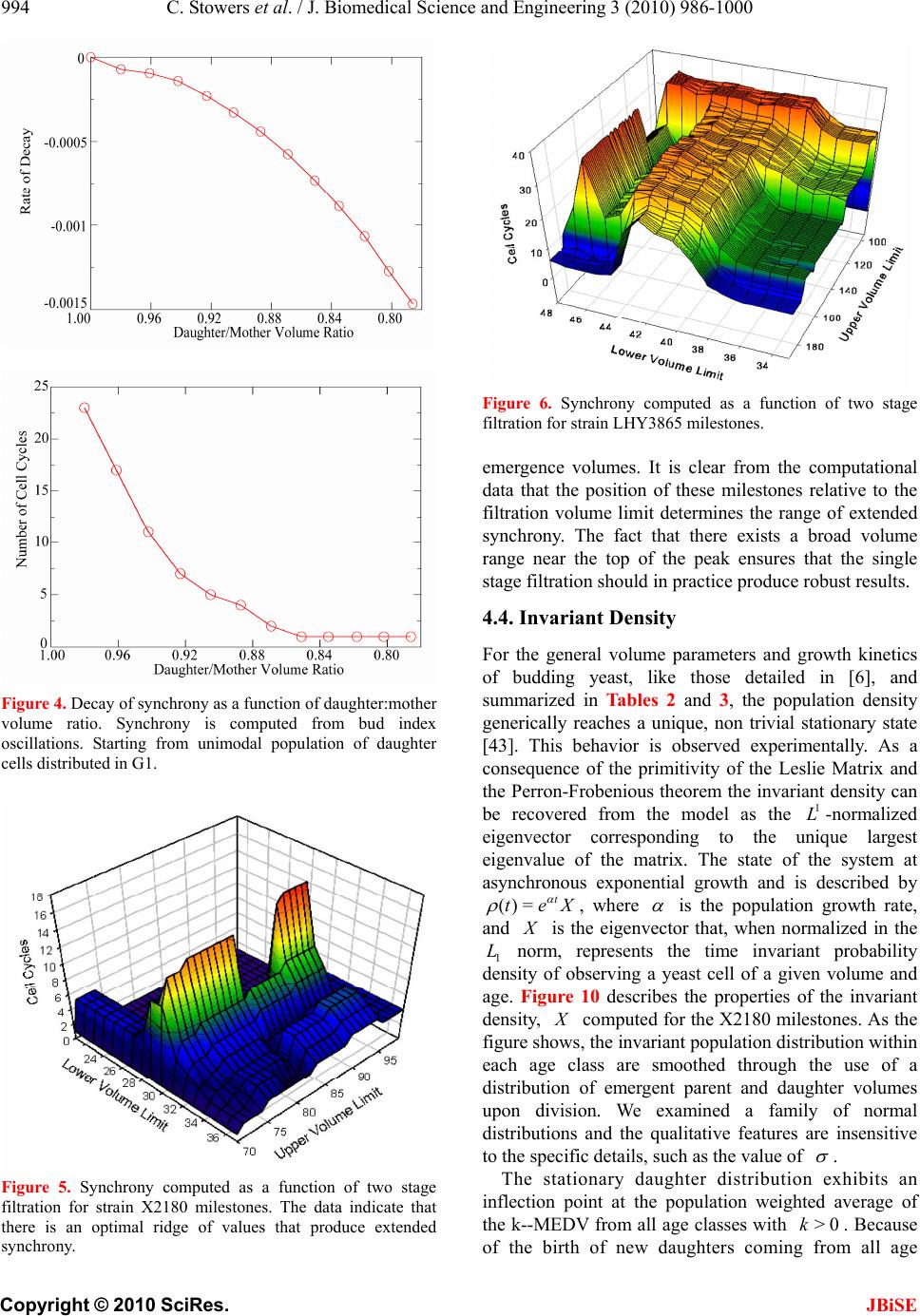

994 C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000
Figure 4. Decay of synchrony as a function of daughter:mother
volume ratio. Synchrony is computed from bud index
oscillations. Starting from unimodal population of daughter
cells distributed in G1.
Figure 5. Synchrony computed as a function of two stage
filtration for strain X2180 milestones. The data indicate that
there is an optimal ridge of values that produce extended
synchrony.
Figure 6. Synchrony computed as a function of two stage
filtration for strain LHY3865 milestones.
emergence volumes. It is clear from the computational
data that the position of these milestones relative to the
filtration volume limit determines the range of extended
synchrony. The fact that there exists a broad volume
range near the top of the peak ensures that the single
stage filtration should in practice produce robust results.
4.4. Invariant Density
For the general volume parameters and growth kinetics
of budding yeast, like those detailed in [6], and
summarized in Tables 2 and 3, the population density
generically reaches a unique, non trivial stationary state
[43]. This behavior is observed experimentally. As a
consequence of the primitivity of the Leslie Matrix and
the Perron-Frobenious theorem the invariant density can
be recovered from the model as the 1 L-normalized
eigenvector corresponding to the unique largest
eigenvalue of the matrix. The state of the system at
asynchronous exponential growth and is described by
()= t teX

 , where

is the population growth rate,
and
X
is the eigenvector that, when normalized in the
1
L norm, represents the time invariant probability
density of observing a yeast cell of a given volume and
age. Figure 10 describes the properties of the invariant
density,
X
computed for the X2180 milestones. As the
figure shows, the invariant population distribution within
each age class are smoothed through the use of a
distribution of emergent parent and daughter volumes
upon division. We examined a family of normal
distributions and the qualitative features are insensitive
to the specific details, such as the value of

.
The stationary daughter distribution exhibits an
inflection point at the population weighted average of
the k--MEDV from all age classes with >0k. Because
of the birth of new daughters coming from all age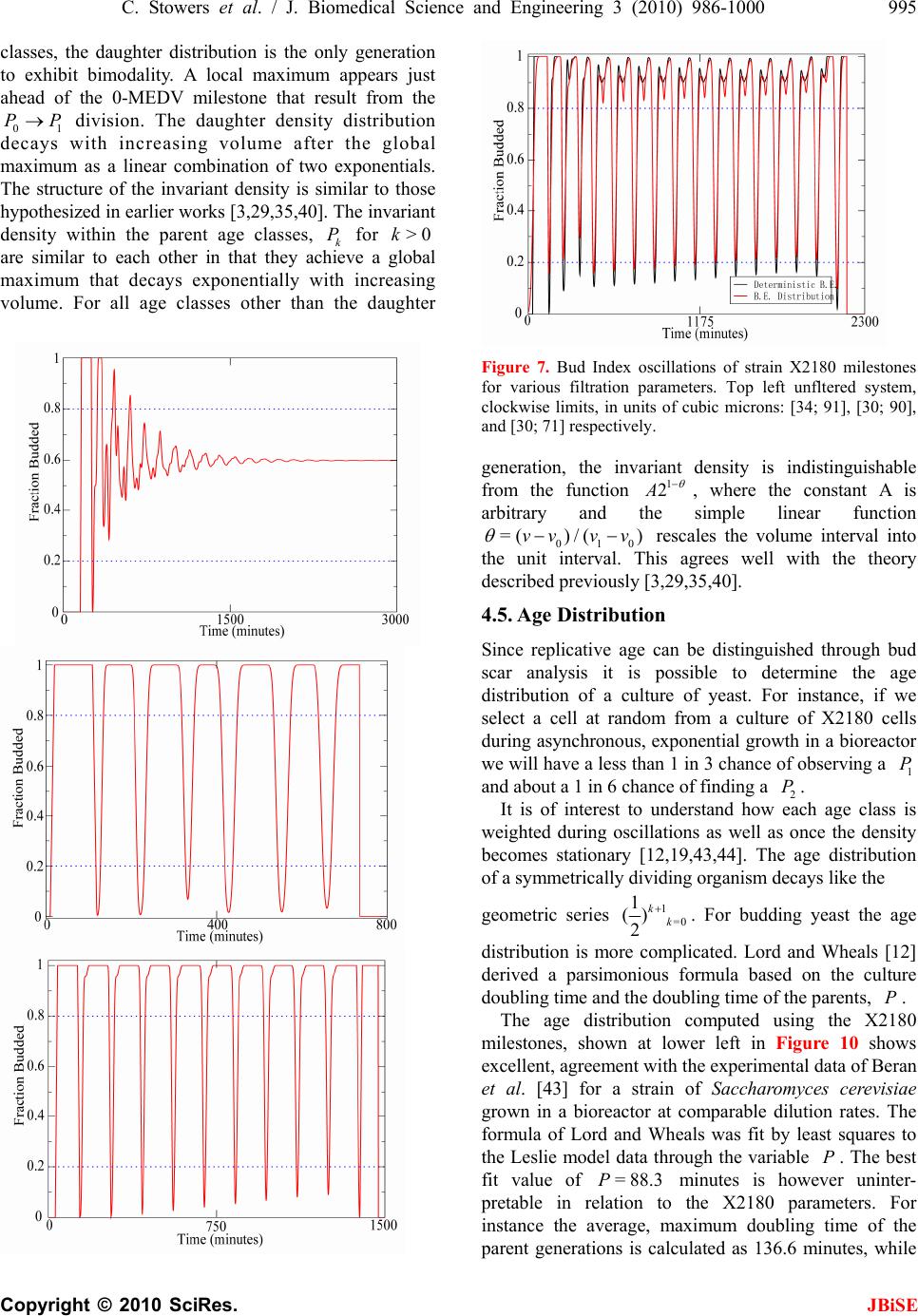

C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000 995
classes, the daughter distribution is the only generation
to exhibit bimodality. A local maximum appears just
ahead of the 0-MEDV milestone that result from the
01
PP division. The daughter density distribution
decays with increasing volume after the global
maximum as a linear combination of two exponentials.
The structure of the invariant density is similar to those
hypothesized in earlier works [3,29,35,40]. The invariant
density within the parent age classes, k P for >0k
are similar to each other in that they achieve a global
maximum that decays exponentially with increasing
volume. For all age classes other than the daughter
Figure 7. Bud Index oscillations of strain X2180 milestones
for various filtration parameters. Top left unfltered system,
clockwise limits, in units of cubic microns: [34; 91], [30; 90],
and [30; 71] respectively.
generation, the invariant density is indistinguishable
from the function 1
2
A


, where the constant A is
arbitrary and the simple linear function
010
=( )/()vvv v


 rescales the volume interval into
the unit interval. This agrees well with the theory
described previously [3,29,35,40].
4.5. Age Distribution
Since replicative age can be distinguished through bud
scar analysis it is possible to determine the age
distribution of a culture of yeast. For instance, if we
select a cell at random from a culture of X2180 cells
during asynchronous, exponential growth in a bioreactor
we will have a less than 1 in 3 chance of observing a 1 P
and about a 1 in 6 chance of finding a 2 P.
It is of interest to understand how each age class is
weighted during oscillations as well as once the density
becomes stationary [12,19,43,44]. The age distribution
of a symmetrically dividing organism decays like the
geometric series 1
=0
1
()
2
kk . For budding yeast the age
distribution is more complicated. Lord and Wheals [12]
derived a parsimonious formula based on the culture
doubling time and the doubling time of the parents,
P
.
The age distribution computed using the X2180
milestones, shown at lower left in Figure 10 shows
excellent, agreement with the experimental data of Beran
et al. [43] for a strain of Saccharomyces cerevisiae
grown in a bioreactor at comparable dilution rates. The
formula of Lord and Wheals was fit by least squares to
the Leslie model data through the variable P. The best
fit value of = 88.3P minutes is however uninter-
pretable in relation to the X2180 parameters. For
instance the average, maximum doubling time of the
parent generations is calculated as 136.6 minutes, while

996 C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000
the average minimum doubling time time is 96.8
minutes. These latter two values should realistically
bookend the mean doubling times.
Based on a consideration of population flux and flux
transit time we have been able to derive a recurrence
relation that explains the observed non-geometric decay
of the age distribution in terms of the growth parameters
Figure 8. Bud index oscillations of LHY3865. Top panels
single stage, bottom are two stage filtration. Right panels are
best achievable. Parameters cubic microns are clockwise from
top right: 39, 42, [37; 100] and [33; 178].
that extends previous works [12,44]. This analysis is to
be presented elsewhere.
Given the general exponential decay of the age
distribution we have contented ourselves to represent 14
generations computationally. Experimentally mortality
curves for replicative age has been measured for some
strains of budding yeast [18,29,30]. It has been observed
there that some yeast can survive upwards of 60
divisions. From the decline in the age distribution we
have observed that practically, 20,30,40 generations or
more, need not be represented in the model to precisely
capture the dynamics of the system. We know of no
experimental data sets that have completely charac-
terized more than the first 8 age classes. The precise
connection between senescence and replicative aging is
currently undecided and is an interesting area of intense
activity.
5. DISCUSSION
The Leslie model captures the dynamics of bud index
oscillations and their decay. We have shown that there is
good agreement between measured data and the
predicted bud index oscillations for two different sets of
strain milestones, one haploid and one diploid, of
different volume extents and growth rates. The different
strains of yeast display quantitatively different behavior
with regard to their decay of synchrony as we have
defined it. The X2180 strain exhibits 1 synchronous
cycle while the LHY3865 strain displays 3. The model
captures this difference. This instills confidence in the
model predictions of synchrony. The strain milestones in
both cases contain measurement error and are
incomplete especially in generations higher than the
fourth age class. The agreement of the model and the

C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000 997
experimental data, despite these errors, exposes the
robustness of the processes and the ability of the Leslie
model to capture the essentials of the asymmetric growth
and division process. These claims are supported by the
results of a sensitivity analysis.
It is well known that theoretically volume symmetric
division is a degenerate case that leads to persistent
synchrony [31,42]. Several well known avenues allow
the manipulation of the division volume asymmetry.
Lord and Wheals observed [12], as have many others,
that age class growth rates depend linearly on the culture
doubling time and estimated that there exists a growth
rate that if achievable would produce balanced and
presumably synchronous growth. Growth rates are most
typically affected through variation of nitrogen or carbon
source. It has also been observed that drugs such as
hydroxyurea can induce nearly symmetric division [39].
It is well known that strain variations influence division
volume asymmetry. We have explicitly examined the
relationship between division volume asymmetry and the
number of synchronous cycles of bud index oscillations.
Our intentions in doing so are two fold. First, we
imagine that if a legitimate relationship exists then it
may be possible through a judicious mutation to create
strains of yeast with predefined synchrony. Second, we
see a direct relationship between the control of syn-
chrony through continuous volume filtration and the
natural synchrony that results from volume symmetric
division. What this means is that a volume filter is seen
in the abstract as a mechanism for restoring partial
symmetry to an underlying volume asymmetric system.
For instance, consider Figure 2. The volume grids of the
different generations are not a priori commensurate,
however the volume grids that live between the filter
cutoffs are more so. Those cells that are far from the
symmetry conditions are removed from the system,
leaving the remainder more synchronous. The intrinsic
asymmetry that volume filtration cannot influence are
the volume milestones such as k-MEDV, k-BE and
k-MDV. These however can be influenced by mutation
and or nutrients. The combination of mutation, media
composition and continuous volume filtration is
therefore expected to be able to produce budding yeast
that are remain synchronous for long periods of time
starting from a homogeneous initial condition.
We have explored both single and double stage
filtration. We explored single stage filtration and present
it here because it is far easier to implement in practice
and it appears to produces results that could be observed
with even a crude device. The results indicate that there
exist robust windows of volume that can be used to
control synchrony. An example can be seen in the single
stage results, Figure 9. There is a broad peak around
3
μm 41, approximately 3
μm 4 in width that produces a
roughly 4 fold extension in synchrony. This result if
correct implies that even a crude filtration device should
Figure 9. Single stage filtration for LHY3865. Cells below cutoff continuously removed. Synchrony measures successive cycles of
Bud index oscillation that maintains at least 60% of its total amplitude.

998 C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000
produce observable changes. We are currently exploring
design equations for such a device.
Continuous filtration is a control mechanism that
will alter the population structure relative to a unfiltered
Figure 10. Invariant density for X2180. Clockwise from upper:
P0, P6 and P13 distributions. Lower left compares model age
distribution with data of Beran et al. [43] and formula of Lord
and Wheals [24].
population. A population structure that will be altered in
the filtered population are the volume distributions and
the overall age distribution. How, and to what extent the
age distribution is affected can be analyzed with the
model. The results of this analysis are to appear else-
where. Continuous filtration, we think, can be accomp-
lished experimentally without inducing a general stress
response in the individual cells of the population.
We observe that while we have explored here the very
specific application of volume filtration, the Leslie
model can be used to explore a much broader range of
questions that are of continuing interest in yeast
physiology and in the larger picture of systems biology.
For instance, as has been observed previously [19,22], it
is possible to use the model to investigate how signals
from single cells manifest themselves at the populations
level. With the addition of volume filtration it will be
possible to study cell cycle dependent protein expression
more extensively.
A use that has been little explored to date is how a
signal, periodic in the cell cycle, such might be
conceived for a gene expression, manifests itself at the
population level. When signals are routinely evaluated
by grinding up large numbers of cells and pooling their
mRNA for instance, such questions seem reasonable. We
have previously observed that how one grinds up the
cells in such a situation has quantifiable effects that
depend on the cell cycle [45]. Any extensive quantity
that varies in a single cell with the cell cycle can be
examined with this model. For example oxygen con-
sumption, glucose uptake, or mRNA production of the
population can be studied given measured or putative
data from single cells. Conversely, it is also possible to

C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000 999
use the model to deconvolve population ensemble ave-
rages into individual cell signals.
Finally, a physiological component that has not been
included into the current model are the putative
asymmetric effects that are now emerging in the study of
chronological aging and senescence [7]. It is well known
that aging occurs in organisms such as Escherichia coli
and fission yeast that undergo morphogenically sym-
metric division [1]. Given the success of the Leslie
model in matching the dynamics of the bud index
oscillations for a few cell cycles, it is tempting to sug-
gest that deviations between the Leslie model and the
dynamics of yeast with a variety of aging phenotypes
may provide new and otherwise difficult to attain insight
into the rate and effects of senescence.
6. ACKNOWLEDGEMENTS
We thank Linda Breeden for the gift of the LHY3865
strain. We thank Konstantin Mischaikow for coding an
early version of the model and helpful discussions. EMB,
and CS, were partially supported through NSF-DMS
0443855.
REFERENCES
[1] Stewart, E.J., Madden, R., Paul, G. and Taddei, F. (2005)
Aging and death in an organism that reproduces by mor-
phologically symmetric division. PLoS Biology, 3(2),
295- 300.
[2] Bellgardt, K.H. (1994) Analysis of synchronous growth
of bakers yeast. Part I: Development of a theoretical
model for sustained oscillations. Journal of Biotechnol-
ogy, 35(1), 19-33.
[3] Keulers, M., Sazuki, T., Satroutdinov, A.D., Kuriyama, H.
(1996) Autonomous metabolic oscillations in continuous
culture of saccharomyces cerevisiae grown on ethanol.
FEMS Micro Letters, 142(2-3), 253-258.
[4] Murray, D.B., Klevecz, R.R. and Lloyd, D. (2003) Gen-
eration and maintenance of synchrony in saccharomyces
cerevisiae continuous culture. Experimental Cellular Re-
search, 287(1), 10-15.
[5] Tu, B.P., Kudlicki, A., Rowicka, M. and McKnight, S.L.
(2006) Logic of the yeast metabolic cycle: Temporal
compartmentalization of cellular processes. Science, 310
(5751), 1152-1158.
[6] Woldringh, C.L., Huls, P.G. and Vischer, N. (1993) Vol-
ume growth of daughter and parent cells during the cell
cycle of saccharomyces cerevisiae /a

as determined
by image cytometry. Journal of Bacteriology, 175(10),
3174- 3181.
[7] Ackerman, M., Chao, L., Berstrom, C. and Doebeli, M.
(2007) On the evolutionary origin of aging. Aging Cell,
6(2), 235-244.
[8] Agilaniu, H., Gustafsson, L., Rigoulet, M. and Nystrom,
T. (2003) Asymmetric inheritance of oxidatively dam-
aged proteins during cytokinesis. Science, 299(5613),
1751-1753.
[9] Eisen, M.B., Spellman, P.T., Brown, P.O. and Botstein, D.
(1998) Cluster analysis and display of genome-wide ex-
pression patterns. Proceedings of National Academy Sci-
ences, 95(25), 14863-14868.
[10] Boczko, E.M., Cooper, T.G., Gedeon, T., Mischaikow, K.,
Murdock, D.G., Pratap, S. and Wells, K.S. (2005) Struc-
ture Theorems and the Dynamics of Nitrogen Catabolite
Repression in Yeast. Proceedings of National Academy
Sciences, 102(16), 5647-5652.
[11] Boczko, E.M., Gedeon, T. and Mischaikow, K. (2007)
Dynamics of a simple regulatory switch. Journal of
Mathematical Biolo gy, 55(5-6), 679-719.
[12] Lord, P.G. and Wheals, A.E. (1980) Asymmetrical divi-
sion of saccharomyces cerevisiae. Journal of Bacterial
142(3), 808-818.
[13] Slater, M.L., Sharrow, S.O. and Gart, J.J. (1977) Cell
cycle of saccharomyces cerevisiae in populations growing at
different rates. Proceedings of National Academy Sci-
ences, 74(9), 3850-3854.
[14] Harris, T.E. (1967) The theory of branching processes.
Die Grundlehren der Mathematischen Wissenschaften,
band 119. Springer-Verlag, Berlin; Prentice-Hall, Inc.,
Englewood Cliffs, New Jersey.
[15] Kimmel, M. and Axelrod, D.E. (2002) Branching proc-
esses in biology. Interdisciplinary Applied Mathematics,
Springer-Verlag, New York.
[16] Hartwell, L.H. and Unger, M.W. (1977) Unequal division
in saccharomyces Cerevisiae and its implications for the
control for the cell division. Journal of Cellular Biology,
75(2), 422-435.
[17] Chen, K.C., Calzone, L., Ccikasz, N.A., Cross, F.R.,
Novak, B. and Tyson, J.J. (2004) Integrative analysis of
cell cycle control in budding yeast. Molecular Biology
Cellular, 15(8), 3841-3862.
[18] Egilmez, N.K. and Jazwinski, S.M. (1989) Evidence for
the involvement of a cytoplasmic factor in the aging of
the yeast saccharomyces cerevisiae. Journal of Bacteri-
ology, 171(1), 37-42.
[19] Vanoni, M., Vai, M., Popolo, L. and Alberghina, L. (1983)
Structural heterogeneity in populations of the budding
yeast saccharomyces cerevisiae. Journal of Bacteriology,
156(3), 1282-1291.
[20] Jorgensen, P. and Tyers, M. (2004) How cells coordinate
growth and division. Current Biology, 14, R1014-R1027.
[21] Hatzis, C. and Porro, D. (2006) Morphologically struc-
tured models of growing budding yeast populations.
Journal of Biotechnology, 124(2), 420-438.
[22] Walker, G. (1999) Synchronization of yeast cell popula-
tions. Methods in Cell Science, 21(2-3), 87-93.
[23] Davis, R.H. and Gecol, H. (1996) Classification of con-
centrated suspensions using inclined settlers. Interna-
tional Journal of Multiphase Flow, 22(3), 563-574.
[24] Walsh, T.J. and Bungay, H.R. (1979) Shallow depth
sedimentation of yeast cells. Biotechnology and Bioen-
gineering, 21(6), 1081-1084.
[25] Wickramasinghe, S.R., Lin W.C. and Dandy D.S. (2001)
Seperation of different sized particles by inertial migra-
tion. Biotechnical Lette rs, 23(17), 1417-1422.
[26] Caswell, H. (2001) Matrix Population Models. 2nd Edi-
tion, Sinauer Associates Inc. Sunderland.
[27] Pringle, J.R. (1991) Staining of bud scars and other cell
wall chitin with calcoflour. Methods in Enzymology, 194,

1000 C. Stowers et al. / J. Biomedical Science and Engineering 3 (2010) 986-1000
732-735.
[28] Pohley, H.J. (1987) A formal mortality analysis for
populations of unicellular organisms (saccharomyces
cerevisiae). Mechanisms of Ageing and Development,
38(3), 231-243.
[29] Sinclair, D., Mills, K. and Guarente, L. (1998) Aging in
saccharomyces cerevisiae. Annual Revised Microbiology,
52, 533-560.
[30] Tyson, C.B., Lord, P.G. and Wheals, A.E. (1979) De-
pendency of size in saccharomyces cerevisiae cells on
growth rate. Journal of Bacteriology, 138(1), 92-98.
[31] Smith, J.A. and Martin, L. (1973) Do cells cycle? Proceed-
ings of National Academy Sciences, 70(4), 1263-1267.
[32] Hersh, R.T. and Kitos, P.A. (1980) Is 1 G normally dis-
tributed? Journal of Theoretical Biology, 86(1), 117-122.
[33] Wheals, A.E. (1982) Size control models of saccharo-
myces cerevisiae cell proliferation. Mollecular and Cel-
lular Biology, 2(4), 361-368.
[34] Barford, J.P. and Hall, R.J. (1976) Estimation of the
length of cell cycle phases from asynchronous cultures of
saccharomyces Cerevisiae. Experimental Cell Research,
102(2), 276-284.
[35] Brewer, B.J., Chlebowicz, S.E. and Fangman, W.L. (1984)
Cell cycle phases in the unequal mother/daughter cell
cycles of saccharomyces Cerevisiae. Molecular and Cel-
lular Biology, 4(11), 2529-2531.
[36] Johnston, G.C., Pringle, J.R. and Hartwell, L.H. (1977)
Coordination of growth with cell division in the yeast
Saccharomyces Cerevisiae. Experimental Cellular Re-
search, 105(1), 79-98.
[37] Johnston, G.C., Ehrhardt, C.W., Lorincz, A. and Carter,
B.L.A. (1979) Regulation of cell size in the yeast Sac-
charomyces Cerevisiae. Journal of Bacteriology, 137(1),
1-5.
[38] Singer, R.A. and Johnston, G.C. (1981) Nature of the G1
phase of the yeast saccharomyces cerevisiae. Proceeding s o f
National Ac ademy Sciences , 78(5), 3030-3033.
[39] Helmstetter, C. A. (1991) Description of a baby machine
for Saccharomyces cerevisiae. The New Biologist, 3(11),
1089-1096.
[40] Koshwanez, J., Holl, M., Marquardt, B., Dragavon, J.,
Burgess, L. and Meldrum, D. (2004) Identification of
budding yeast using a fiber-optic imaging bundle. Re-
vised Scientific Instruction, 75(5), 1363-1365.
[41] Breeden, L.L. (1997)

-Factor synchronization of bud-
ding yeast. Methods in Enzymology, 283, 332-342.
[42] Diekmann, O., Heijmans, H.J.A.M. and Thieme, H.R.
(1984) On the stability of the cell size distribution. Jour-
nal of Mathematical Biology, 19(2), 227-248.
[43] Beran, K., Malek, I., Steiblova, E. and Lieblova, J. (1967)
The distribution of the relative age of cells in yeast
populations. Microbial Physiology and Continuous Cul-
ture: 3rd International Symposium Held at the Microbi-
ological Research Establishment (Ministry of Defense),
Porton Down, Salisbury, Wiltshire.
[44] Gover, N.B. and Woldringh, C.L. (1995) Relationship
between the fraction of cell of different genealogical ages
and their cycle times in saccharomyces Cerevisiae: A
theoretical analysis. Journal of Theoretical Biology,
174(2), 223-225.
[45] Stowers, C. and Boczko, E.M. (2007) Reliable cell dis-
ruption in yeast. Yeast, 24(6), 533-541.
[46] Johnston, G.C. and Singer R.A. (1983) Growth and the
cell cycle of the yeast saccharomyces Cerevisiae. Ex-
perimental Cellular Research, 149(1), 1-13.
[47] Kaeberlein, M. (2005) Regulation of yeast replicative life
span by TOR and Sch9 in response to nutrients. Science
310(5751), 1193-1196.