Global pattern of pairwise relationship in genetic network

doi:10.4236/jbise.2010.310128

Paper Menu >>

Journal Menu >>

J. Biomedical Science and Engineering, 2010, 3, 977-985 JBiSE

doi:10.4236/jbise.2010.310128 Published Online October 2010 (http://www.SciRP.org/journal/jbise/).

Published Online October 20 10 in SciRes. http://www.scirp.org/journal/jbise

Global pattern of pairwise relationship in genetic network

Ao Yuan, Qingqi Yue, Victor Apprey, George E. Bonney

National Human Genome Center, Howard University, Washington DC, USA.

Email: yuanao@hotmail.com; ayuan@howard.edu

Received 6 April 2010; revised 22 April 2010; accepted 10 May 2010.

ABSTRACT

In recent times genetic network analysis has been

found to be useful in the study of gene-gene inter-

actions, and the study of gene-gene correlations is a

special analysis of the network. There are many

methods for this goal. Most of the existing methods

model the relationship between each gene and the

set of genes under study. These methods work well

in applications, but there are often issues such as

non-uniqueness of solution and/or computational

difficulties, and interpretation of results. Here we

study this problem from a different point of view:

given a measure of pair wise gene-gene relationship,

we use the technique of pattern image restoration to

infer the optimal network pair wise relationships.

In this method, the solution always exists and is

unique, and the results are easy to interpret in the

global sense and are computationally simple. The

regulatory relationships among the genes are in-

ferred according to the principle that neighboring

genes tend to share some common features. The

network is updated iteratively until convergence,

each iteration monotonously reduces entropy and

variance of the network, so the limit network

represents the clearest picture of the regulatory

relationships among the genes provided by the data

and recoverable by the model. The method is illus-

trated with a simulated data and applied to real

data sets.

Keywords: Convergence, Gene-Gene relationship, Neigh-

borhood, Pattern analysis, Relationship measure.

1. INTRODUCTION

A gene regulatory network (also called a GRN or genetic

regulatory network) is a collection of DNA segments in

a cell which interact with each other (indirectly through

their RNA and protein expression products) and with

other substances in the cell, thereby governing the rates

at which genes in the network are transcribed into

mRNA. From methodology point of view, genetic net-

works are models that, in a simplified way, describe

some biological phenomenon from interactions between

the genes. They provide a high-level view and disregard

most details on how exactly one gene regulates the ac-

tivity of another. The gene-gene pair wise relationships

provide a special insight of the network and are of inter-

est in the study.

Our work is closely related to that of genetic network

analysis, and we first give a brief review of the methods.

Some methods are deterministic, such as differential

(difference) equation models [1-3], which may not be

easy to solve nor have unique solutions. Since the ge-

netic network is a complex system, any artificial model

can only explain part of its mechanism; the unexplained

parts are random noises, so we prefer a stochastic model.

Existing stochastic methods for this problem including

the linear models [4,5] or generalized linear models [6,7],

the Bayesian network [8,9] etc. All these methods have

their pros and cons, but have the common disadvantage

that the solution may not be unique and the results are

not easy to interpret. Also, when the network size ex-

ceeds that of the data, these methods break down. In

genetic work the pair wise regulatory relationships

among the genes are important. For such data, it is of

interest to investigate the underlying patterns that may

have biologic significance, in particular those arising

from pair wises regulatory relationships among the

genes. Here we study this problem from a different point

of view. Given a measure of pair wise gene-gene rela-

tionship, we compute the measures from the data, and

use the technique of pattern recognition and image res-

toration to infer the underlying network relationships.

The pair wise regulatory relationships among the genes

are inferred according to the principle that neighboring

genes tend to share some common features, as neigh-

boring genes tend to be co-regulated by some enhancers

because of their close proximity [10]. In this method, the

solution is unique and computationally simple, the re-

sults are easy to interpret and the network can be of any

size. In the following we describe our method, study its

978 A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

basic properties, and illustrate its application. This me-

thod is used to reveal the true relationships of structured

high dimensional data array [11-14].

2. MATERIALS AND METHODS

The gene expression data are generally time dependent,

as in Iyer et al. [15]. Let ()

t (1,..., ;1,imj

...,;1,... )nt k be the observed gene expression re-

sponse for subject i, gene j at time t. Denote

( )(( ),...,( ))'

ii in

txtxt be the observations across all

the genes for subject i, and we use ()

t to denote a

general sample of the ()

t’s. Often for this type of data,

m and k are in the low tens, and n in the tens to thousands.

The commonly used differential equation model for

genetic network analysis is a set of first order homogeneous

differential equations with constant coefficients, in the

simple case, has the form

() ()

dx tWx t

dt ,

where ()

Ww is the n × n matrix of unknown regu-

latory coefficients to be solved. This type of models and

its more specific and complicated variations characterize

well the dynamic of the network over time. The base

solution of the above equation set is the matrix exponen-

tial 1

:/!:(( ),...,( ))'

tWr r

etWrvtvt







, and the general

solution of it has the form

() ()

ijj

tcvt



x_{i} (t),

(i = 1,...,m), where the

c’s are constants to be deter-

mined by initial conditions from the data. So there are in

total n² + n = n(n + 1) coefficients, n2 of them from W

and n from the

c’s, to be determined from a total of

mnk data points. When mnk < n(n + 1) these coefficients

can not be determined; when mnk ≥ n(n + 1) they may

be uniquely or non-uniquely determined, or may still be

not determined. For differential (difference) equation

models more complicated than this, solutions are more

difficult to get.

The commonly used stochastic model is the multi-

variate linear model

(1)() ,

iii

xt Wxt



 () 0,





(i = 1, …, m; t = 1, …,

k-1)

where 1

(,...,)'

iin





 is the random deviations unex-

plained by the model. Denote () ( ())

txt, if X′(t)X(t)

is non-singular, the least-squares solution of the above

model is W = X’(t + 1) X(t) (X’(t) X(t))-¹, and it may have

multiple solutions for different t. For '( )( )

tXt to be

non-singular, one must have n ≤ m. Even for n < m,

'( )()

tXt may not necessarily be non-singular. This

puts an immediate restriction on the size of the network

to be analyzed. Also, the solution of the above model

may not be unique due to different time points.

For these reasons, we study the problem from a dif-

ferent point of view; by analyze the pair wise gene-gene

relationships in the network. In the following we de-

scribe our model in which there is always an unique so-

lution, the result is easy to interpret, and there is no re-

striction on the size of the network. Since the pattern in

the genetic network is based on the principle of neigh-

boring similarity, the order of the genes matters in the

study, and generally we assume the genes are arranged in

their chromosome order.

First we need a measurement for the relationship be-

tween any pair of genes, and the network can be repre-

sented by the matrix of the pair wise relationships. For

large network, linear relationship is not adequate to use,

as most of the coefficients will be very small. Also, as

mentioned above, such model in this case has no solu-

tion because of the small sample size. Pearson’s correla-

tion is a good choice for this purpose, other choices in-

cluding Kendal’s tau and Spearman’s rho, etc. Here we

illustrate the method with Pearson’s correlation, and our

goal is to infer the triangular correlation matrix

()

ijijn





 from the observed data, where ij

r is the

Pearson’s correlation coefficient between genes i and j.

As usually the number m of individuals is small (some-

times as few as 2), estimate the correlations using the

data at each time point alone is inadequate. So we use all

the data to estimate them. An empirical initial version of

these correlations are

()

(( )( ))(()())

(())(())

mk rii sjj

rs ij

txtxtxt

rmk Var xtVar xt





 ,

((1 )ijn



 (1)

where

() (),

iri

txt

m



(())( ()()),

irii

Varx txtx t

m



 (i = 1,...,n; s=1,...,k).

here the ()

t’s are not i.i.d. over the time t’s, and the

sample size mk is often not large, so the above empirical

correlations are very crude evaluations of the true corre-

lations ij

r’s. The initial table (0) (0)

(:1 )

Rr ijn

is used as the raw data for the next step analysis. For

each fixed i the observations ()

ts at different time

conditions reduced the common features in the data, this

table is biased as an estimate of R. We need to restore

their values according to the basic property of the ge-

netic regulatory system. Many reports have shown that

nearby genes tend to have similar expression profiles

[16-19], thus nearby pairs of genes tend to have similar

relationships, and their correlations tend to be close. This

A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

979

is just the same principle as used in image restoration of

data arrays of any size. In the following we use this

technique to reduce the bias and improve the estimate of

R based on the observation (0)

Meloche and Zammar [14] considered a method for

image restoration of binary data, here we adopt their idea

and revise their method to gene expression analysis for

continuous data. We assume the following model

(0) ,

ijij ij



 ij



~ 2

(0, )N



, (1 ≤ i < j ≤ n) (2)

for some unknown 2



> 0, where the ij



’s represent

the part of measurements unexplained by the true reg-

ulatory relationships in the model. Define the neighbor

(0)

R of (0)

r to be the collection of the nine immedi-

ate members of (0)

R of (0)

r = {(0) :|| 1,

rai





||1bj}, which includes (0)

r itself at the center.

For (0)

r’s on the boundary of (0)

Rthe definition is

modified accordingly. For example, (0)

1,2

R and

(0)

1,nn

R has only three members, (0)

1, j

R (3 < j < n-1)

has six members, etc. Larger neighbors of different

shapes can also be considered; here we only illustrate

using the above neighbor systems. We assume the

(0)

r’s only depend on their neighbors (0)

R’s. The aim

is to provide estimates ij



’s for the true ij

r’s based on

the records (0)

R. We assume the estimates have the

form for some function h(

⋅

) to be specified. The per-

formance of the estimates will be measured by the aver-

age conditional mean squared error.

(0)

()

ij ij

rhR, (1≤ i < j ≤ n), (3)

2(0)

2[() |]

(1)ij ij

ijn

Er rR

nn  







(4)

The optimal set of estimates is the one which mini-

mizes (4). Although ij

r is deterministic, we may view

it as a realization of the random variable

r with (I, J)

uniformly distributed over the integer set

{(,) :1}Sijijn. So (4) can be rewritten as

2(0) 2(0)

(0)2 (0)

[() |][() |]

[( ())|]

IJIJ IJIJ IJ

EErr RErr R

EhRr R







Thus by (3), the minimizer of (4) is achieved by

* (0)(0)(0)

:()(| )(|)

IJIJIJIJ IJ

rhRErRErR 



, and so

*(0) (0)

()(|).

ij ijIJ

rhR ErR



To evaluate the above conditional expectation, we

need a bit more preparation. Note 2



is estimated by

2(0)2

(, )

2()

(1) ij

ij S











, (0)

(, )

(1) ij

ij S

nn 

.

Denote 2

(| )t





the normal density function with

mean 0 and variance 2



. Denote ij

S as the collection

of indices for (0)

R. Given (0)

R, for (,)ij



, view

(0)

r as a random vector over indices (I,J). We define

the conditional distribution of (0)

r as

(0)(0) (0)

(0) (0)

(|)

{#} 1

|| ||

IJuv ij

ij uv

ij ij

PrrR

member inRr







In the above we used the fact that the (0)

rare con-

tinuous random variables, so the collection {members in

(0)

R= (0)

r}={ (0)

r} almost surely. The correspond-

ing conditional probability is defined as

(0)

(0)(0) 2(0)(0)

(,)

((,)(,) |)

(|)(|)

uv ijuvij

uv S

PIJuv R

rrPr R











, (u,v) ij



By (2), we deduce (0) (0)

(| ,(,)(,))

IJ IJuv

Er RIJuvr,

so we have

(0) (0)

(,)

(0)

(| )(| ,(,)

(,))((,)(,)|)

ijIJijIJ ij

uv S

rErRErR IJ

uvPI JuvR









(0)(0)(0) 2(0)(0)

(,)

(0)(0) 2(0)(0)

(,)

(|)(|)

uvuv ijuvij

uv S

uv ijuvij

uv S

rrr PrR

rrPrR











(0)(0)(0) 2(0)(0)(0) 2

(,) (,)

(0)(0) 2(0)(0) 2

(,) (,)

(|)(|)

(|) (|)

ij ij

uvuv ijuvuv ij

uv Suv S

uv ijuv ij

uv Suv S

rrr rrr

rr rr





 















,

(i, j)ij



(5)

The matrix ()

Rr



is our one-step restored esti-

mate of the genetic correlation network R, we also de-

note it by (1) (1)

()

RR r .

Denote F(⋅) the operator given in (5), as

(1) (1)

()

ij ij

rFR, and denote (1) (1)

()

ij ij

rFR

(1) (0)(0)

()(|)RFR ERR .

We view F(⋅) as a filter for the noises, so (1)

R is a

smoothed version of (0)

R. Let

Rr be the random

variable of the ij

r’s over the random index (I,J) and the

variation of possible values of the ij

r’s, with density p(⋅),

its uncertainty can be characterized by variance and en-

tropy, which is defined as

H(p) = –E[log p(R)]= –p(r)log p(r)dr.

It is maximized or most uncertain when R is uni-

formly distributed, and has smaller value when the dis-

tribution of r is more certain. It has some relationship

with variance. The former depends on more innate fea-

tures, such as moments, of the distribution than the latter,

which only measures the disparity from the mean. When

980 A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

p(⋅) is a normal density with variance 2



, then

() 12Hp





 . For many commonly used parametric

distributions, entropy and variance agree with each other,

i.e. an increase in one of them implies so for the other.

But this is not always true and a general closed form

relationship between variance and entropy does not exists.

Variance is more popular in practice because of its sim-

plicity.

Although generally, in the image restoration context,

R is estimated by just applying F once, a natural question

is what will happen if we use the operator F repeatedly?

i.e. let (1) (1)()()

()()(|)

kk kk

Rr FRERR



  for k ≥ 0.

To investigate this question, we impose the model

()() ,

ij ijij



 ()k



~ ),0( )(2 k



, (1 ≤ i < j ≤ n)

(6)

The estimators ()k

r ‘s are obtained by minimizing

2()

2[() |]

(1)

ij ij

ijn

Er rR

nn  







(7)

and are given by

() ()

(| )

ijIJ ij

rErR.

similarly 2()k



is estimated by

2( )( )( )2

(, )

2()

(1)

kkk

ij S











() ()

(, )

(1)

ij S

nn 

.

Since n is usually large, 2( )k





is a good estimator of

2( )k



. Corresponding to (5), we have

(1)()()

(|)

kkk

ijIJ ij

rErR



()(0) (0)2

(,)

(0)(0) 2

(,)

( )(0)(0)2()

(,)

(0)(0)2()

(,)

(|)

uvuv ij

uv S

uv ij

uv S

uvuv ij

uv S

uv ij

uv S

rrr













, (i,j) ij

S , k1 (8)

In the above we do not replace the (0)

r’s by the

()k

r’s in (|)



 but with 2(0)



replaced by the step k

estimator 2()k



, only for the reason of simplicity in the

proof of the Proposition below. Finally, 2( )k



is re-

placed by 2()k





in actual computation.

Although few density functions are convex, many of

them are log-convex. For example, the normal, exponen-

tial (in fact any quadratic exponential families), Gamma,

Beta, chisquare, triangle, uniform distributions. But

some are not, such as the T and Cauchy distributions.

Condition A) does not require all the ()

()

p’s to belong

to the same parametric family, nor even to be parametric.

Condition B) is satisfied for almost all parametric fami-

lies as few parametric families require more than the

first two moments to determine. The only restriction we

make is that all the ()

()



’s belong to the same para-

metric family.

View ()k

r as a random realization of the ()k

r’s and

as of (0)

R, let ()

()



be the density function of ()k

To study the property of the algorithm, we say a

non-negative function f(⋅) is log-convex if log f(

⋅

) is

convex, and assume the following conditions

A) ()

()



is log-convex for all k.

B) All the ()

()



’s belong to a parametric family

which is determined by the fist two moments.

Our algorithm has the following desirable property

(see Appendix for the proof)

Proposition. 1) Assume either A) or B), then

(1)()

()(),

Hp Hp

 k ≥0.

2) 2(1)2()kk



, k ≥0.

3) As k →∞, the table ()k

R converges in

the component wise sense:

() *k

RR

for some stationary array **(0)

(,)RRRF.

This Proposition tells us that, if the assumption of

neighboring similarity is valid for (0)

R, then the esti-

mates ()k

R become more and more clear (less entropy),

and more and more accurate as an estimator of R (less

variance). So (*)

R is the sharpest picture the data (0)

provide and can be restored by the filter F, the innate

regulatory relationships among the genes can be recov-

ered by filter F and provided by the data (0)

R under the

ideal situation of no noise. Intuitively, this picture has

some close relationship with the haplotype block struc-

tures.

As of small sample size (mk) and large number (n(n –

1)/2) of parameters, there is no way of talking about the

consistency of R to R. So in general (*)

R and R may not

equal, however our algorithm enable us to do the best

effort we can. Convergence of ()k

R can be accessed by

the distance criteria: for a given > 0 (usually =1/100 or

1/1000)

(1)

(1) ()()

(,)| |

(1)

kk k

ij ii

dR Rrr













(1)

(1)()()1/2

(,)(())

(1)

kk k

ij ii

dR Rrr











.

A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

981

Network at each time. We may also investigate the

problem at each different time point t. In this case (1)

is replaced by

()

(()())(()())

(( ))(( ))

mrii rjj

rij

txtxtxt

rmVar xtVar xt





,(1 )ijn 

where,

() (),

iri

txt

m



(())( ()()),

irii

Varx txtx t

m



 (i = 1,...,n; t =

1,...,k)

and (0)

R(t) = ((0)()

rt: 1 ≤ i < j ≤n) be the corre-

sponding initial table at each t, and the neighborhood

for (0) ()

rt is (0) ()

Rt = {(0)

r: |a – i| ≤ 1, |b – j| ≤

1}. In this case (6) is

() ()

() ()(),

ij ijij

rtrt t



 ()()

ij t



~ 2( )

(0,( ))



(1 ≤ i < j ≤ n)

and ()()()

() (()|()).

kkk

ijIJ ij

rtEr tRt



let 2()( )( )2

(, )

()( ()())

(1)

kkk

ij S

trtrt











() ()

(, )

() ()

(1)

ij S

rt rt

nn 

.

(8) is now (1)()()

() (()|)

kkk

ijIJ ij

rtErtR



()(0)(0)2

(,)

(0)(0) 2

(,)

()(0)(0) 2()

(,)

(0)(0)2( )

(,)

() (()()|)

(() ()|)

() (()()|())

(()()|())

uvuv ij

uv S

uv ij

uv S

uvuv ij

uv S

uv ij

uv S

r trtrt

rtrt

r trtrtt

rtrtt













, (i,j) ij



k1

The matrix ()()

() (())

Rtr t is the k-step re-

stored estimate of the genetic correlation network

()( ())

Rtr t at time t. The proposition is then hold

for each fixed t.

3. SIMULATION STUDY

We simulate 40 genes over 12 time conditions at time

(hour) points 112

( ,...,)tt = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,

12) for 6 individuals by mimicking the setting of the data

analyzed in Iyer et al. [15]. We simulate the genes from

6 clusters, the numbers of genes in each cluster are given

by the vector 16

( ,...,)nn = (8, 6, 4, 4, 6, 12). The base-

line values of the gene expressions over time t ∈ [0,12]

in cluster k are generated by functions of the form













12 3

sinsin/2sin(/3)

kk kk

htat atat , (k =

1,....,6).

Let h(t) be the vector of length 40, with first n₁ com-

ponents given by h1(t), second n2 components by h2(t),....,

last n6 components by h6(t). Denote 123

(, , )

kkkk

aaaa.

We arbitrarily choose the k

a’s as a1 = (0.54, –0.18,

1.23), a2 = (–0.12, –0.25, 0.45), a3 = (1.0, –0.55, –0.15),

a4 = (–0.32, –0.15, –0.65), a5 = (0.15, 0.25, 0.35) and a6

= (–0.52, –0.45, –0.55). First we need to simulate the ij

r’s

with coordinated patterns. We divide the 40 genes into the

6 clusters, and assume independence among the clusters.

Then for given a covariance matrix 16

  

we generate the data using this and the time condi-

tions, where k



is the covariance matrix for the genes

in cluster k. Directly specifying a high dimensional posi-

tive matrix is not easy, we let each k

 has the structure

kkk



, for some k

Q non-singular, so that k



is positive definite. Note that the 'kk

QQ’s may not be

correlation matrices, but they are covariance matrices, so



. Let k

Q be upper diagonal with dimension k

The non-zero elements of Q1 are drawn from U(0.5,0.8);

those for Q2 from U(0.2,0.4); those for Q3 from

U(0.2,0.6), those for Q4 from U(–0.3, –0.1); those for Q5

from U(0.6,0.9); and those for Q6 from U(–0.8, –0.6).

Then let 1/2

QQ  . The 6 individuals are i.i.d,

so we only need to describe the simulation of observa-

tion 11

{():1,...,40;1,...,12}

xxtj t



of the first indi-

vidual. Note for each fixed t, 1111,40

( )((),...,( ))

txtxthas

covariance matrix



. We first generate 140

( ,...)yyy

with the components i.i.d. N(0,1), then

1/2

1() ()()

thty t





is the desired sample, where for each fixed t,

140

( )((),...,( ))tt t







is the noise, with the ()



’s i.i.d

N(0,1) and independent over t. Convert the covariance

matrix ()





to a correlation matrix()



ijijii jj





only for i < j. Using the data

(())



, we compute the ()k

R’s from (8) then use

perspective plots to compare the restored correlations

after convergence at step k, ()k

R, the one-step restored

(1)

R, the initial estimated (0)

R and the true simulated

correlations R.

After computation, the algorithm meets the conver-

gence criterion at iteration 14 with = 10–4. The distances

between the observed, first step estimate and last step

estimate are: d1((0)

R, R) = 0.125, d1((1)

R,R) = 0.108 and

d1((14)

R, R) = 0.094. We see that the estimate after con-

vergence is closest to the true correlations. The results

are displayed in Figure 1. We only display the correla-

tions ij

r for j > i. Those values for ij

r is 1’s, and those

for ij

r (i > j) are set to zero’s, which can be obtained by

symmetry.

982 A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

From this figure we see that the correlations computed

from the raw data, panel (b), are very noisy, the true pat-

tern, panel (a), in the network is messed up. The

one-step estimate, panel (c), gives some limited sense,

while the final estimates, panel (d), recover the true pic-

ture with reasonably well. Considering the large number

of 40(40+1)/2 = 820 parameters and the small number of

15 individuals on 40 genes, the last step estimates are

quite a success. Large number of simulations yield simi-

lar results, the convergence criterion is met with 10 to 15

iterations.

Note we only used networks of 40 genes, as large

networks are not easy to display graphically. The com-

putations of a network with n genes is in the order

n(n-1)/2, so there should be no computational problem

for ordinary computer using this method to restore even

the whole genome.

4. RESULTS

We use the proposed method to analyze the data with 30

microarray chips from the Stanford microarray database:

http:// smd.stanford.edu/cgi-bin/search/QuerySetup.pl.

The Category is Normal tissue and the subcategory is

PBMC, the following 30 files are the Raw data in the

database: 19430.xls, 19438.xls, 19439.xls, 19446.xls,

19447.xls, 19448.xls, 19449.xls, 19450.xls, 19451.xls,

19500.xls, 19505.xls, 19506.xls, 19507.xls, 21407.xls,

21408.xls, 21409.xls, 21410.xls, 21411.xls, 21412.xls,

21413.xls, 21414.xls, 21415.xls, 21416.xls, 21424.xls,

21425.xls, 21426.xls, 21427.xls, 21428.xls, 21429.xls,

21430.xls. The data we used are the overall intensity

(mean), the 67th column in the 30 excel files. We choose

three subsets of genes on the 30 arrays: set I is genes

0-49, set II is genes 1000-1049 and set III is genes

5000-5049 from the original data set. There are 80 variable

for each array. We choose the intensity from normal

people for our analysis. The initial correlation coeffi-

cients among the genes computed from the raw data in

each set, and those estimated after convergence by our

algorithm are shown in Figures 2-4. Clearly the initial

correlations are noisy and difficult to see any patterned

Figure 1. Network Correlations: (a). Simulated R, (b) Initial (0)

R, (c) One-step Restored (1)

R, (d) k-step

Converged ()k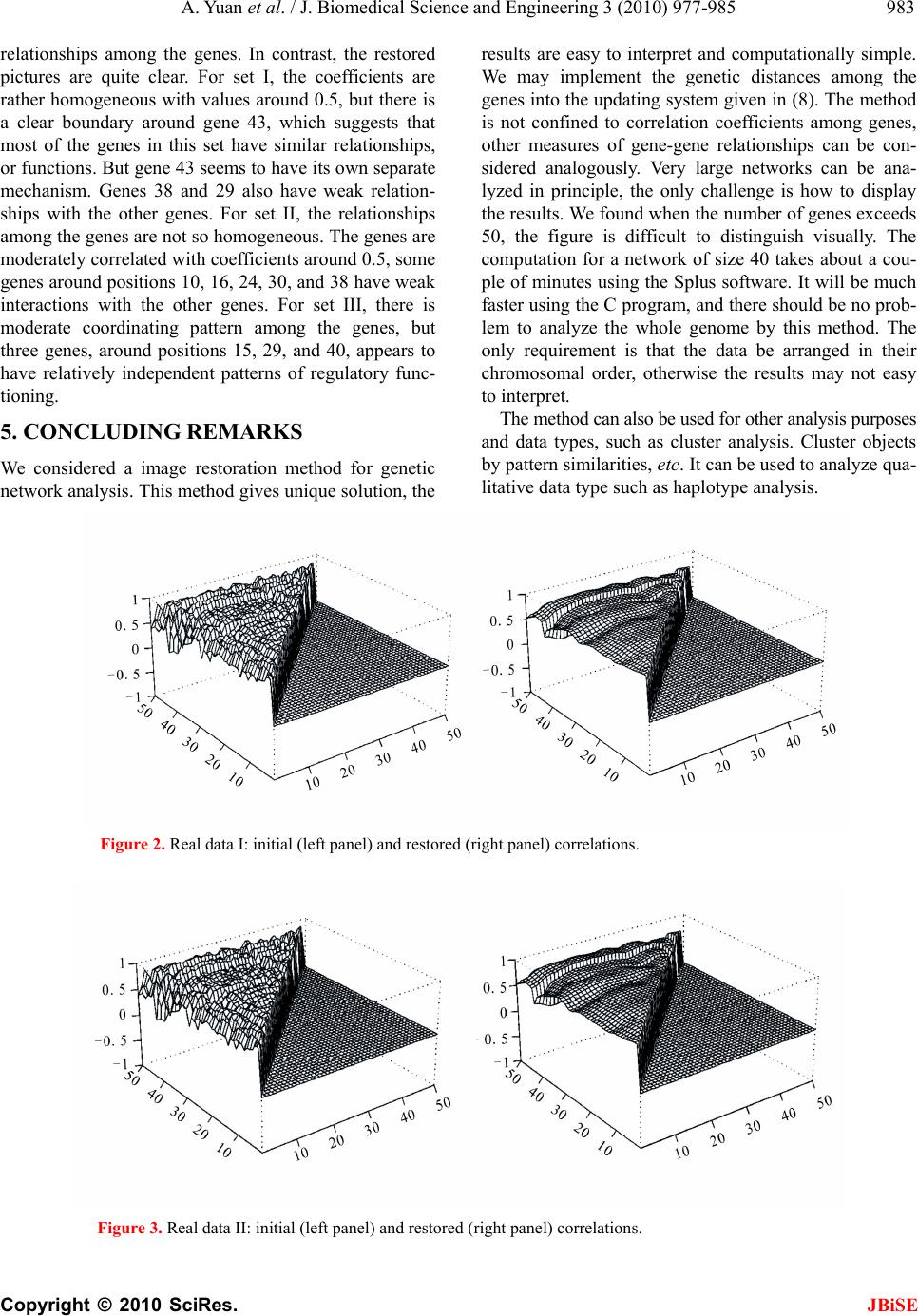

A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

983

relationships among the genes. In contrast, the restored

pictures are quite clear. For set I, the coefficients are

rather homogeneous with values around 0.5, but there is

a clear boundary around gene 43, which suggests that

most of the genes in this set have similar relationships,

or functions. But gene 43 seems to have its own separate

mechanism. Genes 38 and 29 also have weak relation-

ships with the other genes. For set II, the relationships

among the genes are not so homogeneous. The genes are

moderately correlated with coefficients around 0.5, some

genes around positions 10, 16, 24, 30, and 38 have weak

interactions with the other genes. For set III, there is

moderate coordinating pattern among the genes, but

three genes, around positions 15, 29, and 40, appears to

have relatively independent patterns of regulatory func-

tioning.

5. CONCLUDING REMARKS

We considered a image restoration method for genetic

network analysis. This method gives unique solution, the

results are easy to interpret and computationally simple.

We may implement the genetic distances among the

genes into the updating system given in (8). The method

is not confined to correlation coefficients among genes,

other measures of gene-gene relationships can be con-

sidered analogously. Very large networks can be ana-

lyzed in principle, the only challenge is how to display

the results. We found when the number of genes exceeds

50, the figure is difficult to distinguish visually. The

computation for a network of size 40 takes about a cou-

ple of minutes using the Splus software. It will be much

faster using the C program, and there should be no prob-

lem to analyze the whole genome by this method. The

only requirement is that the data be arranged in their

chromosomal order, otherwise the results may not easy

to interpret.

The method can also be used for other analysis purposes

and data types, such as cluster analysis. Cluster objects

by pattern similarities, etc. It can be used to analyze qua-

litative data type such as haplotype analysis.

Figure 2. Real data I: initial (left panel) and restored (right panel) correlations.

Figure 3. Real data II: initial (left panel) and restored (right panel) correlations.

984 A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

Figure 4. Real data III: initial (left panel) and restored (right panel) correlations.

6. ACKNOWLEDGEMENTS

The research has been supported in part by the National

Center for Research Resources at NIH grant 2G12

RR003048.

REFERENCES

[1] Goodwin, B.C. (1965) Oscillatory behavior in enzymatic

control processes. In Weber, G., Ed., Advances in Enzyme

Regulation, Pergamon Press, Oxford, 425-438.

[2] Tyson, J.J. and Othmer, H.G. (1978) The dynamics of

feedback cellular control circuits in biochemical path-

ways. Progress in Biophysics, Academic Press, New

York, 1-62.

[3] Reinitz, J., Mjolsness, E. and Sharp, D.H. (1995) Model

for cooperative control of positional information in Dro-

sophila by bicoid and maternal hunchback. Journal of

Experimental Zoology, 271(1), 47-56.

[4] Wessels, L.F.A., Van Someren, E.P. and Reinders, M.J.T.

(2001) A comparison of genetic network models. Pacific

Symposium on Biocomputing, 6(4), 508-519.

[5] D’haeseleer, P., Liang, S. and Somogyi, R. (1999) Gene

expression data analysis and modeling. Pacific Sympo-

sium on Biocomputating, Hawaii, USA.

[6] Savageau, M.A. (1976) Biochemical System Analysis: A

Study of Function and Design in Molecular Biology. Ad-

dison-Wesley, Reading, Massachusetts.

[7] Voit, E.O. (2000). Computational Analysis of Biochemi-

cal Systems, Cambridge University Press, Cambridge.

[8] Friedman, N., Linial, M., Nachman, I. and Pe’er, D.

(2000) Using Bayesian network to analyze expression

data. Journal of Computational Biology, 7(3-4), 601-620.

[9] Zhang, B.T. and Hwang, K.B. (2003) Bayesian network

classifiers for gene expression analysis. In: Berrar D.P.,

Dubitzky W. and Granzow M. Ed., A Practical Approach

to Microarray Data Analysis, Kluwer Academic Publish-

ers, Netherlands, 150-165.

[10] Chen, L. and Zhao, H. (2005) Gene expression analysis

reveals that histone deacetylation sites may serve as par-

titions of chromatin gene expression domains. BMC Ge-

netics, 6(1), 44.

[11] Owen, A. (1984) A neighborhood based classifier for

LANDSAT data. Canadian Journal of Statistics, 12(3),

191-200.

[12] Ripley, B.D. (1986) Statistics, images, and pattern recog-

nition. Canadian Journal of Statistics, 14(2), 83-111.

[13] Besag, J. (1986) On the statistical analysis of dirty pic-

tures. Journal of the Royal Statistical Society, 48(3), 259-

302.

[14] Meloche, J. and Zammar, R. (1994) Binary-image resto-

ration. Canadian Journal of Statistics, 22(3), 335-355.

[15] Iyer, V.R., Eisen, M.B., Ross, D.T., Schuler, G., Moore, T.,

Lee, J.C., Trent, J.M., Staudt, L.M., Hudson J.J., Boguski,

M.S., Lashkari, D., Shalon, D., Botstein, D. and Brown,

P.O. (1999) The transcriptional program in the response

of human fibroblast to serum. Science, 283(5398), 83-87.

[16] Cohen, B.A., Mitra, R.D., Hughes, J.D. and Church, G.M.

(2000) A computational analysis of whole-genome ex-

pression data reveals chromosomal domains of gene ex-

pression. Nature Genetics, 26(2), 183-186.

[17] Caron, H., Schaik, B., Mee, M., Baas, F., Riggins, G.,

Sluis, P., Hermus, M.C., Asperen, R., Boon, K., Voute,

P.A., et al. (2001) The human transcriptome map: clus-

tering of highly expressed genes in chromosomal do-

mains. Science, 291(5507), 1289-1292.

[18] Lercher, M.J., Urrutia, A.O. and Hurst, L.D. (2002)

Clustering of housekeeping genes provides a unified

model of gene order in the human genome. Nature Ge-

netics, 31(2), 180-183.

[19] Spellman P.T., Rubin G.M. (2002) Evidence for large

domains of similarly expressed genes in the Drosophila

genome. Journal of Biology, 1(1), 5.

[20] Ebrahimi, N., Maasoumi, E. and Soofi, E. (1999) Order-

ing univariate distributions by entropy and variance.

Journal of Econometrics, 90(2), 317-336.

A. Yuan et al. / J. Biomedical Science and Engineering 3 (2010) 977-985

985

Appendix

Proof of the Proposition. Recall

(1)(1) (1)()

()

kkkk

IJ IJ

rr rR



 is random in (I,J) and

()k

R; for fixed (I,J)=(i,j), (1)(1) ()

()

kkk

ij ji

rrR



 is ran-

dom in ()k

R; (1)(1)()(0)

(|)

kkk

IJ IJ

rrRR



 is random in

(I,J) (discrete); also

(1) ()()()()

(|)[|]

kkk kk

IJUVIJ

rErR ErR

 for random

index (I,J)

∈

S and random index (, )

UV S.

1) We first prove the result under condition A). We

have

(1)(1)() (1)

(1)

(1)(1)()

()

log( )log( )

()

()log(||)0,

()

kk kk

kkk

Ep rEpr

prdrDpp













which is the relative entropy between (1)

()

p



and

()

p. It is known that (1) ()

(||)0

Dpp

with “=”

if and only if (1)()

() ()

 . Note log-convexity of

()

p imply, for each given ()k

()()()() ()()

log([| ])[log()| ]

kkkkk k

IJ IJ

pErREprR.

Thus by the above two inequalities we get

( 1)(1)(1)()( 1)

()() ()()() ()

()log ()log()

log([|])( [log(|])

kkkkk

kkkkkk

IJ IJ

HpE prE pr

EpErREEprR



 

 

(1)()()

log()().

kk k

Ep rHp





Under condition B), the result in Ebrahimi et al. [20]

states that entropy and variance agree each other. i.e. one

increase/decrease implies the other. Now the conclusion

is immediate from 2).

2) By the total variance formula, we have

() ()

() ()() ()

()

[( |)] ([ |])

kk kk

UV IJUV IJ

Var r

EVar rRVar ErR







()()()

()()(1)(1)

[(|)]()

[( |)]

kk k

UV IJIJ

kk kk

UV IJ

EVar rRVarr

EVar rR









(0,1, 2,...).k

3) We only need to prove the convergence of the

component ()k

r for any fixed (i,j). In fact from (8), for

any integer m and k we have

(1 )(0)(0)2(1)

(,)

()

(0)(0)2( 1)

(,)

(1 )

(|)

()

km km

uvuv ij

uv S

ij km

uv ij

uv S

rrr



 



















,

(i,j)

∈

S, k,m = 0,1,2...

Since (0)





 and () 0



, by ii), we have

() *k



 for some 0 ≤*



< ∞. So if we let

(1 )(0)(0)2*

(,)

()

(0)(0) 2*

(,)

(1 )

(|)

()

uvuv ij

uv S

uv ij

uv S

rrr





























(i,j)

∈

S, k,m = 0,1,2...

then ()() (1)

km km

ij ij

rro





 as k →∞, thus we only need

to prove the convergence of

{()km

r

}.

Note

(1 )2*

(1 )(0)(0)2*

(,)

() (0 |):

(|)

ijuv ij

uv S

FR C

rrr

















We have 01



, and for all m,

(1)()(1)(1)()(0)

||| |||

ll kmkkm

ijijij ijijij ijij

rrCr rCrr



 

 

(1)()(1)(0)

(1) (0)

|| ||

||,

kllkl

ijijijijij ijij

ij ij

Crr CCrr

Crr







 







 



thus ()

1,2 ,...

{}

ij k





is a Cauchy sequence, and the con-

vergence follows.