Paper Menu >>
Journal Menu >>
 J. Biomedical Science and Engineering, 2010, 3, 963-976 JBiSE doi:10.4236/jbise.2010.310127 Published Online October 2010 (http://www.SciRP.org/journal/jbise/). Published Online October 20 10 in SciRes. http://www.scirp.org/journal/jbise Computer system for simulation of human perception. Some implications for the pathophysiology of the schizophrenic syndrome Bernhard J. Mitterauer Bernhard Mitterauer, MD Volitronics-Institute for Basic Research, Psychopathology and Brain Philosophy, Gotthard Guenther Ar- chives, Wals (Salzburg), Austria. Email: mitterauer@wasi.tv Received 16 June 2010; revised 25 June 2010; accepted 29 June 2010. ABSTRACT After the description of a brain model based on glial-neuronal interactions, a computer system for simulation of human perception, called clocked perception system, is proposed. The computer sys- tem includes a receptor field with sensors, each of which receives data with specific characteristics. These data are passed to processors, whereby only those connections between sensors and processors are released that are suited for an evaluation of the data according to a combination of specific data dictated by a phase program circuit. The computer system also includes a selector circuit that discards those dictated program commands that lead to a “senseless” computation result. A motor program circuit for the control of effectors may be connected to the computer system which at least contributes to the movement of the receptor field in order to bring the receptor field closer to suitable data with spe- cific characteristics for better execution of the pro- gram. From disorders of the computer system im- plications are deduced for the pathophysiology of the schizophrenic syndrome. Finally, a novel treat- ment approach to this syndrome is proposed. Keywords: Glial-Neuronal Interactions; Clocked Per- ception System; Technical Implementation; schizo- phrenic Syndrome 1. INTRODUCTION The construction of artificial perception systems dates back to the 1960s [1]. Over the years, far better learning algorithms were developed and much more powerful hardware provided, hence rendering neural networks, or neurocomputing, the method of choice for most pat- tern-recognition applications or robotics [2,3]. Sophisti- cated pattern-recognition systems are now available in all perception qualities. The present paper is one of a series investigating the time-coding principle from a biological and formal- technical point of view [4-8]. Here, the biological and formal background is further elaborated and some im- plications for the pathophysiology of schizophrenia are deduced from disorders of the mechanism. 2. CLOCKED PERCEPTION SYSTEM 2.1. Brain Biological Background The biological brain model for the proposed clocked perception system is based on glial-neuronal interactions [5,7]. The nervous tissue of the brain consists of the neuronal systems (neurons, axons, dendrites) and the glial system (astrocytes, oligodendrocytes with myelin sheaths enfolding axons, radial glia, and microglia). Ex- perimental results are inspiring a major reexamination of the role of glia in the regulation of neural integration in the central nervous system [9,10]. Figure 1 shows a schematic diagram of the glial-neuronal interaction: two astrocytes (Ac1,2) are shown in this very simple model, whereby in each case only one neuron (N1,2) belonging to an astrocyte is taken into consideration. Halassa et al. [11] identified how a single astrocyte contacts only four to eight neurons, but 300 to 600 synapses via its processes. The glial network (syncytium) consists in this schema of two astrocytes and two oligodendrocytes (Oc1,2) inter- connected via gap junctions (g.j.). The neuronal system shows two neurons (N1,2) with two afferent axons (Axi,j) and two afferent axodendritic synapses (Sai,j), two efferent axons (Ax1,2) with myelin sheaths (Ms) and a node of Ranvier (N.R.), as well as two dendro-dendritic synapses (Sd1,2,3,4) with the corresponding dendrites (D1, D 2, D 3, D4). Although a true understanding of how the astrocyte, the dominant glial cell type, interacts with neurons is  B. J. Mitterauer / J. Biomedical Science and Engineering 2 (2008) 963-976 Copyright © 2010 SciRes. JBiSE 964 still missing, several models have been published. Here, I focus on a modified model proposed by Newman [12]. Figure 2 depicts a schematic diagram of possible gli- al-neuronal interactions at a glutamatergic tripartite synapse. Release of glutamate (GLU) from the pre- synaptic terminal activates glial receptors (glR) and postsynaptic receptors (poR) 1) (for the sake of clarity only one receptor is shown). The occupancy of glial re- ceptors evokes a Ca2+ increase 2) and the release of glu- tamate from the astrocyte. Glutamate excitation of pre- synaptic receptors (prR) 3) modulates glutamate release while activation of postsynaptic receptors 4) directly depolarizes the postsynapse. Activation of the astrocyte also elicits the release of adenosine-triphosphat (ATP), which depolarizes the postsynaptic neuron 5) and inhib- its the presynaptic terminal 6) via occupancy of the cog- nate receptors [13]. Hence, glia may exert a temporal boundary-setting function in synaptic information proc- essing [5]. For understanding the clock mechanism of the percep- tion system, the rhythmic contraction waves of glial cells (astrocytes and oligodendrocytes) are decisive. Glial cells, when they get swollen and/or depolarized, can potentially release accumulated K+, neurotransmitters, neuromodulators (e.g. taurine), and water into interstitial fluid in a pulsatile manner. Such discharge processes represent mechanisms by which glial cell networks could influence neuronal firing in a coordinated fashion [14]. In addition to modulating synaptic transmission in neuronal cells, astrocytes and oligodendrocytes may play a direct role in generating pacemaker rhythms [15]. This originally speculative assumption has already been verified. Parri et al. [16] showed that astrocytes in situ could act as a primary source for generating neu- ronal activity in the mammalian central nervous system. Slow glial calcium oscillations (every 5 to 6 minutes) occur spontaneously and can cause excitations in nearby neurons. Although experimental evidence shows that neuronal-glia interactions also occur in the millisecond range [17], until now spontaneous rapid glial oscillations within a second are not found. However, slow rhythmic pulsations of glial cells, especially of astrocytes, could influence cognitive processes such as thinking and could also play a role in neuronal pacemaker circuits [18]. Since phase programming represents a basic mecha- nism in the clocked perception system that may be gene- rated in the astrocytic syncytium, the underlying bio- logical structure and function must be described. Figure 3 shows a diagrammatic schema depicting an astrocytic syncytium composed of two astrocytes (Ac1, Ac2) inter- connected via gap junctions (g.j.). Each astrocyte con- tacts four synapses (Sy) with four different qualities (a, b, c, d) building an astrocytic-neuronal compartment. A Two astrocytes (Ac1,2) are shown in this very simple model, whereby in each case only one neuron belonging to an astrocyte is taken into consideration. The glial network (syncytium) consists of two astrocytes and two oligodendrocytes (Oc1,2) belonging to them. Gap junctions (g.j.) exist between the astrocytes and the oligodendrocytes. The neuronal system shows two neurons (N1,2) with two affer- ent axons (Axi,j) and two afferent axo-dendritic synapses (Sai,j), two efferent axons (Ax1,2) with myelin sheaths (Ms) and a node of Ranvier (N.R.), as well as two dendro-dendritic synapses (Sd1,2;3,4) with the corresponding dendrites (D1, D2, D3, D4). Figure 1. Schematic diagram of the glial-neuronal interaction. 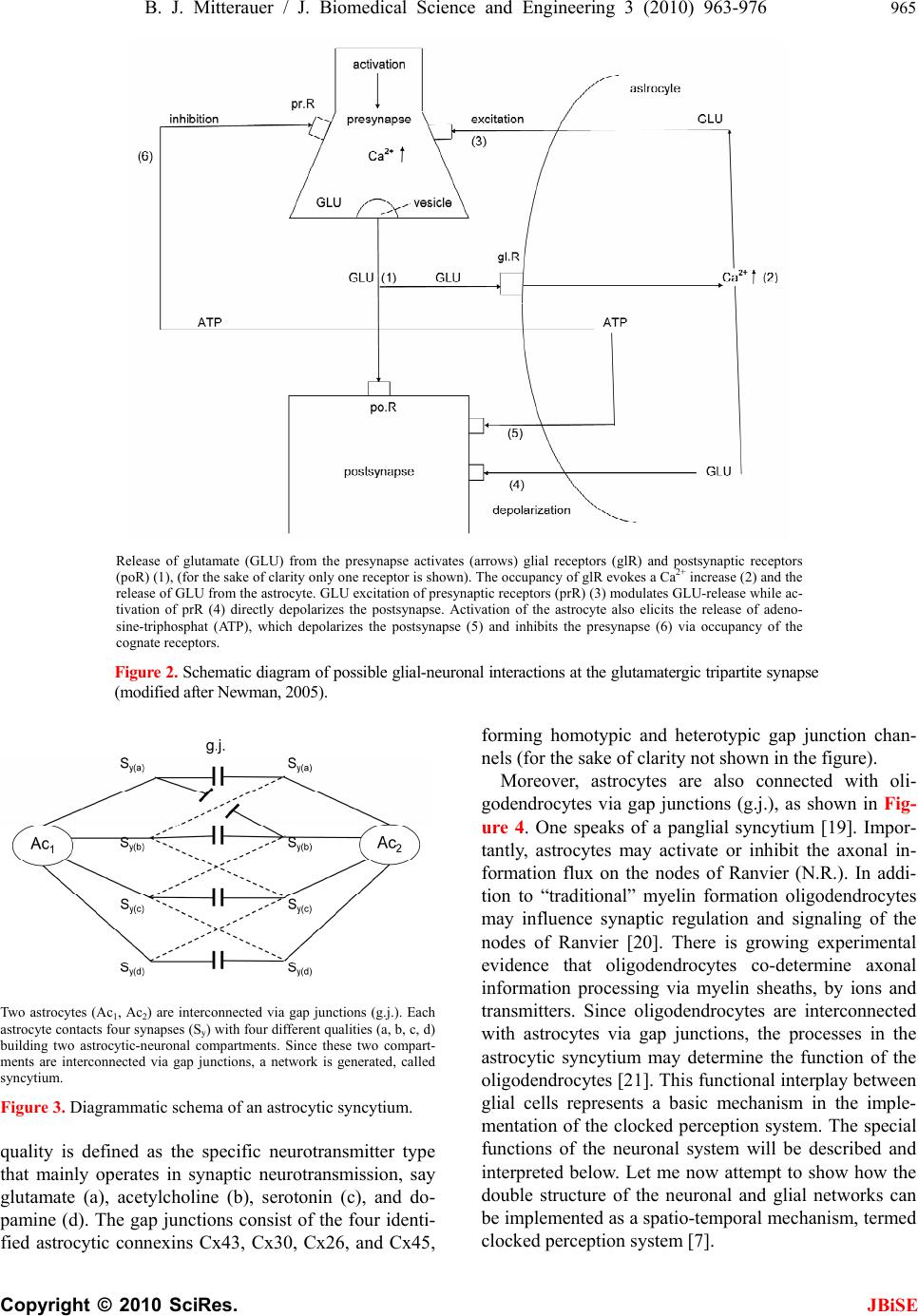 B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 965 Copyright © 2010 SciRes. JBiSE Release of glutamate (GLU) from the presynapse activates (arrows) glial receptors (glR) and postsynaptic receptors (poR) (1), (for the sake of clarity only one receptor is shown). The occupancy of glR evokes a Ca2+ increase (2) and the release of GLU from the astrocyte. GLU excitation of presynaptic receptors (prR) (3) modulates GLU-release while ac- tivation of prR (4) directly depolarizes the postsynapse. Activation of the astrocyte also elicits the release of adeno- sine-triphosphat (ATP), which depolarizes the postsynapse (5) and inhibits the presynapse (6) via occupancy of the cognate receptors. Figure 2. Schematic diagram of possible glial-neuronal interactions at the glutamatergic tripartite synapse (modified after Newman, 2005). Two astrocytes (Ac1, Ac2) are interconnected via gap junctions (g.j.). Each astrocyte contacts four synapses (Sy) with four different qualities (a, b, c, d) building two astrocytic-neuronal compartments. Since these two compart- ments are interconnected via gap junctions, a network is generated, called syncytium. Figure 3. Diagrammatic schema of an astrocytic syncytium. quality is defined as the specific neurotransmitter type that mainly operates in synaptic neurotransmission, say glutamate (a), acetylcholine (b), serotonin (c), and do- pamine (d). The gap junctions consist of the four identi- fied astrocytic connexins Cx43, Cx30, Cx26, and Cx45, forming homotypic and heterotypic gap junction chan- nels (for the sake of clarity not shown in the figure). Moreover, astrocytes are also connected with oli- godendrocytes via gap junctions (g.j.), as shown in Fig- ure 4. One speaks of a panglial syncytium [19]. Impor- tantly, astrocytes may activate or inhibit the axonal in- formation flux on the nodes of Ranvier (N.R.). In addi- tion to “traditional” myelin formation oligodendrocytes may influence synaptic regulation and signaling of the nodes of Ranvier [20]. There is growing experimental evidence that oligodendrocytes co-determine axonal information processing via myelin sheaths, by ions and transmitters. Since oligodendrocytes are interconnected with astrocytes via gap junctions, the processes in the astrocytic syncytium may determine the function of the oligodendrocytes [21]. This functional interplay between glial cells represents a basic mechanism in the imple- mentation of the clocked perception system. The special functions of the neuronal system will be described and interpreted below. Let me now attempt to show how the double structure of the neuronal and glial networks can be implemented as a spatio-temporal mechanism, termed clocked perception system [7].  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 Copyright © 2010 SciRes. JBiSE 966 Two astrocytes (Ac1,2) contact two neurons (N1,2). The astrocytes are interconnected via gap junctions (g.j.) building an astrocytic syncytium. In addition, the astrocytes (Ac1,2) are interconnected with oli- godendrocytes (Oc1,2) via gap junctions (g.j.) forming a general glial network, called panglial syncytium. Only two axons (Ax1,2), two myelin sheaths (Ms) and nodes of Ranvier (N.R.) are shown (see Figure 1). Figure 4. Schematic diagram of the panglial syncytium. 3. CLOCKED PERCEPTION SYSTEM 3.1. Description of the Preferred Embodiments Figure 5 shows a computer system for the simulation of human perception via sense organs that contains a large number of sensors Rn, namely R1, R2, R3,…R10, R11,…Rn in a receptor field 2. These sensors are sensitive to data a, b, or c, which are represented here by different configu- rations of the sensors; thus, the sensors, such as R1, R4, etc. which have a triangular receptor surface, are sensi- tive to specific data that are simulated in the illustration by STa. Correspondingly, sensors R2, R5, R11, etc. are sensitive to specific data b supplied by stimuli STb, which here are shown to have a semi-circular receptor surface and a similar stimulus. Further sensors such as sensors R3, R6, …Rn are sensitive to specific data c, which here are shown to have a quadrilateral receptor surface or correspondingly quadrilateral stimuli STc. All stimuli are compiled in a stimulus field 3. It is clear that the stimuli are not produced by an arranged stimulus field as shown in the illustration; rather, they are pre- sented to the computer system within the scope of a si- mulation of the environment in a non-arranged fashion. Each sensor Ri is connected with a processor Pi via a line Li, whereby the index i progresses from 1 to n. Instead of a processor, an entire processor group PG, consisting of several processors Pi, as shown by dotted lines in Figure 6 may be provided. Such a processor group consisting of processors P6.1, P6.2, to P6.6 is shown in Figure 6. The results calculated by processors Pi are stored in a mem- ory buffer 4. A circuit configured as a line circuit 5 is provided that is controlled by a phase circuit 6. Lines A1 to An proceed from the line circuit 5 to corresponding lines L1 to Ln, where they affect switches S1 in the lines L1, of which only the switches S1, S6, S7 and Sn are shown. These switches are pure on/off switches, so that the lines Li are either interrupted or connected by the switches. Along with the control circuit C for the line switching 5, the phase circuit 6 includes a large number of output lines B, of which the lines B1 to B11 and Bn are shown here. These lines Bi also lead to the connection lines Li be- tween the sensors Ri and the processors P1, and control the switches SWi located in the lines there, of which only switches SW1, SW6, SW7, and SWn are shown. As switch Si, these switches SWi are pure on/off switches, so that lines Li are either interrupted or connected by the switches as they are controlled. The central element of this computer system is a phase program circuit 7 in which an intended program for the total computer system is embedded and that con- trols the phase circuit 6 via control line C2 and also the line switching directly via control line C1. Cycles are dictated to phase circuit 6 via the phase program circuit 7, whereby a cycle corresponds to the time phase in which a certain switching applies. Depending on the programming, a primary, secondary, or tertiary analysis of the status of the sensors is performed, for example, by the phase circuit. Thus, the cycled programming has a sampling function in that all monographs, digraphs, or trigraphs are played through or intentionally imple- mented, so that a certain combination of sensor statuses is sought in the simulated environment. The processors are arranged such that exactly as many processors are assigned to each receptor as there are phases being processed by the phase program. In the simplified case represented in Figure 6, there are six processors per group PGi that are connected with one of the sensors Ri 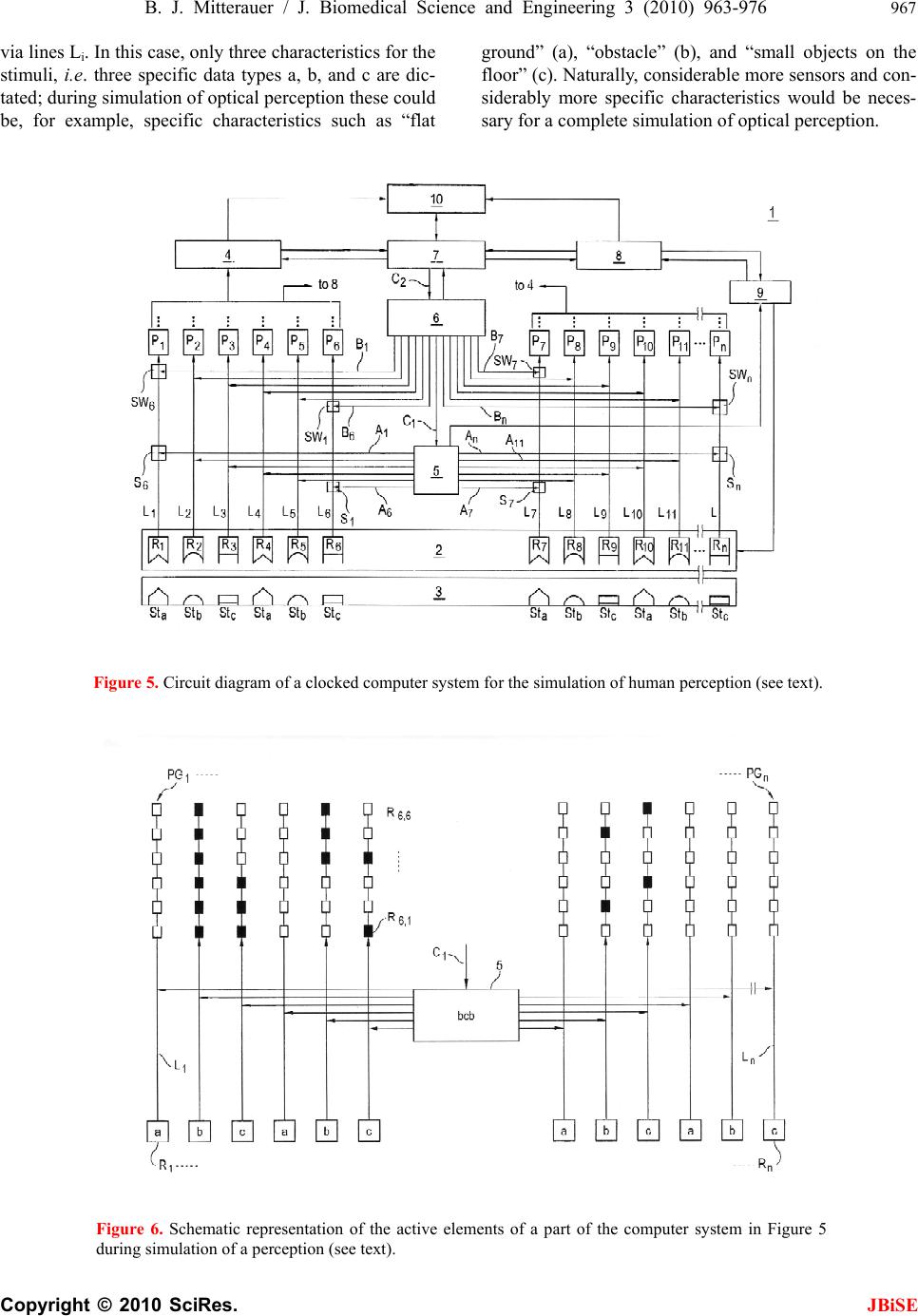 B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 967 Copyright © 2010 SciRes. JBiSE via lines Li. In this case, only three characteristics for the stimuli, i.e. three specific data types a, b, and c are dic- tated; during simulation of optical perception these could be, for example, specific characteristics such as “flat ground” (a), “obstacle” (b), and “small objects on the floor” (c). Naturally, considerable more sensors and con- siderably more specific characteristics would be neces- sary for a complete simulation of optical perception. Figure 5. Circuit diagram of a clocked computer system for the simulation of human perception (see text). Figure 6. Schematic representation of the active elements of a part of the computer system in Figure 5 during simulation of a perception (see text).  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 Copyright © 2010 SciRes. JBiSE 968 In the simplified representation in Figure 6, only those sensors that may be assigned the named chracteris- tics R1 to Rn are shown as small boxes, each connected to a processor group PG1 to PGn. Each processor group PGi consists of six processors, whereby, as mentioned above, only those processors of the sixth group are designated as P6.1 through P6.6. Figure 6 shows only the line circuit 5 from the computer system in the upper part of Figure 5, whereby a trigraph of the specific charac- teristics b, c, b are specified on the line circuit block, which are processed in six steps corresponding to the six processors based on the phase program. One may see from Figure 6 that the sensors occupied by specific characteristics “b” and “c” are switched through, and that some processors are already acting in the pertinent processor groups (designated by black boxes). It is also clear that no processor is active in the processor group PGn, which leads to the conclusion that the sensor Rn is not occupied. Since neither the sensors nor the proces- sors executing the specific characteristics “a” are being queried by the trigraph, the corresponding processor groups are not active. During the processing of the dis- tribution of specific characteristics specified by the tri- graph, the line circuit 5 must perform the following number of switchings in the arrangement of sensors for the computer system shown: ‐ For primary analysis (“Is a suitable stimulation of the three specific characteristics occurring at all?”), two switchings; ‐ For secondary analysis (“What is the distribution of the specific characteristics queried?”), 24 switchings; and ‐ For tertiary analysis (“How many of the specific characteristics are present at the sensor?”), 12 switchings. As may be derived from the diagram in Figure 6, only matching stimuli are accepted for the pre-determined phase program, while non-matching stimuli, i.e. those that do not correspond to the phase program, are dis- carded. This alternation between acceptance and rejec- tion is a characteristic of subjective intentional systems. A system’s ability to reject is an “index of its subjectivity”, which means that the implementation of intentions re- quires not only the identification of matching objects, but also the simultaneous discarding of present objects not intended. In order to dynamically configure the sta- tistical computer system described, and thus to optimally simulate perception, as mentioned above, a motor pro- gram circuit 8 is connected with the computer system that interacts with the phase program circuit 7 via bi- directional lines, and is controlled by it in accordance with each phase program step. This motor program cir- cuit controls effectors 9 that affect the receptor field 2, for example, in order to display it, thus achieving a bet- ter reception of stimuli by the individual sensors. The effectors might also serve to reposition a complete robot. The line circuit 5 also acts directly on the effectors 9 or their control circuits, which report each phase program step to be processed to the effectors, so that these may be controlled correspondingly. It must be mentioned for the sake of completeness that another comparator circuit 10 may be provided that con- tains data from the memory buffer 4, the motor program circuit 8, and the phase programming circuit 7, whereby communication with the phase program circuit 7 is bi-directional. The available data may be compared after suitable transformation in order to determine how well the intended phase program was processed. Based on this result, the phase program may be altered, or the computer system may be placed into another condition, e.g. by movement of the sensors or repositioning the robot. In this case, the decision is sent to the computer system whether it should continue to attempt to find the characteristics corresponding to the phase program, or whether it should alter the phase program with the help of the memory buffer 4. The perception mechanism presented may be viewed as a guitarist who hears a melody in his head and wants to hear how it really sounds. He wants to perceive it. He picks up his guitar and with his left hand presses the strings at exactly those points that correspond to his de- sired melody. The melody therefore dictates where the strings must be pressed. Regarding the perception me- chanism, this means that the phase program determines which lines must be released by the switching mecha- nism for a certain time period. Since the melody consists of varying combinations of sounds or notes, the grip on the guitar must be constantly changed, which correspond to a change in the phase program. Earlier, the guitar did not produce any sound by itself except for the minor sounds caused by placing the fingers on the strings. The guitar player must first strike the strings with his right hand (or guitar pick). This process corresponds to sti- mulation of the sensors. This takes into account the combination of how the guitarist uses the strings of his instrument. This mechanism of creating a melody re- quires no logical calculations, but rather takes advantage of the possibilities of use of the instrument in time cycles. However, from a biological point of view we are faced with the problem how and where these phase programs may be generated in the brain [22]. 3.2. Generation of the Phase Programs within the Astr ocytic Syncytium First of all, if one speaks of intentional programs, one has to define the formalism on which these programs are based. According to Guenther [23], a negative language  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 969 Copyright © 2010 SciRes. JBiSE can be formalized in an n-valent permutation system. Generally, a permutation of n things is defined as an ordered arrangement of all the members of the set taken all at a time according to the formula n! (! means facto- rial). Ta ble 1 shows a quadrivalent permutation system in a lexicographic order. It consists of the integers 1, 2, 3, 4. The number of permutations is 24 (4! = 1.2.3.4 = 24). The permutations of the elements 1 4 2 to 3 3 2 4 1 can be generated with three different NOT operators N1 , N2 , N3 , that exchange two adjacent (neighbored) inte- gers (values) by the following scheme: 1 ↔ 2; 2 ↔ 3; 3 ↔ 4 (N1) (N2) (N3) Generally, the number of negation operators (NOT) is dependent on the valuedness of the permutation system minus 1. For example, in a pentavalent permutation sys- tem four negation operators (N1-N4) (n = 5 – 1 = 4) are at work. It is possible to form loops, each of which passes through all permutations of the permutation system once (Hamilton loop). In a quadrivalent system they are computable (44 Hamilton loops), but in higher valent systems they are not computable. Ta b l e 2 shows an ex- ample of a Hamilton loop [23]. The first permutation (P = 1234) is permutated via a sequence of negation opera- tors (N1×2×3,…,2×1×2) generating all the permutations once until the loop is closed. Such permutation systems can be mathematically formalized as negation networks, called permutographs [24]. Figure 7 shows a quadrivalent permutograph. The individual NOT or negation functions N1-N3 are repre- sented between the permutations (1,…,24). The various Hamilton loops differ in NOT or negation operator se- quence. An example of a Hamilton loop is indicated in this permutograph by a dash-dotted line. It is defined by the following negation operator sequence: N1–N2–N3–N2–N3–N2–N1–N2–N1–N2-N3-N2-N3-N2-N1- N2-N1-N2-N3-N2-N 3-N2-N1-N 2 Figure 7. Example of a Hamilton loop in a quadrivalent per- mutograph. Table 1. Quadrivalent (n = 4) permutation system arranged in a lexocographic order. 1 1 1 1 11 2 2 2 2223333334 4 4 444 2 2 3 3 44 1 1 3 3441122441 1 2 233 3 4 2 4 23 3 4 1 4132414122 3 1 312 4 3 4 2 32 4 3 4 1314241213 2 3 121 number of the permutation 1 2 3 4 56 7 8 9 101112 13 14 15 161718 19 20 21 22 2324 This permutation system consists of 24 permutations (1 x 2 x 3 x 4, ….., 4 x 3 x 2 x 1) according to the formula n = 4! (factorial) = 1 The 24 permutations are lexicographically arranged. Table 2. Example of a Hamilton loop generated by a sequence of negation operators (Guenther, 1980) and designation of a phase program. Phase program in triplets: a b cb c b a babcbcbabab c b c b ab P N 1. 2. 3. 2. 3. 2. 1. 2. 1. 2. 3. 2. 3. 2. 1. 2. 1. 2. 3. 2. 3. 2. 1. 2. P 1 2 3 44 3 2 1 1 2 3 44 3 2 1 1 2 3 4 4 3 2 1 1 2 1 1 11 1 1 2 3 3 2 23 4 4 4 4 4 4 3 2 2 3 3 2 3 3 2 23 4 4 4 4 4 4 32 2 3 3 2 1 1 1 1 1 1 2 3 4 4 4 32 2 3 3 2 1 1 11 1 1 2 3 3 2 2 3 4 4 4 4 This first permutation (P = 1 × 2 × 3 × 4) is permutated via a sequence of negation operators (N1×2×3,…,2×1×2) generating all the permutations once until it is closed (1234) in the sense of a Hamiltion loop. It represents a phase program consisting of triplets, where N1, N2, N3 stand for the characteristics a, b, c.  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 Copyright © 2010 SciRes. JBiSE 970 Already in the 1980s we were able to show that the negative language may represent an appropriate formal model for a description of intentional programs gener- ated in neuronal networks of biological brains. Based on this formalism, computer systems for robot brains have also been proposed [25,26]. Here, I will try to further elaborate on this possible intentional programming in our brains, focusing on glial-neuronal interaction. 3.2.1. Glial Gap Junctions Could Embody Negation Operators In situ, morphological studies have shown that astrocyte gap junctions are localized between cell bodies, between processes and cell bodies, and between astrocytic end- feet that surround brain blood vessels. In vitro, junc- tional coupling between astrocytes has also been ob- served. Although less frequently observed than junctions between astrocytes, gap junctions also occur between oligodendrocytes, as observed in situ and in vitro. Moreover, astrocyte-to-oligodendrocyte gap junctions have been identified between cell bodies, cell bodies and processes, and between astrocyte processes and the outer myelin sheath. Thus, the astrocytic syncytium extends to oligodendrocytes, allowing glial cells to form a general- ized glial syncytium, also called “panglial syncytium”, a large glial network that extends radially from the spinal cord and brain ventricles, across gray and white matter regions, to the glia limitans and to the capillary epithe- lium. Ependymal cells are also part of the panglial syncytium. Additionally, activated microglia may also be interconnected with astrocytes via gap junctions. How- ever, the astrocyte is the linchpin of the panglial syncytium. It is the only cell that interconnects to all other glia. Furthermore, it is the only one with peri- synaptic processes. Gap junctions are now recognized as a diverse group of channels that vary in their permeability, voltage sensi- tivities, and potential for modulation by intracellular factors; thus, heterotypic coupling may also serve to coordinate the activities of the coupled cells by provid- ing a pathway for the selective exchange of molecules below a certain size. In addition, some gap junctions are chemically rectifying, favoring the transfer of certain molecules in one direction versus the opposite direction. The main gap junction protein of astrocytes is connexin Cx43, whereas Cx32 is expressed in oligodendrocytes in the CSN as well as another type of connexin, Cx45. Heterelogous astro-oligodendrocyte gap junctions may be composed of Cx43/Cx32, if these connexins form functional junctions [27]. Recent experimental results suggest roles of glial gap junction-mediated anchoring of signalling molecules in a wide variety of glial homeo- static processes [28]. Gap junctions are showing properties that differ sig- nificantly from chemical synapses [29]. The following enumeration of gap junctional properties in glial syn- cytia may support my hypothesis that gap junctions could embody negation operators in the sense of a gen- eration of negative language in glial syncytia: First, gap junctions communicate through ion currents in a bi-directional manner, comparable to negation op- erators defined as exchange relations. Bidirectional in- formation occurs between astrocytes and neurons at the synapse. This is primarily chemical and based on neuro- transmitters. It is not certain that all glial gap junction communications are bidirectional due to rectification. This is a poorly understood area because of extremely severe technical difficulties, especially in vivo [30]. Second, differential levels of connexin expression reflect region-to-region differences in functional requirements for different astrocytic gap junctional coupling states. The presence of several connexins enables different permeabilities to ions and molecules and different con- ductance regulation. Such differences of gap junctional functions could correspond to the different types of ne- gation operators. Third, neuronal gap junctions do not form syncytia and are generally restricted to one synapse. Fourth, processing within a syncytium is driven by neu- ronal input and depends on normal neuronal functioning. The two systems are indivisible. It is important to em- phasize that neuronal activity-dependent gap junctional communication in the astrocytic syncytium is long-term potentiated. This is indicative of a memory system as proposed in neuronal synaptic activity by Hebb over five decades ago [31]. Fifth, the diversity of astrocytic gap junctions results in complex forms of intercellular com- munication because of the complex rectification between such numerous combinatorial possibilities. Sixth, the astrocytic system normally functions to induce precise efferent (e.g. behaviorally intentional or appropriate motor) neuronal responses. Admittedly, the testing of this conjecture is also faced with experimental difficulties. Now, let us tie junctional functions and negative lan- guage together. Negation operators represent exchange relations between adjacent values or numbers. So they operate like gap junctions bi-directionally. Dependent on the number of values (n) that constitute a permutation system, the operation of different negation operators (n–1) is necessary for the generation of a negative lan- guage. With concern to gap junctions, they also show functional differences basically influenced by the con- nexins. Therefore, different types of gap junctions could embody different types of negation operators. Further- more, a permutation system represents—like the glial syncytium—a closed network generating a negative language. So we have a biomimetic interpretation of the negative language. If it is supposed that Hamilton loops are generated in the astrocytic syncytium, how can these be interpreted as  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 971 Copyright © 2010 SciRes. JBiSE working phase programs in glial-neuronal interactions? Let us take the Hamilton loop shown in Tabl e 2 as an example. It consists of a sequence of 24 negation opera- tors (N1-N3). In the computer system proposed, the phase programming is clocked and based on characteristic triplets (a, b, c) in various combinations [7]. If the nega- tion operators N1, N2, N3 stand for the characteristics a, b, and c, then a Hamilton loop consists of eight triplets representing a phase program (Table 2). Now, a phase programming in various combinations of triplets (e.g. aaa; baa, etc.) occurs [7]. Interestingly, in a quadrivalent permutation system all possible Hamilton loops (n = 44) are computable. In higher valued systems one is faced with a NP (non-deterministic polynomial time) problem so that the number of all possible Hamilton loops is uncomputable. What the implementation of this biomi- metic model of phase programming concerns, we can expect promising biotechnical developments [32]. 3.3. Coping with “Nonsense” Phase Programs In undisturbed dynamics the perception system is capa- ble of coping with “nonsense” phase programs. In order to shorten the time required to process the overall phase program, and to calculate sigificant results from the phase program quickly, the computer system includes a selection circuit that quasi “jumps over” such commands during readout of those individual program commands whose execution would lead to senseless or non-execu- table results, thereby discarding them. Such “nonsense” program commands are buffered, so that the meaningful commands are compared with the buffered “nonsense” program commands when the program commands are read out, and may thus be removed from program execu- tion. The computer system starts, for example, with any particular phase program and tests which program com- mands created significant perception images within a certain environment. The criterion for “meaningful” might be, for instance, that the computer system inten- tionally conducts an action corresponding to the percep- tion. For example, the proper motor is actuated in a robot that leads to meaningful handling. The computer system determines over time that certain program commands corresponding to a time cycle in the phase program lead to “senseless” perception images which also evince themselves in purposeless, i.e. “nonsense” actions, e.g. motor processes. However, such program commands executed in another environment might cause meaning- ful actions, so that consideration of the current environ- ment is significant. The computer system’s learning process consists of having the phase programs created for a specific, targeted environment, and, based on sys- tem feedback, having program commands ignored that are unsuitable for each task in the current environment, and thereby creating a suitable action, e.g. movement of sensors. The sensors address three different properties or data types, whereby the individual program commands are compiled as triplets, i.e. as a triple data set composed of a, b, and c. When triplets, for example, that have the property b in the first position are unsuitable for the creation of meaningful actions in the current environ- ment, they are removed from the phase program. If, for example, the following phase program is present: aaa/baa/cba/bcc/aca, then the second and fourth triplets beginning with b will be cancelled, i.e. removed, so that the following imple- mentable phase program remains: aaa/cba/aca. From this very brief example, one may see that the act of ignoring part of the phase program can significantly shorten it, so that the calculation time for the entire sys- tem is also shortened. Actions that are suitable and meaningful for the environment may be quickly calcu- lated. The function of this phase program circuit, which is modified by this selection circuit, is oriented to genetic code: a gene carries so-called codones, i.e. genetic words consisting of four (or possibly five) nucleotides A, T, C, and G (and possibly U), which represent a reading framework for amino acids from which in turn a certain protein is created. Comparable to this genetic mecha- nism, command programs are encoded as phase program triplets that represent the structure of a perception image. Note, a gene consists of sections of nucleotides which may factor a gene (so-called exons), and sections which cannot factor a protein (so-called intrones). In order to create a functional protein at all, the intrones must be “spliced out” of the nucleotide sequence. In science, one speaks of a so-called “splicing mechanism”. As soon as this mechanism is destroyed in that intrones are not ac- tually cut out, non-functional “Chimera” proteins or only short-lived supported proteins (truncated proteins) come into existence. In the phase programming for the com- puter system based on the invention, this genetic princi- ple means that program commands encode in the form of trigraphs, e.g. triplets of time cycles which encode un- suitable positions for a qualitative image construction for the objects of a certain environment, or tend to lead to sense deceptions within the meaning of false perceptions if these program commands are not spliced out. 4. IMPLICATIONS FOR THE PATHOPHYSIOLOGY OF THE SCHIZOPHRENIC SYNDROME Since in schizophrenia various phenomenologies are observed, it is more appropriate to speak of a schizo- phrenic syndrome [33]. From the perception system  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 Copyright © 2010 SciRes. JBiSE 972 proposed three main disorders can be deduced that could play a role in the pathophysiology of the schizophrenic syndrome. First, a disorder of phase programming in the glial syncytium occurs. Second, phase programs cannot be transferred to the neuronal system in synapses. Third, the switching mechanism is defective so that the oli- godendrocyte-axonic system is affected. These disorders can also be combined which determines the severity of the schizophrenic syndrome. 4.1. Incomplete Generation of Phase Programs Caused by a Loss of Gap Junctions If the function of an amount of gap junctions in the glial syncytium is genetically or (and) by stress disturbed, the network is incomplete (“leaky”) [34]. Hence, complete cycles of phase programs cannot be generated. Even if the synaptic glial-neuronal interactions would remain intact, phase programs cannot work, since incomplete triplets are unable to conduct analyses of the various object qualities in the environment. Hallucinations may be caused by this perception disorder. In visual halluci- nations, for example, uncanny scenes arise where unreal objects are composed, corresponding to neologisms in the semantic domain. Such severe cognitive impairment also affects thinking, emotions and motor behaviour. 4.2. Phase Programs cannot be Transferred in Synapses Caused by Non-Functional Astrocytic Receptors As shown in Figure 2, astrocytes exert a modulatory function in synaptic information transmission via their receptors accompanied by gliotransmission. As in Fig- ure 8 depicted, the glial receptors (glR) are non-func- tional (crosses) and cannot be occupied by neurotrans- mitters (NT), so that the activation of the gliotransmit- ters (GT) is impossible. Hence, they cannot negatively feedback to the receptors on the presynapse (prR). As a consequence, the glia lose their inhibitory or bound- ary-setting function and the neural transmitter flux is unconstrained, as the flux of thought on the phenome- nological level [35]. The glial system in its interaction with the neuronal system generates glial-neuronal compartments in the sense of specific functional units or operational domains [5,36]. The interactional structure of an astrocyte with n-neurons can be defined as an elementary compartment of nerve cells. By simultaneously activating and deacti- vating neurotransmission in all of the synapses envel- oped by an astrocyte, the astrocyte calcium wave may coordinate synapses into synchronously firing groups, interpretable as harmonization [7,37]. A loss of the glial boundary-setting function is de- picted in Figure 9. The astrocytes (Aci; Acj) of com- partment x and compartment y have non-functional glial receptors (crosses), so that glia cannot influence neu- ronal information processing. This genetically deter- mined disturbance results in a compartmentless neuronal network displayed as a group of eight neurons with 28 connecting lines (according to the formula [n2-n] 2). Such a brain is unable to structure the environmental information. One may argue that a glial determination of neuronal networks into functional units is not necessary because the neuronal system is compartmentalized per se [38]. However, there is a qualitative difference between the purely neuronal compartments and the glia-deter- mined compartments. Neuronal compartments may be merely functional for information processing, whereas glial-neuronal compartments may in addition have an information-structuring potency that we need for recog- nizing the qualitative differences between objects and individuals in our environment. That capacity may be lost in schizophrenic patients. Therefore, one can also speak of a loss of conceptual boundaries in schizophre- nia. This disorder can affect cognitive processes such as thinking. If a schizophrenic patient is unable to delimit conceptual boundaries among words, thoughts, or ideas with different meanings, then meaningless word con- structs (neologisms) or disorganized speech are the typi- cal phenomenological manifestations, called “thought dis- order”. From an ontological point of view, delusions are the consequence of the loss of boundaries between the self and the others (nonselves). Here, the self is defined as a living system capable of self-observation. One could also say that our brain embodies a distinct ontological locus of self-observation. Everything taking place in the brains of schizophrenic patients is reality because they cannot differentiate between their inner world and the outer world. Therefore, they cannot see ontological dif- ferences between the selves and the nonselves. This loss of ontological boundaries may lead to a delusional mis- interpretation of reality. Hallucinations may be caused by the same disorder. However, the perception systems are phenomenologi- cally affected. A schizophrenic who hears the voice of a person in his head is absolutely convinced that this per- son is really speaking to him. The loss of ontological boundaries or inner/outer confusion shows its phe- nomenological manifestation in the auditory system. Such a disorder can also occur in other sensory systems. The loss of the glial boundary-setting function may also be responsible for motoric and emotional symptoms in schizophrenia as catatonia and affective flattening. Im- portantly, Kondziella et al. [39] argued that astrocytes 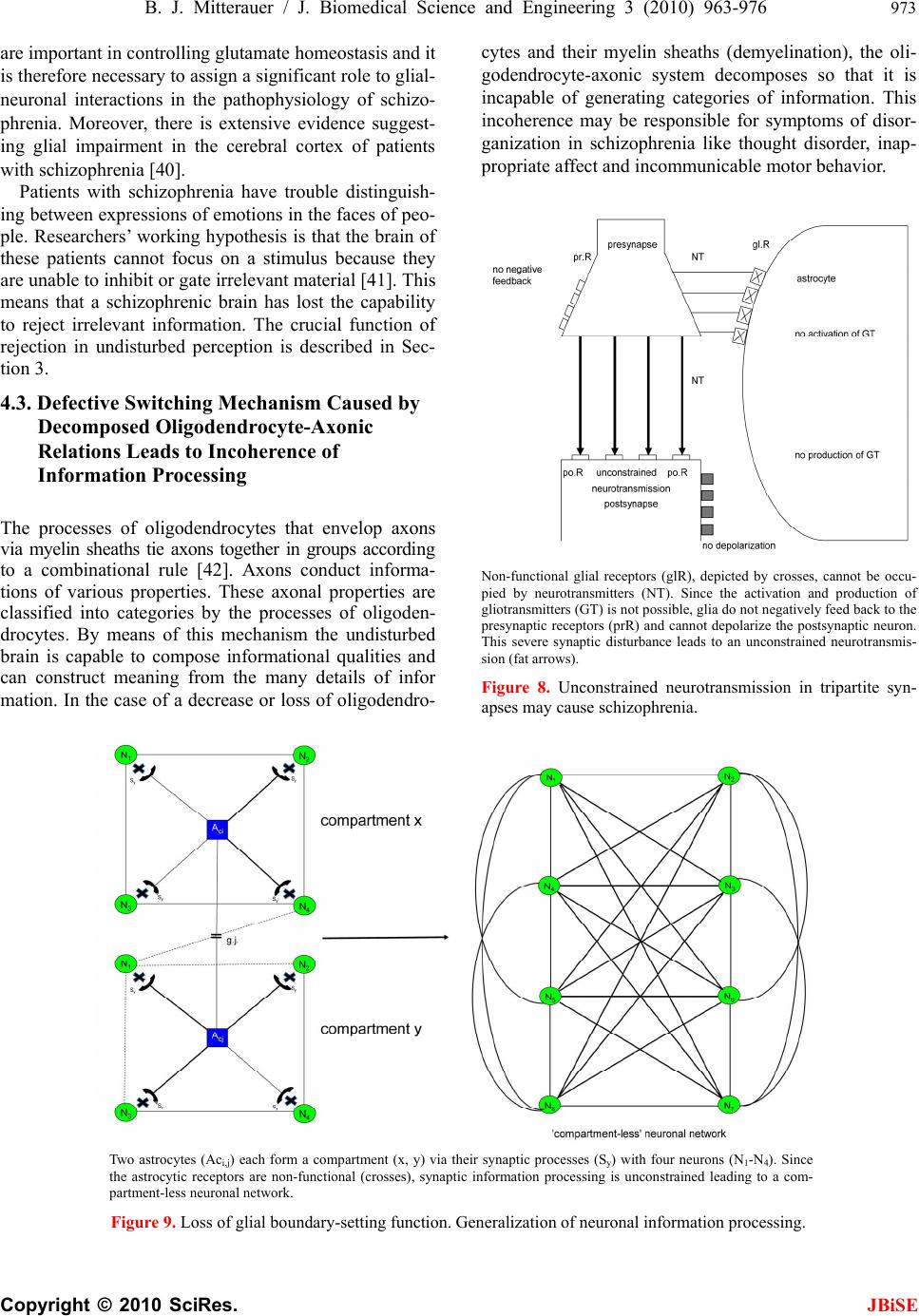 B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 973 Copyright © 2010 SciRes. JBiSE are important in controlling glutamate homeostasis and it is therefore necessary to assign a significant role to glial- neuronal interactions in the pathophysiology of schizo- phrenia. Moreover, there is extensive evidence suggest- ing glial impairment in the cerebral cortex of patients with schizophrenia [40]. Patients with schizophrenia have trouble distinguish- ing between expressions of emotions in the faces of peo- ple. Researchers’ working hypothesis is that the brain of these patients cannot focus on a stimulus because they are unable to inhibit or gate irrelevant material [41]. This means that a schizophrenic brain has lost the capability to reject irrelevant information. The crucial function of rejection in undisturbed perception is described in Sec- tion 3. 4.3. Defective Switching Mechanism Caused by Decomposed Oligodendrocyte-Axonic Relations Leads to Incoherence of Information Processing The processes of oligodendrocytes that envelop axons via myelin sheaths tie axons together in groups according to a combinational rule [42]. Axons conduct informa- tions of various properties. These axonal properties are classified into categories by the processes of oligoden- drocytes. By means of this mechanism the undisturbed brain is capable to compose informational qualities and can construct meaning from the many details of infor mation. In the case of a decrease or loss of oligodendro- cytes and their myelin sheaths (demyelination), the oli- godendrocyte-axonic system decomposes so that it is incapable of generating categories of information. This incoherence may be responsible for symptoms of disor- ganization in schizophrenia like thought disorder, inap- propriate affect and incommunicable motor behavior. Non-functional glial receptors (glR), depicted by crosses, cannot be occu- pied by neurotransmitters (NT). Since the activation and production of gliotransmitters (GT) is not possible, glia do not negatively feed back to the presynaptic receptors (prR) and cannot depolarize the postsynaptic neuron. This severe synaptic disturbance leads to an unconstrained neurotransmis- sion (fat arrows). Figure 8. Unconstrained neurotransmission in tripartite syn- apses may cause schizophrenia. Two astrocytes (Aci,j) each form a compartment (x, y) via their synaptic processes (Sy) with four neurons (N1-N4). Since the astrocytic receptors are non-functional (crosses), synaptic information processing is unconstrained leading to a com- partment-less neuronal network. Figure 9. Loss of glial boundary-setting function. Generalization of neuronal information processing.  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 Copyright © 2010 SciRes. JBiSE 974 The research criteria for alternative dimensional de- scriptors for schizophrenia [43] differentiate between a psychotic (hallucinations, delusions) dimension, a dis- organized dimension and a negative (deficit) dimension of schizophrenia. The disorganized dimension describes the degree to which disorganized speech, disorganized behaviour or inappropriate affect have been present. This kind of schizophrenic symptomatology can be deduced from the incoherence of brain functions that may be caused by decomposed oligodendrocyte-axonic relations. Thought disorder is the main symptom of cognitive disorganization. This appears in incoherent words, termed neologisms, and in incoherent sentences (word salad) [44]. These symptoms of incoherence may be caused by decomposed oligodendrocyte-axonic relations, if the cognitive systems are affected. However, one may argue that multiple sclerosis is also based on a demyeli- nating disorder of the brain where oligodendroglia is decreased or lost, comparable to the mechanism that is hypothesized for symptoms of incoherence in schizo- phrenia. In addition, patients with multiple sclerosis show not only the typical motoric symptoms, but can also suffer from cognitive impairments, affective disor- ders, and even psychotic symptoms [45]. First of all, although the pathophysiology of schizophrenia is as yet unknown, there is a consensus that the core symptoms (delusions and hallucinations) of schizophrenia may be basically caused by a disorder in the synaptic informa- tion processing, so that the astrocyte-neuronal interac- tion in tripartite synapses must primarily be disordered, which is not the case in multiple sclerosis. In line with this argumentation all macroglial cells (astrocytes and oligodendrocytes) with their syncytia must be considered in their interaction with the neuronal system with regard to research of the pathophysiology of schizophrenia. Therefore, abnormalities of white matter in brains with schizophrenia may be mainly responsible for symptoms of incoherence and not for the whole schizophrenic syn- drome. Structural magnetic resonance imaging research sug- gests that schizophrenia is associated with grey matter reductions in a network of frontal, temporal, limbic, tha- lamic, and striatal areas [46]. In addition, abnormalities of cerebral white matter, oligodendrocytes and myelin have been observed in schizophrenia with in-vivo imag- ing and post-mortem biochemistry [47]. White matter abnormalities are also frequently associated with cogni- tive impairment in both healthy and diseased individuals, and cognitive dysfunction is an important component of schizophrenia [48,49]. Although the neurobiological origins of the abnor- malities in white matter of brains with schizophrenia are unclear, gene studies involved in the maintenance of white matter structures may be particularly fruitful in schizophrenia. Recently, data gathered in a number of model systems indicated that axonal RNAs are synthe- sized in the surrounding glial cells. Experiments on the perfused squid giant axon have definitely proven that axoplasmic RNAs are transcribed on periaxonal glia. Their delivery to the axon occurs by a modulatory mechanism based on the release of neurotransmitters from the stimulated axon and on their binding to glial receptors [20,50]. 5. FUTURE PROSPECTS Since the computer system for simulation of human per- ception is implementable in a robot brain [8], an alterna- tive approach to experimental biological brain research is available. Moreover, the underlying brain model is based on the structures and functions of both the neu- ronal and the glial system. The latter may generate in- tentional or phase programs that characterize subjective systems. Therefore, a robot brain endowed with inten- tions may show features of subjectivity in its behaviour. Importantly, the perception mechanism proposed does not primarily work as a pattern-recognition system but as a pattern-generation system. What the so-called mental disorders concerns, we can also implement these disorders in a robot brain as de- scribed for schizophrenia. Then the robot could teach us what we know about these disorders, what we should further investigate and what probably remains unknown. The hypothesis that the schizophrenic syndrome may essentially be caused by non-functional astrocytic re- ceptors is experimentally testable. Since the splicing code has recently been deciphered [51], the hypothesis that non-functional, truncated astrocytic receptors are caused by a non-splicing of introns can be investigated at least in post-mortem brains with schizophrenia. Should these non-functional receptors be identified, the substitution of proteins identical with astrocytic receptor types could represent a novel therapeutic approach to the schizophrenic syndrome. REFERENCES [1] Rosenblatt, F. (1962) Principles of neurodynamics: Per- ception and the theory of brain mechanisms. Spartan Books, Washington, D.C. [2] Nolfi, S. and Floreano, D. (2000) Evolutionary robotics. The Biology, Intelligence, and Technology of Self-Orga- nizing Machines, MIT Press, Cambridge. [3] Sarhan, A.M. (2009) Iris recognition using discrete co- sine transform and artificial neural networks. Journal of Computer Science, 5(5), 369-373. [4] Mitterauer, B., Leitgeb, H. and Reitboeck, H.J. (1996)  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 975 Copyright © 2010 SciRes. JBiSE The neuro-glial synchronization hypothesis. Recent Re- search Developments in Biological Cybernetics, 1(1), 137-155. [5] Mitterauer, B. (1998) An interdisciplinary approach to- wards a theory of consciousness. Bio-systems, 45(1), 99-121. [6] Mitterauer, B. (2000) Some principles for conscious ro- bots. Journal of Intelligent Systems, 10(1), 27-56. [7] Mitterauer, B. (2001) Clocked perception system. Jour- nal of Intelligent Systems, 11 (4 ), 269-298. [8] Mitterauer, B. (2004) Computer system, particularly for simulation of human perception via sense organs. United States Patent, 6, 697, 789B2. [9] Kettenmann, H. and Ransom, B.R. (2005) Neuroglia. Oxford University Press, Oxford. [10] . Halassa, M.M and Haydon, P.G. (2010) Integrated brain circuits: Astrocytic networks modulate neuronal activity and behaviour. Annual Review of Physiology, 72, 335- 355. [11] Halassa, M.M., Fellin, T., Takano, H., Dong, J. and Hay- don, P.G. (2007) Synaptic islands defined by the territory of a single astrocyte. The Journal of Neuroscience, 27(24), 6473-6477. [12] Newman, E.A. (2005) Glia and synaptic transmission. In: Kettenmann, H. and Ransom, B.R., Eds., Neuroglia, Ox- ford University Press, Oxford, 355-366. [13] Haydon, P.G. and Carmignoto, G. (2006) Astrocyte con- trol of synaptic transmission and neurovascular coupling. Physiological Review, 86(3), 1009-1031. [14] Newman, E.A. and Zahs, K.R. (1997) Calcium waves in retinal glial cells. Science, 275(5301), 844-846. [15] Mitterauer, B., Garvin, A.M. and Dirnhofer, R. (2000) The sudden infant death syndrome: A neuro-molecular hypothesis. Neuroscientist, 6(3), 154-158. [16] Parri, H.R., Gould, T.M and Crunelli, V. (2001) Spon- tanous astrocytic Ca2+ oscillations in situ drive NMDAR- mediated neuronal excitation. Nature Neuroscience, 4(8), 803-812. [17] Winship, I.R., Plaa, N. and Murphy, T.H. (2007) Rapid astrocyte calcium signals correlate with neuronal activity and onset of the hemodynamic response in vivo. The Journal of Neuroscience, 27(23), 6268-6272. [18] Mitterauer, B. (2010) Possible Role of Astrocytes in the Sudden Death Infant Syndrome. Artificial Ingenuity. http://www.artificialingenuity.com/BB/viewtopic.php?t= 102 [19] Rash, J.E. (2010) Molecular disruptions of the panglial syncytium block potassium siphoning and axonal salta- tory conduction: Pertinence to neuromyelitis optica and other demyelinating diseases of the central nervous sys- tem. Neuroscience, 168(4), 982-1008. [20] DeFelipe, J., Fields, R.D., Hof, P.R., Höstad, M., Kos- tovic, I., Meyer, G. and Rockland, K.S. (2010) Cortical white matter: Beyond the pale remarks, main conclusions and discussion. Frontiers in Neuroanatomy, 4, 4. [21] Fields, R.D. (2009) The other brain. Simon and Schuster, New York. [22] Mitterauer, B. (2007) Where and how could intentional programs be generated in the brain? A hypothetical mod- el based on glial-neuronal interactions. BioSystems, 88(3), 101-112. [23] Guenther, G. (1980) Martin Heidegger und die Weltge- schichte des nichts. In: G. Guenther, Ed., Beiträge zur Grundlegung einer operationsfähigen Dialektik, Meiner, Hamburg, 260-296. [24] Thomas, G.G. (1982) On Permutographs. Supplemente ai Rendiconti del Circulo Matematico di Palermo, 2(2), 275-286. [25] Mitterauer, B. (1988) Computer system for simulating reticular formation operation. United States Patent, 4, 783,741. [26] Thomas, G.G. and Mitterauer, B. (1989) Computer for simulating complex processes. United States Patent, 4, 829,451. [27] Baumann, N. and Dinh, D.P. (2001) Biology of oli- godendrocyte and myelin in the mammalian central nervous system. Physiological Reviews, 81(2), 871-927. [28] Giaume, C. and Theis, M. (2009) Pharmacological and genetic approaches to study connexin-mediated channels in glial cells of the central nervous system. Brain Re- search Reviews, 63(1-2), 160-176. [29] Theis, M., Söhl, G., Elberger, J. and Willecke, K. (2005) Emerging complexities in identity and function of glial connexins. Trends in Neurosciences, 28(4), 188-195. [30] Perea, G. and Araque, A. (2005) Glial calcium signalling and neuron-glia communication. Cell Calcium, 38(3-4), 375-382. [31] Hebb, D.O. (1949) The organization of behaviour. Wiley, New York. [32] Rambidi, N.G. and Yakovenchuk, D. (2001) Chemical reaction-diffusion implementation of finding the shortest paths in a labyrinth. Physical Reviews, 63(2 Pt 2), 026607. [33] Dean, B., Boer, S., Gibbons, A., Money, T. and Scarr, E. (2009) Recent advances in post-mortem pathology and neurochemistry in schizophrenia. Current Opinion in Psychiatry, 22(2), 154-160. [34] Mitterauer, B. (2009) Loss of function of glial gap junc- tions may cause severe cognitive impairments in schizo- phrenia. Medical Hypotheses, 73(7), 393-397. [35] Mitterauer, B. (2010) Synaptic imbalances in endogenous psychoses. Bio-systems, 100(1), 113-121. [36] Mitterauer, B. (2003) The loss of self-boundaries: To- wards a neuromolecular theory of schizophrenia. Bio- systems, 72(2), 209-215. [37] Mitterauer, B. and Kopp, C. (2003) The self-composing brain: Towards a glial-neuronal brain theory. Brain and Cognition, 51(4), 357-367. [38] Rall, W. (1995) Theoretical significance of dendritic trees for neuronal input-output relations. In: I. Segev, J. Rinzel, G.M. Shephard, Eds., The Theoretical Foundation of Dendrite Function, MIT Press, Cambridge, 122-146. [39] Kondziella, D., Brenner, E., Eyjolfsson, E.M. and Son- newald, U. (2007) How do glial-neuronal interactions fit into current neurotransmitter hypotheses of schizophrenia. Neurochemistry International, 50(3), 291-301. [40] Rametti, G., Jungue, C., Falcon, C., Bargalló, N., Catalán, R., Penadés, R., Garzon, B. and Bernado, M. (2009) A voxel-based diffusion tensor imaging study of temporal white matter in patients with schizophrenia. Psychiatry Research, 171(3), 166-176. [41] Holden, C. (2003) Deconstructing schizophrenia. Science, 299(5605), 333-335. [42] Thomas, G.G. (1985) Introduction to kenogrammatics. Proceedings of the 13th Winter School on Abstract Anal-  B. J. Mitterauer / J. Biomedical Science and Engineering 3 (2010) 963-976 Copyright © 2010 SciRes. JBiSE 976 ysis, section of Topology, Rendiconti del Circolo Mate- matico di Palermo, 2(11), 113-123. [43] Diagnostic and statistical manual of mental disorders. American Psychiatric Association, Washington, D.C., 1998. [44] Frith, C.D. (1999) The cognitive neuropsychology of schizophrenia. Psychology Press, Sussex. [45] Beatty, W.W. (1993) Cognitive and emotional distur- bances in multiple sclerosis. Neurologic Clinics, 11( 1) , 189-204. [46] Fornito, A., Yűcel, M. and Pantelis, C. (2009) Reconciling neuroimaging and neuropathological findings in schizo- phrenia and bipolar disorder. Current Opinion in Psy- chiatry, 22(3), 312-319. [47] Kubicki, M., McCarley, R.W. and Shenton, M.E. (2005) Evidence for white matter abnormalities in schizophrenia. Current Opinion in Psychiatry, 18(2 ) , 121- 134. [48] Dwork, A.J., Mancevski, B. and Rosoklija, G. (2007) White matter and cognitive function in schizophrenia. International Journal of Neuropsychopharmacology, 10 (4), 513-536. [49] Wolf, R.C., Höse, A., Frasch, K., Walter, H. and Vasic, N. (2008) Volumetric abnormalities with cognitive deficits in patients with schizophrenia. European Psychiatry, 23 (8), 541-548. [50] Giuditta, A., Chun, J.I., Eyman, M., Cefaliello, C., Bruno, A.P. and Crispino, M. (2008) Local gene expression in axons and nerve endings: The glia-neuron unit. Physio- logical Reviews, 88(5), 515-555. [51] Barash, Y., Calarco, J.A., Gao, W., Pan, Q., Wang, X., Shai, O., Blencowe, B.J. and Frey, B.J. (2010) Decipher- ing the splicing code. Nature, 465(7294), 53-59. |

