Paper Menu >>
Journal Menu >>
 J. Biomedical Science and Engineering, 2010, 3, 931-941 JBiSE doi:10.4236/jbise.2010.310124 Published Online October 2010 (http://www.SciRP.org/journal/jbise/). Published Online October 20 10 in SciRes. http://www.scirp.org/journal/jbise Comparative analysis of various modularization algorithms and species specific study of VEGF signaling pathways Namrata Tomar, Losiana Nayak, Rajat K. De Machine Intelligence Unit, Indian Statistical Institute, Kolkata, India. Email: namrata_t@isical.ac.in; losiana_t@isical.ac.in; rajat@isical.ac.in Received 24 August 2009; received 9 September 2009; accepted 30 August 2010. ABSTRACT In biology, signal transduction refers to a process by which a cell converts one kind of signal or sti- mulus into another. It involves ordered sequences of biochemical reactions inside the cell. These cas- cades of reactions are carried out by enzymes and activated by second messengers. Signal transduc- tion pathways are complex in nature. Each pathway is responsible for tuning one or more biological functions in the intracellular environment as well as more than one pathway interact among themselves to carry forward a single biological function. Such kind of behavior of these pathways makes under- standing difficult. Hence, for the sake of simplicity, they need to be partitioned into smaller modules and then analyzed. We took VEGF signaling path- way, which is responsible for angiogenesis for this kind of modularized study. Modules were obtained by applying the algorithm of Nayak and De (Nayak and De, 2007) for different complexity values. These sets of modules were compared among themselves to get the best set of modules for an optimal com- plexity value. The best set of modules compared with four different partitioning algorithms namely, Farhat’s (Farhat, 1998), Greedy (Chartrand and Oellermann, 1993), Kernighan-Lin’s (Kernighan and Lin, 1970) and Newman’s community finding algorithm (Newman, 2006). These comparisons en- abled us to decide which of the aforementioned al- gorithms was the best one to create partitions from human VEGF signaling pathway. The optimal com- plexity value, on which the best set of modules was obtained, was used to get modules from different species for comparative study. Comparison among these modules would shed light on the trend of de- velopment of VEGF signaling pathway over these species. Keywords: Signal Transduction Pathway, VEGF Path- way, Complexity Value, KEGG Database, Modulariza- tion, Newman’s Community Finding Algorithm, Ker- nighan-Lin’s Algorithm, Farhat’s Algorithm, and Greedy Algorithm. 1. INTRODUCTION The ability of cells to receive and act on signals from beyond the plasma membrane is fundamental to life. This ability of cells to respond correctly to their micro- environment is the basis of development, tissue repair, immunity and normal tissue homeostasis. Cells respond to their environment by recognizing their structure, re- gulating the activity of proteins and finally by altered gene expression. The stimulus for such type of responses is known as signal. Signals interact with the responding cell through molecules, called receptors [1]. For example, cells receive constant input from membrane proteins that act as information receptors, sampling the surrounding medium for pH, osmotic strength, and the availability of food, oxygen and light and the presence of noxious chemicals, predators or competitors for food. These sig- nals elicit appropriate responses like motion towards food or away from toxic substances [2]. In multi-cellular organisms, cells with different functions, exchange a wide variety of signals. For example, plant cells respond to growth hormones and to variations in sunlight. Ani- mal cells exchange information through the concentra- tions of ions and glucose in extra-cellular fluids, the in- terdependent metabolic activities, taking part in different tissues, and in an embryo, the correct placement of cells during development. So, we can get the concept that in all the cases, signal represents information that is de- tected by specific receptors and converted to a chemical process. This conversion of information into a chemical change or signal transduction is a universal property of living cells. Errors in cellular information processing are responsible for diseases such as cancer, autoimmunity and diabetes. By understanding cell signaling, diseases may be treated effectively. Systems biology research helps us to understand the underlying structure of cell  N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 932 signaling networks and how changes in these networks may affect the transmission and flow of information. Signal transduction is specific and exquisitely sensi- tive [2]. In unicellular organisms, signals are of envi- ronmental origin and diffusible in nature. Signals, in metazoans, are paracrine (e.g. neurotransmitters); they release from the nearby cells and diffuse over short dis- tances. In the case of endocrine signals (e.g. hormones), they may be released from distant cells and vascular system sends them to their targets. Macromolecular sig- nals are associated with the extra-cellular matrix or on the surface of the neighboring cells, and they are called juxtacrine signals. It requires two adjacent cells to make physical contact in order to communicate. Some cells require direct cell-cell contact; others form gap junctions to connect to the cytoplasm of other cells’ cytoplasm for communication. A molecular signal that binds to a re- ceptor is a ligand. As signaling pathway is made up of many different input and output nodes that make it, complex network, it is difficult to study and analysis. So the idea to divide it into small bio-significant modules, through the process called modularization came into light. A module is a subset of the original pathway, which has minimal dependency on the rest part of the network [3]. Here, the idea is to divide a pathway in such a way that the complexity of resulting modules is much less than that of the entire pathway, which pro- vides an easier way to study the entire pathway. Many methods are developed to divide a network into smaller divisions. Here, we considered Vascular Endothelial Growth Factor (VEGF) pathway for applying different partition- ing algorithms. It has a receptor, i.e., VEGFR, which is activated by ligand. Ligand binding to the receptor leads to receptor homodimerization or heterodimerization. Dimerization of receptors leads to their activation and subsequent autophosphorylation on certain tyrosine re- sidues. It has many types of receptors. The receptors for vascular epithelial growth factor (VEGF) and related ligands are VEGFR-1 (Flt-1), VEGFR-2 (KDR/Flk-1), VEGFR-3 (Flt-4), neuropilin-1 and neuropilin-2. The interaction of VEGFR with either neuropilin-1 (NRP-1) or heparan sulfate proteoglycan helps in binding VEGF to its receptor. These receptors have multiple immu- noglobulin G-like extra-cellular domains and intracellu- lar tyrosine kinase activity. The human gene for VEGF resides on chromosome 6p21. The coding region spans 14 kb and contains eight exons. Alternative splicing of a single pre-mRNA generates several distinct VEGF spe- cies. There are several splice variants of VEGF, like VEGF 121, 145, 165, 189, and 206. Among them, VEGF 165 is the predominant form [4]. VEGF family has other members also. These are VEGF-B, -C, and -D, and Pla- cental Growth Factor (PlGF). VEGF binds to VEGFR-1 and 2, and triggers angiogenesis. PlGF is localized to the placenta and binds only to VEGFR-1. VEGF-B also binds only to VEGFR-1, and has function in coronary vascularization and growth. VEGF-C and VEGF-D activate VEGFR-2 and -3 but not VEGF-1. VEGF-C is involved in lymphangiogenesis. The function of VEGF-D is unknown [5]. For activation of the signaling pathway, VEGF binds to at least two transmembrane Flt-1 (VEGF receptor-1) and Flk-1/KDR (VEGF receptor-2). Both these are tyrosine kinase re- ceptors. This results in tyrosine phosphorylation, and activation of phosphatidylinositol 3-kinase (PI3K) and phospholipase Ca2+ (PLC-γ). PLC-γ forms two mole- cules, Diacylgylcerol (DAG) and Inositol (1, 4, 5)-trisphosphate (IP3). These two further activate PKC and release Ca2+. PI3K activates Akt. PKC, calcium and Akt activate endothelial Nitric Oxide Synthase (eNOS). It releases NO that is responsible for vasodilation and increased vascular permeability. The role for PLC-γ, PKC, calcium and NO in VEGF-induced hyper perme- ability has been confirmed in isolated coronary venules, and the involvement of PI3K/Akt and NO was demon- strated in human umbilical vein endothelial cell (HU- VEC) monolayer [6]. Further, it also triggers intracellu- lar signaling cascade that are able to recognize and dock at phosphorylated tyrosine residues of the activated re- ceptors. These interactions are mediated by Src, phos- phatidylinositol 3-kinase (PI3K), Shc, Grb2, and the phosphates SHP-1 and SHP-2 and other domains of the signaling proteins. VEGF receptor activation can induce activation of the MAPK cascade via Raf stimulation. It leads to gene ex- pression and cell proliferation. Activation of PI3K leads to PKB activation and cell survival; activation of PLC-γ leads to cell proliferation, vasopermeability and angio- genesis. VEGF regulates several endothelial cell func- tions, including proliferation, differentiation, permeabil- ity, vascular tone and the production of vasoactive mo- lecules [5]. H. sapiens VEGF pathway taken from KEGG database is given in Figure 1. The organization of this article is as follows. The next section describes the methodology of algorithm of Nayak and De in detail, and then introductory descrip- tion of Kernighan-Lin’s, Farhat’s, Greedy and Commu- nity finding algorithms has been given. After that, we provide results in which we analyzed output got through implementing different partitioning algorithms. Species’ evolution based comparison has also been done over the modules got through applying the algorithm of Nayak and De.  N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 933 Figure 1. VEGF signaling pathway of H. sapiens present in KEGG pathway database. 2. METHODOLOGY Many algorithms are proposed for the partition of a net- work. We compared the algorithm of Nayak and De [3] with community finding algorithm of Newman, Farhat’s, Greedy and Kernighan-Lin’s algorithms. Farhat’s, Greedy and Kernighan-Lin’s algorithms are graph partitioning algorithms and they need cut size and cut number for partitioning a network. Newman’s community finding algorithm has been applied to one category of bioche- mical networks (metabolic pathways). The chosen set provided a good mix of algorithms that belong to atleast three categories. They provide a uniform platform for the comparative study. But by no means, this set of chosen algorithms is an exhaustive one. Algorithm of Nayak and De works on a biochemical pathway which has gene products and chemical com- pounds. Here, the pathway is considered as a graph, gene products and chemical compounds are nodes. Edges show protein-protein interaction, protein-compound in- teraction or link to another map. The total number of relations with n as either a preceding or succeeding node is given by Tn = Rnp+Rns, where Rnp and Rns are out- degree and indegree, respectively, of a node n. The term Tn is the total degree of the node. According to algo- rithm, a node is detected which has maximum number of relations in the node pool E for a given network. This detected node is considered as a “starting node”. This is always considered as a “permanent member”. Permanent member is removed from the pool E. By defining the starting node, an initial module is created for relation r. Here, n may be a predecessor or a successor. After ini- tialization of the module, the total number of relations of every individual member is considered. Now, a node is checked for its permanency. If the number of relation lying inside the module is equal to the total number of relation associated with the node, then, it is permanent member. If a node in a module has more than c relations lying outside the module, it is ex- cluded from the module with decreasing the previous non permanent nodes’ total relation by one. This certain number of relations is known as complexity level c which can be set by the user. This process is continued until we have no new immediate neighboring node to be included or no node is left to be declared permanent. One important fact is that if a member X is present four times in a network, it will be considered four times like X1, X2, X3 and X4. After formation of a module, it searches for another starting point and repeat all above mentioned steps. This process will terminate when all the nodes of node pool E are exhausted. This algorithm had been applied for different c-values  N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 934 for VEGF KEGG pathway database http://www.ge- nome.jp/kegg/pathway.html#environmental. Then, ap- propriate c-value had been selected for comparative analysis of different species present in KEGG. KEGG has KGML layout which has XML files. These XML files’ coding was used to give input for the algorithm. Species of which KGML layout and XML coding were present in KEGG were considered for the comparative study of VEGF pathway. The species were H. sapiens (human), P. troglodytes (Chimpanzee), M. musculus (mouse), R. norvegicus (rat), C. familiaris (dog), B. tau- rus (cow), S. scrofa (pig). Kernighan-Lin’s algorithm is a heuristic algorithm applied for graph partitioning problems. It has important applications in the layout of digital circuits and compo- nents in VLSI. B. W. Kernighan and S. Lin has proposed an heuristic method in paper [7] to partition of the graph in such a way that it would be effective in finding opti- mal partitions. They deal with a combinatorial problem and partition of a graph G into subsets those would be no larger than a given maximum size. In this way, total cost of the edge cut is minimized. Greedy algorithm [8] works well when a problem has greedy choice property and optimal substructure. It makes local optimal choice at each stage and tries to find global optimum. Farhat in 1988 has presented an algo- rithm which is an efficient non-numerical algorithm for the automatic decomposition of an arbitrary finite ele- ment domain into a specified number of balanced sub- domains [9]. It is found to be effective for the imple- mentation of concurrent solution strategies on high per- formance architectures. Community structure detection is used for social net- works, internet and web data, biochemical networks or gene network. Here, it is assumed that the network of interest divides naturally into subgroups, and the re- searchers find those groups. So, we can say that the number and size of the subgroups are determined by the network itself and not by the researcher. It has been ap- plied to metabolic pathways. It divides a network in which good modules are not present. So, we can say that it is based on the properties of the network. Modularity score is directly dependent on the network architecture, adjacency matrix and eigenvalues of a symmetric matrix calculated from the adjacency matrix. Positive value of modularity means there is presence of modules in a net- work and a negative value shows that division is not possible [10]. 3. RESULTS AND COMPARATIVE ANALYSIS Species those were available in KEGG database had been considered for the comparative study. They are H. sapiens (human), P. troglodytes (Chimpanzee), M. mus- culus (mouse), R. norvegicus (rat), C. familiaris (dog), B. taurus (cow), S. scrofa (pig). The gradual development of this pathway in some species had been studied with respect to VEGF pathway of H. sapiens using the algo- rithm of Nayak and De. We applied all selected algo- rithms to VEGF signaling pathway of H. sapiens as ob- tained from KEGG database and compared their per- formances. 3.1. Modularization of VEGF Signaling Pathway of H. Sapiens using Different Algorithms We took different c-values and studied various modules obtained by the algorithm of Nayak and De. Then, by analyzing all the modules for different c-values, we chose a particular c-value for the comparative study of organisms. VEGF signaling pathway of H. sapiens has 40 nodes and 34 relations. Modules were created for c = 1, 2, 3, 4 and 5. For c = 1, we had 12 modules shown in Table 1. Number of modules was reduced, as complexity level was increased. For c = 2, node MAK1 merged with cen- tral node (PLCG1, PLC1) as shown in Table 2. Now, this node had function of cell survival and migration of vesicular endothelial cell [11]. For the same complexity value, another central node, MAPK14 merged into cen- tral node KDR. KDR has role in cell proliferation and growth function along with previous function of focal adhesion turnover and cell migration. It had paxillin and FAK as node members. Paxillin acts as a focal adhesion adaptor in focal adhesion dynamics and cell migration. Paxillin-FAK interaction is involved in Erk activation [12]. For c = 2, we had 6, and for c = 3, we had 4 mod- ules as shown in Ta b l e 3 . The node AKT3 was present as central node for c = 2 but it combined with PIK3R5 as we changed complexity to c = 3. It resulted in having multiple functions for the node AKT3. For c = 3, PIK3R5 functioned for permeability, vasodilatation as well as for cell survival and nitric oxide release [13]. For c = 2, there was a central node called CHP that had members (NFAT5), (PTGS2). But for c = 3, it merged with central node (PLCG1, PLC1). CHP, a central node for c = 2, had NFAT as a member, which is a family of transcription factors. It has at least four structurally sim- ilar members, e.g., NFATp (NFAT1), NFATc (NFAT2), NFAT3 and NFAT4. NFATc is present in endocardium, and is involved in morphogenesis of cardiac valves, septum and also in heart organization during develop- ment [14]. It regulates the properties of reserve cells. SMC uses NFAT signaling for adaptation. Calcineurin (CHP) is a Ca2+/CAM dependent phosphatase that regu- lates the process of dephosphorylation and nuclear im-  N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 935 port of NFAT. Another member PTGS2 is a target of NFAT and is involved in prostaglandin synthesis during angiogenesis. It is necessary for the migration of endo- thelial cells to allow the proper formation of endothelial tubes and postnatal angiogenesis in vivo [15]. For c = 2, (PRKCA) was a central node which had members (RAF1), (SPHK 2) and (HRAS, HRAS1), but for c = 3, the same central node had no members and as complexity was increased, it became a single node. For c = 4 and c = 5, the number of modules created were the same but this number was less as many central nodes merged. These modules were large enough to study and analysis. 3.2. Changes Found with the Increased Complexity Values We found that different c-values gave different number and complexity of modules. Number of modules was decreased as we increased the c-value. This resulted in over splitting. Many different modules were combined Table 1. Modularization for c = 1 for H. sapiens VEGF sig- naling pathway. S. No. Central Node Other Nodes 1 (KDR) (VEGFA,VEGF),(SHC2), (PTK2), (PXN) 2 (PLCG1, PLC1) (SH2D2A) 3 (AKT3) (NOS3), (CASP9), (BAD) 4 (PRKCA) - 5 (CHP) - 6 (PIK3R5) (RAC1),(SRC) 7 (RAF1) - 8 (MAPK1) (PLA2G2D), (MAP2K1) 9 (MAPK14) (CDC42) 10 (HRAS, HRAS1) (SPHK2) 11 (MAPKAPK3) (HSPB1) 12 (NFAT5) ( PTGS2) Table 2. Modularization for c = 2 for H. sapiens VEGF sig- naling pathway. S. No. Central Node Other Nodes 1 (KDR) (VEGFA, VEGF), (SH2D2A), (SHC2), (PTK2), (PXN), (CDC42), (SRC), (MAPK14), (MAPKAPK3), (HSPB1) 2 (PLCG1, PLC1) (PLA2G2D), (NOS3), (MAPK1), (MAP2K1) 3 (PRKCA) (RAF1), (SPHK2), (HRAS, HRAS1) 4 (PIK3R5) (RAC1) 5 (CHP) (NFAT5), (PTGS2) 6 (AKT3) (CASP9), (BAD) Table 3. Modularization for c = 3 for H. sapiens VEGF sig- naling pathway. S. No.Central Node Other Nodes 1 (KDR) (VEGFA, VEGF), (SH2D2A), (SHC2), (PTK2), (PXN), (CDC42), (SRC), (MAPK14), (MAP- KAPK3), (HSPB1) 2 (PLCG1, PLC1) (CHP), (PLA2G2D), (NOS3), (NFAT5), (MAPK1), (PTGS2), (MAP2K1), (RAF1), (HRAS,HRAS1), (SPHK2) 3 (PRKCA) - 4 (PIK3R5) (RAC1), (AKT3), (CASP9), (BAD) and increased in size with increase in c-value. With in- crease in c-value, new members were inserted in a cer- tain module or changed its earlier central node. As we took the case of VEGF signaling pathway of H. sapiens, we found just half number of modules with decrease in c-value by one, i.e., for c-value of two, we had six mod- ules whereas, the number was 12 for c = 1. But, for c = 4 and 5, size and number of modules, and the number of their members became static (in Ta b le s 4 and 5 respec- tively). The names of central nodes and their members for different c-values are given in Tables 1-5. 3.3. Fixing the Complexity Values Now, by assigning different c-values, we had different sets of modules. So, by analyzing all the modules thor- oughly, we understood that for c = 5, we should have Table 4. Modularization for c = 4 for H. sapiens VEGF sig- naling pathway. S. No.Central Node Other Nodes 1 (KDR) (VEGFA, VEGF), (SH2D2A), (SHC2), (PTK2), (PXN), (CDC42), (PIK3R5), (SRC),(MAPK14), (RAC1), (AKT3), (MAPKAPK3), (NOS3), (CASP9), (BAD), (HSPB1) 2 (PLCG1, PLC1) (CHP), (PRKCA), (PLA2G2D), (NFAT5), (RAF1), (SPHK2), (MAPK1), (PTGS2), (HRAS,HRAS1), (MAP2K1) Table 5. Modularization for c = 5 for H. sapiens VEGF sig- naling pathway. S. No.Central Node Other Nodes 1 (KDR) (VEGFA, VEGF), (SH2D2A),(SHC2), (PTK2), (PXN), (CDC42), (PIK3R5), (SRC), (MAPK14), (RAC1), (AKT3), (MAPKAPK3), (NOS3), (CASP9), (BAD), (HSPB1) 2 (PLCG1, PLC1) (CHP), (PRKCA), (PLA2G2D), (NFAT5), (RAF1), (SPHK2), (MAPK1), (PTGS2), (HRAS, HRAS1), (MAP2K1)  N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 936 stopped modularization process. Because for c = 4 and c = 5, we had the same set of modules. Even for c = 3, number of modules were less and they were merged, and thereby, it was unworthy to proceed. As per above anal- ysis, it was clear that for higher c-values, number of nodes and relations were greater than that we got for c = 1 as nodes started merging with other nodes. For c = 1, we had sufficient nodes, and relations for most of the nodes of this pathway. By analysis of all the modules for dif- ferent c-values, we assumed that increase in c-value gave almost similar output as nodes got merged. Module names, their number of nodes and relations for different c-values for H. sapiens VEGF signaling pathway are shown in Table 6. We were getting a simplified and bio- logically significant network for c = 1. We found c = 1 to be an optimal one, because for this c-value, network was modularized properly and not too much over splitting was occurred. This made us to fix c-value to 1 for VEGF signaling pathway of H. sapiens . 3.4. Comparison of Algorithm of Nayak and De with Newman’s Community Finding Algorithm For the algorithm of Nayak and De, we got modules where central nodes were defined but it was not the case with Newman’s algorithm. By applying Newman’s algo- rithm, we got four modules while it was 12 for the algo- rithm of Nayak and De for c = 1. Thus, we found less number of modules by Newman’s algorithm. Hence, the complexity of the modules obtained by Newman’s algo- rithm was quite high compared to those generated by the algorithm of Nayak and De. This may defeat the objec- tive of modularizing a signal transduction pathway. Nodes of a created module obtained by Newman’s algo- Table 6. Module names and their number of nodes and rela- tions for H. sapiens VEGF signaling pathway. `N’ represents number of nodes and `R’ stands for number of relations. S.No Module Name c = 1c = 2 c = 3 c = 4c = 5 NRNR N R N RNR 1 (KDR) 541110 11 10 17 161716 2 (PLCG1, PLC1) 2154 11 11 11 101110 3 (AKT3) 4332 1 0 1 010 4 (PRKCA) 1344 1 0 0 000 5 (CHP) 1232 1 0 0 000 6 (PIK3R5) 3221 5 4 0 000 7 (RAF1) 1310 0 0 0 000 8 (MAPK1)3210 0 0 0 000 9 (MAPK14)2110 0 0 0 000 10 (HRAS, HRAS1) 2110 0 0 0 000 11 (MAP- KAPK3) 2110 0 0 0 000 12(NFAT5) 2110 0 0 0 000 Figure 2. Modules of human VEGF signaling pathway created by the algorithm of Nayak and De for c-value of 1. 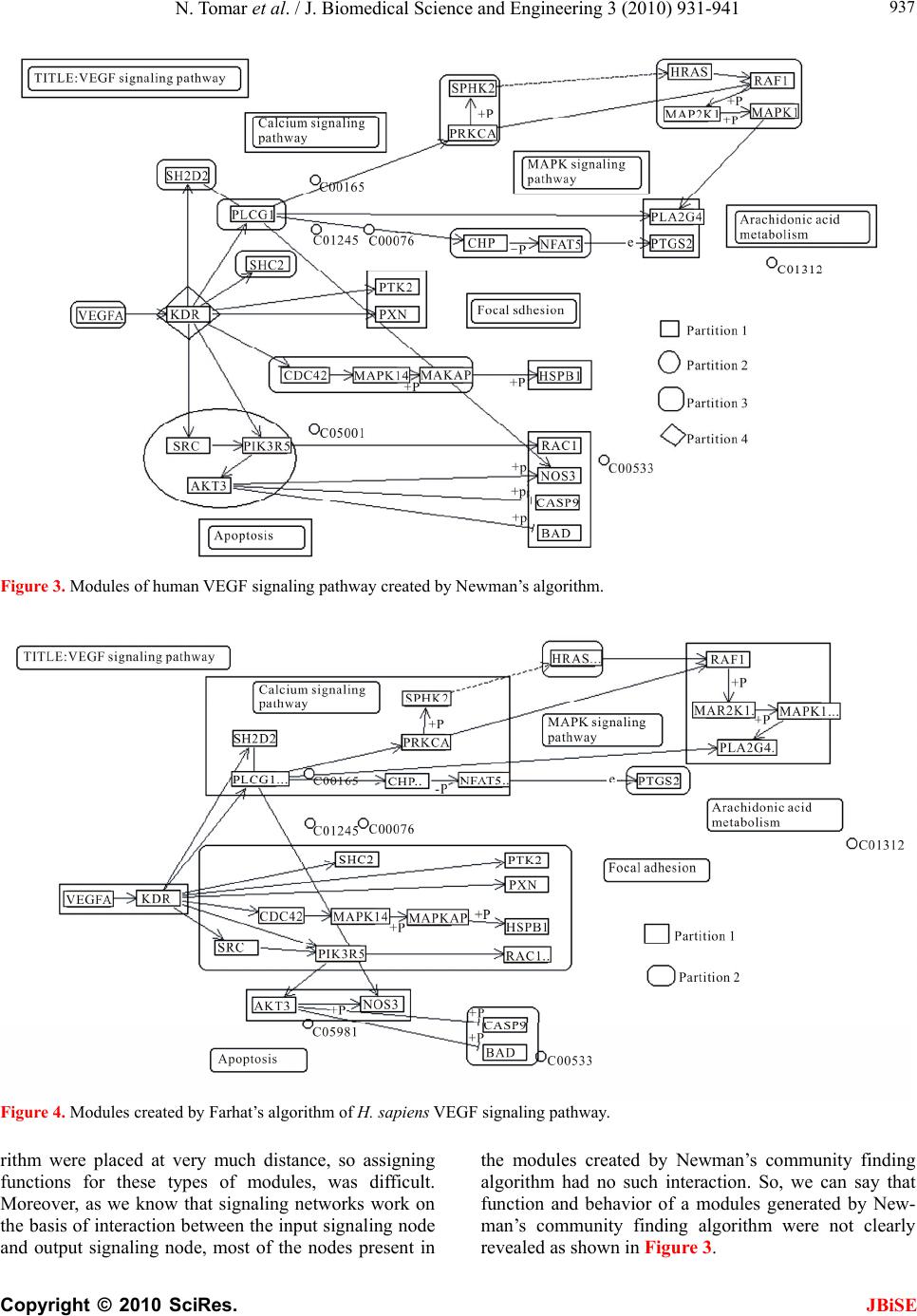 N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 937 Figure 3. Modules of human VEGF signaling pathway created by Newman’s algorithm. Figure 4. Modules created by Farhat’s algorithm of H. sapiens VEGF signaling pathway. rithm were placed at very much distance, so assigning functions for these types of modules, was difficult. Moreover, as we know that signaling networks work on the basis of interaction between the input signaling node and output signaling node, most of the nodes present in the modules created by Newman’s community finding algorithm had no such interaction. So, we can say that function and behavior of a modules generated by New- man’s community finding algorithm were not clearly revealed as shown in Figure 3. 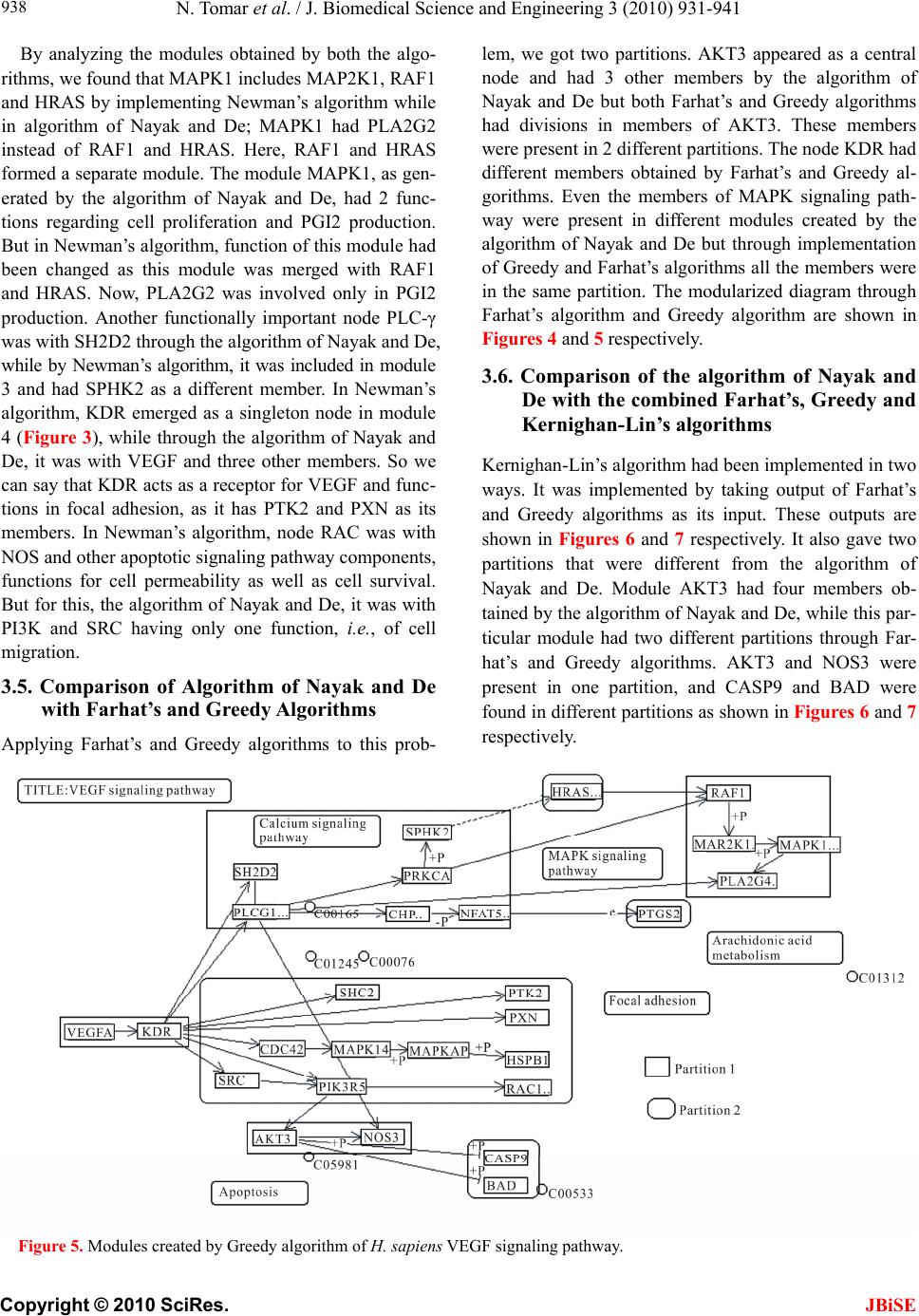 N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 938 By analyzing the modules obtained by both the algo- rithms, we found that MAPK1 includes MAP2K1, RAF1 and HRAS by implementing Newman’s algorithm while in algorithm of Nayak and De; MAPK1 had PLA2G2 instead of RAF1 and HRAS. Here, RAF1 and HRAS formed a separate module. The module MAPK1, as gen- erated by the algorithm of Nayak and De, had 2 func- tions regarding cell proliferation and PGI2 production. But in Newman’s algorithm, function of this module had been changed as this module was merged with RAF1 and HRAS. Now, PLA2G2 was involved only in PGI2 production. Another functionally important node PLC-γ was with SH2D2 through the algorithm of Nayak and De, while by Newman’s algorithm, it was included in module 3 and had SPHK2 as a different member. In Newman’s algorithm, KDR emerged as a singleton node in module 4 (Figure 3), while through the algorithm of Nayak and De, it was with VEGF and three other members. So we can say that KDR acts as a receptor for VEGF and func- tions in focal adhesion, as it has PTK2 and PXN as its members. In Newman’s algorithm, node RAC was with NOS and other apoptotic signaling pathway components, functions for cell permeability as well as cell survival. But for this, the algorithm of Nayak and De, it was with PI3K and SRC having only one function, i.e., of cell migration. 3.5. Comparison of Algorithm of Nayak and De with Farhat’s and Greedy Algorithms Applying Farhat’s and Greedy algorithms to this prob- lem, we got two partitions. AKT3 appeared as a central node and had 3 other members by the algorithm of Nayak and De but both Farhat’s and Greedy algorithms had divisions in members of AKT3. These members were present in 2 different partitions. The node KDR had different members obtained by Farhat’s and Greedy al- gorithms. Even the members of MAPK signaling path- way were present in different modules created by the algorithm of Nayak and De but through implementation of Greedy and Farhat’s algorithms all the members were in the same partition. The modularized diagram through Farhat’s algorithm and Greedy algorithm are shown in Figures 4 and 5 respectively. 3.6. Comparison of the algorithm of Nayak and De with the combined Farhat’s, Greedy and Kernighan-Lin’s algorithms Kernighan-Lin’s algorithm had been implemented in two ways. It was implemented by taking output of Farhat’s and Greedy algorithms as its input. These outputs are shown in Figures 6 and 7 respectively. It also gave two partitions that were different from the algorithm of Nayak and De. Module AKT3 had four members ob- tained by the algorithm of Nayak and De, while this par- ticular module had two different partitions through Far- hat’s and Greedy algorithms. AKT3 and NOS3 were present in one partition, and CASP9 and BAD were found in different partitions as shown in Figures 6 and 7 respectively. Figure 5. Modules created by Greedy algorithm of H. sapiens VEGF signaling pathway. 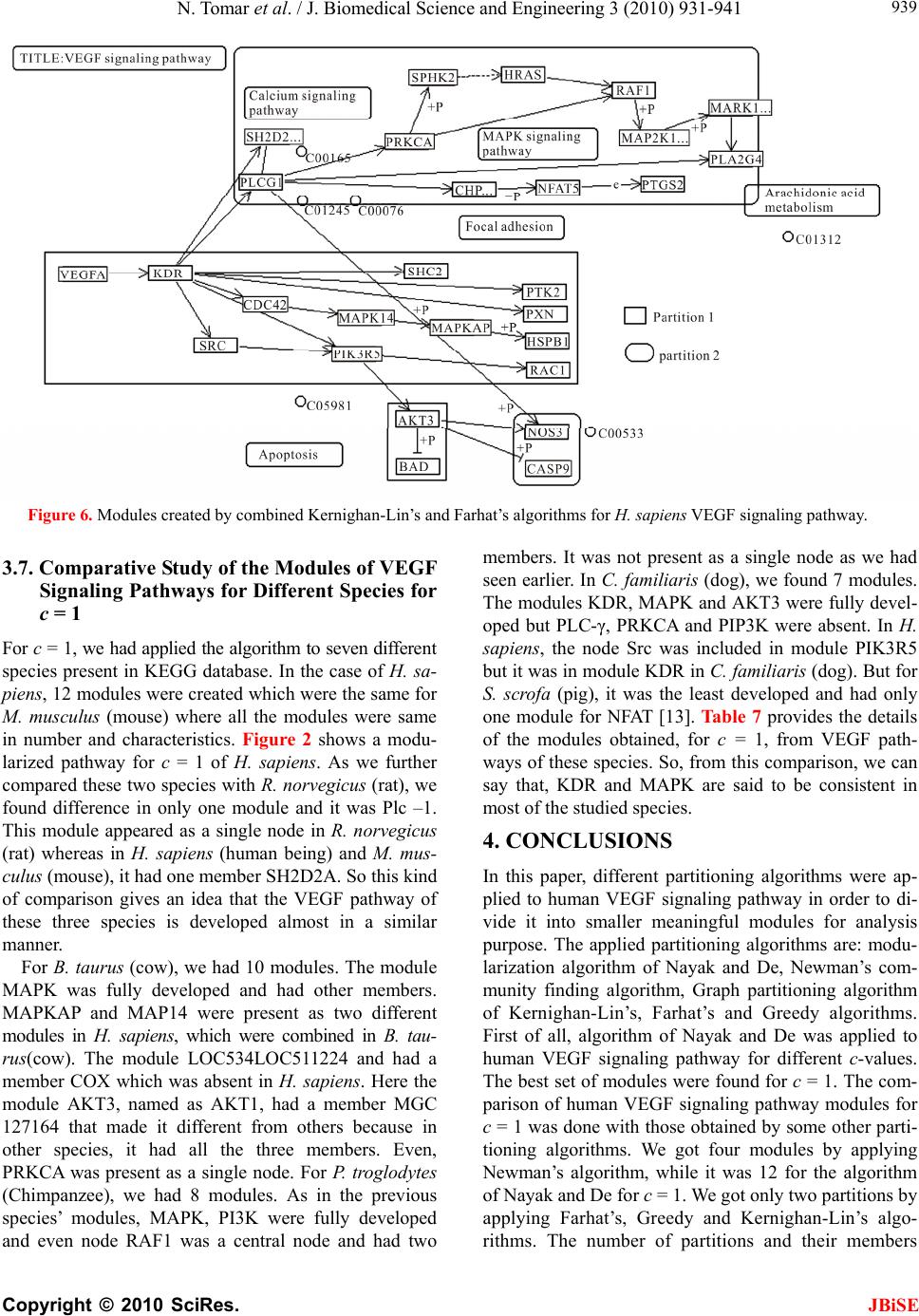 N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 939 Figure 6. Modules created by combined Kernighan-Lin’s and Farhat’s algorithms for H. sapiens VEGF signaling pathway. 3.7. Comparative Study of the Modules of VEGF Signaling Pathways for Different Species for c = 1 For c = 1, we had applied the algorithm to seven different species present in KEGG database. In the case of H. sa- piens, 12 modules were created which were the same for M. musculus (mouse) where all the modules were same in number and characteristics. Figure 2 shows a modu- larized pathway for c = 1 of H. sapiens. As we further compared these two species with R. norvegicus (rat), we found difference in only one module and it was Plc –1. This module appeared as a single node in R. norvegicus (rat) whereas in H. sapiens (human being) and M. mus- culus (mouse), it had one member SH2D2A. So this kind of comparison gives an idea that the VEGF pathway of these three species is developed almost in a similar manner. For B. taurus (cow), we had 10 modules. The module MAPK was fully developed and had other members. MAPKAP and MAP14 were present as two different modules in H. sapiens, which were combined in B. tau- rus(cow). The module LOC534LOC511224 and had a member COX which was absent in H. sapiens. Here the module AKT3, named as AKT1, had a member MGC 127164 that made it different from others because in other species, it had all the three members. Even, PRKCA was present as a single node. For P. troglodytes (Chimpanzee), we had 8 modules. As in the previous species’ modules, MAPK, PI3K were fully developed and even node RAF1 was a central node and had two members. It was not present as a single node as we had seen earlier. In C. familiaris (dog), we found 7 modules. The modules KDR, MAPK and AKT3 were fully devel- oped but PLC-γ, PRKCA and PIP3K were absent. In H. sapiens, the node Src was included in module PIK3R5 but it was in module KDR in C. familiaris (dog). But for S. scrofa (pig), it was the least developed and had only one module for NFAT [13]. Table 7 provides the details of the modules obtained, for c = 1, from VEGF path- ways of these species. So, from this comparison, we can say that, KDR and MAPK are said to be consistent in most of the studied species. 4. CONCLUSIONS In this paper, different partitioning algorithms were ap- plied to human VEGF signaling pathway in order to di- vide it into smaller meaningful modules for analysis purpose. The applied partitioning algorithms are: modu- larization algorithm of Nayak and De, Newman’s com- munity finding algorithm, Graph partitioning algorithm of Kernighan-Lin’s, Farhat’s and Greedy algorithms. First of all, algorithm of Nayak and De was applied to human VEGF signaling pathway for different c-values. The best set of modules were found for c = 1. The com- parison of human VEGF signaling pathway modules for c = 1 was done with those obtained by some other parti- tioning algorithms. We got four modules by applying Newman’s algorithm, while it was 12 for the algorithm of Nayak and De for c = 1. We got only two partitions by applying Farhat’s, Greedy and Kernighan-Lin’s algo- rithms. The number of partitions and their members 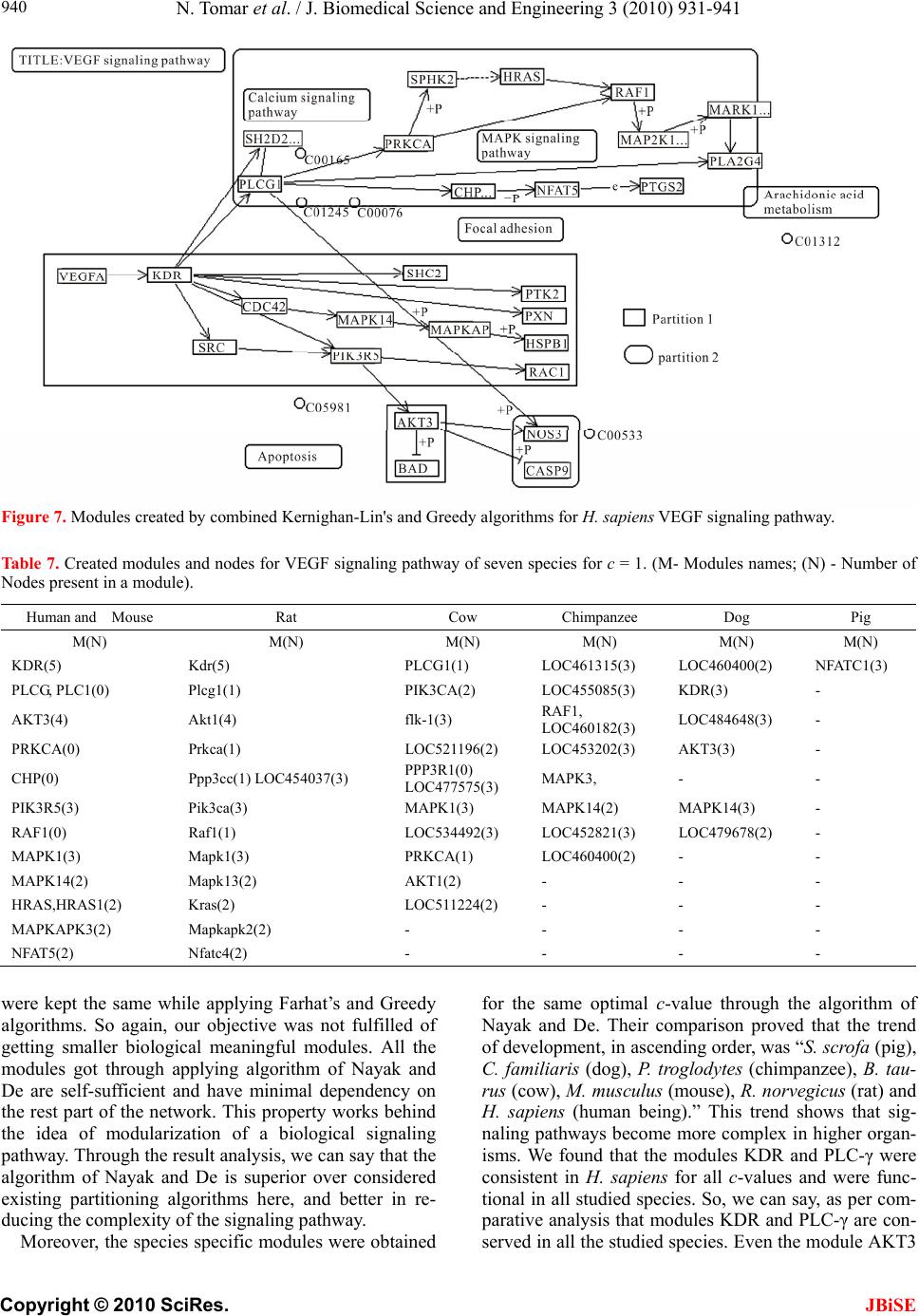 N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 940 Figure 7. Modules created by combined Kernighan-Lin's and Greedy algorithms for H. sapiens VEGF signaling pathway. Table 7. Created modules and nodes for VEGF signaling pathway of seven species for c = 1. (M- Modules names; (N) - Number of Nodes present in a module). Human and Mouse Rat Cow Chimpanzee Dog Pig M(N) M(N) M(N) M(N) M(N) M(N) KDR(5) Kdr(5) PLCG1(1) LOC461315(3) LOC460400(2) NFATC1(3) PLCG, PLC1(0) Plcg1(1) PIK3CA(2) LOC455085(3) KDR(3) - AKT3(4) Akt1(4) flk-1(3) RAF1, LOC460182(3) LOC484648(3) - PRKCA(0) Prkca(1) LOC521196(2) LOC453202(3) AKT3(3) - CHP(0) Ppp3cc(1) LOC454037(3) PPP3R1(0) LOC477575(3) MAPK3, - - PIK3R5(3) Pik3ca(3) MAPK1(3) MAPK14(2) MAPK14(3) - RAF1(0) Raf1(1) LOC534492(3) LOC452821(3) LOC479678(2) - MAPK1(3) Mapk1(3) PRKCA(1) LOC460400(2) - - MAPK14(2) Mapk13(2) AKT1(2) - - - HRAS,HRAS1(2) Kras(2) LOC511224(2) - - - MAPKAPK3(2) Mapkapk2(2) - - - - NFAT5(2) Nfatc4(2) - - - - were kept the same while applying Farhat’s and Greedy algorithms. So again, our objective was not fulfilled of getting smaller biological meaningful modules. All the modules got through applying algorithm of Nayak and De are self-sufficient and have minimal dependency on the rest part of the network. This property works behind the idea of modularization of a biological signaling pathway. Through the result analysis, we can say that the algorithm of Nayak and De is superior over considered existing partitioning algorithms here, and better in re- ducing the complexity of the signaling pathway. Moreover, the species specific modules were obtained for the same optimal c-value through the algorithm of Nayak and De. Their comparison proved that the trend of development, in ascending order, was “S. scrofa (pig), C. familiaris (dog), P. troglodytes (chimpanzee), B. tau- rus (cow), M. musculus (mouse), R. norvegicus (rat) and H. sapiens (human being).” This trend shows that sig- naling pathways become more complex in higher organ- isms. We found that the modules KDR and PLC-γ were consistent in H. sapiens for all c-values and were func- tional in all studied species. So, we can say, as per com- parative analysis that modules KDR and PLC-γ are con- served in all the studied species. Even the module AKT3  N. Tomar et al. / J. Biomedical Science and Engineering 3 (2010) 931-941 Copyright © 2010 SciRes. JBiSE 941 was found in all the studied species except in S. scrofa (pig) and B. Taurus (cow). This analysis makes one to study a conserved or con- sistent module rather than considering the complex sig- naling pathway as a whole. It is easier to determine un- derlying mechanism of normal development as well as in certain disorders or diseased conditions. In a certain dis- ease, only one molecule or a small group of molecules gets deregulated, so modularized study makes one to concentrate over a few modules containing responsible molecules only. This type of implementation also saves time and cost for experimental analysis. REFERENCES [1] Twyman, R.M. (2000) Advanced molecular biology. Garland/BIOS Scientific Publishers, UK. [2] David, L.N. and Cox, M.M. (2008) Lehninger principles of biochemistry. 5th Edition, W. H. Freeman & Company, New York. [3] Nayak, L. and De, R. (2007) An algorithm for modulari- zation of MAPK and calcium signaling pathways: Com- parative analysis among different species. Journal of Biomedical Informatics, 40(6), 726-749. [4] Robinson, C.J. and Stringer, S.E. (2001) The splice vari- ants of vascular endothelial growth factor (VEGF) and their receptors. Journal of Cell Science, 114(5), 853-865. [5] Kowanetz, M. and Ferrara, N. (2006) Vascular endothe- lial growth factor signaling pathways: Therapeutic per- spective. Clinical Cancer Research, 12(17), 5018-5022. [6] Breslin, J.W., Pappas, P.J., Cerveira, J.J., Hobson, R.W. and Durn, W.N. (2002) VEGF increases endothelial per- meability by separate signaling pathways involving ERK-1/2 and nitric oxide. American Journal of Physiol- ogic Heart Circ Physiology, 284(1), H92-H100. [7] Kernighan, B.W. and Lin, S. (1970) An efficient heuristic procedure for partitioning graphs. The Bell System Tech- nical Journal, 49(1 ) , 291-307. [8] Chartrand, G. and Oellermann, O.R. (1993) Applied and algorithmic graph theory. International Series in Pure and Appli ed Mathe mati cs. McGraw Hill, New York. [9] Farhat, C.G. (1988) A simple and efficient automatic fem domain decomposer. Computers & Structures, 28(5), 579-602. [10] Newman, M.E.J. (2006) Modularity and community structure in networks. PNAS, 103(23), 8577-8582. [11] McLaughlin, A.P. and Vries, G.W.D. (2001) Role of PLCg and Ca2+ in VEGF and FGF-induced choroidal endothelial cell proliferation. American Journal of Phy- siologic Cell Physiology, 281(5), C1448-C1456. [12] Hunag, C., Jacobson, K. and Schallerl, M.D. (2004) MAP Kinases and cell migration. Journal of Cell Science, 117(20), 4619-4628. [13] Blum, S., Issbrucker, K., Willuweit, A., Hehlgans, S., Lucerna, M., Mechtcheriakova, D., Walsh, K.V.D., Ahe, D., Hofer, E. and Clauss, M. (2001) An inhibitory role of the phosphatidylinositol 3-kinase-signaling pathway in vascular endothelial growth factor-induced tissue factor expression. The Journal of Biochemistry, 276(36), 33428-33434. [14] Horsley, V. and Pavlath, G.K. (2002) NFAT: Ubiquitous regulator of cell differentiation and adaptation. The Journal of Cell Biology, 156(5), 771- 774. [15] Armesilla, A.L., Lorenzo, E., Arco, P.G.D., Martinez S., Alfranca, A. and Redondo, J.M. (1999) Vascular endo- thelial growth factor activates nuclear factor of activated T cells in human endothelial cells: A role for tissue factor gene expression. Molecular and Cellular Biology, 19(3), 2032-2043. |

