Circuits and Systems, 2010, 1, 71-75
doi:10.4236/cs.2010.12012 Published Online October 2010 (http://www.SciRP.org/journal/cs)
New Communication Bands Generated by Using a Soliton
Pulse within a Resonator System
P. P. Yupapin1, M. A. Jalil2,3, I. S. Amiri3, I. Naim3, J. Ali3
1Advanced Research Center for Photonics, Faculty of Science King Mongkut’s Institute of Technology Ladkrabang,
Bangkok, Thailand
2Ibnu Sina Institute for Fundamental Science Studies, Universiti Teknologi Malaysia,
Johor Bahru, Malaysia
3Institute of Advanced Photonics Science, Nanotechnology Research Alliance, Universiti Teknologi Malaysia,
Johor Bahru, Malaysia
Received August 5, 2010; revised September 8, 2010; accepted September 15, 2010
Abstract
We propose a novel system of a broadband source generation using a common soliton pulse (i.e. with center
wavelength at 1.55 m) propagating within a nonlinear microring and nanoring resonators system. A system
consists of a micro ring resonator system incorporating an add/drop filter, whereas the large bandwidth sig-
nals can be generated, stored and regenerated within the system. By using the appropriate parameters relating
to the practical device such as micro ring radii, coupling coefficients, linear and nonlinear refractive index,
we found that the obtained multi soliton pulses have shown the potential of application for dense wavelength
division application, whereas the different center wavelengths of the soliton bands can be obtained via the
add/drop filter, which can be used to increase the channel capacity in communication network.
Keywords: Ring Resonator, Photonic Device, Optical Waveguide
1. Introduction
The demand of communication channels and network
capacity has been increased significantly for three dec-
ades, however, up to now, the large user demand remains.
Therefore, the searching of new techniques is needed,
which is focused on the communication channel and
network capacity. Recently, Pornsuwancharoen et al. [1]
have reported the very interesting result of the technique
that can be used to fulfill the large demand. They have
shown that the signal bandwidth can be stretched and
compressed by using the nonlinear micro ring system [2-
4]. By using such a scheme, the increasing in communi-
cation channels using soliton communication is plausible.
Furthermore, the long distance communication link is
also available. However, several problems are required to
solve and address, for instance, the problem of soliton-
soliton interaction and collision [5], and the waveguide
structure that the broadband soliton can be confined [6].
In this letter, we propose the technique that can be used
to generate the new soliton communication bands (wave-
length bands), whereas the common soliton pulse, i.e., a
soliton source is at the center wavelength of 1.55 m. The
soliton bands at the required center wavelengths can be
stored [7] and filtered by using the add/drop filter [5]. In
application, the use of super dense wavelength multi-
plexing, with the long distance link is available. Fur-
thermore, the personnel channel and network may be
plausible due to the very available bandwidths. However,
the problem of the soliton interaction and collision is
required to solve, which can be avoided by the specific
free spectrum range design [5].
2. Theoretical Background
To maintain the soliton pulse propagating within the ring
resonator, the suitable coupling power into the device is
required, whereas the interference signal is a minor effect
compared to the loss associated to the direct passing
through. A soliton pulse, which is introduced into the
multi-stage micro ring resonators as shown in Figure 1,
the input optical field (Ein) of the soliton input is given
by an Equation (1) [7].

0
0
secexp 2
in
D
Tz
EtA hit
TL


 

 
 




(1)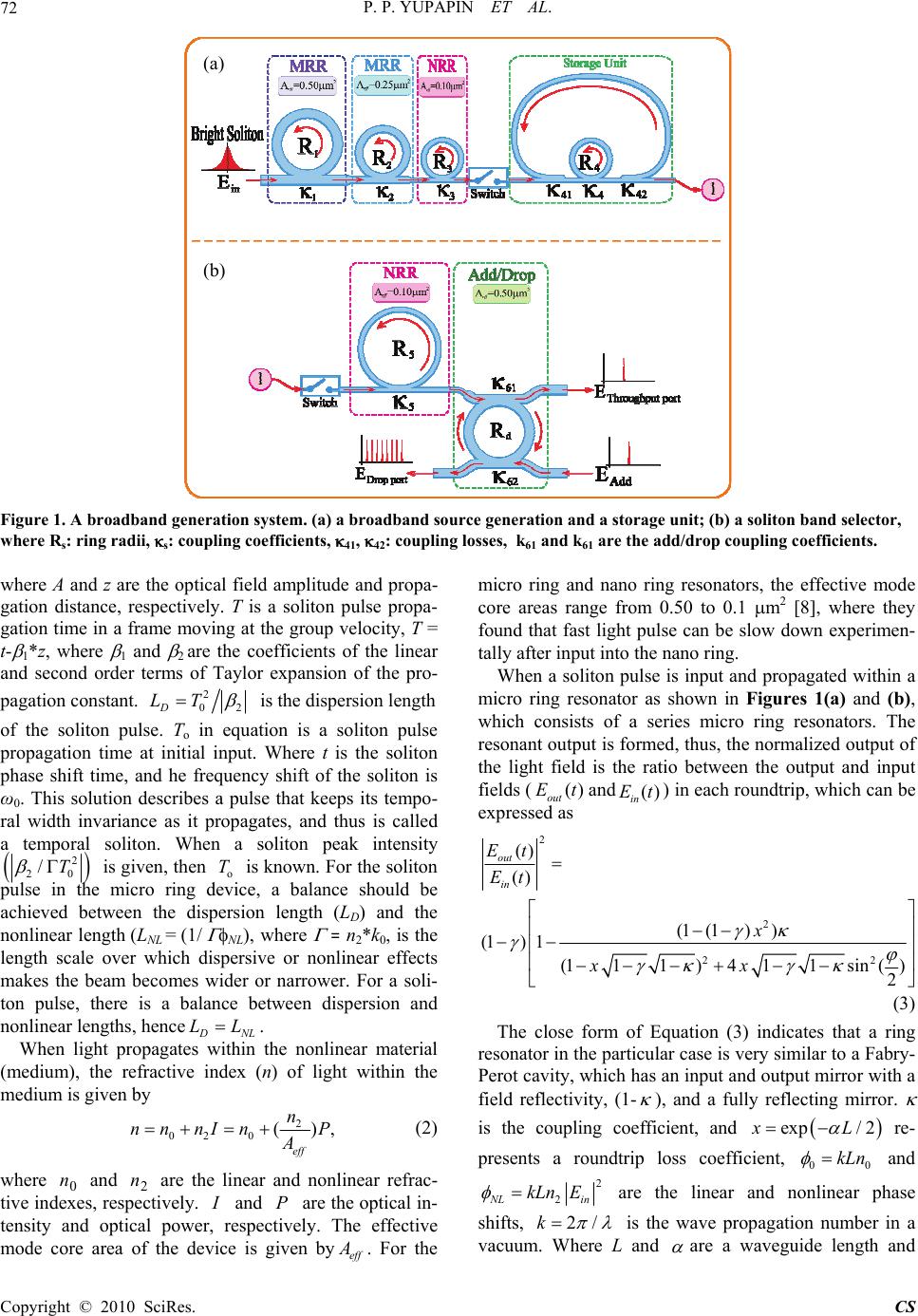

P. P. YUPAPIN ET AL. 72
Figure 1. A broadband generation system. (a) a broadband source generation and a storage unit; (b) a soliton band selector,
where Rs: ring radii, s: coupling coefficients, 41, 42: coupling losses, k61 and k61 are the add/drop coupling coefficients.
where A and z are the optical field amplitude and propa-
gation distance, respectively. T is a soliton pulse propa-
gation time in a frame moving at the group velocity, T =
t-

1*z, where

1 and

2 are the coefficients of the linear
and second order terms of Taylor expansion of the pro-
pagation constant. 2
02D
LT

 is the dispersion length
of the soliton pulse. To in equation is a soliton pulse
propagation time at initial input. Where t is the soliton
phase shift time, and he frequency shift of the soliton is
ω0. This solution describes a pulse that keeps its tempo-
ral width invariance as it propagates, and thus is called
a temporal soliton. When a soliton peak intensity


2
20
/T   is given, then o T is known. For the soliton
pulse in the micro ring device, a balance should be
achieved between the dispersion length (LD) and the
nonlinear length (LNL = (1/  NL), where  =n2*k0, is the
length scale over which dispersive or nonlinear effects
makes the beam becomes wider or narrower. For a soli-
ton pulse, there is a balance between dispersion and
nonlinear lengths, hence
D
NL
LL.
When light propagates within the nonlinear material
(medium), the refractive index (n) of light within the
medium is given by
2
02 0
(),
eff
n
nn nInP
A
  (2)
where 
n and  n are the linear and nonlinear refrac-
tive indexes, respectively.
I
and P are the optical in-
tensity and optical power, respectively. The effective
mode core area of the device is given byeff
A
. For the
micro ring and nano ring resonators, the effective mode
core areas range from 0.50 to 0.1 m2 [8], where they
found that fast light pulse can be slow down experimen-
tally after input into the nano ring.
When a soliton pulse is input and propagated within a
micro ring resonator as shown in Figures 1(a) and (b),
which consists of a series micro ring resonators. The
resonant output is formed, thus, the normalized output of
the light field is the ratio between the output and input
fields (()
out
Etand )(tEin ) in each roundtrip, which can be
expressed as
2
2
22
()
()
(1 (1))
(1) 1
(111)411sin()
2
out
in
Et
Et
x
xx



 











 


(3)
The close form of Equation (3) indicates that a ring
resonator in the particular case is very similar to a Fabry-
Perot cavity, which has an input and output mirror with a
field reflectivity, (1-

), and a fully reflecting mirror. 
is the coupling coefficient, and

exp/2xL   re-
presents a roundtrip loss coefficient, 00 kLn

 and
2
2
N
Lin
kLn E   are the linear and nonlinear phase
shifts, 2/k



is the wave propagation number in a
vacuum. Where L and

are a waveguide length and
(
a
)
(
b
)

P. P. YUPAPIN ET AL. 73
linear absorption coefficient, respectively. In this work,
the iterative method is introduced to obtain the results as
shown in Equation (3), similarly, when the output field is
connected and input into the other ring resonators.
After the signals are multiplexed with the generated
chaotic noise, then the chaotic cancellation is required by
the individual user. To retrieve the signals from the cha-
otic noise, we propose to use the add/drop device with
the appropriate parameters. This is given in details as
followings. The optical circuits of ring-resonator add/
drop filters for the throughput and drop port can be given
by Equations (4) and (5), respectively [9].





2
2
112 2
2
121 2
1211cos 1
11 1211cos
t
in
L
L
n
L
L
n
E
E
ekL e
eekL




 
 




 

(4)
 
2
2
12
2
121 2
11 1211cos
d
in
L
L
L
n
E
E
e
eekL









 
(5)
where Et and Ed represents the optical fields of the
throughput and drop ports respectively. eff kn

 is the
propagation constant, eff n is the effective refractive
index of the waveguide and the circumference of the ring
is 2LR

, here R is the radius of the ring. In the
following, new parameters will be used for simplification:
L

  is the phase constant. The chaotic noise cancel-
lation can be managed by using the specific parameters
of the add/drop device, which the required signals can be
retrieved by the specific users. 
1 and

1 are coupling
coefficient of add/drop filters, 2/
n
k

  is the wave
propagation number for in a vacuum, and where the
waveguide (ring resonator) loss is  = 0.5 dBmm-1. The
fractional coupler intensity loss is  = 0.1. In the case of
add/drop device, the nonlinear refractive index is ne-
glected.
3. Results and Discussion
In operation, the large bandwidth signal within the micro
ring device can be generated by using a common soliton
pulse input into the nonlinear micro ring resonator. This
means that the broad spectrum of light can be generated
after the soliton pulse is input into the ring resonator
system. The schematic diagram of the proposed system is
as shown in Figure 1. A soliton pulse with 50 ns pulse
width, peak power at 2 W is input into the system. The
suitable ring parameters are used, for instance, ring radii
R1 = 15.0 μm, R2 = 10.0 μm, R3 = Rs = 5.0 μm and R5 = Rd
= 20.0 μm. In order to make the system associate with
the practical device [8], the selected parameters of the
system are fixed to 
0 = 1.55 m, n0 = 3.34 (In-
GaAsP/InP), Aeff = 0.50, 0.25 m2 and 0.10 m2 for a
micro ring and nano ring resonator, respectively,  = 0.5
dBmm-1,  = 0.1. The coupling coefficient (kappa,
 ) of
the micro ring resonator ranged from 0.1 to 0.95. The
nonlinear refractive index is n2 = 2.2 × 10-13 m
2/W. In
this case, the wave guided loss used is 0.5 dBmm-1. The
input soliton pulse is chopped (sliced) into the smaller
signals spreading over the spectrum (i.e., broad wave-
length) as shown in Figures 2(b) and 2(g), which is
shown that the large bandwidth signal is generated
within the first ring device. The biggest output amplifi-
cation is obtained within the nano-waveguides (rings R3
and R4) as shown in Figures 2(d) and 2(e), whereas the
maximum power of 10 W is obtained at the center wave-
length of 1.5 m. The coupling coefficients are given as
shown in the figures. The coupling loss is included due
to the different core effective areas between micro and
nano ring devices, which is given by 0.1 dB.
We have shown that a large bandwidth of the optical
signals with the specific wavelength can be generated
within the micro ring resonator system as shown in Fig-
ure 1. The amplified signals with broad spectrum can be
generated, stored and regenerated within the nano-
waveguide. The maximum stored power of 10 W is ob-
tained as shown in Figures 2(d) and 2(e), where the av-
erage regenerated optical output power of 4 W is achi-
eved via and a drop port of an add/drop filter as shown in
Figures 2(h)-2(k), which is a broad spectra of light
cover the large bandwidth as shown in Figure 2(g).
However, to make the system being realistic, the wave-
guide and connection losses are required to address in the
practical device, which may be affected the signal ampli-
fication. The storage light pulse within a storage ring (Rs
or R4) is achieved, which has also been reported by Ref.
[7]. In applications, the increasing in communication
channel and network capacity can be formed by using the
different soliton bands (center wavelength) as shown in
Figure 2, where 2(h) 0.51 m, 2(i) 0.98 m, 2(j) 1.48
m and 2(k) 2.46 m are the generated center wave-
lengths of the soliton bands. The selected wavelength
center can be performed by using the designed add/drop
filter, where the required spectral width (Full Width at
Half Maximum, FWHM) and free spectrum range (FSR)
are obtained, the channel spacing and bandwidth are
represented by FSR and FWHM, respectively, for in

P. P. YUPAPIN ET AL. 74
Figure 2. A soliton band with center wavelength at 1.5 m, where (a) input soliton; (b) ring R1; (c) ring R2; (d) ring R3; (e)
storage ring (Rs); (f) ring R5; (g) drop port output signals. The output of different soliton bands (center wavelength) are as
shown, where (h) 0.51 m; (i) 0.98 m; (j) 1.99 m; (k) 2.48 m.
stance, the FSR and FWHM of 2.3 nm and 100 pm are
obtained as shown in Figure 2(i).
4. Conclusions
In conclusion, apart from communication application, the
idea of personnel wavelength (network) being realistic
for the large demand user due to un-limit wavelength
discrepancy, whereas the specific soliton band can be
generated using the proposed system. The potential of
soliton bands such as visible soliton (color soliton), UV-
soliton, X-ray soliton and infrared soliton can be gener-
ated and used for the applications such as multi color
holography, medical tools, security imaging and trans-
parent holography and detection, respectively.
5. Acknowledgements
One of the authors (Muhammad Arif Jalil) would like to
acknowledge Nanoscale Science and Engineering Re-
search Alliance (N’SERA), King Mongkut’s Institute of
Technology Ladkrabang, Bangkok (KMITL), Thailand
for research facility, and he would also like to extend his
appreciation to UTM for funding this research work.
6. References
[1] N. Pornsuwancharoen, U. Dunmeekaew and P. P. Yu-
papin, “Multi-Soliton Generation Using a Micro Ring
Resonator System for DWDM Based Soliton Communi-
cation,” Microwave and Optical Technology Letters, Vol.

P. P. YUPAPIN ET AL. 75
51, No. 5, 2009, pp. 1374-1377.
[2] P. P. Yupapin, N. Pornsuwanchroen and S. Chaiyasoon-
thorn, “Attosecond Pulse Generation Using Nonlinear
Micro Ring Resonators,” Microwave and Optical Tech-
nology Letters, Vol. 50, No. 12, 2008, pp. 3108-3011.
[3] N. Pornsuwancharoen and P. P. Yupapin, “Generalized
Fast, Slow, Stop, and Store Light Optically within a Nano
Ring Resonator,” Microwave and Optical Technology Let-
ters, Vol. 51, No. 4, 2009, pp. 899-902.
[4] N. Pornsuwancharoen, S. Chaiyasoonthorn and P. P. Yu-
papin, “Fast and Slow Lights Generation Using Chaotic
Signals in the Nonlinear Micro Ring Resonators for
Communication Security,” Optical Engineering, Vol. 48,
No. 1, 2009, p. 50005-1-5.
[5] P. P. Yupapin, P. Saeung and C. Li, “Characteristics of
Complementary Ring-Resonator Add/Drop Filters Mod-
eling by Using Graphical Approach,” Optics Communica-
tions, Vol. 272, No. 1, 2007, pp. 81-86.
[6] M. Fujii, J. Leuthold and W. Freude, “Dispersion Relation
and Loss of Subwavelength Confined Mode of Metal-Di-
electri-Gap Optical Waveguides,” IEEE Photonics Tech-
nology Letters, Vol. 21, No. 6, 2009, pp. 362-364.
[7] P. P. Yupapin and N. Pornsuwancharoen, “Proposed
Nonlinear Micro Ring Resonator Arrangement for Stop-
ping and Storing Light,” IEEE Photonics Technology Let-
ters, Vol. 21, No. 6, 2009, pp. 404-406.
[8] Y. Su, F. Liu and Q. Li, “System Performance of Slow-
light Buffering and Storage in Silicon Nano-Waveguide,”
Proceedings of SPIE, Vol. 6783, 2007, p. 67832.
[9] P. P. Yupapin and W. Suwancharoen, “Chaotic Signal
Generation and Cancellation Using a Micro Ring Reso-
nator Incorporating an Optical Add/Drop Multiplexer,”
Optics Communications, Vol. 280, No. 2, 2007, pp. 343-
350.