 Journal of Signal and Information Processing, 2013, 4, 51-56 http://dx.doi.org/10.4236/jsip.2013.41006 Published Online February 2013 (http://www.scirp.org/journal/jsip) 51 Short-Term Sinusoidal Modeling of an Oriental Music Signal by Using CQT Transform Lhoucine Bahatti1, Mimoun Zazoui1, Omar Bouattane2, Ahmed Rebbani1 1Faculté des Sciences et Techniques, Mohammedia, Morocco; 2Ecole Normale Supérieure d’Enseignement Technique, Université Hassan II Mohammedia, Mohammedia, Morocco. Email: lbahatti@gmail.com Received October 16th, 2012; revised November 28th, 2012; accepted December 10th, 2012 ABSTRACT In this paper, we propose a method for characterizing a musical signal by extracting a set of harmonic descriptors re- flecting the maximum information contained in this signal. We focus our study on a signal of oriental music character- ized by its richness in tone that can be extended to 1/4 tone, taking into account the frequency and time characteristics of this type of music. To do so, the original signal is slotted and analyzed on a window of short duration. This signal is viewed as the result of a combined modulation of amplitude and frequency. For this result, we apply short-term the non-stationary sinusoidal modeling technique. In each segment, the signal is represented by a set of sinusoids charac- terized by their intrinsic parameters: amplitudes, frequencies and phases. The modeling approach adopted is closely related to the slot window; therefore great importance is devoted to the study and the choice of the kind of the window and its width. It must be of variable length in order to get better results in the practical implementation of our method. For this purpose, evaluation tests were carried out by synthesizing the signal from the estimated parameters. Interesting results have been identified concerning the comparison of the synthesized signal with the original signal. Keywords: Oriental Music Signal; Short Time Fourier Transform; Constant Q Transform; Modulation; Sinusoidal Modeling; Weighting Window; 1/4 Tone 1. Introduction In the field of the music signal transcription, the extrac- tion of the parameters remains of paramount importance. This transcription requires a model which best reflects the signal to be studied. In this regard, the sinusoidal analysis, based on the decomposition in Fourier series, is used from the outset, for the processing of sounds and their generation. The sinusoidal model is very suitable for modeling harmonic signals and their superposition where their changes in frequency and amplitude are low. The sinusoidal modeling is also the best way able to analyze and synthesize audio sounds. It is therefore an invertible representation of the sound, if all parameters are kept. However, due to variations of the characteristics of sound signals according to time, it is irrelevant to con- sider that the parameters of the model components are constant throughout the duration of the signal. Also to be valid even for highly variable signals, transient signals, and non-stationary signals, the sinusoidal modeling has been perfected, leading to the noisy sinusoids model [1]. The latter model is both simplest and most general to represent a musical signal where the sinusoids are char- acterized by a set of parameters to be estimated. For this, the method QIFFT (quadratic interpolation FFT) [2], used mainly due to its simplicity and accuracy, should be studied and improved, especially for an oriental music signal whose tonality can be up to 1/4 tone. In our case, we will exploit the sinusoidal model to extract a set of parameters of a signal from an Arabic lute. The extracted parameters will allow us to synthesize an- other signal that will be compared to the original one. The first section of this manuscript will address the ba- sics of sinusoidal modeling, short term and long term aspects modeling. The analysis of the short term estima- tion and the signal parameters modeling will be dis- cussed in third section. Section 4 presents the commented experimental results for a real music signal. The final section gives some concluding, remarks and future per- spectives. 2. Sinusoidal Modeling The sinusoidal modeling is, initially, an application of Fourier’s theorem that shows that any periodic signal can be represented by a sum of sinusoids with different fre- quencies and amplitudes. In the real context, the audio Copyright © 2013 SciRes. JSIP  Short-Term Sinusoidal Modeling of an Oriental Music Signal by Using CQT Transform 52 signals (music in particular) are characterized by vibra- tions. Also this vibrating signals aspect can be effectively modeled by a sum of generalized sinusoids whose am- plitudes and phases may change over the time. (Equation (1) or Equation (2)) 1 exp P i i i tAt j t (1) 1 cos P ii i tAt t (2) where: t P : the signal to be analyzed, : number of partials, i t t : instantaneous amplitude of partial i, and i However, in most cases where the signals are highly variable, or transitional, and also in order to take into account the non-deterministic part [1], the model of Equation (1) is insufficient, then the signal is a superpo- sition of a quasi harmonic part followed by a noise, in according to the following equation: : instantaneous phase of partial i. 1 exp P ii i tAtjtn t (3) where represents the non-deterministic residual of the signal nt t. Certainly, the forms assigned to the partial amplitudes i t and the phases have a very important role regarding the performance of sinusoidal modeling. This model is then characterized by a series of parameters to be estimated, and whose number depends on the expres- sions of it i t and . it 2.1. Short-Term Modeling Short-term modeling is especially designed to obtain a stationary modelIndeed to valid this model, the signal to be analyzed must be slotted into small fragments where the signal parameter variations will be considered small. Then, in each segment, of duration T, starting at , the signal can be represented by a plurality of sinusoids of the form: tnT 1 Ni n i St St n i n (4) cos 2π for ii i nn n St aftnT nTtnT T (5) Non stationary extensions of the signal can be envis- aged to follow faithfully the signal variations along the viewing window that can last up to 32 ms [3]. 2.2. Long-Term Modeling For quasi-periodic signal sounds, correlations between the parameters of the sinusoids issued from successive frames can be exploited. Then, it is useful, and required, to consider a long-term sinusoidal model where the am- plitudes and frequencies of the sinusoids change slowly and continuously over time, in order to keep and insure continuity of phase [1]. 1 cos P kk i tAt t (6) 0 02πd t kk k tF uu (7) The parameters Fk, Ak and Φk the frequencies, ampli- tudes and phases of instantaneous partial Pk respectively, are estimated instantly using the short term model. 3. Short Term Analysis The short-term sinusoidal analysis consists of two tasks: The first, consists of detecting the presence of a sinusoi- dal components in the analyzed signal (peaks in the Fou- rier spectrum). The second task is used to estimate the signal parameters (amplitude, frequency and phase). This analysis process can be represented by the fol- lowing algorithm: For n = 1 to number of frames do Begin -Isolate the frame of index n -Select the spectral peaks corresponding to the partial of signal -Model the signal concerning each partial -Estimate the model parameters end Each step of this algorithm is described below. 3.1. Frame Isolation The frame isolation, known as the windows weighting, is considered to isolate a frame of index n and its width T. To do so we take: n St n St stwtnT (8) wt nT is a weighting window such that: 1 0when an 2 1 2 wt nTtnT tn T d (9) It is of symmetrical shape so that its phase spectrum is zero. In addition to extracting a signal frame, the window weighting should allow best estimates of the model pa- rameters assigned to that frame. The window depends strongly on the signal to be analyzed according to its temporal features and especially frequency characteris- tics. It is completely defined by its type (expression) and length (size). Copyright © 2013 SciRes. JSIP  Short-Term Sinusoidal Modeling of an Oriental Music Signal by Using CQT Transform 53 3.2. Window Sizing A longer window generally increases the bias, while a short window is useless in the steady state of an audio signal. Therefore the same kind of window; with the same length along the entire signal is study case to be avoided. Several solutions are possible, for example: A single window kind of variable frequency Window of the same type with variable length, or Windows belonging to different classes of signals. In [4], to properly estimate the instantaneous fre- quency of a signal, the solution used is to select a win- dow wi from a finite set W: 12i www wm according to a criterion named Maximum Correlation Criterion (MCC). In our approach, we choose one kind of window hav- ing variable length by using on the CQT Transform (constant Q transform), in which the temporal resolution increases with frequency. So, a large analysis window is used at low frequencies and when frequency increases, the window size will decrease. The basic tool of the sinusoidal modeling is the short term Fourier transform (STFT) as follow: 2π ,e jf w Stfs wt d (10) In the case of initial STFT, w is the window of fixed length: e N L , (N: fixed size and Fe sample rate), while in the opposite case, the length of the window CQT be- comes variable. In the case of a time signal n sampled at the fre- quency Fe, The constant Q transform (CQT) can be di- rectly determined by: 1 2π 0 ,e k k N mf w m Sk wmksm (11) where w Sk k is the kth CQT component, and the analy- sis window , of the size Nk, depending on fre- quency (“bin” k). The frequencies corresponding to the CQT bins are geometrically spaced, related to the Orien- tal musical scale: So if we denote fmin the starting fre- quency analysis, the other frequencies are derived from the relation: ,wmk k min Af With: A: ratio for the resolution 1/4 tone: 37 1.027 36 A [5] For the CQT form, the ratio k k Q is constant [6], where, 1 kk k ff . In the Oriental range we have: min 1 min min 137. 1 k kk Af QA Af Af And the size of the analysis window is determined by: . e k k NQ 3.3. Window Kind Determination To isolate a frame k t of index k and width Tk, we use the following expression: kk tstwtkT . So in the frequency domain, we have: . k This convolution must cause the minimum possible strain on SfSfWf Sf . To do so, the window w(t) must largely decrease too its lobe sides and increase the selectivity of the main lobe. The analysis window is also conditioned by the adopted model QIIFT [2] (the phase is of a quadratic form) to the frame signal as: 1 cos P kk k tAt t (12) where: 2 2 k kkk tt t . (13) Arbitrarily, the rectangular window is adopted, but, for more accuracy, the Gaussian window is considered as a reference in the literature, since it allows accurate esti- mation of model parameters QIFFT [2]. However, the Hann window, in addition to be of C∞ (infinitely con- tinuous and differentiable), remains a good candidate for estimating sinusoidal parameters [7]. (See Figure 1 and Table 1). Thus it is adopted in our approach, its basic expression is: 0.50.5cos 2πPour 2 0elsewh h tT t wt T 2 ere T (14) 3.4. Selection of Spectral Peaks and Modeling After isolating the frame n t, we proceed by deter- mining its amplitude spectrum. The selection of the spectral peak, and filtering the frame n t around this peak, aims to reduce the signal to a single partial (exam- ple k = 1 for the fundamental signal). For music signal of an Arabic lute, the fundamental frequencies of the dif- ferent basic notes, subject of study and analysis, in the first octave, are summarized in Table 2. The filter used is a pass band having a variable cutoff frequency to track the fundamental frequency of the de- tected note. Under these conditions, each partial can be represented by several models [3]. The chosen model is of the form: 2 0 00 00 log exp 2 tat t ttjt t (15) Copyright © 2013 SciRes. JSIP 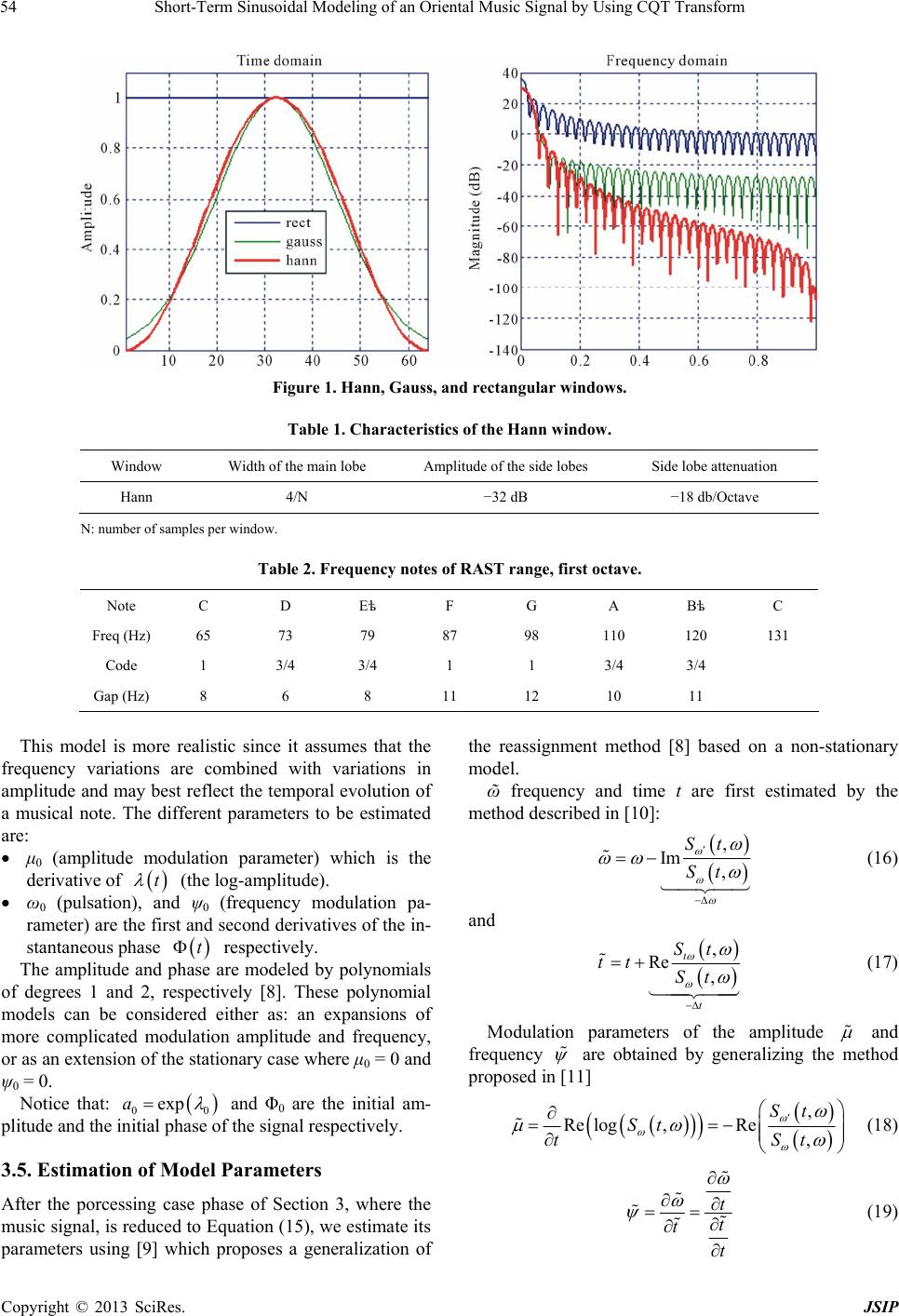 Short-Term Sinusoidal Modeling of an Oriental Music Signal by Using CQT Transform Copyright © 2013 SciRes. JSIP 54 Figure 1. Hann, Gauss, and rectangular windows. Table 1. Characteristics of the Hann window. Window Width of the main lobe Amplitude of the side lobes Side lobe attenuation Hann 4/N −32 dB −18 db/Octave N: number of samples per window. Table 2. Frequency notes of RAST range, first octave. Note C D Eѣ F G A Bѣ C Freq (Hz) 65 73 79 87 98 110 120 131 Code 1 3/4 3/4 1 1 3/4 3/4 Gap (Hz) 8 6 8 11 12 10 11 This model is more realistic since it assumes that the frequency variations are combined with variations in amplitude and may best reflect the temporal evolution of a musical note. The different parameters to be estimated are: μ0 (amplitude modulation parameter) which is the derivative of t (the log-amplitude). ω0 (pulsation), and ψ0 (frequency modulation pa- rameter) are the first and second derivatives of the in- stantaneous phase t respectively. The amplitude and phase are modeled by polynomials of degrees 1 and 2, respectively [8]. These polynomial models can be considered either as: an expansions of more complicated modulation amplitude and frequency, or as an extension of the stationary case where μ0 = 0 and ψ0 = 0. Notice that: 0 0 expa and Φ0 are the initial am- plitude and the initial phase of the signal respectively. 3.5. Estimation of Model Parameters After the porcessing case phase of Section 3, where the music signal, is reduced to Equation (15), we estimate its parameters using [9] which proposes a generalization of the reassignment method [8] based on a non-stationary model. ῶ frequency and time t are first estimated by the method described in [10]: m, , ISt St (16) and Re , , t t St tt St (17) Modulation parameters of the amplitude and frequency are obtained by generalizing the method proposed in [11] , Re log,Re, St St tS t (18) t t t t (19) 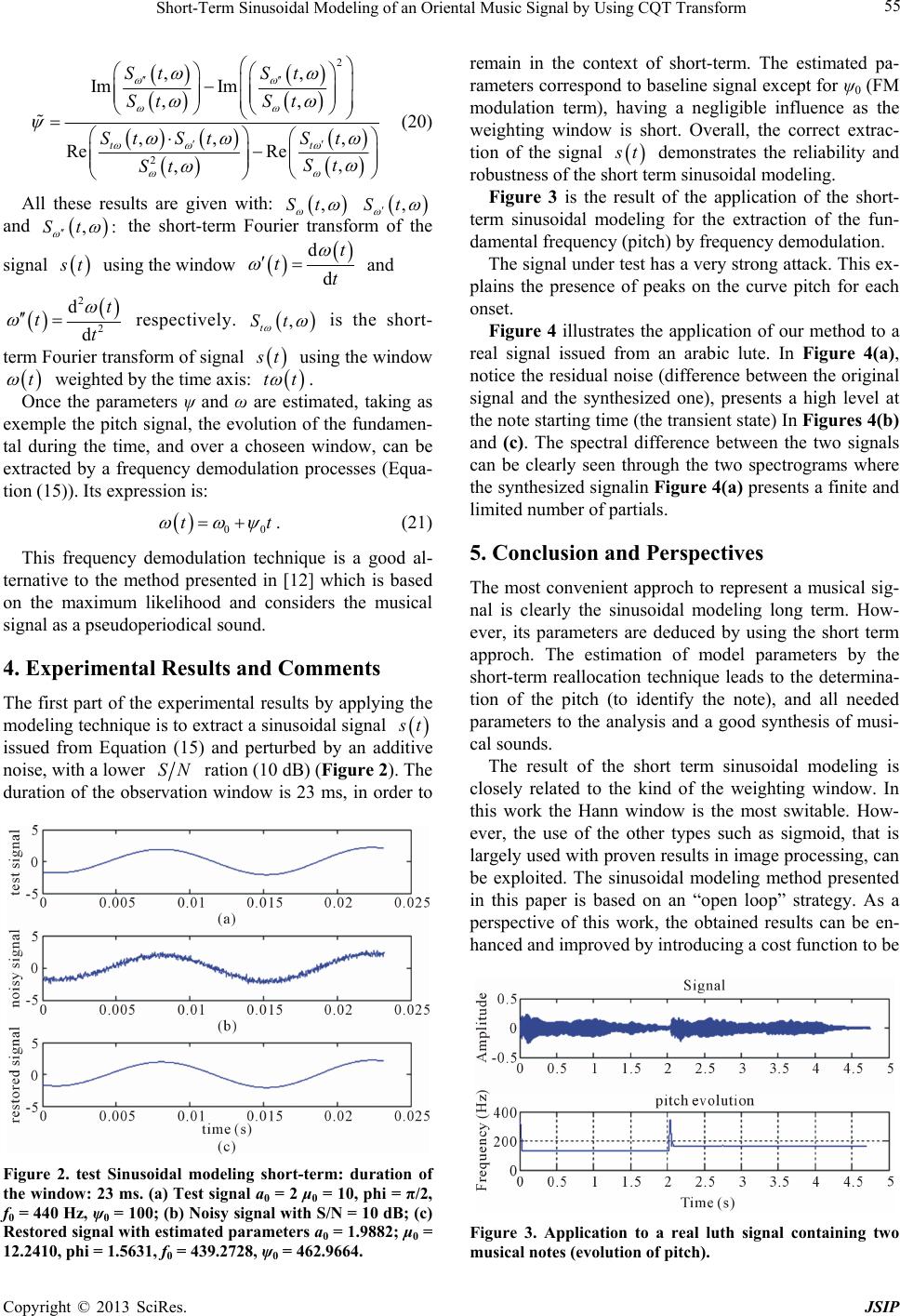 Short-Term Sinusoidal Modeling of an Oriental Music Signal by Using CQT Transform 55 2 2 ,, Im Im ,, ,, , ReRe , , t St St St St StStS t St St t (20) All these results are given with: ,St ,St and ,St : the short-term Fourier transform of the signal t using the window dt d tt and 2 2 d d t tt respectively. , t St is the short- term Fourier transform of signal t t using the window weighted by the time axis: . t t Once the parameters ψ and ω are estimated, taking as exemple the pitch signal, the evolution of the fundamen- tal during the time, and over a choseen window, can be extracted by a frequency demodulation processes (Equa- tion (15)). Its expression is: 00 tt . (21) This frequency demodulation technique is a good al- ternative to the method presented in [12] which is based on the maximum likelihood and considers the musical signal as a pseudoperiodical sound. 4. Experimental Results and Comments The first part of the experimental results by applying the modeling technique is to extract a sinusoidal signal t issued from Equation (15) and perturbed by an additive noise, with a lower SN ration (10 dB) (Figure 2). The duration of the observation window is 23 ms, in order to Figure 2. test Sinusoidal modeling short-term: duration of the window: 23 ms. (a) Test signal a0 = 2 μ0 = 10, phi = π/2, f0 = 440 Hz, ψ0 = 100; (b) Noisy signal with S/N = 10 dB; (c) Restored signal with estimated parameters a0 = 1.9882; μ0 = 12.2410, phi = 1.5631, f0 = 439.2728, ψ0 = 462.9664. remain in the context of short-term. The estimated pa- rameters correspond to baseline signal except for ψ0 (FM modulation term), having a negligible influence as the weighting window is short. Overall, the correct extrac- tion of the signal t demonstrates the reliability and robustness of the short term sinusoidal modeling. Figure 3 is the result of the application of the short- term sinusoidal modeling for the extraction of the fun- damental frequency (pitch) by frequency demodulation. The signal under test has a very strong attack. This ex- plains the presence of peaks on the curve pitch for each onset. Figure 4 illustrates the application of our method to a real signal issued from an arabic lute. In Figure 4(a), notice the residual noise (difference between the original signal and the synthesized one), presents a high level at the note starting time (the transient state) In Figures 4(b) and (c). The spectral difference between the two signals can be clearly seen through the two spectrograms where the synthesized signalin Figure 4(a) presents a finite and limited number of partials. 5. Conclusion and Perspectives The most convenient approch to represent a musical sig- nal is clearly the sinusoidal modeling long term. How- ever, its parameters are deduced by using the short term approch. The estimation of model parameters by the short-term reallocation technique leads to the determina- tion of the pitch (to identify the note), and all needed parameters to the analysis and a good synthesis of musi- cal sounds. The result of the short term sinusoidal modeling is closely related to the kind of the weighting window. In this work the Hann window is the most switable. How- ever, the use of the other types such as sigmoid, that is largely used with proven results in image processing, can be exploited. The sinusoidal modeling method presented in this paper is based on an “open loop” strategy. As a perspective of this work, the obtained results can be en- hanced and improved by introducing a cost function to be Figure 3. Application to a real luth signal containing two musical notes (evolution of pitch). Copyright © 2013 SciRes. JSIP 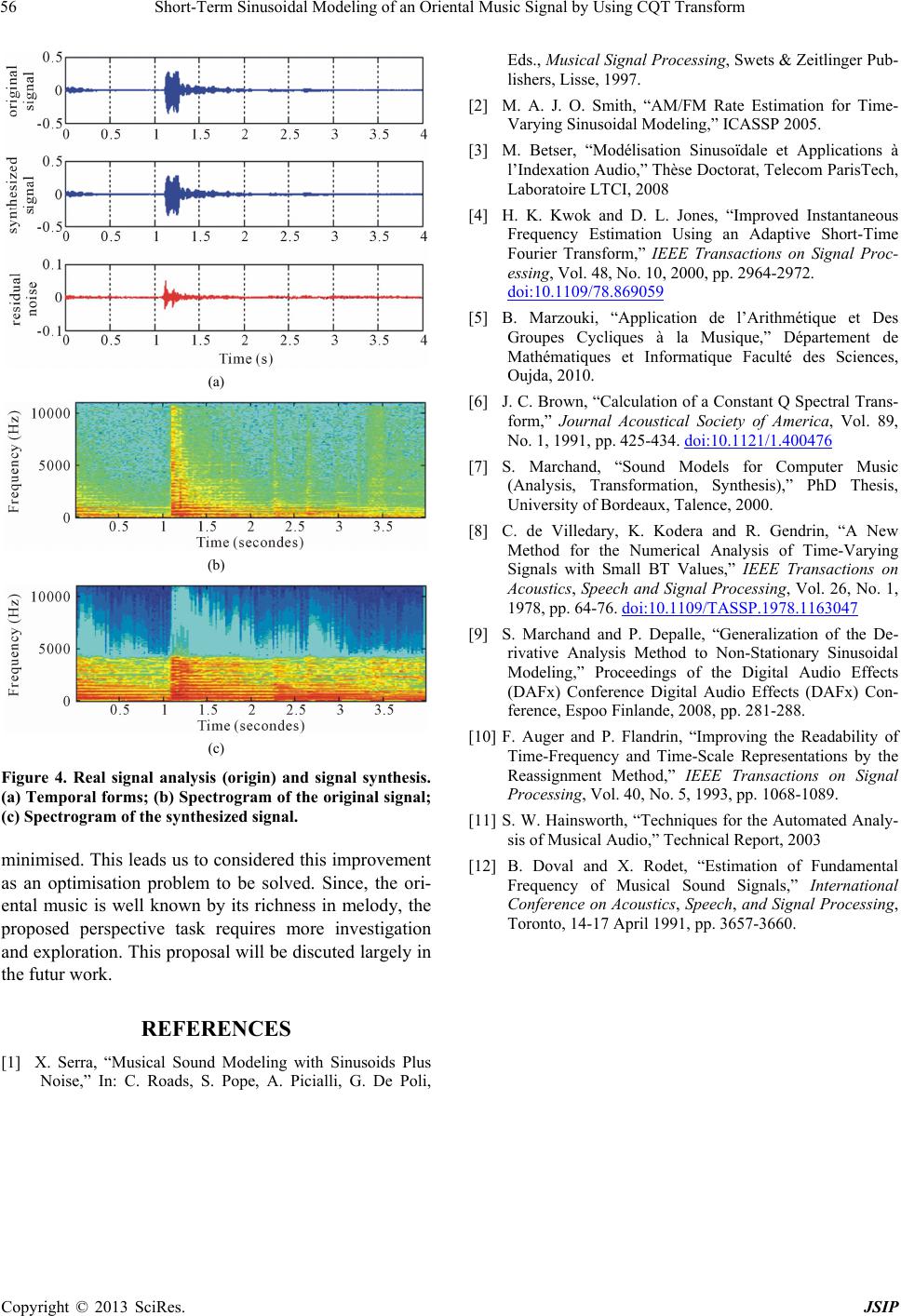 Short-Term Sinusoidal Modeling of an Oriental Music Signal by Using CQT Transform Copyright © 2013 SciRes. JSIP 56 (a) (b) (c) Figure 4. Real signal analysis (origin) and signal synthesis. (a) Temporal forms; (b) Spectrogram of the original signal; (c) Spectrogram of the synthesized signal. minimised. This leads us to considered this improvement as an optimisation problem to be solved. Since, the ori- ental music is well known by its richness in melody, the proposed perspective task requires more investigation and exploration. This proposal will be discuted largely in the futur work. REFERENCES [1] X. Serra, “Musical Sound Modeling with Sinusoids Plus Noise,” In: C. Roads, S. Pope, A. Picialli, G. De Poli, Eds., Musical Signal Processing, Swets & Zeitlinger Pub- lishers, Lisse, 1997. [2] M. A. J. O. Smith, “AM/FM Rate Estimation for Time- Varying Sinusoidal Modeling,” ICASSP 2005. [3] M. Betser, “Modélisation Sinusoïdale et Applications à l’Indexation Audio,” Thèse Doctorat, Telecom ParisTech, Laboratoire LTCI, 2008 [4] H. K. Kwok and D. L. Jones, “Improved Instantaneous Frequency Estimation Using an Adaptive Short-Time Fourier Transform,” IEEE Transactions on Signal Proc- essing, Vol. 48, No. 10, 2000, pp. 2964-2972. doi:10.1109/78.869059 [5] B. Marzouki, “Application de l’Arithmétique et Des Groupes Cycliques à la Musique,” Département de Mathématiques et Informatique Faculté des Sciences, Oujda, 2010. [6] J. C. Brown, “Calculation of a Constant Q Spectral Trans- form,” Journal Acoustical Society of America, Vol. 89, No. 1, 1991, pp. 425-434. doi:10.1121/1.400476 [7] S. Marchand, “Sound Models for Computer Music (Analysis, Transformation, Synthesis),” PhD Thesis, University of Bordeaux, Talence, 2000. [8] C. de Villedary, K. Kodera and R. Gendrin, “A New Method for the Numerical Analysis of Time-Varying Signals with Small BT Values,” IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. 26, No. 1, 1978, pp. 64-76. doi:10.1109/TASSP.1978.1163047 [9] S. Marchand and P. Depalle, “Generalization of the De- rivative Analysis Method to Non-Stationary Sinusoidal Modeling,” Proceedings of the Digital Audio Effects (DAFx) Conference Digital Audio Effects (DAFx) Con- ference, Espoo Finlande, 2008, pp. 281-288. [10] F. Auger and P. Flandrin, “Improving the Readability of Time-Frequency and Time-Scale Representations by the Reassignment Method,” IEEE Transactions on Signal Processing, Vol. 40, No. 5, 1993, pp. 1068-1089. [11] S. W. Hainsworth, “Techniques for the Automated Analy- sis of Musical Audio,” Technical Report, 2003 [12] B. Doval and X. Rodet, “Estimation of Fundamental Frequency of Musical Sound Signals,” International Conference on Acoustics, Speech, and Signal Processing, Toronto, 14-17 April 1991, pp. 3657-3660.
|