Circuits and Systems, 2010, 1, 35-40
doi:10.4236/cs.2010.12006 Published Online October 2010 (http://www.SciRP.org/journal/cs)
Universal Current-Controlled Current-Mode Biquad Filter
Employing MO-CCCCTAs and Grounded Capacitors
Sajai Vir Singh1, Sudhanshu Maheshwari2, Durg Singh Chauhan3
1Department of Electronics and Communications, Jaypee University of Information Technology,
Waknaghat, India
2Department of Electronics Engineering, Z. H. College of Engineering and Technology, Aligarh Muslim University,
Aligarh, India
3Department of Electrical Engineering, Institute of Technology, Banaras Hindu University,
Varanasi, India
Received May 22, 2010; revised July 19, 2010; accepted July 23, 20 10
Abstract
This paper presents a universal current-controlled current-mode biquad filter employing current controlled cur-
rent conveyor trans-conductance amplifiers (CCCCTAs). The proposed filter employs only three MO-
CCCCTAs and two grounded capacitors. The proposed filter can simultaneously realize low pass (LP), band
pass (BP), high pass (HP), band reject (BR) and all pass (AP) responses in current form by choosing appropriate
current output branches. In addition, the pole frequency and quality factor of the proposed filter circuit can be
tuned independently and electronically over the wide range by adjusting the external bias currents. The circuit
possesses low active and passive sensitivity performance. The validity of proposed filter is verified through
PSPICE simulations.
Keywords: Biquad, Current-Mode, Universal Filter
1. Introduction
It is well accepted that universal biquad filter is a very im-
portant functional block which is widely used in various
parts such as communication, measurement, instrumenta-
tion and control systems [1]. Because of the well known
advantages such as reduced distortions, low input imped-
ance, high output impedance, less sensitive to switching
noise, better ESD immunity, high slew rate and larger
bandwidth, the design and implementation of current-mode
active filters using current-mode active elements [2] have
become quite popular for wide variety of applications due
to their inherent advantages over the voltage-mode counter
parts. Recently, a new current-mode active element, name-
ly the current controlled current conveyor trans-conductan-
ce amplifiers (CCCCTAs) has been introduced [3]. Its
trans-conductance and parasitic resistance can be adjusted
electronically, hence it does not need a resistor in practical
applications. This device can be operated in both current
and voltage-modes, providing flexibility. In addition, it can
offer several advantages such as high slew rate, high speed,
wider bandwidth and simpler implementation. All these
advantages together, its current-mode operation makes the
CCCCTA, a promising choice for realizing active filters [4].
During the last one decade and recent past a number of
universal current-mode active filters have been reported in
the literature [5-23], using different current-mode active
elements. Unfortunately these reported current-mode filters
[5-23] suffer from one or more of the following drawbacks:
1) Lack of electronic tunability [5,7,9,11,20].
2) Can not provide completely standard filter functions
simultaneously [8,13,15,18,21-23].
3) Excessive use of active and/or passive elements [5,6,9,
11,12,14,16-19].
4) Can not provide explicit current outputs [8,13,15].
5) Pole frequency and quality factor can’t be controlled
orthogonally [8,10,22].
In this paper a new universal current-controlled cur-
rent-mode biquad filter using three MO-CCCCTAs and
two grounded capacitors is proposed. The proposed filter
can simultaneously realize LP, BP, HP, BR and AP re-
sponses in current form. In addition, the pole frequency
and quality factor of the proposed filter circuit can be
tuned independently and electronically over the wide

S. V. SINGH ET AL. 36
range by adjusting the external bias currents. Both the
active and passive sensitivities are less and no longer
than one. The validity of proposed filter is verified
through PSPICE, the industry standard tool.
2. Proposed Circuit
The CCCCTA properties can be described by the fol-
lowing equations
XiYiXi Xi
V=V+IR ,
Z
iXi
I
=I , =
±Omi Zi
I
gV (1)
where RXi and gmi are the parasitic resistance at X
termi-
nal and transconductance of the i
th
CCCCTA, respec-
tively. RXi and gmi depend upon the biasing currents IBi
and ISi of the CCCCTA, respectively. The schematic
symbol of MO-CCCCTA is illustrated in Figure 1. For
BJT model of MO-CCCCTA [3] shown in Figure 2, RXi
and gmi can be expressed as
2
T
Xi
B
i
V
R=
I
and 2
Si
mi
T
I
g=
V (2)
The proposed current-mode universal filter is shown in
Figure 3. It is based on three MO-CCCCTAs and two
grounded capacitors. Routine analysis of proposed filter
yields the circuit transfer functions TLP(s), TBP(s), THP(s),
TBR(s) and TAP(s) for the current outputs ILP(s), IBP(s),
IHP(s), IBR(s) and IAP(s) and can be formulated as

2
11
2
1221122
()
()
LP
LP
in
m
mX
XmX m
Is
Ts= =
Is
g
gR
s
CC R+sgRC+g

(3)

2
12 2
11
2
1221122
()
()
HP
HP
in
X
mX
XmX m
Is
Ts= =
Is
sCCR
gR
s
CC R+sgRC+g
(4)

23 3
11
2
1221122
()
()
2
BP
BP
in
mX
mX
XmX m
Is
Ts==
Is
sC gR
gR
s
CC R+sgRC+g

(5)

2
12 22
11
2
1221122
()
()
BR
BR
in
Xm
mX
XmX m
Is
Ts==
Is
sCCR +g
gR
s
CC R+sgRC+g
(6)

223 3
12 22
11
2
1221122
()
()
2
AP
AP
in
mX
Xm
mX
XmX m
Is
Ts= =
Is
sC gR
s
CC R-+g
gR
s
CC R+sgRC+g

(7)
Figure 1. CCCCTA symbol.
Figure 2. Internal topology of MO-CCCCTA.
It is noted from (7) that simple current matching con-
dition is required to get AP response which is IS3IB1 =
2IS1IB3. The pole frequency (ωo), the quality factor (Q)
and Bandwidth (BW) ωo/Q of each filter response can be
expressed as
1
2
2
o
12 2
m
X
g
ω=CC R



,
1
2
122
11 2
Xm
mX
CR g 1
Q= gR C



,
011
12
mX
X
ω
g
R
BW ==
QCR
(8)
Substituting intrinsic resistances as depicted in (2), it
yields
1
2
22
o
12
1SB
T
II
ω=VCC



,
1
2
21 1
122
2S
B
SB
IC I
Q= IIC



(9)
From (9), by maintaining the ratio IB2 and IS2 to be
constant, it can be remarked that the pole frequency can
be adjusted by IB2 and IS2 without affecting the quality
factor. Moreover, the Quality factor can also be adjusted
by IB1 or IS1 or both, without affecting the pole frequency.
In addition, bandwidth (BW) of the system can be ex-
pressed by
012
11
1SB
TB
ω
I
I
BW ==
QVCI (10)
Equations (9) and (10) show that the pole frequency
and quality factor of the proposed filter circuit can be tuned
independently and electronically with out affecting the
bandwidth over the wide range by adjusting the external
bias current IS2.
3. Non-Ideal Analysis
For non-ideal case, the CCCCTA can be, respectively,

S. V. SINGH ET AL. 37
characterized with the following equations
Xii YiXiXi
V=βV+IR (11)
Z
iiXi
I=α
I
(12)
Oipimi Zi
I=γ
g
V (13)
-Oinimi Zi
I=-γ
g
V (14)
where βi, αi, γpi, and γni are transferred ratios of ith
CCCCTA (I = 1, 2, 3) which deviate from ‘unity’ by the
transfer errors. In the case of non-ideal and re-analyzing
the proposed filter in Figure 3, it yields the transfer func-
tions as

22 1 22
11
2
111 222 21112112 222
()
()
pp m
LP
LPm X
in XpmXnm
αβγ γg
Is
Ts= =gR
Is sαβCC R+sαβγgRC+αβαβ γ
g
 (15)


213
332
3
11
2
111 222 21112112 222
1
()
()
pp
mX
BP
BPm X
in XpmXnm
βγ γgRCs
+α
Is
Ts= =gR
Is sαβCC R+sαβγ gRC+αβαβγ
g
 (16)

2
11222221 212
11
2
111 222 2111 2112 222
()
()
nX mnnpp
HP
HPm X
in XpmXnm
sγCC R+αβg(γγγγ )
Is
Ts= =gR
Is sαβCCR+sαβγ gRC+αβαβγ
g
 (17)

2
112222 1 22
11
2
111 222 21112112 222
) ()
()
nX nnm BR
BRm X
in XpmXnm
(s γCC R+αβγ γg Is
Ts= =gR
Is sαβCC R+sαβγgRC+αβαβ γ
g
(18)


213
2
112233 222122
3
11
2
111 222 21112112 222
()
1
()
()
pn
pXmX pnm
AP
APm X
in XpmXnm
βγγ
sγCC RgRC s+αβγ γg
+α
Is
Ts= =gR
Is sαβCC R+sαβγgRC+αβαβ γ
g

 (19)
Figure 3. Proposed universal current-controlled current-mode biquad filter employing MO-CCCCTAs and grounded capacitors.

S. V. SINGH ET AL. 38
In this case, the ωo and Q are changed to
1
2
222 2
o
12 2
nm
X
αγ βg
ω=CC R



,
1
2
2221 11
11 1222
nXm
pmX
γRgC αβ
Q= γgR αβC



(20)
The active and passive sensitivities of the proposed
circuit can be found as
12 2
1
2
o
X
ω
C,C ,R
S=,222 2
1
2
o
mn
ω
g,α,β,γ
S=,o
1131313 0 Xmm
ω
R,g,g,α,α,β,β
S=,
313 1230
o
Xnnppp
ω
R,γ,γ,γ,γ,γ
S=
(21)
222
1
2
Q
C,α,β
S=, 2212
1
2
Xm n
Q
R,g,C,γ
S= , 11 11
pm X
Q
γ,g ,R
S=

,
11 1
Q
α,β
S= 313233 30
nn p pm
Q
α,γ,γ,γ,γ,β,g
S= (22)
From the above results, it can be observed that all the
sensitivities are low and no longer than one in magnitude.
4. Simulation Results
The proposed universal current-mode filter was verified
through PSPICE simulations. In simulation, the MO-
CCCCTA was realized using BJT model as shown in
Figure 2, with the transistor model of HFA3096 mixed
transistors arrays [12] and was biased with ±1.85 V DC
power supplies. The SPICE model parameters are given
in Table 1. The circuit was designed for Q = 1 and fo =
ωo/2π = 3.68 MHz. The active and passive components
were chosen as IB1 = IB2 = 60 µA, IB3 = 30 µA IS1 = IS2 =
IS3 = 240 µA and C1 = C2 = 0.2 nF. Figure 4 shows the
simulated gain responses of the LP, HP, BP, BR and AP
in current form. Figure 5 shows the phase response of
AP. The simulation results show the simulated pole fre-
quency as 3.58 MHz that agree quite well with the theo-
retical analysis.
Figure 6 shows magnitude responses of BP function
where IB2 and IS2 are equally set and changed for several
values, by keeping its ratio to be constant for constant
Q(= 2). Other parameters were chosen as IB1 = 240 µA,
IB3 = 30 µA, IS1 = IS3 = 240 µA, and C1 = C2 = 0.2 nF. The
pole frequency (in Figure 6) is found to vary as 1.75
MHz, 3.43 MHz and 7.52 MHz for three values of IB2 =
IS2 as 60 µA, 120 µA and 280 µA, respectively, which
shows that pole frequency can be electronically adjusted
without affecting the quality factor. Figure 7 shows the
magnitude responses of BP function for different values
of IS1, by keeping IB1 = IB2 = 60 µA, IB3 = 30 µA, IS2 = IS3 =
240 µA, and C1 = C2 = 0.2 nf. The quality factor was
found to vary as 7.2, 3.81, 1.91, 0.96, 0.49, by keeping
constant pole frequency as 3.35 MHz for five values of
IS1 as 30 µA, 60 µA, 120 µA, 240 µA and 480 µA, re-
spectively, which shows that the quality factor of the BP
Figure 4. Simulated results of circuit in Figure 3.
Figure 5. Phase response of AP of circuit in Figure 3.
Figure 6. Band Pass responses for different value of IB2 = IS2.
Figure 7. Band Pass responses for different value of IS1.
response can be electronically adjusted without affecting
the pole frequency by input bias current IS1. Further
simulations were carried out to verify the total harmonic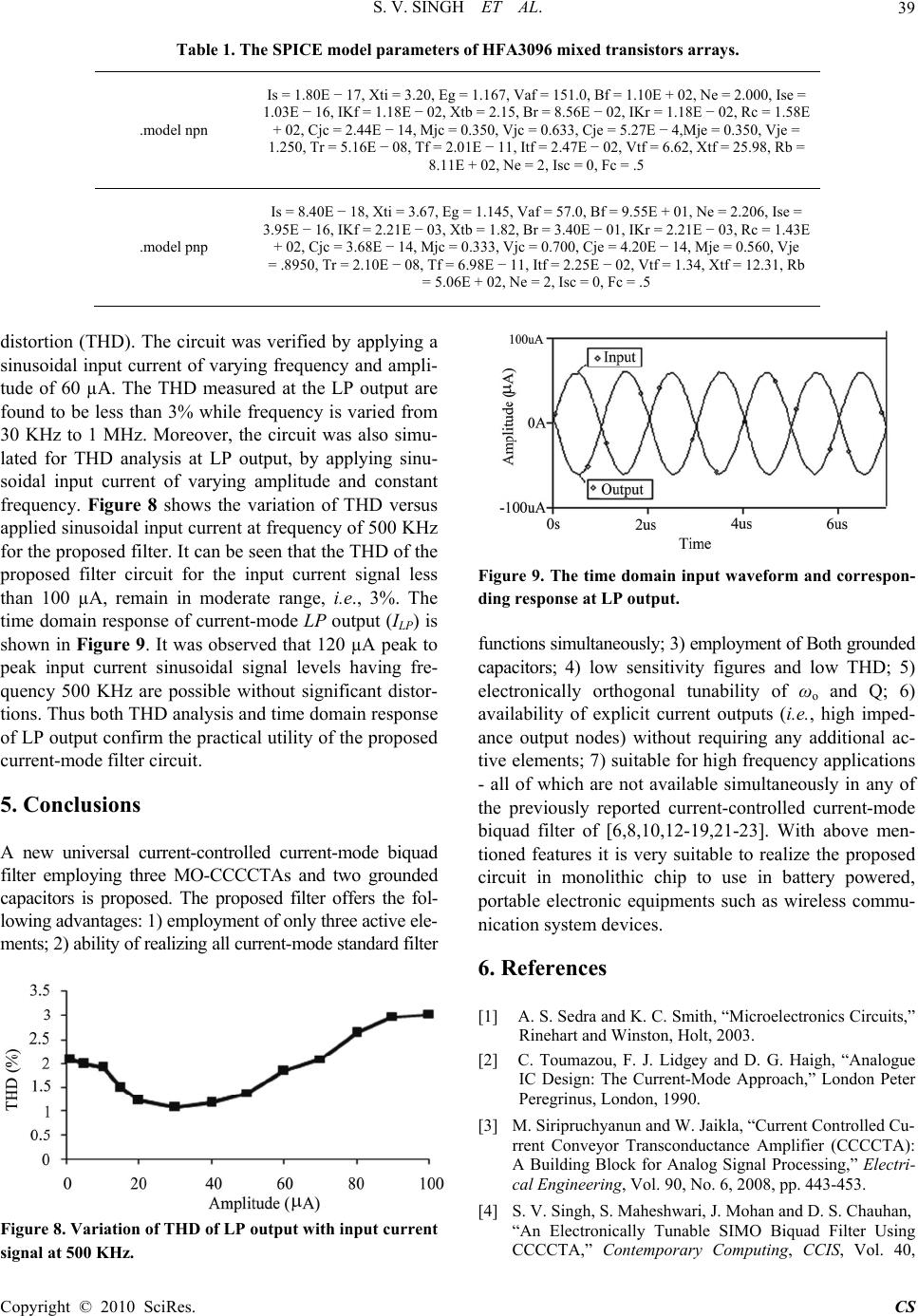

S. V. SINGH ET AL. 39
Table 1. The SPICE model parameters of HFA3096 mixed transistors arrays.
.model npn
Is = 1.80E − 17, Xti = 3.20, Eg = 1.167, Vaf = 151.0, Bf = 1.10E + 02, Ne = 2.000, Ise =
1.03E − 16, IKf = 1.18E − 02, Xtb = 2.15, Br = 8.56E − 02, IKr = 1.18E − 02, Rc = 1.58E
+ 02, Cjc = 2.44E − 14, Mjc = 0.350, Vjc = 0.633, Cje = 5.27E − 4,Mje = 0.350, Vje =
1.250, Tr = 5.16E − 08, Tf = 2.01E − 11, Itf = 2.47E − 02, Vtf = 6.62, Xtf = 25.98, Rb =
8.11E + 02, Ne = 2, Isc = 0, Fc = .5
.model pnp
Is = 8.40E − 18, Xti = 3.67, Eg = 1.145, Vaf = 57.0, Bf = 9.55E + 01, Ne = 2.206, Ise =
3.95E − 16, IKf = 2.21E − 03, Xtb = 1.82, Br = 3.40E − 01, IKr = 2.21E − 03, Rc = 1.43E
+ 02, Cjc = 3.68E − 14, Mjc = 0.333, Vjc = 0.700, Cje = 4.20E − 14, Mje = 0.560, Vje
= .8950, Tr = 2.10E − 08, Tf = 6.98E − 11, Itf = 2.25E − 02, Vtf = 1.34, Xtf = 12.31, Rb
= 5.06E + 02, Ne = 2, Isc = 0, Fc = .5
distortion (THD). The circuit was verified by applying a
sinusoidal input current of varying frequency and ampli-
tude of 60 µA. The THD measured at the LP output are
found to be less than 3% while frequency is varied from
30 KHz to 1 MHz. Moreover, the circuit was also simu-
lated for THD analysis at LP output, by applying sinu-
soidal input current of varying amplitude and constant
frequency. Figure 8 shows the variation of THD versus
applied sinusoidal input current at frequency of 500 KHz
for the proposed filter. It can be seen that the THD of the
proposed filter circuit for the input current signal less
than 100 µA, remain in moderate range, i.e ., 3%. The
time domain response of current-mode LP output (ILP) is
shown in Figure 9. It was observed that 120 µA peak to
peak input current sinusoidal signal levels having fre-
quency 500 KHz are possible without significant distor-
tions. Thus both THD analysis and time domain response
of LP output confirm the practical utility of the proposed
current-mode filter circuit.
5. Conclusions
A new universal current-controlled current-mode biquad
filter employing three MO-CCCCTAs and two grounded
capacitors is proposed. The proposed filter offers the fol-
lowing advantages: 1) employment of only three active ele-
ments; 2) ability of realizing all current-mode standard filter
Figure 8. Variation of THD of LP output with input current
signal at 500 KHz.
Figure 9. The time domain input waveform and correspon-
ding response at LP output.
functions simultaneously; 3) employment of Both grounded
capacitors; 4) low sensitivity figures and low THD; 5)
electronically orthogonal tunability of ωo and Q; 6)
availability of explicit current outputs (i.e., high imped-
ance output nodes) without requiring any additional ac-
tive elements; 7) suitable for high frequency applications
- all of which are not available simultaneously in any of
the previously reported current-controlled current-mode
biquad filter of [6,8,10,12-19,21-23]. With above men-
tioned features it is very suitable to realize the proposed
circuit in monolithic chip to use in battery powered,
portable electronic equipments such as wireless commu-
nication system devices.
6. References
[1] A. S. Sedra and K. C. Smith, “Microelectronics Circuits,”
Rinehart and Winston, Holt, 2003.
[2] C. Toumazou, F. J. Lidgey and D. G. Haigh, “Analogue
IC Design: The Current-Mode Approach,” London Peter
Peregrinus, London, 1990.
[3] M. Siripruchyanun and W. Jaikla, “Current Controlled Cu-
rrent Conveyor Transconductance Amplifier (CCCCTA):
A Building Block for Analog Signal Processing,” Electri-
cal Engineering, Vol. 90, No. 6, 2008, pp. 443-453.
[4] S. V. Singh, S. Maheshwari, J. Mohan and D. S. Chauhan,
“An Electronically Tunable SIMO Biquad Filter Using
CCCCTA,” Contemporary Computing, CCIS, Vol. 40,

S. V. SINGH ET AL. 40
2009, pp. 544-555.
[5] A. M. Soliman, “New Current-Mode Filters Using Current
Conveyors,” International Journal of Electronics and
Communications (AEÜ), Vol. 51, No. 3, 1997, pp. 275-
278.
[6] S. Minaei and S. Türköz, “New Current-Mode Current-
Controlled Universal Filter with Single Input and Three
Outputs,” International Journal of Electronics, Vol. 88,
No. 3, 2001, pp. 333-337.
[7] R. Senani, “New Current Mode Biquad Filter,” Interna-
tional Journal of Electronics, Vol. 73, No. 4, 1992, pp.
735-742.
[8] A. U. Keskin, D. Biolek, E. Hancioglu and V. Biolkova,
“Current-Mode KHN Filter Employing Current Differ-
encing Transconductance Amplifiers,” International
Journal of Electronics and Communications (AEÜ), Vol.
60, No. 6, 2006, pp. 443-446.
[9] M. Soliman, “Current Mode Universal Filters with Grou-
nded Passive Elements and Using Single Output Current
Conveyors,” Journal of Active and Passive Electronics
Devices, Vol. 4, 2009, pp. 55-62.
[10] S. Maheshwari and I. A. Khan, “Novel Cascadable Cur-
rent-Mode Translinear-C Universal Filter,” Active Pas-
sive Electronics Components, Vol. 27, No. 4, 2004, pp.
215-218.
[11] C. Wang, Y. Zhao, Q. Zhang and S. Du, “A New Current
Mode SIMO-Type Universal Biquad Employing Multi-
Output Current Conveyors (MOCCIIs),” Radioengineer-
ing, Vol. 18, No. 1, 2009, pp. 83-88.
[12] R. Senani, V. K. Singh, A. K. Singh and D. R. Bhaskar,
“Novel Electronically Controllable Current-Mode Uni-
versal Biquad Filter,” The Institute of Electronics, Infor-
mation and Communication Engineers, Vol. 1, No. 14,
2004, pp. 410-415.
[13] W. Kiranon, J. Kesorn and N. Kamprasert, “Electroni-
cally Tunable Multi-Function Translinear-C Filter and
Oscillators,” Electronics Letters, Vol. 33, No. 7, 1997, pp.
573-574.
[14] S. Maheshwari and I. A. Khan, “High Performance Ver-
satile Translinear-C Universal Filter,” Journal of Active
and Passive Electronics Devices, Vol. 1, No. 2, 2005, pp.
41-51.
[15] M. T. Abuelma’atti and N. A. Tassaduq, “New Current-
Mode Current Controlled Filters Using Current-Controll-
ed Conveyor,” International Journal of Electronics, Vol.
85, No. 4, 1998, pp. 483-488.
[16] T. Katoh, T. Tsukutani, Y. Sumi and Y. Fukui, “Electro-
nically Tunable Current-Mode Universal Filter Employ-
ing CCCIIs and Grounded Capacitors,” International
Symposium on Intelligent Signal Processing and Com-
munications Systems, 2006, pp. 107-110.
[17] C. Wang, H. Liu and Y. Zhao, “A New Current-Mode
Current-Controlled Universal Filter Based on CCCII (±),”
Circuits System Signal Processing, Vol. 27, No. 5, 2008,
pp. 673-682.
[18] S. Minaei and S. Türköz, “Current-Mode Electronically
Tunable Universal Filter Using Only Plus-Type Current
Controlled Conveyors and Grounded Capacitors,” Elec-
tronics and Telecommunications Research Institute Jour-
nal, Vol. 26, No. 4, 2004, pp. 292-296.
[19] M. T. Abuelma’atti and N. A. Tassaduq, “A Novel Sin-
gle-Input Multiple-Output Current-Controlled Universal
Filter,” Microelectronics Journal, Vol. 29, No. 11, 1998,
pp. 901-905.
[20] S. Maheshwari, “Current-Mode Filters with High Output
Impedance and Employing only Grounded Components,”
WSEAS Transactions on Electronics, Vol. 5, No. 1, 2008,
pp. 238-243.
[21] W. Jaikla and M. Siripruchyanun, “A Cascadable Cur-
rent-Mode Universal Biquadratic Filter Using MO-
CCCCTAs,” IEEE Conference, Pisa, 2008, pp. 952-955.
[22] D. Biolek and V. Biolkova, “CDTA-C Current-Mode
Universal 2nd Order Filter,” Proceeding of the 5th Inter-
national Conference on Applied Informatics and Com-
munications, Malta, 2003, pp. 411-414.
[23] W. Tangsrirat and W. Surakampontorn, “Systematic of
Cascadable Current-Mode Filters Using CDTAs,” Fre-
quenz, Vol. 60, No. 11-12, 2006, pp. 241-245.