Journal of Modern Physics
Vol.3 No.9(2012), Article ID:22682,8 pages DOI:10.4236/jmp.2012.39143
Nonabelian Dualization of Plane Wave Backgrounds
Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
Email: hlavaty@fjfi.cvut.cz, turekm@km1.fjfi.cvut.cz
Received June 30, 2012; revised July 31, 2012; accepted August 10, 2012
Keywords: Sigma Model; String Duality; pp-Wave Background
ABSTRACT
We investigate plane-parallel wave metrics from the point of view of their (Poisson-Lie) T-dualizability. For that purpose we reconstruct the metrics as backgrounds of nonlinear sigma models on Lie groups. For construction of dual backgrounds we use Drinfel’d doubles obtained from the isometry groups of the metrics. We find dilaton fields that enable to satisfy the vanishing beta equations for the duals of the homogenous plane-parallel wave metric. Torsion potentials or B-fields, invariant w.r.t. the isometry group of Lobachevski plane waves are obtained by the Drinfel’d double construction. We show that a certain kind of plurality, different from the (atomic) Poisson-Lie T-plurality, may exist in case that metrics admit several isometry subgroups having the dimension of the Riemannian manifold. An example of that are two different backgrounds dual to the homogenous plane-parallel wave metric.
1. Introduction
Sigma models can serve as models of string theory in curved and time-dependent backgrounds. Solution of sigma-models in such backgrounds is often very complicated, not to say impossible. On the other hand, there are many backgrounds whose properties were thoroughly investigated and it is therefore interesting to find if they can be transformed to some others. Important example of such transformation is so called Poisson Lie T-duality.
In their seminal work [1] Klimčík and Ševera set conditions for dualizability of backgrounds and gave formulas for their transformation. Since then several examples of dualizable sigma models were constructed, see e.g. [2- 4]. Unfortunately, most of the examples are not physically interesting. The purpose of this paper is to show that physical backgrounds that admit sufficiently large group of isometries are naturally dualizable and therefore equivalent in a sense to some others. In this paper we are going to investigate four-dimensional plane-parallel wave metrics [5-8] from this point of view.
The basic concept used for construction of dualizable sigma models is Drinfel’d double-Lie group with additional structure. The Drinfel’d double for a sigma model living in curved background can sometimes be found from the knowledge of symmetry group of the metric. More precisely, in the Drinfel’d double there are two equally dimensional subgroups whose Lie algebras are isotropic subspaces of the Lie algebra of the Drinfel’d double. In case that the metric has sufficient number of independent Killing vectors, the isometry group of the metric (or its subgroup) can be taken as one of the subgroups of the Drinfel’d double. The other one then must be chosen abelian in order to satisfy the conditions of dualizability. Short summary of the dualization procedure described e.g. in [9] is given in the next section.
2. Elements of Poisson-Lie T-Dual Sigma-Models
Let G be a Lie group and  its Lie algebra. Sigma model on the group G is given by the classical action
its Lie algebra. Sigma model on the group G is given by the classical action
 (1)
(1)
where F is a second order tensor field on the Lie group G. The functions 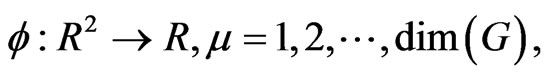 are determined by the composition
are determined by the composition  where
where  and
and  are components of a coordinate map of neighborhood
are components of a coordinate map of neighborhood  of element
of element .
.
Equivalently the action can be expressed as
 (2)
(2)
where  are right-invariant fields
are right-invariant fields
 . The relationship between E and F is given by the formula
. The relationship between E and F is given by the formula
 (3)
(3)
where 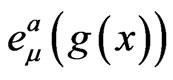 are the components of right invariant forms
are the components of right invariant forms . The equations of motion derived from the action (1) have the following form
. The equations of motion derived from the action (1) have the following form
 (4)
(4)
where  are components of the Levi-Civita connection associated with the second order tensor field F This tensor field is a composition of the metric (a symmetric part) and the torsion potential (an antisymmetric part). The condition of dualizability of sigma-models on the level of the Lagrangian is given by the formula [1]
are components of the Levi-Civita connection associated with the second order tensor field F This tensor field is a composition of the metric (a symmetric part) and the torsion potential (an antisymmetric part). The condition of dualizability of sigma-models on the level of the Lagrangian is given by the formula [1]
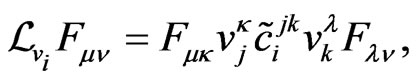 (5)
(5)
where  are structure coefficients of the dual algebra
are structure coefficients of the dual algebra 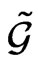 and
and  are left-invariant fields on the Lie group G. The algebras
are left-invariant fields on the Lie group G. The algebras  and
and  then define the Drinfel’d double that enables to construct tensor F satisfying (5).
then define the Drinfel’d double that enables to construct tensor F satisfying (5).
2.1. The Drinfel’d Double and Poisson-Lie T-Duality
As mentioned in the Introduction the Drinfel’d double D is defined as a connected Lie group whose Lie algebra  can be decomposed into pair of subalgebras
can be decomposed into pair of subalgebras ,
,  maximally isotropic with respect to a symmetric ad-invariant nondegenarate bilinear form
maximally isotropic with respect to a symmetric ad-invariant nondegenarate bilinear form  on
on .
.
Under the condition (5) the field Equations (4) for the  -model can be rewritten as equation for the mapping
-model can be rewritten as equation for the mapping 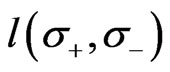 from the world-sheet
from the world-sheet  into the Drinfel’d double D
into the Drinfel’d double D
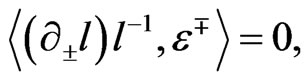 (6)
(6)
where subspaces ,
,
 are orthogonal w.r.t.
are orthogonal w.r.t.  and span the whole Lie algebra
and span the whole Lie algebra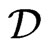 .
. ,
,  are the bases of
are the bases of  and
and .
.
Due to Drinfel’d, there exists unique decomposition (at least in the vicinity of the unit element of D) of an arbitrary element l of D as a product of elements from  and
and . The solutions of Equation (6) and solution
. The solutions of Equation (6) and solution  of the Equation (4) are related by
of the Equation (4) are related by
 (7)
(7)
where ,
,  fulfil the equations
fulfil the equations
 (8)
(8)
 (9)
(9)
The matrix  of the dualizable
of the dualizable  -model is of the form
-model is of the form
 (10)
(10)
where  is a constant matrix,
is a constant matrix, 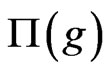 is given by the formula
is given by the formula
 (11)
(11)
and matrices ,
,  ,
,  are given by the adjoint representation of the Lie subgroup G on the Lie algebra of the Drinfel’d double in the basis
are given by the adjoint representation of the Lie subgroup G on the Lie algebra of the Drinfel’d double in the basis  1
1
 (12)
(12)
Let us note that 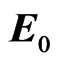 is the value of
is the value of  in the unit
in the unit  of the group
of the group  because
because .
.
The dual model can be obtain by the exchange
 (13)
(13)
Solutions of the equations of motion of dual models are mutually associated by the relation
 (14)
(14)
2.2. Poisson-Lie T-Plurality
Generally, more than two decompositions2 (Manin triples) of Lie algebra  of the Drinfel’d double can exist. This possibility leads to Poisson-Lie T-plurality. Let
of the Drinfel’d double can exist. This possibility leads to Poisson-Lie T-plurality. Let  is another decomposition of the Drinfel’d algebra
is another decomposition of the Drinfel’d algebra  into a pair of maximal isotropic subalgebras. Then the Poisson-Lie T-plural sigma model is given by the following formulas [10]
into a pair of maximal isotropic subalgebras. Then the Poisson-Lie T-plural sigma model is given by the following formulas [10]
 (15)
(15)
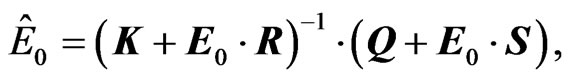 (16)
(16)
where the matrices  determine the relationship between the bases of the appropriate decompositions
determine the relationship between the bases of the appropriate decompositions  and
and
 (17)
(17)
The relationship between the classical solutions of the two Poisson-Lie T-plural sigma-models is given by a possibility of two decompositions of the element  as
as
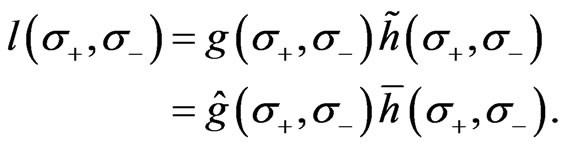 (18)
(18)
The Poisson-Lie T-duality is then a special case of Poisson-Lie T-plurality for .
.
3. Homogenous Plane Wave Metrics
Homogenous plane wave is generally defined by the metric of the following form [5,6]
 (19)
(19)
where  is the standard metrics on Euclidean space
is the standard metrics on Euclidean space  and
and  The form of this metric seems to be simple, but explicit construction of sigma models can be very complicated. Therefore, we have focused on the special case of isotropic homogenous plane wave metric
The form of this metric seems to be simple, but explicit construction of sigma models can be very complicated. Therefore, we have focused on the special case of isotropic homogenous plane wave metric
 (20)
(20)
Metric (20) has a number of symmetries important for the construction of the dualizable sigma models. It admits the following Killing vectors
 (21)
(21)
where  satisfies
satisfies
 (22)
(22)
The Killing vectors  are generators of orthogonal rotations in
are generators of orthogonal rotations in . For special choice of
. For special choice of
 (23)
(23)
there are further isometries related to the scaling of the light-cone coordinates
 (24)
(24)
The specific form of  enables us to calculate the function
enables us to calculate the function 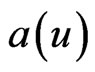 explicitly. The Killing vectors of the metric (20) for
explicitly. The Killing vectors of the metric (20) for  are
are
 (25)
(25)
where D is the generator associated with the scaling symmetry and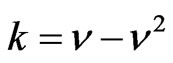 .
.
In the following we shall investigate the case . It means that the metric tensor in coordinates
. It means that the metric tensor in coordinates  reads
reads
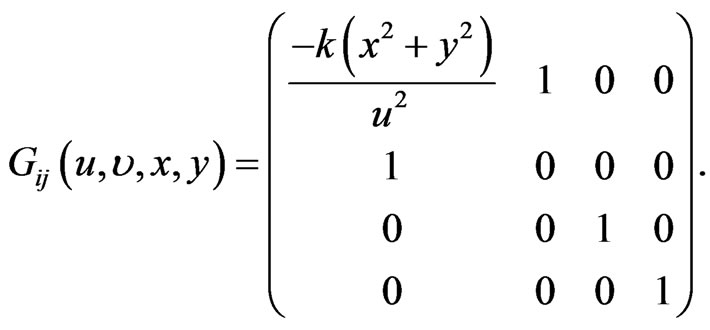 (26)
(26)
This metric is not flat but its Gaussian curvature vanishes. Note that it has singularity in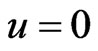 . It does not satisfy the Einstein equations but the conformal invariance conditions equations for vanishing of the
. It does not satisfy the Einstein equations but the conformal invariance conditions equations for vanishing of the  -function
-function
 (27)
(27)
 (28)
(28)
 (29)
(29)
where the covariant derivatives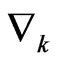 , Ricci tensor
, Ricci tensor  and Gauss curvature
and Gauss curvature  are calculated from the metric
are calculated from the metric  that is also used for lowering and raising indices. Torsion
that is also used for lowering and raising indices. Torsion  in this case vanishes and dilaton field is [5]
in this case vanishes and dilaton field is [5]
 (30)
(30)
The metric (26) admits the following Killing vectors3
 (31)
(31)
One can easily check that the Lie algebra spanned by these vectors is the semidirect sum  where
where  and ideal
and ideal  . The algebra
. The algebra 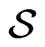 is abelian and its generators can be interpreted as dilation in
is abelian and its generators can be interpreted as dilation in  and rotation in
and rotation in . Generators of the algebra
. Generators of the algebra  commute as two-dimensional Heisenberg algebra with the center
commute as two-dimensional Heisenberg algebra with the center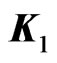 .
.
Construction of Dual Metrics
As explained in Section 2, dualizable metric can be constructed by virtue of Drinfel’d double. For this goal the Lie algebra  of the Drinfel’d double can be composed from the four-dimensional Lie subalgebra
of the Drinfel’d double can be composed from the four-dimensional Lie subalgebra  isomorphic to the four-dimensional subalgebra of Killing vectors and four-dimensional Abelian algebra4
isomorphic to the four-dimensional subalgebra of Killing vectors and four-dimensional Abelian algebra4 . Moreover, the four-dimensional subgroup of isometries must act freely and transitively [1] on the Riemannian manifold M where the metric (20, 23) is defined so that
. Moreover, the four-dimensional subgroup of isometries must act freely and transitively [1] on the Riemannian manifold M where the metric (20, 23) is defined so that .
.
Using the method described in [11] for semisimple algebras we find that up to the transformation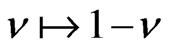 , i.e.
, i.e.  there are six classes of four-dimensional subalgebras of the isometry algebra of the homogeneous plane wave metric isomorphic to
there are six classes of four-dimensional subalgebras of the isometry algebra of the homogeneous plane wave metric isomorphic to
• 
• 
• 
• 
• 

where 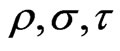 are arbitrary parameters.
are arbitrary parameters.
Infinitesimal form of transitivity condition can be formulated as requirement that four independent Killing vectors can be taken as basis vectors of four-dimensional vector distribution in M. In other words, these Killing vectors must form a basis of tangent space in every point of M. It means that in every point of M there is an invertible matrix 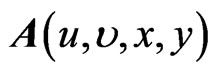 that solves the equation
that solves the equation
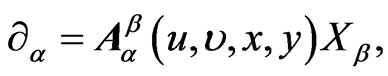 (32)
(32)
where ,
,  and
and  form a basis of the subalgebra.
form a basis of the subalgebra.
Infinitesimal form of requirement that the action of the isometry subgroup is free says that if in any point of M there is a vector of the corresponding Lie subalgebra such that its action on the point vanishes then it must be null vector.
By inspection we can find that the only four-dimensional subalgebras that generate transitive actions on M are isomorphic to  or
or  . Their non-vanishing commutation relations are
. Their non-vanishing commutation relations are
 (33)
(33)
and
 (34)
(34)
respectively where  and
and 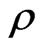 are real parameters. One can also check that the action of both corresponding groups of isometries is free. In the following we shall find metric dual to (26) that follows from its Drinfel’d double description where
are real parameters. One can also check that the action of both corresponding groups of isometries is free. In the following we shall find metric dual to (26) that follows from its Drinfel’d double description where  is isomorphic either to algebra spanned by
is isomorphic either to algebra spanned by 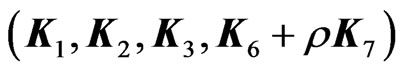 or by
or by  .
.
Let us start with construction of the Drinfel’d double following from the algebra isomorphic to (33) and dual Abelian algebra. Assume that the Lie algebra  is spanned by elements
is spanned by elements  with commutation relations
with commutation relations
 (35)
(35)
where  and
and  are arbitrary real parameters. The basis of left-invariant vector fields of the group generated by
are arbitrary real parameters. The basis of left-invariant vector fields of the group generated by  is
is
 (36)
(36)
where  are group coordinates used in parametrization
are group coordinates used in parametrization
 (37)
(37)
To be able to obtain the metric (26) by the Drinfel’d double construction first we have to transform it into the group coordinates. Transformation between group coordinates x1, x2, x3, x4, and geometrical coordinates u, 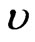 , x, y is
, x, y is
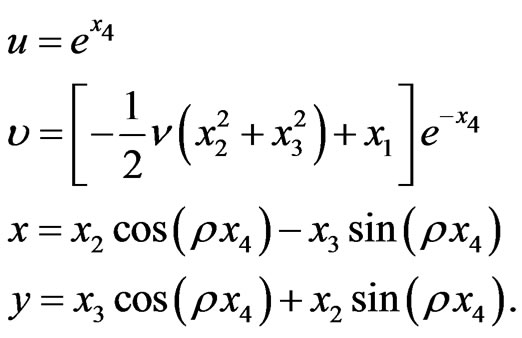 (38)
(38)
It converts the Killing vectors  into the left-invariant vector fields (36) and the metric (26) into the form
into the left-invariant vector fields (36) and the metric (26) into the form
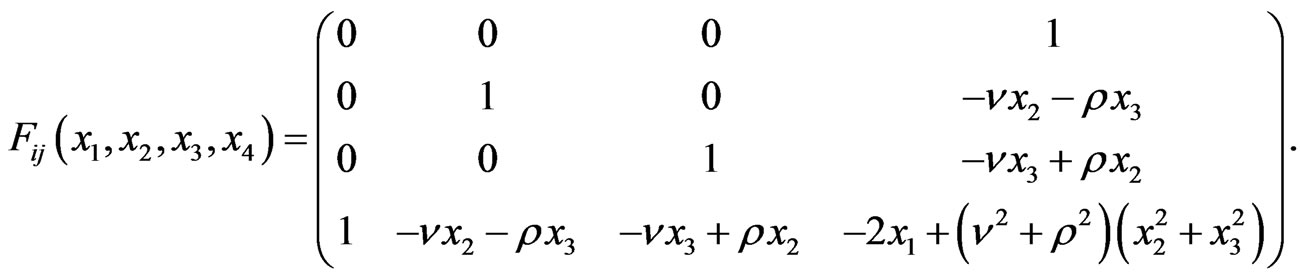 (39)
(39)
that is obtainable by (3) and (10). To get the matrix  necessary for construction of the dual model we note that it is given by the value of
necessary for construction of the dual model we note that it is given by the value of  in the unit of the group, i.e. by value of
in the unit of the group, i.e. by value of  for
for .
.
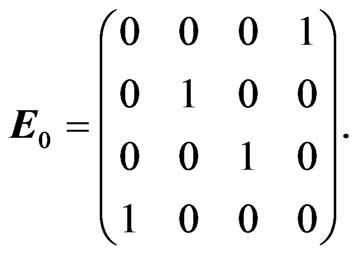 (40)
(40)
The dual tensor on the Abelian group  constructed by the procedure explained in the Section 2, namely by using (3), (10) and (13) is
constructed by the procedure explained in the Section 2, namely by using (3), (10) and (13) is
 (41)
(41)
One can see that the dual tensor has also antisymmetric part ( -field or torsion potential)
-field or torsion potential)
 (42)
(42)
and its torsion  is
is
 (43)
(43)
The Gauss curvature of its symmetric part vanishes but the Ricci tensor is nontrivial. Dual metric that is symmetric part of (41) does not solve the Einstein equations either but again we can satisfy conformal invariance conditions (27)-(29) by the dilaton field
 (44)
(44)
If we use the subalgebra of isometries spanned by  instead of that spanned by
instead of that spanned by  then the transformation between group coordinates x1, x2, x3, x4, and geometrical coordinates u,
then the transformation between group coordinates x1, x2, x3, x4, and geometrical coordinates u,  , x, y is
, x, y is
 (45)
(45)
the matrix 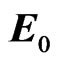 gets again the form (40) and we get another tensor dual to (26)
gets again the form (40) and we get another tensor dual to (26)
 (46)
(46)
Even though it is not symmetric its torsion is zero. It satisfies the conformal invariance conditions (27)-(29) with the dilaton field
 (47)
(47)
4. Lobachevsky Plane Waves
Another type of metrics that have rather large group of isometries are so called Lobachevsky plane waves [7,8]. They are of general form
 (48)
(48)
They satisfy Einstein equation with cosmological constant  iff
iff
 (49)
(49)
The Gauss curvature of this metric is . For special forms of function H the metric (48) admits various sets of Killing vectors. All of them are subalgebras of a vector space spanned by
. For special forms of function H the metric (48) admits various sets of Killing vectors. All of them are subalgebras of a vector space spanned by
 (50)
(50)
A bit surprisingly, all these seven independent vector fields found in [7] form a Lie algebra even though they are not Killing vectors of the same metrics (it depends on the form of ). We are interested in metrics that admit at least four independent Killing vectors because they can be interpreted as dualizable backgrounds for sigma models in four dimensions.
). We are interested in metrics that admit at least four independent Killing vectors because they can be interpreted as dualizable backgrounds for sigma models in four dimensions.
As mentioned in the Section 3.1, for construction of dualizable metrics we need a four-dimensional subalgebra of Killing vectors that generates group of isometries that acts freely and transitively on the four-dimensional Riemannian manifolds. Here we shall investigate metrics of the form (48) where that , i.e.
, i.e.
 (51)
(51)
It solves the Einstein equation with the cosmological constant  for
for  [12].
[12].
4.1. Construction of the Dual Metric
The metric (51) has five-dimensional Lie group of isometries generated by the Killing vectors KI, KII, KIII, KIV, KV, KVI. Their nonzero commutators read
 (52)
(52)
Four-dimensional subalgebras of the Lie algebra (52) for generic  are isomorphic to one of the following algebras:
are isomorphic to one of the following algebras:
• 
• 

It is easy to check that the only subalgebra of these that satisfy the condition of transitivity (32) in every point of M is the first one. Its action is free on M as well so that we can use it for dualization of the metric (51).
In the following we shall consider the case  because
because  do not bring anything qualitatively different. It means that for dualization we shall use the algebra
do not bring anything qualitatively different. It means that for dualization we shall use the algebra 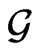 spanned by KI, KIII, KIV, KVI with nonzero commutation relations
spanned by KI, KIII, KIV, KVI with nonzero commutation relations
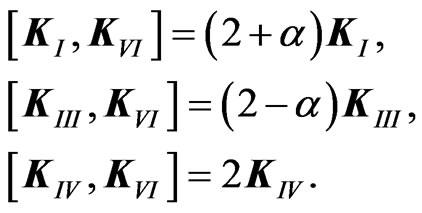 (53)
(53)
The corresponding Drinfel’d double is generated by the algebra  defined by the commutation relations (53) and four-dimensional Abelian algebra. The basis of leftinvariant vector fields of the group generated by
defined by the commutation relations (53) and four-dimensional Abelian algebra. The basis of leftinvariant vector fields of the group generated by 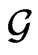 is
is
 (54)
(54)
where x1, x2, x3, x4 are group coordinates used in parametrization

and X1, X2, X3, X4 are generators of  satisfying
satisfying
 (55)
(55)
Transformation between group coordinates and coordinates u,  , x, y of the Lobachevsky manifold is
, x, y of the Lobachevsky manifold is
 (56)
(56)
This transformation converts the Killing vectors KI, KIII, KIV, KVI into the left-invariant vector fields (54) and the metric (51) into

The value of this metric for , i.e. in the unit of the group, gives the matrix
, i.e. in the unit of the group, gives the matrix
 (57)
(57)
Having this matrix we can construct the dual tensor. It is again obtained using (3), (10) and (13) and has the form
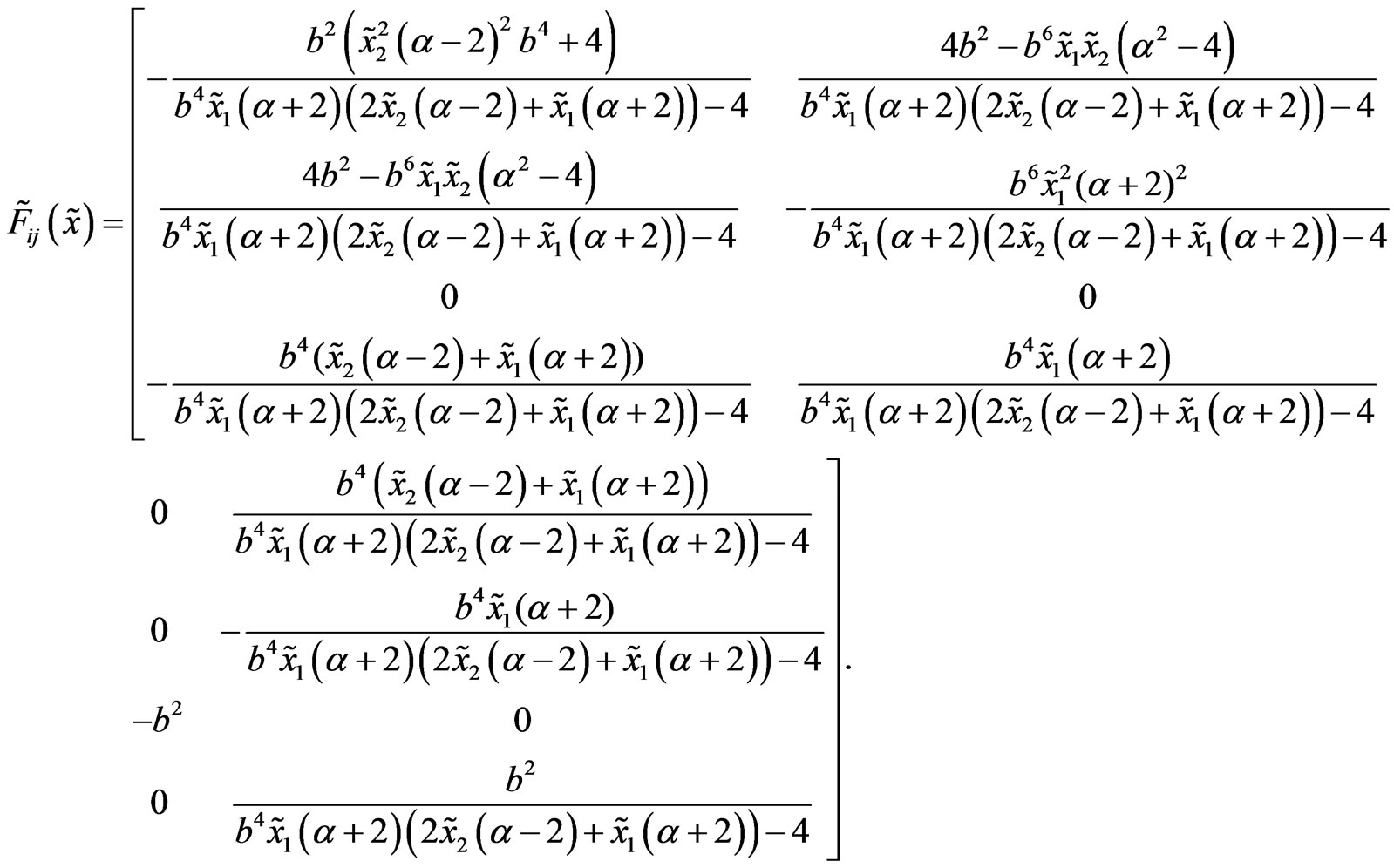
This tensor has nonzero and nonconstant Gauss curvature and torsion.
4.2. B-Field
The Drinfel’d double construction enables to add the Bfield (torsion potential) to the metric so that the resulting tensor  is invariant with respect to the same isometry group as the metric itself. Namely, changing
is invariant with respect to the same isometry group as the metric itself. Namely, changing  to5
to5
 (58)
(58)
and applying the formula (3), (10), we get covariant tensor that after the transformation (56) acquires the form
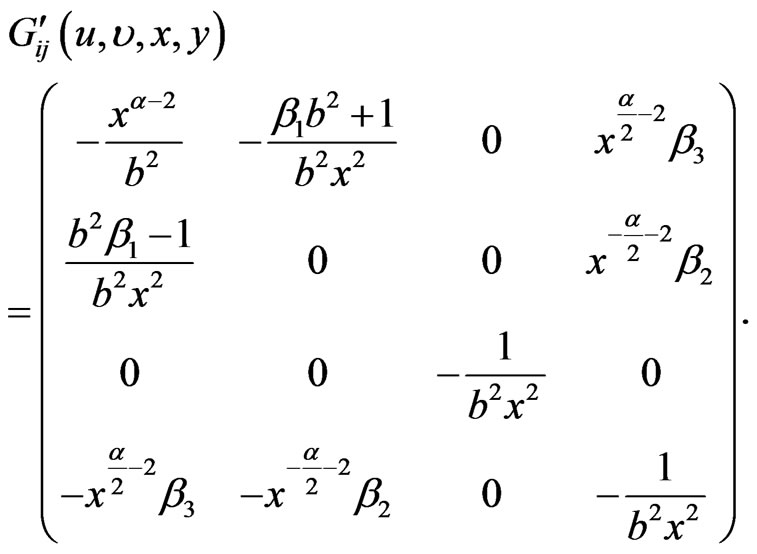 (59)
(59)
Its symmetric part is the metric (51). This tensor is again invariant with respect to the isometry group generated by KI, KIII, KIV, KVI. For  the invariant group can be extended by the generator KV.
the invariant group can be extended by the generator KV.
Torsion  obtained from the antisymmetric part of
obtained from the antisymmetric part of  is
is
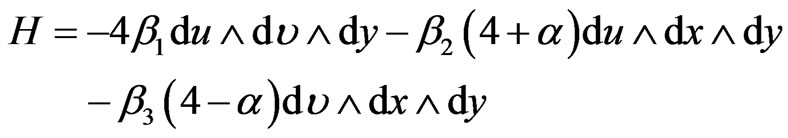 (60)
(60)
As the tensor (59) was obtained by the Drinfel’d double construction it is possible to dualize it but the result is too extensive to display.
5. Conclusions
Isometry groups of metrics can be used for construction of their (nonabelian) T-dual backgrounds. Sufficient condition for that is that the metric have an isometry subgroup whose dimension is equal to the dimension of the Riemannian manifold and its action on the manifold is transitive and free.
We have shown that for the plane wave metrics (26) and (51) such isometry subgroups exist and the metrics can be dualized by the Poisson-Lie T-duality transformation. We have determined the metrics and B-fields dual to the plane waves. For homogeneous plane waves (26) we have also found the dilaton field that guarantees conformal invariance of the dual metric.
Metrics that possess isometry group whose dimension is greater than the dimension of the Riemannian manifold may have several duals. More precisely, if the metric admits various isometry subgroups with above given properties then we can construct several backgrounds dual to the metric. This phenomenon is another kind of plurality of sigma models different from the Poisson-Lie T-plurality described in the Section 2.
An example of this type of plurality is provided by the plane wave metric (26) with isometry subgroups generated by Killing vectors  or by
or by  (see (31) producing two dual backgrounds (41) and (46)). To decide if this plurality is different from the Poisson-Lie T-plurality one has to check whether the eight-dimensional Drinfel’d double s generated by the four-dimensional abelian algebra and algebras spanned by
(see (31) producing two dual backgrounds (41) and (46)). To decide if this plurality is different from the Poisson-Lie T-plurality one has to check whether the eight-dimensional Drinfel’d double s generated by the four-dimensional abelian algebra and algebras spanned by  or
or 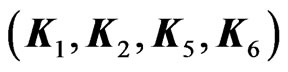 are isomorphic by a transformation that leave the constant matrix (40) invariant. This is, however, very difficult task that might be investigated in the future.
are isomorphic by a transformation that leave the constant matrix (40) invariant. This is, however, very difficult task that might be investigated in the future.
6. Acknowledgements
This work was supported by the research plan LC527 of the Ministry of Education of the Czech Republic. Consultation with P. Winternitz and L. Šnobl on classification of subalgebras are gratefully acknowledged.
REFERENCES
- C. Klimčík and P. Ševera, “Dual Non-Abelian Duality and the Drinfeld Double,” Physics Letters B, 1995, pp. 455-462.
- M. A. Lledo and V. S. Varadarajan, “SU(2) Poisson-Lie T-Duality,” Letters in Mathematical Physics, Vol. 45, No. 3, 1998, pp. 247-257. doi:10.1023/A:1007498803198
- K. Sfetsos, “Poisson-Lie T-Duality beyond the Classical Level and the Renormalization Group,” Physics Letters B, Vol. 432, No. 3-4, 1998, pp. 365-375. doi:10.1016/S0370-2693(98)00666-2
- L. Hlavatý and L. Šnobl, “Poisson-Lie T-Plurality of ThreeDimensional Conformally Invariant Sigma Models II: Nondiagonal Metrics and Dilatonpuzzle,” Journal of High Energy Physics, No. 10, 2004.
- G. Papadopoulos, J. G. Russo and A. A. Tseytlin, “Solvable Model of Strings in a Time-Dependent Plane-Wave Background,” Classical and Quantum Gravity, pp. 969- 1016, [hep-th/0211289].
- M. Blau and M. O’Loughlin, “Homogeneous Plane Waves,” Nuclear Physics B, Vol. 652, No. 1-2, 2003, pp. 135-176. doi:10.1016/S0550-3213(03)00055-5
- S. T. C. Siklos, “Lobatchewski Plane Gravitational Waves in Galaxies, Axisymmetric Systems and Relativity,” M. A. H. MacCallum, Ed., Cambridge University Press, Cambridge, 1985, p. 247.
- J. Podolský, “Interpretation of the Siklos Solutions as Exact Gravitational Waves in the Anti-De Sitter Universe,” Classical and Quantum Gravity, Vol. 15, No. 3, 1998, pp. 719-733. doi:10.1088/0264-9381/15/3/019
- C. Klimčk, “Poisson-Lie T-Duality,” Nuclear Physics A, 1996, pp. 116-121, [hepth9509095].
- R. von Unge, “Poisson-Lie T-Plurality,” Journal of High Energy Physics, 2002, [hepth0205245].
- J. Patera, P. Winternitz and H. Zassenhaus, “Continuous Subgroups of the Fundamental Groups of Physics. I. General Method and the Poincaré Group,” Journal of Mathematical Physics, Vol. 16, No. 8, 1975, pp. 1597- 1614.
- V. R. Kaigorodov, “Einstein Spaces of Maximum Mobility,” Soviet Physics Doklady, Vol. 7, 1963, p. 893.
NOTES
1The superscript t means transposition of the matrix.
2Two decompositions always exist,  ,
, .
.
3If , i.e.
, i.e.  then
then .
.
4It is easy to see, that the Equation (5) is then fulfilled.
5Other antisymmetric elements do not change torsion.

