Paper Menu >>
Journal Menu >>
 Engineering, 2010, 2, 705-709 doi:10.4236/eng.2010.29091 Published Online September 2010 (http://www.SciRP.org/journal/eng) Copyright © 2010 SciRes. ENG Some Aspects of Non-Orthogonal Stagnation-Point Flow towards a Stretching Surface Motahar Reza1, Anadi Sankar Gupta2 1Department of Mathematics, National Institute of Science & Technology, Berhampur, India 2Department of Mathematics, Indian Institute of Technology, Kharagpur, India E-mail: reza@nist.edu Received May 12, 2010; revised July 21, 2010; accepted August 3, 2010 Abstract The problem of steady two-dimensional oblique stagnation-point flow of an incompressible viscous fluid towards a stretching surface is reexamined. Here the surface is stretched with a velocity proportional to the distance from a fixed point. Previous studies on this problem are reviewed and the errors in the boundary conditions at infinity are rectified. It is found that for a very small value of shear in the free stream, the flow has a boundary layer structure when/1ac, where ax and cx are the free stream stagnation-point velocity and the stretching velocity of the sheet, respectively, x being the distance along the surface from the stag- nation-point. On the other hand, the flow has an inverted boundary layer structure when /1ac. It is also observed that for given values of /ac and free stream shear, the horizontal velocity at a point decreases with increase in the pressure gradient parameter. Keywords: Oblique Stagnation-Point Flow, Stretching Surface 1. Introduction The study of the flow of an incompressible viscous fluid over a stretching surface has important bearing on sev- eral technological and industrial processes. Problems such as the extrusion of polymers in melt-spinning, glass blowing, spinning of fibers a several metallurgical as well as metal-working processes involve certain aspects of flow over stretching sheets. Crane [1] obtained a simi- larity solution in closed analytical form for steady two- dimensional flow of an incompressible viscous fluid caused solely by the stretching of an elastic sheet which moves in its own plane with a velocity varying linearly with distance from a fixed point. Chiam [2] investigated steady two-dimensional or- thogonal and oblique stagnation-point flow of an incom- pressible viscous fluid towards a stretching surface in the case when the parameterbrepresenting the ratio of the strain rate of the stagnation-point flow to that of the stretching surface is equal to unity. By removing this highly restrictive assumption (1b), Mahapatra and Gupta [3] analyzed the steady two-dimensional orthogo- nal stagnation-point flow of an incompressible viscous fluid to-wards a stretching surface in the general case 1b. They observed that the structure of the boundary layer depends crucially on the value of b. Reza and Gupta [4] generalized the problem of an oblique stagna- tion-point flow over a stretching surface by Chiam [2] to include surface strain rate different from that of the stagnation flow. But since the displacement thickness arising out of the boundary layer on the surface was ig- nored in their boundary condition at infinity, the analysis in [4] is of doubt full validity. This was rectified in a paper by Lok, Amin and Pop [5]. However, these authors [5] did not take into account the pressure gradient pa- rameter in the boundary condition at infinity. This is a serious omission since the pressure gradient parameter is linked to the free stream shear in the oblique stagna- tion-point flow (Drazin and Riley [6]). Hence the results of the paper in [5] are also of doubtful validity. It is noted that planar oblique stagnation-point flow of an incompressible viscous flow of an incompressible vis- cous fluid towards affixed rigid surface was first studied by Stuart [7]. This problem was later independently in- vestigated by Tamada [8] and Dorrepaal [9]. The ana- logue of the planar oblique stagnation-point flow to stag- nation flow obliquely impinging on a rigid circular cyl- inder was discussed by Weidman and Putkaradze [10]. Exact similarity solutions for impingement of two vis- cous immiscible oblique stagnation flows forming a flat  M. REZA ET AL. Copyright © 2010 SciRes. ENG 706 interface was given by Tilley and Weidman [11]. On the other hand heat transfer in oblique stagnation-point flow of an incompressible viscous fluid towards stretching surface was investigated by Mahapatra, Dholey and Gupta [12]. Further oblique stagnation-point flow of a viscoelastic fluid towards a stretching surface was stud- ied by Mahapatra, Dholey and Gupta [13]. The objective of the present paper is to rectify the er- rors in [4] and [5] and give a correct solution to the above problem. It is worth pointing out that an oblique stagnation-point flow occurs when a separated viscous flow reattaches to a surface. 2. Flow Analysis Consider the steady two-dimensional flow near a stagna- tion point when an incompressible viscous fluid im- pinges obliquely on an elastic surface coinciding with the plane 0y, the flow being confined to 0y. Two equal and opposite forces are applied along the x-axis so that the surface is stretched keeping the origin fixed, as shown in Figure 1. The velocity components in the in- viscid free stream along the x and y directions are 0102 2( ),()UaxbyV ay , (1) respectively, where a and b are constants. Further 2 is the displacement thickness arising out of the boundary layer on the stretching surface and1 is the parameter which controls the horizontal pressure gradi- ent that produces the shear flow. Note that the whole flow field given by (1) may be viewed as being com- posed of an orthogonal stagnation-point flow combined with a horizontal shear flow. The corresponding stream function for the above velocity distribution is 2 021 ()()ax yby (2) There appears a boundary layer on the surface at high Reynolds number. At the stretching surface, the no-slip condition gives ucx,0v at 0y, (3) where c is a positive constant and u and v are the velocity components along x and y directions, re- spectively. In Reza & Gupta [4], stream function in the boundary layer was assumed in the form () (),FW (4) where is the kinematic viscosity and 11 22 , cc xy , (5) This gives the dimensionless velocity components from (4) and (5) as () ()UF W ,(),VF (6) where 12 Uuc and 12.Vvc Using (6) in the Navier-Stokes equations it was shown in [4] that ()F and ()W satisfy the following equations 2 1, F FF Fc (7) 2, F WFWW c (8) where 1 cand 2 care constants. From (6), no-slip condi- tions (3) become (0)0,(0) 1,FF (9) (0) 0,(0) 0.WW (10) Further from (1) and (6), the boundary condition for ()F and ()W at infinity are () a Fc ; 2 () () a Fd c as , (11) 1 ()2 () b Wd c as , (12) where 1 2 22 /dc is the dimensionless displace- ment thickness parameter and 1 2 11 /dc is the dimensionless pressure gradient parameter linked to the free stream shear flow. Reza and Gupta [4] ignored both the constants δ1 and δ2 in (1). While pointing out that δ2 should be taken into account (as mentioned in the Introduction), Lok, Amin & Pop [5] rectified this error in [4]. However, these authors in [5] lost sight of the constant δ1 in (1) and consequently arrived at governing equations for the velocity distribu- tion one of which is incorrect. Hence their analysis is of doubtful validity. Using the boundary conditions (11) and (12) in (7) and (8), we get Figure 1. A sketch of the physical problem. 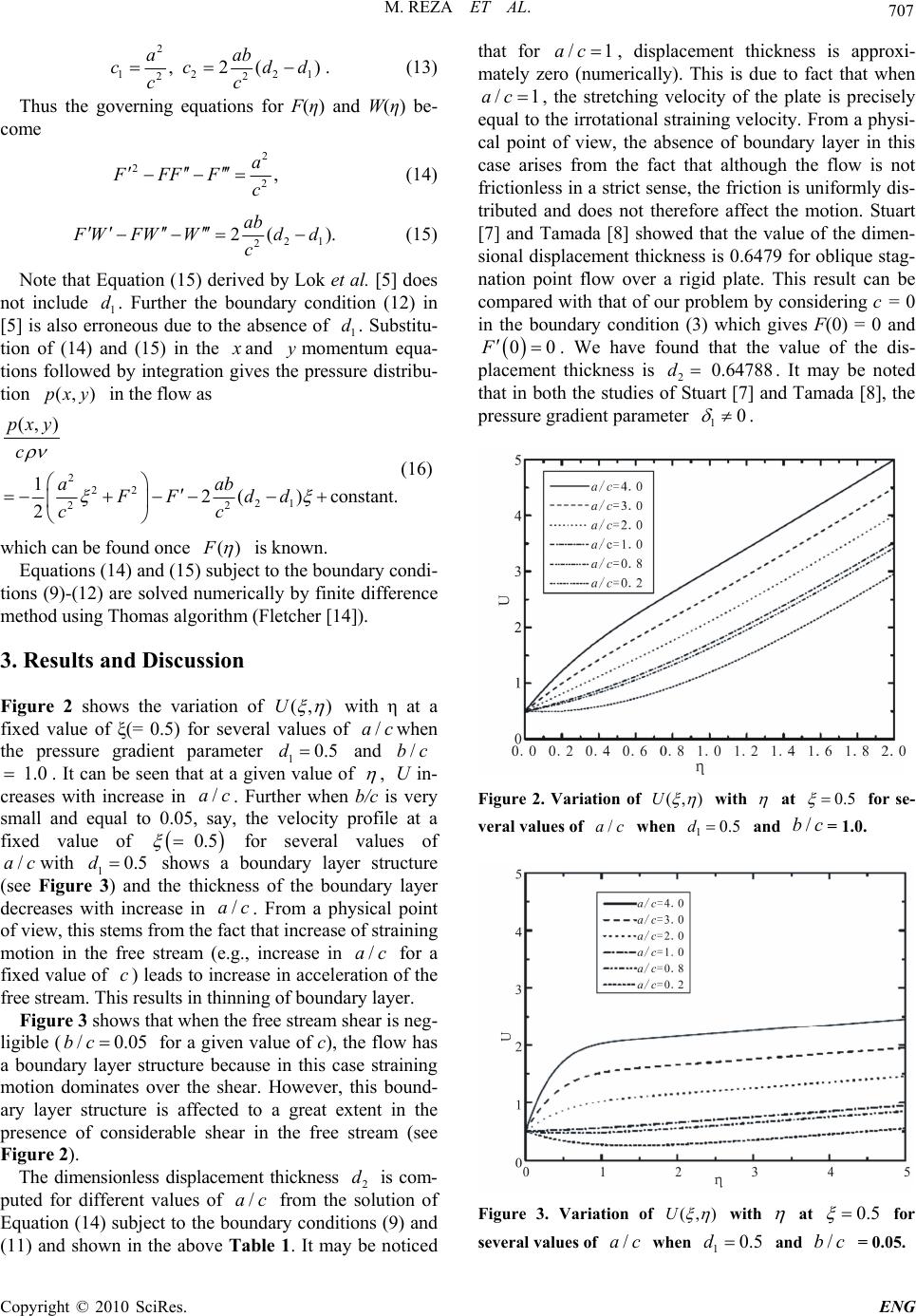 M. REZA ET AL. Copyright © 2010 SciRes. ENG 707 2 12 21 22 ,2( ) aab cc dd cc . (13) Thus the governing equations for F(η) and W(η) be- come 2 2 2, a FFFFc (14) 21 2 2( ). ab F WFWW dd c (15) Note that Equation (15) derived by Lok et al. [5] does not include 1 d. Further the boundary condition (12) in [5] is also erroneous due to the absence of 1 d. Substitu- tion of (14) and (15) in the x and ymomentum equa- tions followed by integration gives the pressure distribu- tion (,) p xy in the flow as 2 22 21 22 (, ) 12 ()constant. 2 pxy c aab FF dd cc (16) which can be found once ()F is known. Equations (14) and (15) subject to the boundary condi- tions (9)-(12) are solved numerically by finite difference method using Thomas algorithm (Fletcher [14]). 3. Results and Discussion Figure 2 shows the variation of (, )U with η at a fixed value of ξ(= 0.5) for several values of /ac when the pressure gradient parameter 10.5d and / bc 1.0. It can be seen that at a given value of , Uin- creases with increase in /ac . Further when b/c is very small and equal to 0.05, say, the velocity profile at a fixed value of 0.5 for several values of /ac with 10.5d shows a boundary layer structure (see Figure 3) and the thickness of the boundary layer decreases with increase in /ac . From a physical point of view, this stems from the fact that increase of straining motion in the free stream (e.g., increase in /ac for a fixed value of c) leads to increase in acceleration of the free stream. This results in thinning of boundary layer. Figure 3 shows that when the free stream shear is neg- ligible (/0.05bc for a given value of c), the flow has a boundary layer structure because in this case straining motion dominates over the shear. However, this bound- ary layer structure is affected to a great extent in the presence of considerable shear in the free stream (see Figure 2). The dimensionless displacement thickness 2 d is com- puted for different values of /ac from the solution of Equation (14) subject to the boundary conditions (9) and (11) and shown in the above Table 1. It may be noticed that for /1ac , displacement thickness is approxi- mately zero (numerically). This is due to fact that when /1ac , the stretching velocity of the plate is precisely equal to the irrotational straining velocity. From a physi- cal point of view, the absence of boundary layer in this case arises from the fact that although the flow is not frictionless in a strict sense, the friction is uniformly dis- tributed and does not therefore affect the motion. Stuart [7] and Tamada [8] showed that the value of the dimen- sional displacement thickness is 0.6479 for oblique stag- nation point flow over a rigid plate. This result can be compared with that of our problem by considering c = 0 in the boundary condition (3) which gives F(0) = 0 and 00F . We have found that the value of the dis- placement thickness is 2 0.64788d . It may be noted that in both the studies of Stuart [7] and Tamada [8], the pressure gradient parameter 10 . Figure 2. Variation of (,)U with at 0.5 for se- veral values of /ac when 10.5d and /bc = 1.0. Figure 3. Variation of (,)U with at 0.5 for several values of /ac when 10.5d and /bc = 0.05. 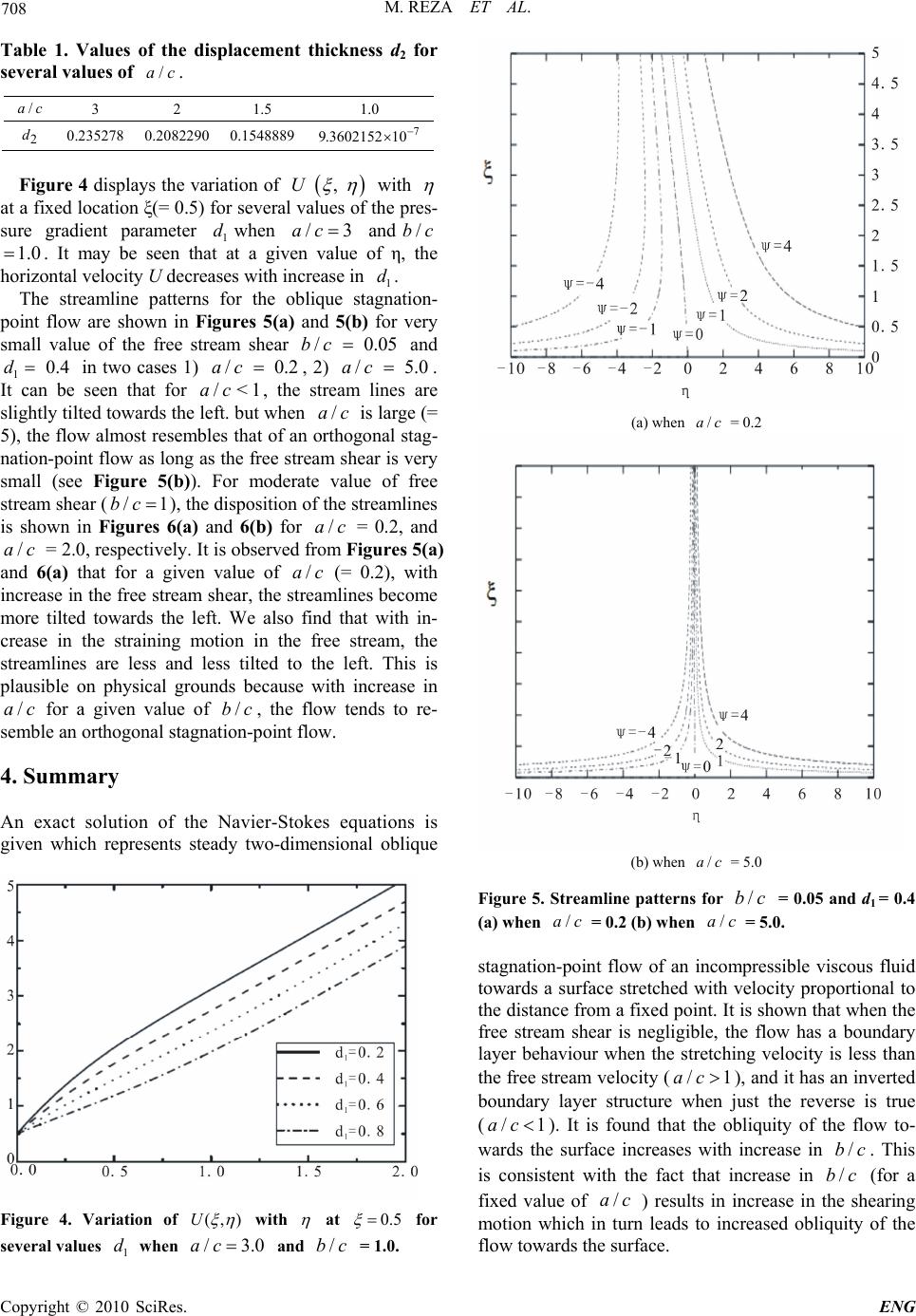 M. REZA ET AL. Copyright © 2010 SciRes. ENG 708 Table 1. Values of the displacement thickness d2 for several values of /ac. /ac 3 2 1.5 1.0 2 d 0.235278 0.2082290 0.1548889 7 9.3602152 10 Figure 4 displays the variation of , U with at a fixed location ξ(= 0.5) for several values of the pres- sure gradient parameter 1 dwhen /3ac and/bc 1.0. It may be seen that at a given value of η, the horizontal velocity U decreases with increase in 1 d. The streamline patterns for the oblique stagnation- point flow are shown in Figures 5(a) and 5(b) for very small value of the free stream shear / 0.05bc and 1 0.4d in two cases 1) / 0.2ac, 2) / 5.0ac . It can be seen that for / < 1ac , the stream lines are slightly tilted towards the left. but when / acis large (= 5), the flow almost resembles that of an orthogonal stag- nation-point flow as long as the free stream shear is very small (see Figure 5(b)). For moderate value of free stream shear (/1bc), the disposition of the streamlines is shown in Figures 6(a) and 6(b) for / ac= 0.2, and / ac= 2.0, respectively. It is observed from Figures 5(a) and 6(a ) that for a given value of / ac(= 0.2), with increase in the free stream shear, the streamlines become more tilted towards the left. We also find that with in- crease in the straining motion in the free stream, the streamlines are less and less tilted to the left. This is plausible on physical grounds because with increase in / acfor a given value of /bc, the flow tends to re- semble an orthogonal stagnation-point flow. 4. Summary An exact solution of the Navier-Stokes equations is given which represents steady two-dimensional oblique Figure 4. Variation of (,)U with at 0.5 for several values 1 d when /3.0ac and /bc = 1.0. (a) when / ac= 0.2 (b) when / ac= 5.0 Figure 5. Streamline patterns for /bc = 0.05 and d1 = 0.4 (a) when / ac = 0.2 (b) when / ac = 5.0. stagnation-point flow of an incompressible viscous fluid towards a surface stretched with velocity proportional to the distance from a fixed point. It is shown that when the free stream shear is negligible, the flow has a boundary layer behaviour when the stretching velocity is less than the free stream velocity (/1ac), and it has an inverted boundary layer structure when just the reverse is true (/1ac ). It is found that the obliquity of the flow to- wards the surface increases with increase in /bc . This is consistent with the fact that increase in /bc (for a fixed value of / ac) results in increase in the shearing motion which in turn leads to increased obliquity of the flow towards the surface. 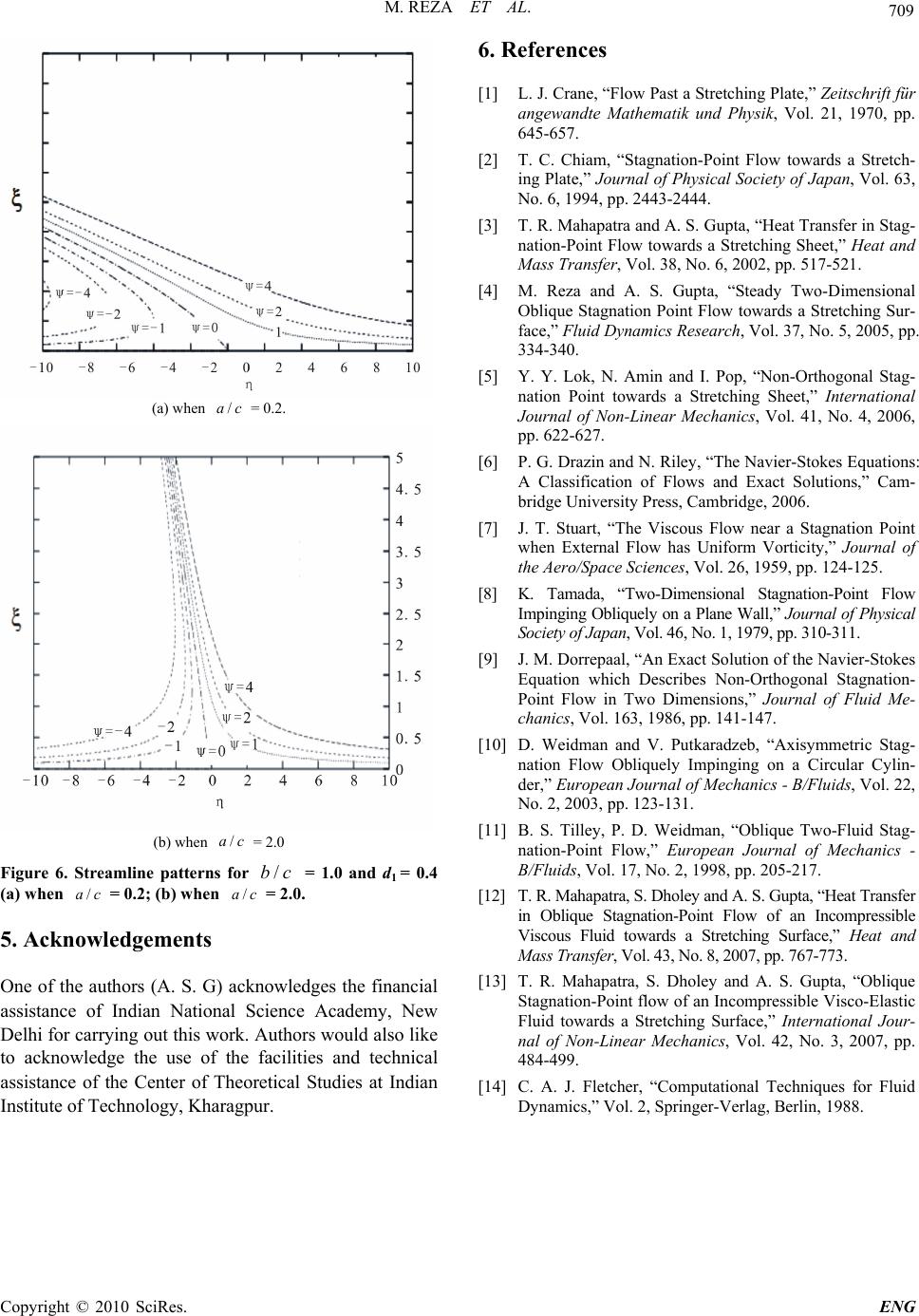 M. REZA ET AL. Copyright © 2010 SciRes. ENG 709 (a) when / ac= 0.2. (b) when / ac= 2.0 Figure 6. Streamline patterns for /bc = 1.0 and d1 = 0.4 (a) when / ac= 0.2; (b) when / ac= 2.0. 5. Acknowledgements One of the authors (A. S. G) acknowledges the financial assistance of Indian National Science Academy, New Delhi for carrying out this work. Authors would also like to acknowledge the use of the facilities and technical assistance of the Center of Theoretical Studies at Indian Institute of Technology, Kharagpur. 6. References [1] L. J. Crane, “Flow Past a Stretching Plate,” Zeitschrift für angewandte Mathematik und Physik, Vol. 21, 1970, pp. 645-657. [2] T. C. Chiam, “Stagnation-Point Flow towards a Stretch- ing Plate,” Journal of Physical Society of Japan, Vol. 63, No. 6, 1994, pp. 2443-2444. [3] T. R. Mahapatra and A. S. Gupta, “Heat Transfer in Stag- nation-Point Flow towards a Stretching Sheet,” Heat and Mass Transfer, Vol. 38, No. 6, 2002, pp. 517-521. [4] M. Reza and A. S. Gupta, “Steady Two-Dimensional Oblique Stagnation Point Flow towards a Stretching Sur- face,” Fluid Dynamics Research, Vol. 37, No. 5, 2005, pp. 334-340. [5] Y. Y. Lok, N. Amin and I. Pop, “Non-Orthogonal Stag- nation Point towards a Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 41, No. 4, 2006, pp. 622-627. [6] P. G. Drazin and N. Riley, “The Navier-Stokes Equations: A Classification of Flows and Exact Solutions,” Cam- bridge University Press, Cambridge, 2006. [7] J. T. Stuart, “The Viscous Flow near a Stagnation Point when External Flow has Uniform Vorticity,” Journal of the Aero/Space Sciences, Vol. 26, 1959, pp. 124-125. [8] K. Tamada, “Two-Dimensional Stagnation-Point Flow Impinging Obliquely on a Plane Wall,” Journal of Physical Society of Japan, Vol. 46, No. 1, 1979, pp. 310-311. [9] J. M. Dorrepaal, “An Exact Solution of the Navier-Stokes Equation which Describes Non-Orthogonal Stagnation- Point Flow in Two Dimensions,” Journal of Fluid Me- chanics, Vol. 163, 1986, pp. 141-147. [10] D. Weidman and V. Putkaradzeb, “Axisymmetric Stag- nation Flow Obliquely Impinging on a Circular Cylin- der,” European Journal of Mechanics - B/Fluids, Vol. 22, No. 2, 2003, pp. 123-131. [11] B. S. Tilley, P. D. Weidman, “Oblique Two-Fluid Stag- nation-Point Flow,” European Journal of Mechanics - B/Fluids, Vol. 17, No. 2, 1998, pp. 205-217. [12] T. R. Mahapatra, S. Dholey and A. S. Gupta, “Heat Transfer in Oblique Stagnation-Point Flow of an Incompressible Viscous Fluid towards a Stretching Surface,” Heat and Mass Transfer, Vol. 43, No. 8, 2007, pp. 767-773. [13] T. R. Mahapatra, S. Dholey and A. S. Gupta, “Oblique Stagnation-Point flow of an Incompressible Visco-Elastic Fluid towards a Stretching Surface,” International Jour- nal of Non-Linear Mechanics, Vol. 42, No. 3, 2007, pp. 484-499. [14] C. A. J. Fletcher, “Computational Techniques for Fluid Dynamics,” Vol. 2, Springer-Verlag, Berlin, 1988. |

