 Journal of Applied Mathematics and Physics, 2013, 1, 1-5 doi:10.4236/jamp.2013.11001 Published Online February 2013 (http://www.scirp.org/journal/jamp) Copyright © 2013 SciRes. JAMP A Ranking Method of Extreme Efficient DMUs Using Super-Efficiency Model* Dariush Akbarian Department of Mathematics, Arak Branch, Islamic Azad University, Arak, Iran. Email: d_akbarian@yahoo.com, d-akbarian@iau-arak.ac.ir Received 2013 Abstract In this paper, we present a method for ranking e xtreme efficient dec ision making units (DMUs) in data envelopment analysis (DEA) models based on measuring distance between them and new PPS (after omissio n extreme efficie nt DMUs ) along the input -axis or outp ut axis. Keywords: Data envelopment ana lysis; Effici ency; Rank i ng. 1. Introduction Data envelopment analysis (DEA) is a non-parametric method for measuring efficiency of a set of Decision Making Units (DMUs) such as firms or a public sector agencies, first introduced by Charnes, Cooper and Rhod es (CCR) [1] and extended by Banke r, Cha rnes, and Cooper (BCC) [2]. One important issue in DEA which has been studied by many DEA researchers, is to discri- minate between efficient DMUs. Several authors have proposed methods for ranking the best performers ([3]-[10] among others). Ying-Ming Wang et al. [10] pro pose d a ranki ng methodology for DMUs by imposing an appro priate minimum weight restriction on all inp uts and outputs, which is decided by a decision maker (DM) or an assessor in terms of the solutions to a series of li- near programming (LP) models that are specially con- structed to determine a maximin weight for each DEA efficient unit. Jahanshahloo et al. [4] proposed a ranking system based on changing reference set. in the proposed ranking system, the evaluation for efficient DMUs is dependent of the efficiency changes of all inefficient units due to its absence in the reference set while the estimate for inefficient DMUs depends on the influence of the e xclus ion of each efficient unit from the reference set. Fo r a review of ra n ki ng me tho d s, re ad ers are referred to Adler et al. [8]; in which the previous methods were divided into six categories. One of the six areas is well-known as the super-efficiency approach, which was first proposed by Andersen and Petersen (AP) [9] to rank extreme efficient DMU s. The main idea of this approach is to evaluate a DMU after this performer itself is ex- cluded from the reference set. However, in some cases, especially under the condition of variable returns to scale (VRS) , the met hod ma y fail due to the i nfeasibili ty prob- lem associated with the super-efficiency models. In this paper, we intend to introduce a new ranking system for extreme efficien t DMUs under the co ndition of VRS and CRS. For this aim, we use a variance of super-efficiency models (see models (6) and (7)) and obtai n the most dis- tance between them and new PPS (after omission ex- treme efficient DMUs) along the input-axis or out- put-axis. Also, our proposed method is able to rank ex- treme efficient DMUs even in presence of infeasibility. This paper is organized as follows. Section 2 presents some basic DEA models. Section 3 introduces our pro- posal and states and proves some facts related to proper- ties and characteristics of it. A numerical example is given in Section 4 and Section 5 comprehends our con- clusions. 2. Background Consider a set of n DMUs which is associated with m inputs and s outputs. Particularl y, ( ϵ= {1, ..., n}) consume s amount xij of input i and produces amount yrj of output r. Let =(1,… , ) in which ≥ 0 & 0 and =1,…, in which ≥ 0 & ≠0. The production possibility set (PPS) of CCR model de- fine as follows: ( ) 1 1 {, |,,0,} nn cj j jjj j j TXY XXYYjJ λ λλ = = =≥≤ ≥∈ ∑∑ and similarly the productio n possibility set of BCC mod- el define as follows:  D. Akbarian ET AL. Copyright © 2013 SciRes. JAMP ( ) 1 11 {, |,,1,0,} n nn vjjjj jj j jj TXY XX YXjJ λλλλ == = =≥≤= ≥∈ ∑ ∑∑ By omitting , fro m , the new pro ducti on pos- sibility set is as follows: {} {} {(,)|,,0,{ }}. nn cjjjJpj jj jJ p TXYXX YYjJp λ λλ ∈− ∈− = ≥∈−≥≤ ∑∑ In fig ur e (1) the polyhedral and are and , respectively. The inp ut-o ri e nte d BC C and i np ut -oriented CCR models, corresponds to, , is given by (1) and (2), re- spectively: 1 min () ms ir ia r ss θ +− = = −∈ + ∑∑ . .1,, 1,, (1) 1 j ijiik jJ j rjrrk jJ j jJ stxsx im y syrs λθ λ λ − ∈ + ∈ ∈ += =… −= =… = ∑ ∑ ∑ 11 min min() m ir s ir tt θ = = +− −∈ + ∑∑ . .1,, 1,, (2) j ijiik jJ j rjrrk jJ stxtx im y tyrs λθ λ − ∈ + ∈ += =… −= =… ∑ ∑ where ϵ is non-Archimedean small and positive number and +, , +and , =1, …, , =1, … ,are called slack variables belong to ≥0. Note that and represent input excesses; also +and + represent output shortfalls. The models (1) and (2) are called envelopment forms (with non-Archimedean number). is said to b e strong efficient (CCR-efficie nt) if and only if: * = 1 and t*+ = 0, t*- = 0. Where the superscript (*) indicates optimalit y. In similar manner the BCC- effi- cient DMUs can be defined. The AP model is as follows [9 ]: {} {} . .1,, 1,, (3) j ijip jJ p j rjrp jJ p stxxim y yrs λθ λ ∈− ∈− ≤=… ≥=… ∑ ∑ The Jahanshahloo’s method corresponding inefficient is as foll ows : [4] ,, 1 } 1 { min min() . .1,, ms ab abi ir r j ijiia jJ b ss stxsx im θ λθ +− = − = − ∈ ∂ ∂=−+ += =… ∑∑ ∑ {} 1,, (4) j rjrra jJ b y syrs λ + ∈− −= =… ∑ The efficiency of strong efficiency will be de- noted by Ω and will be given by: in which is the set of non-strong efficienc y DMUs and is the number of non-strong efficiency DMUs. Jaha nsha hlo o et al. [1 4] used 1-nor m in or der to ra nk the extremely efficient DMUs in DEA models with constant and variable returns to scale, and the proposed method can remove the difficulties arising from AP and MAJ models. Their proposed model is as follows: 11 minΓ(,) ms c pi iprrp ir XYx xyy = = = −+− ∑∑ {} . .1,, j iji jJ p stxxim λ ∈− ≤=… ∑ {} 1,, (5) j rjr jJ p y yrs λ ∈− ≥=… ∑ In this paper we rank DMUs in CCR model; in a similar way one can also rank DMUs in BCC model. The fol- lowing super-efficiency models are used for ranking ex- treme efficient DMUs [12]:  D. Akbarian ET AL. Copyright © 2013 SciRes. JAMP min { } .. pp j ljllk jJ p stx x λθ ∈− ≤ ∑ {} 1, (6) p j ijik jJ p xximi l λ ∈− ≤ =…≠ ∑ {} 1, , p j rjrk jJ k y yrs λ ∈− ≥=… ∑ {} . .1,, p j ijip jJ k stxxim µ ∈− ≤=… ∑ {} ,1,, (7) p j rjrp jJ p yy rsrq µ ∈− ≤ =…≠ ∑ in whi c h =1, … , and =1, … ,. In ord er to rank DMUs in BCC model t he constraint = {}1 is is added to (6) and (7) (see [13]). Remark 1: In (6) and (7), for each and , = = 1 if and only i f st rong e ffi cient lies on the str ong defining hyperplane of PPS. In fact it is an interio r point of strong defini ng h yper p lane . Figure 1: The value distance of from new PP S (′v) a long t he x-a xis and y-axis Remark 2: In (6) (or (7)), if for some (or ), >1 (or <1) or if for some l(or q), model (6) (or model (7)) is infeasible then, stro ng efficient lies on the extreme ray (edge) of PPS and vice versa. (For more details on models (6) and (7) see [12].) We call all efficie nt DMUs lying on extreme ray (edge) of PPS of CCR model as extreme efficient DMUs, he- reafter. Remark 3: In multiple output case, if for some model (7) is infeasible then, virtual DMU ( ) '11 ,,, ,,,, kkmk kqksk DMUxx yyy γ =……−… in which > 0, is on the weak defining hyperplane of PPS vertical to hyperp lane =0. Remark 4: In multiple inputs case, if for a t le a st one , model (6) is infeasible then v irtual DMU ′=(1,…,+,…,,1,…,) in whic h > 0, is on the weak defining hyperplane which passes through th axis of input .1 3. A proposed method for ranking by su- per-efficiency model We state the following theorem without proof. Theorem 1: If there exist at least two DEA-efficient DMUs then, there is at least one (or ) so that model (6) (or model (7)) is feasible. First, we evaluate each , ( ϵ ), by models (2). Suppose that DMUs are strong efficient. Without lose of generality we can assume that these efficient DMUs are 1 ,…, . Consider the set = {1 , ..., }. Then, corr espondi ng to each , ( ϵ ), we solve the models (6) and (7). In view of remarks 1,2 we can iden- tify all extreme efficient DMUs. Corresponding each extreme efficient we ob- tain and , = 1,…, , = 1,..., . Note that for so me and the models (6) and (7) may be infeasible. But by theorem 1 for there exist at least for one or so that the models (6) or (7) have fi- nite optimal solution. We have: 1=The value distance of from new PPS (′Tc) along the th axis of input. 1 =The value distance of from new PPS (Tc) along the th axis of output. Where it is understood that the above value distances are taken ove r existing and (see Fig. 1). Let =max ,{ 1, 1 } In order to judge which DMU has better rank in compar- ison with other DMUs, the following definition is given: Definition. has a better rank in comparison with if > . The following theorem shows that our proposed method has more influence to the PPS of DEA models than 1-method has . 1For mor e det ail see [12 ]. 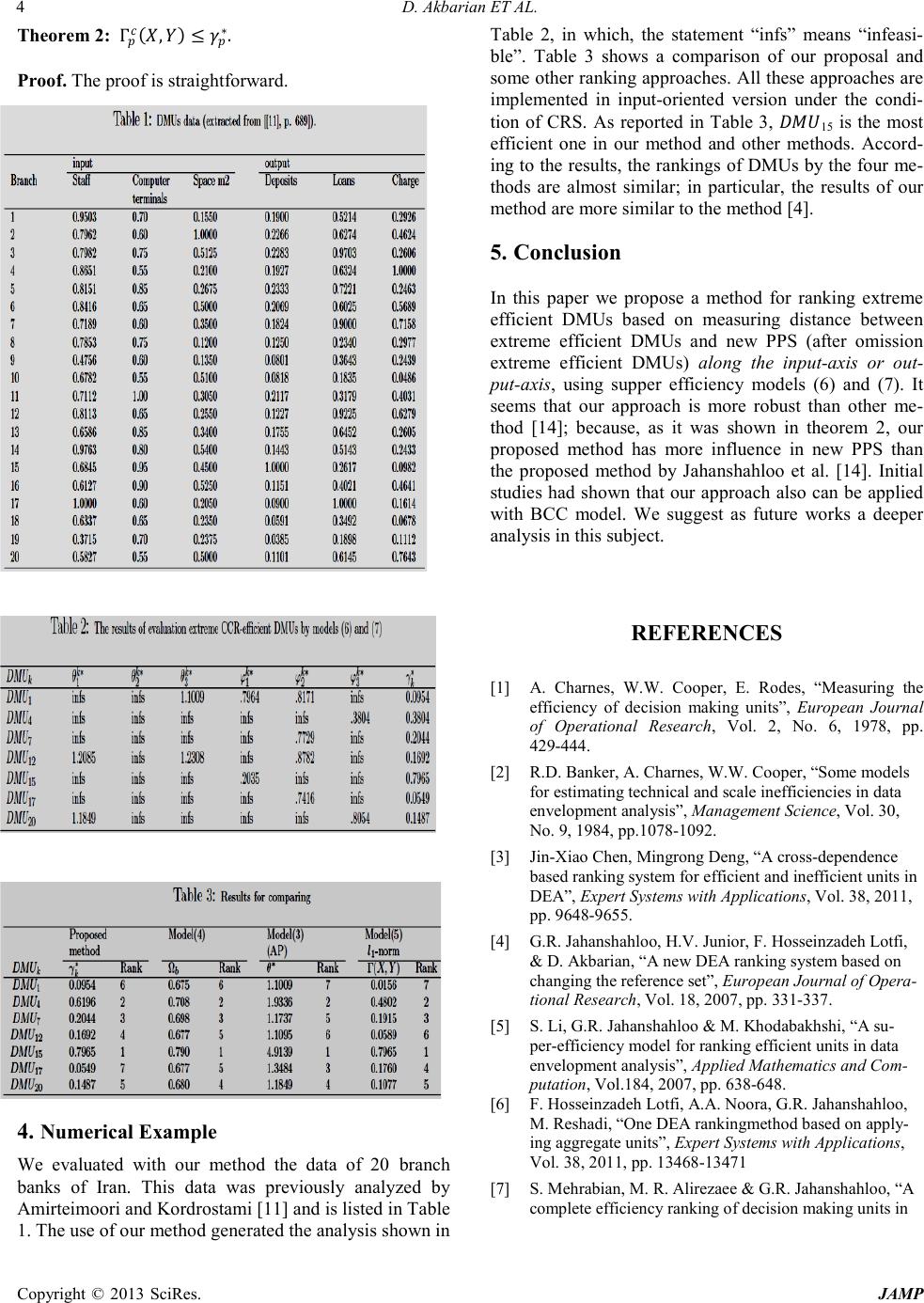 D. Akbarian ET AL. Copyright © 2013 SciRes. JAMP Theorem 2: (,) . Proof. The proof is straightforward. 4. Numerical Example We evaluated with our method the data of 20 branch banks of Iran. This data was previously analyzed by Amirteimoori and Kordrostami [11] and is listed in Ta ble 1. The use of our method generated the analysis shown in Table 2, in which, the statement “infs” means “infeasi- ble”. Table 3 shows a comparison of our proposal and some other ranking approaches. All these approaches are implemented in input-oriented version under the condi- tion of CRS. As reported in Table 3, 15 is the most efficient one in our method and other methods. Accord- ing to t he results , the ran kings o f DMUs by the four me- thods are almost similar; in particular, the results of our method are more similar to the method [4]. 5. Conclusion In this paper we propose a method for ranking extreme efficient DMUs based on measuring distance between extreme efficient DMUs and new PPS (after omission extreme efficient DMUs) along the input-axis or out- put-axis, using supper efficiency models (6) and (7). It seems that our approach is more robust than other me- thod [14]; because, as it was shown in theorem 2, our proposed method has more influence in new PPS than the proposed method by Jahanshahloo et al. [14]. Initial studies had shown that our approach also can be applied with BCC model. We suggest as future works a deeper analysis in t hi s subject. REFERENCES [1] A. Charnes, W.W. Cooper, E. Rodes, “Measuring the efficiency of decision making units”, European Journal of Operational Research, Vol. 2, No. 6, 1978, pp. 429-444. [2] R.D. Banker, A. Charnes, W.W. Cooper, “Some models for estimating tech nical and scale i nefficiencies in data envelopment analysis”, Management Science, Vol. 30, No. 9, 1984, pp.1078-1092. [3] Jin-Xiao Chen, Mingrong Deng, “A cross-dependence based r anking system for efficient and inefficient units in DEA”, Expert Systems with Applications, Vol. 38, 2011, pp. 9648-9655. [4] G.R. Jahanshahloo, H.V. Junior, F. Hosseinzadeh Lotfi, & D. Akbarian, “A new DEA ranking system based on changing the reference set”, European Journal of Opera- tional Resea rch, Vol. 18, 2007, pp. 331-337. [5] S. Li, G.R. Jahanshahloo & M. Khodabakhshi, “A su- per-efficiency model for ranking efficient units in data envelopment analysis”, Applied Mathematics and Com- putation, Vol .184, 20 07, pp. 638-648. [6] F. Hosseinzadeh Lotfi, A.A. Noora, G.R. Jahanshahloo, M. Reshadi, “One DEA rankingmethod based on apply- ing aggregate un its”, Expert Systems with Applications, Vol. 38, 2011, pp. 13468-13471 [7] S. Mehrabian, M. R. Alirezaee & G.R. Jahanshahloo, “A complete efficiency ranking of decision making units in  D. Akbarian ET AL. Copyright © 2013 SciRes. JAMP data en vel opment analysis”. Computational Optimization and Applications, Vol. 14, 1999, pp. 261-266. [8] N. Adl er, L. Fri edman & Z. Sinuany-Stern, “Review of ranking methods in the data envelopmentanalysis con- text”, European Journal of Operational Research, Vol. 140, 2000, pp. 249-265. [9] P. Andersen & N .C. Pet er s en, “A procedure for ranking efficient unit s in data en vel opment analysis”, Manage- ment S cience, Vol. 39, 1993, pp. 1261-1264. [10] Y.M. Wanga, Y. Luob, L. Liang, “Ranking decision making units by imposing a minimum weight restriction in the data envelopment analysis”, Journal of C om p ut a- tional an d A ppli ed Mathematics, Vol. 223, 2009, pp. 469-484. [11] A. Amirteimoori & S. Kordrostami, “Efficient surfaces and an efficiency index in DEA: A const a nt re tur ns to scale”, Applied Mathe m at ic s and Com put at ion , Vol. 163, 2005, pp. 683-691. [12] G.R. Jahanshahloo, F. Hosseinzadeh Lotfi & D. Akbarian, “Finding weak defining hyperplanes of PPS of the CCR model”, submited to journal Applied Mathematical Mod- elling, Vol. 34, 2010, pp. 3321-3332. [13] G.R. Jahanshahloo, F. Hosseinzadeh Lotfi & D. Akba- rian, ”Finding weak defining hyperplanes of PPS of the BCC model”, Applied Mathematical Modelling, Vol. 34, No.11, 20 10, pp. 3321-3332. [14] G.R. Jahanshahloo, F. Hosseinzadeh Lotfi, N. Shoja, G. Tohidi, S. Razavian, “Ranking by sing 1-norm in data envelopment analysis”, Applied Mathematics and Com- putation, Vol. 153, 2004, pp. 215-224.
|