Paper Menu >>
Journal Menu >>
 J. Service Science & Management, 2010, 3, 373-382 doi:10.4236/jssm.2010.33044 Published Online September 2010 (http://www.SciRP.org/journal/jssm) Copyright © 2010 SciRes. JSSM 373 Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Mohamad K. Hasan1*, Ahmad A. Al Hammad2 1Department of Quantitative Methods and Information Systems College of Business Administration, Kuwait University, Safat, Ku- wait; 2Quantitative Analysis Department College of Business Administration King Saud University, Riyadh, Saudi Arabia. Email: mkamal@cba.edu.kw, ahammad@ksu.edu.sa Received April 22nd, 2010; revised May 29th, 2010; accepted July 8th, 2010. ABSTRACT The Saudi Public Transport Company (SAPTCO) intercity bus schedule comprises a list of 382 major trips per day to over 250 cities and villages with 338 buses. SAPTCO operates Mercedes 404 SHD and Mercedes 404 RI-IL fleet types for the intercity trip. The fleet assignment model developed by American Airlines was adapted and applied to a sample of the intercity bus schedule. The results showed a substantial saving of 29% in the total number of needed buses. This encourages the decision makers at SAPTCO to use only Mercedes 404 SHD fleet type. Hence, the fleet assignment model was modified to incorporate only one fleet type and applied to the sample example. Due to the increase in the problem size, the model was decomposed by stations. Finally, the modified decomposed model was applied to the whole schedule. The model results showed a saving of 16.5% in the total number of needed buses of Mercedes 404 SHD. A sensitivity analysis was carried out and showed that the predefined minimum connection time is critical for model effi- ciency. A modification to the connection time for 11 stations showed a saving of 14 more buses. Considering our rec- ommendation of performing a field study of the trip connection time for every station, the expected saving of the total number of needed buses will be about 27.4% (90 buses). This will yield a net saving of 16.44 million Saudi Riyals (USD 4.4 million) per year for SAPTCO in addition to hiring new employees. The revenue analysis shows that these 90 sur- plus buses will yield about USD 20,744,000 additional revenue yearly. Keywords: Fleet Assignment Model, Bus Scheduling, Integer Programming, Transportation Service, Revenue Management 1. Introduction 1.1. Problem Definition SAPTCO has 382 intercity major trip departures every day. This excludes the local services and the international services to Egypt, Kuwait, Jordan, Sudan, Qatar, Bahrain, Syria, Turkey, and The United Arab Emirates. This Inter- city schedule is produced by considering an existing set of trips, traffic revenue forecasts, available resources such as buses, drivers’ base, maintenance shop base, and associ- ated operating cost. SAPTCO is applying an assignment system such that the buses and drivers are assigned to 14 main stations, i.e., each station has its own bus fleet and drivers. According to that system’s work regulations, the drivers are assigned to the trip schedule, then, a bus is assigned to one or two scheduled drivers, depending on the length of the trip to operate his (their) scheduled trip. The work regulations require that: a) Each driver takes a minimum number of hours off work before he takes another trip which may be to another station or to his original (base) station. b) Each driver has to take one day off work per week. According to a) of work regulations, during driver’s rest time the bus which is assigned to him cannot be assigned to another driver, the bus is idle at this rest time which can sometimes be more than 12 hours, whereas, b) means that the bus is idle for a whole day during its driver’s rest. Since the trips are scheduled for all week days, an additional number of buses are required to cover this rest day for all drivers. These additional buses are estimated to be 16.6% of the daily used scheduled buses.  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 374 At SAPTCO, two points of view can be identified: one is expressed by the maintenance department who wants to retain this existing assignment system. The other point of view is expressed by the operations department who seeks “better” assignment system. This research paper proposes a new assignment system which takes into account maxi- mizing the utilization of any bus in the fleet. This means that it should take a few hours (three are proposed for the most stations) after the bus’s arrival at any station to be prepared (e.g., maintenance checking, bus cleaning... etc.) for operating any other scheduled trip by any scheduled driver for this trip. In contrast, the proposed assignment system first assigns buses to the trips schedule, and then assigns drivers to those scheduled buses. 1.2. Literature Review The fleet assignment problem for airline industries ad- dresses the question of how to best assign aircraft fleet types to an airline’s schedule of flight legs. A flight leg is defined as a journey consisting of a single take off and landing, and thus constitutes the smallest unit of opera- tion that can be assigned an aircraft. A flight schedule is a set of light legs with specified departure and arrival air- ports and times (arrival times can be fleet specific). A fleet assignment is a function that assigns a fleet type to each flight leg [1]. The scale and complexity of fleet assignment problems and their large cost implications have motivated the de- velopment of optimization-based methods to solve them. Abara [2] presents a formulation for a general flight Net- work based on a partial enumeration of “feasible turns”, that is, connection opportunities between pairs of fl ight legs. The model was formulated and solved the fleet assignment problem as an integer linear programming model, permitting assignment of two or more fleets to a flight schedule simultaneously. The objective function of the model can take a variety of forms including profit maximization, cost minimization, and the optimal utili- zation of a particular fleet type. Several departments at American Airlines use the model to assist in fleet plan- ning and schedule development. Subramanian et al. [3] developed a model for Delta Airlines that assigns fleet types, not individual aircraft tail numbers, to the flight legs. They showed that actual aircraft are routed after the model is solved to ensure that the solution is operational. Because of the hub- and-spoke nature of operations and large fleet sizes, it is always possible to obtain a feasible tail routing from the assignment recommended by the model. Kontogiorgis and Acharya [4] developed schedule plan- ners for US Airway that balanced between meeting week- end passenger demand, which is different from weekday demand, and also minimize the costs of realigning airport facilities and personnel that we would incur by changing fight patterns too much. They built a specialized fleet- assignment model and integrated it into a graphical en- vironment for schedule development. The US Airway’s planners used the system to create safe, profitable, and robust flight plans. Rexing et al. [5] developed a generalized fleet assign- ment model for simultaneously assigning aircraft types to flights and scheduling flight departures. Their model, a simple variant of basic fleet assignment models, assigns a time window to each flight and then discretizes each window, allowing flight departure times to be optimized. Because problem size can become formidable, much larger than basic fleet assignment models, they devel- oped two algorithmic approaches for solving the model. Ahuja et al. [6] developed a new approach that is ba- sed on generalizing the swap-based neighborhood search approach of Talluri [7] for FAM, which proceeds by swapping the fleet assignment of two flight paths flown by two different plane types that originate and terminate at the same stations and the same times. An important feature of their approach is that the size of our neighbor- hood is very large; hence the suggested algorithm is in the category of very large-scale neighborhood search al- gorithms. Sherali and Zhu [8] proposed a two-stage stochastic mixed-integer programming approach in which the first stage makes only higher-level family-assignment deci- sions, while the second stage performs subsequent family based type-level assignments according to forecasted market demand realizations. By considering demand un- certainty up-front at the initial fleeting stage, they in- jected additional flexibility in the process that offers more judicious opportunities for later revisions. They conducted a polyhedral analysis of the proposed model and developed suitable solution approaches. Their results of some numerical experiments were presented to exhibit the efficacy of using the stochastic model as opposed to the traditional deterministic model that considers only expected demand, and to demonstrate the efficiency of the proposed algorithms as compared with solving the model using its deterministic equivalent. Jacobs et al. [9] presented a new methodology for in- corporating origin and destination (O&D) network ef- fects into the fleet assignment process. The methodology used a decomposition strategy to combine a modified version of a leg-based fleet assignment model (Leg-FAM) with the network flow aspects of probabilistic O&D yield management. By decomposing the problem, the nonlin- ear aspects of the O&D market effects and passenger flow were isolated in O&D yield management and in-  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 375 corporated in FAM using linear approximations to the total network revenue function. Barnhart et al. [1] presented a subnetwork fleet assign- ment model that employs composite decision variables representing the simultaneous assignment of fleet types to subnetworks of one or more flight legs. Their formulation is motivated by the need to better model the revenue side of the objective function. They presented a solution me- thod designed to balance revenue approximation and model tractability. Computational results suggested that the approach yields profit improvements over comparable models and that it is computationally tractable for prob- lems of practical size. In addition to the above literature reviews, many local public transport studies that were done for SAPTACO were reviewed. The main objective of this paper is to evaluate the two points of view of the maintenance department and the operations department through developing a new fleet assignment model (new bus schedule). In next section, the fleet assignment problem (the proposed assignment system) is formulated and solved as an Integer Linear Programming (ILP) problem. This was done by adapting the fleet assignment model developed at American Airlines [2]. Section 3 shows the result of the assignment model application on a sample example and the whole schedule. It also shows model efficiency, cost analysis, sensitivity analysis and revenue management that are conducted for both existing and proposed as- signment systems. Section 4 summarizes and identifies the main findings and conclusions. Finally, Section 5 gives some directions for futher reaearch. 2. The Assignment Model The existing assignment system, first, assigns the drivers to the service schedule, then assigns a bus to one or two scheduled drivers to operate his (their) scheduled trip in this way the bus and the driver is one unit that cannot be separated even at the driver’s rest time. Therefore, a proposed assignment system should take into account splitting this unit to maximize the utilization of any bus in the fleet. In another words, the proposed system should first assign the buses to the service schedule, then assign drivers to those scheduled buses. This means that the bus can be used by more than one or two scheduled drivers during one day cycle. This can be done by taking into account after the bus finished its scheduled trip to any station , it should take a few hours (three are proposed by maintenance department for most stations) to be prepared (e.g., normal maintenance checking, bus cleaning,...etc.) to operate any other scheduled trip by any scheduled driver for this trip. In case of major maintenance repair that takes more than three hours, the bus should be re- placed by another unscheduled bus. To design this proposed assignment system, the fleet assignment model developed at American Airlines was adapted. The goal of our fleet assignment model is to assign as many trip segments as possible in the SAPTCO’s intercity bus schedule to one or more bus fleet types. (SAPTCO operates Mercedes 404 SHD and Mercedes 404 RHL fleet types for the Intercity trip) while optimiz- ing some objective (e.g., maximize the utilization of Mercedes 404 SHD fleet type, minimize the total number of needed buses, minimize the cost of imbalance schedule) and meeting sets of constraints (e.g., trip coverage, con- tinuity of equipment, schedule balance, and bus count). The model uses integer linear programming to solve the fleet assignment problem. Given a service schedule, with departure and arrival times indicated, it determines which bus trip should be assigned to which bus types to optimize the objective function. 2.1. Model Formulation 2.1.1. Constraints 1) Trip coverage: After many interviews with the decision makers of maintenance department of SAPTCO, it was determined that a minimum of three hours time will be enough for any arriving trip at a specific station to finish normal bus maintenance checking and bus cleaning, so that this trip (bus) can be connected with any departing trip from the same station whose departure time permits this minimum three hours for connection. We will refer to Trip-to-Trip by turns. Typically, an arriving trip can turn to more than one departing trip. Figure 1 shows four arriving trips to the Riyadh station (Trips: 1318, 763, 765 and 1931) and five departing trips (Trips: 768, 772, 1313, 1317 and 1948) from the same station. Allowing a minimum connection time of three hours, 22 turn variables per bus type are possible as follows: 0000-768, 0000-772, 0000-1313, 0000-1317, 0000- 1948, 1318-772, 1318-1313, 1318-1317, 1318-1948, 763- 772, 763-1313, 763-1317, 763-1948, 765-1313, 765-1317, 765-1948, 1931-1317, 1931-1948, 1318-0000, 763-0000, 765-000, 1931-0000, where the turn 1318-0000 represents a termination trip in Riyadh, i.e.. the bus that operated trip 1318 should be overnighting in Riyadh and cannot be connected to any other departing trip on the same day. While, the turn 0000-768 represents an origination trip from Riyadh, i.e. , the bus that will operate trip 768 is already in the Riyadh station from last night and not ar- riving from any other station on the same day. Now, we can define the decision variable ,, ijk X to represent a feasible turn where the arriving trip i turns to the departing trip j on bus type k . If 0 i = , then j is a sequence origination and, if 0 j = , then i is a sequence  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 376 Arriving Trip Arriving Departing Trip Departing From No Time Time No To Jeddah 1318 11:00 12:30 768 Dammam Dammam 763 12:30 15:30 772 Dammam Dammam 765 14:00 18:00 1313 Jeddah Abha 1931 19:00 22:00 1317 Jeddah Arrivals 23:00 1948 Abha Departures Figure 1. Four arrivals and five departures trips (Riyadh Station). termination where sequence represents the daily routing for a bus. If 1 k = represents Mercedes 404 SHD bus type and 2 k = represents Mercedes 404 RHL bus type, then 1318.772.1 1 X = means that the trip 1318 arriving to Riyadh from Jeddah can be turned (connected) to trip 772 departing from Riyadh to Dammam using Mercedes 404 SHD bus type. While 1318.772.1 0 X = means that the trip 1318 cannot be connected to trip 772 using Mercedes 404 SHD bus type (i.e., it may use Mercedes 404 RHL bus type or connected to any trip other than 772). Hence, ,, 0 1 ijk Xor = . To prevent trips being counted twice, each trip must be served exactly once. That is, each departing trip must be a turn of only one arriving trip or being an originating trip and use only one bus type. This means, for example, neither 1318.772.1 1 X = and 763.772.1 1 X = nor 1318.772.1 1 X = and 1318.772.2 1 X = can happen. Suppose that T repre- sents the total number of scheduled trips, then the first constraint can be written as follows: 2 ,, 01 =1 Tk ijk ik Xj = == ∀ ∑∑ (1) 2) Continuity of equipment: To assure the integrity of the network, each trip being served must begin (sequence origination or continued from another trip) and end (sequence termination or turn into another trip) on the same bus type. This constraint can be stated as follows: ,,,, 00 , TT ilkljk ij XXlk == =∀ ∑∑ (2) 3) Schedule balance by station and bus type: An excess of arrivals over departures at a given station results in a sequence origination shortage; the reverse situation leads to a sequence termination shortage. Figure 2 shows an example of this case where there are three sequences for three stations Riyadh, Dammam, and Jed- dah: 1350-771-1317, 761-1309-1352, 765-1313. Riyadh station is balanced while Dammam and Jeddah Stations are not. Jeddah station has one origination trip represented by OR (trip 1350) and two termination trips represented by TE (trip 1313 and trip 1317), i.e., there is a sequence origination shortage at Jeddah station. There is a reverse situation at Dammam station where a sequence termina- tion shortage happens. A difference between the schedule’s total departures and total arrivals represents a physical imbalance. To overcome this imbalance, we introduce the following decision variables: sk O = No. of origination shortages at station s for bus type k . sk R = No. of terminations shortages at station s for bus type k . Therefore, the sum of sequence originations and the origination shortage variable ( sk O ) must be equal to the sum of sequence terminations and the termination short- age variable ( sk R ) for each station s and bus type k . Hence, the third constraint can be written as follows: 0,,,0, = , ss jkskiksk jDiA XOXRks ∈∈ ++∀ ∑∑ (3) where s D = Set of departures from station s s A = Set of arrivals at station s . 4) Bus count The main objective of the assignment model, as we will see later, is to minimize the number of buses used. Therefore, if the schedule is too small for the available buses, only the number needed should be used. In con- trast, if the schedule is too large, then the available buses of the two types should be exhausted before any addi- tional buses can be added. The constraint can be stated as follows: 0,, 1 T jkkk j XEMk = −≤∀ ∑ (4) where k M = Number of available buses of type k in all  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 377 Figure 2. Imbalance schedule. stations. k E = Number of the additional buses of type k in all stations that are needed beyond the available number to cover the service schedule. 2.1.2. Objective Function After many interviews with the decision makers in the SAPTCO operations department, the following goals that should be satisfied by the model were determine: 1) Mercedes 404 SHD bus type must be used for a specific trip (e.g., Riyadh-Jeddah, Riyadh-Makkah, Ri- yadh- Madinah, etc). After covering all of these specified trips, it is preferred to use this bus type for any others trips until it is exhausted. Then, Mercedes 404 RHL bus type should cover the remaining trips. To incorporate this goal into the model the following parameter is defined: jk b = Benefit of operating trip j on bus type k where values of jk b for the following cases can be as- sumed: • If Mercedes 404 SHD bus type must be used, then 1 4 j b = and 2 0 j b = . • If Mercedes 404 SI-1D bus type is preferred to be used, then 1 3 j b = and 2 2 j b = . Hence, this goal can be written as: 2 ,, 001 TTK jkijk ijk MaximizebX = === ∑∑∑ 2) A minimum number of buses must be used to mini- mize the total operation cost or to maximize the total profit (the revenue is fixed). This goal consists of two parts; in the first part, the use of the available buses (the origination trips) must be reduced. In the second, the use of the additional buses ( k E ) must be reduced by impos- ing a large cost or penalty of using it. This can be stated as follows: 22 0,,1 111 Tkk jkk jkk MinimizeXCE == === + ∑∑∑ where 1 C is a large penalty value, say, 1 1000000 C=. 3) Shortages in sequence originations and terminations result in dead-heading and incur costs. To reduce the chance of producing an imbalance schedule, a large pen- alty value is imposed for the decision variables sk O and sk R in the objective function as follows: ( ) 2 211 Sk sksk sk MinimizeCOR = == + ∑∑ where S is the total number of stations and 2 C is a large penalty value , say, 2 500000 C=. Combining all of the above model ingredients, the ILP assignment model is: ILP: ( ) 22 ,,2 00111 22 0,,1 111 TTKSk jkijksksk ijksk Tkk jkk jkk MaximizebXCOR XCE == ===== == === −+ −− ∑∑∑∑∑ ∑∑∑  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 378 Subject to: 2 ,, 01 1 Tk ijk ik Xj = == =∀ ∑∑ ,,,, 00 = , TT ilkljk ij XXlk == ∀ ∑∑ 0,,,0, = , ss jkskiksk jDiA XOXRks ∈∈ ++∀ ∑∑ 0,, 1 T jkkk j XEMk = −≤∀ ∑ where ,,, kskskk EORandE are decision variables taking the following values: ,, 0,1 ijk X= and ,, 0,1,2,3,... skskk ORandE = 3. The Results 3.1. Sample Example Results for Two Fleet Types To validate the model before its application to the whole schedule, we selected a sample of 40 trips which satisfy all the model requirements. This sample example con- sists of five main stations: Riyadh, Jeddah, Dammam, Madinah, and Abha, and four minor stations: Bishah, Jawf, Khafji, and Qurayyat. A three-hour period was chosen as minimum time for any arrival trip to turn (be connected) to any departure trip at the same station. Two buses types Mercedes 404 SHD ( 1 K = in the model) and Mercedes 404 RHL ( 2 K = in the model), were used. The results of this application showed that all con- straints were satisfied, that is, for each bus type each de- parting trip was indeed, a connection (turn) of only one arriving trip or an origination trip which satisfies the first trip coverage constraint. Each arriving trip was turned (connected) to only one departing trip, or it was a termi- nation trip on the same bus type, which satisfies the sec- ond constraint. Constraint (4), bus count, was satisfied for each station where the number of origination trips never exceeded the number of the available buses plus the additional ones. Table 1 shows that the number of origination (orig.), connection (con.), termination (term.), and departure (dep.) trips for each main and minor sta- tion where the number of origination trips plus the num- ber of connection trips is equal to the total number of departure trips, while the number of termination trips plus the number of connection trips is equal to the total number of arrival trips. Since the total number of depar- ture trips is equal to the total number of arrival trips for each station and the satisfaction of constraint (3) of the assignment model, in addition to forcing the values of sk O and sk R in the last part of the objective function to be zero through the penalty value 2 500000 C=, then the total number of origination trips is always equal to the total number of termination trips. This means that for any terminated arrival trip, the bus will be overnighting in the station then operate the next day origination trip. This makes a balanced sched- ule. To compute the needed number of bused to cover the 40 trips sample example, as shown in Table 2, we added the trip time (the time that the trip took from the depar- ture station to the arrival station) and the connection time (the actual time that elapsed for any arrival trip to a spe- cific station to connect another departure trip from the same station) for all trips, then divided these number of hours by 24. That is, the total number of needed buses is given by the following: 24 438.75329.25 32 24 Totalnumberofneededbuses TotaltripstimeTotaltripsconnectiontime buses + = + == Using the existing assignment system, the actual number of needed buses was 45 buses of both types. This means 13 (29% saving) buses were saved using the pro- posed assignment system. 3.2. Model Modification to Incorporate Only One Bus Type (Mercedes SHD 404) The good saving in the total number of needed buses encourages the decision makers at SAPTCO to decide to use only Mercedes 404 SHD bus type. Therefore, we Table 1. Summary results of the application of the assignment model on the sample example. Main Stations Minor Stations Riyadh Jeddah Dammam Abha Madinah Bishah Jawf Khafji Qurayyat Total Orig. 2 1 1 0 0 2 0 2 0 8 Con. 7 4 6 5 3 1 3 0 3 32 Term. 2 1 1 0 0 2 0 2 0 8 Dep. 9 5 7 5 3 3 3 2 3 40 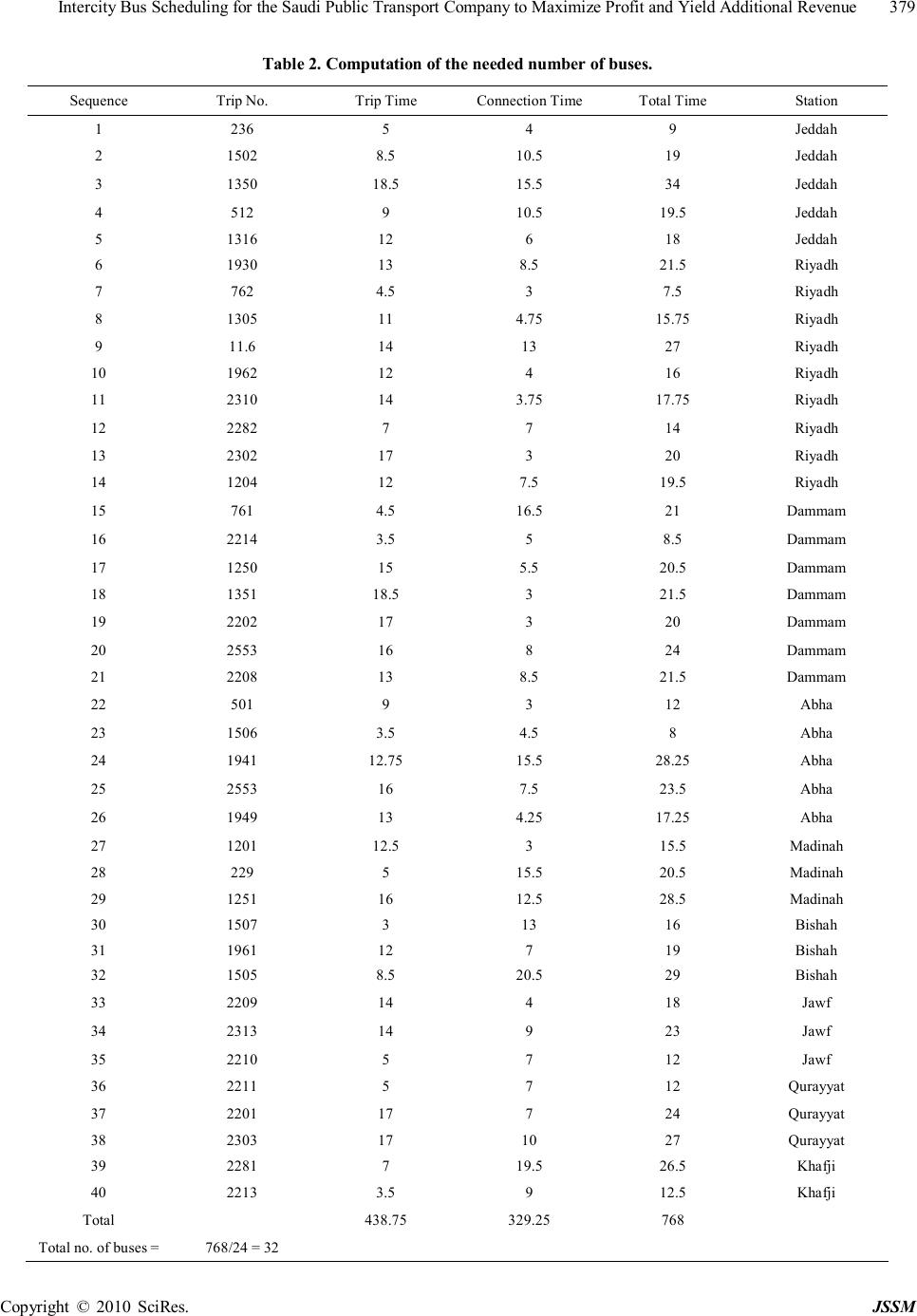 Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 379 Table 2. Computation of the needed number of buses. Sequence Trip No. Trip Time Connection Time Total Time Station 1 236 5 4 9 Jeddah 2 1502 8.5 10.5 19 Jeddah 3 1350 18.5 15.5 34 Jeddah 4 512 9 10.5 19.5 Jeddah 5 1316 12 6 18 Jeddah 6 1930 13 8.5 21.5 Riyadh 7 762 4.5 3 7.5 Riyadh 8 1305 11 4.75 15.75 Riyadh 9 11.6 14 13 27 Riyadh 10 1962 12 4 16 Riyadh 11 2310 14 3.75 17.75 Riyadh 12 2282 7 7 14 Riyadh 13 2302 17 3 20 Riyadh 14 1204 12 7.5 19.5 Riyadh 15 761 4.5 16.5 21 Dammam 16 2214 3.5 5 8.5 Dammam 17 1250 15 5.5 20.5 Dammam 18 1351 18.5 3 21.5 Dammam 19 2202 17 3 20 Dammam 20 2553 16 8 24 Dammam 21 2208 13 8.5 21.5 Dammam 22 501 9 3 12 Abha 23 1506 3.5 4.5 8 Abha 24 1941 12.75 15.5 28.25 Abha 25 2553 16 7.5 23.5 Abha 26 1949 13 4.25 17.25 Abha 27 1201 12.5 3 15.5 Madinah 28 229 5 15.5 20.5 Madinah 29 1251 16 12.5 28.5 Madinah 30 1507 3 13 16 Bishah 31 1961 12 7 19 Bishah 32 1505 8.5 20.5 29 Bishah 33 2209 14 4 18 Jawf 34 2313 14 9 23 Jawf 35 2210 5 7 12 Jawf 36 2211 5 7 12 Qurayyat 37 2201 17 7 24 Qurayyat 38 2303 17 10 27 Qurayyat 39 2281 7 19.5 26.5 Khafji 40 2213 3.5 9 12.5 Khafji Total 438.75 329.25 768 Total no. of buses = 768/24 = 32  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 380 modified the fleet assignment model by deleting the first part of the objective function and let all the decision va- riables not depend on bus type. This modified model was applied to the same sample example using only Mercedes 404 SHD bus type. 3.2.1. Problem Size and Decomposed Model As mentioned in Abara’s paper, the approximate number of ,, ijk X variable decision variables is 5 TK , where T is the total number of trips and K is the total number of fleet (bus) types. There are also 2 KS shortage variables ( , sksk OR ) and K additional bus variables ( k E ). To compute the total number of constraints, the first con- straint comprise T trip coverage constraints, the second constraint comprises TK continuity of equipment con- straints, the third constraint comprise KS schedule ba- lance constraints, and the forth constraint comprises K bus count constraints. Table 3 shows the actual number of variables and con- straints for the application of the original (two bus types used) and modified (one bus type used) models on the sample example. It also show the expected number of decision variables and the number of constraints if the modified model applies to whole schedule which consists of 382 trips and 28 stations. From Table 3, the problem size becomes larger for the application of the modified model to the whole schedule. This encouraged the decomposition of the modified model by station. The assignment results for the three models, original, modified and decomposed, were different but the total connection times were the same (329.25 hours). This means that the three models utilized the same number of buses to operate the given schedule. 3.2.2. Application of the Decomposed Modified Model to the Whole Schedule SAPTCO’ intercity bus schedule comprise a list of 382 major trips per day to over 250 cities and villages utiliz- ing 328 buses of the Mercedes 404 SHD and Mercedes 404 RHL types (using the existing assignment system). This schedule consists of 14 main and 14 minor stations. From the previous discussion the decomposed modi- fied model was applied to this whole schedule using only Mercedes 404 SHD bus type taking 4 hours as the mini- mum time for connection in Riyadh and Jeddah stations Table 3. Problem size for different models. Original Model Modified Model Models Problem Size Sample Example Sample Example Whole Schedule Total No. of Variables 432 21 6 1 967 (expected) Total No. of Constraints 140 90 793 and three hours for other stations, The results showed that all constraints were satisfied as mentioned in the sample example and the total number of needed buses to cover the whole schedule was 274 buses of Mercedes 404 SHD type. 1) Model Efficiency: The existing assignment system uses 328 buses to cover the 382 trips per day. The total trip time (working hours) was 2951 hours. For the proposed assignment system, the total connection times (lay-over hours) was 3625 hours. To compare the existing and proposed as- signment system, the following measures of effectiveness (MOE) were computed: For the existing assignment System: Average working hours per bus per day 2951 9 328 == hours Average lay-over hours per bus per day = 15 hours Percent of daily working time 9 10037.5% 24 =×= For the proposed assignment system: Average working hours per bus per day = 2951 274 = 10.77 hours Average lay-over hours per bus per day 3625 274 = = 13.23 hours Percent of daily working time= 10.77 10044.88% 24 ×= The increase in the percent of daily working time = 7.38% Model efficiency 328274 16.5% 328 − == The above results shows that increasing the average working hours per bus per day using the proposed as- signment system by only 1.77 hours (or 7.38%) saved 54 buses (16.5% of the existing used buses). 2) Sensitivity Analysis The predefined minimum connection time (four hours for Riyadh and Jeddah stations and three hours for others stations) was judgmental and was not based on any field studies. The predefined minimum connection time for 11 stations (most of them are minor stations that the people at SAPTCO think that they really do not need three hours as a connection time) were reduced to one hour instead of three hours and the proposed assignment model was re- applied to these stations. Then, the total real connection time for each station were computed and compared to that before modification. The results showed that there was a saving of 336 hours for the 11 stations. This means that 14 more buses were saved. Moreover, the predefined  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 381 minimum connection time for Abha and Makkah stations were reduced to two hours and the results of the reappli- cation of the proposed assignment model showed that there was a saving of 3 more buses. This gives us the following MOE for the proposed assignment model: Average working hours per bus per day 2951 257 = = 11.48 hours Average lay-over hours per bus per day 3217 257 = = 12.52 hours Model efficiency 328257 21.6% 328 − == The more interested results from the above sensitivity analysis are: • The real connection times varies from its minimum, 3 hours, to more than 20 hours and few of them were 3 hours. This means that the rush demand for maintenance is not really true. • For Makkah station when the predefined minimum connection was reduced to two hours, only 5 de- parture trips out of 43 ( the total number of depar- ture trips) needed real connection time less than three hours. The same was happen for Abha station where only 5 departure trips out of 33 needed real connection time less than three hours. If these spe- cific departure trips take a high priority for bus checking and cleaning, the reduction of the prede- fined minimum connection will not be very critical for the maintenance department. • For Abha station when we try to reduce the prede- fined minimum connection by one more hour (after it was reduced to two hours), the total connection time was the same as for two hours predefined minimum connection. This means that the prede- fined minimum connection limit behind it we can- not save any buses From the above results, by performing a field study of this predefined minimum connection time for every sta- tion, the expected saving of the total number of needed buses will be about 90 buses (Model efficiency = 27.4%). This will yield a net saving of 16 million Saudi riyals per year for SAPTCO as will be illustrated in the cost analy- sis next. 3) Cost Analysis Since the revenues are the same for the existing and the proposed systems as both systems operate the same number of daily trips (i.e., the same intercity schedule), the comparison between both systems concentrate on the operation cost for both systems. The operation costs con- sist of two parts, the first is the direct (variable) costs which are divided to kilometer cost that equal to 0.32 SR/km and hour cost that equal to 35.15 SR/hr. The sec- ond part is the fixed cost which is counted for the daily (24 hours) use of the bus. This fixed cost estimated to be 668 SR/day. That is, for example, a trip from Riyadh to Jeddah take about 12 hours and its length about 1000 kilometers will cost: 0.32100035.15126681409.8 SR ×+×+= . Since the existing and the proposed systems operate the same number of kilometers and the same number of hours, then our comparison will depend on the fixed cost that depend on the number of buses used. The ex- isting system use 328 buses to cover the service sched- ule, while from the model results the proposed system need 238 buses. This means that there is a saving of ( ) 32823866860120 −×= SR/day or about 21.94 million SR per year. The proposed system incur hiring new employees for bus checking, filing, and reporting bus status during the connection time (the proposed three hours) before an- other driver operates the bus for the next trip. The total hiring costs were estimated to be about SR 5.5 million per year. This means the net saving cost will be about SR 16.44 million (USD 4.4 million) per year. 4) Revenue Management As we mentioned in the cost analysis the revenue from the proposed system is not changed, but as a result of the proposed system, SAPTCO will have 90 buses surplus and these buses can be utilized to yield new additional revenue as follows using the revenue data in Table 4: • There are seasonal demands for the SAPTCO buses for about four months during a year. Three months for what is called “O’Mara”, which is Muslim re- ligion custom, to visit Al Kaaba in Makkah city and its peak demand in Ramadan, Shaban, and Ragab months of Hagree calendar. In these months SAP- TCO outsources buses form other transport compa- nies. Using all or part of their surplus buses will yield additional revenue. Yearly (1) 90 60903800 20,520,000USD 5,472,000 AdditionalRevenue NumberofbusesDaysbusrevenueperday SR =×× =××== • There is also one month that has the highest demand Table 4. Average daily bus revenue for different trip type. Trip Type Revenue/Bus/day Intercity Trip SR 2000 International Trip SR 3800 O’Mara Season Trip SR 3800 Pilgrim (Hajj) Season Trip SR 5500 City School or Company Trip SR 400  Intercity Bus Scheduling for the Saudi Public Transport Company to Maximize Profit and Yield Additional Revenue Copyright © 2010 SciRes. JSSM 382 for buses during pilgrim (Hajj) season which is also a Muslim religion custom to visit Al Kaaba in Makkah city at least one time in the Muslim person life. In this month they can use their surplus buses instead of outsourcing. Yearly (2) 30 60305500 9,900,000USD 2,640,000 AdditionalRevenue NumberofbusesDaysbusrevenueperday SR =×× =××== • Around the year, there are high demands from others agencies, like schools, manpower companies, and others small companies to outsourcing buses from SAPTCO. Using some of their surplus buses will yield new revenue. Yearly (3) 240 60240400 5,760,000USD 1,536,000 AdditionalRevenue NumberofbusesDaysbusrevenueperday SR =×× =××== • Around the years there are a medium demand for international trip to Egypt, Jordon, Iraq, Syria, Le- banon, and Yemen countries Yearly (4) 365 303653800 41,610,000USD 11,096,000 AdditionalRevenue NumberofbusesDaysbusrevenueperday SR =×× =××== • Therefore the total yearly additional revenue will be: Yearly (1) (2) (3) (4) USD 20,744,000 TotalAdditionalRevenue AdditionalRevenueAdditionalRevenue AdditionalRevenueAdditionalRevenue =++ + = 4. Summary and Conclusions In this paper, a new intercity bus schedule for the Saudi Public Transport Company (SAPTCO) has developed. Conversely to the existing assignment system, the new assignment system assigns buses to the given intercity bus schedule first, and then assigns drivers to those scheduled buses in such way that maximizes the utiliza- tion of buses. The main finding of this application can be summarized as follows: 1) Only 274 out of 328 buses of Mercedes 404 SHD are needed to cover the service schedule (a total saving of 54 buses). 2) By performing a field study of the trip predefined minimum connection time for every station, the expected saving of the total number of needed buses will be about 90 buses. 3) The new schedule system yielded the following for SAPTCO: • A net saving of USD 4.4 million per year. • Hiring new employees with no additional cost for bus checking, filing, and reporting bus status during the connection time. • Additional revenue of USD 20,744,000 per year from the use of the 90 surplus buses. 5. Directions for Further Research Based on the results and the analysis, directions for fur- ther research can be summarized as follows: 1) The new assignment system is based on the given service intercity schedule which may be optimal (it may be built in the spirit of the existing system). This encourages developing a new optimal service schedule and reapplying the assignment model for it. 2) The determination of three hours as a minimum connection time for all station is judgmental and need field studies. 3) The existing drivers’ assignment system which used to assign drivers to the scheduled buses need to be adapt- ed to take into account the advantages of the new bus assignment system. 4) Developing a maintenance bus schedule so that bus has its maintenance schedule time depending on the pro- posed assignment system. REFERENCES [1] C. Barnhart, A. Farahat and M. Lohatepanont, “Airline Fleet Assignment with Enhanced Revenue Modeling, ” Opera- tions Research, Vol. 57, No. 1, 2009, pp. 231-244. [2] J. Abara, “Applying Integer Linear Programming to the Fleet Assignment Problem,” Interfaces, Vol. 19, No. 4, 1989, pp. 20-28. [3] R. Subramanian, R. Scheff, J. Quillinan, S. Wiper and R. Marsten, “Coldstar: Fleet Assignment at Delta Air Lines,” Interfaces, Vol. 24, No. 1, 1994, pp. 104-120. [4] S. Kontogiorgis and S. Acharya, “US Airways Automates Its Weekend Fleet Assignment, ” Interfaces, Vol. 29, No. 3, 1999, pp. 52-62. [5] B. Rexing, C. Barnhart, T. Kniker, A. Jarrah and N. Krish- namurthy, “Airline Fleet Assignment with Time Windows,” Transportation Science, Vol. 34, No. 1, 2000, pp. 1-20. [6] R. Ahuja, J. Goodstein, A. Mukherjee, J. Orlin and D. Sharma, “A Very Large-Scale Neighborhood Search Al- gorithm for the Combined Through-Fleet-Assignment Mo- del, ” INFORMS Journal on Computing, Vol. 19, No. 3, 2007, pp. 416-428. [7] K. T. Talluri, “Swapping Applications in a Daily Fleet As- signment,” Transportation Science, Vol. 30, No. 3, 1996, pp. 237-248. [8] H. Sherali and H. Zhu, “Two-Stage Fleet Assignment Mo- del Considering Stochastic Passenger Demands,” Opera- tions Research, Vol. 56, No. 2, 2008, pp. 383-399. [9] T. Jacobs, B. Smith and E. Johnson, “Incorporating Network Flow Effects into the Airline Fleet Assignment Process,” Transportation Science, Vol. 42, No. 4, 2008, pp. 514-529. |

