 Vol.2, No.9, 968-978 (2010) Natural Science http://dx.doi.org/10.4236/ns.2010.29118 Copyright © 2010 SciRes. OPEN ACCESS Thermal buckling analysis of ceramic-metal functionally graded plates Ashraf M. Zenkour1,2*, Daoud S. Mashat1 1Department of Mathematics, Faculty of Science, King AbdulAziz University, Jeddah, Saudi Arabia; *Corresponding Author: zenkour@kau.edu.sa 2Department of Mathematics, Faculty of Science, Kafrelsheikh University, Kafr El-Sheikh, Egypt Received 7 March 2010; revised 20 April 2010; accepted 26 April 2010. ABSTRACT Thermal buckling response of functionally graded plates is presented in this paper using sinusoidal shear deformation plate theory (SPT). The material properties of the plate are assumed to vary according to a power law form in the thickness direction. Equilibrium and stability equations are derived based on the SPT. The non-linear governing equations are solved for plates subjected to simply supported boundary conditions. The buckling analysis of a function- ally graded plate under various types of thermal loads is carried out. The influences of many plate parameters on buckling temperature dif- ference will be investigated. Numerical results are presented for the SPT, demonstrating its importance and accuracy in comparison to other theories. Keywords: Thermal Buckling; Non-Linear Strains; Functionally Graded Material; Sinusoidal Plate Theory; Thermal Load 1. INTRODUCTION The rapid development of composite materials and structures in recent years has drawn increased attention from many engineers and researchers. These materials are broadly used in aerospace, mechanical, nuclear, ma- rine, and structural engineering. In conventional lami- nated composite structures, homogeneous elastic laminas are bonded together to obtain enhanced mechanical and thermal properties. However, the abrupt change in mate- rial properties across the interface between different ma- terials can result in large inter-laminar stresses leading to delimitation, cracking, and other damage mechanisms which result from the abrupt change of the mechanical properties at the interface between the layers. To remedy such defects, functionally graded materials (FGMs), within which material properties vary continuously, have been proposed. The concept of FGM was proposed in 1984 by a group of materials scientists, in Sendai, Japan, for ther- mal barriers or heat shielding properties. Initially FGM was designed as a thermal barrier material for aerospace application and fusion reactors. Later on FGM was de- veloped for the military, automotive, biomedical and semiconductor industries, and as a general structural element in high thermal environments. FGM is one of the advanced high temperature materials capable of withstanding extreme temperature environments. FGMs are composite and microscopically heterogeneous in which the mechanical properties vary smoothly and con- tinuously from one surface to the other. This is achieved by gradually varying the volume fraction of the con- stituent materials. Typically, these materials are made from a mixture of ceramics and metal or a combination of different materials. The ceramic constituent of the material provides the high-temperature resistance due to its low thermal conductivity and protects the metal from oxidation. The ductile metal constituent, on the other hand, prevents fracture caused by stresses due to high-temperature gradient in a very short period of time. Further, a mixture of a ceramic and a metal with a con- tinuously varying volume fraction can be easily manu- factured [1-4]. A comprehensive work on the FGMs was presented in the literature. The response of FG ceramic-metal plates has been investigated by Praveen and Reddy [5] using a plate finite element. They investigated the static and dynamic thermoelastic responses of the FGMs by vary- ing the volume fraction using a simple power law distri- bution. Reddy [6] developed the Navier’s solutions for FG plates using the third-order shear deformation plate theory (TSDT) and an associated finite element model. Amini et al. [7] described a method for three-dimensio- nal free vibration analysis of rectangular FGM plates  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 969 969 resting on an elastic foundation using Chebyshev poly- nomials and Ritz’s method. This analysis has been based on a linear, small-strain, three-dimensional elasticity theory. Analysis of FG plates under static and dynamic loads has been presented by Sladek et al. [8] using the meshless local Petrov-Galerkin method and Reissner- Mindlin theory to describe the plate bending problem. Kim et al. [9] investigated finite element computation of fracture parameters in FGM assemblages of arbitrary geometry with stationary cracks. In Altenbach and Ere- meyev [10], a viscoelastic FG polymer foam has been studied using a new plate theory based on the direct ap- proach. The large deflection response of simply sup- ported rectangular FG plates under normal pressure loading has been analyzed by Ovesy and Ghannadpour [11] using a finite strip method. In Han [12], a numerical method was proposed for analyzing transient waves in plates of FGM excited by impact loads. The bending problem of transverse load acting on FGM rectangular plate using both two-dimensional trigonometric and three-dimensional elasticity solutions was investigated by Zenkour [13]. Zenkour [14,15] studied the bending response, buckling and free vibration of simply sup- ported FG sandwich plate using the SPT. Zenkour [16] presented the derivation of equations for free vibration of FG plates expressing the displacement components by trigonometric series representation through the plate thickness. Other researches into FGMs have included the nonlinear analysis of FG plates [17], large deformation analysis of FG shells [18], static and vibration analysis of FG beams [19,20]. In view of the advantages of FGMs, a number of in- vestigations dealing with thermal buckling had been published in the scientific literature. In recent years, the mechanical and thermal buckling analysis of FG ce- ramic-metal plates has been presented by Zhao et al. [21] using the first-order shear deformation plate theory, in conjunction with the Ritz method. A two-dimensional global higher-order deformation theory has been em- ployed by Matsunaga [22] for thermal buckling of plates made of FGMs. Morimoto et al. [23] presented the ther- mal buckling analysis of FG rectangular plates subjected to partial heating in a plane and uniform temperature rise through its thickness. In Ref. [24], Shariat and Eslami presented the thermal buckling analysis of rectangular FG plates with geometrical imperfections using the clas- sical plate theory to derive the equilibrium, stability, and compatibility equations of an imperfect FGM. Thermal buckling of rectangular and circular plates compose of FGM was also studied based on the first- and higher-order shear deformation plate theory [25-27]. Various plate theories, depending upon the through- thickness displacement pattern considered, have been used to determine thermal buckling loads of composite plates. The classical plate theory [24], which is based on Kirchhoff’s hypothesis, overestimates the thermal buck- ling load when applied to even moderately thick plates. This is particularly true for composite plates in which transverse shear moduli are small in comparison to the in-plane Young’s moduli [28]. In such cases, it becomes necessary to take into account shear deformation effects. Thus, various improved plate theories such as first-order shear deformation [25,26], higher order shear deforma- tion [5,6] and sinusoidal shear deformation [13-16,29- 31] plate theories have been developed to predict the behavior of plates with thickness shear deformation. In this article, thermal buckling analysis of rectangular FG ceramic-metal plates is investigated. The material prop- erties of the FG plates are assumed to vary continuously through the thickness, according to a simple power law distribution of the volume fraction of the constituents. The SPT is used to obtain the buckling of the plate under different types of thermal loads. The thermal loads are assumed to be uniform, linear and non-linear distribution through the thickness. Additional numerical results are presented for FGM plates that show the effects of vari- ous parameters on thermal buckling response. 2. MATHEMATICAL MODEL Consider a rectangular plate of length a, width b and thickness h made of FGM. The plate is subjected to a thermal load (, ,)Txyz. The material properties of the FGM plate, such as Young’s modulus E and thermal ex- pansion coefficients are assumed to be functions of the volume fraction of the constituent materials. The FGM plate is supported at four edges defined in the (, ,) yz coordinate system with x- and y-axes located in the middle plane (0)z and its origin placed at the corner of the plate. The modulus of elasticity E, the coefficient of thermal expansion and Poisson’s ratio are assumed as [5] mcm mcm 0 () , (), (), k k EzEE V zVvzv (1) where cmc m cmc m , , 1, 2 EEE z Vh (2) and m E and m denote the elastic moduli and the coefficient of thermal expansion of metal; c E and c denote the elastic moduli and the coefficient of thermal  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 970 expansion of ceramic, and k is the volume fraction ex- ponent. The value of k equal to zero represents a fully ceramic plate. The above power law assumption reflects a simple rule of mixtures used to obtain the effective properties of the ceramic-metal plate. The rule of mix- tures applies only to the thickness direction. The density of the plate varies according to the power law, and the power law exponent may be varied to obtain different distributions of the component materials through the thickness of plate. Note that the volume fraction of the metal is high near the bottom surface of the plate, and that of ceramic high near the top surface. In addition, Eq.1 indicates that the bottom surface of the plate (/2)zh is metal-rich whereas the top surface (/2)zh of the plate is ceramic-rich. For simplicity, is assumed constant across the plate thickness. The displacements of a material point located at (x, y, z) in the FGM plate might better be illustrated as [29, 30]: 11 22 3 (, ,)(), (, ,)(), (, ,), w uxyzu zz x w uxyz vzz y uxyzw (3) where u, v and w are the displacements of the middle surface along the axes x, y and z, respectively, and 1 and 2 are the rotations about the y and x-axes and account for the effect of transverse shear. The coefficient of 1 or 2 which is given by ()z should be odd function of z. All of the generalized displacements 12 (,, ,,)uvw are functions of the (x, y). The dis- placement of the classical thin plate theory (CPT) can easily be obtained by setting () 0z. The displace- ments of the first-order shear deformation plate theory (FPT) are obtained by setting ()zz . In addition, the higher-order shear deformation plate theory (HPT) [6] is obtained by setting 2 4 ()1 3 z zz h . (4) Also, the SPT is obtained by setting [14,15]: () sin hz zh . (5) Note that the present SPT, as well as HPT, is simpli- fied by enforcing traction-free boundary conditions at the plate faces. The SPT accounts according to a co- sine-law distribution of the transverse shear deformation through the thickness of the FGM plate. The SPT, HPT and FPT contain the same number of dependent un- knowns. No transversal shear correction factors are needed for both SPT and HPT because a correct repre- sentation of the transversal shearing strain is given. The non-linear strain components ij compatible with the displacement field in Eq.3 are 0 11 111111 0 22 222222 0 12 121212 () ,zz (6) 0 23 23 33 ,3 0 13 13 0,( ),z (7) where 020 200 1 11,1,1 22,2,2232 131 2 1 , , , , 2 uwv w 0 12,1,2,1,2 11,11 22,22 12,12 , , , 2, vu ww ww w 111,122 2,2122,11,2 , , . (8) The stress-strain relations for the FGM plate are given by 11 11 2 22 22 23131223 13 12 1 () , 11 () {,,} {,,}, 2(1 ) T Ez T Ez (9) where (,,)Txyz is the temperature rise through the thickness. The stress and moment resultants of the FGM plate can be obtained by integrating Eq.9 over the thickness, and are written as 0 2 11 , 1 1 ikkkiT ikkkiT ikkkiT NABC A MBDF B SCFGC (10) 0 12 12 12 12 12 12 1, 2(1 ) kkk kkk kk k NABC MBDF SCFG (11) and  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 971 971 0 13 13 0 23 23 , 2(1 ) k QH Q (12) where 1, 2i and 00 0000 1 11222 2211 1 112222211 1 112222211 ,, ,, ,. (13) In Eqs.10-1 2, 12 ,,NN and 12 N and 12 ,, M and 12 are the basic components of stress resultants and stress couples; 12 ,,SS and 12 S are additional stress couples associated with the transversal shear effects; and 13 Q and 23 Q are transversal shear stress resultants. The coefficients ,,,... kkk ABC etc. are defined by /2 2 /2 /2 /2 /2 /2 /2 2 ,3 /2 {, ,}(){1,,}d, {,,}() (){1,,()}d, {,,}()() (,,){1,,()}d, ()( ())d. h kk kh h kk kh h TTT h h kh ABDEzzzz CFGzEzzzz BCzEzTxyzzzz HEzzz (14) 3. EQUILIBRIUM AND STABILITY EQUATIONS The total potential energy of a plate subjected to thermal loads is defined as [27] , mbcT VUU U U (15) where ,, mbc UUU and T U are membrane strain en- ergy, bending strain energy, coupled strain energy and thermal strain energy. The strain energy for FGM plate based on the SPT is defined as given below in Eq.16. The equilibrium and stability equations of FGM plates may be derived by the variational approach. The expan- sion of V about the equilibrium state by the Taylor series is 23 11 2!3! ... .VVVV (17) The governing equations of equilibrium can be de- rived by using the first variation .V The non-linear equilibrium equations associated with the present SPT are 1,112,2 0,NN 12,12,2 0,NN 1,1112,122,221 ,112,2212,12 220,MMMNwNwNw 1,112,213 0,SS Q 12,12,223 0.SSQ (18) To establish the stability equations, the condition 20V used to derive the stability equations of many practical plate buckling problems is also used here. The external load acting on the original configuration is con- sidered to be the critical buckling temperature if the above equation 2 (0)V is satisfied. Assuming that the state of stable equilibrium of a general plate under thermal load may be designated by 000 0 0 12 ,, ,,uvw . The displacements of the neighboring state are 0101 111 010 1 222 01 ,, ,, , uu u vv v ww w (19) where 11 1 1 1 ,, ,uvw and 1 2 are arbitrarily small increment of displacements. The stability equations are represented by using the above total displacement given in Eq.19 in the equation 20V and collecting the second-order terms. They read 11 1,112,20,NN 11 12,12,2 0,NN 111010101 1,1112,122,221,112,2212 ,12 220,MMMNwNwNw 11 1 1,112,213 0,SS Q 111 12,12,223 0,SSQ (20) where the superscript 1 refers to the state of stability and the superscript 0 refers to the state of equilibrium condi- tions. The terms 00 12 ,NN and 0 12 N are the pre-buckling force resultants obtained as 000 1112 ,,0 11 TT AA NNN . (21) 4. EXACT SOLUTIONS FOR THERMAL BUCKLING OF FGM PLATES Rectangular plates are generally classified in accordance 1111222212 12232313 13 v 1dv. 2 VTT (16)  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 972 with the type support used in the absent of the body forces and lateral loads except the external temperature load. The following boundary conditions are imposed at the side edges 111 111 21 11 111 111 12 22 0at0, , 0at0, , vwNM Sxa uwNM Syb (22) Following Navier solution procedure, we assume the following solution form for 1111 1 12 (, , ,,)uvw that satisfies the simply-supported boundary conditions, 1 1 1 1 1 1 ,1 1 1 1 1 1 2 cos( )sin() sin() cos() , sin()sin() cos( )sin() sin() cos() mn mn mn mn mn mn Uxy u Vxy v Wxy w xy Yxy (23) where ma , nb ; m and n are mode num- bers; 1111 ,, ,, mn mnmnmn UVWX and 1 mn Y are arbitrary pa- rameters to be determined subjected to the condition that the solution in Eq.23 satisfies the conditions in Eq.22. Substituting Eq.23 into Eq.20 , one obtains []{} 0,L (24) where {} denotes the column 11 111 {} {,,,,}, t mnmnmnmn mn UVWXY (25) and elements rs sr LL of the coefficient matrix []L are given by: 22 11 [2(1)], k LA 12 (1 ), k LA 22 13 2( ), k LB 22 14 [2(1) ], k LC 15 (1 ), k LC 22 22 [(1)2 ], k LA 22 23 2( ), k LB 2415 ,LL 22 25 [(1)2], k LC 22 22 33 2()[ ()(1)], kT LDA 22 34 2( ), k LF 22 35 2( ), k LF 22 44 [2(1) ](1), kk LG H 45 (1 ), k LG 22 55 [(1)2](1). kk LG H (26) For non-trivial solutions of Eq.24, the determinant L should be zero. This equation (0)L is stated for the determination of the lowest critical load. In the fol- lowing, the solutions of the equation 0L for differ- ent types of thermal loading conditions are presented. The plate is assumed simply supported in bending and rigidly fixed in extension. The temperature change is varied only in the thickness direction. 4.1. Thermal Buckling for FGM Plates under Uniform Temperature Rise The initial uniform temperature of the plate is assumed to be i T. The temperature is uniformly raised to a final value T in which the plate buckles. The temperature change is i TTT . Substituting Eq.26 into the equation 0L , the buckling temperature change using the shear deformation theories is obtained as 222 22222 2 12 222222 11 2 ()[(1)()] (1 )[(1)()] T nsm PaPnsm TaAPaPns m , (27) where 2 12 , 2(), kkkk k PAHPAGC 2 11 2 22 , 22(2), kkk kkk kkkkk PPDBH PPD AFBBG FC (28) /2 1/2 ()()d, /. h Th zEzz sa b The critical buckling temperature change cr T, is the smallest value of T which is obtained when m =1 and n = 1. Therefore, 22 222 12 2222 11 2 (1)[(1)(1)] . (1 )[(1)(1)] cr T sPaPs TaAPaPs (29) For the classical plate theory, the critical buckling temperature difference cr T is given as 22 2 1 (1)() (1 ) kkk cr kT ADB TaAA . (30) 4.2. Thermal Buckling for FGM Plates Subjected to a Graded Temperature Change across the Thickness For an FG plate, the temperature change is not uniform. The temperature varies according to the power law variation. Usually, the temperature rises much higher at  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 973 973 the ceramic side than that in the metal side of the plate. In this case, the temperature through the thickness is given by m ()TzTV T , (31) where m T is the temperature of the bottom surface which is metal-rich and is the power law exponent (0 ). Similar to the previous loading case, solving the equa- tion 0L, the buckling temperature difference (/2)( /2)TTh Th using the shear deformation plate theories can be determined, and then we can obtain the critical buckling cr T as 22222 1 12 2222 2 21 2 (1)[(1) (1)], (1 )[(1)(1)] mT cr T T TA sPaPs TA aAPaPs (32) where /2 2/2 ()()d. h Th zVE zz (33) Also, the critical buckling temperature difference cr T for the classical plate theory, is deduced as 22 1 2 2 2 (1)() . (1 ) kk kmT cr T kT ADBT A TA aAA (34) Note that the value of equal to unity represents a linear temperature change across the thickness. While the value of excluding unity represents a non-linear temperature change through the thickness. 5. RESULTS AND DISCUSSION The general approach outlined in the previous sections for the thermal buckling analysis of the homogeneous and FGM plates under uniform, linear and non-linear temperature rises through the thickness is illustrated in this section using the SPT. The correlation between the present theory and different higher- and first-order shear deformation theories and classical plate theory is estab- lished. To illustrate the proposed method, a ceramic-metal FG plate is considered. The combination of materials consists of aluminum and alumina. The Young’s modu- lus and the coefficient of thermal expansion for alumina are c380 GPa,E 6 c7.410/C, and for alu- minum are m70 GPa,E 6 m23 10/C, respec- tively. Note that, Poisson's ratio is selected constant for both aluminum and alumina and it equal to 0.3. The shear correction factor for FPT is set equal to 5/6. For the linear and non-linear temperature rises through the thickness, the temperature rises 5C in the metal-rich surface of the plate (i.e. m5CT). We will assume in all analyzed cases (unless otherwise stated) that /2,ab /10,ah and 3. Numerical results of the present investigation are given in Tables 1-4 and Figures 1-4. In Tables 1 and 2, the side to thickness ratio of the plate is set as /100ah . In these tables the critical buckling temperature differ- ence cr T of the plate under uniform and linear tem- perature rises is shown for different values of the power law index k using various plate theories. The results ob- tained as per the present HPT and CPT are compared with the corresponding ones presented by Javaheri and Eslami [32]. Excellent agreement is achieved between the two solutions. It is seen that, for all theories, the critical temperature difference increases monotonically as the aspect ratio /ab increases. Moreover, the criti- cal buckling cr T decreases until it reaches minimum values and then increases as the values of the volume fraction exponent k increases. Tables 3 and 4 exhibit the critical temperature difference 3 10 cr cr tT for differ- ent values of the aspect ratio /ab, the temperature ex- ponent and the power law index k under non-linear temperature loads at /10ah and 5, respectively. The nonlinearity temperature exponent is taken here as 2, 5 and 10. The effect of /ab on the critical buckling cr t is similar to that in the case of uniform and linear temperature difference across the thickness. As the power law index k increases, the critical buckling cr t decreases to reach lowest values and then increases ex- cluding cr t of the rectangular plates for 10 . Also, it is noticed that cr t increases as the nonlinearity index increases. In general, the values of the critical tem- perature difference calculated by using the shear defor- mation theories are lower than those calculated by using the classical plate theory, indicating the shear deforma- tion effect. The SPT without using any shear correction factor gives results very close to HPT and closer than those obtained using FPT. The critical buckling temperature difference cr t of the ceramic-metal FG rectangular plate (5)k versus the side-to-thickness ratio /ah calculated by all theo- ries under a uniform, linear and non-linear temperature load are shown in Figure 1. For plates with small /ah ratio, very large differences between the results of both SPT and HPT and those of both FPT and CPT are ob- served. Moreover, the differences between the higher- order shear deformation theories (SPT and HPT) and FPT are lower than those between any of them and CPT. However, for a large value of the side-to-thickness ratio the difference between the values predicted by the shear deformation theories and CPT is low significant because the plate is essentially thin. Because of permitting shear deformation in SPT, HPT and FPT, the plate becomes more flexible and thus the critical buckling temperatures calculated by these theories are smaller than those cal- 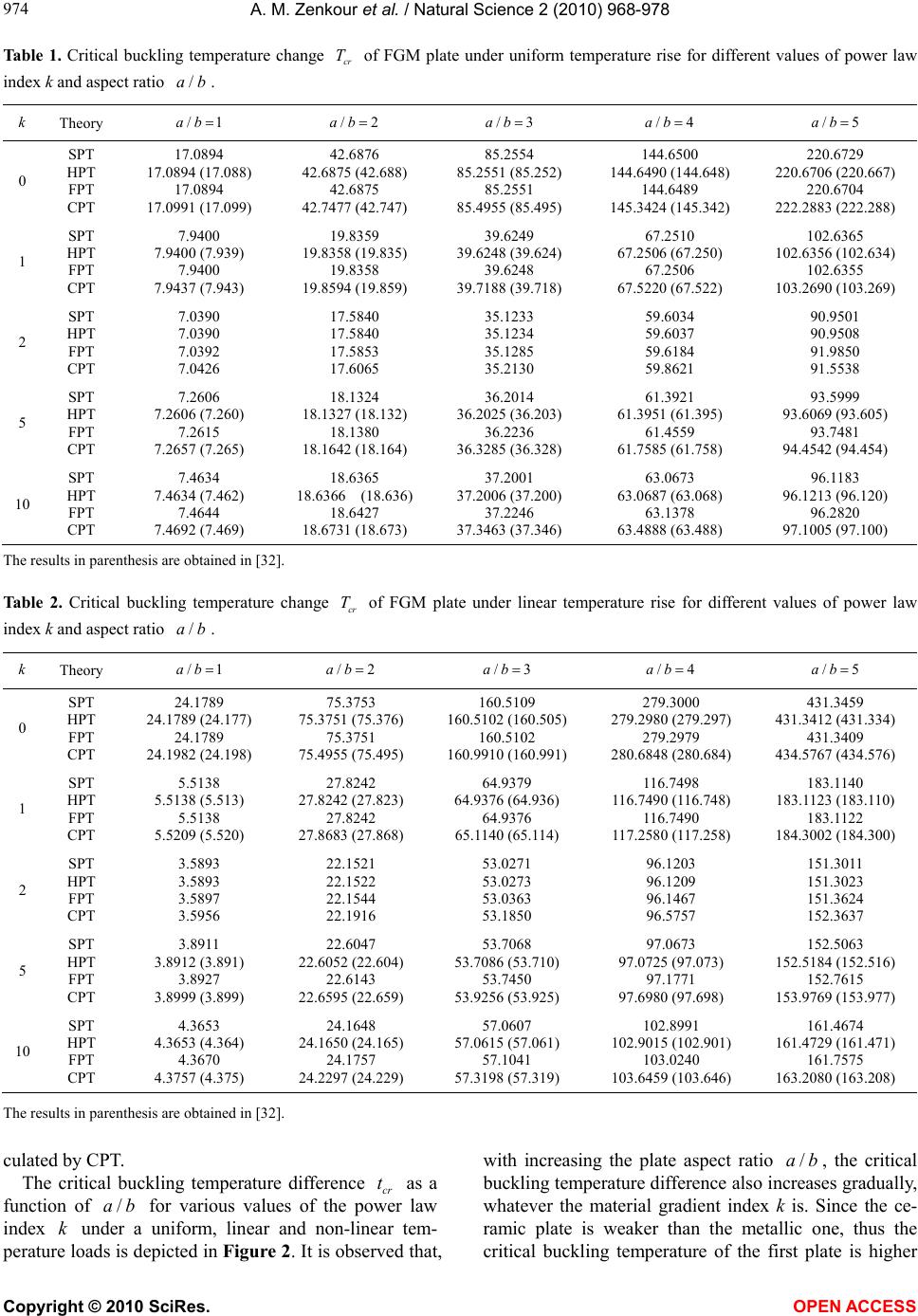 A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 974 Table 1. Critical buckling temperature change cr T of FGM plate under uniform temperature rise for different values of power law index k and aspect ratio /ab. k Theory /1ab /2ab /3ab /4ab /5ab 0 SPT HPT FPT CPT 17.0894 17.0894 (17.088) 17.0894 17.0991 (17.099) 42.6876 42.6875 (42.688) 42.6875 42.7477 (42.747) 85.2554 85.2551 (85.252) 85.2551 85.4955 (85.495) 144.6500 144.6490 (144.648) 144.6489 145.3424 (145.342) 220.6729 220.6706 (220.667) 220.6704 222.2883 (222.288) 1 SPT HPT FPT CPT 7.9400 7.9400 (7.939) 7.9400 7.9437 (7.943) 19.8359 19.8358 (19.835) 19.8358 19.8594 (19.859) 39.6249 39.6248 (39.624) 39.6248 39.7188 (39.718) 67.2510 67.2506 (67.250) 67.2506 67.5220 (67.522) 102.6365 102.6356 (102.634) 102.6355 103.2690 (103.269) 2 SPT HPT FPT CPT 7.0390 7.0390 7.0392 7.0426 17.5840 17.5840 17.5853 17.6065 35.1233 35.1234 35.1285 35.2130 59.6034 59.6037 59.6184 59.8621 90.9501 90.9508 91.9850 91.5538 5 SPT HPT FPT CPT 7.2606 7.2606 (7.260) 7.2615 7.2657 (7.265) 18.1324 18.1327 (18.132) 18.1380 18.1642 (18.164) 36.2014 36.2025 (36.203) 36.2236 36.3285 (36.328) 61.3921 61.3951 (61.395) 61.4559 61.7585 (61.758) 93.5999 93.6069 (93.605) 93.7481 94.4542 (94.454) 10 SPT HPT FPT CPT 7.4634 7.4634 (7.462) 7.4644 7.4692 (7.469) 18.6365 18.6366 (18.636) 18.6427 18.6731 (18.673) 37.2001 37.2006 (37.200) 37.2246 37.3463 (37.346) 63.0673 63.0687 (63.068) 63.1378 63.4888 (63.488) 96.1183 96.1213 (96.120) 96.2820 97.1005 (97.100) The results in parenthesis are obtained in [32]. Table 2. Critical buckling temperature change cr T of FGM plate under linear temperature rise for different values of power law index k and aspect ratio /ab. k Theory /1ab /2ab /3ab /4ab /5ab 0 SPT HPT FPT CPT 24.1789 24.1789 (24.177) 24.1789 24.1982 (24.198) 75.3753 75.3751 (75.376) 75.3751 75.4955 (75.495) 160.5109 160.5102 (160.505) 160.5102 160.9910 (160.991) 279.3000 279.2980 (279.297) 279.2979 280.6848 (280.684) 431.3459 431.3412 (431.334) 431.3409 434.5767 (434.576) 1 SPT HPT FPT CPT 5.5138 5.5138 (5.513) 5.5138 5.5209 (5.520) 27.8242 27.8242 (27.823) 27.8242 27.8683 (27.868) 64.9379 64.9376 (64.936) 64.9376 65.1140 (65.114) 116.7498 116.7490 (116.748) 116.7490 117.2580 (117.258) 183.1140 183.1123 (183.110) 183.1122 184.3002 (184.300) 2 SPT HPT FPT CPT 3.5893 3.5893 3.5897 3.5956 22.1521 22.1522 22.1544 22.1916 53.0271 53.0273 53.0363 53.1850 96.1203 96.1209 96.1467 96.5757 151.3011 151.3023 151.3624 152.3637 5 SPT HPT FPT CPT 3.8911 3.8912 (3.891) 3.8927 3.8999 (3.899) 22.6047 22.6052 (22.604) 22.6143 22.6595 (22.659) 53.7068 53.7086 (53.710) 53.7450 53.9256 (53.925) 97.0673 97.0725 (97.073) 97.1771 97.6980 (97.698) 152.5063 152.5184 (152.516) 152.7615 153.9769 (153.977) 10 SPT HPT FPT CPT 4.3653 4.3653 (4.364) 4.3670 4.3757 (4.375) 24.1648 24.1650 (24.165) 24.1757 24.2297 (24.229) 57.0607 57.0615 (57.061) 57.1041 57.3198 (57.319) 102.8991 102.9015 (102.901) 103.0240 103.6459 (103.646) 161.4674 161.4729 (161.471) 161.7575 163.2080 (163.208) The results in parenthesis are obtained in [32]. culated by CPT. The critical buckling temperature difference cr t as a function of /ab for various values of the power law index k under a uniform, linear and non-linear tem- perature loads is depicted in Figure 2. It is observed that, with increasing the plate aspect ratio /ab, the critical buckling temperature difference also increases gradually, whatever the material gradient index k is. Since the ce- ramic plate is weaker than the metallic one, thus the critical buckling temperature of the first plate is higher  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 975 975 Table 3. Critical buckling temperature change cr t of FGM plate under non-linear temperature rise for different values of index k, aspect ratio /ab, and temperature exponent /10ah. /1ab /2ab /3ab k Theory 2 5 10 2 5 10 2 5 10 0 SPT HPT FPT CPT 4.8414 4.8410 4.8408 5.1147 9.6829 9.6821 9.6817 10.2294 17.7520 17.7505 17.7498 18.7540 11.2294 11.2269 11.2246 12.8093 22.4589 22.4538 22.4492 25.6186 41.1747 41.1654 41.1568 46.9675 20.0164 20.0066 19.9919 25.6336 40.0328 40.0133 39.9838 51.2673 73.3935 73.3577 73.3037 93.9900 1 SPT HPT FPT CPT 2.1068 2.1066 2.1065 2.2072 4.3182 4.3179 4.3178 4.5241 8.1906 8.1900 8.1898 8.5812 4.9517 4.9508 4.9499 5.5391 10.1496 10.1476 10.1458 11.3534 19.2512 19.2475 19.2440 21.5346 8.9711 8.9673 8.9615 11.0921 18.3880 18.3802 18.3684 22.7355 34.8774 34.8626 34.8402 43.1235 2 SPT HPT FPT CPT 1.6765 1.6766 1.6812 1.7627 3.2736 3.2738 3.2828 3.4419 6.1232 6.1235 6.1404 6.4379 3.9243 3.9246 3.9493 4.4256 7.6627 7.6633 7.7116 8.6417 14.3327 14.3339 14.4242 16.1638 7.0655 7.0659 7.1433 8.8640 13.7962 13.7970 13.9483 17.3080 25.8051 25.8066 26.0895 32.3737 5 SPT HPT FPT CPT 1.5955 1.5964 1.6141 1.7083 2.8485 2.8500 2.8816 3.0498 4.9990 5.0017 5.0571 5.3522 3.6479 3.6521 3.7444 4.2885 6.5126 6.5202 6.6849 7.6562 11.4292 11.4425 11.7317 13.4363 6.3635 6.3755 6.6569 8.5888 11.3609 11.3822 11.8847 15.3337 19.9377 19.9751 20.8569 26.9097 10 SPT HPT FPT CPT 1.6766 1.6770 1.6974 1.8092 2.8844 2.8851 2.9202 3.1126 4.7717 4.7728 4.8310 5.1492 3.7953 3.7970 3.9016 4.5414 6.5293 6.5322 6.7122 7.8130 10.8015 10.8062 11.1040 12.9250 6.5362 6.5402 6.8510 9.0951 11.2448 11.2515 11.7862 15.6470 18.6022 18.6134 19.4980 25.8848 Table 4. Critical buckling temperature change cr t of FGM plate under non-linear temperature rise for different values of index k, aspect ratio /ab, and temperature exponent /5ah . /1ab /2ab /3ab k Theory 2 5 10 2 5 10 2 5 10 0 SPT HPT FPT CPT 16.7416 16.7353 16.7270 20.5039 33.4833 33.4706 33.4541 41.0078 61.3861 61.3628 61.3325 75.1810 32.8985 32.8633 32.7842 51.2823 65.7971 65.7266 65.5685 102.5646 120.6281 120.4989 120.2090 188.0351 48.6540 48.5388 48.1978 102.5796 97.3080 97.0776 96.3955 205.1592 178.3980 177.9756 176.7252 376.1253 1 SPT HPT FPT CPT 7.4586 7.4561 7.4529 8.8709 15.2878 15.2827 15.2762 18.1827 28.9971 28.9875 28.9751 34.4879 15.0945 15.0800 15.0476 22.1983 30.9390 30.9094 30.8430 45.4997 58.6835 58.6274 58.5014 86.3014 22.9714 22.9214 22.7734 44.4106 47.0843 46.9819 46.6785 91.0281 89.3070 89.1127 88.5373 172.6573 2 SPT HPT FPT CPT 5.8880 5.8885 5.9430 7.0886 11.4979 11.4981 11.6045 13.8415 21.5048 21.5065 21.7057 25.8898 11.7774 11.7751 11.9755 17.7406 22.9970 22.9923 23.3838 34.6407 43.0146 43.0059 43.7381 64.7936 17.7227 17.7018 18.0864 35.4938 34.6058 34.5650 35.3160 69.3061 64.7282 64.6519 66.0566 129.6333 5 SPT HPT FPT CPT 5.3654 5.3742 5.5741 6.8687 9.5789 9.5945 9.9515 12.2627 16.8104 16.8378 17.4644 21.5203 10.1426 10.1682 10.8794 17.1895 18.1076 18.1534 19.4230 30.6885 31.7779 31.8582 34.0863 53.8566 14.4932 14.5269 15.9245 34.3909 25.8748 25.9349 28.4301 61.3982 45.4087 45.5142 49.8932 107.7502 10 SPT HPT FPT CPT 5.5369 5.5400 5.7630 7.2736 9.5255 9.5308 9.9144 12.5134 15.7580 15.7669 16.4014 20.7009 10.2387 10.2435 11.0005 18.2025 17.6144 17.6226 18.9250 31.3150 29.1395 29.1530 31.3076 51.8043 14.3554 14.3463 15.7723 36.4172 24.6965 24.6810 27.1342 62.6510 40.8554 40.8297 44.8880 103.6433 than that of the second. For the FGM plate, cr t de- creases as the metallic constituent in the plate increases. Figure 3 investigates the critical buckling temperature difference cr t of homogeneous and FG plates versus the side-to-thickness ratio /ah under various types of temperature loads. Figure 4 gives similar for FG plates versus the aspect ratio /ab. The buckling temperature of the homogeneous plate is considerably higher than  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 976 Figure 1. Critical buckling temperature difference cr t due to uniform, linear and non-linear tempera- ture rise across the thickness versus the side-to- thickness ratio /ah. Figure 2. Critical buckling temperature difference cr t due to uniform, linear and non-linear tempera- ture rise across the thickness versus the aspect ratio /ab. 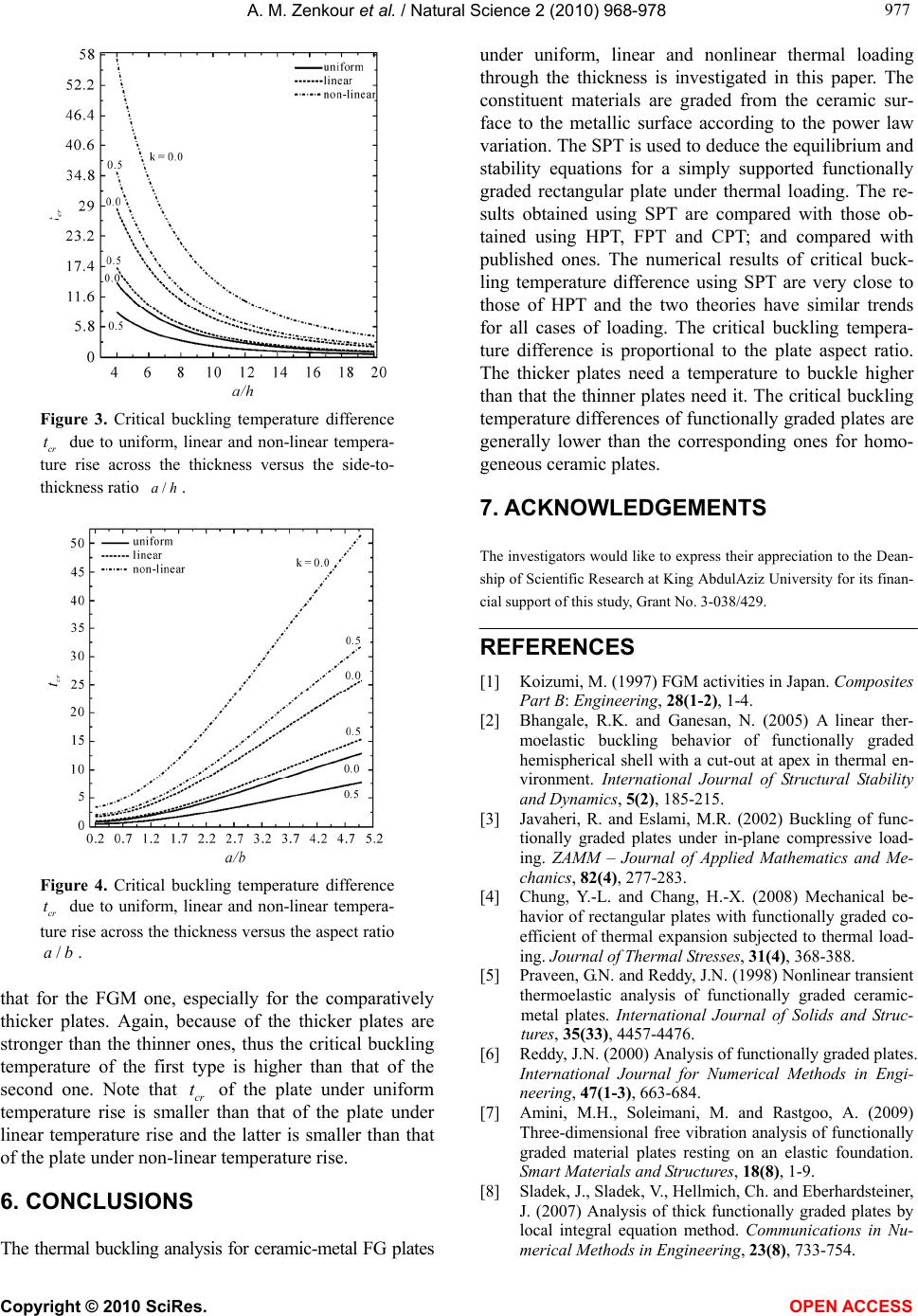 A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 977 977 Figure 3. Critical buckling temperature difference cr t due to uniform, linear and non-linear tempera- ture rise across the thickness versus the side-to- thickness ratio /ah . Figure 4. Critical buckling temperature difference cr t due to uniform, linear and non-linear tempera- ture rise across the thickness versus the aspect ratio /ab. that for the FGM one, especially for the comparatively thicker plates. Again, because of the thicker plates are stronger than the thinner ones, thus the critical buckling temperature of the first type is higher than that of the second one. Note that cr t of the plate under uniform temperature rise is smaller than that of the plate under linear temperature rise and the latter is smaller than that of the plate under non-linear temperature rise. 6. CONCLUSIONS The thermal buckling analysis for ceramic-metal FG plates under uniform, linear and nonlinear thermal loading through the thickness is investigated in this paper. The constituent materials are graded from the ceramic sur- face to the metallic surface according to the power law variation. The SPT is used to deduce the equilibrium and stability equations for a simply supported functionally graded rectangular plate under thermal loading. The re- sults obtained using SPT are compared with those ob- tained using HPT, FPT and CPT; and compared with published ones. The numerical results of critical buck- ling temperature difference using SPT are very close to those of HPT and the two theories have similar trends for all cases of loading. The critical buckling tempera- ture difference is proportional to the plate aspect ratio. The thicker plates need a temperature to buckle higher than that the thinner plates need it. The critical buckling temperature differences of functionally graded plates are generally lower than the corresponding ones for homo- geneous ceramic plates. 7. ACKNOWLEDGEMENTS The investigators would like to express their appreciation to the Dean- ship of Scientific Research at King AbdulAziz University for its finan- cial support of this study, Grant No. 3-038/429. REFERENCES [1] Koizumi, M. (1997) FGM activities in Japan. Composites Part B: Engineering, 28(1-2), 1-4. [2] Bhangale, R.K. and Ganesan, N. (2005) A linear ther- moelastic buckling behavior of functionally graded hemispherical shell with a cut-out at apex in thermal en- vironment. International Journal of Structural Stability and Dynamics, 5(2), 185-215. [3] Javaheri, R. and Eslami, M.R. (2002) Buckling of func- tionally graded plates under in-plane compressive load- ing. ZAMM – Journal of Applied Mathematics and Me- chanics, 82(4), 277-283. [4] Chung, Y.-L. and Chang, H.-X. (2008) Mechanical be- havior of rectangular plates with functionally graded co- efficient of thermal expansion subjected to thermal load- ing. Journal of Thermal Stresses, 31(4), 368-388. [5] Praveen, G.N. and Reddy, J.N. (1998) Nonlinear transient thermoelastic analysis of functionally graded ceramic- metal plates. International Journal of Solids and Struc- tures, 35(33), 4457-4476. [6] Reddy, J.N. (2000) Analysis of functionally graded plates. International Journal for Numerical Methods in Engi- neering, 47(1-3), 663-684. [7] Amini, M.H., Soleimani, M. and Rastgoo, A. (2009) Three-dimensional free vibration analysis of functionally graded material plates resting on an elastic foundation. Smart Materials and Structures, 18(8), 1-9. [8] Sladek, J., Sladek, V., Hellmich, Ch. and Eberhardsteiner, J. (2007) Analysis of thick functionally graded plates by local integral equation method. Communications in Nu- merical Methods in Engineering, 23(8), 733-754.  A. M. Zenkour et al. / Natural Science 2 (2010) 968-978 Copyright © 2010 SciRes. OPEN ACCESS 978 [9] Kim, J.-H. and Paulino, G.H. (2002) Finite element evaluation of mixed mode stress intensity factors in func- tionally graded materials. International Journal for Nu- merical Methods in Engineering, 53(8), 1903-1935. [10] Altenbach, H. and Eremeyev, V.A. (2008) Analysis of the viscoelastic behavior of plates made of functionally graded materials. ZAMM – Journal of Applied Mathe- matics and Mechanics, 88(5), 332-341. [11] Ovesy, H.R. and Ghannadpour, S.A.M. (2007) Large deflection finite strip analysis of functionally graded plates under pressure loads. International Journal of Structural Stability and Dynamics, 7(2), 193-211. [12] Han, X., Liu, G.R. and Lam, K.Y. (2001) Transient waves in plates of functionally graded materials. International Journal for Numerical Methods in Engineering, 52(8), 851-865. [13] Zenkour, A.M. (2007) Benchmark trigonometric and 3-D elasticity solutions for an exponentially graded thick rec- tangular plate. Archive of Applied Mechanics, 77(4), 197-214. [14] Zenkour, A.M. (2005) A comprehensive analysis of func- tionally graded sandwich plates: Part 1-Deflection and stresses. International Journal of Solids and Structures, 42(18-19), 5224-5242. [15] Zenkour, A.M. (2005) A comprehensive analysis of func- tionally graded sandwich plates: Part 2-Buckling and free vibration. International Journal of Solids and Structures, 42(18-19), 5243-5258. [16] Zenkour, A.M. (2005) On vibration of functionally graded plates according to a refined trigonometric plate theory. International Journal of Structural Stability and Dynamics, 5(2), 279-297. [17] Aliaga, J.W. and Reddy, J.N. (2004) Nonlinear thermoe- lastic analysis of functionally graded plates using the third-order shear deformation theory. International Jour- nal of Computational Engineering Science, 5(4), 753- 779. [18] Arciniega, R.A. and Reddy, J.N. (2007) Large deforma- tion analysis of functionally graded shells. International Journal of Solids and Structures, 44(6), 2036-2052. [19] Kadoli, R., Akhtar, K. and Ganesan, N. (2008) Static analysis of functionally graded beams using higher order shear deformation theory. Applied Mathematical Model- ling, 32(12), 2509-2525. [20] Sina, S.A., Navazi, H.M. and Haddadpour, H. (2009) An analytical method for free vibration analysis of function- ally graded beams. Materials & Design, 30(3), 741-747. [21] Zhao, X., Lee, Y.Y. and Liew, K.M. (2009) Mechanical and thermal buckling analysis of functionally graded plates. Composite Structures, 90(2), 161-171. [22] Matsunaga, H. (2009) Thermal buckling of functionally graded plates according to a 2D higher-order deformation theory. Composite Structures, 90(1), 76-86. [23] Morimoto, T., Tanigawa, Y. and Kawamura, R. (2006) Thermal buckling of functionally graded rectangular plates subjected to partial heating. International Journal of Mechanical Sciences, 48(9), 926-937. [24] Shariat, B.A.S. and Eslami, M.R. (2006) Thermal buck- ling of imperfect functionally graded plates. Internation- al Journal of Solids and Structures, 43(14-15), 4082- 4096. [25] Ganapathi, M. and Prakash, T. (2006) Thermal buckling of simply supported functionally graded skew plates. Composite Structures, 74(2), 247-250. [26] Lanhe, W. (2004) Thermal buckling of a simply sup- ported moderately thick rectangular FGM plate. Com- posite Structures, 64(2), 211-218. [27] Najafizadeh, M.M. and Heydari, H.R. (2004) Thermal buckling of functionally graded circular plates based on higher order shear deformation plate theory. European Journal of Mechanics A/Solids, 23(6), 1085-1100. [28] Babu, C.S. and Kant, T. (2000) Refined higher order finite element models for thermal buckling of laminated composite and sandwich plates. Journal of Thermal Stresses, 23(2), 111-130. [29] Zenkour, A.M. (2006) Generalized shear deformation theory for bending analysis of functionally graded plates. Applied Mathematical Modelling, 30(1), 67-84. [30] Zenkour, A.M. (2004) Buckling of fiber-reinforced vis- coelastic composite plates using various plate theories. Journal of Engineering Mathematics, 50(1), 75-93. [31] Zenkour, A.M. (2004) Thermal effects on the bending response of fiber-reinforced viscoelastic composite plates using a sinusoidal shear deformation theory. Acta Mecha- nica, 171(3-4), 171-187. [32] Javaheri, R. and Eslami, M.R. (2002) Thermal buckling of functionally graded plates based on higher order the- ory. Journal of Thermal Stresses, 25(7), 603-625.
|