Circuits and Systems, 2013, 4, 97-105
http://dx.doi.org/10.4236/cs.2013.41015 Published Online January 2013 (http://www.scirp.org/journal/cs)
A Novel Time Domain Noise Model for Voltage Contr olled
Oscillators
Li Ke, Peter Wilson, Reuben Wilcock
Electronics and Computer Science, University of Southampton, Southampton, UK
Received September 25, 2012; revised October 25, 2012; accepted November 3, 2012
ABSTRACT
This paper describes a novel time domain noise model for voltage controlled oscillators that accurately and efficiently
predicts both tuning behavior and phase noise performance. The proposed method is based on device level flicker and
thermal noise models that have been developed in Simulink and although the case study is a multiple feedback four de-
lay cell architecture it could easily be extended to any similar topology. The strength of the approach is verified through
comparison with post layout simulation results from a commercial simulator and measured results from a 120 nm fabri-
cated prototype chip. Furthermore, the effect of control voltage flicker noise on oscillator output phase noise is also
investigated as an example application of the model. Transient simulation based noise analysis has the strong advantage
that noise performance of higher level systems such as phase locked loops can be easily determined over a realistic ac-
quisition and locking process yielding more accurate and reliable results.
Keywords: Voltage Controlled Oscillators; Noise Model; Simulation
1. Introduction
Low jitter reference frequency generation is a key re-
quirement for high performance analogue and mixed-
signal integrated circuits and is usually achieved using a
stable reference crystal and phase locked loop (PLL). An
important trade-off exists between PLL phase noise and
loop bandwidth and it is vital to explore this balance,
particularly when targeting low output jitter [1]. At the
heart of every PLL is a voltage controlled oscillator
(VCO) which greatly influences the performance of the
PLL itself and is typically the biggest noise contributor in
the system [2]. In order facilitate PLL noise analysis,
therefore, a VCO noise model is required which will ac-
curately predict noise performance under realistic closed
loop conditions whilst maintaining simulation efficiency.
It is widely agreed that time domain transistor level
simulations provide the most reliable and accurate means
to examine the performance of closed loop PLLs [3].
One approach for noise analysis is to include noise be-
havior for each transistor within the transient simulation,
in a technique known as transient noise analysis. Unfor-
tunately, however, few commercial simulators include
support for noise as part of a transient simulation, focus-
ing on less accurate linearized approaches instead. In-
deed, transient noise analysis tends to be impractical for
realistic circuit designs due to the huge simulation re-
sources required [3]. To address this problem, a number
of alternative approaches have been proposed in the lit-
erature based on a variety of design platforms including
Matlab-Simulink [3-4], C [5], and VHDL [6]. All these
methods extract behavioral model parameters from tran-
sistor level simulations first, which can lead to inaccu-
racy since the parameters are only valid for limited oper-
ating conditions. With the decrease in technology node
size this problem is exacerbated as devices are becoming
increasingly difficult to characterize.
In this paper, a novel time domain VCO noise model is
proposed, which incorporates transistor level noise be-
havior whilst maintaining simulation efficiency. In order
to accurately define true dynamic behavior the VCO
model accepts an instantaneous control voltage input and
dynamically generates the correct output waveform,
whilst incorporating the relevant noise sources to ensure
an accurate representation of the phase noise perform-
ance. Further post processing of the VCO output wave-
form then provides both the oscillation frequency and
signal purity. A careful balance is struck between accu-
racy and complexity to ensure meaningful results yet
manageable simulation times. Section 2 introduces the
VCO structure used in this work and derives the com-
bined VCO tuning behavior and noise performance
model. Section 3 presents a case study complete with
transistor level simulations and measurements from a
prototype chip to demonstrate the work on a realistic
example. Finally, Section 4 discusses the significance of
C
opyright © 2013 SciRes. CS

L. KE ET AL.
98
the work, with some concluding remarks.
2. VCO Architecture and Tuning Model
A high performance VCO architecture is at the core of
this approach and is detailed in this section. Both the
frequency tuning behavior and noise performance char-
acteristics are considered and combined into a complete
time domain model that facilitates accurate and efficient
system simulation.
2.1. VCO Tuning Model
Passive inductor and capacitor (LC) based VCO struc-
tures offer excellent phase noise performance yet can be
difficult and expensive to integrate on deep sub-micron
CMOS processes due to their large physical size and ad-
ditional processing requirements. Conversely, inverter
based oscillators (also referred to as RC or ring oscilla-
tors) are easily integrated onto standard CMOS processes
but generally suffer from inferior phase noise perform-
ance [7]. Despite this, their compact size and additional
advantages of wider tuning range and direct quadrature
output has led to great interest in RC oscillators. Recent
research has focused on achieving phase noise perform-
ance in RC oscillators that is close to equivalent LC
based designs [1]. Given the importance of modeling the
phase noise of RC oscillator accurately, they are a suit-
able candidate for the development of an improved
model, as described in this paper.
The oscillator architecture employed in this work is
shown in Figure 1 and is based on a multiple feedback
four delay cell topology in order to achieve a wide tuning
range [8]. Within each delay cell, the two internal tran-
sistors, Mp1 and Mn1, operate as an inverter and the two
current control transistors, Mp2 and Mn2, in each stage
are responsible for frequency control. Transistors Mp3
and Mp4 form a secondary feedback loop to increase the
oscillator frequency. Since the on-resistance (Ronn and
Ronp) and lumped gate capacitance C of the two invert-
ing transistors (Mp 1 and Mn1) are independent of the
frequency of oscillation, they can be modeled as fixed
values defined by Equations (1)-(3) [9].
 
2
GS th
VV  

1
2
DS
DSn ox
DS
V
RonnVCWni Lni
I


 
 (2)
 
2
GS th
VV  

1
2
DS
DSn ox
DS
V
RonpVCWpi Lpi
I


 
 (3)
where Cox is the unit-area gate oxide capacitance, Cgdo is
the gate-drain overlap capacitance per unit-length, μn is
the mobility parameter and Vth is the transistor threshold
voltage, WniLni and Wpi are the transistor di-
mensions for NMOS and PMOS inverter transistors re-
spectively. VDS and VGS are the effective drain-source and
gate-source voltage difference for each transistor. Defin-
ing VDS and VGS within Equations (2) and (3) is difficult
since the voltages at the gate and drain nodes of the de-
vice dynamically change within each oscillation cycle.
The gate and drain voltages of Mni increase from VDD/2
to VDD and decrease from VDD to VDD/2 respectively
within each propagation delay. For simplicity, therefore,
it is assumed that both drain and gate nodes are fixed at
3VDD/4 within the propagation delay, ensuring that Mn i
stays in saturation. The two control transistors, Mpc and
Mnc, are modeled as variable resistors Rctp and Rctn with
values defined by the external control voltage, and the
linearity of this relationship governs the linearity of the
VCO’s tuning function. The resistance relationship de-
pends on the operating region of the transistor and for
Mnc is given by Equations (4) and (5) for the saturation
and deep triode regions respectively. Equations (6) and
(7) give the corresponding equations for Mpc.
Lpi

2
_1
2nox th
Vct
Rctn satWnc
CVctV
Lnc



(4)

1
_
Dnox th
Vct
Rctn triWnc
ICVctV
Lnc



(5)

2
_1
2nox th
Vct
Rctp satWpc
CVctV
Lpc



(6)

1
_
Dnox th
Vct
Rctp triWpc
ICVctV
Lpc




(7)
As illustrated in Figure 1, Wnc/Lnc and Wpc/Lpc are
the dimensions of the current controlling transistors.
During each period of oscillation the drain source voltage
of the control transistors Mpc and Mnc can vary by sev-
eral hundred mV and so the region of operation is diffi-
cult to define. A good compromise is to assume that the
effective ON resistance of the control transistor Mnc is a
combination of Equations (4) and (5) (or (6) and (7) for
transistor Mpc). The combination is determined linearly
by the instantaneous control voltage, Vct, and is given by
Equation (8) for Rctn and Equation (9) for Rctp.


in
out
3
22
2
C
C
gdogdooxox gdogdo
WniCWpiWniLniCWpi LpiCCWniCWpi


C C (1)

L. KE ET AL. 99
Figure 1. Modeling of effective RC delay for a VCO delay cell.
__
DD
Vct
tn tri
VV




DD
DD
VVct
RctnRctn satRc




 (8)
_
DD
DD
VVct
RctpRctp satRc
V
 



_
DD
Vct
tp triV




(9)
Now that the effective capacitive and resistive com-
ponents have been modelled, the corresponding propaga-
tion delays, td_push and td_pull , can be obtained directly
from Equations (10) and (11). The time constant is ob-
tained from the product of the effective resistance


eff
R

and capacitance

eff
C in each case

_
2
2
d
DD DD
eff efsh fpu
VV
C
II
C
Rctn
t CR 2
DD
DD
V
VC
o nnR




(10)

_
2
2
DD DD
d pulleffeff
VV
tR C C
IIC
Rctp
2
DD
DD
V
VC
Ronp





t

(11)
As the pull-up path uses the same principle and struc-
ture as the push-down path for the dual inverter based
ring oscillator, it is straightforward to combine 2N stages
(as it is a dual feedback loop structure) of push delay
_pushd and 2N stages of pull delay

_pulld to obtain
the nominal oscillation cycle, To which is given in Equa-
tion (12). Figure 2 illustrates the complete tuning model,
which has been implemented in Simulink.
t

_pull _pushdd
t t
(12)
To verify the accuracy of the tuning
iour has been compared with schema
si
pically result in a reduced oscil-
la
02TN
model, its behave-
tic level transistor
mulations using standard foundry models. This com-
parison is shown in Figure 3, where the correlation
across the range of Vct of the oscillation frequency is
good between the proposed model and the more detailed
transistor level circuit.
In practice, the circuit will also suffer from layout
parasitics, which will ty
tion frequency. Realistic estimation of the performance
with parasitic components taken into account can be
achieved through post layout extraction simulations. A
simple extension to the model can be included to cor-
rectly predict the performance reduction, in the form of a
parasitic delay factor that can be added to the overall
oscillation period as shown in Equation (13). The value
of parasitic delay can be quickly obtained from simple dc
analyses, and the more accurate model used for later
noise analysis, increasing confidence in the noise results.
The effect of the parasitic delay can be seen in Figure 4,
where the extracted simulation results are compared with
the revised model and a clear reduction in the maximum
oscillation frequency from over 1 GHz to 840 Mhz was
observed.


0_pull _push
2 parasitic_delay
dd
TNt t (13)
2.2. Transistor Level Noise Model
ate a transistor’s
y Equation (14)
power spectral density (PSD) for thermal and flicker
Thermal noise and flicker noise domin
noise spectrum and can be summarised b
where Sin_thermal and Sin_flicker are the drain current noise

L. KE ET AL.
100
Figure 2. Complete VCO tuning model.
l schematic and
model simulation results.
Figure 1. Comparison of transistor leve
delay simula-
tion and model including parasitic delay.
is the absolute
mperature in Kelvin and g is the device transconduc-
on MOSEFTs. The point of intersection
between the flicker noise and thermal noise contributions
Figure 4. Comparison of extracted parasitic
noise, k is the Boltzmann constant, T
te m
tance. The flicker noise coefficient Kf is a process inde-
pendent parameter of the order of 10−24 and γ is a
bias-dependent factor which may be set at 2/3 for long
channel transistors and must be replaced by a larger
value for submicr
is referred to as the device’s corner frequency, fc, and is
given in Equation (15). Above the corner frequency, the
noise level is dominated by thermal noise, whereas below
the corner frequency flicker noise dominates with an
increasing factor of 20 dB/decade [9,10].


22
,out-thermal -flicker
nn
ni i
VSS R
22
4f
mm
OX eff eff
K
kT ggR
CWLf






(14)
MATLAB code has been made available in the litera-
ture [11] to model this relationship and is used as a start-
ing point in this work. Firstly, the thermal noise is cre-
ated by a random number generator based on a variance
given in Equation (16), which is determined by both the
absolute thermal noise level, Sin-thermal, and the system
sampling time, systs.
-thermal
22
in m
4
Variance SkTg
s
ysts systs
 (16)
Secondly, using the mathematical fun
in [11], a bank of single-pole low pass filters was created
to


ctions proposed
produce a noise-shaping filter, which can approxi-
mately generate the correct flicker noise response. The
transfer function of this noise-shaping filter is given by
Equation (17).

0.5
12π
110
1
n
K
c
f
Hs
02π10
2n
nc
s
f



 (17)
where fc is the device’s corner frequency, giv
tion (15), and a K value of approximately 10 is required



en in Equa-
for correct modelling of the flicker noise. The model
realization of this noise-shaping filter is illustrated in
Figure 5(a). Separate output ports are used for the ther-
mal and flicker noise contributions to allow a better un-
derstanding of how these different noise types affect the
2
corner
1
44
ffm
mmc
ox effeffox effeff
g
kT ggff
CW LfCW LkT

KK

 (15)

L. KE ET AL. 101
(a)
(b)
Figure 5. Simulink model of thermal and flicker noise
sources (a) and PFD of single device noise (b).
, confirming
g model and
device level noise model the final stage is to combine
oth the tun-
VCO noise as a whole. A power spectral density com-
parison of the single device noise model and a simulation
Spectre is shown together in Figure 5(b)
in
correct operation of the model at this level.
Combined VCO Noise and Tuning Model
Having developed both the VCO level tunin
both aspects in a model which will predict b
ing and noise performance of the VCO. The first chal-
lenge in achieving this is to relate the noise quantity,
currently in the form of current (A) to the VCO time do-
main jitter (s) and frequency domain phase noise (dBc/
Hz@offset). The jitter, Δtd occurring within a single
propagation delay can be calculated by integrating the
noise current, in(t), over the time interval td and dividing
by the pull-up/push-down current, I, as described by
Equations (18) and (19) [10]. The propagation delay and
pull-up/push-down current can be obtained directly from
the model in Figure 2.

0
1d
d
t
nn
vitt
C
 (18)

0
1d
d
t
dn
itt
II
 (19)
It is possible at this stage to combine 4N noise gen-
erators from the previous
model where each delay cell has four transistors (Mn1,
Mn2, Mp5, Mp6). However, with each noise block re-
quiring 11 transfer functions for fli
the total of 44 transfer functions would degrade the
simulation efficiency. Furthermore, having to adjust the
model structure as the number of stages
sirable, so instead N should be an input variable. For this
re
n
v
tC
section for an N stage VCO
cker noise generation,
changes is unde-
ason, three simplifications are performed on the model
to improve efficiency. First, it is possible to combine
pairs of noise contributors into one lumped transistor by
making the reasonable assumption that the inverting and
control transistors share the same dimensions. This
halves the number of noise generators, which greatly
enhances the efficiency of the model. Secondly, assume-
ing a lumped transistor noise model it is important to
establish the relationship between the control voltage and
the trans-conductance of the lumped transistor as this
will have an impact on its noise characteristics. As a re-
sult of this, the altered noise profile of this lumped tran-
sistor can be determined by Equations (20) and (21)
where gm_lump is its trans-conductance.

_mlumpnoxth
Wni
g
CVctV
Lni
  (20)
_1
4
fmlump
c
ox
Kg
fCWniLni kT


 (21)
Thirdly, for short td time intervals it can be assumed
that the noise current stays at a constant value within the
interval meaning that Equation (19) can be reduced to
Equation (22). If the change in noise current within the
time interval is noticeable, however, th
amplitude spread is known to be pro
length of the time interval and trans-conductance, but
inversely proportional to the load capa
thermore, it is known that the jitter amplitude spread is
pr
is so-called jitter
portional to the
citance [10]. Fur-
oportional with the order of device’s corner frequency
allowing Equation (22) to be extended to the more gen-
eral case of Equation (23).

0
1d
d
t
n
dn d
i
tittt
I
I
 
 (22)
  

_log1 0 dmlump
n
dd
tg fc
it
tt t
IC

  (23)
Based on the above refinement the proposed jitter
generator is shown in Figure 6 which is a combination of
the propagation delay generator and the noise generator.
The accuracy of this model can be attributed to the noise
current, the push current and the len
tion delay all being a function of the control voltage,
rather than assuming independence from this important
gth of the propaga-

L. KE ET AL.
102
circuit parameter. The resulting full VCO model results
in 2N PMOS and 2N NMOS based noise gen
an N stage oscillator. Summing all squares of the noise
co
hows the developed model phase noise re-
e case study circuit dimensions based on
tions of the fully extracted
erators for
ntributors gives the total noise which is then trans-
formed into the jitter value. In order to determine the
phase noise, the instantaneous oscillation frequency and
output phase is also available at the model output. The
phase noise, which is the parameter of ultimate interest,
can be approximated by the power spectral density (PSD)
function of extra phase.
3. Results
In this section the novel VCO noise model is tested and
compared to results from an industry standard simulator.
A case study circuit was designed for this purpose with
the dimensions given in Table 1, which refer to the
schematic of Figure 1.
Phase Noise Simulations
Figure 7(a) s
sults using th
just flicker noise. Here the new model is shown to agree
well with post layout simula
circuit. Both curves have a roll-off factor of 30 dB/dec-
ade, which demonstrates that the device flicker noise is
being modeled correctly. For further analysis the noise
source in the model was changed from flicker to thermal,
which correctly resulted in a shallower roll-off factor of
20 dB/decade [10] as shown in Figure 7(b). The behave-
ioral models in both cases took 1 minutes and 45 seconds
to generate, whereas the transistor level simulations took
from 3 - 4 minutes. Although this demonstrates an effi-
ciency saving of 50% - 60%, it is important to point out,
as discussed in Section 1, that the real benefit of the pro-
posed model is its suitability for simulating the noise of
complex systems such as PLLs, due to its time domain
nature.
It is well known that flicker noise in the VCO control
voltage plays a more significant role than any other noise
source in the oscillator circuit [10] which makes it an
interesting aspect to investigate with the proposed model.
Within the current mirror structure that generates the
control voltage, the diode connected transistor is the ma-
jor noise contributor and can be modeled by another in-
stance of the device noise model. In order to translate the
Figure 6. Combination of the noise generator with the VCO behavioral model.
and thermal noise
(a) (b)
Figure 7. Comparison between the proposed Simulink model and Spectre based r esults for flicker noise (a)
(b) induced phase noise.

L. KE ET AL. 103
current noise of the device model to control voltage noise
is it multiplied by the transistor’s output resistance which
is obtained through a simple DC simulation.
Table 2 shows four example designs where the current
mirror transistors are varied, keeping all other design
parameters the same. For the purposes of fair comparison,
the differential control voltages generated from the con-
trol module were designed to be almost identical (Vct =
1.2 V), resulting in almost identical oscillation frequent-
cies. However, a significant difference is apparent for the
phase noise performances of these four design examples,
which are shown in Figure 8. As in the previous design
example, both the circuit simulator based post layout
simulation results and the pro
VCO output phase noise without paying a penalty in
simulation time. The recommended design going forward
would be Design 3 which achieves excellent phase noise
without the compromise of a large transistor area and
correspondingly large gate capacitance, which could
cause stability problems in a larger system.
4. Prototype Chip
To verify the proposed VCO model further, the VCO
design example of the previous section with the recom-
mended control module sizing of Design 3 was realized
with a prototype chip fabricated on a standard0 nm
re 9(a) shows the layut view
highlighted, and Figure 9(b)
0 are consis-
results and simulation results
posed model results were 1.2 V CMOS process. Figu
of the chip with the VCO
obtained. The phase noise results obtained from these
wo methods agree strongly for these four analytical de- shows the die being probed on a high speed wafer prob-
t
sign cases, confirming the accuracy of the proposed VCO
model.
As expected, the results clearly show that lowering the
transistor output resistance through a greater W/L ratio is
an essential requirement for reducing the VCO output
phase noise, highlighting the well-known trade-off be-
tween power and noise performance. In this example the
proposed model has allowed accurate analysis of the
12
o
ing station. Bench tests used an Agilent E4443A 3
Hz-6.7 GHz spectrum analyser and gave the phase noise
plot in Figure 10. A battery was used for the power
source to ensure very low noise from the supply.
The phase noise spectrum shows a roll off of −30
dBc/Hz/decade, indicating that flicker noise is dominant
in the design. The results shown in Figure 1
tent with the modeling
Figure 8. Phase noise with different transistor dimensions.
Table 1. Transistor dimensions of design example.
Transistor: W/L (mm): Transistor: W/L (mm):
Table 2. Varying the control current mirror transistors in
four design examples.
Design 3 Design 4 DeviceDesign 1 Design 2
Mcn 0.15 µm/0.13 µm2 µm/0.4 µm
Mp1, Mp2 100/0.4 Mn1, Mn2 64/0.4
Mp3, Mp4 100/0.4 Mn3, Mn4 32/0.4
Mp5, Mp6 199/0.4 Mn5, Mn6 32/0.4
16 µm/0.4 µm 160 µm/1 µm
Mcp 0.45 µm/0.13 µm6 µm/0.4 µm
gds of Mcp 23 µ 44.77 µ
48 µm/0.4 µm 480 µm/1 µm
374.4 µ 849.2 µ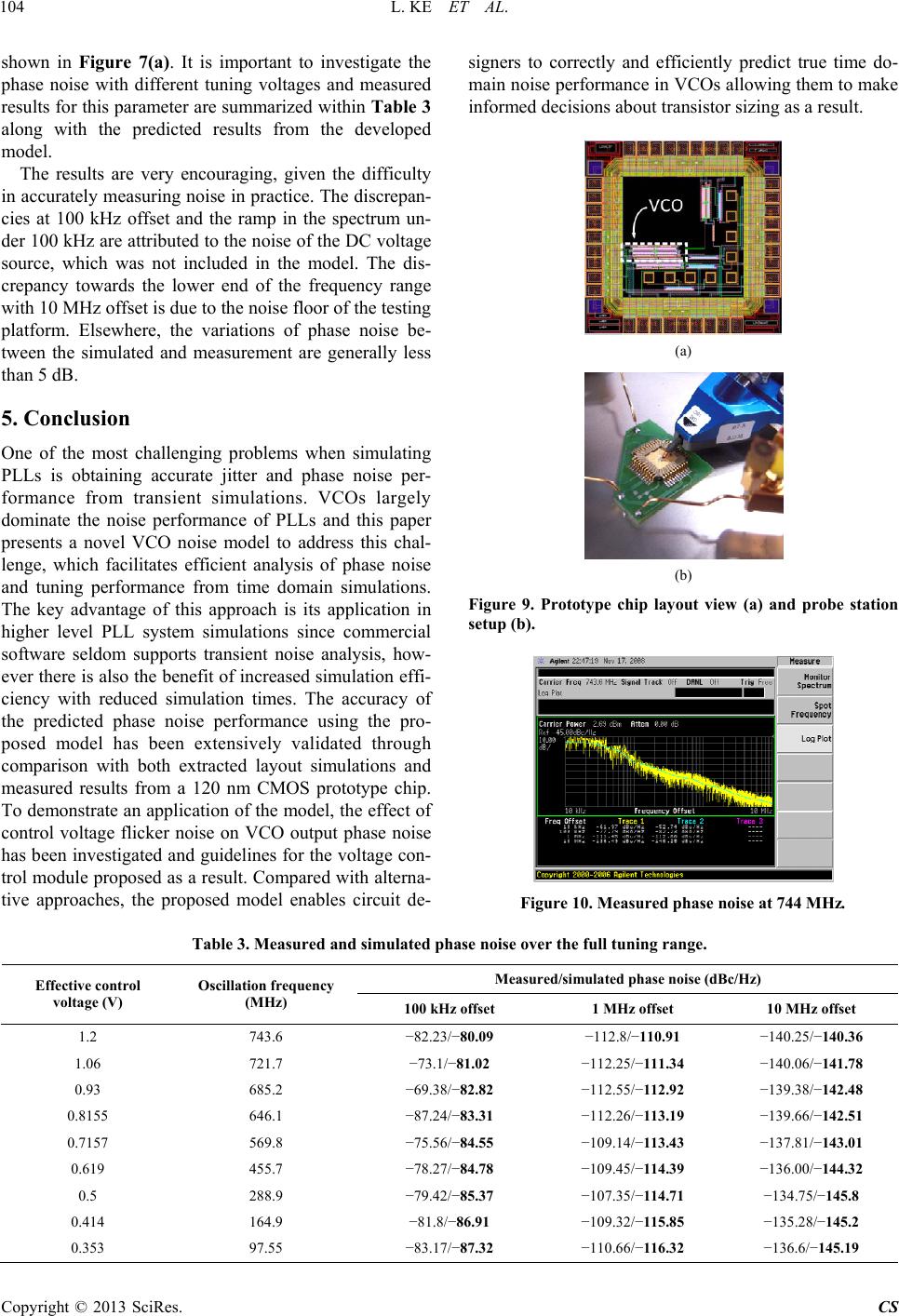

L. KE ET AL.
104
shown in Figure 7(a). It is important to investigate the
phase noise with different tuning voltages and measured
results for this parameter are summarized within Tab le 3
along with the predicted results from the developed
model.
The results are very encouraging, given the difficulty
in accurately measuring noise in practice. The discrepan-
cies at 100 kHz offset and the ramp in the spectrum un-
der 100 kHz are attributed to the noise of the DC voltage
source, which was not included in the model. The dis-
crepancy towards the lower end of the frequency range
with 10 MHz offset is due to the noise floor of the testing
platform. Elsewhere, the variations of phase noise be-
tween the simulated and measurement are generally less
than 5 dB.
5. Conclusion
One of the most challenging problems when simulating
PLLs is obtaining accurate jitter and phase noise per-
formance from transient simulations. VCOs largely
inate the noise performanc
resenal-
lengise
anerfoom ain s.
The key advantage of this approach is its application in
hig PLL system simunce cocial
sofdom sransnalow-
ever thso thefit of inula-
en extensively validated through
csonth laulad
mre
To onstrat
cont vol
inv anlinesvoln-
signers to correctly and efficiently predict true time do-
main noise performance in VCOs allowing them to make
informed decisions about transistor sizing as a result.
(a)
dom
p
e of PLLs and this paper
ts a novel VCO noise model to address this ch
e, which facilitates efficient analysis of phase no
d tuning prmance frtime domsimulation
her levellations simmer
tware selupports tient noise aysis, h
ere is ale bencreased simtion effi
ciency with reduced simulation times. The accuracy of
the predicted phase noise performance using the pro-
posed model has be
ompari with boextractedyout simtions an
easud results from a 120 nm CMOS prototype chip.
dem
rol
e an application
tage flicker noi
of t
se on VC
he model, the e
O output phase n
ffect of
oise
has beenestigatedd guide for the tage co
trol module proposed as a result. Compared with alterna-
tive approaches, the proposed model enables circuit de-
(b)
Figure 9. Prototype chip layout view (a) and probe station
setup (b).
Figure 10. Measured phase noise at 744 MHz.
se noise over the full tuning range.
Measured/simulated phase noise (dBc/Hz )
Table 3. Measured and simulated pha
Effective control
voltage (V) Oscillation frequency (MHz) 100 kHz offset 1 MHz offset 10 MHz offset
1.2 743.6 −82.23/−80.09 −112.8/−110.91 −140.25/−140.36
1.06 721.7 −73.1/
0.93 685.2 −69.38
0.8155 646.1 −87.2
0.7157 569.8 −75.56
0.619 455.7 −78.27
0
−81.02 −112.25/−111.34 −140.06/−141.78
/−82.82 −112.55/−112.92 −139.38/−142.48
4/−83.31 −112.26/−113.19 −139.66/−142.51
/−84.55 −109.14/−113.43 −137.81/−143.01
/−84.78 −109.45/−114.39 −136.00/−144.32
9 −79.42/−85.37 −107.35/−114.71 −134.75/−145.8
164.9 −81.8/−86.91 −109.32/−115.85 −135.28/−145.2
97.55 −83.17/−87.32 −110.66/−116.32 −136.6/−145.19
.5 288.
0.414
0.353

L. KE ET AL. 105
REFERENCES
[1] Z. H. Gao, Y. C. Li and S. L. Yan, “A 0.4 ps-RMS-Jitter
1 - 3 GHz Ring Oscillator PLL Using Phase-Noise Pre-
amplification,” IEEE Journal of Solid-State Circuits, Vol.
43, No. 9, 2008, pp. 2079-2089.
doi:10.1109/JSSC.2008.2001873
[2] G. Manganaro, S. UngKwak, S. H. Cho and A. Pulin-
cherry, “A Behavioral Modelling Approach to the Design
a Low Jitter Clock Source,” IEEE Transactions on Cir-
cuit and Systems II, Vol. 50, No. 11, 2003, pp. 804-814.
[3] L. Bizjak, N. Da Dalt, P. Thurner, R. Nonis, P. Paletri and
L. Selmi, “Comprehensive Behavioral Modeling of Con-
ventional and Dual-Tunig PLLs,” IEEE Transactions on
Circuit and System I, Vol. 55, No. 6, 2008, pp. 1628-
1638.
[4] S. Brigati, F. Francesconi, A. Malvasi, A. Pesucci and M.
Polerri, “Modeling of Franctional-N Division Frequency
Synthesizers with Simulink and Matlab,” The 8th IEEE
International Conference on Electronics, Circuits and
Systems, Vol. 2, 2001, pp. 1081-1084.
[5] M. H. Perrott, “Fast and Accurate Behaviotal Simulation
of Fractional-N Frequency Synthesizers and Other PLL/
DLL Circuits,” Proceedings of the 39th annual Design
Automation Conference, New York, 10-1 June 2002, pp.
498-503.
n Simulation and Modeling of Phase Noise of an RF
Oscillator,” IEEE Transactions on Circuit and Systems I,
Vol. 52, No. 4, 2005, pp. 723-733.
[7] D. A. Badillo and S. Kiaei, “A Low Phase Noise 2.0 V
900 MHz CMOS Voltage Controlled Ring Oscillator,”
Proceedings of the 2004 International Symposium on
Circuits and Systems, Vol. 4, 2004, p. 533
[8] K. Li, R. Wilcock and P. Wilson, “Improved 6.7 GHz
CMOS VCO Delay Cell with up to Seven Octave Tuning
Range,” IEEE International Symposium on Circuits and
Systems, Seattle, 18-21 May 2008, pp. 444-447.
[9] R. J. Baker, “CMOS Circuit Design, Layout and Simula-
tion,” 2nd Edition, IEEE Press, Wiley, Hoboken008.
d
4
[6] R. B. Staszewski, C. Fernando and P. T. Balsara, “Event-
Drive
, 2
oi:10.1109/9780470547106
[10] A. A. Abidi, “Phase Noise and Jitter in CMOS Ring Os-
cillators,” IEEE Journal of Solid-State Circuits, Vol. 41,
No. 8, 2006, pp. 1803-1816.
doi:10.1109/JSSC.2006.876206
[11] S. C. Terry, J. Blalock, J. M. Rochelle, M. N. Ericson and
S. D. Caylor, “Time-Domain Noise Analysis of Lineat
Time-Invariant and Linear Time-Variant Systems Using
MATLAB and HSPICE,” IEEE Transactions on Nuclear
Science, Vol. 52, No. 3, 2005, pp. 1418-1422.