Paper Menu >>
Journal Menu >>
 Int. J. Communications, Network and System Sciences, 2010, 3, 767-772 doi:10.4236/ijcns.2010.39102 Published Online September 2010 (http://www.SciRP.org/journal/ijcns) Copyright © 2010 SciRes. IJCNS An Efficient Noisy-ICA Based Approach to Multiuser Detection in IDMA Systems Abdelkrim Hamza1,2 , Salim Chitroub1, Gérard Salut2 1LCPTS Laboratoire de Communication et du Traitement du Signal, FEI-USTHB, Alger, Algeria 2Laboratoire d’Analyse et d’Architecture des Systèmes-CNRS;LAAS, F-31077 Toulouse, France E-mail: ahamza@usthb.dz Received July 3, 2010; revised August 7, 2010; accepted September 5, 2010 Abstract Interleaved Division Multiple Access (IDMA) is a new access scheme that has been proposed in the literature to increase the capacity of wireless channels. The performance of such systems depends on the accuracy of the channel state information at the receiver. In this paper, a Noisy-Independent Component Analysis (N-ICA) based IDMA receiver for multiple access communication channels is proposed. The N-ICA com- ponent is applied as a post processor. Unlike other IDMA receivers, the proposed scheme detects and separates the transmitted symbols without channel state information tracking. The performance of the proposed tech- nique is presented in terms of raw bit error rate (BER) without channel coding for different signal to noise ratios (SNR). Simulation results demonstrate that N-ICA post processor provides an improvement in perfor- mance in BER in loaded systems. When the system is not loaded, the proposed post processor has the same performance as conventional IDMA receiver with less iterations leading to a complexity reduction. Keywords: IDMA, ICA, Multi-User Detection 1. Introduction One of the challenges of next generation wireless sys- tems is the spectral efficiency. The goal is to provide sufficient quality and capacity to the diverse and rich multimedia content that need to be transmitted. Recently proposed Interleave-Division Multiple-Access (IDMA) communication system is one of the most promising technologies for high data rate wireless networks [1]. IDMA can be regarded as a special case of Code Divi- sion Multiple Access (CDMA). In CDMA systems, users are separated using signatures or spreading codes; while in IDMA systems, distinct interleavers are employed to separate users [2]. At the receiver of IDMA system, the signal of the user of interest needs to be extracted out of the Multiple Access Interference (MAI) and the Inter Symbol Interfe- rence (ISI). Moreover, since conventional IDMA detec- tor is sensitive to channel estimation errors [3], a good channel tracking algorithm is mandatory. This might drastically increase the overall complexity at the receiver. To overcome those drawbacks, in this paper, we propose a new blind receiver for IDMA systems. In our approach, a noisy Independent Component Analysis (N-ICA) scheme is introduced as a post processor. Independent Component Analysis (ICA) has attracted special attentions in the wire- less communication fields for interference suppression of CDMA systems [4,5]. In this paper, we propose to detect and separate the transmitted symbols without channel tracking and by in- cluding the noise in the global model; leading to the N-ICA model. We will show that our model is very suitable for symbol detection and separation in the IDMA context. In terms of complexity, as a post processor, the proposed solution starts the processing just after conventional IDMA processing. In this case, a hardware reuse is possible if an FPGA implementation is carried on for example (currently being finalized). Therefore, the proposed N-ICA block does not represent a complexity increase in the overall system. The remainder of this paper is organized as follows. The next section is devoted to the IDMA system model. In Sec- tion 3, we detail the proposed N-ICA model for IDMA. In Section 4, an estimation algorithm is presented for N-ICA in an IDMA context. Using some evaluation criteria, computer simulation results are presented in Section 5 to  768 A. HAMZA ET AL. Copyright © 2010 SciRes. IJCNS provide a comparative study. Conclusions are drawing in Section 6. 2. IDMA System Model As shown in Figure 1 (the upper plot is the transmitter and the lower one is the receiver), we consider an IDMA system with K users. A single path channel hk and BPSK modulation are considered here. The nth bit in the se- quence dk of kth user is spread, generating a sequence vector denoted ck=[ck(1), ck(2), ..., ck(J)]T where J is the frame length, C is the spreading factor and the super- script T is the transpose operator. Then ck is permuted by an interleaver πk and at the output of the interleaver, the vector xk=[ xk(1), xk(2), ..., xk(J)]T is obtained. The ele- ments in ck and xk are considered as chips. The chip rate is C times higher than the bit rate. Users are distin- guished mainly by their respective interleavers πk. Each user can have its own signature sequence or all users can share the same spreading code [3]. The received signal can be modeled as: 1() K kk k rjhx jnj j=1…J (1) As illustrated in figure 1, this sub optimal receiver consists of an elementary signal estimator (ESE) and K single user a posteriori probability (APP) decoders (DEC) [1]. The multiple access and coding constraints are con- sidered separately in the ESE and DEC. The outputs of the ESE and DEC are extrinsic log likelihood ratios (LLRs) about {xk(j)} defined in [2]. These LLRs are fur- ther distinguished by subscripts, eESE(xk(j)) and Figure 1. IDMA-N-ICA system model. eDEC(xk(j)), depending on whether they are generated by the ESE or DEC. A global turbo-type iterative process is then applied to process the LLRs generated by the ESE and DEC, as detailed below [1,3]. Pr |1, () log, Pr |1, kk k kk rx jh ex jkj rx jh (2) 2.1. The Basic ESE The Equation (1) can be rewritten as: () kk k rjhx jj (3) () kkk j rjhx j (4) where k is the distortion including interference plus noise in r(j) with respect to user-k [3]. The mean and the variance functions are noted by E(.) and Var(.) respec- tively. k j can be approximated by a random Gaussian va- riable. with mean and variance : () (()) kkk EjErjhExj (5) () k Varj Var (2 ()) ||(()) kk rjhVarxj (6) where 1(()) K kk k Er jEhxjEnj (7) 22 1 K kk k Var rjhVarxj (8) Therefore, the log likelihood ratio [1] is given by: 2.() /(()) ESE kkkk exjhrjE jVarj (9) 2.2. The DEC Function The Dec in our structure performs despreading operation and the extrinsic LLRs eDEC(ck(j)) are used to update E(xk(j)) and V ar(xk(j)) as [3]: ()tanhtanh()/2 kDECk Ex jex j (10) 2 1( ) kk VarEx jEx j (11) This iterative process is repeated a preset number of times. 2.3. The ESE Function for Multi-Path Channels When we consider a multipath fading channel with L paths; the received signal is represented by: 1 , 10 KL kl kl rjhxjlnjj (12) where hk,l are the coefficients related to user k. Following a similar principle as that for single path we obtain Algorithm 1 below for detection in a multipath channel: Algorithm 1: Detection in a Multi-Path Channel 1) Estimation of interference Mean  A. HAMZA ET AL. 769 Copyright © 2010 SciRes. IJCNS 1 , 10 ()( ) KL kl kl ErjhEx jl (13) ,, ( klkl k EjErjlhExj (14) 2) Estimation of interference variance 2 12 , 10 () KL kl kl Var rjhVarxjl (15) 2 ,,klkl k VarjVar rjlhVarxj (16) 3) LLR generation , , , ()2.kl ESEklk l kl rj lEj exjh Var j (17) 1 0() L E SEkESE kl l exj exj (18) 3. ICA and N-ICA Principle The application of ICA consists of estimating the un- known input signals from the output signals without prior knowledge of the channel state information [6]. Let’s suppose that the sources are statistically in- dependent. This is a fundamental assumption for using ICA that is generally verified in communication systems [6]. The extraction of the sources can be done by ICA by exploiting the essential features of the sources and system [7]. In the simplest form of ICA, we observe n scalar variables r1, r2, … rn which are linear combinations of l unknown independent sources or components ICs de- noted by b1, b2, ..., bl. If we express the observed random variables with the vector, r = (r1, r2, ..., rn)T and the ICs variables bj with the vector b = (b1, b2, ..., bl)T then the relationship is given by [8]: mmm rGbn (19) where m r is the mth observed data vector, G is an unknown full rank mixing matrix, m bis an unknown non Gaussian source vector and m n is an additive Gaussian noise process. The goal is to estimate the noise free ICsm busing only the observations m r and the assumption of the inde- pendence of the sources. This means that a set of vectors w1, w2, should be estimated such that W = [w1,w2, ...] is the separating matrix; therefore, the output source esti- mations 1, 2, ., . TT mm rrww... i.e.: T mm yWr (20) are independent and each of them can be used to represent one of the sources. 3.1. Mathematical Representation of IDMA by N-ICA Model In this subsection, we develop the theoretical frame- work and show the similarity between Noisy ICA model and IDMA system model. We focus our atten- tion on synchronous IDMA systems for simplicity and brevity. However, the method can be extended to an asynchronous system by extending the observation interval. After chip rate sampling i.e. C equal spaced samples per symbol are taken, the sampled data is processed within a window of specific size. For synchronous model, data propagated through a single path channel fall into the same window of size Tb for desired and interfering symbols. The samples are then collected into a C×1 vectors rm. , 1 K mkkmkm k rhdsn (20) here k s is the C×1 vector representation of kth user’s interleaved signature sequence andm ndenotes the noise vector. The last equation can be rewritten in a matrix form: bm = [d1,m, d2,m, ..., dK,m] s1 = [s1,1, s2,1, ..., sC,1]T C×1 vector 11,1 1 , 0 ,, 0 m mK KKm K hbn rss hb n 11 ,, mKKmm rshshbn (22) Equation (22) can be represented in a more compact form: mmm rGbn (23) where the C×K matrix G is assumed full rank. We can see the similarity between the IDMA model of Equa- tion (23) and the N-ICA model of Equation (19). The goal of the Noisy-ICA based IDMA detection is to recover the symbol vector bm for each user k without knowing the parametric form of G which depends on the channel coefficients. 4. N-ICA Estimation Algorithm The proposed system is a hybrid structure composed of two parts where a classical IDMA receiver is combined with a N-ICA block as shown in figure 1. Block IDMA, described in the previous section, works for a number of iterations (it) after which the block N-ICA takes over. The proposed N-ICA will act as a post processor attached to an IDMA receiver in the presence of noise. The aim of our N-ICA block is to avoid continuous tracking of channel state information [9]. In this section, we will derive estimation algorithms for the proposed N-ICA post processor in IDMA context. 4.1. Principal Component Analysis Processing The Principal Component Analysis (PCA) based part of the model consists of whitening the input signals. This  770 A. HAMZA ET AL. Copyright © 2010 SciRes. IJCNS step of processing is achieved by using the PCA in [10] to extract the Principal Components (PCs). This can be done for the noiseless case as follows: 1/2 T YUGB (24) where the matrix U corresponds to the Eigen vector of the data covariance matrix C and the diagonal matrix that contains the related Eigen values : 1/2 = diag [1/2 1/21/2 12 ,,, n ] (25) This PCA processing can be extended to noisy data using bias removal technique [8]. In the regular ICA process, the covariance matrix of the noise free data nf m r can be given by: () nfnfTT mm CErr GG (26) On the other hand, the covariance matrix of the observed noisy data can be written as: TT mm Err GG +2n I CC (27) where 2 is the noise power andn C is the diagonal noise covariance matrix. In the noise bias removal tech- nique, the Eigen values and vectors of matrix n C is used for whitening instead of matrix which is called quasi-whitening [10]. In fact, quasi whitening can be performed on the noisy data as follows: 21/2 () Tm zIUr (28) The covariance matrix of quasi white data is then given by: 221 () T Ezz II (29) From (29), we notice that the covariance matrix is different from the identity matrix. Therefore, we have to take into account the non-whiteness of the data. This is achieved by using the fast ICA algorithm that is presented in the next subsection. 4.2. Fast ICA Algorithm Since only the second order statistics are used to com- pute the matrix, the PCA used in the first part of the model does not provide the best results. Higher order statistics of the received signals contain additional in- formation about the non Gaussian properties of the noise. The purpose of this work is to establish a new scheme in which the system can take into account such random deformations in the detection step. To improve the per- formance, the presence of the noise should be reduced to the minimum using the extracted PCs without additional prior knowledge of their statistical properties. This is the purpose of the ICA based part of the model. Therefore, the ICA model should include a noise term as well in its linear transform matrix. The ICA approach that we present here is our contri- bution to take into account the noise in the ICA model. This means that the bias due to noise should be removed, or at least reduced. Noisy-FastICA has been applied to the blind source separation and interference suppression in multiple access communications before in [11] and FastICA in [9], [10]. The Noisy-FastICA algorithm performs as follows (Algorithm 2): Algorithm 2: Noisy-FastICA Let k be the desired user,m r, m = 1, .., M the received block data and b denotes the estimate of the symbol b. 1) First perform PCA for dimension reduction 2) Quasi- whitened the noisy data using (28) 3) Start ICA Let t=1 and update 13 (( 1)) T mm wtEzwtz 2 3((1) )(1) Tm Ewtz wt where 221 () I I Normalize w(t) : T (t)() wt wt wt w If | (1) T wt wt | < (1 – 10-4), let t= t+1 and go to step 3. 4. Output the estimated desired user’s bit: ,km b = sgn (Zm) 5. Simulation Results In this section, we present the simulation results of the proposed Noisy-Independent Component Analysis (N-ICA) based Interleaved Division Multiple Access (IDMA) presented in this paper. In all simulation results, the following notations have been adopted: It is the iterations number used in IDMA block. Τ represents the percentage of load rate defined by the ratio between the number of users and the spreading factor (K/C). IDMA is the conventional IDMA receiver described in Section 2. IDMA-ICA is the hybrid structure described in [12]. IDMA-N-ICA is the proposed hybrid structure described in Section 3 using the noisy fast ICA algorithm. To evaluate the detection and separation ability of the proposed N-ICA model, performances are presented in terms of raw Bit Error Rate (BER) before decoding for different Signal to Noise Ratios (SNR). We consider a time varying channel, BPSK modulation and Gold spreading codes of length C. Among the parameters that influence the performances are the effect of load rate and the number of iterations for IDMA block. The obtained results are presented in Figures 2-6. In Figures 2 and 3 we show a comparison between our proposed post processor N-ICA and the IDMA re- ceiver for single path and multipath channel respectively. In Figure 4, performances of our proposed receiver are presented for different values of τ (rate of load) and a spreading factor of 63. 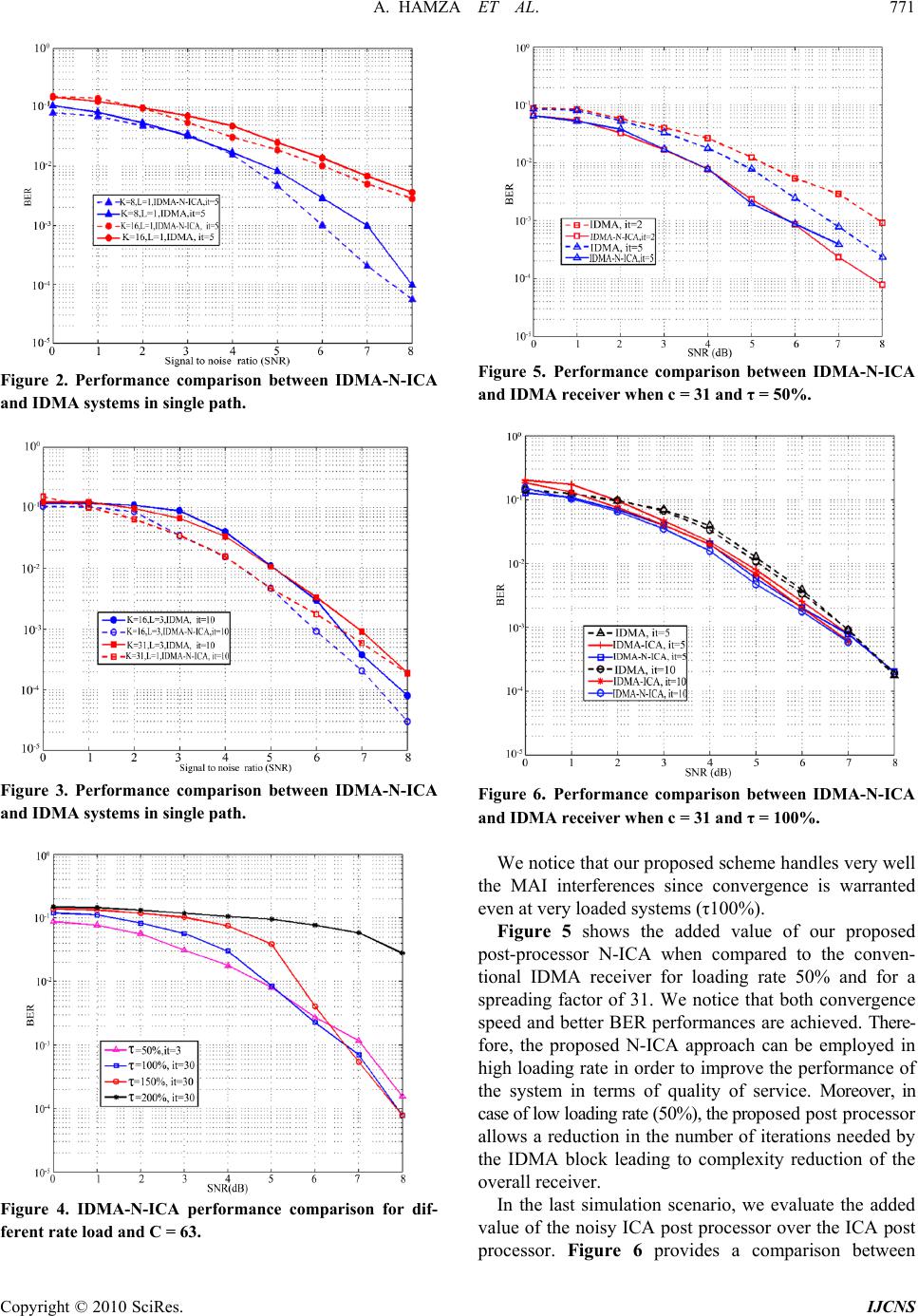 A. HAMZA ET AL. 771 Copyright © 2010 SciRes. IJCNS Figure 2. Performance comparison between IDMA-N-ICA and IDMA systems in single path. Figure 3. Performance comparison between IDMA-N-ICA and IDMA systems in single path. Figure 4. IDMA-N-ICA performance comparison for dif- ferent rate load and C = 63. Figure 5. Performance comparison between IDMA-N-ICA and IDMA receiver when c = 31 and τ = 50%. Figure 6. Performance comparison between IDMA-N-ICA and IDMA receiver when c = 31 and τ = 100%. We notice that our proposed scheme handles very well the MAI interferences since convergence is warranted even at very loaded systems (τ100%). Figure 5 shows the added value of our proposed post-processor N-ICA when compared to the conven- tional IDMA receiver for loading rate 50% and for a spreading factor of 31. We notice that both convergence speed and better BER performances are achieved. There- fore, the proposed N-ICA approach can be employed in high loading rate in order to improve the performance of the system in terms of quality of service. Moreover, in case of low loading rate (50%), the proposed post processor allows a reduction in the number of iterations needed by the IDMA block leading to complexity reduction of the overall receiver. In the last simulation scenario, we evaluate the added value of the noisy ICA post processor over the ICA post processor. Figure 6 provides a comparison between  772 A. HAMZA ET AL. Copyright © 2010 SciRes. IJCNS IDMA, IDMA-ICA and IDMA-N-ICA receivers when the spreading factor is 31 and the load rate is 100%. When SNR is low, N-ICA outperforms the ICA post processor. However, when SNR is high, both receivers present the same performance. These observations are expected since N-ICA takes into account the presence of noise. It is worth noting also that both IDMA-ICA and ID- MA-N-ICA receivers outperforms the conventional IDMA receiver. 6. Conclusions In this paper, N-ICA post processor is proposed in ID- MA context. N-ICA algorithm constitutes an efficient tool for symbol recovery and it offers an efficient alter- native to the IDMA systems with block channel estima- tion. The major contribution of this work is the application of blind detection technique in the IDMA context. The proposed algorithm has better performance compared to the IDMA receiver in loaded systems because it allows dimension reduction (PCA) which helps to reduce the amount of noise in the system. For unloaded systems, the proposed post processor allows a complexity reduction by reducing the number of iterations needed by the IDMA block. In future work, to better analyze the complexity of the proposed scheme, FPGA implementation of IDMA and proposed post pro- cessor will be realized. 7. References [1] P. Li, L. Liu, K. Wu and W. K. Leung, “Interleave Divi- sion Multiple Access,” IEEE Transactions on Wireless Communication, Vol. 5, No. 4, 2006, pp. 938-945. [2] I. Mahafeno, C. Langlais and C. Jego, “Reduced Com- plexity Iterative Multi-User Detector for IDMA (Inter- leave Division Multiple Access) System,” Proceedings of IEEE Global telecommunication Conference, Vol. 1, San Francisco, 2006, pp. 530-540. [3] H. Schoeneich and P. Hoeher, “Semi-Blind Pilot-layer Aided Channel Estimation with Emphasis on Interleave Division Multiple Access Systems,’’ Proceedings of IEEE Global telecommunication Conference, Vol. 3, St. Louis, 2005, pp. 110-118. [4] T. Ristaniemi and J. Joutsensalo, “Advanced ICA Based Receivers for DS-CDMA Systems,” Signal Processing, Vol. 82, 2002, pp. 417-431. [5] M. Gupta and B. Santhanam, “ICA Based Blind Adaptive MAI Suppression in DS-CDMA Systems,” Proceedings of IEEE-DSP Workshop, New Mexico, 2004, pp. 204- 210. [6] J.-F. Cardoso, “Blind Signal Separation: Statistical Prin- ciples,” Proceedings of the IEEE, Vol. 86, No.10, June 1978, pp. 2009-2025. [7] A. Hyvarinen, “Fast and Robust Fixed-Point Algorithms for Independent Component Analysis,” IEEE Transac- tions on Neural Networks, Vol. 10, No. 3, 1999, pp. 626-634. [8] T. Huovinen, A. Shahed and M. Valkama, “Blind Diver- sity Reception and Interference Cancellation Using ICA,” Proceedings of International Conference on Acoustics, Speech and Signal Processing, Vol. 3, 2007, pp. 685-688. [9] A. O. Dahmane, “A New MMSE Based Cascade Fliter MUD Tracking Mode in Time-Varying Channels,” Pro- ceedings of IEEE Conference on Wireless and Mobile Computing, Networking and Communications, Vol.5, 2005, pp. 103-107. [10] M. E. Davies, “Identifiability Issues in Noisy ICA,” Pro- ceedings of IEEE Signal Processing letters, Vol. 11, No. 5, 2004, pp. 470-473. [11] O. Ekici and A. Yongacoglu, “Application of Noisy In- dependent Component Analysis for CDMA Signal Sepa- ration, Proceedings of IEEE-DSP Workshop, Vol. 3, July 2004, pp. 3812-3816. [12] A. Hamza, G. Salut and S. Chitroub, “Independent Com- ponent Analysis in IDMA Systems,” Proceedings of IEEE NEWCAS-TAISA, Toulouse, July 2009, pp. 64-68. [13] R. H. Mahadevappa, “Interference Cancellation Tech- nique for Multi-User Communication System”, PhD the- sis, Northeaster University, Massachusetts, 2002. |

