Int. J. Communications, Network and System Sciences, 2010, 3, 737-744
doi:10.4236/ijcns.2010.39098 Published Online September 2010 (http://www.SciRP.org/journal/ijcns)
Fuzzy Integral Based Information Fusion for Water
Quality Monitoring Using Remote Sensing Data
Huibin Wang1, Tanghuai Fan2, Aiye Shi1, Fengchen Huang1, Huimin Wang3
1College of Computer and Informa tion Engineering, Hohai University, Nanjing, China
2Department of Computer Science and Techno logy, Nanchang Institute of Technology, Nanchang, China
3State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing, China
Received June 16, 2010; revised July 22, 2010; accepted August 17, 2010
Abstract
To improve the monitoring precision of lake chlorophyll a (Chl-a), this paper presents a fusion method based
on Choquet Fuzzy Integral (CFI) to estimate the Chl-a concentration. A group of BPNN models are designed.
The output of multiple BPNN model is fused by the CFI. Meanwhile, to resolve the over-fitting problem
caused by a small number of training sets, we design an algorithm that fully considers neighbor sampling
information. A classification experiment of the Chl-a concentration of the Taihu Lake is conducted. The
result shows that, the proposed approach is superior to the classification using a single neural network classifier,
and the CFI fusion method has higher identification accuracy.
Keywords: Water Quality Monitoring, Remote Sensing, Neural Networks, Fuzzy Integral, Information
Fusion
1. Introduction
The reason of eutrophication is that the excess nutrients
accumulation leading to high biological productivity
(such as algae, aquatic plants, reeds, fish, plankton) in
the water, which includes natural factors and human fac-
tors. Eutrophication can cause deterioration of water quality
and change the water ecology, and in severe cases can
cause the original function of the lake losing, change the
lake's ecological environment. Therefore, Lake eutro-
phication monitoring [1] is an important part of water
environment monitoring. However, it is difficult to iden-
tify the lake eutrophication distribution information
exactly for relying solely on the ground sensors, or by
way of point source measurement. It needs to take the
advantages of remote sensing, using remote sensing
fusion manner through the eutrophication monitoring.
Remote sensing water quality monitoring is to get the
distribution of water quality by establishing the qualitative
or quantitative relationship between water spectral
characteristics and water quality parameters, and the
migration and changes of water quality by comparing the
information in different time. Lake water quality inver-
sion through combining remote sensing data with the
measured data of ground monitoring is the main form of
the present research.
But most inversion models are just single model, only
the inversion precision of the monitoring point itself is
analyzed, and the inversion precision of the non-monitoring
points which are adjacent to the monitoring point have
not been fully considered. Therefore, the precision of
inversion and robustness are very poor, which makes a
great affection to the result of information analysis.
One of the research challenges is how to create an
appropriate inversion model for water quality parameters
inversion of different regions and different characteristics.
Conventional inversion methods include empirical me-
thod, semi-empirical method and analysis method [2].
These methods are essentially achieving the water quality
inversion via the establishment of linear regression model.
However, since the non-linear relationship between re-
mote sensing image data and water quality parameters,
the estimation using linear regression and the small com-
plementary between the data will lead to a poor accuracy.
Therefore, many scholars conduct water quality inver-
sion by nonlinear regression method. Non-linear regres-
sion method can be both explicit and implicit. The pa-
rameters of explicit one are often difficult to determine,
while the parameters of implicit one avoid the above
problems. The implicit regression models commonly used

H. B. WANG ET AL. 738
are neural network regression model [3,4] and genetic
algorithm regression model [5]. To improve the accu-
racy of water quality inversion, some scholars establish the
water quality inversion model using other methods com-
bined with the neural network method [6].
However, all of the existing results establish the
inverse model by using the internal relations between
water quality spectral characteristics and remote sensing
image data. In addition, the existing inversion models
only analyze the accuracy of the local monitoring point
without considering the water quality inversion accuracy
of neighboring non-monitoring points.
Eutrophication evaluation commonly uses chlorophyll
a (Chl-a) as an indicator [7], the concentration of Chl-a is
an important parameter to measure the degree of eutro-
phication. The method using TM remote sensing data to
inverse Chl-a concentration can often be divided into two
categories: one is linear estimation model, and the other
is non-linear estimation model. The former algorithm is
less complex, while the inversion precision of the Chl-a
concentration is lower. The latter algorithm is more
complex, while the inversion precision of the Chl-a con-
centration is higher.
This paper focuses on the water environment moni-
toring information fusion classification of remote sensing
combined with ground monitoring data, the monitoring
data is classified by a group of water quality classifiers,
and the multiple output results of a group of water quality
classifiers are fused based on fuzzy integral fusion model
to get the Chl-a concentration estimates. This is based on
TM remote sensing image information extraction, com-
bining with the monitoring information from ground
sensors, to optimize information processing.
2. The Proposed Fuzzy Integral Model for
Water Quality Monitoring
Using remote sensing for water quality monitoring and
water quality status recognition, essentially, is an uncertain
problem. Because it is usually hard to determine the
regression model of water quality parameters between
remote sensing and ground monitoring, which requires a
lot of testing. Meanwhile, the water environmental
information is strongly related and has many complex
factors. Since it is difficult to extract the thematic infor-
mation of water quality parameters and status, the moni-
toring information from only one class of remote image
is incomplete, and the monitoring is not very robust. To
improve the robustness of water quality recognition, an
improved method is used. First, the data fusion process
using multi-spectral, radar and other remote sensing image
data are conducted, then, the water quality based on fu-
sion results is recognized. However, most recognition
applications are based on a single inversion model structure
which causes lower identification accuracy.
This paper designs a new fusion model based on Choquet
Fuzzy Integral (CFI) (showed in Figure 1) to estimate the
Chl-a concentration of Taihu Lake.
This model uses a group of inversion models, firstly,
multiple ground monitoring data and remote sensing data
n are input into the various inversion models (water
quality classification) n, the output is the initial Chl-a
concentration classification estimation, then the CFI is
used to fuse the outputs which come from different
inversion models to get the final result of Chl-a concen-
tration classification estimation. Water quality classification
can be composed of semi-empirical methods, neural
network, SVM and other models.
The fuzzy integral based fusion model is adopted,
mainly considering the fact that the fusion algorithm of
water quality classification needs not only the objective
results provided by inversion models, but also the
importance of inverse models in the fusion process. The
Choquet Fuzzy Integral (CFI) can obtain the importance
of inverse models by defining the fuzzy measure.
Accordingly, the fusion process transforms to the generalized
Lebesgue integral of objective results provided by inversion
models related to the importance of the corresponding
inverse models. As the importance of inversion models
has been taken into account, the CFI fusion method can
make the results more objective and accurate. In the
implementation process, the importance of inversion
models is obtained from the remote sensing data of mon-
itoring points and the training samples which consist of
Chl-a concentration. The value of importance level is
between region [0,1]. The closer to 1 the value is, the
more important inversion model is. On the other hand,
the smaller value indicates the less importance of the
inversion model. Meanwhile, CFI fully considers the
impact of various factors. The inversion model which has
great impact on one category, but has a small importance
level can also affect the fusion results by fuzzy integral.
Ground monitoring data
Remote sensing data 1
Remote sensing data 2
Remote sensing data n
Inversion
model 1
Inversion
model 2
Inversion
model n
Fuzzy
Integra l
Water
qua lity
Figure 1. Water quality monitoring model based on fuzzy
integral.

H. B. WANG ET AL. 739
3. NN Based Water Quality Classification
Artificial Neural Network (ANN) is an effective non-
linear approximation method. We select the back- prop-
agation neural network (BPNN) model as a water quality
classifier. Although the BP neural network has some
inherent shortcomings, it still has a good generalization
performance since it’s a global approximation algorithm.
Usually, the transfer function used by neurons of BP
neural network is sigmoid type differentiable function,
which can achieve any nonlinear mapping between the
input and output. In this method, all of the inversion
models use BP neural network.
This research uses multi-layer BPNN, which is de-
fined as follows: if the network is shown as 3-3-4, that is,
there are 3 nodes in the input layer, one hidden layer and
also 3 nodes in the hidden layer, and 4 nodes in the out-
put layer, and so the others. The input variables are data
from band 1 to band 3 of the Land sat TM image, while
the output ones are inversion of the Chl-a concentration
category. Each of the BPNN used has three input nodes
which have the same value, while it has four output
nodes. But it is different for the numbers of hidden layer
and its nodes in each BPNN. In addition, each BPNN
uses different learning rules, in order to ensure the inde-
pendence of the BPNN.
The approach uses 11 training sets (through Chl-a
concentration category collected on field and the corre-
sponding values of TM radiation). So far, there is no
general rule to select the appropriate number of training
set, but the more the number and decidability of training
set can be, the more promotion neural network has. In
general, the number of training set must be twice more
than the number of free variables. In the research, as the
number of available training set is relatively small, there
may be “over-fitting” problem during the network train-
ing. To solve that, we consider that it should utilize the
near information of each sampling site, shown in Figure 2.
Assume that each monitoring point and its four nearest
neighbor of Chl-a concentration are in the same category.
(Representative sampling site, Representative neighbor site,
between sampling site and neighbor site about 30 meters)
Figure 2. Sampling site and four neighbor sites.
This is because the spatial resolution of the Landsat TM
images from band 1 to band 3 is 30m, and correspondingly
the distance between its monitoring point of its ground
with the same name and its four nearest neighbor point is
also 30 meters (Landsat TM images have been registered
with the coordinate of ground monitoring point). Due to
the short distance, this assumption is reasonable. In the
research we select 11 monitoring points, and the nearest
4 points in the neighborhood of each monitoring points,
which 55 pairs of training set are composed of. The
Chl-a concentration category of 8 monitoring points and
their corresponding 4 points in the neighborhood, and the
value of radiation corresponding to TM images with the
same name are used as the training set (that is, 40 training
sets). The Chl-a concentration category of other 3 moni-
toring points and their corresponding values of TM ra-
diation are used as a test set. We select training set con-
sidering its representation in the entire lake region.
The traditional interpolation method of the neural
network may result in poor fitting or over-fitting of data.
Poor fitting will result in more training error, while the
over-fitting would lead to much larger inspection error.
Therefore, in the training network, we must make appro-
priate adjustments to the network's size, in order to make
training error similar to testing error.
Network input and output vectors have been normalized
to between 0 and 1 so that the input and output maintain
a certain dynamic range when the network is training.
4. Fuzzy Integral Based Fusion Method
CFI fuzzy integral is a nonlinear function with the fuzzy
measure. The distinction between Fuzzy integral and
other examples is that it takes the objective evidence
provided by the various sources and the desired value of
the sources’ subsets into account.
The two most commonly-used fuzzy integrals are Su-
geno [9] fuzzy integrals and Choquet [10] fuzzy integrals.
The Sugeno fuzzy integral is the nonlinear function de-
fined on the fuzzy measure, and it eliminates the effect of
the secondary factors. Compared with the weighted av-
erage, it enhances the effect of the main factors, but
completely ignores the secondary factors. Choquet fuzzy
integral takes various factors into account, in order to
avoid the defects of Sugeno fuzzy integral. The applica-
tion of the Choquet fuzzy integral in multi-source infor-
mation fusion has been emphasized and widely used [11].
As this paper selects the water quality by fuzzy integral,
considering the interaction of the different water quality
grades, this article carries out the information fusion by
Choquet fuzzy integral.
Fuzzy integral can be interpreted as a fuzzy expecta-
tion, or the maximum degree of consistency between two

H. B. WANG ET AL. 740
opposite trends or between objective evidence with the
expectation. In this paper, the fuzzy integral is under-
stood as a vague expectation that it expects the high
recognition accuracy of the water quality classes by
means of the fuzzy integral calculation.
The basic principle of fuzzy integral [12] is as follows:
Suppose that Sis a random set, ()PS is the power
set ofS, If Set Function
g
meets following conditions:
1) ()0,() 1ggS


2) () (),,,()
g
AgBifAB andA BP S 
3)

1
(),
ii
i
fAP SandA

 is monotonous, so
lim ()(lim)
2
ii
ii
g
Ag A

 

 (1)
Then
g
is one of fuzzy measures on()PS .
According to the above definition, Sugeno introduced
g

fuzzy measure. It satisfies the following conditions:
()() ()()()ig ABg AgBg AgB

   (2)
To any1

 , ,()
A
BPSand AB

, Suppose
that Sis a set formed by information source, Where,

12
,, ,
m
Sss s, And written as


()
ii
g
gs

,

i1, 2,,
g
imis called as fuzzy-density.
Suppose

12
,,,
m
A
sss X, so ()
g
A

is de-
fined as:
11
12
111
()
imm mm
iij m
iijj
g
Ag ggggg


 

 

(3)
When 0

, according to the property of Fuzzy measure,
the value of

is determined by the following polynomial
1
1(1)
m
i
i
g


 
 (4)
For a fixed set

,0 1
ii
gg, there is exclusive
(1,)

 and 0

, in conformity with (4).
So, the fuzzy measure is totally decided by its
fuzzy-density
g

. Murofushi and Sugeno proposed
Choquet Fuzzy integral, called CFI, showing by (5):
1
0
()()[()()] ()
()0
ii i
shsdghs hsgA
hs

 


 (5)
where 12 {, , ,}
ii
A
ss s, the order of the ()h

is de-
scending, that is12
0()()()1
n
hs hshs.
In the new-proposed method, the output of BPNN is
fused by CFI. Firstly, for ith Water quality classifier, its
correct recognition rate to water qualification is i
g
.So,
the fuzzy measure of every class different water quality
classifier can be deduced from (3) and (4).
In order to calculate CFI, we need to make certain
belief functionh, its value is determined by the output of
BPNN. Finally these BPNN are fused. According to (5),
the Fuzzy integral values of every water quality classifi-
cation are calculated. Then the class corresponding to the
maxima value is chosen as the correct recognition class.
5. Experimental Results and Analysis
This work is conducted at the Taihu Lake, which is in the
Yangtze River Delta in China. The Taihu Lake is the
third largest fresh water lake and is the typical plain type
shallow lake with its average depth 1.89 m. The area of
the Taihu Lake body is 2338.1 km2. The water body
volume probably is 0.47 km3; the change coefficient of
the water body is 1.18. The prevailing wind of Taihu
region is southeaster in spring and summer, the concen-
tration of Chl-a is a little high in its west and northwest
region; additionally, the pollution of industry, household
garbage and the circle net catches fish make the Chl-a
concentration nearby the lake is comparably high, too.
5.1. Data Sampling and Processing
The data of TM is the most used multi-spectral remote
sensing data in inland water quality monitoring. The unit
of TM data is scene, a scenery data, which compared to
the earth area, is the area of 185 km×185 km, and space
resolution is 30 m. The data of every scene is decided by
the satellite orbit number and central latitude, the system,
using the orbit and coordinate to decide the scene center,
is called Global index system.
Data usually offer users with CCT. Each unit of data
(which called the pixels) records reflective luminance on
the ground reflection area in each band, that are almost
the same as the resolution of sensors, the quantitative
series are 256. The parameters are shown in Table 1.
Locate direction about representative’s point of
research region respectively by using GPS, and measured
transparency and reflective spectra of water in each point
simultaneously. Meanwhile, in order to ensure the reli-
ability of the water quality research, the ground water
quality parameters acquisition time by sensors, should
consistent with the TM remote sensing data acquisition
time.
Due to the large surface of Taihu Lake, the width and
spatial resolution of a set of data from the TM are suffi-
cient to cover the entire region. The TM data is obtained
on 1997-05-04; its pseudo color composition diagram is
shown in Figure 3.

H. B. WANG ET AL. 741
Table 1. The observation parameters of landsat -4/5.
Wave
band
Wavelength
(μm)
Calibration of spec-
tral
regions
spatial
resolution
(m)
1 0.45~0.52 blue 30
2 0.52~0.60 green 30
3 0.63~0.69 red 30
4 0.76~0.90 near infrared 30
5 1.55~1.75 mid-infrared 30
6 10.4~12.5 infrared 60
7 2.08~2.35 mid-infrared 30
Figure 3. The 432 band Color composition diagram
of Taihu Lake (on 4 May,4,1997).
Before estimating the Chl-a concentration, we should
made atmospheric correction of the TM data. Here the
Dark-Object methods is used, it is assumed that the
radiation received by TM sensors including the wa-
ter-leaving radiance and the radiation caused by atmos-
pheric effects. If there is no atmospheric interference,
then the gray value of clean water (the general location is
mid-lake) in the near infrared band (the forth band) im-
age should be set to 0, otherwise, we assume the value is
n4, it indicates that the TM data suffered atmospheric
interference, so the forth band value of atmospheric
correction is radiation value subtract n4. Correspondingly,
the 1, 2, and 3 bands then made atmospheric correction
on the basis of n4 (generally according to the specific
image to adjust).
Furthermore, the ground space coordinate and the im-
age coordinate should be aligning. This article use Map-
Info7.0 to align coordinate. Figure 4 is composition dia-
gram of the original TM image and ground monitoring
point after alignment.
As shown in Figure 5, there is 11 monitoring points in
Taihu Lake in May 1997. Table 2 shows the Chl-a con-
centration value of the sampling points.
When we use TM multi-spectral remote sensing data
to study lake water quality, the band of choice is very
Figure 4. The effect picture of monitoring point and remote
sensing image after alignment.
Figure 5. The distribution of monitoring points in
Tai hu Lake.
Table 2. The concentration value of Chl-a of the sampling
points in Taihu lake.
Sampling points Concentration value of Chl-a
（μg/L）
S1 39
S2 22
S3 16
S4 17
S5 13
S6 16
S7 17
S8 8
S9 22
S10 47
S11 16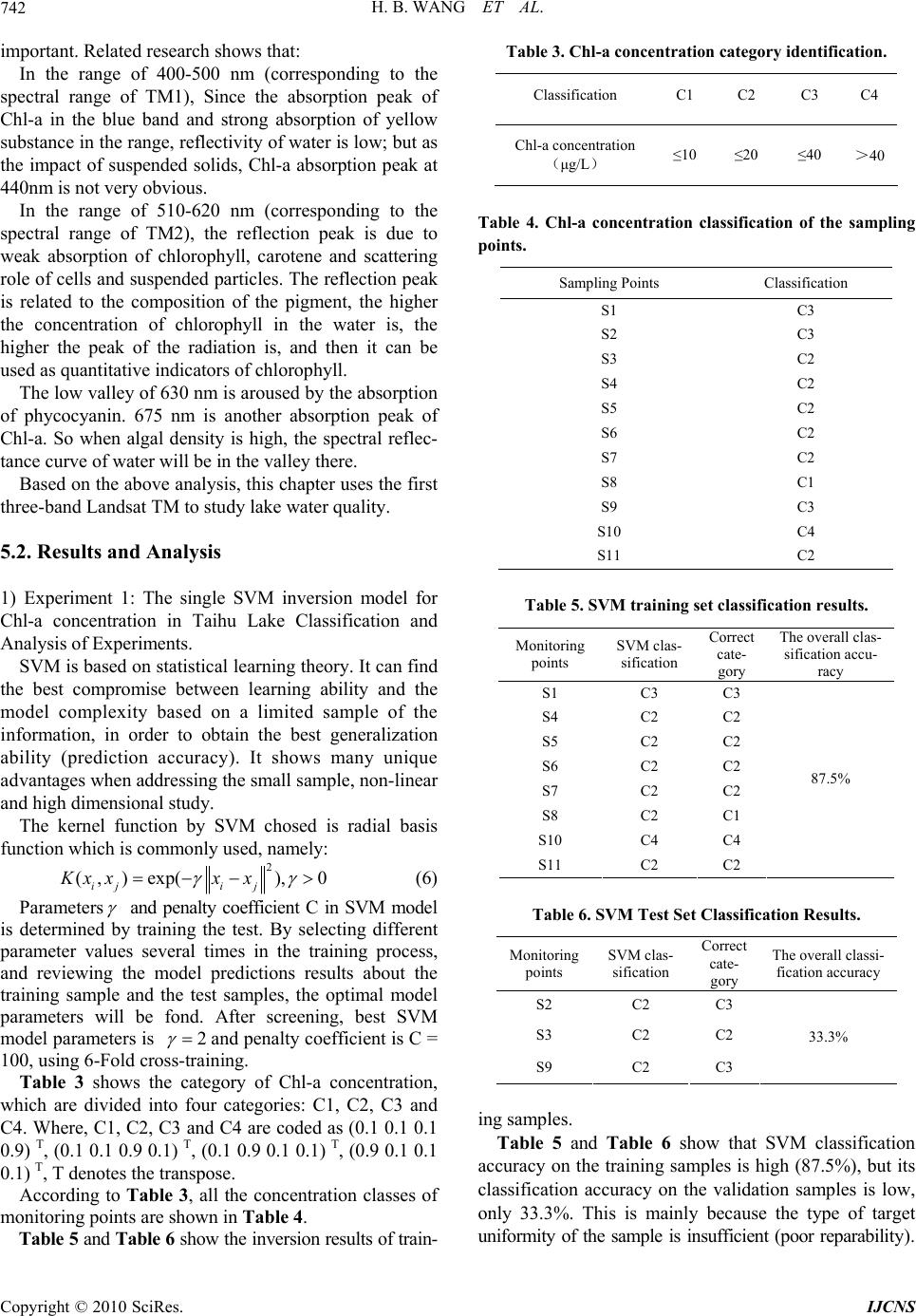

H. B. WANG ET AL. 742
important. Related research shows that:
In the range of 400-500 nm (corresponding to the
spectral range of TM1), Since the absorption peak of
Chl-a in the blue band and strong absorption of yellow
substance in the range, reflectivity of water is low; but as
the impact of suspended solids, Chl-a absorption peak at
440nm is not very obvious.
In the range of 510-620 nm (corresponding to the
spectral range of TM2), the reflection peak is due to
weak absorption of chlorophyll, carotene and scattering
role of cells and suspended particles. The reflection peak
is related to the composition of the pigment, the higher
the concentration of chlorophyll in the water is, the
higher the peak of the radiation is, and then it can be
used as quantitative indicators of chlorophyll.
The low valley of 630 nm is aroused by the absorption
of phycocyanin. 675 nm is another absorption peak of
Chl-a. So when algal density is high, the spectral reflec-
tance curve of water will be in the valley there.
Based on the above analysis, this chapter uses the first
three-band Landsat TM to study lake water quality.
5.2. Results and Analysis
1) Experiment 1: The single SVM inversion model for
Chl-a concentration in Taihu Lake Classification and
Analysis of Experiments.
SVM is based on statistical learning theory. It can find
the best compromise between learning ability and the
model complexity based on a limited sample of the
information, in order to obtain the best generalization
ability (prediction accuracy). It shows many unique
advantages when addressing the small sample, non-linear
and high dimensional study.
The kernel function by SVM chosed is radial basis
function which is commonly used, namely:
2
(, ) exp(),0
iji j
Kx xxx    (6)
Parameters

and penalty coefficient C in SVM model
is determined by training the test. By selecting different
parameter values several times in the training process,
and reviewing the model predictions results about the
training sample and the test samples, the optimal model
parameters will be fond. After screening, best SVM
model parameters is 2

and penalty coefficient is C =
100, using 6-Fold cross-training.
Table 3 shows the category of Chl-a concentration,
which are divided into four categories: C1, C2, C3 and
C4. Where, C1, C2, C3 and C4 are coded as (0.1 0.1 0.1
0.9) T, (0.1 0.1 0.9 0.1) T, (0.1 0.9 0.1 0.1) T, (0.9 0.1 0.1
0.1) T, T denotes the transpose.
According to Table 3, all the concentration classes of
monitoring points are shown in Table 4.
Table 5 and Table 6 show the inversion results of train-
Table 3. Chl-a concentration category identification.
Classification C1 C2 C3 C4
Chl-a concentration
（μg/L） ≤10 ≤20 ≤40 ＞40
Table 4. Chl-a concentration classification of the sampling
points.
Sampling Points Classification
S1 C3
S2 C3
S3 C2
S4 C2
S5 C2
S6 C2
S7 C2
S8 C1
S9 C3
S10 C4
S11 C2
Table 5. SVM training set classification results.
Monitoring
points
SVM clas-
sification
Correct
cate-
gory
The overall clas-
sification accu-
racy
S1 C3 C3
S4 C2 C2
S5 C2 C2
S6 C2 C2
S7 C2 C2
S8 C2 C1
S10 C4 C4
S11 C2 C2
87.5%
Table 6. SVM Test Set Classification Results.
Monitoring
points
SVM clas-
sification
Correct
cate-
gory
The overall classi-
fication accuracy
S2 C2 C3
S3 C2 C2
S9 C2 C3
33.3%
ing samples.
Table 5 and Table 6 show that SVM classification
accuracy on the training samples is high (87.5%), but its
classification accuracy on the validation samples is low,
only 33.3%. This is mainly because the type of target
uniformity of the sample is insufficient (poor reparability).

H. B. WANG ET AL. 743
In 11 samples sets, 54.55% is C2. Although the SVM is
suitable for fitting a small sample data, but its generali-
zation performance is also poor because of the poor
divisibility of target category. In addition, the encoding
for the target sample of SVM classifier is inferior to
neural networks. Such as for the class of the target sam-
ple m, encoded is the only positive integer m, which also
makes the category fitting degree of water quality pa-
rameters lower in the case of too few training samples
using SVM method. The result is show as in Figure 6.
2) Experiment 2: We use fuzzy integral proposed in
this paper combining with neural network model to
compare and analyze the Chl-a concentration category in
Taihu Lake. Besides, it is compared with the single neural
network model.
In this research, the training sets include Chl-a con-
centration category of eight monitoring points: S1, S4,
S5, S6, S7, S8, S10, S11 and their four neighbor points
and the corresponding TM image radiance. Test set is
constituted with The Chl-a concentration classification of
other three monitoring points and corresponding TM
image radiation.
Three BPNN used to generate the initial value of Chl-a
concentration category. To ensure the independence of
three BPNN, the first BPNN structure is 3-4-4, the second
BPNN structure is 3-5-4, and the third BPNN structure is
3-3-4-4. The three BPNN input vectors are the value of
atmospheric correction radiance in band TM1, TM2,
TM3. In addition, the learning rules of each BPNN are
different. The first BPNN is momentum of back propa-
gation gradient descent; second BPNN is decreasing
gradient adaptive learning rate back propagation; third
using Bayesian back propagation rule. The expected
output of BPNN is the Chl-a concentration category.
All of the BPNN is trained using the MATLAB soft-
ware. Test set for each BPNN model results and the
results of CFI are shown in Table 7.
As can be seen from Table 7, the classification
obtained using the CFI model results better than the single
BPNN classifier. Although each BPNN can give the correct
classification to the test set, while CFI gives better
classification of test results.
For sampling point S2, correct classification is given
by BPNN according to the principle of selecting the
maximum, However, for the reason that the confidence
values of class 3 (C3) and class 4 (C4) (outputs of BPNN)
are similar (confidence values of C3 and C4 are 0.534
and 0.526 respectively), it is not easy to distinguish the
two classes. Moreover, by using model CFI, not only can
we distinguish sampling point S3 well, but also can
distinguish C3 from other categories.
Figure 7 shows the Chl-a concentration distribution
produced by the model this paper proposed. As is shown
Figure 6. SVM method of inversion of the Taihu Lake
water quality categories.
Figure 7. Chl-a concentration distribution of TaiHu Lake.
in Figure 7, the highest concentration of Chl-a are in the
northern area, northeast corner, southwest corner, and the
whole eastern coastal area of Taihu Lake, while the value
of Chl-a concentration is 0-10μg/L in central southwest
area.
From the comparison by Figure 6 and Figure 7,
there is a great difference between the water quality cat-
egory of SVM inversion and the new method. When us-
ing SVM method, there are only water C2, C3 and C4 in
Taihu Lake, by comparison, C1, C2, C3, C4 all exist
when using the new method. From concentration of
Chl-a of monitoring sites, The case of four classes of
water all existing in Taihu Lake, is consistent with the
actual situation. It shows that, for TM data of 1997, the
category precision of water quality inversion using new
method is superior to using a single inversion model
(such as SVM).
6. Conclusions
For water environment monitoring based on remote
C1:0~10
C2:10~20
C3:20~40
C4:＞40
g/L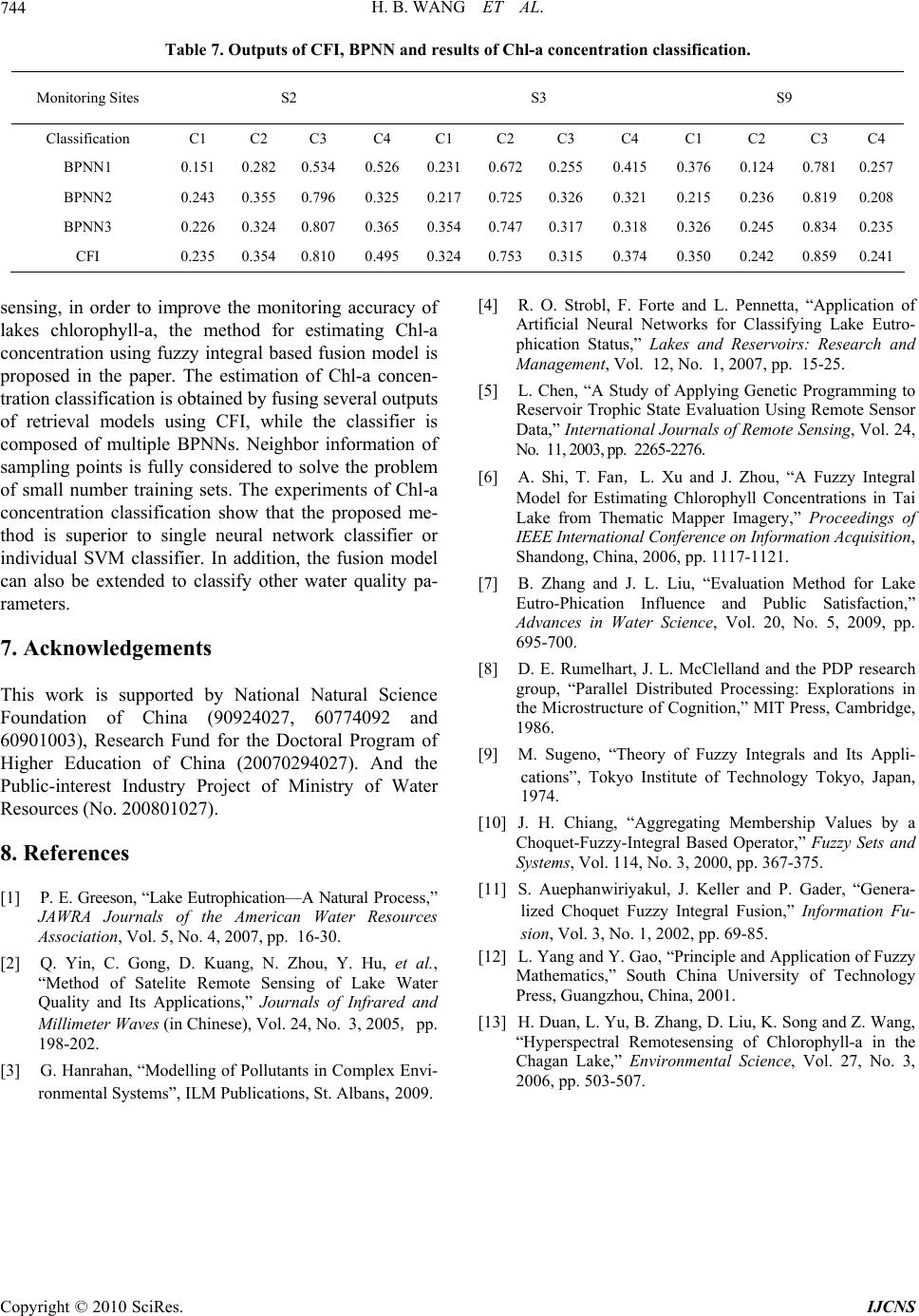

H. B. WANG ET AL. 744
Table 7. Outputs of CFI, BPNN and results of Chl-a concentration classification.
Monitoring Sites S2 S3 S9
Classification C1 C2 C3 C4 C1 C2 C3 C4 C1 C2 C3 C4
BPNN1 0.151 0.282 0.534 0.5260.2310.6720.2550.415 0.376 0.124 0.7810.257
BPNN2 0.243 0.355 0.796 0.3250.2170.7250.3260.321 0.215 0.236 0.8190.208
BPNN3 0.226 0.324 0.807 0.3650.3540.7470.3170.318 0.326 0.245 0.8340.235
CFI 0.235 0.354 0.810 0.4950.3240.7530.3150.374 0.350 0.242 0.8590.241
sensing, in order to improve the monitoring accuracy of
lakes chlorophyll-a, the method for estimating Chl-a
concentration using fuzzy integral based fusion model is
proposed in the paper. The estimation of Chl-a concen-
tration classification is obtained by fusing several outputs
of retrieval models using CFI, while the classifier is
composed of multiple BPNNs. Neighbor information of
sampling points is fully considered to solve the problem
of small number training sets. The experiments of Chl-a
concentration classification show that the proposed me-
thod is superior to single neural network classifier or
individual SVM classifier. In addition, the fusion model
can also be extended to classify other water quality pa-
rameters.
7. Acknowledgements
This work is supported by National Natural Science
Foundation of China (90924027, 60774092 and
60901003), Research Fund for the Doctoral Program of
Higher Education of China (20070294027). And the
Public-interest Industry Project of Ministry of Water
Resources (No. 200801027).
8. References
[1] P. E. Greeson, “Lake Eutrophication—A Natural Process,”
JAWRA Journals of the American Water Resources
Association, Vol. 5, No. 4, 2007, pp. 16-30.
[2] Q. Yin, C. Gong, D. Kuang, N. Zhou, Y. Hu, et al.,
“Method of Satelite Remote Sensing of Lake Water
Quality and Its Applications,” Journals of Infrared and
Millimeter Waves (in Chinese), Vol. 24, No. 3, 2005, pp.
198-202.
[3] G. Hanrahan, “Modelling of Pollutants in Complex Envi-
ronmental Systems”, ILM Publications, St. Albans, 2009.
[4] R. O. Strobl, F. Forte and L. Pennetta, “Application of
Artificial Neural Networks for Classifying Lake Eutro-
phication Status,” Lakes and Reservoirs: Research and
Management, Vol. 12, No. 1, 2007, pp. 15-25.
[5] L. Chen, “A Study of Applying Genetic Programming to
Reservoir Trophic State Evaluation Using Remote Sensor
Data,” International Journals of Remote Sensing, Vol. 24,
No. 11, 2003, pp. 2265-2276.
[6] A. Shi, T. Fan，L. Xu and J. Zhou, “A Fuzzy Integral
Model for Estimating Chlorophyll Concentrations in Tai
Lake from Thematic Mapper Imagery,” Proceedings of
IEEE International Conference on Information Acquisition ,
Shandong, China, 2006, pp. 1117-1121.
[7] B. Zhang and J. L. Liu, “Evaluation Method for Lake
Eutro-Phication Influence and Public Satisfaction,”
Advances in Water Science, Vol. 20, No. 5, 2009, pp.
695-700.
[8] D. E. Rumelhart, J. L. McClelland and the PDP research
group, “Parallel Distributed Processing: Explorations in
the Microstructure of Cognition,” MIT Press, Cambridge,
1986.
[9] M. Sugeno, “Theory of Fuzzy Integrals and Its Appli-
cations”, Tokyo Institute of Technology Tokyo, Japan,
1974.
[10] J. H. Chiang, “Aggregating Membership Values by a
Choquet-Fuzzy-Integral Based Operator,” Fuzzy Sets and
Systems, Vol. 114, No. 3, 2000, pp. 367-375.
[11] S. Auephanwiriyakul, J. Keller and P. Gader, “Genera-
lized Choquet Fuzzy Integral Fusion,” Information Fu-
sion, Vol. 3, No. 1, 2002, pp. 69-85.
[12] L. Yang and Y. Gao, “Principle and Application of Fuzzy
Mathematics,” South China University of Technology
Press, Guangzhou, China, 2001.
[13] H. Duan, L. Yu, B. Zhang, D. Liu, K. Song and Z. Wang,
“Hyperspectral Remotesensing of Chlorophyll-a in the
Chagan Lake,” Environmental Science, Vol. 27, No. 3,
2006, pp. 503-507.