Identification of Noisy Utterance Speech Signal using GA-Based Optimized 2D-MFCC Method and a Bispectrum Analysis

doi:10.4236/jsea.2012.512B037

Paper Menu >>

Journal Menu >>

Journal of Software Engineering and Applications, 20 12, 5, 193-199

doi:10.4236 /js ea.2012.512b037 Published Online December 2012 (http://www.SciRP.org/journal/jsea)

193

Identification of Noisy Utterance Speech Signal using

GA-Based Optimized 2D-MFCC Method and a

Bispectrum Analysis

Benyamin Kusumoputro1, Agus Buono2, Lina3

1Departmen t of Elect rical En gineerin g, Uni versitas In donesi a, Jakart a, Indonesia; 2Department o f Computer S cience, Bogor Agricu l-

tural University, Bogor, Indonesia; 3Department of Computer Science, Tarumanagara University, Jakarta, I ndonesia..

Email: kusum o@ e e . ui. a c .i d, pu desha @yahoo. c o. i d, l ina @ untar . a c .id

Received 2012

ABSTRACT

One -dimensional Mel-Frequency Cepstrum Coefficients (1D-MFCC) in conjunction with a power spectrum analysis

method is usually used as a feature extraction in a speaker identification system. However, as this one dimensional fea-

ture e xtract ion subs ystem shows low recognition rate for identifying an utterance speech signal under harsh noise con-

ditions, we have developed a speaker identification system based on two-dimensional Bispectrum data that was theo-

retically more robust to the addition of Gaussian noise. As the processing sequence of ID-MFCC method could not be

directly used for processing the two-dimensional Bispectrum data, in this paper we proposed a 2D-MFCC method as an

extension of the 1D-MFCC method and the o pti mization o f the 2D filter de sig n using Genetic Algorithms. By using the

2D-MFCC method with the Bispectrum analysis method as the feature extraction technique, we then used Hidden

Markov Model as the pattern classifier. In this paper, we have experimentally shows our developed methods for ide nti-

fying an utterance speech signal buried with various levels of noise. Experimental result shows that the 2D-MFCC

method without GA optimization has a comparable high recognition rate with that of 1D-MFCC method for utterance

signal without noise addition. However, when the utterance signal is buried with Gaussian noises, the developed

2D-MFCC shows higher recognition capability, especially, when the 2D-MFCC optimized by Genetics Algorithms is

utilized.

Keywords: 2D Mel-Frequency Cepstrum Coefficients; Bispectrum; Hidden Markov Model; Genetics Algorithms

1. Introduction

Research on automatic speech and voice identification

system has attracted much interest in the last few years,

motivated b y the gro wth o f its app licatio ns in man y areas

such a s in diagnosis of a ro tor crack [1], classification o f

unknown radar targets [2], medical disease [3], and for

personal and gender identification for security system

[4,5]. Speaker based personal identification is the process

of determining a registered speaker when an utterance

speech signal is provided. In this machine-based speech

identification, a gallery of speeches is firstly enrolled to

the s ystem and cod ed for sub sequent searchi ng. W hen an

unide nt i fied sp e ec h is fe tche d to the s yste m, a tho ro u ghl y

comparison with the each coded speech in the gallery,

and the identi ficatio n is then a ccompli shed when a suita-

ble match occurs.

Speaker identification system can be divided into two

subsystems, i.e., a feature extraction subsystem and a

classifier subsystem. The main function of a feature ex-

traction subsystem is to transform the input utterance

speech signal into a set of features, while a classifier

subsystem have to identify and classify the speaker by

comparing the extracted-features from his/her speech

signa l input with the ones from a set of known speakers

database.

Conventional feature extraction subsystem usually

used Mel-Freq uency Cepst rum Coe fficients (M FCC) and

power spectrum analysis methods [6]. Power spectrum

analysis method, however, shows low recognition rate

for classifying the utterance speech signal under harsh

noise condition [7]. To solve this problem, higher order

signal analysis, i.e. bispectrum analysis method is util-

ized, since the bispectrum value is theoretic ally robust to

Gaussian noise [8], which can be empirically proved by

researchers such as in [7,9]. As the utterance speech in

bispectrum data is represented as a pattern in 2D decision

space, bispectrum analysis required two-dimensional

filter design, and for that purpose, we have developed

2D-MFCC filter design method that will be explained

here.

Identification of Noisy Utterance Speech Signal using GA-Based Optimized 2D -MFCC

Method and a Bispectrum Analysis

194

The remainder of this paper is organized as follows. In

Section 2, we formulate the development of 2D-MFCC

filter develop ment. Section 3 p resents t he op timizatio n o f

2D-MFCC filter development by using Genetic Algo-

rithms. Section 4 shows the experimental setup and re-

sults to demonstrate the effectiveness of the proposed

method. Finally, Section 5 is dedicated to a summary of

this study and suggestions for future research directions.

2. Speaker Identification System

The focus of this paper is to develop a feature extraction

subsystem that could increased the recognition rate of the

classifier subsystem (HMM method), to classify an ut-

terance speech buried in a harsh noise condition. In the

developed method, the feature extracting subsystem is

composed of a 2D-MFCC filter design to extract the 2D

information contained in the Bispectrum data. The Bis-

pectrum data is represented as a 2D vector with MxM

elements in a 2D frequency space of f1 and f2, respec-

tively. In this section we will present a brief review of

1D-MFCC filter construction and the developed of

2D-MFCC filter construction for representing the Bis-

pectrum data.

We developed further the feature extraction subsystem

by using a Genetic Algorithm (GA) method. GA is used

to optimize the filter characteristics in such that the dif-

ference between the feature vector of a speech signal

without noise addition and the feature vector of a speech

signal with Gaussian noise addition will be as small as

possible. By reducing the difference between these two

signals from the same speaker, the possibility of the

speaker to be recognized correctly will be higher. As the

learning method of the classifier subsystem is important

aspect for increasing the recognition rate as in the soft

computing methods, in this research, a Hidden Markov

Model (HMM) trained by Baum Welch Algorithm is

utilized [10 ].

In the learning phase, samples of the speaker’s speech

for a certain phrase of a word is inputted to the speech

database, and by using these samples, the classifier sys-

tem is trained to develop the reference models for those

determined-speakers. In the application phase, the input

utterance speech signal is compared with each of the

models that has already been stored (as a reference model)

on the database, and the classifier decided the winning

speaker by determining the highest recognition rate for

all the reference models.

2.1. Power Spectrum Analysis with 1D-MFCC

Method

Suppose each tone of an utterance speech signal with an

actual frequency f (Hz) is represented in Mel-frequency

scale, following the relation ship of:

ˆ2595*log1 700

mel

f

= +





(1)

when the actual frequency f is higher than 1000 Hz, and

linear when the actual frequency is lower than 100 Hz.

The 1D-MFCC filter design method provides a trian-

gular filter with height of 1 at its middle point, and 0 at

their left and right parts for filtering the 1D

Mel-frequency data. As can be seen in the Fig.2,

1D-MFCC filter can be depicted as three vertex points:

(fi-1,0 ), (fi, 1), and (fi+1,0) for the ith filter, with i = 1 , …, M.

It is clearly seen that determining the center point of each

filter and the distance between the two adjacent center

points of the filter is essential [7,9 ,10].

The Mel-frequency spectrum coefficients MFSi is cal-

culated as the sum of the filtered 1D Mel-frequency X(j)

that can be expressed as:

log(( ))*()

MFSabs XjHf

−



=



∑

(2)

where i=1,…,M, M the number of the triangular filter, N

the number of FFT coefficients. The abs(X(j)) is the

magnitude of jth of the FFT pro cess o f the inp ut utter anc e

signal, and Hi(f) is the height of ith triangular at point f.

The MFCCk value is then calculated by using Discrete

Cosine Transform to transform the Mel-frequency spec-

trum coefficients back into its ti me domain throug h:

*( 0.5)*

*cos 20

MFCC MFS

−



=



∑

(3)

where k=1,…,K the number of coefficients.

2.2. Bispectrum Analysis with 2D-MFCC

Method

Bispectrum analysis of an utterance speech signal can be

explained as follows. If {X(k)}, k=0,±1,...,±2 is a real

random process, then the cumulants of order 3 is

)2,1(

ττ

( 1,2)(1)(1)!

Xpk

piS

iS is

C pEX

EXEX

ττ

−

=∈

∈∈



=−−











∑∏

∏∏

(4)

where the summation extends over all partitions

(s1,s2,…,sp), p=1,2,3, of the set of integers (1,2,3). Bis-

pectrum, referred to as cummulant spectra, is a Fourier

transform of cummulant sequence, and formulated as:

( )

31 23 12

1122

(, ),

*exp{(,)}

ττ

ωω ττ

ωτ ωτ

+∞ +∞

=−∞ =−∞

−

∑∑

(5)

Identification of Noisy Utterance Speech Signal using GA-Based Optimized 2D-MFCC

Method and a Bispectrum Analysis

195

In the case of stationary process, the cummulant order

3 can be formulated as:

{ }

( ,)()()()

3121 2

cE xtxtxt

τττ τ

= ++

(6)

Basically, there are two approaches to predict the Bis-

pectrum, i.e. a parametric approach and a conven- tional

approach. The conventional approach consists of the fol-

lowing three classes, i.e. an indirect technique, a direct

technique and a complex demodulates method. Because

of its simplicity, in this research, the Bispectrum data is

predicted using the conventional indirect method, in

which the detail of this algorithm is presented elsewhere

[11].

Since Bispectrum data is represented in two dimen-

sions o f fre q uenc y f1a nd f2, a 2D-MFCC filter , instead of

a 1D-MFCC filter, should be used to process the data. To

develop 2D-MFCC filter, we firstly construct a 1D-

MFCC filter in each of f1 and f2 dimension, with in the

first dimension f1 as f1i ; i=1,. . .,M and in the second

dimension f2 as f2j; j=1,. .., N, with M=N. We then com-

bined the two separate 1D-MFCC Hi(f1m) and the other

1D-MFCC Hj(f2n) into an integrated 2D-MFCC

Hij(f1m,f2n) as a pyramid shape, that can be depicted in

Figure 1a. The base o f this pyra mid shape is a square with

its corner positions are (f1i-1,f2 j-1), (f1 i +1 , f2 j-1), (f1 i-1,f2 j +1)

and ( f1i +1 , f2 j+1), respectively, as can be seen in Figure 1b.

The connected lines between the center of the square

shape and each of the corner points determined as the

line a, line b, line c and line d, respectively, which its

line equation ca n be written as :

Figure 1. The construction of 2D-MFCC filter and its cal-

culation for Bispec tru m data B(f1m,f2n).

line a:

( )

211 2

fff f

−



= −+



−

 (7)

line b:

( )

211 2

fff f

−



= −+



−

 (8)

line c:

( )

211 2

fff f

−



= −+



−

 (9)

line d:

( )

211 2

fff f

−



= −+



−

 (10)

Using these lines, the square shape of the pyramid fil-

ter can be divided into four quadrants as can be seen in

Figure 1c. Suppose we have a Bispectrum data B(f1m,f2n)

in the t wo d imens io n freq uenc y space such as depicted at

Figure 1d. The height of the 2d filter is calculated by

firstly determined the quadrant of the data and then cal-

culate the Hi,j(f1m,f2n), using algorithm written below.

1. If B(f2n) > f2 j-1, and

( )

(2)( 1)12

nmij

BfBff f

−



< −+



−



( )

(2)( 1)12

nmij

BfBff f

−



< −+



−



Then B(f1m,f2n) Є quadrant I;

( 2)2

( 1,2)22

ij mnjj

Bf f

Hf fff

−

=−

(11)

2. If B(f2n) < f2j+1 , and

( )

(2)( 1)12

nmi j

BfBff f

−



> −+



−



−



> −+



−



Then B(f1m,f2n) Є quadrant II;

2( 2)

( 1,2)22

ij mnjj

f Bf

Hf fff

−

=−

(12)

3. If B(f1m)>f1i-1, and

( )

(2)( 1)12

nmi j

nmij

BfBfff

−



> −+



−



−



< −+



−



Then B(f1m,f2n) Є quadrant III;

(1) 1

( 1,2)11

ij mnii

Bf f

Hf fff

−

=−

(13)

Identification of Noisy Utterance Speech Signal using GA-Based Optimized 2D -MFCC

Method and a Bispectrum Analysis

196

4. If B(f1m)<f1i+1, and

( )

(2)( 1)12

nmi j

nmij

BfBfff

BfBff f

−



> −+



−



−



< −+



−



Then B(f1m,f2n) Є quadrant IV;

1 (1)

( 1,2)11

ij mnii

f Bf

Hf fff

−

=−

(14)

Using the same calculation such as in the 1D-MFCC

method (see Eq. (2)), the Mel-frequency Bispectrum

coefficients MFS(i,j) is calculat ed thr ough:

128 128

( ,)log[(1,2)

*(1,2)]

ij mn

MFS ijBff

Hf f

= =

=∑∑

(15)

for the 2D-filter height Hi,j(f1m,f2n), with m=1,…,M,

n=1,…,N, and M=N=128. The MF CC(i,j) for 2D-MFCC

is then calculated through 2D-cosine transform, as:

( )

( 0,5)

(,) *cos

( 0.5)

*cos

kij

MFCCMFS ijN



−

=



−

∑∑

(16)

where k=1,2,3,…,K the number of the coefficient.

3. Optimization of 2D-MFCC Filter using

Genetic Algori t hms

The 2D-MFCC method is developed for calculating the

Mel-Bispectrum coefficients MFCCk (in Eq. 21) of

t wo-dimensions Bispectrum Mel-frequency B(f1m,f2n), b y

calculating the 2D-filter height Hi,j(f1m,f2n). Since the

center position of each filter is very essential in deter-

mining this 2D-filter height Hi,j(f1m,f2n), optimizing the

position of the filter’s center is necessary for reducing the

total error. Thus the goal of the optimization process, i.e.

Genetic Algorithms [17], is to minimize the difference

between the Mel-Bispectrum coefficients of a speech

signal buried with a Gaussian noise and that without a

Gaussian noise by designing the optimized 2D-filter

height Hi,j(f1m,f2n).

The chromosome representation is constructed as fol-

lows. Suppose M is the maximum number of triangular

filters on each frequency dimension f1 and f2, respec-

tively, and F is the maximum frequency for both each

dimensions. Suppose the distance between each of the

center positio n of those filter s, as x1, x2, x3, …, xM+1 such

that x1+x2+x3+ …+xM+1=F, where xi is the distance be-

tween ith filter center with the next (i +1)th filter center,

with i=2,3,4,…,M. For representing the optimized set of

these filters that will be used in the 2D-MFCC, the dis-

tance between two filters center is coded into 7 binary

digits. Then the chromosome that represents a set of fil-

ters could be coded by binary digit with a length of

7*(M+1) digits, i.e., the first seven digits for x1, the

second seven digits for x2, and so on. A simple illustra-

tion of the chromosome representation process is ex-

plained here. Suppose we have four triangular filters on

one-dimension frequency domain, with its center position

are 2.5, 4.5, 6.5 and 8.0, resp ectively, with the ma ximum

frequency F is 10. The distance between each of filter’s

center are x1=2.5, x2=4.5-2.5=2, x3=6.5-4.5=2,

x4=8-6.5=1.5, and x5=10-8=2. The chromosome then

consists of 5 locus, i.e. x1, x2, x3, x4, and x5, in which each

locus is coded by binary digit with length of 7 to be

7*5=35 digits.

The Fitness Function is calculated so that the deter-

mined set of filters produced the Mel-Bispectrum coeffi-

cient MFCCk, that have with very similar characteristics

between the input speech signal added with Gaussian and

that without a G aussian noise addition. T his fitness func-

tion can be mathematically formulated as follow:

),(*),(

)(

4321

4231BBdBBd

BBdBBd

ifitness =

(17)

where B1 is the Bispectrum data B(f1m,f2n) of the signal

without noise addition, B2 is the Bispectrum data

B(f1m,f2n) of the signal added with 20dB Gaussian noise,

B3 is the B2 - B1, B4 is the Bispectrum data B(f1m,f2n) of

20dB Gaussian noise, and d(B k,Bl) the distance between a

feature vector of Bispectrum data Bk and a feature vector

of Bispectrum data Bl.

A conventional roulette whee l is then used to select th e

winning chromosome in population. Chance for any

chromosome to be selected is proportional to their fitness

value. The Crossover technique is then used to alter two

chromosomes into their o ffspring, and in this res earch, an

arithmetic crossover technique is utilized. Suppose two

parents X=(x1,x2,x3,…, xN+1) and Y=(y1,y2,y3,…, yN+1) and

by using an arithmetic crossover technique, their

offspring are X=(x1,x2,x3,…, xN+1) and Y=(y1,y2,y3,…, yN+1)

with aЄ(0,1).

Mutation is a process of transforming any chromo-

some to its offspring through a changing of the internal

gene. The mutation is started by selecting a certain

chromosome to be mutated, followed by randomly gen-

erated two integer numbers p and q, p,q Є [0,N+1] with

N the number of the filter used. The mutation process is

done by inverting the order of locus between those se-

lected points.

Figure 2 shows a sample of the comparison of a 1D-

MFCC filter -bank design by using the conventional method

and a GA-based optimization met hod. It is clea rly shows

Identification of Noisy Utterance Speech Signal using GA-Based Optimized 2D-MFCC

Method and a Bispectrum Analysis

197

that different pattern of the filter-bank are achieved,

which is lead to better per formance on its application.

4. Experiment Setup and Results

Several experiments were conducted to evaluate the

performance of the developed system. The utterance

speech signals were recorded as WAV files, conducted

by ten Indonesian people, within the ages range of 12 –

28 years old. They were asks to say ’pudesha’ with

normaly tones and intuation, but allowed to lengthening

their pronountiation. Each speaker uttered 80 times and

digitized by sampling rate of 11 kHz within duration of

1.28 second, and each frame that consists of 512 samples

per frame is read frame by frame with an overlaps of 256

samples between the adjacent frames. Training/testing

paradigm is taken to be 50%: 50%, in which 400

utterance speeches are used as the training set, while the

other 400 utterance speeches are taken as the testing data

set.

The bispectrum analysis of each frame is conducted by

using conventional indirect method as explained in [8].

We calculated the filtered bispectrum of each frame at

frequency B(f1m,f2n), and converted into MFCCk

coefficients such as in Eq. 3. Number of coefficients K is

determined to be 13, and as the consequence, the

bispectrum value of each frame could be written as a

feature vector that consists of 13 elements. For a balance

comparison, this value is also used for the other feature

extraction methods, including the conventional 1D-

MFCC method.

Hidden Markov Model is used as the classifier in all of

the experiments conducted here, and three different methods

of feature extraction subsystems, i.e. the conventional

1D-MFCC method, 2D-MFCC method and 2D-MFCC-

GA method are examined and compared. Figure 7 sh ows

(a)

(b)

Figure 2. (a) Conventional one-dimensional MFCC filter-

ban k, (b) MFCC filterbank optimized by using GA.

Figure 3. Comparison of recognition rate between 1D-

MFCC with 2D-MFCC for a speech signal without noise

addition.

a comparison of recognition rate between 1D-MFCC

with 2D-MFCC for uttered speech signal without an

addition of a Gaussian noise. Noted that in these

experiments, we ha ve used numerous hidden units in the

HMM classifier for comparison. Experimental results

depicted in Figure 3 show that when the three different

methods are used to classify an utterance speech signal

without Gaussian noise addition, the recognition rates

were very high, i.e. 98.4%, 99.4% and 99.0% for 1D-

MFCC, 2D-MFCC and 2D-MFCC-GA, respectively.

These comparable results sho w that the 2D -MFCC method

is not necessary be used, when it is used to classify an

utterance speech signal without noise addition.

This result also co nfirmed that the 1D-MFCC method,

which was usually used in the conventional system,

works appropriate enough to classify speakers when

there were no noise disturbances. It is also clearly seen

from this figure that the different number of hidden unit

used in the HMM classifier has no influence to the rec-

ognition rate of the system. In the next experiments af-

terward, we have determined to use a three hidden unit

HMM, for convenience.

When a Gaussian noise of 20dB is added to the utter-

ance speech signal, however, the recognition rate of the

1D-MFCC method is dropped significantly. In order to

increase the recognition rate of the systems, we have

analyzed the MFCCk values for both methods as a func-

tion of each coefficient k = 1,…,K, for both methods;

such as depicted in Figure 4. Clearly seen from these

figures, that the first coefficient of both methods is very

sensitive to the ad dition of the Ga ussian noise, sugge sted

that omitting this coefficient on calculating the MFCC

values increases the recognition rate of both methods.

In the next experiments, we have removed the first

coefficient of the MFCC methods, and by using the ut-

terance speech signal without Gaussian noise as the in-

putted signal, the experimental results are depicted in

Figure 5. As can be seen here, it is very clear that the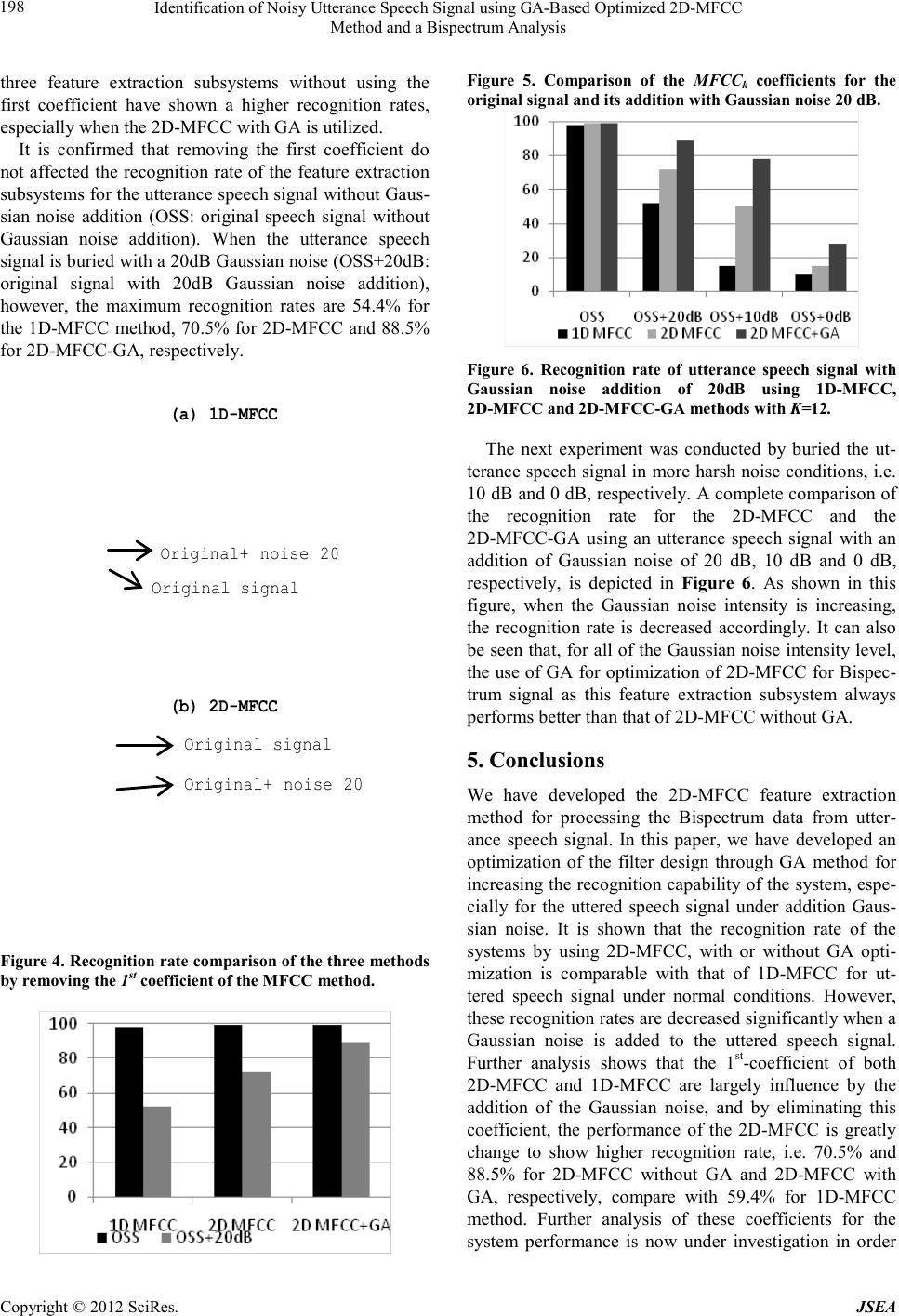

Identification of Noisy Utterance Speech Signal using GA-Based Optimized 2D -MFCC

Method and a Bispectrum Analysis

198

three feature extraction subsystems without using the

first coefficient have shown a higher recognition rates,

especially when the 2D-MF CC with GA is utilized.

It is confirmed that removing the first coefficient do

not affected the recognition rate of the feature extraction

subs yste ms fo r t he utt era nce sp eec h signa l witho ut Ga us-

sian noise addition (OSS: original speech signal without

Gaussian noise addition). When the utterance speech

signal is buried with a 20dB Gaussian noise (OSS+20dB:

original signal with 20dB Gaussian noise addition),

however, the maximum recognition rates are 54.4% for

the 1D-MFCC method, 70.5% for 2D-MFCC and 88.5%

for 2D-MFCC -G A, respectively.

(a) 1D-MFCC

(b) 2D-MFCC

Original signal

Original+ noise 20

Original signal

Original+ noise 20

Figure 4 . Recogniti on rate compari son of t he three methods

by removing t he 1st coefficient of the MFCC method.

Figure 5. Comparison of the MFCCk coefficients for the

original signal and its addi tion w ith Gaussian noise 20 dB.

Figure 6. Recognition rate of utterance speech signal with

Gaussian noise addition of 20dB using 1D-MFCC,

2D-MFCC and 2D-M F CC-GA meth ods wi th K=12.

The next experiment was conducted by buried the ut-

terance speech signal in more harsh noise conditions, i.e.

10 dB and 0 dB, respectively. A complete comparison of

the recognition rate for the 2D-MFCC and the

2D-MFCC-GA using an utterance speech signal with an

addition of Gaussian noise of 20 dB, 10 dB and 0 dB,

respectively, is depicted in Figure 6. As shown in this

figure, when the Gaussian noise intensity is increasing,

the recognition rate is decreased accordingly. It can also

be se en that, for a ll of the G aussia n noise i ntensit y level,

the use of GA for optimization of 2D-MFCC for Bispec-

trum signal as this feature extraction subsystem always

performs better than that of 2D -MFCC wit hout GA.

5. Conclusions

We have developed the 2D-MFCC feature extraction

method for processing the Bispectrum data from utter-

ance speech signal. In this paper, we have developed an

optimization of the filter design through GA method for

increasing the recognition capability of the system, espe-

cially for the uttered speech signal under addition Gaus-

sian noise. It is shown that the recognition rate of the

systems by using 2D-MFCC, with or without GA opti-

mization is comparable with that of 1D-MFCC for ut-

tered speech signal under normal conditions. However,

these recognition rates are decreased significantly when a

Gaussian noise is added to the uttered speech signal.

Further analysis shows that the 1st-coefficient of both

2D-MFCC and 1D-MFCC are largely influence by the

addition of the Gaussian noise, and by eliminating this

coefficient, the performance of the 2D-MFCC is greatly

change to show higher recognition rate, i.e. 70.5% and

88.5% for 2D-MFCC without GA and 2D-MFCC with

GA, respectively, compare with 59.4% for 1D-MFCC

method. Further analysis of these coefficients for the

system performance is now under investigation in order

Identification of Noisy Utterance Speech Signal using GA-Based Optimized 2D-MFCC

Method and a Bispectrum Analysis

199

to develop more robust speaker identification system,

especial ly under harsh noise envir onmen ts .

6. Acknowled ge ment

The Authors would like to acknowledge the Universitas

Indonesia for funding this research. Part of this research

is also supported by Ministry of National Education of

Indonesia.

REFERENCES

[1] Z. Li, J. Sun, J. Han, f. Chu and Y. He, Parametric bis-

pectrum analysis of cracked rotor based on blind identifi-

cation of time series models, IEEE Proceeding of Intelli-

gent Control and Automation, Vol. 2, 2006,

pp.5729-5733.

[2] I. Jouny, E.D. Garber and R.L. Moses, Radar target iden-

tification using the bispectrum: a comparative study,

IEEE Trans. Aerospace and Electronic Systems, Vol. 31,

No. 1, 1995, pp. 69-77.

[3] E.S. Fonseca, R.C. Guido, A.C. Silvestre and J.C. Pereira,

Discrete wavelet transform and support vector machine

applied to pathological voice signals identification, IEEE

Proceeding of International Symposium on Multimedia,

2005

[4] Z. Wang and H. Wang, Voice identification system based

on ser ver, IEEE Proceeding of Intern. Conf. on Computer

Application and System Modeling, Vol. 9, 2010, pp.

384-387.

[5] M. Abdollahi, E. Valavi and H.A. Noubari, Voice-based

gender identification via multiresolution frame classifica-

tion of spectro-temporal maps, IEEE Proceeding of Intern.

Joint Conf. on Neural Networks, 200 9, pp . 1-4.

[6] T.D. Ganchev, Speaker Recognition, PhD Dissertation,

Wire Communications Laboratory, Department of Com-

puter and Electrical Engineering, University of Patras

Greece, 2005

[7] B. Kusumoputro, A. Triyanto, M.I. Fanany and W. Jat-

miko, Speaker identification in noisy environment using

bispectrum analysis and probabilistic neural networks,

IEEE Proceeding of Intern. Conf. on Computational In-

telligence and Multimedia Application, 2001, pp.118-123.

[8] C.L. Nikeas and A.P. Petropulu, Higher order spectra

analysis: A Nonlinear Signal Processing Framework,

Prentice-Hall, Inc. New Jersey, 1993.

[9] T.E. Ozkurt and T. Akgul, Robust text-independent

speaker identification using bispectrum slice, IEEE Pro-

ceeding of Signal Processing and Communications Ap-

plications, 2004, pp. 418-421.

[10] L. Luo and L.F. Chaparro, Parametric identification of

systems using a frequency slice of the bispectrum, IEEE

Proceeding of Intern. Conf. on Acoustic, Speech and

Signal Processing, Vol. 3, 199 1, pp. 3481-3484

[11] L. Rabiner. A Tutorial on Hidden Markov Model and

Selected Applications in Speech Recognition. Proceed-

ing IEEE, Vol 77 N o. 2. Fe br uary 1989.

[12] Cornaz, C. dan U. Hunkeler. An Automatic Speaker

Recognition System. Mini-Project.

http://www.ifp.uiuc.edu/~minhdo/teaching/speaker_recog

nition, access : August, 15, 2008.

[13] Zbigniew M. Genetic Algorithms + Data structures =

Evolution Programs, 3th Edition , Spr inger , 19 96.