A Journal of Software Engineering and Applications, 2012, 5, 181-187
doi:10.4236/jsea.2012.512b035 Published Online December 2012 (http://www.scirp.org/journal/jsea)
Method of Detection Ab normal Features in
Ionosp here Critica l Frequency Data o n the
Basis of Wavelet Transformation and Neural
Networks Combin ation
O. V. Mandrikova1,2, Yu. A. Polozov1,2, V. V. Bogdanov1, E. A. Zhizhiki na2
1Institute of Cosmophysical Researches and Radio Wave Propagation FEB RAS, Petropavlovsk-Kamchatskij, Russia; 2Kamchatka
State Technical Univer sity, Petropavlovsk-Kamchatskij, Russia.
Received 2012.
ABSTRACT
The research is focused on the development o f automatic detection method of abnor mal features, that occur in recorded
time series of ionosphere critical frequency fOF2 during periods of high solar or seismic activity. The method is based
on joint application of wavelet-transformation and neural networks. On the basis of wavelet transformation algorithms
for the detection of features and estimation of their parameters were developed. Detection and analysis of characteristic
components of time series are performed on the basis of joint application of wavelet transformation and neural networks.
Method's approbation is performed on fOF2 data obtained at the observatory “Paratunka” (Paratunka settlement,
Ka mchatskiy Kray).
Keywords: Wavelet Transformation; Neural Networks; Critical Frequency of Ionosphere; Ab no rmalities; Earthquakes
1. Introduction
The subject of the investigationsis recorded time series
of ionospheric parameters, which include components
with different internal structure and determined by den-
sity of at mo sphere, its chemical compound and the sp ec-
tral characteristics of solar radiation [1,2]. Ionosphere
research is carried out by distant methods, one of which
is vertical radio probing. Frequency of carrier radio im-
pulse for which the given area of ionosphere becomes
transparent, is called critical (fOF2) and it characterises
electron concentration.
Against the regular changes caused by a daily and
seasonal course, abnormal features with duration from
some tens minutes till several hours [2-13] are observed
in the fOF2 data. These anomalies have various structure
and arise against powerful ionospheric disturbances
which are caused by solar activity, in seismoactive areas
they can arise during the seismic activity increase
periods [2-13]. Complex structure of the ionospheric data
makes traditional methods of the time series analysis
inefficient for their analysis and abnormalities detection,
because these methods are based on the procedure of
smoothing and lead the important information loss [2,5].
Main tools for abnormalities detection are based on the
analysis of the average and median values that does not
allow to find out internal dependences in the data and
single abnormal features.
In connection with the wide variety of basis functions
with compact carriers, wavele t-transformation is an
effective tool for complex time series analysis [3,4,14-
19]. Using the discrete wavelet-transformation construc-
tion, the algorithm allo wing to allo cate abnor mal feature s
and to define their parametres in fOF2 data in an
automatic mode is offered in this paper.
For characteristic components of fOF2 time series
detection and analysis this paper proposes the method
based on joint application of wavelet-transfor mation with
neural networks. Neural networks have well proved in
complex nonlinear dependences reproduction [6,21-23].
The efficiency of this mathematical tool application for
ionospheric d ata processing and analysis is demonstrated
in [6,11,12,22,23]. These authors offer ways o f fOF2 data
analysis and prognosis on the basis of neural networks
and show that in many respects their work result is
defined b y properties of training set. Experimental search

Method of Detection Abnormal Features in Ionosphere Critical Frequency Data on the
Basis of Wavelet Trans fo rmation and Neural Networks Combination
182
of suitable training set and neural network architecture is
carried out in [22,23 ]. If modelled data are complex and
noisy it is necessary to perform their preprocessing and
to solve problems of uninformative and redundant data
[5,6,13]. In [6,13] offered ways of joint application of
wavelet-transformation and neural networks for uninfor-
mative data removal, developed algorithms of training
set formation on the basis of a wavelet-filtration, and
showed that the given approach allows to optimise
process of network training and to increase length of data
anticipation interval. This paper, where the method of
fOF2 characteristic components detection and prognosis
on the basis of wavelet-packages constructio n and neura l
networks joint application is developed, is continuation
of these investigations.
In process of proposed method approbation, abnormal
features in fOF2 data, arising during the periods of
increased solar activity or caused by processes in
lithosphere (seismic events of a power class with k>12
analysis) were detected.
2. Method description
Detection of abnormal features and their parametres
definitio n on t he basis o f discrete wavelet-transforma-
tion. Formally complex time series can be presented as
sum of different-scale components with various internal
structure [5]
∑
=
j
j
tftf )()(
, where
j
is scale.
As the
j
f
components structure is subject to change
in random time moments, the most effective way for
their description is application of approximation methods,
based on deco mposition of function on basis. Considering
analyzed features local character, their different-scale
and forms variety, the most suitable space for their
representation is wavelet-space [5,13,14].
On the basis of discrete wavelet-transformation for
j
f
components the following representation in the form of
the wavelet-scheme is obtained [14, 23]:
∑
Ψ=
n
njnjj tctf ),()( ,, (1)
where
{ }
2
),(
,Ζ∈
Ψ
nj
nj
is orthonormalized basis of the
)(
2RL
Lebega space,
( ) nt
jj
nj
−Ψ=Ψ 22
2/
,
,
)(
2RLf j∈
.
{ }
Ζ∈
=
n
njj
cc
,
coefficients are result of
mapping of
f
into the space with resolution
j
,
njnj fc,, ,Ψ= .
Without breaking general coherence, we will consider
that an initial discrete time series belong to space with
scale
0=j
. The importance of representation f as
Equation (1) is defined by sorting and storing of
different-scale components of complex time series in
various spaces
j
W
with resolution
j
:
j
J
j
jWW −−= =⊕= 1 0
,
{ }
Zn
nj ∈
Ψ
,
is basis of
j
W
space.
For the purpose of possibility to construct adaptive
approximating wavelet-schemes, we will use nonlinear
mappings [5, 14]:
)()( ,
),(
,tсtf nj
Inj
njM
M
Ψ= ∑
∈
, (2)
where
M
f
is projection of f onto
M
vectors
which indexes are contained in some set M I. In this
case f function approximation is carried out by M
vectors depend ing on it s structure.
The error of approximation (2) is the sum of the
remained coefficients
[ ]
2
),(
,
2∑
∉
=−=
M
Inj
njM
cffM ε
.
Assuming that
)()(
,
),(
,
tcte
nj
Inj
nj
M
Ψ= ∑
∉
component is
a consequence of the noise factor influence, we receive
representation of random time series in wavelet-space:
( )
∑
∈
+Ψ=
M
Inj
njnj
tetctf
,
,,
)()()(
.
As a time series includes characteristic components and
abnormal features, we will present it as follows:
e(t)(t))(
)()()()(
21
),( ),
(
,,,,
++=
=+Ψ+Ψ=
∑∑
∈ ∈
ftf
tet dtatf
A D
Inj Inj
njnjnjnj
, (3)
where
∑
∈
Ψ=
A
Inj
njnj
tatf
),(
,,1
)()(
,
∑
∈
Ψ=
D
Inj
njnj tdtf
),(
,,2 )()( ,
{ }
A
Inj
nj
a∈),(
,
are set of approximating coefficients, describing
characteristic features of data,
{ }
D
Inj
nj
d∈),(
,
is set of
the detailing coefficients describing abnormal features,
MDA III =∪ .
In [14,24] demonstrated that absence of amplitude
coefficients decrease when
0→j
, characterises
presence of local features in
)(tf
and operation of their
detection can be realized on the basis of requirement
check
Td
nj
≥
,
, when
0→ j
, where
T
is some
threshold value. Meantime, the least analyzed scale is
limited by step of discrete tim e series sampling.
If wavelet
Ψ
has compact carrier equal to
[ ] CC,−
,
then assemblage of
( )
nj, point pairs, such that some
point
ν
is contained in
nj,
Ψ
carrier, defines influence
cone of point
ν
in scale-spatial plane [14]. As the

Method of Detection Abnormal Features in Ionosphere Critical Frequency Data on the
Basis of Wavelet Transformation and Neural Networks Combination
183
carrier
nj,
Ψ
on the scale
j
is equal to
[ ]
jj CnCn −− +− 2*,2*
,
then influence cone of point
ν
on the scale
j
is
defined by inequality:
JjCvn
j
−−−=∗≤−
−
,...,2,1,2
.
Let's consider that function
f
in the neighbourhood
of some point
v
has abnormal feature of scale
j
, if in
the neighbourhood of the point
v
with the sizes de fined
by an influence c one, the conditio n is sa tisfied:
jnj Td≥ ,, (4)
where
j
T
is threshold value on scale
j
, time duration
of abnormality is defined by the influence cone of point
ν
.
Operation of scale
j
abnormal features detection can
be realized on the basis of threshold functions
applicatio n
.
,0
,
)( 




<
≥
=
j
j
T
Txесли
Txеслиx
xP
j
The sets of detailing components
{ }
( )
D
Inj
nj
d
∈,
,
allocated in such a way define the component )(
2tf of
model Equation (3).
Intensity of abnormality on scale
j
in point
v
neighborhood we will define as
nj
n
fdE j,
max
,= ν
, where
:n
j
Cvn
−
∗≤− 2
.
Changes of intensity in time can be analyzed on the
basi s of value
)(tf
E
∑
=
j
nj
с
,
. (5)
The construction of wavelet-packages [14, 24] assumes
recursive splitting of space
j
W
:
i
i
p
j
I
ij WW 1=
⊕=
. Space
i
i
p
j
W
admits orthonormalized basis
=Ψ
i
i
p
j
( )
{ }
Zk
j
p
j
j
kt
i
i
i
i
∈
−Ψ22
2/
.
Integration of corresponding basises of wavelet-packages
( ) { }
IiZk
j
p
j
j
kt
i i
i
i
≤≤∈
−Ψ
1,
2/
22
defines orthonormalized
basis
j
W
, that allows to restore function completely.
Detection and analysis of characteristic components
of time series on the basis of wavelet-packages and
neural net works joint applicat ion.
The Neural network creates m ap p ing
'
:ffy →
.
The set of weight coefficients of neuron input
connections represents a column-vector [21]
[ ]
T
N
uuU ,...,
1
=
,
where
N
is length o f network input vector.
If
'
ˆ
f
is a real network output, and
'
f
is a desired
one, then
( )
fyf =
'
is an unknown function, and а
( )
UfGf,
ˆ
'
=
is its approximation which is reproduced
by neural network. Procedure of network training is
reduced to minimisation of approximation mean-square
error on parameter
U
.
Giving to the inp ut of the t raine d neura l net work val ues
of function f from an interval
[ ] lTl ,1+−
, network
becomes capable to compute anticipated function values
on time interval
[ ] α ++ ll ,1
, where
l
is a current
discrete moment of time;
α
is length of anticipation
interval. The decision error is defined as difference
between desired
'
f
and real
'
ˆ
f
output values during
the discrete time moment
l
.
The error vector is the vector where
i
element is
)()(
ˆ
)(
''
lflfl
i
ii
−= ε
, (6)
where
l
is a current time moment,
i
is a current
position on antic ipation interva l.
Algorithm of training and control sets formation:
1. An initial data array
( ){}
K
k
kf
1=
, where
K
is a
sampling length, is divided on
L
blocks
Q
:
( ){}(){}( ){}( ){} ( )
KQKk Q
k
Q
k
K
kkfkfkfkf −=
+
=== =,...,, 1 211
long.
2. On the basis of wavelet-packages construction, for
each block
s
we have representation
f
in the form of
a linear combination different -scale components:
s
p
sss
ffff +++= ...
21
, where every component
i
i
i
i
i
p
si
i
i
i
p
j
p
j
Ikj
p
j
skj s
iWf ∈ΨΨ=
∑
∈
,
),(
,
β
in wavelet-space is
uniquely defined by coefficients sequence
{ }
i
p
s
i
i
i
Ikj
skj
s
j∈
=
),(
,
ββ
,
i
i
i
p
j
sskj
fΨ=,
,
β
,
i
i
p
j
W
are
wavelet-package spaces.
3. Every detected component defines a subspace of time
series features space. As i
p
j
W
are wavelet-packages
spaces, then is obtained:
{ } 0
1
=
=

I
i
p
i
i
W
,

I
i
p
iVW
i
1=
=
.
Thus, for each unit
s
separation of data features in
space is received Figure 1. Using the following sets of
detected features
{ }
____
11 ,1
,Ls
spj
f=;
{ }
____
21 ,1
,Ls
spj
f=
;…;
{ }
____
1,1
,Ls
spjI
f=
;...;
{ }
____
,1
,Ls
spjII
f=
;
{ }
____
2111
,1
,,
,
Ls
spj spj
ff
=
;…;
{ }
____
21
,1
,,
,
Ls
spj spj
IIff
=
;

Method of Detection Abnormal Features in Ionosphere Critical Frequency Data on the
Basis of Wavelet Trans fo rmation and Neural Networks Combination
184
{ }
____
312111 ,1
,,, ,, Ls
spj spj spjfff =
;…
{ }
____
12111
,1
,,,
,...,,
Ls
spj spj spj
I
fff
=
;…;
{ }
____
21 ,1
,,, ,...,, Ls
spj spj spjIIIIfff =we form training and
control sets for neural networks.
Figure 1. The scheme of data separation in wavelet-images
space.
Algorithm of “the best" network construction:
Step 1: Carry out wavelet-restoration of a component
spj
f
11
,
for each data unit
s
and fo rm tr aining se t on the
basis of combinations of the restored data from various
units. Construct network 1 of variable structure [21]
(variable structure network is a multilayer feed forward
network, which architecture is defined by minimisation
of decision error on training vectors set), tr a in and te st it.
Step 2: Carry out wavelet-restoration of components
spj
II
f
,
for each data unit
s
and fo r m t ra inin g se t o n t he
basis of combinations of the restored data from various
units. Construct a network 2 of variable structure, train
and test it.
Etc.
Step r: Carry out wavelet-restoration of components
spj spj spj
IIII
fff
,,,
,...,,
21
for each data unit
s
and form
training set on the basis of combinations of the restored
data from various units. Construct network r of variable
structure, tra in and test it.
On the basis of the analysis of results of received neural
networks operation the “best” network is defined: "the
best" is considered to be the network having the least
decision error on te st s et
( )
∑∑
Μ
= =
ΜΜ
=
1 1
2
min,)
1
(min
l
f
i
ilE
ε
α
, (7)
where
α
is a neural network number,
____
,1 r= α
,
Μ
is a length of analyzed network output vector,
f
is a
length of an anticipation inter val.
The training data set is a set of observations containing
features of studied process. On the basis of wavelet-
packages construction, we have data features separation
in space. During training and designing each network
learns a subset of input data features and approximates
them. " The best" networ k is t he net work ha ving t he lea st
decision error on test set. Therefore data subset used at
training of the "best" network will contain the most
typical features of studied process. In wavelet-space this
subset is represented by set of coefficients
{ }
A
Inj
nj
a∈),(
,
, defining component
)(
1tf
of time series
model Equa tio n (3).
If there is an abnormal feature in the data, then a change
of their structure occurs. Therefore operation of
abnormal features detection on the basis of a neural
network can be c onstructe d b y processing and analysis of
decision errors i ε
: if
( ) Ρ≥= ∑∑
= =
Z
l
f
i
iZ l
Z
E
1 1
2
1
ε
, (8)
where
Z
is an observation frame length,
Ρ
is a
beforehand specified threshold value, then within an
analyzed time frame we have abnormality.
3. Results of experiments
In experiments fOF2 data were used, received by
automatic ionospheric station located in Paratunka
settlement, Kamchatka peninsula. Data recording occurs
once an hour. For experiments results of fOF2
measurements dated 1979 - 2011 were taken. In the
process of analysis, data of the Earth magnetic field
(H-component) were used to define magnetospheric
disturbances degree, characterising Solar activity. As
basic functions the class of Daubechies orthogonal
wavelets: db2, db3, db4 was used.
Following the results obtained in [3], for detection of
abnormalities on the basis of operation Equation (4)
were used the threshold values defined in the process of
algorithm ope ration by formula:
( )
jnj
Vnn
j
StdmedT *
,
,1,
_____
θ +=
=
, where
( )
∑
=
−
−
=
V
n
nj
njj
dd
V
St
1
2
,
,
1
1
, nj
d, is the average
value defined within the analyzed sliding time frame of
length
V
,
168=V
readouts,
med
is a median
defined within the analyzed sliding time frame of length
V
. The coefficient
= θ
3 has been defined statistically.
The detected time-and-frequency intervals containing
abnormal features, are shown on Figure 2-5 (b) by
shades of grey colour. Ionospheric disturbances intensity
changes in time were analyzed on the basis of value
Equation (5), Fig ure 2 -5 (c).
On the bas is o f desc rib ed above algor it hms tr ai ning a nd
control sets for neural networks have been generated and
"the best" network consisting of three layers that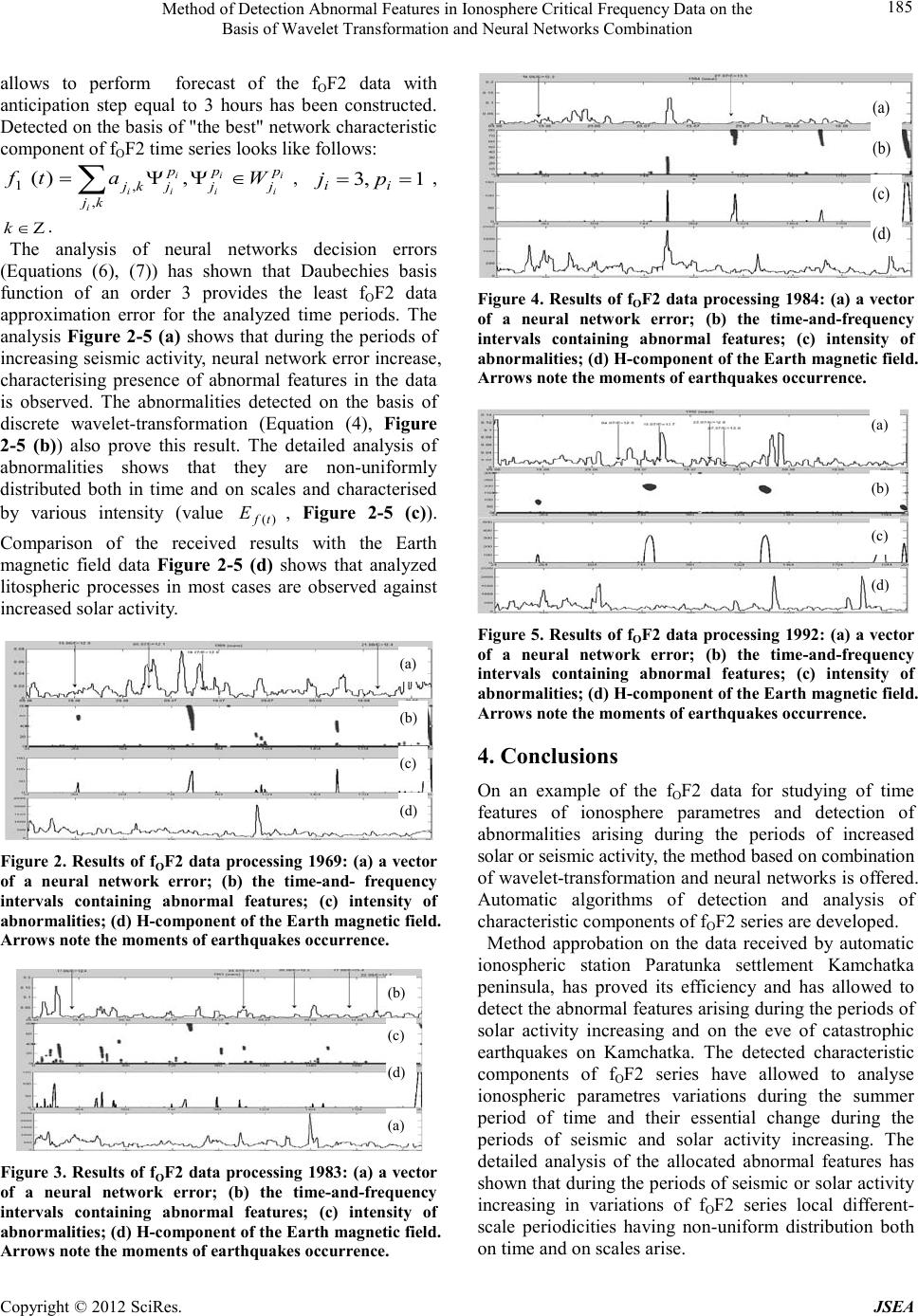

Method of Detection Abnormal Features in Ionosphere Critical Frequency Data on the
Basis of Wavelet Transformation and Neural Networks Combination
185
allows to perform forecast of the fOF2 data with
anticipation step equal to 3 hours has been constructed.
Detected on the basis of "the best" network characteristic
component of fOF2 ti me serie s looks like follows:
i
i
i
i
i
i
ii
p
j
p
j
kj
p
jkj
Watf∈ΨΨ= ∑,)(
,,
1
,
1,3==
ii
pj
,
Ζ∈k
.
The analysis of neural networks decision errors
(Equations (6), (7)) has shown that Daubechies basis
function of an order 3 provides the least fOF2 data
approximation error for the analyzed time periods. The
analysis Figure 2-5 (а) shows that during the periods of
increasing seismic activity, neural network error increase,
characterising presence of abnormal features in the data
is observed. The abnormalities detected on the basis of
discrete wavele t-transformation (Equation (4), Figure
2-5 (b)) also prove this result. The detailed analysis of
abnormalities shows that they are non-uniformly
distributed both in time and on scales and characterised
by various intensity (value
)(tf
E
, Figure 2-5 (c)).
Comparison of the received results with the Earth
magnetic field data Figure 2-5 (d) shows that analyzed
litospheric processes in most cases are observed against
increased solar activity.
(a)
(b)
(c)
(d)
Figure 2. Results of fOF2 data processing 1969: (a) a vector
of a neural network error; (b) the time-and- frequency
intervals containing abnormal features; (c) intensity of
abnormalities; (d) H-component of the Earth mag netic field.
Arrows note the moments of earthquakes occurrence.
(a)
(b)
(c)
(d)
Figure 3. Results of fOF2 data processing 1983: (a) a vector
of a neural network error; (b) the time-and-frequency
intervals containing abnormal features; (c) intensity of
abnormalities; (d) H-component of the Earth magnetic field.
Arrows note the moments of earthquakes occurrence.
(a)
(b)
(c)
(d)
Figure 4. Results of fOF2 data processing 1984: (a) a vector
of a neural network error; (b) the time-and-frequency
intervals containing abnormal features; (c) intensity of
abnormalities; (d) H-component of the Earth magnetic field.
Ar rows note the moments of ea rt hquakes occ urrence.
(a)
(b)
(c)
(d)
Figure 5. Results of fOF2 data processing 1992: (a) a vector
of a neural network error; (b) the time-and-frequency
intervals containing abnormal features; (c) intensity of
abnormalities; (d) H-component of the Earth magnetic field.
Arrows note the moments of earthquakes occurrence.
4. Conclusions
On an example of the fOF2 data for studying of time
features of ionosphere parametres and detection of
abnormalities arising during the periods of increased
solar or seismic activity, the method based o n co mbination
of wavelet-tra nsfor matio n and neural networ ks is o ffered.
Automatic algorithms of detection and analysis of
characteristic compone nts of fOF2 series are developed.
Method approbation on the data received by automatic
ionospheric station Paratunka settlement Kamchatka
peninsula, has proved its efficiency and has allowed to
detect the abnormal features arising during the periods of
solar activity increasing and on the eve of catastrophic
earthquakes on Kamchatka. The detected characteristic
components of fOF2 series have allowed to analyse
ionospheric parametres variations during the summer
period of time and their essential change during the
periods of seismic and solar activity increasing. The
detailed analysis of the allocated abnormal features has
sho wn that dur ing t he per iods of se ismic or solar activit y
increasing in variations of fOF2 series local different-
scale p er iodicities having non-uniform distribution both
on time and on scales arise.

Method of Detection Abnormal Features in Ionosphere Critical Frequency Data on the
Basis of Wavelet Trans fo rmation and Neural Networks Combination
186
5. Acknowledgements
The present paper and the research are supported by the
grant of the President of the Russian Federation
MD-2199.2011.9, the grant of the Russian Foundation
for Basic Research (Far Eastern Branch of the Russian
Academy of Sciences, R ussia) № 11-07-98514-r-vostok_a
and the grant «U.М.N.I.K.» - 8283r/10269 dated
6/30/2010.
Data of the seismic catalogue is kindly given by the
Kamchatka branch of geophysical service of the Russian
Academy of Sciences (Petropavlovsk-Kamchatskiy).
REFERENCES
[1] M.G. Dyomin, “Ionosphere of the Earth. Plasma
Heliophysics,” PhysMathlit, Moscow, 2008.
[2] V.V. Bogdanov, V.V. Geppener and O.V. Mandrikova,
“Modeling of Non-Stationary Time Series of Geophysical
Parameters with a Complex Structure,” St.-Petersburg,
2006.
[3] O. V Mandrikova, Yu.A. Polozov and A.S. Perezhogin,
“Wavelet-Technology of the Ionospheric Data Analysis,”
Scientific Notes of the Belgorod State University, a Series
"History. Political Science. Economy. Computer Science",
Belgorod, No. 19, 2011, pp. 113-11 8.
[4] O. V Mandrikova and Yu.A. Polozov, “Criteria of
Wavelet-Function Choice in Problems of Approximation
Natural Time Series of Complex Structure,” Information
Technology, Mos c ow, No. 1, 2012, pp. 31 - 36.
[5] O. V. Mandrikova, “Multicomponent Model of a Signal
with Complex Structure,” Problems of Evolution of Open
Systems, Issue 10, Vol. 2, 2008, pp.161-172.
[6] Yu. A. Polozov, “Method of Training Set Formation for a
Neural Network on the Basis of a Wavelet-Filtration,”
News of High Schools, the North Caucasian Region, a
Series Natural S ciences, No. 3, 2010, pp. 12-16.
[7] E.V. Liperovskaja, V. А. Liperovsky and O. A.
Pokhotelov, “About Disturbances in Ionosphere F-Area
before Earthquakes,” Geophysical researches, No. 6,
2006, pp . 51-58.
[8] A. A. Namgaladze, “The Physical Mechanism and
Mathematical Modeling of Ionospheris Harbingers of the
Earthquakes Recorded in Full Electronic Maintenance,”
Geom agnetis m and A eronom ia, Vol. 49, No. 2, -2009, pp.
267-277.
[9] O. V. Mandrikova, Yu. A. Polozov and T. L. Zaliaev,
“Methods of Analysis and Interpretation of Ionospheric
Critical Frequency FOf2 Data Based on Wavelet
Transform and Neural Networks,” European
Seismological Commission 33-rd General Assembly (GA
ESC 2012), 19-24 August 2012, Thesis, Moscow.
[10] Y. Polozov, O. Mandrikova and V. Bogdano v, “Det ection
of Anomalies in Ionospheric Increased Seismic Activity,”
International Union of Geodesy and Geophysics (IUGG),
28 June – 07 July 2011, Thesis, Melbourne.
[11] O. V Mandrikova, Yu. A. Polozov, N.V. Glushkova and
T.L. Zalyaev, “Technology of Allocatio n of Anomalies i n
Ionospheric Data on the Basis of Combination
Wavelet-Transformation and Neural Networks,”
International Conference «Intelligent Information
Processing» (IIP-2012), Montenegro, Budva,16-22
September 2012, pp. 524-527.
[12] O. V Mandrikova and Yu. A. Polozov, "Method of
Allocation an d Class if ic ation of Anomalies in Io nospher ic
Parameters on the Basis of Combination of
Wavelet-Transformation and Neural Networks," 14
International Conference «Digital Signal Procssing»
(DSPA - 2012), M osc ow , 28-30 M arch 2012, pp . 353-356.
[13] O.V. Mandrikova, ‘Optimization of a Neural Network
Training Procession on The Basis of Application of a
Design of Wavelet-Transformation (on an Example of
Modeling Ionospheric Signal Representation),”
Automation and Modern Technologies, No. 3, 2009,
pp.14-17.
[14] S. Mallat , “A Wav elet Tour of Sign al P rocessing, ” World ,
Moscow, 2005.
[15] O. V. Mandrikova, I. S. Solovjev, V. V. Geppener and D.
M. Klionskiy, “Analyzing Subtle Features of Natural
Time Series by Means of a Wavelet–Based Approach,”
Pattern Recognition and Image Analysis, Vol. 22, No. 2,
2012, pp . 323–332. doi:10.1134/S1054661812020083
[16] O.V. Mandrikova , I.S. Solovyev, V.V.Geppener, D.M.
Klions k iy and R . T. Al -Kasasbeh, “Analysis of the Earth's
magnetic field variations on the basis of a wavelet-based
approach,” Digit al Si g nal Proces s ing, In Press.
[17] C. K. Chui and J. Z. Wang, “A general framework of
compactly supported splines and wavelets,” CAT Report
219, Texas A&M Univ., 1990.
[18] Ali G. Hafez and Essam Ghamry, “Automatic detection of
geomagnetic sudden Commencements via Time
Frequ ency Clu sters,” Advances Spa ce Research, Vol. 48,
Issue 9, 2011, pp.
1537–1544. doi:10.1016/j.asr.2011.05.025
[19] Ali G. Hafez, Tahir A. Khan and T. Kohda, “Clear P-wave
Arrival of Weak Events and Automatic Onset
Determination Using Wavelet Filter Banks,” Digital
Signal Processing, Vol. 20, Issue 3, 2010, pp.
715-723. doi:10.1016/j.dsp.2009.10.002
[20] D. B. Percival and A. T. Walden, “Wavelet Methods for
Time Series Analysis,” (Cambridge Series in Statistical
and Probabilistic Mathematics), Cambridge University
Press, 20 00.
[21] A.D. Ageev, “Neuromatematika: Studies. The Grant for
High Schools,” IPRJR, Moscow, 2002.
[22] H.A. Barhatov and C.E. Revunov, “Forecasting of
Critical Frequency Ionospheric Layer F2 a Method of
Artificial Neural Networks,” VIII Nizhniy Novgorod
Session of Young Scientists. Natural-Scien ce Disciplin es,
Thesis, Dzerzhinsk, 2003.
[23] H.A. Barhatov, C.E. Revunov and V.P. Urjadov,
“Technology of Artificial Neural Networks for
Forecast ing of Critical F requency Ionospheric La yer F 2,”
News of HIGH SCHOOLS "Radio Physicists", Vol. 48,
2005, pp .1-15.
[24] I. Daubech ies, “Ten Lectures o n Wavelets,” «Regular and
Chaotic Dynamics», Izhevsk, 2001