A Journal of Software Engineering and Applications, 2012, 5, 117-123
doi:10.4236/jsea.2012.512b023 Published Online Decemer 2012 (http://www.scirp.org/journal/jsea)
Quantization of Rough Set Based Attribute Reduction
Bing Li*, Peng Tang, Tommy W. S. Chow
Department of Electronic Engineering, City University of Hong Kong, 83 Tat Chee Avenue, Kowloon, Hong Kong.
Received 2012.
ABSTRACT
We demonstrate rough set based attribute reduction is a sub-problem of propositional satisfiability problem. Since satis-
fiability problem is classical and sophisticated , it is a smart idea to find solutions of attribute reduction by methods of
satisfiability. By extension rule, a method of satisfiability, the distribution of solutions with different numbers of
attributes is obtai ned without findin g all attrib ute r eductio n. T he r elatio n bet ween attribute red uction and missi n g is also
analyzed from computational cost and amount of solutions.
Keywords: Attribute Reduction; Extension rule; Distribution of Solutions; Quantization.
1. Introduction
The size of dataset has been incr easing dra matically, so i t
has been an important issue to reduce huge objects and
large dimensionality. Attribute reduction finds a subset
of attributes to reduce dimensionality. Reducing
attributes ca n save cost of computational t im e a nd mem-
ory. It is also u seful to i mprove classification accuracy as
a result of removing redundant and irrelevant features
[1,2].
A hypothesis done in classical attribute reduction
theory is that all available objects are completely de-
scribed by available attributes. This hypothesis contrasts
with the empirical situation where the information con-
cerning attributes is only partial.
Several methods have been used for handling missing
values. One is complete case analysis ignoring the sam-
ples with missing values [3]. This method can only be
used when the proportion of missing values is not large;
moreover, much effective information is directly dis-
carded. The second approach, called imputation method,
imputes the values of missing data by statistical methods
or machine learning methods [4,5]. This kind of ap-
proach leads to additional bias in multivariate analysis
[6]. Third method assumes a model for the covariates
with mi ssing val ues [7]. A disadvanta ge of t his ki nd me-
thod assu mes implicitly that da ta a r e missed a t random.
For attribute reduction, the above concepts are not
suitable. The y all make assumption, so complete analysis
of missing value is reduced. In addition, it is hard or even
impossible to check the correctness of assumption in
practice. In contrast, rough set can hold complete analy-
sis, since it considers missing value as “everything is
possible” [8, 9]. Rough set i s pr o po sed by Pawlak [10] as
a mathematical theory of set approximation, which is
now widely used in information system. In order to find
the solution of inco mplete syste m by rough set, tolera nce
relation is de fined t hrough rel axing t he equivalenc e rela-
tion [8,11]. It is a NP-hard problem to find an optimal
solution. Heuristic approaches have been proposed, keep-
ing the po sitive r egio n of target decision unchanged [12]
or employing conditional entropy to obtain a sol ution
[13]. Each method aims at some basic requirement ac-
cording to their mechanisms of reduction, so no one can
give a fair e valuat ion among these metho ds.
In this paper, we find that rough set based attribute
reduction with missing value is a sub-problem of propo-
sitional satisfiability problem (SAT). SAT is one of the
most classical problems because of its significance in
both theoretical research a nd practical ap p lic atio n, so it is
smart to find solutions of attribute reduction with miss-
ing value by method of SAT. Exclusion rule [14,15]
checks the satisfiability by inverse of resolution. It can
obtain all satisfiable solutions without trying every com-
bination of attributes. So it provides a possible way to
find all possible reductions. According to the result of
exclusion rule, the distributio n of solution with different
amount of attribute s shows that the to tal number of solu-
tions is decided by the size of minimal reduction. The
total number decreases with addition of missing before
thres hold. I n general, threshol d is smalle r t han 50%. T he
relationship between computational cost and missing is
*Corresponding author.

Quantization of Rough Set Based Attribute Reduction
118
also illustrated.
The rest of paper is organized as follows. The basic
knowledge about attribution reduction using rough set is
given in Section 2. Its relationship with SAT is intro-
duced in Section 3. Experimental results are shown in
section 4. Finally, the c onclusion is drawn in Sec tion 5.
2. Background
In this section, the basic notions [11] related to incom-
plete information s ystems and rough set are p resented.
Definition 2.1: Let
(,)ISU A=
be an information system,
where
U
- a nonempt y, finite set called universe and
A
- a nonempt y, finite set of attributes i.e.
:
a
aU V→
for
aA∈
where
a
V
is called the value set of
a
.
Definition 2.2: In an incomplete infor matio n sys-
tem
(,)ISU A=
, an
nn×
matrix (
ij
c) called discernible
matrix of IS is defined as
{:()()(),
(),,} ,1,,
iji ji
j ij
caAa xa xanda xnull
andaxnullxxUforijn
=∈≠ ≠
≠∈ =
. (1)
The discernible matrix is denoted as
()M IS
. It is
straightforward to find
()M IS
is symmetric and
ii
c= ∅
.
Definition 2.3: A discernible function
IS
f
for an in-
formation system
(,)ISU A=
is a Boolean function of
m
variables
1
,,
m
aa
, which is defined as
{ }
1
(,, )():1,()
IS mijij
faacjin c=∧ ∨≤<≤∨≠∅
, (2)
where
i
a
denotes an attributes in
A
and
()
ij
c∨is the dis-
junction of the variable
a′
such that
ij
ac
′∈
.
Definition 2.4: For any subset of attrib utes
BA⊆
, a
relation
()IND B
called B-indiscern ible relation is defined
as follows:
1
(){{,,,}:()( )()
( ),,,,1}
li
ii
INDBx yya xayora xnull
oraynullaBx yUil
== =
=∀∈∈ ≤≤

. (3)
Definition 2 .5:
()
B
POS a∗
representing B-positive region
of
a∗
is defined as
()
B
POS aBX∗=
(4)
where, for each
()BXIND B∈
,
({ })ZIND aBXZ∃∈∗⊆
.
3. Quantization of attribute reduction
In t h i s wo r k , we just sho w t he concepts between attribute
reduction and SAT. The details of the demonstrations
can b e found in our futur e work.
Definition 3.1: For an information system
(,)ISU A=
,
a
( 1)nn×+
matrix (
ij
C
∗
) called
a∗
-discernible-checked
matrix is defined in two steps:
i.
{ }
{ }
{:()()()
()}()(), 1,,
() ()
ij i
ijji j
ij
aAaa xa xand a xnull
Candaxnullifa xaxforijn
Aaifax ax
∗
∈− ∗≠≠


=≠∗ ≠∗=

−∗∗ =∗



(5)
{ }
{ }
( 1)
1, ,,1, ,
ij
in
if jn c
Cfor in
A aotherwise
∗
∗
+
∅ ∃∈ =∅

= =
−∗



; (6)
ii.
{ }
( 1)( 1)
,,1, ,
iji njn
CAaifccfor ijn
∗ ∗∗
++
=−∗= =∅=
. (7)
a∗
-discernible-c hecked matrix is denoted as
()M IS
∗
,
and 1n+column is called state checking. In step ii., the
ij
c∗
of t wo sample s nei the r in
{ }
Aa−∗
-Positi ve Regi on i s
reduced, making sure that every attribute in minimal re-
duction is necessary.
a∗
-discernible-checking function is
{ }
11
(,,)() :11,
IS mijij
faacijn c
∗ ∗∗
−=∧ ∨≤<≤+≠∅.
Definition 3 .2 [16] An in for mati on s yste m
(,)ISU A=
is consistent if all objects, which have the same value
concerning
{ }
Aa−∗
, also have the same value of deci-
sional attribute
a∗
; otherwise, the information system is
inconsistent.
Theorem 3.1: In a consistent information system, there
is not
∅
in its
a∗
-discernible-checked matrix, and all
samples are in
{}
()
Aa
POS a
−∗
∗.
Theorem 3.2: In an inconsistent information system,
only the sample having
∅
value of state checking is
not in
{}
()
Aa
POS a
−∗
∗.
Definition 3.3: For a subset
B
of
{ }
Aa−∗
, it is an
attribute reductio n when
{}
() ()
B Aa
POS aPOSa
−∗
∗= ∗
.
Theorem 3.3:
B
is an attribute reduction
iff
11
(( ),,())1
IS
B Bm
fVa Va
∗
−
=
, where
{ }
(): 0,1
B
Va⋅→
such
that
aB
∈iff
() 1
B
Va=
.
Definition 3.4
a∗
-improved-discernible functio n
IS
f∗∗ for an information system
(,)ISU A=
is a Boolean
func tio n of
1m−
variables
11
,,
m
aa
−

, which is defined as
{ }
11
( ,,)():1,( )()
IS mijij
faaCijnax ax
∗∗ ∗
−
=∧∨≤<≤∗≠∗ (8)
where
i
a
denotes an attrib utes in
A
.
Theorem 3.4
IS IS
ff
∗∗ ∗
=
.
Definition 3.5 [17] An instance of SAT is a Boolean
for mula in c onju nctive nor mal for mula. E ach disjunction
formula is called a clause, and the instance is called a
clause set.
An example of conjunctive normal formula
is{ }{}{}tlt ltm∨∧ ∨∧∨.
t
,
l
and
m
are Boolean va-
riables; overbar is logical operation denoting
“not”; ,
tl∨
, and
tm∨
are clauses. Each Boolean varia-
ble can be assigned either true o r false.
Theorem 3.5 Attribute reduction based on rough set is
a problem of SAT.
According to Theorem 3.3, a set of attributes is a solu-
tion of reduction iff the related
1
IS
f
∗
=
. The set of
attributes can be translated as an assignment of variables.
The values of attributes are true, when they are included
in the reduction; otherwise, the value s are false.
Not all of instances in SAT are converted into attr ibute
reduction. Give an example to explain this.
( )()()tltltl∨∧ ∨∧ ∨
is an instance of SAT, but it can
not be converted into attribute reduction. There are 3

Quantization of Rough Set Based Attribute Reduction
119
clauses, so the number of objects in the universe is also 3 .
According to the definition of
a∗
-discernible-checking
function, t means the values of two objects are the
same. In the instance, two clauses includet. That is to
say that there are two pairs having the same values con-
cerning the attr ibute
t
. As a result, the 3 objects appear to
have the same value of
t
because of transitivity. But it is
inconsistent with the third clause. So the clause set can
not be written as an instance of attribution reduction.
Based on this analysis, we have concluded that attribute
reduction based on rough set is the subset of SAT.
Definition3.6 [14]:
{ }{}C CtCt
′= ∨∧ ∨
is called the
result of extension rule on a clause
C
, where
t
is an
attribute not in
C
.
Definition 3 .7 [14]: A clause is a maximum term iff it
contains all attributes in either positive form or negative
form.
Theorem 3.6 [14]: For a clause set with
1m−
attributes, the clause set is unsatisfiable iff
1
2
m−
maximum term can be extended by the clauses.
Theorem 3.7 [14]: Given a clause
set
12 n
CC C=∧∧∧
∑
, let
i
P
be the set of all the maxi-
mum terms obtained from
i
C
by using the extension rule,
and set
NM
the number of distinct maximum terms got
from
∑
.
11 1
112
1
1
( 1),
2,
0,
2.
i
ij
n
i ijijl
i ijnijln
nn
mC
i
ij
ij m CC
NM PPPPPP
PP P
P
complementaryforms in CandC
PP otherwise
=≤< ≤≤< <≤
+
−−
−− ∪
=−∩ +∩∩−
+−∩ ∩ ∩
=


∩=



∑∑ ∑
(9)
By knowledge compilation using extension rule, each
pair of clauses in the new clause set contains comple-
mentar y for m of the same attr ibute [15]. So
1
n
i
i
NM P
′
=
′
=∑.
Algorithm 3.1 shows process of knowledge compilation
[15].
Algorithm 3.1 Knowledge compilation usin g the extension r ule
Input: Let
11 2
,,
n
CC C∑=∧∧∧be a set of clauses ,
23
∑=∑=∅
While
1
∑ ≠∅
Loop
Select a clause from
1
∑, say
1
C
, and add it into
2
∑
While i the number of cla us e s in
1
∑
Loop While
j
the number of cla us e s in
2
∑
Loop
If
i
C
and
j
C
contai n co mpl e m e ntar y for ms of the same
attribute, skip.
Else if
i
C
subsumes
j
C
, eliminate
j
C
from
2
∑.
Else if
j
C
subsumes
i
C
, eliminate
i
C
from
1
∑
.
Else extend
j
C
on a variable using extension rule.
1jj=+
End loop
1ii= +
End loop
332
∑=∑ ∪∑
;
2
∑=∅
End loop
Output:
3
∑
is the result of the compilat ion process .
Theorem 3.8: Set11
(, ,)()
c mij
fa aC
∗
−= ∨
and
11
(,,)(( ))(( ))
c mijij
fa aCtCt
∗∗
−
′=∨∨∧∨∨
, where
t
is
an attribute not included
()
ij
C
∗
∨.
11
(( ),,())1
cB Bm
fVa Va
−
=
iff
11
(( ),,())1
c BBm
fVa Va
−
′=
,
where
{ }
(): 0,1
B
Va⋅→ such that
aB
∈iff
() 1
B
Va=
.
Theorem 3.9: If a maximum term of conditional
attributes dose not subsume any clause in
IS
f
∗∗
, the
attributes with negative form in the maximum term is a
solution of attributes reduction; if a maximum term of
conditional attrib utes dose no t subsu me any c lause i n the
extended results of
IS
f
∗∗
, the attributes with negative for m
is a solution of attributes re duction.
Theorem 3.10: The number of attribute reduction
is
1
2
m
NM
−
−
, where
NM
is the number of distinct max-
imu m terms got from IS f∗∗ and
1m−
is the number of con-
ditional attrib utes.
According to the results of complication knowledge,
the distributio n of sol utio n can be found directl y. That is
because every clause has complementary literature of
other clauses. That is to say that the maximum terms
extended by each clause are totall y differe nt from others.
The supplementary of maximum terms extended by the
clauses after complication knowledge is the set of all
solutions. It is not generally necessar y to ob tain all solu-
tions, because it will take memory cost of1 2m−. In this
work, the distribution of solution is found without ex-
tending maximum terms, which is shown in Algorith m
3.2.
Algorithm 3.2 Distribution of a ttribution reduction
Input: Clause set after knowledge compilation
12 n
fCC C
′
′′′ ′
= ∧∧∧
;
a count set include
m
elements, where
1m−
is number of con ditional
attributes.
Set
0i=
.
Initial c o u nt se t:
While 1im
≤−
Loop Value of the
( 1)ith+
element in count set is
set
!
(1,)(1)!(1)!
i
Cm immi −=
− −−
.
End loop
Set 1i= .
While
in
′
≤
Loop
Select
i
C
from
f′
.
Denote the number o f literatures
L
, and number of negative
form
NL
.
The va lue of
( 1)NL th+
element i n count set is decreased 1.
Set
1j NL=+
.
While
1jm−
Loop The
( 1)jth+
element in count set is decreased
( )!
(1, )
( 1)!( 1)!
j NL
C mL jNLmL mjL NL
−
−−−=−−−−−+.
End loop
End loop
Output: The distribution of attribute reduction is in the count set.
4. Experiments
In this section, we show the process finding distribution
of solutions to analyze the characteristics of attribute
reduction. Table 1 shows the details of 3 UCI datase ts.

Quantization of Rough Set Based Attribute Reduction
120
Table 1 Dataset d es cription
Datasets Samples Attribute Classes Proportion of missing
Zoo 101 18 7 0%
Soybean 47 36 4 0%
Voting 435 17 2 14.7%
Table 2 Number of clause
Dataset
Miss ing Zoo Soybean Voting
Equation 8 3873 810 44859
Original datase t 956 615 8460
1% 1144.9 664 -
3% 1458.9 711.3 -
5% 1685.2 744 -
10% 2125.9 771.7 -
20% 2451.1 784.5 4122
30% 2081.8 751 2378
40% 1326.4 694.9 1018
50% 230.1 450.9 465
60% 3.4 114.1 0
70% 0 0 0
80% 0 0 0
90% 0 0 0
4.1. Analysis of
a∗
-improved discernible
a∗
-improved-discernible function depicts the discerni-
ble relationship among samples. It reduces unnecessary
elements of
a∗
-discernible-checked matrix for correct
classification purpose. First, element about 2 samples in
the same class is abandoned. Second, element about 2
samples neither in the
{}Aa−∗
-positive region is omit-
ted. It is not possible that these samples are correctly
classified by rough set. The clauses in
a∗
-improved-
discernible f unction is
112 2
22 222
12
( 1)(1)(1)(1)(1)
22222
()
2
ww
w
nnl lllllnn
n nnlll
−− −−−
− −−−−
+−−+ ++
=


 
, (10)
where
n
is the total number of samples, n
is the number
of samples not in
{}Aa−∗
-positive region, and
i
l
is the
number of samples in the sa m e class.
By the characteristic of conjunction,
a∗
-improved-
discernible function just keeps one copy of the same
clauses to reduce memor y burden. So its exact number of
clauses is smaller tha n Equation 8 in Definitio n 3.4. Null
value is randomly set in order to obverse the variation
rule o f c laus es with var ying of mi ssi ng proportion. Table
2 shows a summary of exact clauses in
a∗
-improved-
discernible function. It can be observed that exact num-
ber of clauses increase with addition of missing. Missing
damages the distrib ution of values i n each attribute. As a
result, the relationship of samples in different class is
more complex with increasing of missing. However, the
addition of clauses stops, whe n the missi ng pro portion is
large enough. That is because that the samples in the
{}Aa−∗
-positive region decreases. The maximum of
clauses are found with missing from 10% to 20%.
4.2. The number of Clauses after Knowledge
Compilation
During the process of knowledge compilation using ex-
tension rule, one clause is deleted from the clause set,
when the clause subsumes another clause [15]. So the
subsuming p lays importa nt rol e in the computational cost
of memory and time. Since the number of clauses in
a∗
-improved-discer nible functio n is large, authors can
not find anything in the figures showing all the clauses.
In Fi g.1, 2 00 c lauses i n the original datasets are random-
ly picked as example to explain subsuming.
Every figure in Fig.1 includes three subfigures. The
middle one describes the 200 clauses of
a∗
-improved-
discernible matrix. Every column expresses one feature;
one ra w is a clause. Red denotes the feature in the related
clause, and blue means the feature not in a clause. For a
clause, its set of red features contains all red features of
another clause. Then, this clause is directly deleted in
knowledge compilatio n. The third subfigure shows this
detail of the first 10 clauses. For example, in the third
sub fig ure o f Fi g. 1a, the red features of the first clause are
included by other 9 clause, so the 9 clauses are deleted.
The first subfigure gives a summary of subsuming in the
second subfigure. The clauses in every two circles are in
a subsu mi ng set where only the first clause is kept. It ca n
be observed that the clauses of Zoo and Voting are dy-
namically del eted, shown in F ig. 1(a) and 1(c).
Fig. 2 illustrates t he amount variatio n of clauses under
increasing of missing during the process of knowledge
compilation. It is very interesting that the variation of
deleted clauses is similar with
a∗
-improved discernible
function. We can conclude that the subsuming characte-
ristic of dataset is not changed by missing proportion. In
Figs. 2(a) and 2(b), clauses in the extended sets increase
with addition of missing, and their increasing stops in
enough large missing proportion. The rule is also found
in Fi gs . 2(c ) although the variation is not dramatic.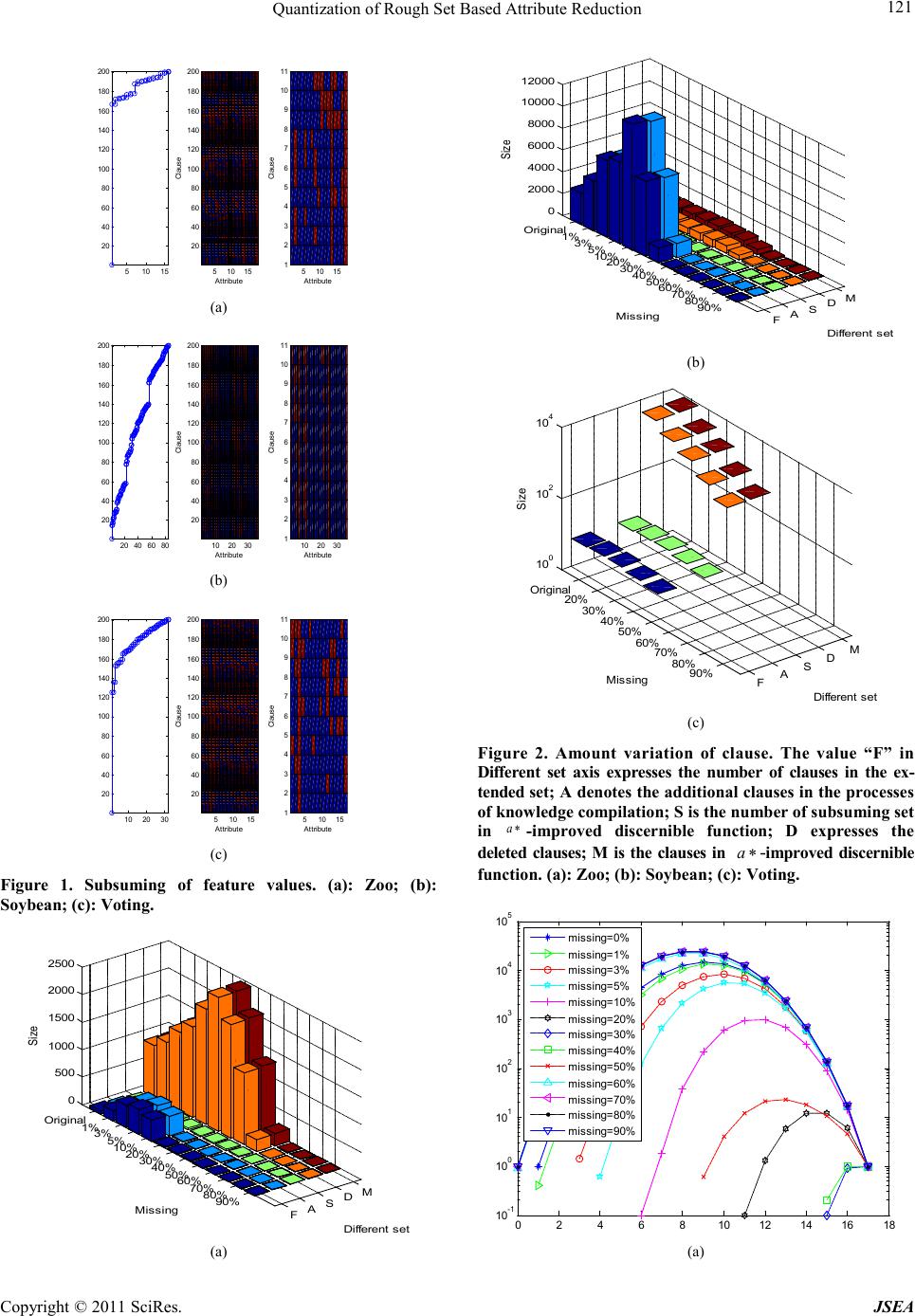

Quantization of Rough Set Based Attribute Reduction
121
510 15
20
40
60
80
100
120
140
160
180
200
Attribute
Clause
510 15
1
2
3
4
5
6
7
8
9
10
11
Attribute
Clause
51015
20
40
60
80
100
120
140
160
180
200
(a)
10 2030
20
40
60
80
100
120
140
160
180
200
Attribute
Clause
10 20 30
1
2
3
4
5
6
7
8
9
10
11
Attribute
Clause
20 40 60 80
20
40
60
80
100
120
140
160
180
200
(b)
510 15
20
40
60
80
100
120
140
160
180
200
Attribute
Clause
510 15
1
2
3
4
5
6
7
8
9
10
11
Attribute
Clause
10 20 30
20
40
60
80
100
120
140
160
180
200
(c)
Figure 1. Subsuming of feature values. (a): Zoo; (b):
Soybean; (c): Voting.
FAS DM
Original
1%
3%
5%
10%
20%
30%
40%
50%
60%
70%
80%
90%
0
500
1000
1500
2000
2500
Different set
Miss ing
Siz e
(a)
FAS DM
Origi nal
1%
3%
5%
10%
20%
30%
40%
50%
60%
70%
80%
90%
0
2000
4000
6000
8000
10000
12000
Different set
Miss ing
Siz e
(b)
FAS DM
Original
20%
30%
40%
50%
60%
70%
80%
90%
10
0
10
2
10
4
Different set
Miss ing
Siz e
(c)
Fig ure 2. Amount variation of clause. The value “F” in
Different set axis expresses the number of clauses in the ex-
tended set; A denotes the additi onal clauses in the proces ses
of knowledge compila tion; S is the number of subsuming set
in
a∗
-improved discernible function; D expresses the
deleted clauses; M is the clauses in
a∗
-improved dis c er n i bl e
function. (a): Zoo; (b): Soybean; (c): Voting.
02468101214 16 18
10
-1
10
0
10
1
10
2
10
3
10
4
10
5
missing=0%
missing=1%
missing=3%
missing=5%
missing=10%
missing=20%
missing=30%
missing=40%
missing=50%
missing=60%
missing=70%
missing=80%
missing=90%
(a)

Quantization of Rough Set Based Attribute Reduction
122
0510 15 20 25 30 35
10
-2
10
0
10
2
10
4
10
6
10
8
10
10
missing=0%
missing=1%
missing=3%
missing=5%
missing=10%
missing=20%
missing=30%
missing=40%
missing=50%
missing=60%
missing=70%
missing=80%
missing=90%
(b)
0246810 12 14 16
10
0
10
1
10
2
10
3
10
4
10
5
missing=14.7%
missing=20%
missing=30%
missing=40%
missing=50%
missing=60%
missing=70%
missing=80%
missing=90%
(c)
Figure 3. Distribution of solutions. (a): Zoo; (b): Soybean;
(c): Voting.
4.3. Distribution of Solutions
According to Algorithm 3.2, the distributio n of all possi-
ble solutions can be found, shown in Fig.3. It can be
observed that the amount of all solutions is decided by
the size of minimal reduction. The number of all solu-
tions is approximated to the area delimited by the cure
and x -axis. For a d ataset, a reduction having the smallest
size among all po ssible solution is minimal reductio n. In
every figure, if the minimal reduction has smaller size,
its number of all solutions is larger. The reason is that
any set containing minimal re d uction is also a solution.
Table 3 is the summary about amount of solutions.
The number of all solutions decreases with addition of
missing before threshold. Then, the number increases.
For each attribute, the original distribution of values in
different class is disordered by missing. This brings
Table 3. Number of solutions.
Dataset
Missing Zoo Soyb ean Voting
Original datase t 74448
10
3.16 10×
32
1% 65622.6 10 3.022 10× -
3% 37285.3 10 2.837 10× -
5% 23799 10 2.659 10× -
10% 3869.9
10
1.916 10×
-
20% 38.3
9
4.622 10×
16
30% 2
9
5.485 10×
16
40% 2.2 4870963.2 64
50% 94.8 445644.8 256
60% 118067.2 144703488 65536
70% 131072
10
3.44 10×
65536
80% 131072
10
3.44 10×
65536
90% 131072
10
3.44 10×
65536
about decrease of discernible ability of every attribute,
so more attributes are needed to provide the same sam-
ples in
{}Aa−∗
- positive region. It results in decrease of
all solution with the addition of missing. However, the
samples in
{}Aa−∗
- positive region are so fewer that
small mount of attributes is enough to provide the same
discernible ab ility, after missing is lar ger t han threshold.
So solution begins increasing. In Table3, the minimum
of solutions is obtained before missing is smaller than
50%.
5. Conclusions
Rough set based attr ibute reduction with missing value is
demonstrated as a sub-problem of satisfiability problem.
Extension rule, a satisfiability method, is employed to
obtain distribution of solutions without finding all
attribute reductions. The relation between attribute re-
duction and missin g is anal yzed from computational co st
and amount of solutions.
REFERENCES
[1] Liu, Y., Dimensionality reduction and main component
extraction of mass spectrometry cancer data. Know-
ledge-Based Systems, 2011.
[2] Lu, J., T. Zh ao, and Y. Zhan g, Feature selecti on based -on
genetic algorithm for image annotation. Knowledge-
Based Systems, 2008. 21(8): p. 887-891.
[3] Chmielewski, M.R., et al., The rule induction system
LERS-a version for personal computers. Foundations of

Quantization of Rough Set Based Attribute Reduction
123
Computing and Decision Sciences, 1993. 18(3-4): p.
181-212.
[4] Booth, D.E., Analysis of Incomplete Multivariate Data.
Te c hnom e t ri c s , 2000. 42(2): p. 213-214.
[5] Hudak, A.T., et al., Nearest neighbor imputation of spe-
cies-level, plot-scale forest structure attributes from Li-
DAR data. Remote Sensing of Environment, 2008.
112(5): p. 2232-2245.
[6] Pelckmans, K., et al., Handling missing values in support
vector machine classifiers. Neural Networks, 2005.
18(5-6): p. 684-692.
[7] Myers, J.W., K.B. Laskey, and T. Levitt. Learning Baye-
sian networks from incomplete data with stochastic
search algorithms. 1999. Morgan Kaufmann Publishers
Inc.
[8] Kryszkiewicz, M., Rough set approach to incomplete
information systems. Information sciences, 1998. 112(1):
p. 39-49.
[9] Slowinski, R. and J. Stefanowski, Rough classification in
incomplete information systems. Mathematical and
Computer Modelling, 1989. 12(10-11): p. 1347-1357.
[10] Pawlak, Z., Rough sets. International Journal of Parallel
Progr a m ming, 1982. 11( 5): p. 341-356.
[11] Leung, Y. an d D. Li, Maximal co nsis tent blo ck technique
for rule acquisition in incomplete information systems.
Information sciences, 2003. 153: p. 85-106.
[12] Meng, Z. and Z. Shi, A fast approach to attribute reduc-
tion in incomplete decision systems with tolerance rela-
tion-based rough sets. Information sciences, 2009.
17 9(16): p. 2774-2793.
[13] Liang, J., Z. Shi, and D. Li, The information entropy,
rough entropy and knowledge granulation in rough set
theory. International Journal of Uncertainty Fuzziness
and Knowledge-Ba sed Systems , 2004. 12 ( 1) : p. 37-46.
[14] Hai, L., S. Jigui, and Z. Yimin, Theorem proving based
on the extension rule. Journal of Automated Reasoning,
2003. 31 ( 1): p. 11-21.
[15] Hai, L. and S. Jigui, Knowledge compilation using the
extension rule. Journal of Automated Reasoning, 2004.
32(2): p. 93-102.
[16] Grzymala-Busse, J.W., Managing uncertainty in expert
systems. Vol. 143. 1991: Springer.
[17] Kirkpatrick, S. and B. Selman, Critical behavior in the
satisfiability of random boolean expressions. Science,
1994. 26 4( 5 16 3) : p. 12 97-1301.