Journal of Water Resource and Protection, 2013, 5, 97-110
http://dx.doi.org/10.4236/jwarp.2013.51012 Published Online January 2013 (http://www.scirp.org/journal/jwarp)
Prediction of Flow Duration Curves for Ungauged Basins
with Quasi-Newton Method
Mutlu Yaşar*, Neset Orhan Baykan
Department of Civil Engineering, Pamukkale University, Denizli, Turkey
Received November 5, 2012; revised December 6, 2012; accepted December 14, 2012
ABSTRACT
Prediction of flow-duration-curves (FDC) is an important task for water resources planning, management and hydraulic
energy production. Classification of the basins as carstic and non-carstic may be used to estimate parameters of the FDC
with predictive tools for catchments with/without observed stream flow. There is a need for obtaining FDC for un-
gauged stations for efficient water resource planning. Thus, study proposes a quite new approach, called the EREFDC
model, for estimating the parameters of the FDC for which the parameters of the FDC are obtained with quasi-Newton
method. Estimation are made for using the bv gauged stations at first than the FDC parameters are estimated for un-
gauged stations based on drainage area, annual mean precipitation, mean permeability, mean slope, latitude, longitude,
and elevation from the mean sea level are used. The EREFDC model consists of various type of linear- and nonlinear
mathematical equations, is able to predict a wide range of the FDC parameters for gauged and ungauged basins. The
method is applied to 72 unimpaired catchments studied are about for 50 years average daily measured stream flow. Re-
sults showed that the EREFDC model may be used for estimating. FDC parameters for ungauged hydrological basins in
order to find FDC for ungauged stations. Results also showed that the EREFDC model performs better in carstic regions
than non-carstic regions. In addition, parameters of FDC for tributaries at the basins with insufficient flow data or
without flow data may be determined by using basin characteristics.
Keywords: Flow Duration Curve; Optimization; BFGS Algorithm; Basin Characteristics
1. Introduction
Efficient use of energy sources is a major problem all
over the world, especially renewable energy that is a core
prerequisite for sustainable development. Hydroelectric
energy is one of the sustainable energy sources that need
to be carefully planned for future generations. Moreover,
technological developments require gradually increasing
energy needs in the future, but, it is usually not equally
distributed in place and time in the world.
Modeling a flow duration curve (FDC) is essential for
the power plants where the measurement could not be
performed and the plants are run-of-the river type. This is
one of the main the reason why hydrologists give so
much importance to this subject. In addition, prediction
of FDCs in ungauged stations are still challenging pro-
blem for hydrological community.
One way of efficient planning and use of hydroelectric
energy require good measured data for all stream flows
around the hydrological basins. This is usually impossible
since it requires considerable amount of money and for
gauging all the basins. Thus it needs to be method that
deals with the parameter estimation of flow-duration-
curves (FDC) for gauged and ungauged basins. The FDC
is a parametric methods that supplies the necessary in-
formation for the various water resource applications [1].
The values of daily FDCs present the most valuable in-
formation for the regional regime of flow during hydroe-
lectric power station application in a streambed [2]. In
addition, a stream flow system can be defined by a FDC
showing the distribution of flow frequencies obtained
from measured flows. If the data are unattainable or lim-
ited, plenty of sources should be evaluated. Therefore,
for the places where measurements cannot be carried out
estimation of FDCs is needed. An experimental FDC can
be easily obtained from flow observations by using stan-
dard nonparametric processes. The regionalization of a
FDC is important when working with basins without
gauging stations and shortage of flow data.
The usefulness of FDC is that it is a main input for
Hydroelectric Power Plants (HEPP) that is classified into
two main groups: 1) The HEPP with stored, regulated,
and directly diverted of natural flows; and 2) The HEPP
with storage reservoirs for which the flows have random
characters in time and they are regulated by means of
*Corresponding author.
C
opyright © 2013 SciRes. JWARP

M. YAŞAR, N. O. BAYKAN 98
storing so that reliable and firm energy may be obtained
by using this regulated amount of water. In the case of
nonstored HEPP’s, energy is to be produced in the pow-
erhouse changes as a function of the existing flow value
in the river bed if there is no storage area due to the to-
pography. Therefore, this type of HEPP requires real-
estimation of flow quantity for relevant design and effi-
cient use of stream flow.
Long term hydrologic data are generally not available
in many hydrological basins. Annual mean flow values
are commonly considered in many hydrologic design-
studies. In order to obtain daily flow data at projected-
point, an index-station of long-term observation values is
selected considering similar geographical conditions. If
the annual flow data are persistent and representative for
the region, the data transfer is assumed to be done prop-
erly. It is known that the FDC are synthetic (artificial)
curves so that the occurrences of the flows are disturbed
by putting the flows to descending or ascending order.
FDC is not a cumulative probability curve because the
time series of the flows in a stream are not stationery for
the intervals less than a year, so that the statistical char-
acteristics change along the year like mean, standard de-
viation, and coefficient of skewness. Therefore, the ex-
ceedence probability of the flow in a certain day depends
on the day where it is placed in [3]. If a generalized
FDC is drawn for each stream basin with observed data,
the FDC with a certain errata may be obtained for the
basins of nongauged stations.
Fennessey and Vogel [4] developed flow duration cur-
ves for the regions without adjustment and gauging sta-
tion in Massachusetts and they analyzed the new models
related with the regional flow duration curves. FDCs they
found that have a complex structure requiring probability
density functions with frequently three or more parame-
ters. They approximated daily FDCs by utilizing two-
parameter lognormal probability density function. Mimi-
kou and Kaemaki [5] regionalized the flow duration
curve by using the morpho-climatological properties of
the drainage basin. They explained the regional variabil-
ity of the flow duration curve associated with every pa-
rameter with the help of multiple regression techniques
by using annual mean regional precipitation, basin area,
hypsometric head and stream length. Alkan [6] suggested
the dimensionless FDC uses from in Equation (1).
et Q



 (1)
where, then, Q is the flow (m3/sec), t is the time series, α
and β are the parameters of the FDC. Alkan [6] found
that there is a nonlinear dependence between the natural
logarithm of the initial value of the exponential model
parameters and natural logarithm of coefficient of annual
flows. This parametric model has been employed to the
stream gauging stations in carstic and non-carstic basins
in Turkey. Singh et al. [7] made modeling of the FDCs
for the small water projects without gauging stations and
the basins with insufficient measurements in the Hima-
layas. Dimensionless FDCs were obtained by using nor-
mal, lognormal and exponential conversions from basins
with gauging stations to the basins without gauging sta-
tions. Yu and Yang [8] obtained FDCs for Cho-Shuei
Creek in Taiwan and they tested the validity of the FDCs.
They determined that polynomial method contains less
uncertainty compared to area index method according to
the analyses of uncertainty of obtained FDCs.
The studies on the deficiencies of flow measurements
are carried out by many researchers in many places in the
world such as Greece [5], the USA [4], Italy [9], India
[7], Taiwan [10] and Portugal [11]. Crocker et al. [11]
aimed to obtain a regional model in order to estimate the
FDC for basins without measurements in some parts of
Portugal. They used cumulative distribution function to
combine a model used in estimation of a FDC when flow
is not zero and a model used in estimation of the period,
in percentage, when there is no stream [11]. Cole et al.
[12] indicated that the users of flow data need independ-
ent qualification indicator in order to use the data safely
and they suggested the use of long term FDCs as an in-
dicator. This method lights the way visually for the dis-
order in flow data and gives the place and the form of the
fault.
Krasovskaia et al. [13] developed a model to estimate
a FDC for the basins without gauging stations. FDCs
were obtained experimentally by using a medium value
and a distribution coefficient and then, they were made
definable as regional FDCs or theoretical regional curves.
Development of first degree moments of FDCs along a
river system and their local scale like a basin area were
analyzed as well as interpolations along the river system
were prepared carefully. Daily flow data of Costa Rica
were used in the study. Estimation errors are relatively
about 30% higher for a period longer than 85%. However,
for a period lower than 20% and in the center of a FDC,
they become smaller about 10% and 8%, respectively.
The differences between experimental and theoretical
FDCs are low and better results were obtained in the
center parts of a FDC.
Bari and Islam [14] applied a stochastic approach in
order to obtain a FDC associated with a one year period
and get rid of difficulties of a traditional FDC in which
the date order of flows are masked. They investigated the
theoretical development of a stochastic FDC and prob-
ability distribution suitable to the average daily flow dis-
tribution. The model was applied to the chosen four
streams of Bangladesh. Small catchment areas are very
important for the development of local water resources.
As long as the global pressure on water resources in-
creases, the potential of the drainage areas will continue
to increase. Generally, the highland catchment areas with

M. YAŞAR, N. O. BAYKAN 99
important water resources are suitable for the develop-
ment of small hydroelectric energies. Estimation of a
FDC is important for the design of hydraulic structures
and related environmental assessment.
Niadas [15] suggested an approach about development
of symbolic daily FDCs for small catchment areas by
combining regional data with real instant flow data. An-
nual mean flow values were estimated by using instant
flow data of the two regions in representation of the flow
regime statistically.
Castellarin et al. [16] showed the relation between the
frequency and dimension of the overflow in a FDC. Their
study also aimed to estimate the FDC of streams without
flow values by evaluating the efficiency and correctness
of the data. The study was carried out for a large area in
east Italy. In order to evaluate the uncertainty of the re-
gional FDCs, they accepted the jack-knife cross valida-
tion method. Results included: a) The evaluation of reli-
ability of regional FDCs for imponderable areas; b) the
closeness of reliability data for the best three regional
models presented; and c) The empirical FDC’s based on
limited data samples generally provide a better fit of the
long-term FDC’s than regional FDC’s.
Ming et al. [17] proposed an index model for pre-
dicting the FDCs. The proposed index model was defined
as nonparametric relationship between each parameter to
the predictive tools and a linear combination of predic-
tors. They found that the index model improved the pre-
diction performance for ungauged stations. Similar study
was due to Ganora et al. [18], where distance-based model
was used to predict FDC for ungauged stations. They
found that the distance-based model produced better es-
timates of the flow duration curves using only few catch-
ment descriptors. Yokoo and Sivapalan [19] proposed an
FDC curve reconstruction with climatic and landscape
controls. Similar study was carried out by Viola et al. [20]
for which the regional FDC was obtained in Sicily. The
regional regression estimates were proposed in that
study.
In all approaches involving the regionalization of FDCs,
the applicability of the estimation methods for the small
catchment areas for ungauged stations is quite limited. In
addition, use of regression techniques developed so far
for the regional estimations may not best represent the
basin characteristics. Therefore, accurate estimations for
small catchment areas need to be made with proper
mathematical equations with commonly obtainable data
for the region such as drainage area, mean precipitation
rate, etc. Moreover there are many studies on the predic-
tion of FDC curve with linear regression techniques and
the statistical methods, but there is limited study on esti-
mation of the FDC with nonlinear equations with re-
gional parameters. One way of estimating the FDC pa-
rameters may be use of numerical method such as quasi-
Newton method. The most popular quasi-Newton algo-
rithm is the BFGS method, named by its discoverers
Broyden, Fletcher, Goldfarb, and Shanno. The BFGS
method is derived from the Newton’s method in optimi-
zation, a class of hill-climbing optimization techniques
that seeks the stationary point of a function, where the
gradient is zero. Newton’s method assumes that the func-
tion can be locally approximated as a quadratic Taylor
expansion in the region around the optimum, and uses
the first and second derivatives to find the stationary
point. Many nonlinear equations for FDC parameter es-
timation are solved with the BFGS algorithm using the
tools in Excel solver [21]. The α and β parameters given
in Equation (1) of the FDC are subsequently solved with
solver tool in Excel by minimizing observed and esti-
mated values of stream flow by using drainage area, an-
nual mean precipitation, mean permeability, mean slope,
latitude, longitude, and elevation from the mean sea level.
During the estimation, the α and β parameters are ob-
tained by an parametric Equation given in (1) at first for
each gauged stations, then by using regional parameters
(such as drainage are, mean slope, etc.) as an independ-
ent variable, α and β parameters are regionalized with set
of linear and nonlinear equations given in Section 2.
The data need for estimating the parameters of FDC
curves are obtained from US Geological Survey (USGS).
The detailed information about the method [22] carried
out in the USA applications in which the data transfer is
performed for the imponderable area with the correlation
between concurrent flows can be attained from USGS
articles and reports [23,24].
The rest of the paper is organized as follows: The next
section is about model development. Section 3 is about
BFGS algorithm. Section 4 is on data collection and
evaluation and finally, conclusions are given in Section 5.
2. Model Development
Modeling procedure is carried out in two steps:
Step I: Obtaining parameters for each gauging sta-
tions
The parameters of FDC for each of the gauged stations
are obtained in Equation (1). In order to obtain the α and
β parameters, in Equation (1) the average daily flows
data are used for each stations that is averaged over 60
years of measured daily flow. Average daily flow for
one-year long period are put into an order from maxi-
mum to minimum as referenced to a beginning of the
January first for that year. Typical FDC curve are given
in Figure 1 for station 1, named Pawnee R. at Rozel, in
Kansas. As can be seen in Figure 1, the fitted FDC and
measured FDC cure are in good agreement with the
theoretical FDC. Estimating the parameters of α and β
are obtained first for each of the stations, and then the
regionalization is made at Step II.

M. YAŞAR, N. O. BAYKAN 100
Figure 1. Typical FDC curve of Pawnee R. at Rozel, in
Kansas.
At Step I, the α and β parameters are calculated for
each gauging stations by minimizing Equation (2) as:
 
1
Min
T
est
t
SSEQ Q




8
(2)
where SS E is the sum of squared errors between ob-
served stream flows, Q, estimated stream flow Qest, and T
is the total number of daily observed stream flow. That is
set as T = 365. During solution quasi-Newton method
with solver toolbox are used.
Step II. Regionalization
By using the α and β parameters obtained. at Step I,
the regionalization is carried out at Step II by using the
regional parameters as drainage area (DA), annual mean
precipitation (AMP), mean permeability (MP), mean slope
(MS), latitude (LAT), longitude (LONG), and elevation
from the mean sea level (EL). Equations are given in
Equations (3) and (4).
26 4
1
10 12 14
0132 53 74
95 116 137
****
***
x
xx
xxx
x

 

 
 
 
 
(3)
26 4
1
10 12 14
0132 53 74
95 116 137
****
***
8
x
xx
xxx
x

 

 
 
 
 
(4)
x1 = Drainage area (km2);
x2 = Annual mean precipitation (mm);
x3 = Mean permeability (mm/h);
x4 = Mean slope (%);
x5 = Latitude(˚); x6= Longitude(˚);
x7 = Elevation (mm).
where, ω are the weighting coefficient of the nonlinear
equations. It is quite difficult for field engineers to use
the FDC directly given in Equations (3) and (4) since
most of them may not have the optimization knowledge;
Thus, the α and β parameters are obtained by quasi-
Newton method so called BFGS given in Section 3. Be-
fore applying Equations (3) and (4), the hydrological
basins are clustered into two groups as carstic and non-
carstic. The reason for clustering is a discharge differ-
ence between carstic and non-carstic regions in terms of
drainage and flow characteristics.
Equations (3) and (4) are used to solve Equations (5)
and (6) during solution process, the following objective
functions are used:


1
min
I

p
re
i
SSE 


 (5)
 
1
min
I

p
re
i
SSE 


 (6)
where, I is the total number of gauged stations for each
carstic and non-carstic groups, α and β are the FDC pa-
rameters obtained from Step I, αpre and βpre are the pre-
dicted values.
Flowchart of the proposed Estimation of REgionalized
Flow Duration Curve (EREFDC) is given in Figure 2.
As can be seen in Figure 2, the EREFDC model starts
with obtaining the parameters of FDC firs and then by
using the regional geographical and hydrological para-
meters, the parameters of the EREFDC are obtained us-
ing the quasi-Newton method as given in Figure 2.
3. BFGS Algorithm
The most popular quasi-Newton algorithm is the BFGS
method, named by its discoverers Broyden, Fletcher,
Goldfarb, and Shanno. The BFGS method is derived from
the Newton’s method in optimization, a class of hill-
climbing optimization techniques that seeks the station-
ary point of a function, where the gradient is zero. New-
ton’s method assumes that the function can be locally
approximated as a quadratic Taylor expansion in the re-
gion around the optimum, and uses the first and second
derivatives to find the stationary point. Detailed discus-
sion of BFGS method can be found in some numerical
optimization textbooks, see the references [25,26]. The
BFGS algorithm can be summarized as follows [26,27]:
Step 1: Estimate an initial design vector Choose a
symmetric positive definite matrix as an estimate for
the Hessian of the cost function. In the absence of more
information, let

0.X

0
H

0.

HI Choose a convergence para-
meter

. Set 0k

, and compute the gradient vector as
 


0
g 0 Xc . Where, k is iteration index and g is the
cost function of the design vector.
Step 2: Calculate the norm of the gradient vector as

k
c. If

,
k


c then stop the iterative process; other-
wise continue.
Step 3: Solve the linear system of equations
to obtain the search direction. Where, d
is search direction vector.
 
kk k
Hd c
Step 4: Compute optimum step size k

  to mini-
mize
 


kk
 gXd .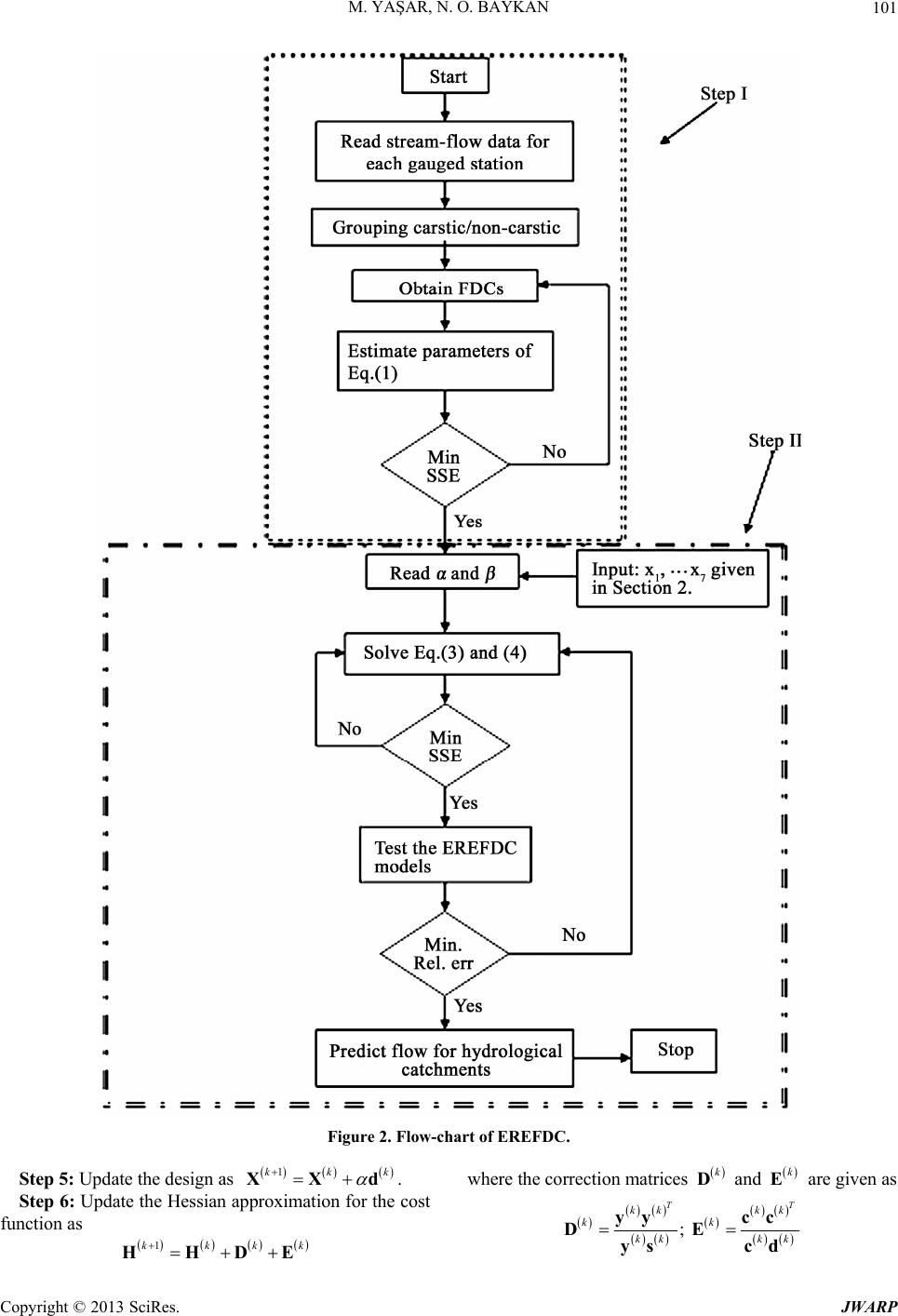

M. YAŞAR, N. O. BAYKAN 101
Figure 2. Flow-chart of EREFDC.
Step 5: Update the design as .
 
1kk

XXd k
k
aawhere the correction matrices

Dnd

Ere given as
k k
Step 6: Update the Hessian approximation for the cost
function as
  

  
 
;
TT
kk kk
kk
kkk k

yy cc
DE
ys cd
  1kkkHHDE

M. YAŞAR, N. O. BAYKAN 102
 
kk
k
 sd (change in design);
k
(change in gradient);
Step 7: Set
4. The EREFDC Model Application
4.lection
ata for 72
America. Kansas is the 15th
with area of 213.089 km2. The
ations used in the EREFDC modeling studies are
selected from those are not affected from the rate of the
rresponding physical and geographical.
Station
Number
Station
Name
Drainage Area Mean Mean SlopeLatitude Longitude
x6 (˚)
Elevation
x7 (mm)
  1kk
yc c


1k
g

c


1k
X
1
and go to Step 2.
kk
1. Data Col
This study uses average daily stream flow d
catchments in Kansas city in
largest state of the USA
stream flow data are for relatively unimpaired catch-
ments. The catchment size ranges from 120 to 30,000 km2
and data length varies from 20 to 100 years. The avail-
able data in Kansas City has been downloaded from the
source: http://waterdata.usgs.gov. Elevation, mean slope
permeability and precipitation are taken from Perry et al.
[28].
4.1.1. Flow Data
The st
flow namely uncontrolled flow. Stations and their corre-
sponding data are given in Table 1. As can be seen in
Table 1 drainage area varies between 10 - 3100 km2,
annual precipitation varies between 100 - 1000 mm, av-
erage basin permeability varies between 10 and 140
mm/h, the slope of the basin varies between 0.8% - 6.0%
and the elevation value varies between 200 - 800 m.
Each of station includes a data from an average daily
stream flow that has a length of 366 data in a year. One
example of the data are given in Appendix for station
number 6814000 Turkey C. 72 station are taken into ac-
count during the EREFDC model developments since
there are no homogenous data on other station in the ba-
sin in Kansas city, USA. Data are classified as carstic
and non-carstic group by putting them into an order ac-
cording to the minimum and maximum station number.
80% of the carstic and non-carstic data are used for
ERECFDC model development and 20% of them are
used for EREFDC model testing.
Carstic map are given in Figure 3. In order to find
Figure 3, each gauged stations are extracted according to
their coordinates, then those coordinates matched with
carst maps taken from
http//:pubs.usgs.gov/of/2004/1352/.
Table 1. Station numbers and their co
Annual Mean
x1 (km2) Precipitation
x2 (mm)
Perme-ability
x3 (mm/h)
x4 (%) x5 (˚)
6814urkey000 T C. 714.8 822 12 3.10 39.9 96.1 316.2
6815000 Big Ne.
6848500 Praire Dog 2608.1 548 35 2.10 40.0 99.5 614.5
9207.100.
1351 100.0
k Sol.
1237
.
.
maha R3468 827 13 2.80 40.0 95.6 261.6
6860000 Smooky Hill R.5 449 39 1.30 38.8 9 799.4
6861000 Smooky Hill 9 468 39 1.40 38.8 669.4
6863500 Big C. 1538.5 554 30 1.40 38.9 99.3 595.5
6866500 Smooky Hill R. 21647 529 37 1.60 38.7 97.6 378.0
6866900 Saline R. 1802.6 523 35 1.50 39.1 99.9 675.9
6867000 Saline R.3890.2 551 35 2.20 39.0 98.9 472.9
6869500 Saline R. 7303.8 602 33 2.50 39.0 97.9 385.7
6871000 N. Fork Sol. R.2198.9 541 34 2.50 39.7 99.3 534.6
6873000 South For2693.6 530 37 2.10 39.4 99.6 589.3
6876700 Salt C. 994.6 685 28 2.60 39.1 97.8 380.1
6878000 Chapman C. 777 785 26 2.20 39.0 97.0 336.0
6879650 Kings C. 714.00 838 12 5.90 39.1 96.6 333.6
6882000 Big Blue R.11517 725 21 1.30 40.0 96.6 354.2
6882510 Big Blue R. 2 728 21 1.40 39.8 96.7 338.4
6884000 Little Blue R6086.5 694 36 1.40 40.1 97.2 389.3
6884025 Little Blue R7127.7 702 35 1.60 40.0 97.0 370.7
6884200 Mill C. 891 778 23 2.40 39.8 97.0 384.5

M. YAŞAR, N. O. BAYKAN 103
Continued
6884400 Little Blue R. 8609.2 717 33 1.70 39.7 96.8 347.5
6885500 B. Vermillion R. 1061.9 846 9 2.40 39.7 96.4 337.4
illion R. 1
ermillion C. 629.4 887 11 3.40 39.3 96.2 302.4
e R. 1
ygnes R.
es R.
C.
s R.
es R.
3
3
.
R.
R.
h R.
.
g C.
6888000 Vermillion C. 629.4 887 11 3.40 39.3 96.2 302.4
6884200 Mill
6884400
C.
Little Blue R.
891
8609.2
778
717
23
33
2.40 39.8
1.70
97.0
96.8
384.5
347.5 39.7
6885500 B. Verm061.9 846 9 2.40 39.7 96.4 337.4
6888000 V
6888500 Mill C. 818.4 881 13 4.20 39.1 96.2 294.1
6889200 Soldier C. 406.6 905 12 3.20 39.2 95.9 281.7
6889500 Soldier C. 751.1 908 14 3.30 39.1 95.7 263.0
6890100 Delawar116.3 914 10 3.10 39.5 95.5 280.7
6891500 Wakarusa R. 1100.8 930 16 2.60 38.9 95.3 243.6
6892000 Stranger C. 1051.5 962 13 3.20 39.1 95.0 244.1
6893080 Blue R. 119.1 999 15 2.10 38.8 94.7 270.1
6910800 M. des C458.4 909 10 2.20 38.6 96.0 319.5
6911000 M.des Cygn909.1 930 11 2.20 38.5 95.7 287.1
6911900 Dragoon C.295.3 916 11 2.70 38.7 95.8 309.7
6912500 H and T Mile 834 920 12 2.30 38.6 95.6 280.1
6913000 M. des Cygne2693.6 928 12 2.20 38.6 95.5 272.4
6913500 M. des Cygn
C.
3237.5 932 13 2.20 38.6 95.3 261.4
6914650 Big Bull 380.7 997 17 2.10 38.7 94.9 260.4
6917000 Little Osage R. 764.1 103 18 2.00 38.0 94.7 235.3
7140850 Pawnee R. 242.68520 28 1.10 38.2 99.6 640.9
7141200 Pawnee R. 5563.3 533 28 1.10 38.2 99.4 621.9
7141780 Walnut C. 087.3 534 30 1.10 38.5 99.4 610.9
7141900 Walnut C. 3651.9 544 30 1.20 38.5 99.0 578.3
7142575 Rattlesnake C. 2711.7 620 150 0.70 38.1 98.5 544.1
7143300 Cow C. 1885.5 664 33 0.90 38.3 98.2 496.3
7143665 Little Arkansas R
sas
1906.2 749 53 0.80 38.1 97.6 424.1
7144200 Little Arkan3436.9 771 51 0.80 37.8 97.4 404.1
7144780 N.Fork Nin.2038.3 682 139 0.70 37.9 98.0 443.8
7145200 S. Ninnesca1683.5 692 78 1.30 37.6 97.9 413.9
7145500 Ninnescah R.5514.1 713 96 1.10 37.5 97.4 372.6
7145700 Slate C.
ter R.
398.9 781 22 0.80 37.2 97.4 352.7
7147070 Whitewa1103.3 839 12 1.20 37.8 97.0 375.4
7147800 Walnut R. 4869.2 871 12 1.40 37.2 97.0 330.1
7149000 Medicine Lodge R. 2338.8 647 65 2.70 37.0 98.5 392.3
7151500 Chikaskia R. 2056.5 729 67 1.10 37.1 97.6 337.7
7152000 Chikaskia R. 4814.8 837 20 1.00 36.8 97.3 294.9
7154500 Cimarron R.
R.
2864.5 414 53 1.00 36.9 103.0 1299.0
7156900 Cimarron22108 428 80 1.10 37.0 100.5 707.2
7157500 Crooked C. 2996.6 521 42 0.72 37.0 100.2 659.5
7157950 Cimarron R31090 496 81 1.30 36.9 99.3 487.6
7166500 Verdigris R. 2947.4 953 17 2.40 37.5 95.7 237.8
7167500 Otter C. 334.1 919 12 2.80 37.7 96.2 298.0
7169500 Fall R. 2141.9 921 16 2.70 37.5 95.8 249.7
7169800 Elk R. 569.8 926 11 0.50 37.4 96.2 273.5
7172000 Caney R. 1152.6 902 14 3.20 37.0 96.3 232.7
7174400 Caney R. 3605.3 933 25 3.10 36.8 96.0 199.1
7179500 Neosho R. 647.5 858 11 1.80 38.7 96.5 367.5
7180500 Cedar C. 284.9 847 13 1.60 38.2 96.8 384.8
7183500 Neosho R.12704 924 15 1.70 37.3 95.1 247.0
7184000 Lightnin510.2 107 26 1.20 37.3 95.0 249.4
7186000 Spring R.3014.8 110 36 1.20 37.2 94.6 254.0
7187000 Shoal C. 1105.9 109 38 2.70 37.0 94.5 270.3
7188000 Spring R. 6500.9 109 36 1.40 36.9 94.7 227.5

M. YAŞAR, N. O. BAYKAN 104
Figure 3. Map of carstic and non-carstic regions.

M. YAŞAR, N. O. BAYKAN 105
After obtaining carstic maps, stations are grouped ac-
cording to carstic and non-carstic region.
4.1.2. Data Generation
Data generation is carried out at Step I in the following
way; Fitted FDC parameters defined at Step I are ob-
tained by solver toolbox and the values are given in Ta-
bles 2(a) and (b). As can be seen in Tables 2(a) and (b),
coefficient of determination R2 varies 44% to 98%. The
reason for low R2 at stations 714275 and 7154500 may
be the measurement error or nonhomogeneity for the
stream flow data
Tables 2(a) and (b) show the non-carstic and carstic
data among the 72 gauged stations and 46 of them are
non-carstic group and 26 of them are carstic.
4.2. The EREFDC Application and
Regionalization
The EREFDC model is applied to 21 carstic and 37 non-
carstic uncontrolled measured flows for estimating the
parameters of the EREFDC models. The 5 of the carstic
and 9 of the non-carstic stations are used for testing the
EREFDC. Considering carstic stations, predicted EREFDC
model parameters for α and β are given in Equations (7)
and (8), respectively. Similarly, EREFDC model para-
meters for α and β considering non-carstic stations, are
given in Equations (9) and (10), respectively.





0.02
1
0.76 0.01
23
4.25 1.27
56
293.67
7
4412.54) (456.05*
5371.2*4078.42*
98.11*0.36*
4893.3*
EREFDC x
xx
xx
x




 




(7)

(8)



0.72
2
0.75 0.44
56
0.07 0.14*
0.69*0.90*
EREFDC x
xx



 
 





0.02
1
25.45 0.76
24
31.45 1.12
56
0.2
7
2569.72) (2061.77*
295.91*10.45*
114.25*0.84*
933.44*
EREFDC x
xx
xx
x




 





(9)

(10)
4.3. The EREFDC Testing
In order to test the EREFDC model, 20% of data in Ta-
bles 2(a) and (b) are randomly selected for which any of
the selected data are not used for during the model devel-
Table 2. (a) Non-carstic grouped and its corresponding esti-
mated parameters at Step I (continued); (b) Carstic grouped
data and its corresponding estimated parameters.
(a)
Estimated α, β parameters for Equation (1)
Station
Number
Carstic
Non-carstic Alfa Beta R2
7142575Non-carstic3.3173 0.0064 0.61
7143300Non-carstic6.4199 0.0076 0.97
7143665Non-carstic19.2220 0.0085 0.98
7144200Non-carstic22.2665 0.0060 0.99
7144780Non-carstic10.0416 0.0061 0.75
7145200Non-carstic10.7604 0.0037 0.92
7145500Non-carstic30.0664 0.0044 0.97
7145700Non-carstic7.5775 0.0092 0.98
7149000Non-carstic8.4529 0.0043 0.97
7151500Non-carstic19.7044 0.0067 0.94
7152000Non-carstic45.7707 0.0065 0.98
7166500Non-carstic17.4648 0.0052 0.99
7169500Non-carstic34.8421 0.0053 0.98
7174400Non-carstic82.5714 0.0060 99
7184000Non-carstic14.6999 0.0080 92
7186000Non-carstic57.9585 0.0048 98
7187000Non-carstic23.7601 0.0042 97
7140850Non-carstic5.2309 0.0654 88
7157500Non-carstic2.4943 0.0097 68
7183500Non-carstic99.7580 0.0029 92
0.
0.
0.
0.
0.
0.
0.
(b)
Estimated α, β parameters fortion (1) Equa
Station
Number
Carstic
Non-carstic
 
R2
6848500Carstic 3.3544 0.0140 92 0.
6861000Carstic 6.6283 0.0185 98
6863500Carstic 3.6823 0.0133 91
6866900Carstic 3.8603 0.0308 87
6871000Carstic 2.7966 0.0112 78
6878000Carstic 7.4679 0.0080 90
6888000Carstic 8.8362 0.0109 0.94
6888500Carstic 15.0576 0.0072 0.95
6889200Carstic 8.3179 0.0083 0.88
6890100Carstic 20.7805 0.0073 0.95
6893080Carstic 4.0328 0.0110 0.87
6910800Carstic 10.5547 0.0092 0.93
6911000Carstic 17.0593 0.0076 0.94
6911900Carstic 6.8470 0.0096 0.95
6912500Carstic 13.7585 0.0067 0.95
7147070Carstic 20.8870 0.0097 0.87
7147800Carstic 67.2417 0.0063 0.95
7154500Carstic 4.0220 0.0300 0.96
7156900Carstic 2.1893 0.0024 0.44
7157950Carstic 7.3423 0.0056 0.92
7167500Carstic 8.3145 0.0090 0.94
7169800Carstic 15.1151 0.0090 0.88
7172000Carstic 24.2369 0.0077 0.97
7179500Carstic 10.2554 0.0078 0.93
7188000Carstic 132.0895 0.0047 0.98
7180500Carstic 4.9053 0.0075 0.90
0.
0.
0.
0.
0.



0.03
3
0.07 0.09
56
0.34 0.05*
0.10*0.02*
EREFDC x
xx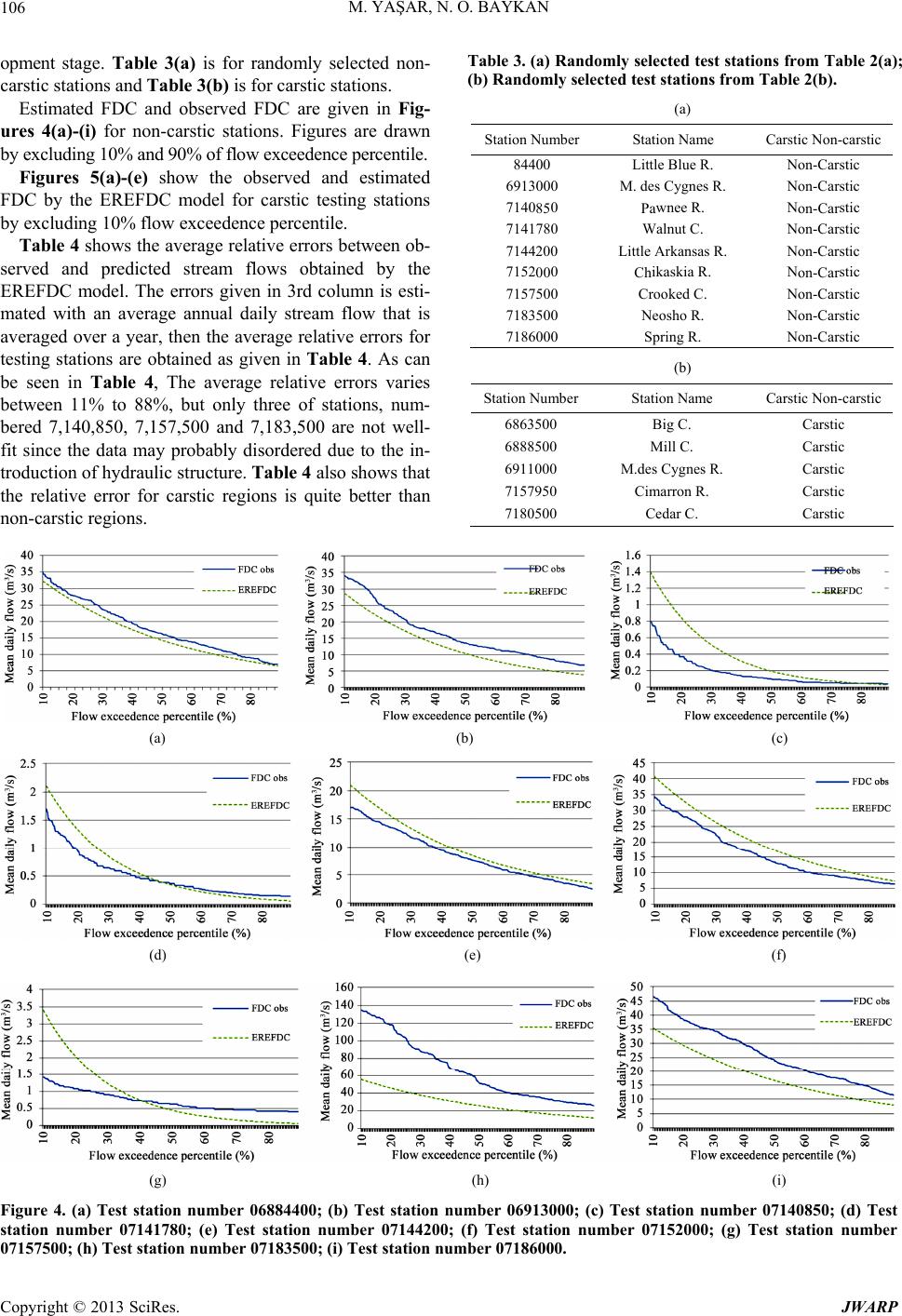



 
 

M. YAŞAR, N. O. BAYKAN 106
op
c stations.
Estimated FDC and observed FDC are given in Fig-
stic stations. Figures are drawn
erage annual daily stream flow that is
av
rrors varies
stations, num-
0 are not well-
fit siobably disordered due to the in-
Station NumberStation Name Carstic Non-carstic
ment stage. Table 3(a) is for randomly selected non-
carstic stations and Table 3(b) is for carsti
ures 4(a)-(i) for non-car
by excluding 10% and 90% of flow exceedence percentile.
Figures 5(a)-(e) show the observed and estimated
FDC by the EREFDC model for carstic testing stations
by excluding 10% flow exceedence percentile.
Table 4 shows the average relative errors between ob-
served and predicted stream flows obtained by the
EREFDC model. The errors given in 3rd column is esti-
mated with an av
eraged over a year, then the average relative errors for
testing stations are obtained as given in Table 4. As can
be seen in Table 4, The average relative e
between 11% to 88%, but only three of
bered 7,140,850, 7,157,500 and 7,183,50
nce the data may pr
troduction of hydraulic structure. Table 4 also shows that
the relative error for carstic regions is quite better than
non-carstic regions.
Table 3. (a) Randomly selected test stations from Table 2(a);
(b) Randomly selected test stations from Table 2(b).
(a)
84400 Little Blue R. Non-Carstic
691300. des s R. Cars
85 Paon-Car
780 Won-Car
20ttle R. on-Car
00 Chon-Car
500 Cron-Car
50 Non-Car
00 Son-Car
0 MCygneNon-tic
71400 wnee R. Nstic
7141alnut C. Nstic
71440 LiArkansas Nstic
71520 ikaskia R. Nstic
7157ooked C. Nstic
71830 eosho R. Nstic
71860 pring R. Nstic
(b)
Station NumStatcberion Name Carstic Non-carsti
6863500Carstic Big C.
6888500 MCarstic
00.de. Carsti
50 CimCarstic
00 CCarstic
ill C.
69110 Ms Cygnes Rc
71579 arron R.
71805 edar C.
(a) (b) (c)
(d) (e ) (f)
(g) (
num300est station number 07140850; (d) Test
0; (f)tioner 0 (g)ation er
mb 000.
h) (i)
Figure 4. (a) Test station number 06884400; (b) Test station
station number 07141780; (e) Test station number 0714420
07157500; (h) Test station number 07183500; (i) Test station nu
ber 06910; (c) T
Test sta numb7152000; Test stnumb
er 07186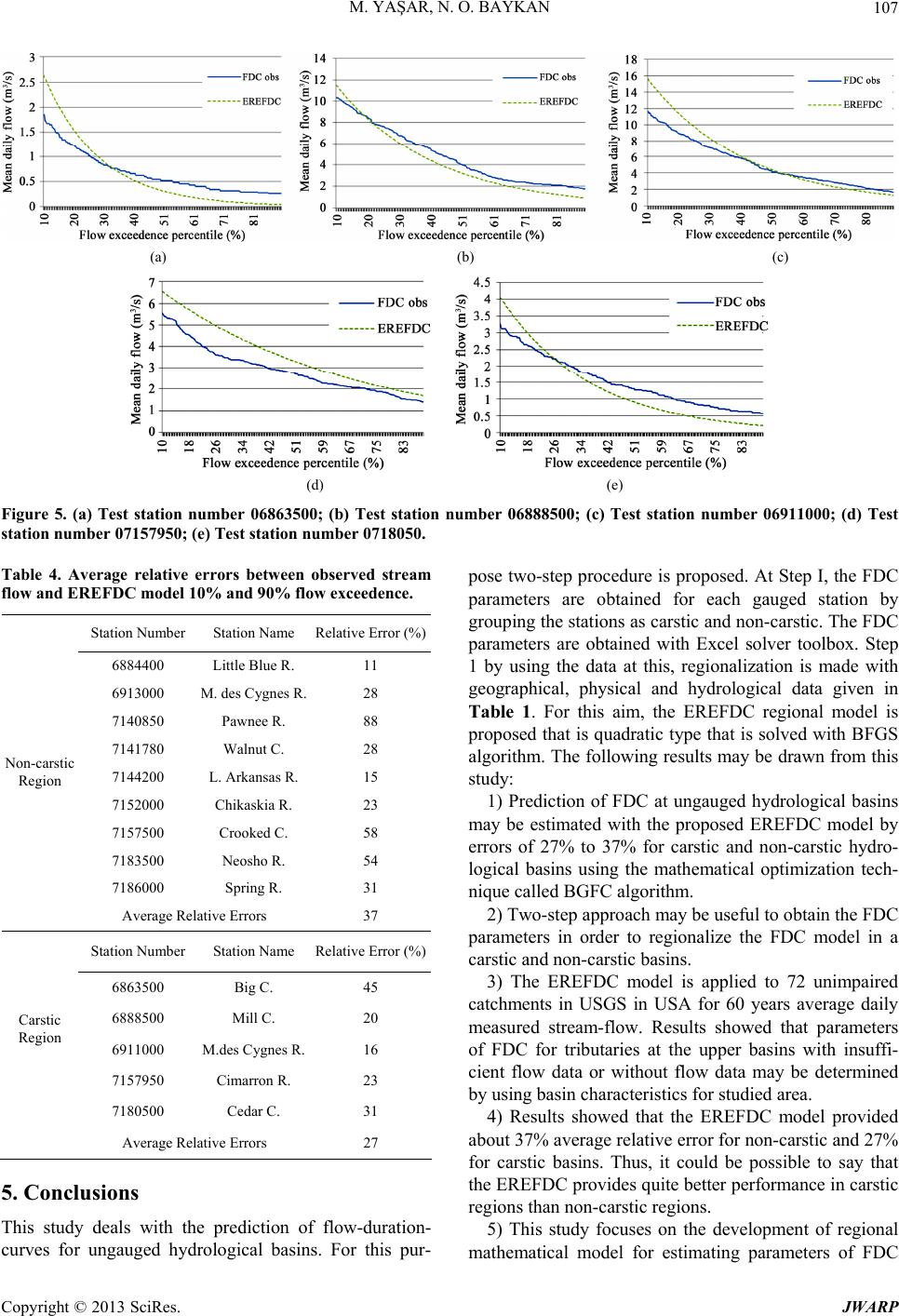

M. YAŞAR, N. O. BAYKAN 107
(a) (b) (c )
(d)
Figure 5. (a) Test stat
ation number 07157
(e)
ion number 06863500; (b) Test station number 06888500; (c) Test station number 06911000; (d) Test
950; (e) Test station number 0718050.
Table 4. Average relative errors between observed stream
flow and EREFDC model 10% and 90% flow exceedence.
Station Number Station Name Relative Error (%)
st
6884400 Little Blue R. 11
6913000 M. des Cygnes R. 28
7140850 Pawnee R. 88
7141780 W
7144200 L. Arkansas R. 15
7152000 Chikaskia R. 23
7157500 Crooked C. 58
7183500 Neosho R. 54
7186000 Spring R. 31
Non-carstic
Region
Average Relative Errors 37
Station N
alnut C. 28
umber Station Name Relative Error (%)
6863500 Big C. 45
6888500 Mill C. 20
6911000 M.des Cygnes R. 16
7157950 Cimarron R. 23
Carstic
Region
7180500 Cedar C. 31
Average Relative Errors 27
5. Conclusions
pose two-step procedure is proposed. At Step I, the FDC
parameters are obtained for each gauged station by
grouping the stations as carstic and non-carstic. The FDC
parameters are obtained with Excel solver toolbox. Step
1 by using the data at this, regionalization is made with
geographical, physical and hydrological data given in
Table 1. For this aim, the EREFDC regional model is
with BFGS
algorithm. The following results may be drawn from this
study:
1) Prediction of FDC at ungauged hydrological basins
may be estimated with the proposed EREFDC model by
errors of 27% to 37% for carstic and non-carstic hydro-
logical basins using the mathematical optimization tech-
nique called BGFC algorithm.
2) Two-step approach may be useful to obtain the FDC
parameters in order to regionalize the FDC model in a
3) The EREFDC model is applied to 72 unimpaired
catchments in USGS in USA for 60 years average daily
measured stream-flow. Results showed that parameters
of FDC for tributaries at the upper basins with insuffi-
cient flow data or without flow data may be determined
by using basin characteristics for studied area.
4) Results showed that the EREFDC model provided
about 37% average relative error for non-carstic and 27%
for carstic basins. Thus, it could be possible to say tha
nce in carstic
model for estimating parameters of FDC
This study deals with the prediction of flow-duration-
curves for ungauged hydrological basins. For this pur-
regions than non-carstic regions.
5) This study focuses on the development of regional
mathematical
proposed that is quadratic type that is solved
carstic and non-carstic basins.
t
the EREFDC provides quite better performa

M. YAŞAR, N. O. BAYKAN 108
curves for carstic and non-carstic regions. The average
relative errors may be considered as a quite high for non-
carstic regions. Future studies should be improvement on
the prediction performance of the ERFDC model for un-
controlled steam flows for various data in the world.
REFERENCES
[1] R. M. Vogel and N. M. Fennessey, “Flow Duration Cur-
ves II: A Revi
Planning,” Journal of the American Water Resources As-
sociation, Vol. 31, No. 6, 1995, pp. 1029-1039.
doi:10.1111/j.1752-1688.1995.tb03419.x
ew of Applications in Water Resources
[2] C. C. Warnick, “Hydropower Engineering,” Englewood
Cliffs, New Jersey, 1984.
[3] D. R. Maidment, “Handbook of Hydrology,” McGraw-
Hill, Colombus, 1992.
[4] N. Fennessey and R. M. Vogel, “Regional Flow Duration
Curves for Ungauged Sites in Massachusetts,” Journal of
Water Resources Planning and Management
No. 4, 1990, pp. 530-549.
, Vol. 116,
doi:10.1061/(ASCE)0733-9496(1990)116:4(530)
[5] M. Mimikou and S. Kaemaki, “Regionalization of Flow
Duration Characteristics,” Journal of Hydrology, Vol. 82,
No. 1-2, 1985, pp. 77-91.
doi:10.1016/0022-1694(85)90048-4
[6] A. Alkr Kl
zeyli ASa A
lerinin Msi,” idroloji ngresi,
İzmir, 2001
[7] R. D. Singh, y, “Regional
Flow-Durels fomber of auged
Himalayan Catchments for Planning Microhydrojects,
l ogic El. 6, No 2001,
10-31
doi:10.106 )1084:4(310)
an, “Karst Pina
kişli Çevirme
atkili Akarsu
ntralları için
arda, Serbest Yü-
kım Sürek Eğri-
odellenmeIII. Ulusal HKo
, pp. 247-255.
S. K. Mishra
ation Mod
and H. Chowdhar
r Large NuUng
ro P
Journa
pp. 3
f Hydrolo
6.
ngineering, Vo. 4,
1/(ASCE -0699(2001)6
[8] P. S. Yu Yangy Analy
gional Flon Curvl of Water Resources
Planning ageme8, No. 6,2, pp.
424-430.
doi:10.1061 02)128:6(424
and T. C., “Uncertaintsis of Re-
w Duratio
and Man
es,” Journa
nt, Vol. 12 200
/(ASCE)0733-9496(20 )
[9] M. Franchini and M. Suppo, “Regional Analysis of Flow
Duratioa g
sources Management, Vol. 10, No. 3, 1996, pp. 199-218.
doi:10.100 4203
n Curves for Limestone Reion,” Water Re-
7/BF0042
[1 . Yu aang, “S Regional Flow Dura-
Curve forical Processes,
Vol. 10, N, pp
doi:10.100099-110:3<37 ID-H
0] P. S
tion
nd T. C. Yynthetic
Southern
o. 3, 1996
Taiwan,” Hydrolog
. 373-391.
2/(SICI)1 085(199603)3::A
YP306>3.0.CO;2-4
[11] K. M. Crocker, Young H. G. Rees
uration Cemeral Catc
Portugal,” Hydrological Sciences, Vol. 48, No. 3, 2003,
:10.1623/hysj.48.3.427.45287
M. D. Z. and, “Flow
Durve Estimation in Ephhments in
pp. 427-439. doi
n and D. J. Robinson, “The
[13] I. Krasovskaia, I. Gottschalk, E. Leblois and A. Pacheco,
“Regionalization of Flow Duration Curves,” In: S. De-
muth, Ed., Climate Variability and Change-Hydrologi-
cal Impacts, IAHS Press, Wallingford, 2006.
[14] M. F. Bari and Kh. M. D. S. Islam, “Stochastic Model of
Flow Duration Curves for Selected Rivers in Bangla-
desh,” Proceedings of the 5th FRIEND World Confer-
ence on Climate Variability and Change-Hydrological
Impacts, Havana, 27 November-1 December 2006, pp.
99-104.
rve Estimation
in Small Ungauged Catchments Using Instantaneous
Flow Measurements and a Censored Data Approach,”
Journal of Hydrology, Vol. 314, No. 1-4, 2005, pp. 48-66.
doi:10.1016/j.jhydrol.2005.03.009
[12] R. A. J. Cole, H. T. Johnsto
Use of Flow Duration Curves as a Data Quality,” Hydro-
logical Sciences, Vol. 48, No. 6, 2003, pp. 939-951.
[15] I. A. Niadas, “Regional Flow Duration Cu
[16] A. Castellarin, G. Galeati, L. Brandimatre, A. Montanari
and A. Brath, “Regional Flow-Duration Curves: Reliabil-
ity for Ungauged Basins,” Advances in Water Resources,
Vol. 27, No. 10, 2004, pp. 953-965.
doi:10.1016/j.advwatres.2004.08.005
i, Z. Lu and H. S. C Francis, “A New
proach and Its Application to Predict
doi:10.1016/j.jhydrol.2010.05.039
[17] L. Ming, S. Quanx
Regionalization Ap
.
Flow Duration Curve in Ungauged Basins,” Journal of
Hydrology, Vol. 389, No. 1-2, 2010, pp. 137-145.
[18] D. Ganora, P. Claps, F. Laio and A. Viglione, “An Ap-
proach to Estimate Nonparametric Flow Duration Curves
in Ungauged Basins,” Water Resources Research, Vol. 45,
2009, W10418. doi:10.1029/2008WR007472
[19] Y. Yokoo and M. Sivapalan, “Towards Reconstruction of
the Flow Duration Curve: Development of a Conceptual
Framework with a Physical Basis,” Hydrology and Earth
System Sciences, Vol. 15, No. 9, 2011, pp. 2805-2819.
[20] F. Viola, L. V. Noto, M. Cannarozzo and G. La Loggia,
“Regional Flow Duration Curves for Ungauged Sites in
Sicily,” Hydrology and Earth System Sciences, Vol. 15,
er-Resources Investigations,
cy Characteristics at Un-
ny Search Algorithm,”
No. 1, 2011, pp. 323-331.
[21] Microsoft, “Microsoft Excel-Visual Basic for Applica-
tions,” Microsoft Press, Washington DC, 1995.
[22] H. C. Riggs, “Low-Flow Investigations,” US Geological
Survey Techniques of Wat
Washington DC, 1972.
[23] L. C. Kjelstrom, “Methods for Estimating Selected Flow-
Duration and Flood-Frequen
gauged Sites in Central Idaho,” USGS Water Resources
Investigations Report 94-4120, Boise, 1998, p. 10.
[24] S. E. Studley, “Estimated Flow Duration Curves for Se-
lected Ungauged Sites in Kansas,” US Geological Survey,
01:4142, Virginia, 2001.
[25] J. Nocedal and S. J. Wright, “Numerical Optimization,”
Springer-Verlag, Berlin, 2006.
[26] J. S. Arora, “Introduction to Optimum Design,” McGraw-
Hill, New York, 1989.
[27] H. Karahan, G. Gurarslan and Z. W. Geem, “Parameter
Estimation of the Nonlinear Muskingum Flood Routing
Model Using a Hybrid Harmo
Journal of Hydrologic Engineering, 2012, in Press.
doi:10.1061/(ASCE)HE.1943-5584.0000608

M. YAŞAR, N. O. BAYKAN 109
[28] C. A. Perry, D. M. Volock and J. C. Artman, “Estimates
of Flow Duration, Mean Flow and Peak-Discharge Fre-
quency Values for Kansas Stream Location,” Scientific
Investigation Report 2004-5033, US Geological Survey,
Virginia, 2004.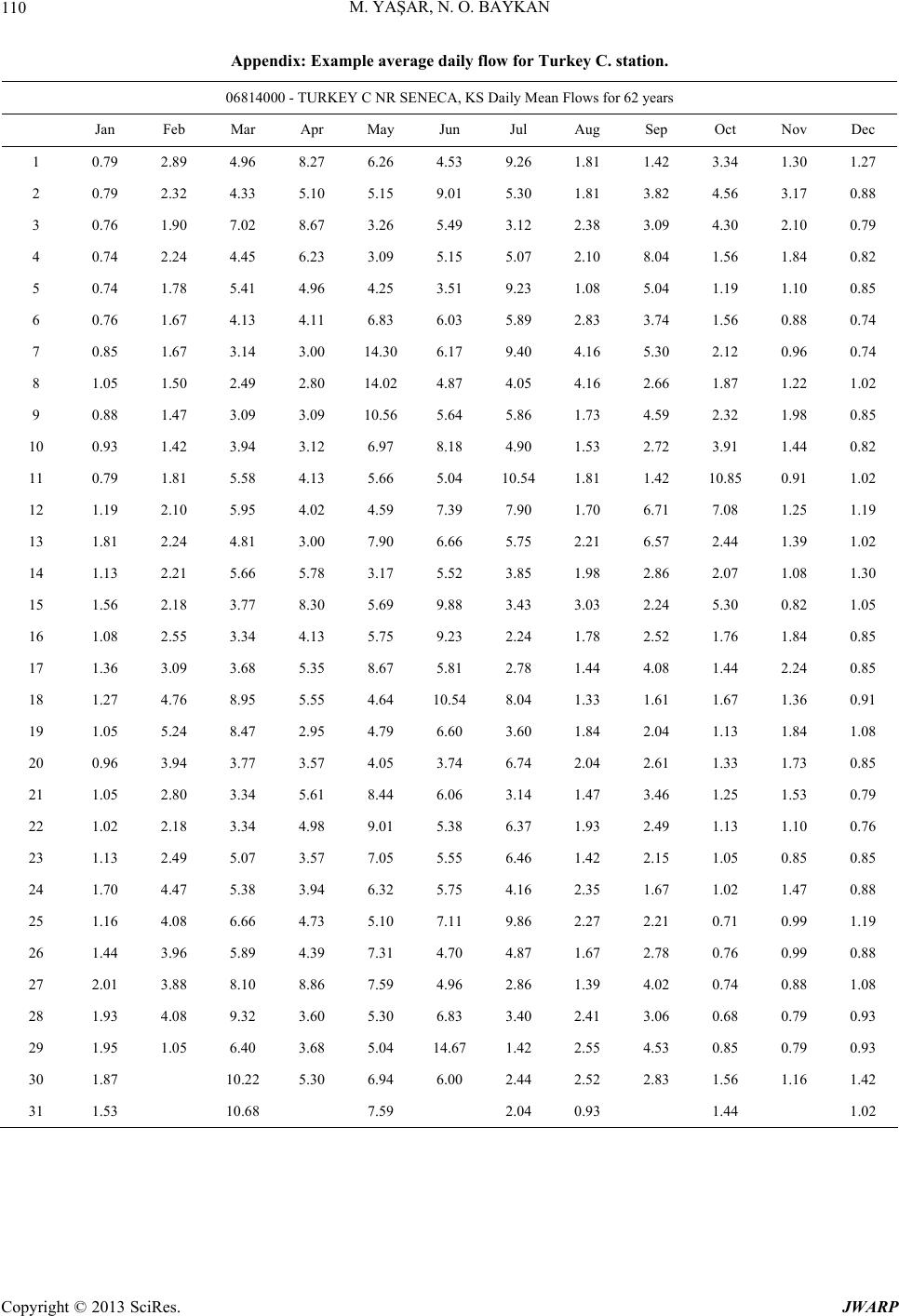

M. YAŞAR, N. O. BAYKAN 110
Appendix: Example average daily flow for Turkey C. station.
06814000 - TURKEY C NR SENECA, KS Daily Mean Flows for 62 years
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1 0.79 2.89 4.96 8.27 6.26 4.53 9.26 1.81 1.42 3.34 1.30 1.27
2 0.79 2.32 4.33 5.10 5.15 9.01 5.30 1.81 3.82 4.56 3.17 0.88
3 0.76 1.90 7.02 8.67 3.26 5.49 3.12 2.38 3.09 4.30 2.10 0.79
4 0.74 2.24 4.45 6.23 3.09 5.15 5.07 2.10 8.04 1.56 1.84 0.82
5 0.74 1.78 5.41 4.96 4.25 3.51 9.23 1.08 5.04 1.19 1.10 0.85
6 0.76 1.67 4.13 4.11 6.83 6.03 5.89 2.83 3.74 1.56 0.88 0.74
7 0.85 1.67 3.14 3.00 14.30 6.17 9.40 4.16 5.30 2.12 0.96 0.74
8 1.05 1.50 2.49 2.80 14.02 4.87 4.05 4.16 2.66 1.87 1.22 1.02
9 0.88 1.47 3.09 3.09 10.56 5.64 5.86 1.73 4.59 2.32 1.98 0.85
10 0.93 1.42 3.94 3.12 6.97 8.18 4.90 1.53 2.72 3.91 1.44 0.82
11 0.79 1.81 5.58 4.13 5.66 5.04 10.54 1.81 1.42 10.85 0.91 1.02
12 1.19 2.10 5.95 4.02 4.59 7.39 7.90 1.70 6.71 7.08 1.25 1.19
13 1.81 2.24 4.81 3.00 7.90 6.66 5.75 2.21 6.57 2.44 1.39 1.02
14 1.13 2.21 5.66 5.78 3.17 5.52 3.85 1.98 2.86 2.07 1.08 1.30
15 1.56 2.18 3.77 8.30 5.69 9.88 3.43 3.03 2.24 5.30 0.82 1.05
16 1.08 2.55 3.34 4.13 5.75 9.23 2.24 1.78 2.52 1.76 1.84 0.85
17 1.36 3.09 3.68 5.35 8.67 5.81 2.78 1.44 4.08 1.44 2.24 0.85
18 1.27 4.76 8.95 5.55 4.64 10.54 8.04 1.33 1.61 1.67 1.36 0.91
19 1.05 5.24 8.47 2.95 4.79 6.60 3.60 1.84 2.04 1.13 1.84 1.08
20 0.96 3.94 3.77 3.57 4.05 3.74 6.74 2.04 2.61 1.33 1.73 0.85
21 1.05 2.80 3.34 5.61 8.44 6.06 3.14 1.47 3.46 1.25 1.53 0.79
22 1.02 2.18 3.34 4.98 9.01 5.38 6.37 1.93 2.49 1.13 1.10 0.76
23 1.13 2.49 5.07 3.57 7.05 5.55 6.46 1.42 2.15 1.05 0.85 0.85
24 1.70 4.47 5.38 3.94 6.32 5.75 4.16 2.35 1.67 1.02 1.47 0.88
25 1.16 4.08 6.66 4.73 5.10 7.11 9.86 2.27 2.21 0.71 0.99 1.19
26 1.44 3.96 5.89 4.39 7.31 4.70 4.87 1.67 2.78 0.76 0.99 0.88
27 2.01 3.88 8.10 8.86 7.59 4.96 2.86 1.39 4.02 0.74 0.88 1.08
28 1.93 4.08 9.32 3.60 5.30 6.83 3.40 2.41 3.06 0.68 0.79 0.93
29 1.95 1.05 6.40 3.68 5.04 14.67 1.42 2.55 4.53 0.85 0.79 0.93
30 1.87 10.22 5.30 6.94 6.00 2.44 2.52 2.83 1.56 1.16 1.42
31 1.53 10.68 7.59 2.04 0.93 1.44 1.02