Graphene, 2013, 2, 18-34
http://dx.doi.org/10.4236/graphene.2013.21004 Published Online January 2013 (http://www.scirp.org/journal/graphene)
Force Field Based MM2 Molecule-Surface Binding
Energies for Graphite and Graphene
Jae H. Son, Thomas R. Rybolt*
Department of Chemistry, University of Tennessee at Chattanooga, Chattanooga, USA
Received November 11, 2012; revised December 12, 2012; accepted January 11, 2013
ABSTRACT
The gas phase adsorption of 118 organic molecules on graphite and graphene was studied by calculating their mole-
cule-surface binding energies, Ecal*, using molecular mechanics MM2 parameters. Due to the general lack of reported
experimental binding energy values for organic molecules with graphene, E*(graphene), it was considered desirable to
have a simple but effective method to estimate these values. Calculated binding energy values using a three-layer model,
Ecal*(3), were compared and correlated to published experimental values for graphitic surfaces, E*(graphite). Pub-
lished values of experimental binding energies for graphite, E*(graphite), were available from gas-solid chromatogram-
phy in the Henry’s Law region over a range of temperature. Calculated binding energy values using a one-layer model,
Ecal*(1), were compared to the three-layer Ecal*(3) values and found to consistently be 93.5% as large. This relation
along with an E*(graphite) and Ecal*(3) correlation was used to develop a means to estimate molecule-graphene bind-
ing energies. Using this approach we report estimated values of 118 molecule-graphene binding energy values.
Keywords: Molecule-Graphene Interaction; Molecule-Graphite Interaction; Molecular Mechanics; Adsorption Energy;
Binding Energy on Graphene; Binding Energy on Graphite
1. Introduction
Graphene is a now well-known single layer of carbons
arranged in a hexagonal configuration. Multiple layers of
graphene stacked upon each other and held together by
van der Waal forces form graphite. Graphene is of great
interest because of its many unique properties [1,2]. Gra-
phene is transparent, light, and an excellent conductor of
electricity and heat. Its transparency and electric conduc-
tivity are desirable properties for touch screen electronic
devices. Graphene’s thermal and electrical conductivity
outperform copper. At room temperature, copper has a
thermal conductivity of 401 Wm−1·K−1 while graphene’s
is 5000 Wm−1·K−1 [3]. The electrical conductivity of
copper is 0.60 × 106 Ω−1·cm−1 and graphene’s is 0.96 ×
106 Ω−1·cm−1 [3]. The breaking strength of graphene is
approximately 42 N/m and an equivalent thickness, steel
has a value of 0.40 N/m [3]. In addition to these striking
graphene properties, one promising application of this
unique two-dimensional material is as a molecular sen-
sor.
Graphene-based devices have been considered for
various electronic and optoelectronic devices as well as
gas sensors and biosensors [4]. A single layer of gra-
phene, bilayer of graphene, few-layers of graphene, or
modified graphene surface can act as a sensor when a
molecule adsorbs on the surface and changes the gra-
phene’s electric conductivity or other measureable prop-
erty. The change in conductivity or other property can
then be correlated with amount of molecules adsorbed
[5]. For example, the electrical conductivity of a gra-
phene fabricated device was observed to increase linearly
with an increase of carbon dioxide in the 10 to 100 ppm
range [6].
In order to exploit the potential applications of gra-
phene as gas sensors, the adsorption of a series of small
gas molecules on pristine graphene and Si-doped gra-
phene have been investigated by ab initio calculations [7].
Their theoretical results indicated that the electronic pro-
perties are sensitive to oxygen and nitrogen dioxide ad-
sorption, but not as much modified by the adsorption of
carbon monoxide and water [7]. The adsorption of inor-
ganic molecules including water, ammonia, carbon mo-
noxide, nitrogen dioxide, and nitrogen oxide on a gra-
phene substrate were considered using first-principles
calculations [8]. Graphene surfaces and variously modi-
fied graphene surfaces have been used to develop gas
sensor devices and successfully have been used to detect
ammonia [9], sulfur dioxide [10], nitrogen dioxide [11],
nitrogen dioxide and ammonia [12], carbon dioxide [6],
acetone [13], hydrogen sulfide [14], and hydrogen [15,
*Corresponding author.
C
opyright © 2013 SciRes. Graphene

J. H. SON, T. R. RYBOLT 19
16]. A variety of surface modifications have been ex-
plored and their detection effects examined [14-20].
Adsorption can be studied theoretically by calculating
the adsorption interaction energy (binding energy) of a
molecule on the surface. A molecule with higher binding
energy should have greater adsorption on the graphene
surface. For example, given the same amounts of two
different molecules in the gas phase (atmosphere sur-
rounding the graphene sensor surface, for example), the
ratio of the amounts of those two molecules physically
adsorbed on the surface would be different depending on
the relative binding energy. The molecule with the
stronger binding energy would be expected to be favored
in surface physisorption. Therefore, the study of binding
energy is important for developing sensors and correlat-
ing sensor responses to amounts physically adsorbed and
further correlating these amounts to the actual concentra-
tions in a complex mixed molecule environment around
the sensor.
It would be useful to be able to predict single layer
graphene binding energies for a variety of organic mole-
cules. There is a lack of gas phase experimental binding
energies for organic molecules on graphene. However,
there have been many experimental studies relating to
molecule adsorption on graphite. Using this molecule-
graphite binding energy data, our approach is to study the
relationship of calculated and experimental graphite ad-
sorption energies and also of calculated graphite and
calculated graphene binding energies. Assuming suitable
relations are found then it should be possible to calculate
molecule-surface binding energies on graphene or graph-
ite and then predict experimental binding energies of
molecules on graphene.
Previous studies showed that MM2 molecular mecha-
nics parameters for atom-carbon van der Waals (vdW)
interactions are suitable to effectively predict molecule-
carbon surface binding energies [21-25]. In these prior
studies of gas-solid interactions, the standard augmented
MM2 parameters developed by Allinger [26,27] were
used to estimate the binding energies of organic mole-
cules interacting with various model carbon surfaces [21-
25]. The adsorption of neutral molecules on a carbon
surface is dominated by dispersive van der Waals (vdW)
forces. In previous studies [21-25] molecule-surface ste-
ric energy differences for an adsorbate molecule adjacent
to or far from a model adsorbent surface were used to
estimate the energy due to adsorption, the binding energy.
Although force field calculations do not reference elec-
tronic behavior, they have been widely used for deter-
mining minimum energies and optimized molecular ge-
ometries [28].
2. Experimental Data
A review of the literature revealed a lack of experimental
organic molecule-graphene interaction energies. How-
ever, a significant number of organic molecule-graphite
interaction energies have been reported. These experi-
ments typically utilized either thermal programmed de-
sorption (TPD) or gas-solid chromatography (GSC). TPD
experiments usually give information about multilayer or
monolayer desorption and so molecule-molecule interac-
tions cannot be ignored [21]. However, many GSC deter-
minations involved finding the low coverage Henry’s
constants and so reflect the interaction of isolated mole-
cules with the carbon surface.
Sample gas corrected retention times can be converted
to a Henry’s law adsorption constant (KH). In various
published studies these Henry law constants were ob-
tained over a range of temperature values [29-42]. A plot
of the natural logarithm of KH versus the reciprocal of the
temperature (d ln KH/d/T) gives a plot whose slope is
E*/R where E* is the molecule-surface binding energy or
adsorption interaction energy and R is the gas constant. If
given as R = 0.001986 kcal·K−1·mol−1 then the slope
times R gives the E* value in kcal/mol. As E* increases
then it indicates stronger molecule surface interactions.
Published Studies using Graphitized Thermal Carbon
Black (GTCB) were selected as suitable graphitic ad-
sorbents. A total of 118 different organic molecules with
a variety of structures and functionality determined from
GSC on suitable graphitic surfaces were identified and
are reported in Table 1. Table 1 gives the assigned mo-
lecule number, molecule name, chemical formula, refer-
ence source for value, experimental value E*, and the
organic group to which the molecule is assigned. Experi-
mental binding energy data are reported in various units
but were converted to kcal/mol for all comparisons. The
experimental binding energies or physisorption interac-
tion energies are commonly reported in eV, meV, kJ/mol,
and Kelvin. The conversion factors used were based on
the relations 1 kcal/mol = 4.336411 × 10−2 eV = 43.36411
meV = 4.184 kJ/mol = 503.217 K.
3. Theory
The energy of a molecule calculated from molecular
mechanics, EMM, (augmented MM2 parameters were
used in this work) is a sum of covalent and noncovalent
energies. The MM2 covalent energy contributions in-
clude stretch, stretch-bend, angle, dihedral, improper
torsion; and the noncovalent energy contributions include
electrostatics, hydrogen-bonding, and van der Waals. The
van der Waals interaction energy, EvdW, is a parameter
that contributes to the noncovalent bond energy, and the
Van der Waals radius of atoms dominates the molecule-
graphite and molecule-graphene interactions. If two
nonbonded atoms are pushed too close together, they will
strongly repel from one other. If they are at a suitable
intermediate range, they will experience a mutual attrac-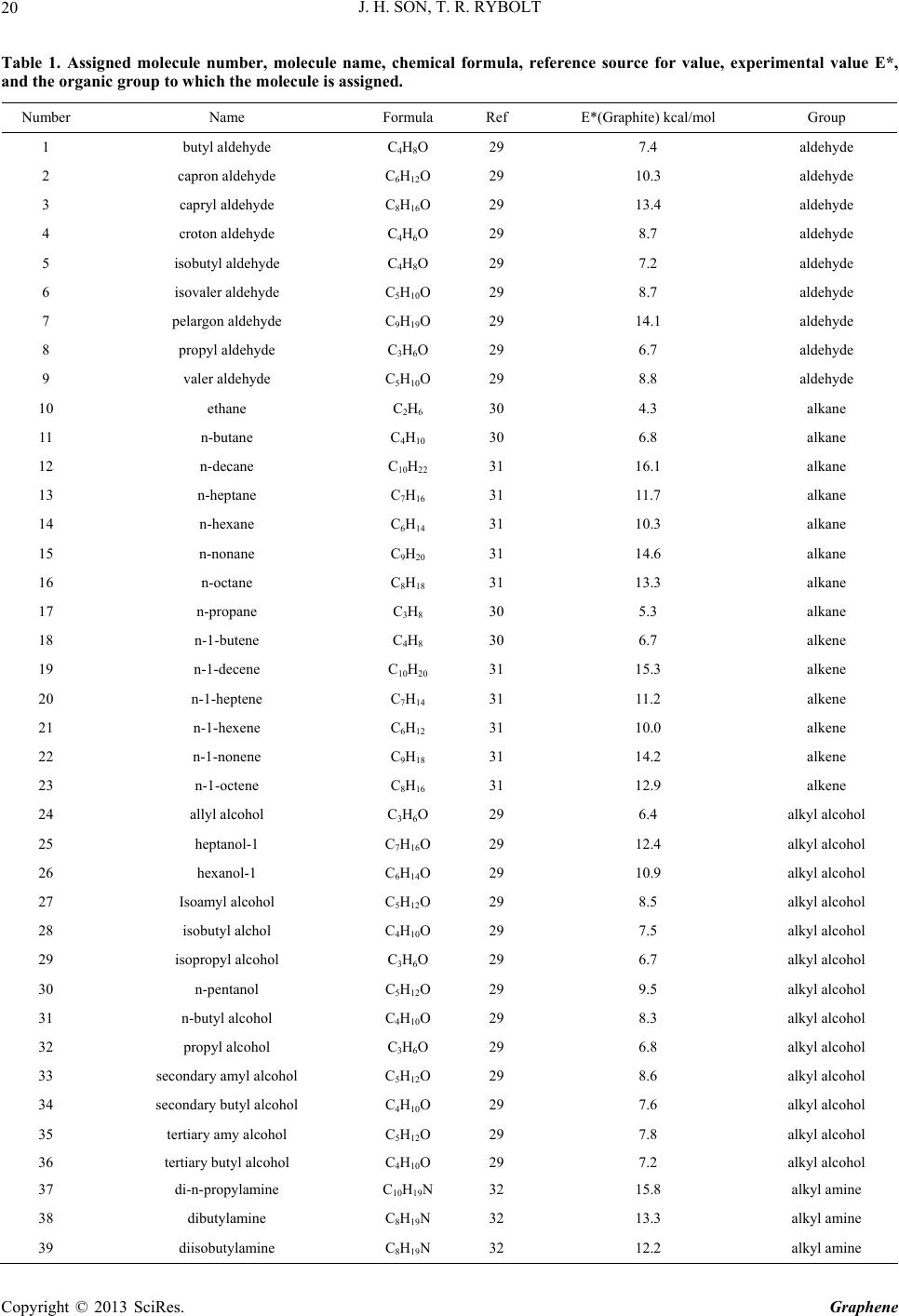

J. H. SON, T. R. RYBOLT 20
Table 1. Assigned molecule number, molecule name, chemical formula, reference source for value, experimental value E*,
and the organic group to which the molecule is assigned.
Number Name Formula Ref E*(Graphite) kcal/mol Group
1 butyl aldehyde C4H8O 29 7.4 aldehyde
2 capron aldehyde C6H12O 29 10.3 aldehyde
3 capryl aldehyde C8H16O 29 13.4 aldehyde
4 croton aldehyde C4H6O 29 8.7 aldehyde
5 isobutyl aldehyde C4H8O 29 7.2 aldehyde
6 isovaler aldehyde C5H10O 29 8.7 aldehyde
7 pelargon aldehyde C9H19O 29 14.1 aldehyde
8 propyl aldehyde C3H6O 29 6.7 aldehyde
9 valer aldehyde C5H10O 29 8.8 aldehyde
10 ethane C2H6 30 4.3 alkane
11 n-butane C4H10 30 6.8 alkane
12 n-decane C10H22 31 16.1 alkane
13 n-heptane C7H16 31 11.7 alkane
14 n-hexane C6H14 31 10.3 alkane
15 n-nonane C9H20 31 14.6 alkane
16 n-octane C8H18 31 13.3 alkane
17 n-propane C3H8 30 5.3 alkane
18 n-1-butene C4H8 30 6.7 alkene
19 n-1-decene C10H20 31 15.3 alkene
20 n-1-heptene C7H14 31 11.2 alkene
21 n-1-hexene C6H12 31 10.0 alkene
22 n-1-nonene C9H18 31 14.2 alkene
23 n-1-octene C8H16 31 12.9 alkene
24 allyl alcohol C3H6O 29 6.4 alkyl alcohol
25 heptanol-1 C7H16O 29 12.4 alkyl alcohol
26 hexanol-1 C6H14O 29 10.9 alkyl alcohol
27 Isoamyl alcohol C5H12O 29 8.5 alkyl alcohol
28 isobutyl alchol C4H10O 29 7.5 alkyl alcohol
29 isopropyl alcohol C3H6O 29 6.7 alkyl alcohol
30 n-pentanol C5H12O 29 9.5 alkyl alcohol
31 n-butyl alcohol C4H10O 29 8.3 alkyl alcohol
32 propyl alcohol C3H6O 29 6.8 alkyl alcohol
33 secondary amyl alcohol C5H12O 29 8.6 alkyl alcohol
34 secondary butyl alcohol C4H10O 29 7.6 alkyl alcohol
35 tertiary amy alcohol C5H12O 29 7.8 alkyl alcohol
36 tertiary butyl alcohol C4H10O 29 7.2 alkyl alcohol
37 di-n-propylamine C10H19N 32 15.8 alkyl amine
38 dibutylamine C8H19N 32 13.3 alkyl amine
39 diisobutylamine C8H19N 32 12.2 alkyl amine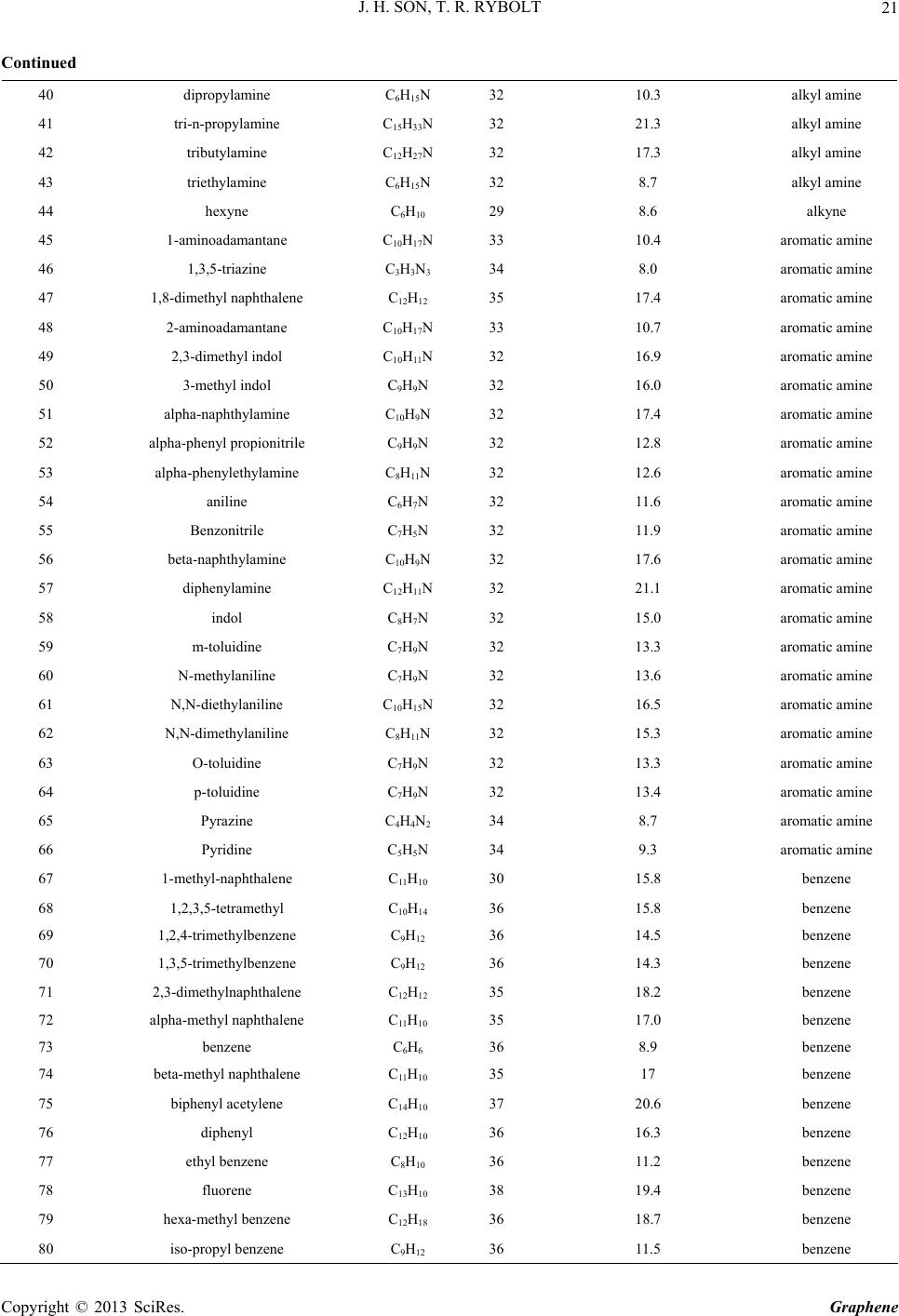

J. H. SON, T. R. RYBOLT 21
Continued
40 dipropylamine C6H15N 32 10.3 alkyl amine
41 tri-n-propylamine C15H33N 32 21.3 alkyl amine
42 tributylamine C12H27N 32 17.3 alkyl amine
43 triethylamine C6H15N 32 8.7 alkyl amine
44 hexyne C6H10 29 8.6 alkyne
45 1-aminoadamantane C10H17N 33 10.4 aromatic amine
46 1,3,5-triazine C3H3N3 34 8.0 aromatic amine
47 1,8-dimethyl naphthalene C12H12 35 17.4 aromatic amine
48 2-aminoadamantane C10H17N 33 10.7 aromatic amine
49 2,3-dimethyl indol C10H11N 32 16.9 aromatic amine
50 3-methyl indol C9H9N 32 16.0 aromatic amine
51 alpha-naphthylamine C10H9N 32 17.4 aromatic amine
52 alpha-phenyl propionitrile C9H9N 32 12.8 aromatic amine
53 alpha-phenylethylamine C8H11N 32 12.6 aromatic amine
54 aniline C6H7N 32 11.6 aromatic amine
55 Benzonitrile C7H5N 32 11.9 aromatic amine
56 beta-naphthylamine C10H9N 32 17.6 aromatic amine
57 diphenylamine C12H11N 32 21.1 aromatic amine
58 indol C8H7N 32 15.0 aromatic amine
59 m-toluidine C7H9N 32 13.3 aromatic amine
60 N-methylaniline C7H9N 32 13.6 aromatic amine
61 N,N-diethylaniline C10H15N 32 16.5 aromatic amine
62 N,N-dimethylaniline C8H11N 32 15.3 aromatic amine
63 O-toluidine C7H9N 32 13.3 aromatic amine
64 p-toluidine C7H9N 32 13.4 aromatic amine
65 Pyrazine C4H4N2 34 8.7 aromatic amine
66 Pyridine C5H5N 34 9.3 aromatic amine
67 1-methyl-naphthalene C11H10 30 15.8 benzene
68 1,2,3,5-tetramethyl C10H14 36 15.8 benzene
69 1,2,4-trimethylbenzene C9H12 36 14.5 benzene
70 1,3,5-trimethylbenzene C9H12 36 14.3 benzene
71 2,3-dimethylnaphthalene C12H12 35 18.2 benzene
72 alpha-methyl naphthalene C11H10 35 17.0 benzene
73 benzene C6H6 36 8.9 benzene
74 beta-methyl naphthalene C11H10 35 17 benzene
75 biphenyl acetylene C14H10 37 20.6 benzene
76 diphenyl C12H10 36 16.3 benzene
77 ethyl benzene C8H10 36 11.2 benzene
78 fluorene C13H10 38 19.4 benzene
79 hexa-methyl benzene C12H18 36 18.7 benzene
80 iso-propyl benzene C9H12 36 11.5 benzene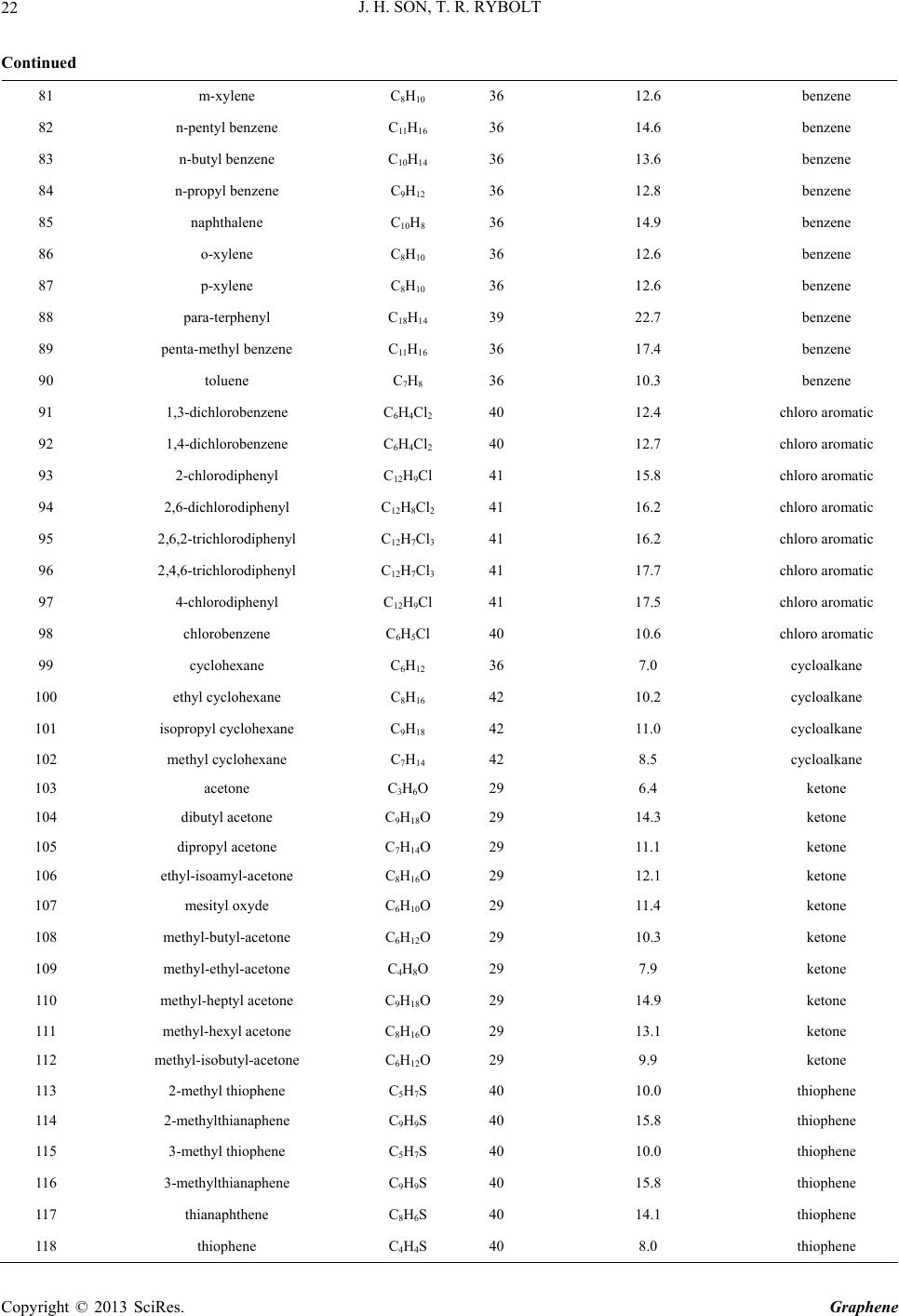

J. H. SON, T. R. RYBOLT 22
Continued
81 m-xylene C8H10 36 12.6 benzene
82 n-pentyl benzene C11H16 36 14.6 benzene
83 n-butyl benzene C10H14 36 13.6 benzene
84 n-propyl benzene C9H12 36 12.8 benzene
85 naphthalene C10H8 36 14.9 benzene
86 o-xylene C8H10 36 12.6 benzene
87 p-xylene C8H10 36 12.6 benzene
88 para-terphenyl C18H14 39 22.7 benzene
89 penta-methyl benzene C11H16 36 17.4 benzene
90 toluene C7H8 36 10.3 benzene
91 1,3-dichlorobenzene C6H4Cl2 40 12.4 chloro aromatic
92 1,4-dichlorobenzene C6H4Cl2 40 12.7 chloro aromatic
93 2-chlorodiphenyl C12H9Cl 41 15.8 chloro aromatic
94 2,6-dichlorodiphenyl C12H8Cl2 41 16.2 chloro aromatic
95 2,6,2-trichlorodiphenyl C12H7Cl3 41 16.2 chloro aromatic
96 2,4,6-trichlorodiphenyl C12H7Cl3 41 17.7 chloro aromatic
97 4-chlorodiphenyl C12H9Cl 41 17.5 chloro aromatic
98 chlorobenzene C6H5Cl 40 10.6 chloro aromatic
99 cyclohexane C6H12 36 7.0 cycloalkane
100 ethyl cyclohexane C8H16 42 10.2 cycloalkane
101 isopropyl cyclohexane C9H18 42 11.0 cycloalkane
102 methyl cyclohexane C7H14 42 8.5 cycloalkane
103 acetone C3H6O 29 6.4 ketone
104 dibutyl acetone C9H18O 29 14.3 ketone
105 dipropyl acetone C7H14O 29 11.1 ketone
106 ethyl-isoamyl-acetone C8H16O 29 12.1 ketone
107 mesityl oxyde C6H10O 29 11.4 ketone
108 methyl-butyl-acetone C6H12O 29 10.3 ketone
109 methyl-ethyl-acetone C4H8O 29 7.9 ketone
110 methyl-heptyl acetone C9H18O 29 14.9 ketone
111 methyl-hexyl acetone C8H16O 29 13.1 ketone
112 methyl-isobutyl-acetone C6H12O 29 9.9 ketone
113 2-methyl thiophene C5H7S 40 10.0 thiophene
114 2-methylthianaphene C9H9S 40 15.8 thiophene
115 3-methyl thiophene C5H7S 40 10.0 thiophene
116 3-methylthianaphene C9H9S 40 15.8 thiophene
117 thianaphthene C8H6S 40 14.1 thiophene
118 thiophene C4H4S 40 8.0 thiophene

J. H. SON, T. R. RYBOLT 23


tive. However, there is no interaction when the atoms are
a long distance from each other.
The calculated binding energy, Ecal*, can be deter-
mined from

mss m
EcalEE E* (1)
where Em is the energy of an isolated gas phase molecule,
Es is the energy of the isolated surface adsorbent material,
and Ems is the energy of the molecule and solid surface
system where the molecule is placed on the surface to
represent the adsorbed state [21]. Considering the equa-
tion above to represent the final minus the initial state,
the molecule has gone from being free in the gas phase to
being adsorbed on the surface. The energy of adsorption
is a negative energy value but the values are reported
here as absolute values and in kcal/mol since these units
are frequently used in molecular modeling. Desorption
energies would be positive values since an input of en-
ergy is required. The equation above is equivalent to
considering the energy difference, ∆E, as
near far
ΔE EE (2)
with respect to the energy of the molecule adsorbed on
the surface, Enear, and the energy of the separated and
non-interacting molecule and surface, Efar. Therefore
Ecal* = ∆E. To distinguish the experimental and calcu-
lated binding energies they are indicated as E* and Ecal*,
respectively.
The experimental binding energies on a single layer
graphene surface and many layer graphite surface are
reported as E*(graphene) and E*(graphite), respectively.
Molecular modeling values of a one layer graphene and a
three layer graphite surface are indicated as Ecal*(1) and
Ecal*(3), respectively. In prior work it has been shown
that a three graphene layer was adequate to represent
molecule-graphite interactions in molecular modeling
calculations [21]. More than 90% of the vdW interaction
is due to the first layer, less than 10% due to the second
layer and 1% or less due to the third layer in the MM2
parameters for molecule carbon surface interactions [21].
Our interest is in predicting E*(graphene) values for or-
ganic molecules. This work considers how E*(graphene),
E*(graphite), Ecal*(1), and Ecal*(3) are all intercom-
nected.
The relationship between the experimental E*(graphite)
and calculated Ecal*(3) can be expressed as

EgraphiteEcal 3*α* (3)
where α is the coefficient or equation multiplied by
Ecal*(3) to approximate E*(graphite). This equation as-
sumes either a simple linear relation with a fixed α or an
α based on an equation to provide a connection between
the experimental and model calculated values and as-
sumes a relation that scales to zero as the values decrease.
Such a relation was observed and various methods used
to generate the α term or equation are discussed subse-
quently.
The relationship between the calculated values for the
graphene one-layer and graphite three-layer model sur-
faces may be expressed as


Ecal 1Ecal3*β*

(4)
where β is the coefficient multiplied by Ecal*(3) to ap-
proximate Ecal*(1). This equation assumes a linear rela-
tion between the molecular modeling binding energies
calculated for our graphene one layer surface model and
our graphite three-layer surface model and a relation that
scales to zero as the values decrease. Such a relation was
observed between these calculated values and will be
discussed.
We further assume that the relationship between the
experimental E*(graphene) and calculated Ecal*(1) will
be analogous to Equation (3) and thus can be expressed
as


EgrapheneEcal 1*α*

. (5)
Based on the above equations, predictions of molecule-
graphene binding energies can be made by calculating
Ecal*(1) and using Equation (5) or instead by calculating
Ecal*(3) and using the relation below that results from
combining Equations (4) and (5) to give


EgrapheneEcal 3*αβ *

. (6)
Such an approach gives a means to reasonable estimate
binding energies on graphene provided Equations (3) and
(4) are found to be valid.
Prior work on flat, rough, and porous surfaces has in-
dicated that MM2 parameters may be used to calculate
molecule-surface binding energies that compare well to
experimental values obtained from gas-solid chromatog-
raphy (GSC) in the Henry’s Law region of low coverage
over a range of temperatures [22-25]. With a modified
model that took into account molecule-molecule nearest
neighbor interactions, monolayer coverage binding ener-
gies were obtained that compared well to values obtained
from thermal program desorption (TPD). For example
the published E* and our calculated Ecal* associated
with monolayer desorption from graphite were found to
be 0.50 and 0.52, 0.72 and 0.71, 1.41 and 1.47, and 2.18
and 1.86 eV for benzene, o-dichlorobenzene, coronene,
and ovalene, respectively [21].
Previously binding energies for DNA/RNA nucleo-
bases adsorbed on single layer graphene were calculated
[43]. These calculations using direct classical MM2 pa-
rameters without modification compared well to more
sophisticated quantum calculations. The molecular me-
chanics Ecal* values were observed to be between the
values from Moller-Plesset perturbation theory which

J. H. SON, T. R. RYBOLT 24
were reported to overestimate and the values from den-
sity functional theory (DFT) which were reported to un-
derestimate molecule-surface binding energies [43].
The goal of this work is to develop a simple and effec-
tive means to estimate molecule-surface binding energy
values for a variety of organic molecules adsorbed on
graphene by comparisons to known molecule-graphite
binding energy values.
4. Analysis and Results
Molecular mechanics MM2 calculations were performed
with Scigress computer software (Fujitsu, Version 7.7.0)
with the geometry optimized in mechanics using aug-
mented MM2 parameters. The graphene model surface
consisted of one layer of 702 benzene rings with no hy-
drogen atoms. The graphite model surface consisted of
three of these layers each containing 702 rings. The lay-
ers were oriented in the form of Bernal graphite with the
first layer and third layer directly aligned and the second
layer offset by half a benzene ring.
To simulate the adsorption of molecules with graphite
or graphene, molecules were oriented parallel to the sur-
face and adjusted to maximize the physical interaction of
molecules on the surface. The rules used for molecule
placement were that first, a carbon from a methyl group
of the molecule was placed above the middle of the cen-
ter benzene ring in the top layer. The carbon was placed
in the middle by making it equidistant from 3 alternating
carbon atoms in the ring. Second, if the molecule was a
cyclo or benzene containing molecules with no attached
alkyl groups attached, then some carbon in the ring was
selected and centered above the surface six member ring.
Third the molecule was further oriented so that the more
polarizable atoms were nearest the surface. The molecule
was then pushed in closer than an expected optimal
separation. With distances between the molecules and the
surfaces of approximately 0.23 - 0.27 nm, the molecules
were pushed out to the optimal distance after the mo-
lecular mechanics energy optimization calculation.
The 118 molecules listed in Tab le 1 were modeled and
optimized as isolated molecules in the gas phase to cal-
culate Em, and as described above, the molecules were
then placed on a graphite model surface to calculate the
Ems energy. For each molecule these two values were
used along with the Es energy for the graphite three-layer
model surface and Equation (1) to calculate Ecal*(3).
The model-based calculated values of Ecal*(3) for 118
molecules are given in Table 2 where they may be com-
pared to the experimental values found in Table 1. The
ratios of E*(Graphite)/Ecal*(3) were found to vary from
0.77 to 1.12 and these values also are given in Table 2.
A series of different approaches were examined to find
the best means of correlation between the E*(graphite)
and Ecal*(3) values. These approaches included (Method
I) direct correlation of all data, (Method II) correlations
of molecule subsets, (Method III) correlation of rigid and
flexible subgroups, and (Method IV) correlation based on
consideration of fraction of non-hydrogen atoms that are
sp3 carbon atoms.
In Method I values of E*(graphite) vs. Ecal*(3) were
plotted and a linear regression through the origin deter-
mined. A graph through the origin is desirable so that the
E*(graphite) and Ecal*(3) values scale to zero appropri-
ately. The resultant linear equation (see Figure 1) is


Egraphite09321 Ecal3*.

* (7)
with R2 = 0.8906 and n = 118.
In Method II comparison, the 118 molecules were di-
vided into 11 different functional groups that included
aldehyde, alkane, alkene/alkyne, alkyl alcohol, alkyl amine,
aromatic amine, benzene derivative, chlorobenzene, cyclo-
alkane, ketone, and thiophene. E*(graphite) data versus
Ecal*(3) data, were plotted for each of the 11 groups of
molecules. As mentioned previously, for appropriate
scaling all linear regressions were required to go through
the origin. Table 3 gives the number of data points, the
slope, and the R2 values for each group. The data points
available within a group varied from a low of 4 mole-
cules in the cycloalkane category to a high of 24 in the
benzene derivative category. As shown in Table 3, the
R2 values varied from a low of 0.8726 for cycloalkane (n
= 4) to a high of 0.9756 for alkene/alkyne (n = 7). The
slopes varied from a low of 0.8729 for alkane to 1.0312
for chloroaromatic. Recall that for the combined set of all
the molecules (n = 118) the R2 value was 0.8906. All the
subset groups have a higher R2 except for the cycloal-
kane at 0.8726.
Method III was based on the observation that the linear
regressions of aromatic amine, benzene derivative, chlo-
roaromatic, and thiophene have slopes of 1.0169, 0.9633,
1.0312, and 0.9936, respectively. This indicates that the
computed interaction energies, Ecal*(3) values that with-
out modification agreed well with the experimental val-
ues of E*(graphite). So if a molecule had a benzene or
other flat ring structure such as the thiophene, the mole-
cule was classified as “rigid.” Therefore the aromatic
amine, benzene derivative, chloroaromatic, and thiophene
groups were combined and considered together as the
rigid group. When all these data (n = 60) are plotted to-
gether, the correlating equation is


Egraphite09918 Ecal3*.

*
(8)
with (R2 = 0.9130).
As shown in Table 3, the data for the remaining
groups of molecules: aldehyde, alkane, alkene/alkyne,
alkyl alcohol, alkyl amine cycloalkane, and ketone had
slopes that varied from 0.8288 for alkyl amine to 0.9057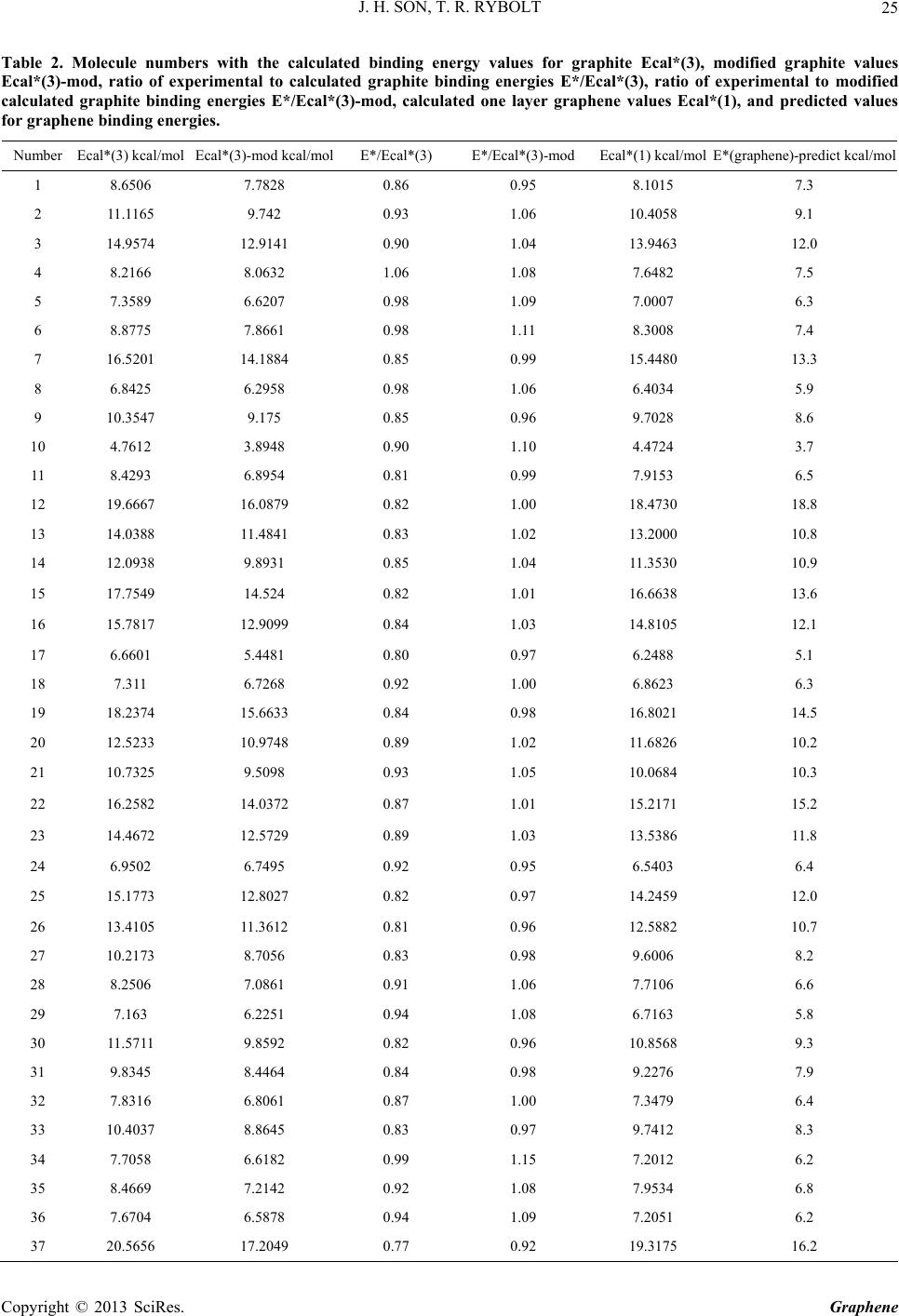

J. H. SON, T. R. RYBOLT 25
Table 2. Molecule numbers with the calculated binding energy values for graphite Ecal*(3), modified graphite values
(3)-mod kcal/mol E*/Ecal*(3) E*/Ecal*(3)-mod Ecal*(1) kcal/mol E*(graphene)-predict kcal/mol
Ecal*(3)-mod, ratio of experimental to calculated graphite binding energies E*/Ecal*(3), ratio of experimental to modified
calculated graphite binding energies E*/Ecal*(3)-mod, calculated one layer graphene values Ecal*(1), and predicted values
for graphene binding energies.
Number Ecal*(3) kcal/mol Ecal*
1 8.6506 7.7828 0.86 0.95 8.1015 7.3
2 11.1165 9.742 0.93 1.06 10.4058 9.1
3 14.9574 12.9141
1
1
0.90 1.04 13.9463 12.0
4 8.2166 8.0632 1.06 1.08 7.6482 7.5
5 7.3589 6.6207 0.98 1.09 7.0007 6.3
6 8.8775 7.8661 0.98 1.11 8.3008 7.4
7 16.5201 14.1884 0.85 0.99 15.4480 13.3
8 6.8425 6.2958 0.98 1.06 6.4034 5.9
9 10.3547 9.175 0.85 0.96 9.7028 8.6
10 4.7612 3.8948 0.90 1.10 4.4724 3.7
11 8.4293 6.8954 0.81 0.99 7.9153 6.5
12 19.6667 16.0879 0.82 1.00 18.4730 18.8
13 14.0388 11.4841 0.83 1.02 13.2000 10.8
14 12.0938 9.8931 0.85 1.04 11.3530 10.9
15 17.7549 14.524 0.82 1.01 16.6638 13.6
16 15.7817 12.9099 0.84 1.03 14.8105 12.1
17 6.6601 5.4481 0.80 0.97 6.2488 5.1
18 7.311 6.7268 0.92 1.00 6.8623 6.3
19 8.237415.6633 0.84 0.98 16.8021 14.5
20 12.5233 10.9748 0.89 1.02 11.6826 10.2
21 10.7325 9.5098 0.93 1.05 10.0684 10.3
22 16.2582 14.0372 0.87 1.01 15.2171 15.2
23 14.4672 12.5729 0.89 1.03 13.5386 11.8
24 6.9502 6.7495 0.92 0.95 6.5403 6.4
25 15.1773 12.8027 0.82 0.97 14.2459 12.0
26 13.4105 11.3612 0.81 0.96 12.5882 10.7
27 10.2173 8.7056 0.83 0.98 9.6006 8.2
28 8.2506 7.0861 0.91 1.06 7.7106 6.6
29 7.163 6.2251 0.94 1.08 6.7163 5.8
30 1.5711 9.8592 0.82 0.96 10.8568 9.3
31 9.8345 8.4464 0.84 0.98 9.2276 7.9
32 7.8316 6.8061 0.87 1.00 7.3479 6.4
33 10.4037 8.8645 0.83 0.97 9.7412 8.3
34 7.7058 6.6182 0.99 1.15 7.2012 6.2
35 8.4669 7.2142 0.92 1.08 7.9534 6.8
36 7.6704 6.5878 0.94 1.09 7.2051 6.2
37 20.5656 17.2049 0.77 0.92 19.3175 16.2

J. H. SON, T. R. RYBOLT 26
Continued
16.9265 14.2303 0.79 0.93 15.8909 14.9 38
39 13.8254 11.6231 0.88 1.05 12.9545 12.3
40 13.1701 11.1576 0.78 0.92 12.3575 11.9
41 24.9434 20.7226 0.85 1.03 23.4343 19.5
42 19.6055 16.3457 0.88 1.06 18.4211 15.1
43 10.54 8.9294 0.83 0.97 9.8632 8.1
44 1
1
1
77 12.1126 11.7629 0.92 0.95 11.2379 10.5
0.40359.2183 0.83 0.93 9.7249 8.6
45 9.9188 8.2979 1.05 1.25 9.3384 7.8
46 7.7967 7.9695 1.03 1.00 7.2819 7.4
47 18.0297 17.8159 0.97 0.98 16.8329 16.6
48 10.1525 8.4934 1.05 1.26 9.5514 8.0
49 17.4376 17.1769 0.97 0.98 16.2713 16.0
50 15.5252 15.5524 1.03 1.03 14.4886 14.5
51 17.3498 17.7343 1.00 0.98 16.1790 16.5
52 12.354 12.1234 1.04 1.06 11.4931 11.3
53 11.2788 11.0171 1.12 1.14 10.2624 9.1
54 12.2977 12.5703 0.94 0.92 11.4819 11.7
55 10.8717 11.1127 1.09 1.07 10.0317 8.9
56 17.3573 17.4199 1.01 1.01 16.2012 16.3
57 19.2333 19.6596 1.10 1.07 17.8932 18.3
58 13.6384 13.9407 1.10 1.08 12.7200 13.0
59 14.3381 14.29 0.93 0.93 13.4207 13.4
60 13.4991 3.45381.01 1.01 12.5911 12.5
61 15.4251 14.6219 1.07 1.13 14.4485 14.7
62 14.6248 14.2855 1.05 1.07 13.6487 13.3
63 14.2315 14.1838 0.93 0.94 13.2930 13.2
64 14.4434 14.395 0.93 0.93 13.4916 13.4
65 8.3784 8.5641 1.04 1.02 7.8201 8.0
66 8.9317 9.1297 1.04 1.02 8.3523 8.5
67 16.3601 16.4191 0.97 0.96 15.2564 15.3
68 16.9358 15.9283 0.93 0.99 15.8278 13.4
69 17.0702 16.287 0.85 0.89 16.1040 16.3
70 15.5725 14.858 0.92 0.96 14.5969 13.6
71 18.2023 17.9864 1.00 1.01 16.9797 14.4
72 16.2701 16.3288 1.04 1.04 15.1739 13.1
73 9.576 9.7882 0.93 0.91 8.8834 9.1
74 6.682916.7431 1.02 1.02 15.5687 15.6
75 19.6911 20.1275 1.05 1.02 18.3850 15.4
76 15.4355 15.7776 1.06 1.03 14.3828 14.4

J. H. SON, T. R. RYBOLT 27
Continued
78 18.2586 18.3766 1.06 1.06 17.0269 17.1
79 20.2064 18.5918 0.93 1.01 18.9263 17.4
1
118 8.5846 8.7749 0.93 0.91 7.9981 8.2
80 11.4603 10.9345 1.00 1.05 10.6949 10.2
81 13.6196 13.2264 0.93 0.95 12.7310 13.0
82 17.5189 16.2816 0.83 0.90 16.3308 15.2
83 15.5873 14.66 0.87 0.93 14.5106 13.9
84 13.8437 13.2085 0.92 0.97 12.8623 10.9
85 14.6034 4.92711.02 1.00 13.6477 14.0
86 13.1729 12.7926 0.96 0.98 12.2962 10.5
87 13.5546 13.1633 0.93 0.96 12.6671 12.3
88 22.6612 23.1635 1.00 0.98 21.1151 21.6
89 18.2592 16.9696 0.95 1.03 17.1053 15.9
90 11.5674 11.4864 0.89 0.90 10.8043 10.7
91 12.9318 13.2184 0.96 0.94 12.0376 12.3
92 12.8689 13.1541 0.99 0.97 11.9701 12.2
93 14.8622 15.1916 1.06 1.04 13.8765 14.2
94 15.2383 15.576 1.06 1.04 14.3751 14.7
95 15.4103 15.7518 1.05 1.03 14.4006 13.7
96 16.3088 16.6703 1.09 1.06 15.2360 15.6
97 17.1266 17.5062 1.02 1.00 15.9001 15.4
98 11.2641 11.5138 0.94 0.92 10.4851 10.0
99 8.7455 7.1541 0.80 0.98 8.2032 6.7
100 11.8776 9.7162 0.86 1.05 11.1466 9.1
101 11.8508 9.6943 0.93 1.13 11.1610 9.1
102 10.5161 8.6025 0.81 0.99 9.8764 8.4
103 7.0548 6.4911 0.91 0.99 6.6022 6.1
104 17.7988 15.2866 0.80 0.94 16.6893 14.3
105 14.0043 12.1706 0.79 0.91 13.1325 11.4
106 14.6858 12.6796 0.82 0.95 13.8034 11.9
107 12.0338 11.2477 0.95 1.01 11.2562 9.3
108 12.4057 10.8718 0.83 0.95 11.6537 10.2
109 8.7048 7.8315 0.91 1.01 8.1405 7.3
110 17.9867 15.448 0.83 0.96 16.8834 16.8
111 16.1562 13.9491 0.81 0.94 15.1430 13.1
112 11.1266 9.7508 0.89 1.02 10.4099 10.7
113 10.7257 10.5985 0.93 0.94 9.9975 9.9
114 15.7348 15.7623 1.00 1.00 14.6754 14.7
115 10.604 10.4782 0.94 0.95 9.8864 9.8
116 15.4225 15.4495 1.02 1.02 14.3652 14.7
117 13.65 13.9525 1.03 1.01 12.7079 12.4

J. H. SON, T. R. RYBOLT 28
Figure 1. Experimental organic molecule-graphitic surface
binding energies versus three layer calculated binding en-
ergies for 118 adsorbate molecules gave a linear regression
of E*(graphite) = 0.9321 Ecal*(3) with (R2 = 0.8906).
ry. R2
Table 3. Number of data points, the slope, and the R2 values
for each group. The data points available within a group
varied from a low of 4 molecules in the cycloalkane cate-
ory to a high of 24 in the benzene derivative categog
values varied from a low of 0.8726 for cycloalkane to a high
of 0.9756 for alkene/alkyne. The slopes varied from a low of
0.8729 for alkane to 1.0312 for chloroaromatic.
Parameters
Functional Group
Slope R2
n
aldehyde 0.9057 0.9308 9
alkane 0.8291
alkene/alkyne 0.6 7
al
ale
ar
c
0.9971 8
0.8751 975
lkyl alcoho0.8564 0.9043 13
kyl amin0.8288 0.96 7
ketone 0.8362 0.9421 10
cycloalkane 0.8581 0.8726 4
omatic amine1.0169 0.9394 22
benzene 0.9633 0.8971 24
hloroaromatic 1.0312 0.9257 8
thiophene 0.9936 0.9728 6
for alere grtogetwhat won-
sidere catehble mo
lacked g structuhe me and had
otentially more conformational flexibility. The average
Whiese R2 val0.9130 for rigid and
0.9621e flexible es are better the R2 of
0.8906 for all the molecule together, a still better correla-
tion is ed to be abively usel*(3) val-
(graphite). From the considerations
above, it is clear that the calculated values
for the “flexible” structures since as shown i
must be multiplied by on average
0.
olecule category was
do
arized as
dehyde and w
d as the “flexible”
ouped
gory. T
her in
e flexi
e c
lecules
a flat rinre in toleculso
p
of the slopes in Table 3 for these seven groups was
0.8556 with a 0.0280 standard deviation. When all these
“flexible” data (n = 58) are plotted together, the correlat-
ing equation is
 
E*graphite0 8500 Ecal*3. (9)
with (R2 = 0.9621).
ues to predict E*
le thues of the
for thmolecul than
needle to effect Eca
are too high
n Figure 2
the Ecal*(3) values
85 to bring their values down to agreement with the
E*(graphite) experimental values. However, there is
more variation within individual molecules than simply
placing into these two groups.
To reconcile the differences observed for the “rigid”
and “flexible” molecules and to have one common equa-
tion and one correlation for all the molecules, a different
approach was needed. We observed that the MM2 vdW
parameters for the sp3 carbon atoms were overestimating
their carbon surface interactions and hence could be cor-
related only by using about 85% of their estimated bind-
ing energy values. The flexible m
minated by tetrahedral bonded carbons which we label
below as C-sp3 atoms. However, the trigonal planar sp2
carbons dominated the so called rigid molecules had
MM2 vdW parameters that matched well with the ex-
perimental interaction energies and hence had slopes
close to one. In examining the individual molecules we
were able to observe variations depending on the number
of C-sp3 atoms and C-sp2 and other atoms. These obser-
vations led to the next approach.
In Method IV for every molecule all non-hydrogen
atoms were counted and placed into one of two catego-
ries. The atom was either a sp3 hybridized carbon or not.
The non sp3 carbon atoms included sp2 trigonal planar
bonding carbon atoms, sp linear bonding carbon atoms,
and all other atoms such as oxygen, nitrogen, sulfur. All
hydrogen atoms were excluded from the counting proc-
ess. So the relations may be summ
Figure 2. Experimental organic molecule-graphitic surface
binding energies versus three layer calculated binding en-
ergies for rigid (n = 60) and flexible (n = 58) adsorbate
molecules gave linear regressions of E*(graphite) = 0.9918
Ecal*(3) with R2 = 0.9130 and E*(graphite) = 0.8500
Ecal*(3) with R2 = 0.9621, respectively.

J. H. SON, T. R. RYBOLT 29
totalC-sp3 other
nn n (10)
C-sp3C-sp3 total
fnn (11)
(12)
(13)
where ntotal is the total number of nonhydrogen atoms,
nC-sp3 is the number of sp3 carbon atoms, nother is the
number of all other nonhydrogen and non sp3 carbon
atoms, fC-sp3-c is the fraction of sp3 carbon atoms, and fother
totalotherothern/nf 
C-sp3 other
1f f
is the fraction of all other nonhydrogen atoms.
Using the above relations then the Equation (3) may be
written as




C-sp3 C-sp3otherother
E*graphitec fc f Ecal*3 (14)
c and care the best fit coefficients
C-sp3 other
the fraction of sp3 carbon atoms and
non-hydrogen atoms, respectively. T
tion (3) is now represented as α = (cC-sp3 f
C-sp3 + cother
fother). The cC-sp3 and cother were derive
regression calculation using E*(g
values in Table 1 along with fC-sp3
tion for α
in
are indicated as Ecal*(3)-modified. For ex-
ample, consider the molecule 1,2,3,5-tetrameth
zene that consist of 4 sp3 carbon atoms and 6 sp2 c
(15)
di
graphene, the second and third layers
were removed from molecules already placed on the
graphite model using the procedure previously des
The Ems was recalculated for each molecule after MM
optim
3.5% of the calculated value on graphite.
Th
multiplied by
fraction of other
he α term in Equa-
d from multilinear
raphite) and Ecal*(3)
and fother values for
each of the 118 molecules. The best fit coefficients for
csp3-C was found to be 0.8180 and for cother was found to
be 1.0221.
The originally calculated Ecal*(3) for each of the 118
molecules could then be modified by the equa
Equation (14) and are given in Table 2. These modi-
fied values
ylben-
arbon
atoms. The fractions are fC-sp3 = 0.4000 and fother = 0.6000.
Using the best fit values of the fractions csp3-C gives
[(0.8180) (0.4000) + (1.0221) (0.6000)] 16.9358 kcal/
mol = [0.9405] [16.9358] = 15.9274 or 15.9 kcal/mol.
Clearly 15.9 is much better estimate of the reported ex-
perimental binding energy of 15.8 kcal/mol.
Figure 3 shows a plot of E*(Graphite) versus Ecal*(3)-
modified where

Ecal* 3 -modified
 
C-sp3 other
08180 f1 0221 f Ecal*3..
The linear regression for E*(graphite) versus Ecal*(3)-
modified (n = 118) gave a slope of 1.0000 and (R2 =
0.9647). While still using the standard MM2 parameters
this approach provides a fairly simple modification that
provides reasonable estimates of E*(graphite). A com-
parison of Figures 1 and 3 shows a change of R2 from
0.8906 to 0.9647 indicating a significant improvement in
the correlation.
Next, it was necessary to determine values of Ecal*(1).
A molecule must have same placement and orientation
for accurate comparison. The only part that should be
fferent was the number of layers for the surface. To
convert graphite to
cribed.
2
ization and then used with Em values and an
Es(graphene) calculated value to find Ecal*(1) using
Equation (1). The average ratio of Ecal*(1)/Ecal*(3) for
the 118 molecules gave an average and standard devia-
tion of 0.9350 ± 0.004. Figure 4 shows a plot of Ecal*(1)
versus Ecal*(3) and the slope based on a linear regres-
sion was 0.9349 with (R2 = 0.9998). The results indicated
the calculated binding energy of a molecule on graphene
is consistently 9
us, the β from Equation (4) is determined to be 0.935
and may the relation may be expressed as


Ecal10 935 Ecal3*. * (16)
Figure 3. Experimental organic molecule-graphitic surface
binding energies versus modified three layer calculated
binding energies for 118 adsorbate molecule
regression of E*(graphite) = 1.0000 Ecal*(
=118) with (R2 = 0.9647).
s gave a linear
3)-modified (n
Figure 4. Plot of Ecal*(1) modeling binding energy on gra-
phene versus Ecal*(3) modeling binding energies on graph-
ite for 118 organic adsorbate molecules gave a linear re-
gression with a slope of 0.9349 and (R2 = 0.9998).

J. H. SON, T. R. RYBOLT 30
So we propose that using MM2 parameters for a
molecule in optimized geometry and then placed on a
three layer graphite surface can give a reasonable esti-
mate of the graphene binding energy using our Equation
(6) expressed after combining Equations (14) and (15) to
give


(17)
Or more directly if a molecule is placed on a single
layer model graphene surface, a reasonable estimate of
the expected molecule-graphene interaction or binding
energy is obtained from
the above as α = (cC-sp3 fC-sp3 + cother fother).
5. Discussion
Th
physical adsorption. Larger
more polarizable atoms tend to increase vdW forces
crease the binding energy. For example, comparing
cules M91 1,3-dichlorobenzene and M73 benzene, one
ob
rface. Since our focus was
t energy for a molecule adsorbed on a
ives an average of 0.93 and a
0.
nd Ecal*(3) with the Ecal*(1) values being
93
h.
other nonhydrogen atoms have values that are on average


C-sp3other
E* graphene
0 93508180 f1 0221 f Ecal*3.. .





C-sp3other
E* graphene
0 8180 f1 0221 fEcal*1..



(18)
It is assumed that the graphite correction also can be
applied to graphene. This assumption is reasonable con-
sidering a single carbon layer accounts for 93.5% of the
MM2 graphite binding energies for the 118 molecules
considered. The cCsp3 and cother above are taken directly
from Equation (15). The α in Equation (3) is now repre-
sented from
e binding energy of an adsorbate molecule on an ad-
sorbent surface can be affected by molecule size, mole-
cule orientation, and the nature of surface. For organic
molecules adsorbed on graphitic surfaces, van der Waals
forces tend to dominate the
in-
mole-
serves E* values of 12.4 and 8.9 kcal/mol, respectively.
More atoms in a molecule increases the vdW forces. For
example, comparing molecules M12 decane and M11
butane, one observes E* values of 16.1 and 6.8 kcal/mol,
respectively. Different orientations of the molecule and
different conformations can also affect the binding en-
ergy. Orientations of molecules were selected to have the
maximum contact with the su
to find the lowes
surface, we chose the most polarizable atom facing the
surface as previously described because the vdW is
stronger with more polarizable atoms near the surface
and a flat orientation to put as much of the molecule on
the surface as possible.
The approach illustrated in Table 3 was to divide the
experimental values into one of nine subgroups based on
the molecular structure of the adsorbate. With the excep-
tion of the cycloalkane group that only had four mole-
cules and R2 = 0.8726, all the remaining R2 values were
better than the set of all 118 molecules with R2 = 0.8906.
The R2 for the eight other groups ranged from 0.8971 up
to 0.9971. However it was desirable to have one general
equation that would allow calculation of Ecal* for what-
ever molecule was selected without regard to functional
group.
As shown in Table 2, our coefficients and the equation
do not make our Ecal* values match with E* exactly.
However, our modification provides a reasonable ap-
proach to interpret the over-calculated values for the at-
oms with sp3 hybridizations and improves the match of
calculated and experimental values. Using the values of
the E*/Ecal*(3) ratios g
09 standard deviation. Using the values of the E*/
Ecal*(3)-modified ratios gives an average of 1.01 and
0.07 standard deviation. This modification was necessary
to successfully predict the binding energy. Figure 1
shows the E* versus Ecal* plots somewhat scattered with
R2 of 0.8906 and a slope of 0.9321. However, Figure 3
shows E* versus Ecal*(3)-modified with a slope of 1.0000
and R2 of 0.9647. So Equation (15) provides an effective
method to estimate E*(graphite) by modifying computed
values of Ecal*(3). There is a regular relation between
Ecal*(1) a
.5% of the Ecal*(3) values as shown in Figure 4 and
in Table 2.
Our initial adjustment for the scatter in Figure 1 was
to place molecules in categories of rigid (ring containing)
or flexible (no ring) as illustrated in Table 3 based on the
slopes that were near one for aromatic amine, benzene
derivatives, chloroaromatic, and thiophene groups but
clearly less than one for the remaining seven groups.
While this division into two categories led to improved
correlation coefficients with R2 equal to 0.9621 and
0.9130 for the flexible and rigid, respectively the cause
of this difference was based on the overestimate of vdW
forces between the surface carbon atoms and sp3 carbon
atoms. For instance, Table 2 shows the ratio of E*
(graphite)/Ecal*(3) is 0.87 for n-butyl benzene (M83) but
for naphthalene (M85) this ratio is 1.02 meaning the cal-
culated and experimental are in close agreement. Both
molecules have same number of carbons but the Ecal* is
about 15% too large due to the calculated vdW energy
being too hig
Since this overestimation occurs in a regular pattern
we were able to adjust the Ecal* simply based on the
fraction of nonhydrogen atoms that were sp3 carbon at-
oms. This adjustment was accomplished by Equation (15)
where the fraction of sp3 carbons is multiplied by 0.8180
Ecal* to give its E* contribution to E* and the fraction of
all other nonhydrogen atoms is multiplied by 1.0221
Ecal* to give its contribution to E*. We see that on av-
erage sp3 carbons have a value that is too high and all

J. H. SON, T. R. RYBOLT 31
slightly low.
To test the application of our approach a molecule not
in the original set of 118 molecules was selected for es-
timation of E*(graphite) and E*(graphene). C. Thier-
felder et al. reported calculated binding energies of me-
thane on graphene with five different methods [44]. They
used a reported experimental value of methane on graph-
ite in the range of 0.12 - 0.14 eV. They also made an
assumption that the binding energy of methane on gra-
ph
6.
orrec-
mers and found
ns with small basis sets tended to
rs. By allowing these errors to offset
n adsorption due to dis-
pe
t of 118 organic molecules
us
ene should be about 0.01 eV less than on graphite so
their estimated binding energy value for methane on gra-
phite was E*(graphite) = 0.12 to 0.14 eV and on gra-
phene they estimated E*(graphene) = 0.11 to 0.13 eV.
Our estimated energy for Ecal*(3) for methane was 3.40
kcal/mol and Ecal*(3)-modified was 2.8 kcal/mol (0.12
eV) and the predicted Ecal*(graphite) was 2.6 kcal/mol
(0.11 eV). So our estimated binding energies of
E*(graphite) = 0.12 eV and E*(graphene) = 0.11 eV
agree with well their suggested values.
Conclusions
The weakness of noncovalent vdW interactions presents
a general challenge for more exact quantum mechanical
methods and density functional theory (DFT) calcula-
tions as indicated by a comparison of 40 density func-
tionals with noncovalent interaction energies [45,46].
DFT results have been reported to underestimate vdW
interactions [47]. However, Moller-Plesset perturbation
theory (MP2) has been reported to overestimate the
binding energies [48]. The basis set used to model a
molecule and a dimer cluster (benzene-coronene for ex-
ample) can greatly affect the interaction energy. This er-
ror is known as the basis set superposition error (BSSE).
For benzene-coronene quantum calculations where coro-
nene can be used to represent a graphene surface the
MP2 results had to be modified by a counterpoise c
tion of about 40% [48]. Tauer and Sherrill examined π-π
interactions for benzene dimers and trim
that MP2 calculatio
have cancelling erro
each other they were able to find interaction energies
close, few tenths of kcal/mol, of a complete basis set
couple cluster CCSD(T) limit [49]. Because of these
computational challenges, for ease of use, for representa-
tions of larger surface areas or multiple molecules, and
for simpler and quicker calculations it can be useful to
make estimates based on molecular mechanics and the
approach outlined in this work.
We used augmented MM2 parameters and classical
molecular modeling to predict molecule-graphene bind-
ing energies of 118 organic molecules. Our results sug-
gest that this method can provide useful estimates of ex-
perimental values that may otherwise be difficult to ob-
tain. In prior work MM2 parameters and molecular me-
chanics calculations have been used to estimate molecule
surface interaction energies on flat, rough, and porous
carbon surfaces [22-25,43].
The calculated binding energies for a molecule on the
single layer graphene model were consistently found to
be 93.5% of the value for the same molecule on the
three-layer graphite model. This is in agreement with
prior work for nucleobases on graphene and graphite that
showed going from 1 to 3 layers increased binding en-
ergy by 8% to 10% [43]. The MM2 calculations for these
binding energies are dominated by vdW forces and these
have been observed to give reasonable correlations when
a standard 0.9 nm cutoff value was used. One implication
for future sensor devices based o
rsive forces on bilayer graphene is that the interaction
energy for a bilayer should be very close, within a few
percent, to the value for graphite.
Although the MM2 parameters were not optimized for
adsorption energy calculations, the values obtained for
vdW dominated adsorption on carbon give good correla-
tions with experimental. It was observed that calculated
Ecal* values had to be corrected to better agree with the
experimental E* for the se
ed. The calculated binding energy was corrected with
simple modification using coefficients that reduced the
energy contribution from all sp3 carbon atoms by multi-
ply the fraction of these atoms by 0.818 and the remain-
ing carbon and heteroatoms (hydrogen atoms were not
included in determining these fractions) were almost un-
changed being multiplied by 1.022, respectively.
The direct MM2 results gave the ratio of E*/Ecal*(3)
as 0.93 (n = 118) with a standard deviation of 0.09. The
modified MM2 results gave the ratio of E*/Ecal*(3)-mod
as 1.01 (n = 118) with a standard deviation of 0.07. So
the direct MM2 model based binding energies were on
average larger than the experimental values by about
7.5% (1/0.93 = 1.075), but after the modification de-
scribed previously and given in Equation (15), the aver-
age of all 118 values was within about one percent. Most
calculated values were within 7% of the corresponding
experimental ones (see Table 2). The slope of E* versus
Ecal*(3)-mod was 1.00 with R2 = 0.965 as shown in Fig-
ure 3.
The modification of the Ecal*(3) calculated values
should apply to the graphene also so the Ecal*(3)-mod
could be multiplied by 0.935 as shown in Equation (16)
to find E*(graphene). Or more directly Ecal*(1) can be
converted to E*(gaphene) using Equation (17). In other
words, a molecule’s interaction energy can be calculated
on a three layer model or a one layer model and effec-
tively converted to a reasonable estimate of the expected
experimental interaction energy on single layer graphene
surface, E*(graphene). Using our data set correlations
and extending it to a molecule not included in the origin-

J. H. SON, T. R. RYBOLT 32
nal set of 118 allowed us to test this method. Binding
energies of 0.12 and 0.11 eV were obtained for methane
and these compared well to published experimental and
estimated values for graphite and graphene, respectively.
Simpler non quantum mechanical calculations based
on classical molecular mechanics continue to be of use to
estimate molecule-surface binding energies based on
weaker dispersion forces. This molecular mechanics ap-
proach does not provide any electronic details but i
us
t is a
eful, computationally simple approach to study mole-
cule interactions on carbon surfaces and should be help-
ful to predict how strongly various molecules may be
held on future single layer graphene or bilayer graphene
sensor detection devices. This approach may also be
useful to predict interactions in other possible applica-
tions such as surface self assembly, molecular separa-
tions, or graphene-molecule storage and delivery devices.
7. Acknowledgements
We gratefully acknowledge the support provided by the
Grote Chemistry Fund and the Wheeler Odor Research
Center at the University of Tennessee at Chattanooga.
REFERENCES
[1] S. W. Pati, T. Enoki and C. N. Rao, “Graphene and Its
Fascinating Attributes,” World Scientific, Singapore, 2011.
[2] W. Choi and J. Lee, “Graphene: Synthesis and Applica-
tions,” CRC Press, Boca Raton, 2012.
[3] Royal Swedish Academy of Sciences, “Scientific Back-
ground on the Nobel Prize in Physics 2010 GRAPH-
ENE,” 2010.
http://www.nobelprize.org/nobel_prizes/physics/laureates
/2010/advancedphysicsprize2010.pdf
[4] P. T. Araujo, M. Terrones and M. S. Dresselhaus, “De-
fects and Impurities in Graphene-Like Materials,” Mate-
rials Today, Vol. 15, No. 3, 2012, pp. 98-109.
doi:10.1016/S1369-7021(12)70045-7
[5] W. Choi, I. Lahiri, R. Seel
thesis of Graphene and Its
aboyina and Y. S. Kang, “Syn-
Applications: A Review,” Cri-
tical Reviews in Solid State Materials Sciences, Vol. 35,
No. 1, 2010, pp. 52-71.
doi:10.1080/10408430903505036
[6] H. J. Yoon, D. H. Jun, J. H. Yang, Z. Zhou, S. S. Yang
and M. M.-C. C
Graphene Shetors B: Chemical
hen, “Carbon Dioxide Gas Sensor Using a
et,” Sensors and Actua,
Vol. 157, No. 1, 2011, pp. 310-313.
doi:10.1016/j.snb.2011.03.035
[7] Y. Zou, F. Li, Z. H. Zhu, M. W. Zhao, X. G. Xu and X. Y.
Su, “An ab Initio Study on Gas Sensing Properties of
Graphene and Si-Doped Graphene,” European Physical
Journal B, Vol. 81, No. 4, 2011, pp. 475-479.
doi:10.1140/epjb/e2011-20225-8
[8] O. Leenaerts, B. Partoens and F. M. Peeters, “Adsorption
of H2O, NH3, CO, NO2, and NO on Graphene: A First-
Principles Study,” Physical Review B
2008, Article ID: 125416.
doi:0.1103/PhysRevB.77.125416
[9] M. Gautam and A. H. Jayatissa, “Adsorption K
Ammonia Sensing by Graphene Film
inetics of
s Decorated with
Platinum Nanoparticles,” Journal of Applied Physics, Vol.
111, No. 9, 2012, Article ID: 094317.
doi:10.1063/1.4714552
[10] Y. Ren, C. Zhu, W. Cai, H. Li, H. Ji, I. Kholmanov, Y.
Wu, R. D. Piner and R. S. Ruoff, “Detection of Sulfur
Dioxide Gas with Graphene Field Effect Transistor,” Ap-
plied Physics Letters, Vol. 100, No. 16, 2012, Article ID:
163114. doi:10.1063/1.4704803
[11] M. G. Chung, D. H. Kim, H. M. Lee,
D. K. Seo, J.-B. Yoo, S.-H. Ho
T. Kim, J. H. Choi,
ng, T. J. Kang and Y. H.
Kim, “Highly Sensitive NO2 Gas Sensor Based on Ozone
Treated Graphene,” Sensors and Actuators B: Chemical,
Vol. 166-167, 2012, pp. 172-176.
doi:10.1016/j.snb.2012.02.036
[12] S. Mao, S. Cui, G. Lu, K. Yu, Z. Wen and J. Chen, “Tun-
ing Gas-Sensing Properties of Reduced Graphene Oxide
Using Tin Oxide Nanocrystals,” Journal of Materials
Chemistry, Vol. 22, 2012, pp. 11009-11013.
doi:10.1039/c2jm30378g
[13] H. Zhang, A. Kulkarni, H. Kim, D. Woo, Y.-J. Kim, B. H.
Hong, J.-B. Choi and T. Kim, “Detection of Acetone Va-
por Using Graphene on Polymer Optical Fiber,” Journal
of Nanoscience and Nanotechnology, Vol. 11, No. 7, 2011,
pp. 5939-5943. doi:10.1166/jnn.2011.4408
, J. S. Chung, E. W. Shin, D. H. [14] T. V. Cuong, V. H. Pham
Yoo, S. H. Hahn, J. S. Huh, G. H. Rue, E. J. Kim, S. H.
Hur and P. A. Kohl, “Solution-Processes ZnO-Chemically
Converted Graphene Gas Sensor,” Materials Letters, Vol.
64, No. 22, 2010, pp. 2479-2482.
doi:10.1016/j.matlet.2010.08.027
[15] J. L. Johnson, A. Behnam, S. J. Pearton and A. Ural,
“Hydrogen Sensing Using Pd-Functionalized Multi-Layer
Graphene Nanoribbon Networks,” Advanced Materials,
Vol. 22, No. 43, 2010, pp. 4877-4880.
doi:10.1002/adma.201001798
[16] W. Wu, Z. Liu, L. A. Jauregui, Q. Yu, R. Pillai, H. Cao, J.
70
Bao, Y. P. Chen and S.-S. Pei, “Wafer-Scale Synthesis of
Graphene by Chemical Vapor Deposition and Its Appli-
cation in Hydrogen Sensing,” Sensors and Actuators B:
Chemical, Vol. 150, No. 1, 2010, pp. 296-300.
doi:0.1016/j.snb.2010.06.0
[17] H. Song, L. Zhang, C. He, Y. Qu, Y. Tian and Y. Lv,
“Graphene Sheets Decorated with SnO2 NanoParticles: In
Situ Synthesis and Highly Efficient Materials for Catalu-
minescence Gas Sensors,” Journal of Materials Chemis-
try, Vol. 21, No. 16, 2011, pp. 5972-5977.
doi:10.1039/c0jm04331a
[18] A. Shimizu and K. Fujii, “Thin Film Gas Sensor,” Japan
Kokai Tokyo Koho, 2011, JP 2011169634 A 20110901.
[19] G. Lu, S. Park, K. Yu, R. S. Ruoff, L. E. Ocola, D. Ro-
senmann and J. Chen, “Toward P
with Highly Reduced Graphene
ractical Gas Sensing
Oxide: A New Signal
Processing Method to Circumvent Run-to-Run and De-
vice-to-Device Variations,” ACS Nano, Vol. 5, No. 2,
2011, pp. 1154-1164. doi:10.1021/nn102803q
, Vol. 77, No. 12,

J. H. SON, T. R. RYBOLT 33
[20] G. Lu, L. E. Ocola and J. Chen, “Gas De
Low-Temperature Reduced Gra
tection Using
phene Oxide Sheets,” Ap-
plied Physics Letters, Vol. 94, No. 8, 2009, Article ID:
083111. doi:10.1063/1.3086896
[21] T. R. Rybolt, C. E. Wells, C. R. Sisson, C. B. Black and
K. A. Ziegler, “Evaluation of Molecular Mechanics Cal-
culated Binding Energies for Isolated and Mono
ganic Molecules on Graphite
layer Or-
,” Journal of Colloid and
Interface Science, Vol. 314, No. 2, 2007, pp. 434-445.
doi:10.1016/j.jcis.2007.05.083
[22] T. R. Rybolt, K. A. Ziegler, H. E. Thomas, J. L. Boyd and
M. E. Ridgeway, “Adsorption Energies for a Nanoporous
Carbon from Gas-Solid Chromatography an
Mechanics,” Journal of C
d Molecular
olloid and Interface Science ,
Vol. 296, No. 1, 2006, pp. 41-50.
doi:10.1016/j.jcis.2005.08.057
[23] T. R. Rybolt and R. A. Hansel, “Determining Molecule-
Carbon Surface Adsorption Energies Using Molecular
Mechanics and Graphene Nanostructures,” Journal of
Colloid and Interface Science, Vol. 300, No. 2, 2006, pp.
805-808. doi:10.1016/j.jcis.2006.04.057
[24] T. R. Rybolt, C. E. Wells, H. E. Thomas, C. M. Goodwin,
J. L. Blakely and J. D. Turner, “Binding Energies for Al-
kane Molecules on a Carbon Surface from Gas-Solid
Chromatography and Molecular Mechanics,” Journal of
Colloid and Interface Science, Vol. 325, No. 1, 2008, pp.
282-286. doi:10.1016/j.jcis.2008.06.043
[25] T. R. Rybolt, K. T. Bivona, H. E. Thomas and C. M.
O’Dell, “Comparison of Gas-Solid Chromatography and
MM2 Force Field Molecular Binding Energies for Green-
house Gases on a Carbonaceous Surface,” Journal of Col-
loid and Interface Science, Vol. 338, No. 1, 2009, pp. 287-
292. doi:10.1016/j.jcis.2009.06.001
[26] N. L. Allinger, “Conformational Analysis. 130. MM2. A
Hydrocarbon Force Field Utilizing V1 and V2 Torsional
Terms,” Journal of the American Chemical Society, Vol.
99, No. 25, 1977, pp. 8127-8134.
doi:10.1021/ja00467a001
[27] J. Lii and N. L. Allinger, “Molecular Mechanics. The
MM3 Force Field for Hydrocarbons. 3. The van der
Waals’ Potentials and Crystal Data for Aliphatic and Aro-
matic Hydrocarbons,” Journal of the American Chemical
Society, Vol. 111, No. 23, 1989, pp. 8576-8582.
doi:10.1021/ja00205a003
[28] F. Jensen, “Introduction to Computational Chemistry,”
John Wiley & Sons, Chichester, 1999.
[29] E. V. Kalashnikova, A. V. Kiselev, A. M. Makogon and
K. D. Shcherbakova, “Adsorption of Molecules of Dif-
ferent Structure on Graphitized Thermal Carbon Black IV.
Gas Chromatographic Investigation of Adsorption of Al-
dehydes, Ketones and Alcohols on Hydrogen-Treated
Graphitized Thermal Carbon Black,” Chromatographia,
Vol. 8, No. 8, 1975, pp. 399-403.
doi:10.1007/BF02269088
[30] C. Vidal-Madjar, M. F. Gonnord and G. Guiochon, “Mo-
)90306-9
lecular Statistical Theory of Adsorption Prediction of the
Thermodynamical Functions of Adsorption of Hydrocar-
bons on Graphitized Thermal Carbon Black,” Journal of
Colloid and Interface Science, Vol. 52, No. 1, 1975, pp.
102-119. doi:10.1016/0021-9797(75
, A. E. Pilt, S. A. Rang and K. [31] O. G. Eisen, A. V. Kiselev
D. Shcherbakova, “Gas Chromatographic Investigation of
Adsorption of Normal Alkenes C6 - C10 on Graphitized
Thermal Carbon Black,” Chromatographia, Vol. 4, No.
10, 1971, pp. 448-454. doi:10.1007/BF02268813
[32] A. V. Kiselev, E. B. Polotnyuk and K. D. Shcher
“Gas Chromatographic Stu
bakova,
dy of Adsorption of Nitrogen-
. 14, No. 8, 1981,
Containing Organic Compounds on Graphitized Thermal
Carbon Black,” Chromatographia, Vol
pp. 478-483. doi:10.1007/BF02263538
[33] S. N. Yashkin, O. B. Grior’eva and A. K. Buryak, “Ex-
perimental and Molecular-Statistical Investigation of Ad-
sorption of Aminoadamantanes on Graphitized Thermal
Carbon Black,” Russian Chemical Bulletin, Vol. 50, No.
6, 2001, pp. 980-985. doi:10.1023/A:1011348730899
[34] S. N. Yashkin, D. A. Svetlov and
modynamic Characteristic
A. K. Buryak, “Ther-
s of Adsorption of Nitrogen-
Containing Heterocycles on Graphitized Thermal Carbon
Black Derived from Molecular Statistical Calculation. 1.
Azines,” Russian Chemical Bulletin, Vol. 52, No. 2, 2003,
pp. 344-353. doi:10.1023/A:1023446513475
[35] E. G. Bychkova, E. V. Kalashnikova, A. V. Kiselev and
K. D. Shcherbakova, “Thermodynamic Characteristics of
, K. D.
12, No. 12, 1979,
Adsorption of the Naphthalene-Type Hydrocarbons on
the Graphitized Thermal Carbon Black,” Vestnik Mosk-
ovskogo Universiteta, Seriya 2: Khimiya, Vol. 27, No. 4,
1986, pp. 382-385.
[36] E. V. Kalashnikova, A. V. Kiselev, R. S. Petrova
Shcherbakova and D. P. Poshkus, “Chromatographic Meas-
urements and Molecular Statistical Calculations of Ther-
modynamic Characteristics of Adsorption of Aromatic
and Polycyclic Hydrocarbons on Graphitized Thermal
Carbon Black,” Chromatographia, Vol.
pp. 799-802. doi:10.1007/BF02260661
[37] E. V. Kalashnikova, A. V. Kiselev and K. D. Shcherba-
kova, “Retention of Some Phenyl-Substituted and Bicy-
clic Hydrocarbons on Graphitized Carbon Black,” Chro-
matographia, Vol. 17, No. 10, 1983, pp. 521-525.
doi:10.1007/BF02261913
[38] A. V. Kiselev, V. I. Nazarova and K. D. Shcherbakova,
“Molecular Structure and Retention Behaviour of Some
Polycyclic Aromatic and Perhydroaromatic Hydrocarbons
on Graphitized Carbon Black,” Chromatographia, Vol.
18, No. 4, 1984, pp. 183-189. doi:10.1007/BF02276730
[39] E. V. Kalashnikova, A. V. Kiselev, K. D. Shcherbakova
and S. D. Vasileva, “Retention of Diphenyls, Terphenyls,
Phenylalkanes and Fluorene on Graphitized Thermal Car-
bon Black,” Chromatographia, Vol.14, No. 9, 1981, pp.
510-514. doi:10.1007/BF02265630
[40] A. K. Buryak, P. B. Dallakyan and A. V. Kiselev, “De-
. Kiselev, “Corre-
lation between the Structure of Chlorinated Biphenyls and
termination of Atom-Atom Potentials of Intermolecular
Interaction and Calculation of the Thermodynamic Char-
acteristics of Adsorption on Graphite of Sulfur- and
Chlorine-Containing Organic Compounds,” Doklady Aka-
demii Nauk SSSR Physical Chemistry, Vol. 282, No.
2,1985, pp. 350-353.
[41] A. K. Buryak, A. N. Fedotov and A. V

J. H. SON, T. R. RYBOLT 34
. S
and A. L. Shilov, “Gas
Their Adsorption on Graphitized Thermal Carbon Black,”
Vestnik Moskovskogo Universiteta, Seriya 2: Khimiya, Vol.
26, No. 6, 1985, pp. 568-571.
[42] W. Engewald, E. V. Kalashnikova, A. V. Kiselev, R
Petrova, K. D. Shcherbakova
.
Chromatographic Investigation of the Adsorption of Po-
lymethylcyclohexanes on Graphitized Thermal Carbon
Black,” Journal of Chromatography A, Vol. 152, No. 2,
1978, pp. 453-466. doi:10.1016/S0021-9673(00)85082-7
[43] T. R. Rybolt and C. E. Wells, “Molecule-Surface Binding
Energies from Molecular Mechanics: Nucleobases on
Graphene,” In: H. E. Chan, Ed., Graphene and Graphite
Materials, Nova Science Publishers, New York, 2009, pp.
95-112.
[44] C. Thierfelder, M. Witte, S. Blankenburg, E. Rauls and W.
G. Schmidt, “Methane Adsorption on Graphene from First
Principles Including Dispersion Interaction,” Surface Sci-
ence, Vol. 605, No. 7-8, 2011, pp. 746-749.
doi:10.1016/j.susc.2011.01.012
[45] O. Engkvist, P. Astrand and G. Karlstrom, “Accurate
Intermolecular Potentials Obtained from Molecular Wave
Functions: Bridging the Gap between Quantum Chemis-
try and Molecular Simulations,” Chemical Reviews, Vol.
100, No. 11, 2000, pp. 4087-4108.
doi:10.1021/cr9900477
[46] Y. Zhao and D. G. Truhlar, “Density Functionals for
Noncovalent Interaction Energies of Biological Impor-
tance,” Journal of Chemical Theory and Computation,
Vol. 3, No. 1, 2007, pp. 289-300.
doi:10.1021/ct6002719
[47] R. Zacharia, H. Ulbricht and T. Hertel, “Interlayer Cohe-
sive Energy of Graphite from Thermal Desorption of Po-
lyaromatic Hydrocarbons,” Physical Review B, Vol. 69,
No. 15, 2004, Article ID: 155406.
doi:10.1103/PhysRevB.69.155406
[48] H. Ruuska and T. A. Pakkanen, “Ab
layer Interaction of Grap
Initio Study of Inter-
hite: Benzene-Coronene and Co-
ronene Dimer Two-layer Models,” Journal of Physical
Chemistry B, Vol. 105, No. 39, 2001, pp. 9541-9547.
doi:10.1021/jp011512i
[49] T. P. Tauer and C. D. Sherrill, “Bey
mer: An Investigation
ond the Benzene Di-
of the Additivity of π-π Interac-
tions,” Journal of Physical Chemistry A, Vol. 109, No. 46,
2005, pp. 10475-10478. doi:10.1021/jp0553479