Graphene, 2013, 2, 13-17
http://dx.doi.org/10.4236/graphene.2013.21003 Published Online January 2013 (http://www.scirp.org/journal/graphene)
Flexible Graphene Devices with an Embedded Back-Gate
Jasper van Veen, Andres Castellanos-Gomez*, Herre S. J. van der Zant, Gary A. Steele*
Kavli Institute of Nanoscience, Delft University of Technology, Delft, The Netherlands
Received November 8, 2012; revised December 11, 2012; accepted January 9, 2013
ABSTRACT
We show the fabrication of flexible graphene devices with an embedded back-gate. The resistance of these devices can
be tuned by changing the strain through the bending of the substrate. These devices can be useful for applications re-
quiring a flexible graphene-based field effect transistor in where the graphene channel is not covered (such as biological
or chemical sensors and photo-detectors).
Keywords: Graphene Device; Flexible Electronics; Back-Gate; Strain Engineering
1. Introduction
Graphene is a two-dimensional material made of carbon
atoms arranged in a honeycomb lattice [1]. Since its iso-
lation by mechanical exfoliation, a great number of ex-
perimental and theoretical works have been carried out to
deeply study this novel material. Due to this effort a lot
of interesting properties and applications have been dis-
covered [2], such as the experimental observation of the
quantum Hall effect even at room temperature [3] and the
possibility to use graphene as a sensor of individual
molecules [4]. Additionally, due to its ambipolar field
effect graphene can be used as the channel material for a
Field Effect Transistor (FET) [5]. Graphene FETs could
have small channel lengths and high mobilities of the
charge carriers. These properties make graphene FETs
advantageous for high-speed applications [6-8].
Together with its electronic properties, graphene also
show exceptional mechanical properties that make this
material very promising for flexible electronic applica-
tions [9-12]. Flexible graphene-based devices will allow
one to modify the electronic properties of the device by
simply bending it [13-15].
A similar strategy, referred as strain engineering has
been successfully employed to modify the electronic pro-
perties of traditional semiconducting materials. In con-
ventional strain engineering, however, the amount of
strain is fixed and it is controlled by epitaxially growing
a certain semiconductor on top of an acceptor substrate
which has a different lattice parameter [16]. It could be
an advantage to be able to have control over the amount
of strain and therewith the electronic properties of a ma-
terial.
However, most of fabricated flexible graphene-devices
lack of a gate electrode which limits its usefulness [17,
18]. In fact, flexible graphene FETs with a local top gate
has been recently reported [19,20] and flexible devices
with a back-gate have not been reported yet. A flexible
back-gated graphene FET could be advantageous in
many applications requiring the graphene surface to be
uncovered such as graphene based chemical sensors or
graphene based photo-detectors.
In this paper we present a method to fabricate gra-
phene flexible FETs with an embedded back-gate. Subse-
quently, basic measurements of the strain dependent
electronic properties of graphene are presented.
2. Sample Fabrication
2.1. Flexible Substrates
The flexible graphene devices are fabricated onto a
commercial 500 µm thick polyimide substrate (Cirlex®).
Prior to the fabrication, the substrates have been polished
with Brasso® polishing solution to reduce the roughness
as much as possible. After that, two fabrication steps are
followed. In the first step a 100 nm thick layer of alumi-
num, which will be used as the back-gate, is evaporated
using electron beam evaporation. A shadow mask can be
used to pattern the back-gate in a strip geometry. In the
second step, a ~5 µm layer of polyimide is spin coated
and cured in vacuum to act as a dielectric layer between
the gate and the graphene. Figure 1 shows a schematic
representation cross-section of the final flexible sub-
strates.
2.2. Graphene Transfer
After the preparation of the flexible substrate with the
embedded gate, graphene is transfer to the substrate sur-
face. This process is schematically depicted in Figure 2
*Corresponding authors.
C
opyright © 2013 SciRes. Graphene

J. VAN VEEN ET AL. 14
Figure 1. Cross-section of the flexible substrate. Also, the
positions of the graphene and the source and drain elec-
trodes are shown. Polyimide is used as the bulk material of
the flexible substrate because of its mechanical properties.
The 100 nm thick Aluminium layer acts as the back-gate of
the FET. The upper layer of polyimide acts as dielectric
between the gate and the graphene.
Figure 2. The transfer of the graphene to the flexible sub-
strate. Panel (a) shows graphene op top of a 30 μm thick
layer of copper. Panel (b) depicts the ensemble after the
PMMA is spin-coated on top of the graphene and the layer
of PDMS is thereafter placed on top of the PMMA. In panel
(c) the copper layer has been dissolved in a solution of fer-
ric-chloride in milli-Q water with a concentration of 1.0 g/L.
Panel (d) shows the process where the ensemble is stamped
on the flexible substrate. In panel (e) the PDMS is slowly
removed from the PMMA. Finally, panel (f) shows the re-
sult of the transfer process. The PMMA has been dissolved
in acetone. Thereafter, the sample has been heated to a
temperature of 150˚C to increase the sticking of the gra-
phene to the flexible substrate.
and it is described in detail in the literature [21]. Briefly,
the transfer process starts with a layer of graphene grown
by Chemical Vapor Deposition (CVD) on top of a copper
foil, see Figure 2(a). A polymethyl metracrylate (PMMA)
layer of 200 nm - 300 nm is spin coated on top of the
graphene and baked at 140˚C for 4 minutes. Thereafter, a
thick layer of polydimethylsiloxane (PDMS) is placed on
top of the PMMA, see Figure 2(b). This facilitates the
handling and transfer of the graphene layer to the sub-
strate. The next step is to remove the copper by etching it
in a solution of ferric-chloride in milli-Q water with a
concentration of 1.0 g/L, see Figure 2(c). Subsequently,
the ensemble is transferred to the flexible substrate. The
graphene is stamped on the desirable location of the sub-
strate, see Figure 2(d). Then, the PDMS is slowly pulled
of the PMMA, see Figure 2(e). It is important that this
step is executed slowly because otherwise the PMMA/
graphene ensemble would remain attach to the PDMS
layer. After this step, the PMMA is dissolved in acetone,
see Figure 2(f). Finally, the sample is placed on a hot
plate at a temperature of 150˚C to remove the traces of
acetone and to increase the sticking of the graphene to
the substrate.
After the transfer process two electrodes, a source and
a drain, are attached to the graphene using silver paint,
see Figure 1.
3. Device Characterization
Right after the device fabrication, we perform a rough
electrical characterization to check that the back-gate is
continuous, the graphene layer is electrically connected
and there is no leakage from the drain-source electrodes
to the back-gate. The electrodes (source, drain and gates)
are shown in Figures 3(a) and (b). The resistance be-
tween G1 and G2 was in the order of R ~ 0 - 50 Ω, which
indicates that the back-gate electrode is continuous. The
source-drain resistance was in the order of R ~ 200 - 500
kΩ. This is a typical resistance for a large area CVD gra-
phene sample. Finally, the drain-gate and the source-
gate resistances where measured giving an open circuit
(R > 10 GΩ). This indicates that there are no pinholes in
the dielectric layer.
The second characterization is done with Atomic
Force Microscopy (AFM). Figure 3(c) shows an AFM
image of the device. The image was obtained from the
region that is indicated with a red box in Figure 3(a).
The AFM image shows that the transferred CVD gra-
phene used in our devices presents some folds and cracks
and also continuous pieces of graphene. From the meas-
urement of the drain-source resistance we know that
there is a continuous path between drain and source elec-
trodes. However, the presence of folded and the cracked
regions may have an influence on the electronic proper-
ties of the device.
4. Experimental Setup
We have further studied the piezoresponse of the flexible
graphene-devices, that is the change in the resistance
with an externally applied strain. The strain is applied by
bending the device. With a simple mechanical model the
applied strain can be related to the radius of curvature of
the device. The mechanical model assumes that the ra-
dius of curvature due to bending the device is larger than
the thickness of the device. Also, the dominant deforma-
tion of the beam should be in the longitudinal direction.
This means that shear stresses and stresses normal to the
neutral axis are negligible. Both these conditions were
met in the performed expeiments. Based on these as r

J. VAN VEEN ET AL. 15
Figure 3. Top view and AFM image of the graphene-based FET. In panel (a) a schematic top view of the graphene FET is
shown. The source S, the drain D and the two electrodes of the continuous back-gate are indicated. The red dashed rectangle
indicates the region where the AFM image is obtained. Panel (b) shows a photograph of the device before the electrodes were
attached. The positions where the electrodes must be placed are shown with red dashed rectangles. Not surprisingly, the
atomically thick graphene is not visible in the photograph. Its position is indicated with a blue rectangle. Panel (c) shows a
AFM image of the device obtained from the region indicated with a red box in panel (a).
where “h” is the substrate thickness and “

” is the cur-
vature radius.
Figure 4 shows photographs of the device taken dur-
ing a measurement at different strain levels. By fitting
the photographs one can extract the radii of curvature and
thus to estimate the applied strain.
5. Experimental Results
Figure 5(a) shows the resistance of graphene plotted
against the applied strain at different gate voltages. From
the figure it appears that for small strains there is a linear
dependence between the resistance and strain. Also, from
measurement at zero gate voltage this behavior was ob-
served to be reversible over different strain apply/release/
apply cycles. More precisely, the slope dR/dε was roughly
constant for the different cycles. For larger strains we
have found that the silver paint electrodes tend to de-
laminate. Therefore, we also fabricated devices with the
source and drain electrodes evaporated using a shadow
mask. Furthermore, the resistance of graphene is an in-
creasing function of strain for all measured values of the
gate voltage. Also, the slope dR/dε is an increasing func-
tion of the gate voltage. This can be seen more clearly in
Figure 5(b) where this slope is plotted against the gate
voltage. This means that the response of the resistance of
graphene to applied strain can be tuned with an exter-
nally applied electric field.
Figure 4. Photographs of the device in the strain cell taken
at different strain levels. In panel (a) no strain is applied to
the sample. The base length L used as reference length is
indicated. In panel (b) about half of the maximum strain is
applied to the sample, here ε = 1.2%. In panel (b) maximum
strain is applied to the sample, in this case ε = 2.2%. In both
panel (b) and (c) the fitted circles used to obtain the radii of
curvature are indicated.
6. Conclusion
sumptions the following relation between the strain and
the radius of curvature can be derived: In this paper we have shown a method to fabricate gra-
phene-based devices with an embedded back-gate. In
these back-gated devices the graphene surface stays un-
covered which can be advantageous in many applications
2
h


 (1)

J. VAN VEEN ET AL. 16
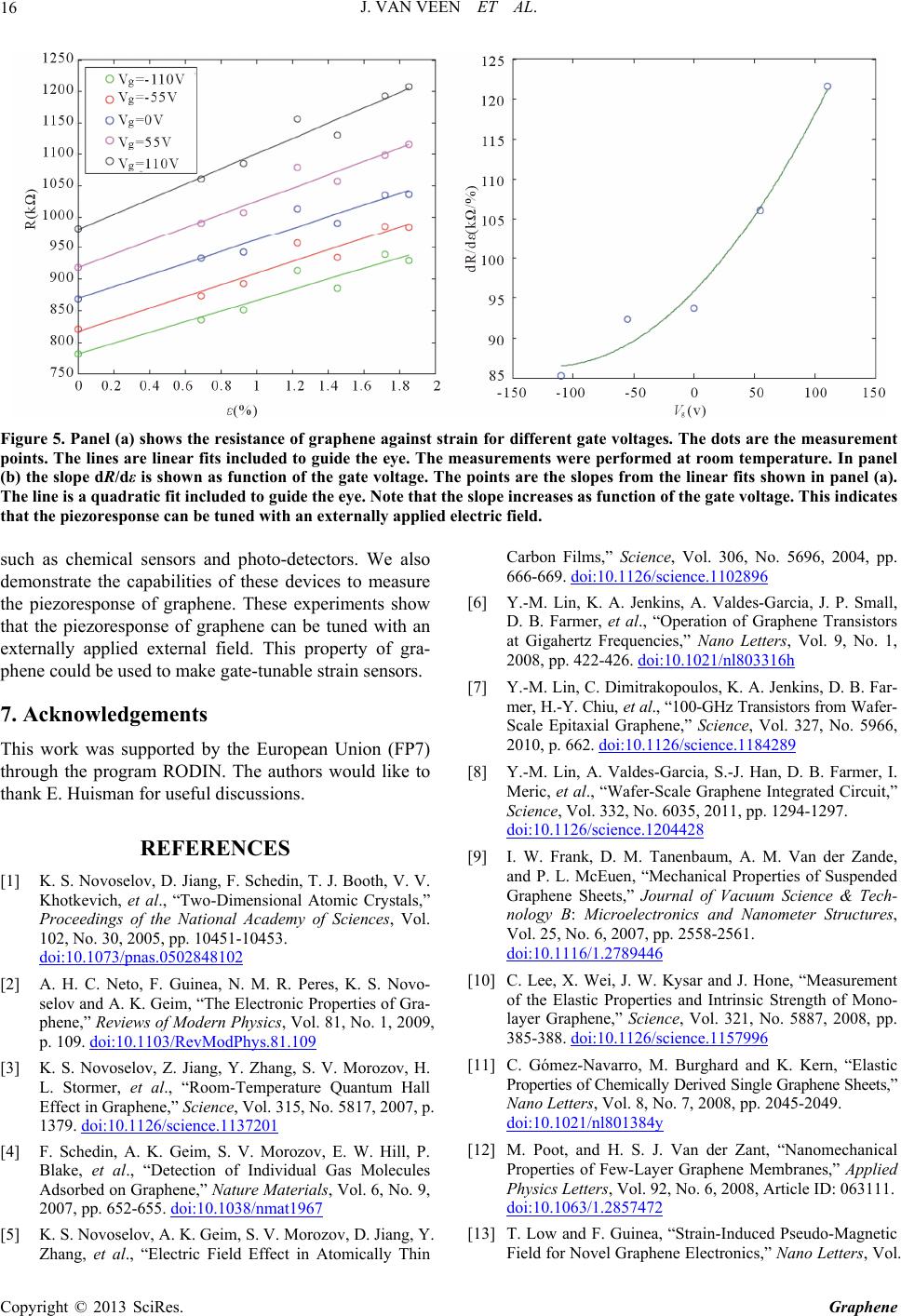
Figure 5. Panel (a) shows the resistance of graphene against strain for different gate voltages. The dots are the measurement
points. The lines are linear fits included to guide the eye. The measurements were performed at room temperature. In panel
(b) the slope dR/dε is shown as function of the gate voltage. The points are the slopes from the linear fits shown in panel (a).
The line is a quadratic fit included to guide the eye. Note that the slope increases as function of the gate voltage. This indicates
that the piezoresponse can be tuned with an externally applied electric field.
such as chemical sensors and photo-detectors. We also
demonstrate the capabilities of these devices to measure
the piezoresponse of graphene. These experiments show
that the piezoresponse of graphene can be tuned with an
externally applied external field. This property of gra-
phene could be used to make gate-tunable strain sensors.
7. Acknowledgements
This work was supported by the European Union (FP7)
through the program RODIN. The authors would like to
thank E. Huisman for useful discussions.
REFERENCES
[1] K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V.
Khotkevich, et al., “Two-Dimensional Atomic Crystals,”
Proceedings of the National Academy of Sciences, Vol.
102, No. 30, 2005, pp. 10451-10453.
doi:10.1073/pnas.0502848102
[2] A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novo-
selov and A. K. Geim, “The Electronic Properties of Gra-
phene,” Reviews of Modern Physics, Vol. 81, No. 1, 2009,
p. 109. doi:10.1103/RevModPhys.81.109
[3] K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H.
L. Stormer, et al., “Room-Temperature Quantum Hall
Effect in Graphene,” Science, Vol. 315, No. 5817, 2007, p.
1379. doi:10.1126/science.1137201
[4] F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P.
Blake, et al., “Detection of Individual Gas Molecules
Adsorbed on Graphene,” Nature Materials, Vol. 6, No. 9,
2007, pp. 652-655. doi:10.1038/nmat1967
[5] K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y.
Zhang, et al., “Electric Field Effect in Atomically Thin
Carbon Films,” Science, Vol. 306, No. 5696, 2004, pp.
666-669. doi:10.1126/science.1102896
[6] Y.-M. Lin, K. A. Jenkins, A. Valdes-Garcia, J. P. Small,
D. B. Farmer, et al., “Operation of Graphene Transistors
at Gigahertz Frequencies,” Nano Letters, Vol. 9, No. 1,
2008, pp. 422-426. doi:10.1021/nl803316h
[7] Y.-M. Lin, C. Dimitrakopoulos, K. A. Jenkins, D. B. Far-
mer, H.-Y. Chiu, et al., “100-GHz Transistors from Wafer-
Scale Epitaxial Graphene,” Science, Vol. 327, No. 5966,
2010, p. 662. doi:10.1126/science.1184289
[8] Y.-M. Lin, A. Valdes-Garcia, S.-J. Han, D. B. Farmer, I.
Meric, et al., “Wafer-Scale Graphene Integrated Circuit,”
Science, Vol. 332, No. 6035, 2011, pp. 1294-1297.
doi:10.1126/science.1204428
[9] I. W. Frank, D. M. Tanenbaum, A. M. Van der Zande,
and P. L. McEuen, “Mechanical Properties of Suspended
Graphene Sheets,” Journal of Vacuum Science & Tech-
nology B: Microelectronics and Nanometer Structures,
Vol. 25, No. 6, 2007, pp. 2558-2561.
doi:10.1116/1.2789446
[10] C. Lee, X. Wei, J. W. Kysar and J. Hone, “Measurement
of the Elastic Properties and Intrinsic Strength of Mono-
layer Graphene,” Science, Vol. 321, No. 5887, 2008, pp.
385-388. doi:10.1126/science.1157996
[11] C. Gómez-Navarro, M. Burghard and K. Kern, “Elastic
Properties of Chemically Derived Single Graphene Sheets,”
Nano Letters, Vol. 8, No. 7, 2008, pp. 2045-2049.
doi:10.1021/nl801384y
[12] M. Poot, and H. S. J. Van der Zant, “Nanomechanical
Properties of Few-Layer Graphene Membranes,” Applied
Physics Letters, Vol. 92, No. 6, 2008, Article ID: 063111.
doi:10.1063/1.2857472
[13] T. Low and F. Guinea, “Strain-Induced Pseudo-Magnetic
Field for Novel Graphene Electronics,” Nano Letters, Vol.

J. VAN VEEN ET AL. 17
10, No. 9, 2010, pp. 3551-3554. doi:10.1021/nl1018063
[14] F. Guinea, A. K. Geim, M. I. Katsnelson and K. S. No-
voselov, “Generating Quantizing Pseudomagnetic Fields
by Bending Graphene Ribbons,” Physical Review B, Vol.
81, No. 3, 2010, Article ID: 035408.
doi:10.1103/PhysRevB.81.035408
[15] F. Guinea, M. I. Katsnelson and A. K. Geim, “Energy
Gaps and a Zero-Field Quantum Hall Effect in Graphene
by Strain Engineering,” Nature Physics, Vol. 6, No. 1,
2009, pp. 30-33. doi:10.1038/nphys1420
[16] P. R. Chidambaram, C. Bowen, S. Chakravarthi, C. Ma-
chala and R. Wise, “Fundamentals of Silicon Material
Properties for Successful Exploitation of Strain Engi-
neering in Modern CMOS Manufacturing,” IEEE Trans-
actions on Electron Devices, Vol. 53, No. 5, 2006, pp.
944-964. doi:10.1109/TED.2006.872912
[17] G. Eda, G. Fanchini and M. Chhowalla, “Large-Area
Ultrathin Films of Reduced Graphene Oxide as a Trans-
parent and Flexible Electronic Material,” Nature Nano-
technology, Vol. 3, No. 5, 2008, pp. 270-274.
doi:10.1038/nnano.2008.83
[18] Y.-H. Lee and Y.-J. Kim, “Electrical and Lattice Vibra-
tional Behaviors of Graphene Devices on Flexible Sub-
strate Under Small Mechanical Strain,” Applied Physics
Letters, Vol. 101, No. 8, 2012, Article ID: 083102.
doi:10.1063/1.4746285
[19] T. Yoon, W. C. Shin, T. Y. Kim, J. H. Mun, T. S. Kim, et
al., “Direct Measurement of Adhesion Energy of Mono-
layer Graphene as-Grown on Copper and Its Application
to Renewable Transfer Process,” Nano Letters, Vol. 12,
No. 3, 2012, pp. 1448-1452. doi:10.1021/nl204123h
[20] J. Lee, L. Tao, K. N. Parrish, H. Yufeng, R. S. Ruoff, et
al., “Highly Bendable High-Mobility Graphene Field Ef-
fect Transistors with Multi-Finger Embedded Gates on Fle-
xible Substrates,” Nanotechnology (IEEE-NANO), 2012,
in Press.
[21] Y. Lee, S. Bae, H. Jang, S. Jang, S. Zhu, et al., “Wafer-
Scale Synthesis and Transfer of Graphene Films,” Nano
Letters, Vol. 10, No. 2, 2010, pp. 490-493.
doi:10.1021/nl903272n