Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21687,5 pages DOI:10.4236/jmp.2012.38113
A Relativistic Density Functional Study of the U2F6 Molecule*
School of Science, Xi’an University of Posts and Telecommunications, Xi’an, China
Email: zhangyunguang2008@yahoo.cn
Received May 26, 2012; revised June 24, 2012; accepted July 19, 2012
Keywords: Molecular Structure; Vibrational Frequency; Bond Dissociation Energy
ABSTRACT
All-electronic relativistic density functional theory (DFT) method has been used to study the U2F6 molecule. Results from calculations predict the existence of U2F6 molecule, which has been found to be stable with a multiply bonded U2 unit. The calculations also predict that D3d symmetry of U2F6 is more stable than D3h. The optimized geometries, vibrational frequencies and infrared intensities are reported for D3d symmetry of U2F6 from Becke Three-parameter Lee-Yang-Parr (B3LYP) function with triple zeta valence plus polarization functions basis set (TZP). The bond dissociation energy (BDE) for U-U bond in the U2F6 was obtained using the same method. In addition, the entropies of U2F6 have been investigated at temperature rang from 0 to 3000 K in 10 steps using the B3LYP method.
1. Introduction
The uranium compounds bring a prodigious challenge for investigation from theory and experiment. Still, uranium compounds are not easy to manage in the laboratory. It is very important that we could gain a good understanding of their chemical properties in many areas. Quantum chemistry is now mature enough to compute uranium compounds properties with good accuracy. Gagliardi and Roos have explored how two uranium atoms bind to form the U2 molecule by multiconfigurational quantum chemistry methods [1,2]. They find that the U2 chemical bond is more complex than any other known diatomic bond, with summation of the bonding electrons suggesting a quintuple bond. In other words, the uranium atom has the ground-state electronic configuration  (six valence electrons), and the U-U bond of U2 molecule is composed of three normal two-electron bonds, four electrons in different bonding orbitals, and two nonbonded electrons leading to a quintuple bond between the two uranium atoms. In addition, its multi-radical nature may support chemical bonds to the framework of diuranium chemistry, such as in F3U2F3.
(six valence electrons), and the U-U bond of U2 molecule is composed of three normal two-electron bonds, four electrons in different bonding orbitals, and two nonbonded electrons leading to a quintuple bond between the two uranium atoms. In addition, its multi-radical nature may support chemical bonds to the framework of diuranium chemistry, such as in F3U2F3.
Not much diuranium compounds have been found experimentally. So far, only the molecules OU2O and H2U2H2 [3] have been detected. However, no real inorganic chemistry based on the U2 unit has been observed. This chemistry could occur in solution, analogous to the widely studied transition metal dimmer chemistry. In theory, Cl3U2Cl3 molecule has been studied by Complete-Active-Space Self-Consistent-Field (CASSCF)/Complete-Active-Space Second-Order-Perturbation Theory (CASPT2) method, the results from calculation predict to be stable with a multiply bonded U2 unit [4]. In the paper, All-electronic DFT has been used to show that diuranium compound F3U2F3 is stable with a multiple U-U bond. The calculations also predict that D3d symmetry of U2F6 is more stable than D3h symmetry. The optimized geometries, BDE and vibrational frequencies are reported for D3d symmetry of U2F6 from B3LYP function with TZP basis set [5]. In addition, the entropies of U2F6 have been investigated at temperature rang from 0 to 3000 K in 10 steps using the same method.
Methods of calculation are given in the next section, and the Result and Discussion are then presented in Section 3. The article ends with the Summary.
2. Computational Details
Our calculations were performed using the Amsterdam density functional (ADF) program. The underlying theory of the program is the Kohn-Sham approach to the DFT. Kohn-Sham DFT is an important computational method to predict chemical properties accurately and to analyze and interpret these in convenient and simple chemical terms [6]. DFT gives superior accuracy to Hartree-Fock theory and semi-empirical approaches, and it is well suited for molecules containing heavy metal atoms.
In this method, scalar relativistic effects are introduced via the zeroth-order regular approximation (ZORA) approach to the Dirac equation [7-9], and that spin-orbit coupling is not included in the present study. It will have only a minor effect on the computed structure for singlet electronic state. Certainly, the spin-orbit coupling effect will further lower the energy but has a negligible effect on the geometry. For the close-shell systems, the spin restricted DFT scheme is used. In this paper, a triple-ζ Slater type basis set augmented with one set of polarization functions, i.e. the triple-zeta polarized(TZP) basis set is employed for all atoms(F and U). Moreover, the calculations were performed using GGA level to [10,11] DFT: B3LYP function in all-electronic method.
ADF has a fragment oriented approach: the polyatomic system to be computed is conceptually built up from fragments, the molecular orbitals are calculated as linear combinations of fragment orbitals, and final analysis of the bonding energy are in terms of fragment properties. The fragments may be single atoms or larger moieties. When we compute a system in terms of its constituent fragments, these fragments must have been computed before and their properties must be passed on to the current calculation. This is done by attaching fragment files, which contain the necessary information. In the paper, the BDE for U-U bond in the U2F6 between the F3U and UF3 radical fragments were obtained using the fragment approach.
3. Results and Discussion
3.1. Structure and Stability
In a previous study of U2 molecule [1,2], it was shown that the ground state configuration is 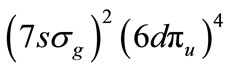
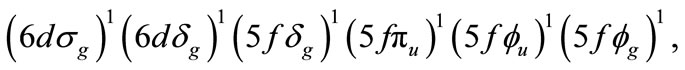 and that the chemical bond is thus more complex than any other known diatomic bond, with summation of the bonding electrons suggesting a quintuple bond. Its multiradical nature (six electrons are available for binding) may support chemical bonds to F3U2F3 molecule. Here we have considered the diuranium compound of U2F6. It can have either an eclipsed or a staggered conformation (see Figures 1 and 2). Preliminary calculations have indicated that the staggered conformation is lower in energy than the eclipsed form, and the calculations were done under limiting symmetry. Moreover, when the molecular structure of U2F6 was optimized under D3d and D3h symmetry respectively (unlimiting symmetry), the final optimum structure was found to be staggered. So the stability of D3d symmetry is better than D3h. We will thus focus our analysis on the staggered structure.
and that the chemical bond is thus more complex than any other known diatomic bond, with summation of the bonding electrons suggesting a quintuple bond. Its multiradical nature (six electrons are available for binding) may support chemical bonds to F3U2F3 molecule. Here we have considered the diuranium compound of U2F6. It can have either an eclipsed or a staggered conformation (see Figures 1 and 2). Preliminary calculations have indicated that the staggered conformation is lower in energy than the eclipsed form, and the calculations were done under limiting symmetry. Moreover, when the molecular structure of U2F6 was optimized under D3d and D3h symmetry respectively (unlimiting symmetry), the final optimum structure was found to be staggered. So the stability of D3d symmetry is better than D3h. We will thus focus our analysis on the staggered structure.
Optimization of the geometry was performed at the B3LYP level of theory using the TZP basis set. The most stable spin-free electronic state was found to be a singlet state. The U-U bond distance is 2.425 Å, the U-F distance is 1.998 Å, and the U-U-F angle is 120.0˚C In addition, we know that scalar relativistic effects are introduced via the ZORA to the Dirac equation, and that spinorbit coupling is not included in the present study. Certainly, the spin-orbit coupling effect will further lower the energy but has a negligible effect on the geometry.
In the U2F6, the formal charge of uranium atom is +3. Thus, 6 of 12 valence electrons remain, and a triple bond can be formed. The electronic configuration for this molecule including all the electrons on U and F atoms is:
 (1)
(1)
where the highest occupied molecular orbitals of each symmetry are indicated.
3.2. Bonding Energy Analysis of F3U-UF3
The energy decomposition between the two radical molecular fragments UF3 in the compound F3U-UF3 have been analyzed with the program package ADF which is found on the methods of Morokuma [12,13] and Ziegler and Rauk [14,15]. The overall bond energy 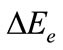 between the two fragments UF3 is given by the summation of
between the two fragments UF3 is given by the summation of 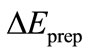 and
and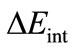 .
.
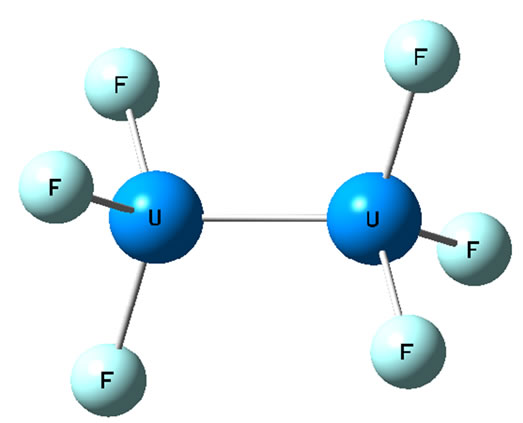
Figure 1. Staggered conformation of U2F6.
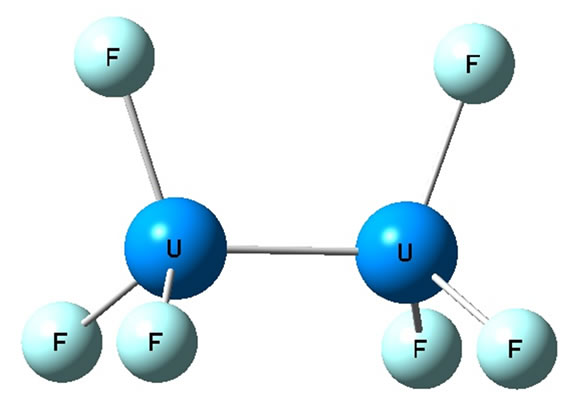
Figure 2. Eclipsed conformation of U2F6.
 (2)
(2)
The preparation energy 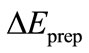 is the sum total of energy which is necessary associated to the structure distortion of both fragments from their equilibrium geometry to the geometry they have when the complex is formed.
is the sum total of energy which is necessary associated to the structure distortion of both fragments from their equilibrium geometry to the geometry they have when the complex is formed.
 (3)
(3)
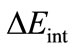 in Equation (2) is the instantaneous interaction energy between the two distorted fragments in the molecule. This term can be further decomposed into three main contributions:
in Equation (2) is the instantaneous interaction energy between the two distorted fragments in the molecule. This term can be further decomposed into three main contributions:
 (4)
(4)
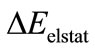 gives the electrostatic interaction energy between the fragments. The term
gives the electrostatic interaction energy between the fragments. The term  is the Pauli repulsion energy that arises from the closed shell repulsion between both fragments.
is the Pauli repulsion energy that arises from the closed shell repulsion between both fragments. 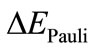 is calculated by enforcing the Kohn-Sham determinant of F3U-UF3, which results from superimposing two fragments UF3, to be orthonormal through antisymmetrization and renormalization. The stabilizing orbital interaction term
is calculated by enforcing the Kohn-Sham determinant of F3U-UF3, which results from superimposing two fragments UF3, to be orthonormal through antisymmetrization and renormalization. The stabilizing orbital interaction term 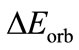 is the term related to the stabilization of the system when the densities of the two fragments UF3 are allowed to relax. It contains charge transfer as well as polarization. This method has been successfully applied to many systems [16-18].
is the term related to the stabilization of the system when the densities of the two fragments UF3 are allowed to relax. It contains charge transfer as well as polarization. This method has been successfully applied to many systems [16-18].
In the paper, we try to understand the trends through detailed analyses of the bonding mechanism in the compounds F3U2F3. The results of our Kohn-Sham MO analyses are calculated by B3LYP method using TZP basis set. The calculated data shows that the values of the repulsive term , the attractive electrostatic term
, the attractive electrostatic term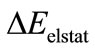 , orbital interaction term
, orbital interaction term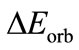 , and preparation energy term
, and preparation energy term 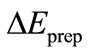 are 250.20 kcal/mol, –63.37 kcal/ mol, –205.33 kcal/mol and 1.24 kcal/mol, respectively. From the Equations (2) and (4), the calculational bond dissociation energy of U-U bond is 17.26 kcal/mol. In this molecule, there is a net flow of electrons from the metal to substituent F3, resulting in a positive atomic charge on U according to both the VDD (0.270) and the Hirshfeld (0.722) [19,20]. In addition, we also give the breakdown of the
are 250.20 kcal/mol, –63.37 kcal/ mol, –205.33 kcal/mol and 1.24 kcal/mol, respectively. From the Equations (2) and (4), the calculational bond dissociation energy of U-U bond is 17.26 kcal/mol. In this molecule, there is a net flow of electrons from the metal to substituent F3, resulting in a positive atomic charge on U according to both the VDD (0.270) and the Hirshfeld (0.722) [19,20]. In addition, we also give the breakdown of the 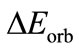 term into contributions of
term into contributions of  (–340.48 kcal/mol),
(–340.48 kcal/mol),  (–2.65 kcal/mol) and
(–2.65 kcal/mol) and  (137.83 kcal/mol). It becomes obvious that the
(137.83 kcal/mol). It becomes obvious that the 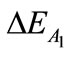 is much bigger than the other interactions.
is much bigger than the other interactions.
The results demonstrate clearly that the atomic partial charges cannot be taken as a measure of the electrostatic interactions between the atoms. The two U atoms in U2F6 carry positive charge. Thus, we obtained an innocent conclusion that the electrostatic interactions between two U atoms are repulsive. In addition, we find that there are strong coulomb attractions between two U atoms. The orbital interaction is greater than the electrostatic attraction.
3.3. Frequencies and Thermodynamic Analysis
The fundamental vibrational frequencies of U2F6 are obtained from the calculations using B3LYP method with TZP basis set, are reported in Table 1. There are not experiments to compare with the computational values up to now. This table also gives the infrared intensities and dipole strength values. Under the D3d symmetry, 12 fundamental vibrational modes of U2F6 are classified as the various symmetry species: 3A1g + A1u + 2A2u + 3E1g + 3E1u. Here, we also give a detailed description of the as

Table 1. Calculated vibrational frequencies and absorption intensity of U2F6.
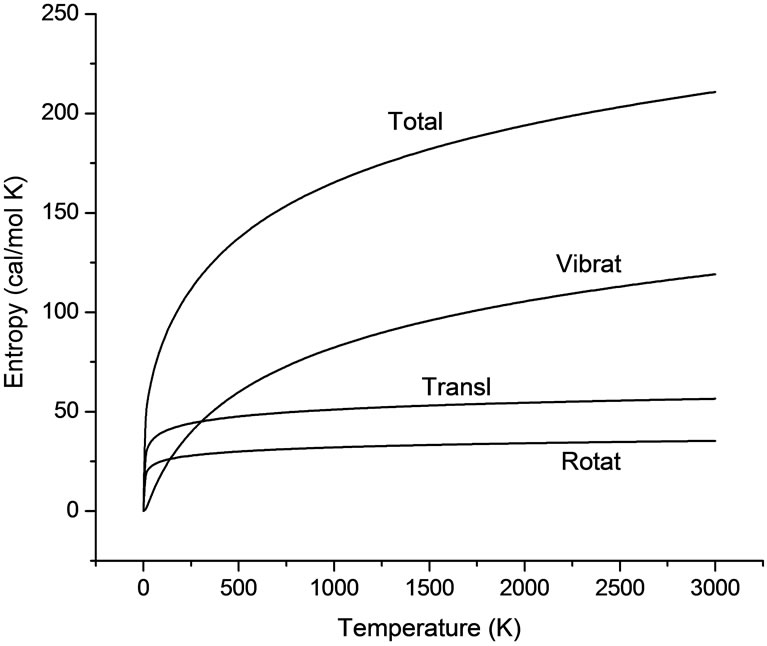
Figure 3. Entropy of U2F6 against temperature.
signment of all vibrational modes of U2F6 molecule in Table 1. Two A2u modes (v6 and v7) and three E1u modes (v1, v11 and v12) have only infrared active under D3d symmetry. The five modes v1, v6, v7, v11 and v12 correspond to the symmetric stretching, deformation symmetric stretching, antisymmetric stretching, deformation antisymmetric stretching and rocking modes, respectively.
After the molecular vibrational frequencies are obtained, some thermodynamic parameters of the U2F6 molecule can be calculated. Figure 3 provide the values of Entropy over a wide temperature range from 0 to 3000 K in 10 steps using a B3LYP method, which obtained good vibrational frequencies. These resulting data, currently not available in the literature, are critical for modeling reaction mechanisms. The entropies are calculated following the anharmonic oscillator approximation. In the calculation, we consider the translational, rotational and vibrational contribution to the molecular entropies, and these calculated results are summarized in Figure 3. As noted in the table, the growth rate of vibrational entropy is the fastest with the increase of temperature among the three forms of movement.
4. Summary
The molecular properties of U2F6 have been investigated using B3LYP function with TZP basis set. Scalar relativistic effects are introduced via the ZORA to the Dirac equation in the present study. The results from quantum chemical calculations that predict the existence of U2F6 molecule, which has been found to be stable with a multiply bonded U2 unit. The calculation also predicts that D3d symmetry of U2F6 is more stable than D3h symmetry. The predicted infrared bands of D3d symmetry at 230.683, 8.289, 373.885, 7.947 and 9.992 cm–1 are assigned to the symmetric stretching mode v1, deformation symmetric stretching mode v6, antisymmetric stretching mode v7, deformation antisymmetric stretching mode v11 and rocking mode v12, respectively. After the molecular vibrational frequencies are obtained, the entropies of U2F6 have been investigated at temperature rang from 0 to 3000 K in 10 steps using the same method. The growth rate of vibrational entropy is the fastest with the increase of temperature among the three forms of movement. In addition, the BDE for U-U bond in the U2F6 molecule was obtained using the B3LYP method.
REFERENCES
- L. Gagliardi and B. O. Roos, “Quantum Chemical Calculations Show That the Uranium Molecule U2 Has a Quintuple Bond,” Nature, Vol. 433, 2005, pp. 848-851. doi:10.1038/nature03249
- B. O. Roos, P. Malmqvist and L. J. Gagliardi, “Exploring the Actinide-Actinide Bond: Theoretical Studies of the Chemical Bond in Ac2, Th2, Pa2, and U2,” Journal of the American Chemical Society, Vol. 128, No. 51, 2006, pp. 17000-17006. doi:10.1021/ja066615z
- P. F. Souter, G. P. Kushto, L. Andrews and M. J. Neurock, “Experimental and Theoretical Evidence for the Formation of Several Uranium Hydride Molecules,” Journal of the American Chemical Society, Vol. 119, No. 7, 1997, pp. 1682-1687. doi:10.1021/ja9630809
- B. O. Roos and L. Gagliardi, “Quantum Chemistry Predicts Multiply Bonded Diuranium Compounds to Be Stable,” Inorganic Chemistry, Vol. 45, No. 2, 2006, pp. 803-807. doi:10.1021/ic051665a
- C. Lee, W. Yang and R. G. Parr, “Development of the Colle-Salvetti Correlation-Energy Formula into a functional of the Electron Density,” Physics Review B, Vol. 37, No. 2, 1988, pp. 785-789. doi:10.1103/PhysRevB.37.785
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A van Gisbergen, J. G. Snijders and T. Ziegler, “Chemistry with ADF,” Journal of Computational Chemistry, Vol. 22, No. 9, 2001, pp. 931-967. doi:10.1002/jcc.1056
- E. van Lenthe, E. J. Baerends and J. G. Snijders. “Relativistic Regular Two Component Hamiltonians.” Journal of Chemical Physics, Vol. 99, No. 6, 1993, pp. 4597- 4610. doi:10.1063/1.466059
- E. van Lenthe, E. J. Baerends and J. G. Snijders, “Relativistic Total Energy Using Regular Approximations,” Journal of Chemical Physics, Vol. 101, No. 11, 1994, pp. 9783-9792. doi:10.1063/1.467943
- E. van Lenthe, A. Ehlers and E. J. Baerends, “Geometry optimizations in the Zero Order Regular Approximation for Relativistic Effects,” Journal of Chemical Physics, Vol. 110, No. 18, 1999, pp. 8943-8953. doi:10.1063/1.478813
- J. P. Perdew, K. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868. doi:10.1103/PhysRevLett.77.3865
- B. Hammer, L. B. Hansen and J. K. Norskov, “Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals,” Physics Review B, Vol. 59, No. 11, 1999, pp. 7413-7421. doi:10.1103/PhysRevB.59.7413
- K. Morokuma, “Molecular Orbital Studies of Hydrogen Bonds. III. C☒O···H☒O Hydrogen Bond in H2CO···H2O and H2CO···2H2O,” Journal of Chemical Physics, Vol. 55, No. 3, 1971, pp. 1236-1244. doi:10.1063/1.1676210
- K. Morokuma, “Why Do Molecules Interact? The Origin of Electron Donor-Acceptor Complexes, Hydrogen Bonding and Proton Affinity,” Account of Chemical Research, Vol. 10, No. 8, 1997, pp. 294-300. doi:10.1021/ar50116a004
- T. Ziegler and A. Rauk, “On the calculation of bonding energies by the Hartree Fock Slater method,” Theorefic Chimica Acta, Vol. 46, No. 1, 1977, pp. 1-10.
- T. Ziegler and A. Rauk, “A Theoretical Study of the Ethylene-Metal Bond in complexes between copper(1+), silver(1+), gold(1+), platinum(0) or platinum(2+) and Ethylene, Based on the Hartree-Fock-Slater TransitionState Method,” Inorganic Chemistry, Vol. 18, No. 6, 1979, pp. 1558-1565. doi:10.1021/ic50196a034
- K. K. Pandey, “Energy analysis of Metal-Metal Bonding in [RM-MR] (M = Zn, Cd, Hg; R = CH3, SiH3, GeH3, C5H5, C5Me5),” Journal of Organometallic Chemistry, Vol. 692, No. 5, 2007, pp. 1058-1063. doi:10.1016/j.jorganchem.2006.10.067
- V. M. Rayon and G. Frenking, “Structures, Bond Energies, Heats of Formation, and Quantitative Bonding Analysis of Main-Group Metallocenes [E(Cp)2] (E = BeBa, Zn, Si-Pb) and [E(Cp)] (E = Li-Cs, B-Tl),” Chemistry-a European Journal, Vol. 8, No. 20, 2002, pp. 4693- 4707.
- O. Kh. Poleshchuk, E. L. Shevchenko, V. Branchadell, M. Lein and G. Frenking. “Energy analysis of the chemical bond in group IV and V complexes: A Density Functional Theory Study,” International Journal of Quantum Chemistry, Vol. 101, No. 6, 2005, pp. 869-877. doi:10.1002/qua.20348
- F. M. Bickelhaupt, N. J. R. van EikemaHommes, C. Fonseca Guerra and E. J. Baerends, “The Carbon-Lithium Electron Pair Bond in (CH3Li)n (n = 1, 2, 4),” Organometallics, Vol. 15, No. 13, 1996, pp. 2923-2931. doi:10.1021/om950966x
- C. Fonseca. Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, “The Nature of the Hydrogen Bond in DNA Base Pairs: The Role of Charge Transfer and Resonance Assistance,” Chemistry-a European Journal, Vol. 5, No. 12, pp. 3581-3594.
NOTES
*Project supported by the young teacher scientific research foundation of Xi’an University of Posts and Telecommunications (Grant No. 0001294).

