Journal of Modern Physics
Vol.3 No.9(2012), Article ID:22680,7 pages DOI:10.4236/jmp.2012.39142
Dirac-Born-Infeld-Einstein Theory with Weyl Invariance
1Japan Women’s College of Physical Education, Tokyo, Japan
2Yamaguchi Junior College, Hōfu, Japan
3Yamaguchi University, Yamaguchi, Japan
Email: *shiraish@yamaguchi-u.ac.jp
Received June 27, 2012; revised July 26, 2012; accepted August 5, 2012
Keywords: Modified Theories of Gravity; Weyl Invariance; Inflation
ABSTRACT
Weyl invariant gravity has been investigated as the fundamental theory of the vector inflation. Accordingly, we consider a Weyl invariant extension of Dirac-Born-Infeld type gravity. We find that an appropriate choice of the metric removes the scalar degree of freedom which is at the first sight required by the local scale invariance of the action, and then a vector field acquires mass. Then non-minimal couplings of the vector field and curvatures are induced. We find that the Dirac-Born-Infeld type gravity is a suitable theory to the vector inflation scenario.
1. Introduction
The cosmological inflation is proposed as some resolutions for the important cosmological problems, e.g. the flatness, horizon and monopole problems. Most of successful models are based on classical scalar fields, although we have not observed such scalar bosons associated with the field.
The inflation can also be caused by other type of fields. The vector inflation has been proposed by Ford [1] and some authors [2-4]. It is emphasized that the massive vector field should non-minimally couple to gravity in such models [1-4].
The reason why the non-minimal coupling is important is as follows. Suppose the equation of motion for the vector field is given by
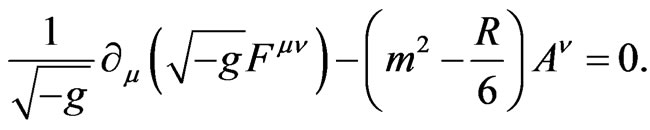 (1.1)
(1.1)
For the background field, we assume1
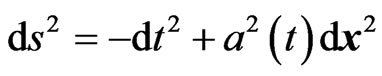 ,(1.2)
,(1.2)
and 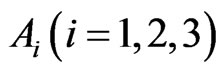 depends only on t and
depends only on t and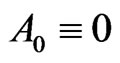 . Then we define
. Then we define  (1.1) becomes
(1.1) becomes
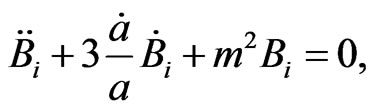 (1.3)
(1.3)
![]() which is very similar to the equation for a homogeneous scalar field in the Friedmann-Lemaître-Robertson-Walker universe. Moreover, the energy density is expressed as ~
which is very similar to the equation for a homogeneous scalar field in the Friedmann-Lemaître-Robertson-Walker universe. Moreover, the energy density is expressed as ~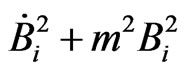 , which is also similar to the one for the scalar field. Thus, the slow evolution of the effective scalar field Bi can occur in the approximately isotropic inflating universe.
, which is also similar to the one for the scalar field. Thus, the slow evolution of the effective scalar field Bi can occur in the approximately isotropic inflating universe.
We have studied [5] Weyl invariant gravity [6-39] as a candidate for the theoretical model of the vector inflation. We found that the choice of the frame yields the mass of the Weyl gauge field, but the non-minimal coupling term is lost [5]. We come to the conclusion that we need further generalization of the gravitational theory.
In the different context, Deser and Gibbons considered Dirac-Born-Infeld (DBI)-Einstein theory [40] almost a decade ago, whose Lagrangian density is of the following type
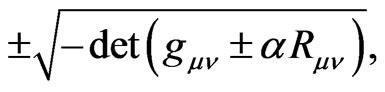 (1.4)
(1.4)
where Rμν is the Ricci tensor and the α is a constant. Originally, electromagnetism of the DBI type has been considered as a candidate of the nonsingular theory of electric fields. Therefore the Dirac-Born-Infeld-Einstein theory as the highly-nonlinear theory is also expected as a theory of gravity suffered from no argument of singularity. The studies on the theory have been done by many authors [41-50]. Because of the nonlinearity in this theory, we expect the extension as the theory of gravity which realizes a successful vector inflation.
Consider the Weyl invariant D-dimensional extension of the Ricci curvature (see the next section) is
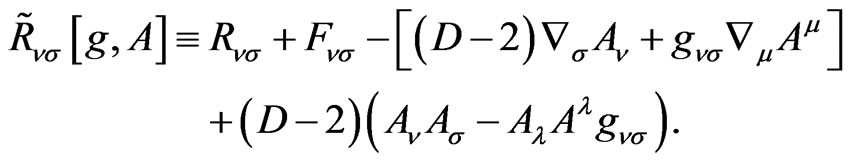 (1.5)
(1.5)
By simple replacement of the Ricci tensor by the Weyl invariant tensor in the action (1.4), the expansion
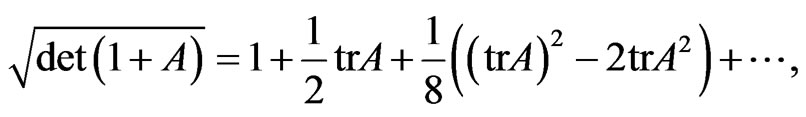 (1.6)
(1.6)
yields the terms RAμAμ and RμνAμAν and so on as well as R and FμνFμν. Other Weyl invariant terms are necessary, because the metric tensor must be combined with a scalar field which compensates the dimensionality. After the frame choice, the freedom of the scalar field is eaten by the vector field, then, the presence of the non-minimal terms mentioned above is still realized2.
In the next section, we review the Weyl invariant gravity with the vector field [11-14,16-21,25-37]. The expression (1.4) is generalized to the Weyl invariant one. The Lagrangian for a Weyl-invariant DBI gravity is proposed in Section 3. In Section 4, the necessity condition for the vector inflation is investigated. In Section 5, another possible inflationary scenario is provided. The last section is devoted to the summary and prospects.
2. Weyl’s Gauge Gravity Theory
In this section, we review the Weyl’s gauge transformation to construct the gauge invariant Lagrangian.
Consider the transformation of metric (in D dimensions)
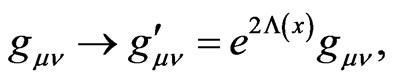 (2.1)
(2.1)
where 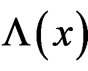 is an arbitrary function of the coordinates xμ.
is an arbitrary function of the coordinates xμ.
We can define the field with weight  which transforms as
which transforms as
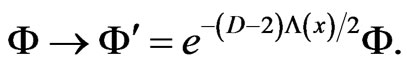 (2.2)
(2.2)
In order to construct the locally invariant theory, we consider the covariant derivative of the scalar field
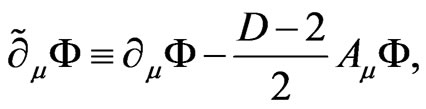 (2.3)
(2.3)
where Aμ is a Weyl’s gauge invariant vector field.
Under the Weyl gauge field transformation
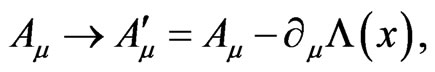 (2.4)
(2.4)
we obtain the transformation of the covariant derivative of the scalar field as
 (2.5)
(2.5)
The field strength of the vector field is given by
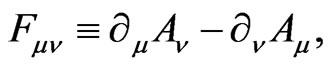 (2.6)
(2.6)
which is gauge invariant as
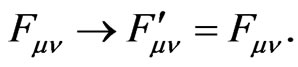 (2.7)
(2.7)
The modified Christoffel symbol is defined as
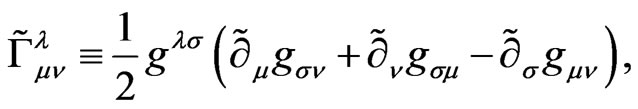 (2.8)
(2.8)
where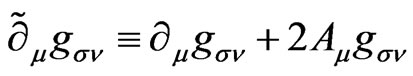 . The modified curvature is given as follows:
. The modified curvature is given as follows:
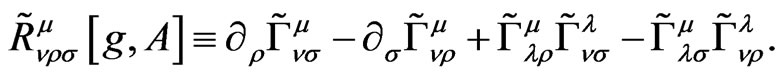 (2.9)
(2.9)
The Ricci curvature in the Weyl invariant version is
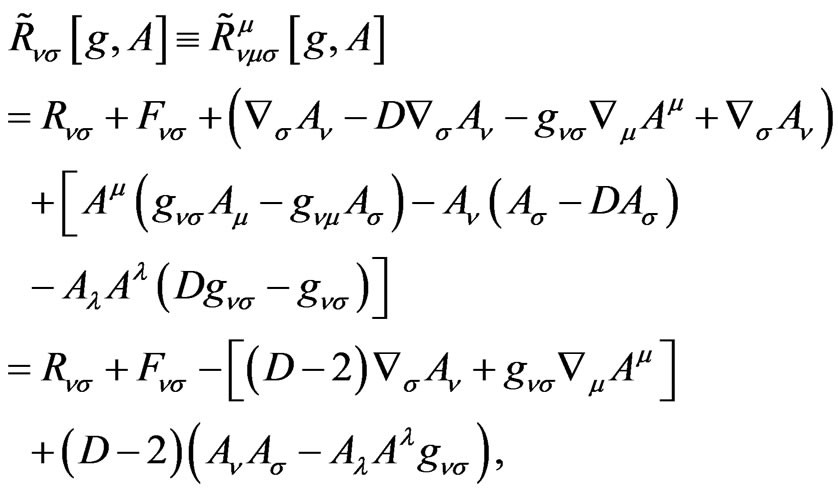 (2.10)
(2.10)
where  denotes the usual generally covariant derivative. Note that under the gauge transformation
denotes the usual generally covariant derivative. Note that under the gauge transformation
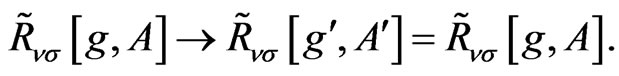 (2.11)
(2.11)
3. Weyl Invariant Lagrangian
Although we can use the Weyl invariant Ricci tensor 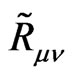 in the DBI gravity, we should note that the metric tensor in the action is not Weyl invariant (which is shown in (2.1)). Thus, we use a combination
in the DBI gravity, we should note that the metric tensor in the action is not Weyl invariant (which is shown in (2.1)). Thus, we use a combination 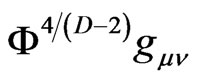 instead of the metric tensor. The scalar Φ compensates the dimension of the metric. Now the use of
instead of the metric tensor. The scalar Φ compensates the dimension of the metric. Now the use of  and
and  in the DBI type action leads to the theory of gravity, a vector field, and unexpectedly, a scalar field.
in the DBI type action leads to the theory of gravity, a vector field, and unexpectedly, a scalar field.
The introduction of the compensating scalar field tells us the action is far from general one. The monomial of the type of the kinetic term, in other words, two coordinate derivatives of the scalar field can be considered, while the curvature includes also two derivatives with no contraction. The possible monomials are
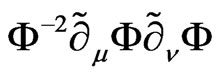 and
and 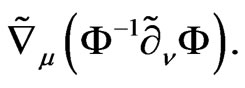 (3.1)
(3.1)
Another notice is in order. The decomposition of a rank two tensor shows that there are three irreducible ones; an anti-symmetric tensor, a traceless symmetric tensor and a trace part.
Now, we must introduce the following independently Weyl invariant tensors into the determinant in the DBI theory:
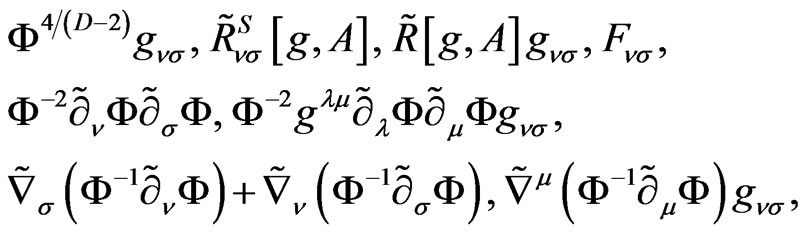 (3.2)
(3.2)
where
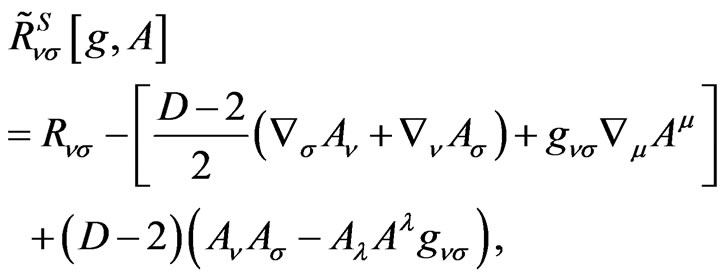 (3.3)
(3.3)
and
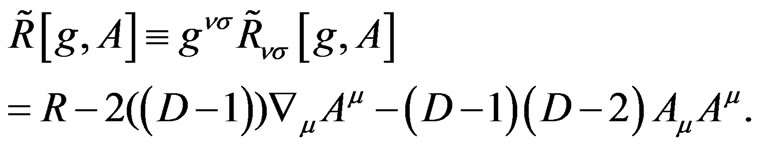 (3.4)
(3.4)
We choose those as symmetric tensors are not traceless3.
Our model of Weyl invariant DBI gravity is described by the Lagrangian density
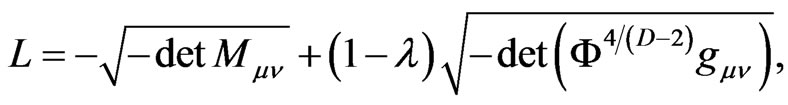 (3.5)
(3.5)
with
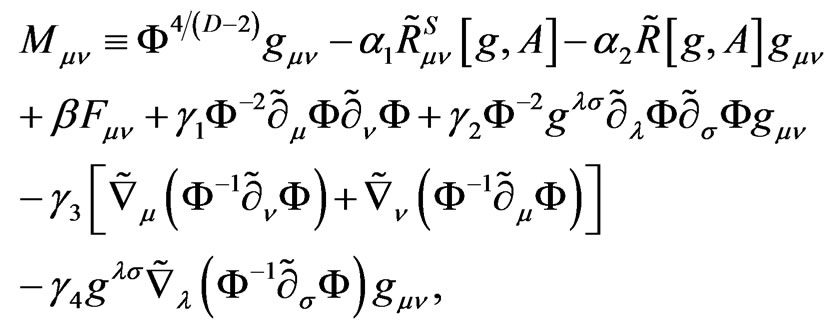 (3.6)
(3.6)
where α1, α2, β, γ1, γ2, γ3, γ4 and λ are dimensionless constants4.
Furthermore the Lagrangian density can be expressed by the new metric conformally related to the original one and new variables. Here we choose
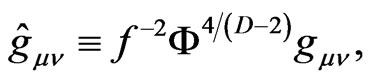 (3.7)
(3.7)
and
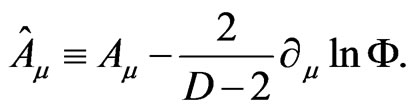 (3.8)
(3.8)
Note that a mass scale f was introduced here. By using the new metric and vector field, we rewrite the each term in the determinant of the Lagrangian as
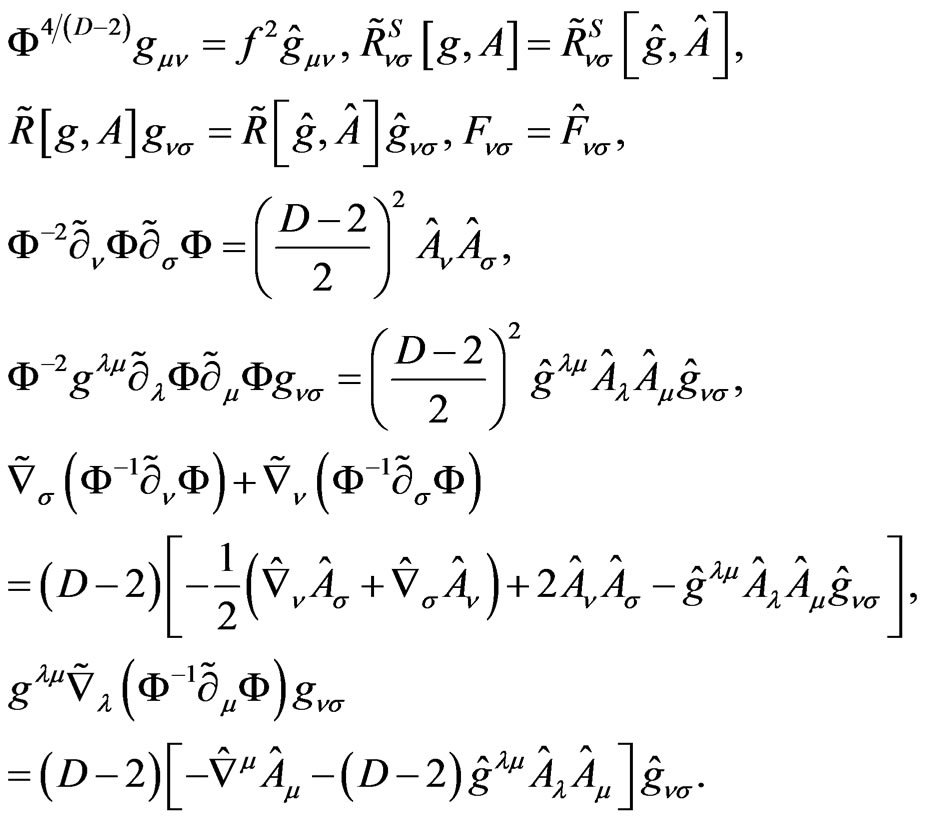 (3.9)
(3.9)
We now can write Mμν as
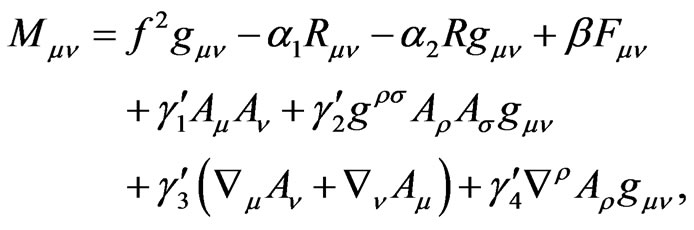 (3.10)
(3.10)
where the “hat”s are dropped and dimensionless constants are
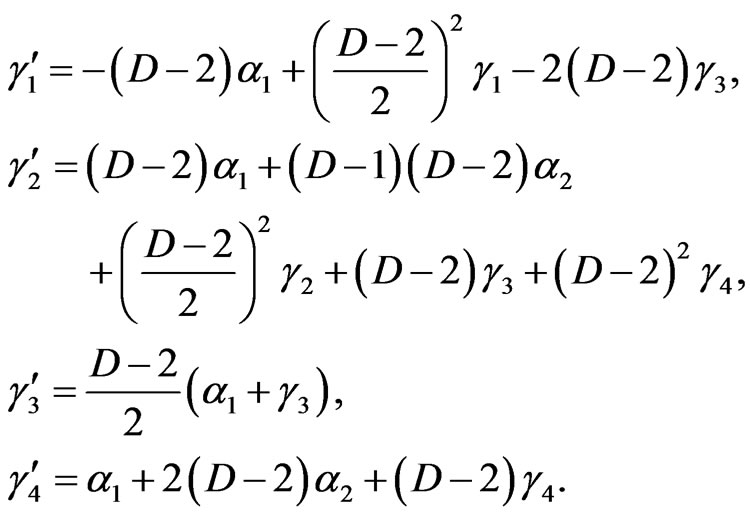
We can rewrite the Lagrangian as
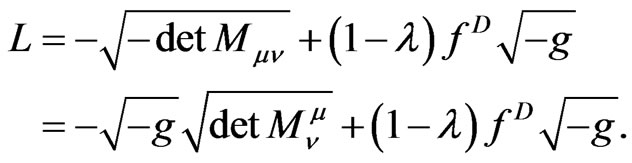 (3.11)
(3.11)
This is the candidate Lagrangian for the vector inflation.
4. Cosmology of Weyl’s Gauge Gravity
In this section, we apply our Weyl invariant DBI theory of gravity to cosmology in four dimensions (D = 4).
We take the metric for the homogeneous flat universe as
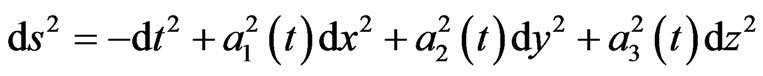 (4.1)
(4.1)
and, moreover, we assume the approximate isotropy 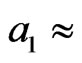
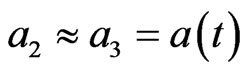 .
.
We consider that only A1(t) is homogeneously evolving, and A2 = A3 = A0 = 0.
By these ansätze, we look for the condition that the vector field behaves much like a scalar field at classical homogeneous level. Substituting the ansätze, we find
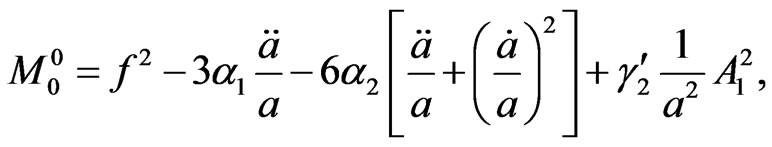 (4.2)
(4.2)
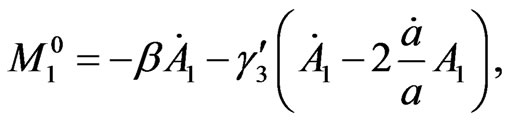 (4.3)
(4.3)
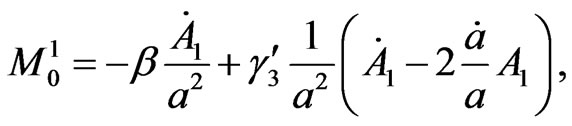 (4.4)
(4.4)
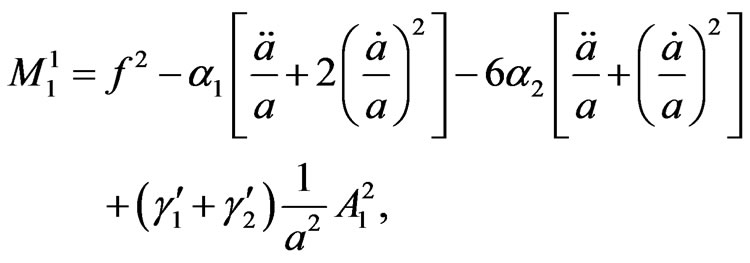 (4.5)
(4.5)
 (4.6)
(4.6)
After some calculations, we can subtract the part of the Lagrangian which includes bilinear and higher-order of the vector field A1. We find that if the parameters are chosen as
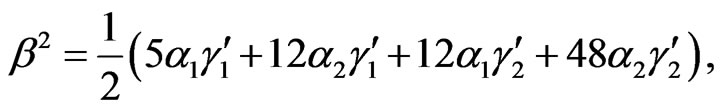 (4.7)
(4.7)
and
 (4.8)
(4.8)
the vector-field part becomes
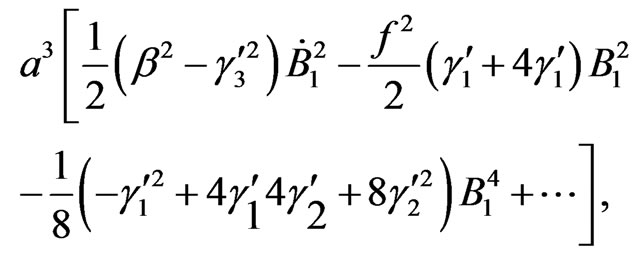 (4.9)
(4.9)
where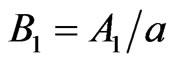 .
.
A simple case is realized when α2 = γ1 = γ2 = γ3 = γ4 = 0, or these parameter take small values in comparison with α1. Then the parameter is α1 only. Equations (4.7) and (4.8) tell us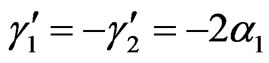 ,
,  and
and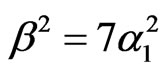 . In this case, this is so simple that the effective mass for B1 may be large. The tuning is possible; say, the choice of γ4 does not affects (4.8) and makes the change in the effective mass.
. In this case, this is so simple that the effective mass for B1 may be large. The tuning is possible; say, the choice of γ4 does not affects (4.8) and makes the change in the effective mass.
An elaborate tuning may give the potential which induces the chaotic inflation [51]. In the next section, however, we show another simple inflation scenario.
5. A Simple Cosmological Scenario
The chaotic inflation in the model can occur by tuning of the parameters. We should remember that the model involves the higher-derivative gravity. Therefore another kind of inflation is worth to be considered.
First let us suppose the flat space. Then the potential, or the energy density for the constant B1, can be easily written down as
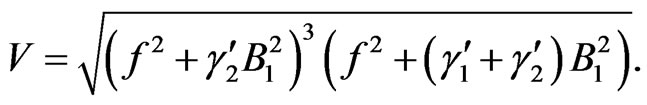 (5.1)
(5.1)
Although other choices are possible, we consider here a simple choice as 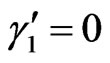 and
and 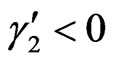 5. In this case, unfortunately, the previous conditions (4.7, 4.8) cannot be satisfied simultaneously, because
5. In this case, unfortunately, the previous conditions (4.7, 4.8) cannot be satisfied simultaneously, because 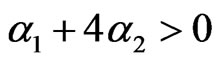 for the positive coefficient of the Einstein-Hilbert term in the action. Then the potential is
for the positive coefficient of the Einstein-Hilbert term in the action. Then the potential is
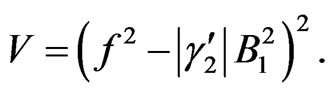 (5.2)
(5.2)
This is the simplest potential. In the true vacuum, the vector field “condensates” and a “natural” choice λ = 1 leads to vanishing cosmological constants6!
This simplest version also has an inflationary phase. That is, for B1 = 0, the scale factor behaves as a(t) ≈ eHt where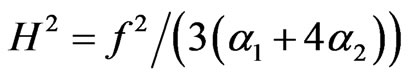 .
.
Unfortunately, this phase is stabilized by the nonminimal coupling between curvatures and the vector field, because the effective potential in this phase becomes
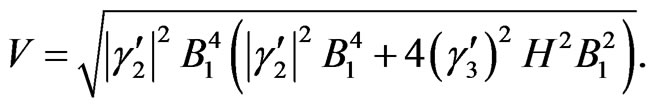 (5.3)
(5.3)
The exit of the de Sitter phase is problematic, like the other higher-derivative models. Though the additional matter fields may play important roles, we will perform further study on them elsewhere.
6. Summary and Outlook
The Weyl invariant DBI gravity is a candidate for a model which causes an inflationary universe. If the vector inflation can explain the possible anisotropy in the early universe, we may seriously investigate the Weyl invariant DBI gravity.
Here we examined slow development of the massive vector field. The inflation along with a fast evolution is shown to be possible in the DBI inflation, where the scalar degrees of freedom which originate from string (field) theory or D brane theory [52,53]. The similar scenario is feasible in our model, though the higher-derivatives make the detailed analysis difficult. Anyway, numerical calculations and large simulations will be needed to understand the minute meaning of the Weyl invariant DBI gravity, because the local inhomogenuity in the spatial directions as well as the strength of vector fields is important for thorough understanding in the early cosmology.
Finally, we think that some marginally related subjects are in order. The higher-dimensional cosmology in the Weyl invariant DBI gravity is worth studying because of its rich content. Incidentally, DBI gravity in three dimensions is eagerly studied [54-57], which is related to New Massive Gravity [58,59]. We think that the Weyl invariant extension of the lower-dimensional theory is also of much mathematical interest.
7. Note Added
After completing this manuscript, we become aware of the paper “Higgs mechanism for New Massive gravity and Weyl invariant extensions of higher derivative theories” by Dengiz and Tekin [60]. They investigated a Weylinvariant DBI gravity in three dimensions.
We also become aware of two recent papers about the cosmology of Weyl invariant theory [61,62].
8. Acknowledgements
The authors would like to thank the organizers of JGRG20, where our partial result ([arXiv:1012.5375]) was presented. We also thank D. Comelli, S. Deser, T. Moon and B. Tekin for informing us about their important and interesting papers.
The present study is supported in part by the Grant-inAid of Nikaido Research Fund.
REFERENCES
- L. H. Ford, “Inflation Driven by a Vector Field,” Physical Review D, Vol. 40, No. 4, 1989, pp. 967-972.
- A. B. Burd and J. E. Lidsey, “An Analysis of Inflationary Models Driven by Vector Fields,” Nuclear Physics B, Vol. 351, No. 3, 1991, pp. 679-694. doi:10.1016/S0550-3213(05)80039-2
- A. Golovnev, V. Mukhanov and V. Vanchurin, “Vector Inflation,” Journal of Cosmology and Astroparticle Physics, No. 6, 2008.
- A. Golovnev and V. Vanchurin, “Cosmological Perturbations from Vector Inflation,” Physical Review D, Vol. 79, No. 10, 2009, Article ID: 103524. doi:10.1103/PhysRevD.79.103524
- T. Maki, Y. Naramoto and K. Shiraishi, “On the Cosmology of Weyl’s Gauge Invariant Gravity,” Acta Physica Polonica B, Vol. 41, No. 6, 2010, pp. 1195-1201.
- H. Weyl, “Electron and Gravitation,” Zeitschrift für Physik, Vol. 56, 1929, pp. 330-352. doi:10.1007/BF01339504
- S. Deser, “Scale Invariance and Gravitational Coupling,” Annals of Physics, Vol. 59, No. 1, 1970, pp. 248-253. doi:10.1016/0003-4916(70)90402-1
- D. K. Sen and K. A. Dunn, “A Scalar-Tensor Theory of Gravitation in a Modified Riemannian Manifold,” Journal of Mathematical Physics, Vol. 12, No. 4, 1971, pp. 578-586. doi:10.1063/1.1665623
- P. A. M. Dirac, “Long Range Forces and Broken Symmetries,” Proceedings of the Royal Society A, Vol. 333, No. 4, 1973, pp. 403-418.
- P. G. O. Freund, “Local Scale Invariance and Gravitation,” Annals of Physics, Vol. 84, No. 1-2, 1974, pp. 440- 454. doi:10.1016/0003-4916(74)90310-8
- R. Utiyama, “On Weyl’s Gauge Field,” Progress of Theoretical Physics, Vol. 50, No. 6, 1973, pp. 2080-2090. doi:10.1143/PTP.50.2080
- R. Utiyama, “On Weyl’s Gauge Field 2,” Progress of Theoretical Physics, Vol. 53, No. 2, 1975, pp. 565-574. doi:10.1143/PTP.53.565
- K. Hayashi, M. Kasuya and T. Shirafuji, “Elementary Particles and Weyl’s Gauge Field,” Progress of Theoretical Physics, Vol. 57, No. 2, 1977, pp. 431-440. doi:10.1143/PTP.57.431
- K. Hayashi and T. Kugo, “Everything about Weyl’s Gauge Field,” Progress of Theoretical Physics, Vol. 61, No. 1, 1979, pp. 334-346. doi:10.1143/PTP.61.334
- D. Ranganathan, “A Geometric Interpretation for the Dirac Field in Curved Space,” Journal of Mathematical Physics, Vol. 28, No. 10, 1987, pp. 2437-2439. doi:10.1063/1.527732
- H. Cheng, “The Possible Existence of Weyl’s Vector Meson,” Physical Review Letters, Vol. 61, No. 19, 1988, pp. 2182-2184. doi:10.1103/PhysRevLett.61.2182
- H. Cheng, “Dark Matter and Scale Invariance,” 2004.
- W. F. Kao, “Inflationary Solution in Weyl Invariant Theory,” Physics Letters A, Vol. 149, No. 2-3, 1990, pp. 76- 78. doi:10.1016/0375-9601(90)90528-V
- W. F. Kao, “Scale Invariance and Inflation,” Physics Letters A, Vol. 154, No. 1-2, 1991, pp. 1-4.
- W. F. Kao, “Higher Derivative Weyl Gravity,” Physical Review D, Vol. 61, No. 4, 2000, Article ID: 047501. doi:10.1103/PhysRevD.61.047501
- W. F. Kao, S.-Y. Lin and T.-K. Chyi, “Weyl Invariant Black Hole,” Physical Review D, Vol. 53, No. 4, 1996, pp. 1955-1962. doi:10.1103/PhysRevD.53.1955
- D. Hochberg and G. Plunien, “Theory of Matter in Weyl Space-Time,” Physical Review D, Vol. 43, No. 10, 1991, pp. 3358-3367. doi:10.1103/PhysRevD.43.3358
- W. R. Wood and G. Papini, “Breaking Weyl Invariance in the Interior of a Bubble,” Physical Review D, Vol. 45, No. 10, 1992, pp. 3617-3627. doi:10.1103/PhysRevD.45.3617
- M. Pawlowski, “Gauge Theory of Phase and Scale,” Turkish Journal of Physics, Vol. 23, No. 5, 1999, pp. 895-902.
- H. Nishino and S. Rajpoot, “Broken Scale Invariance in the Standard Model,” hep-th/0403039.
- H. Nishino and S. Rajpoot, “Standard Model and SU(5) GUT with Local Scale Invariance and the Weylon,” arXiv: 0805.0613 [hep-th].
- H. Nishino and S. Rajpoot, “Implication of Compensator Field and Local Scale Invariance in the Standard Model,” Physical Review D, Vol. 79, No. 12, 2009, Article ID: 125025. doi:10.1103/PhysRevD.79.125025
- H. Nishino and S. Rajpoot, “Weyl’s Scale Invariance for the Standard Model, Renormalizability and the Zero Cosmological Constant,” Classical and Quantum Gravity, Vol. 28, No. 14, 2011, Article ID: 145014. doi:10.1088/0264-9381/28/14/145014
- H. Wei and R.-G. Cai, “Cheng-Weyl Vector Field and Its Cosmological Application,” Journal of Cosmology and Astroparticle Physics, No. 9, 2007.
- P. Jain and S. Mitra, “Cosmological Symmetry Breaking, Pseudo-Scale Invariance, Dark Energy and the Standard Model,” Modern Physics Letters A, Vol. 22, No. 22, 2007, pp. 1651-1661. doi:10.1142/S0217732307023754
- P. Jain and S. Mitra, “One Loop Calculation of Cosmological Constant in a Scale Invariant Theory,” Modern Physics Letters A, Vol. 24, No. 26, 2009, pp. 2069-2079. doi:10.1142/S0217732309031351
- P. Jain and S. Mitra, “Standard Model with Cosmologically Broken Quantum Scale Invariance,” Modern Physics Letters A, Vol. 25, No. 3, 2010, pp. 167-177. doi:10.1142/S0217732310032317
- P. Jain, S. Mitra and N. K. Singh, “Cosmological Implications of a Scale Invariant Standard Model,” Journal of Cosmology and Astroparticle Physics, No. 3, 2008.
- P. K. Aluri, P. Jain and N. K. Singh, “Dark Energy and Dark Matter in General Relativity with Local Scale Invariance,” Modern Physics Letters A, Vol. 24, No. 20, 2009, pp. 1583-1595. doi:10.1142/S0217732309030060
- P. K. Aluri, P. Jain, S. Mitra, S. Panda and N. K. Singh, “Constraints on the Cosmological Constant due to Scale Invariance,” Modern Physics Letters A, Vol. 25, No. 16, 2010, pp. 1349-1364. doi:10.1142/S0217732310032561
- P. Jain, S. Mitra, S. Panda and N. K. Singh, “Scale Invariance as a Solution to the Cosmological Constant Problem,” arXiv:1010.3483 [hep-ph].
- P. Jain, P. Karmakar, S. Mitra, S. Panda and N. K. Singh, “Cosmological Perturbation Analysis in a Scale Invariant Model of Gravity,” Classical and Quantum Gravity, Vol. 28, No. 21, 2011, Article ID: 215010. doi:10.1088/0264-9381/28/21/215010
- E. Scholz, “Cosmological Spacetimes Balanced by a Scale Covariant Scalar Field,” Foundations of Physics, Vol. 39, No. 1, 2009, pp. 45-72. doi:10.1007/s10701-008-9261-x
- E. Scholz, “Weyl Geometric Gravity and ‘Breaking’ of Electroweak Symmetry,” Annalen der Physik, Vol. 523, No. 7, 2011, pp. 507-530. doi:10.1002/andp.201100032
- S. Deser and G. W. Gibbons, “Born-Infeld-Einstein Actions?” Classical and Quantum Gravity, Vol. 15, No. 5, 1998, pp. L35-L39. doi:10.1088/0264-9381/15/5/001
- M. N. R. Wohlfarth, “Gravity a la Born-Infeld,” Classical and Quantum Gravity, Vol. 21, No. 8, 2004, pp. 1927- 1940. doi:10.1088/0264-9381/21/8/001
- D. N. Vollick, “Palatini Approach to Born-Infeld-Einstein Theory and a Geometric Description of Electrodynamics,” Physical Review D, Vol. 69, No. 6, 2004, Article ID: 064030. doi:10.1103/PhysRevD.69.064030
- D. N. Vollick, “Born-Infeld-Einstein Theory with Matter,” Physical Review D, Vol. 72, No. 8, 2005, Article ID: 084026. doi:10.1103/PhysRevD.72.084026
- D. N. Vollick, “Black Hole and Cosmological SpaceTimes in Born-Infeld-Einstein Theory,” gr-qc/0601136.
- J. A. Nieto, “Born-Infeld Gravity in Any Dimension,” Physical Review D, Vol. 70, No. 4, 2004, Article ID: 044042. doi:10.1103/PhysRevD.70.044042
- D. Comelli and A. Dolgov, “Determinant-Gravity: Cosmological Implications,” Journal of High Energy Physics, No. 11, 2004.
- D. Comelli, “Born-Infeld Gravity,” International Journal of Modern Physics A, Vol. 20, No. 11, 2005, pp. 2331- 2335. doi:10.1142/S0217751X05024584
- D. Comelli, “Born-Infeld Type Gravity,” Physical Review D, Vol. 72, No. 6, 2005, Article ID: 064018. doi:10.1103/PhysRevD.72.064018
- E. Rojas, “Higher Order Curvature Terms in Born-Infeld Type Brane Theories,” International Journal of Modern Physics D, Vol. 20, No. 1, 2011, pp. 59-75. doi:10.1142/S0218271811018615
- I. Gullu, T. C. Sisman and B. Tekin, “Unitarity Analysis of General Born-Infeld Gravity Theories,” Physical Review D, Vol. 82, No. 12, 2010, Article ID: 124023. doi:10.1103/PhysRevD.82.124023
- A. D. Linde, “Chaotic Inflation,” Physics Letters B, Vol. 129, No. 3-4, 1983, pp. 177-181. doi:10.1016/0370-2693(83)90837-7
- E. Silverstein and D. Tong, “Scalar Speed Limits and Cosmology: Acceleration from D-cceleration,” Physical Review D, Vol. 70, No. 10, 2004, Article ID: 103505. doi:10.1103/PhysRevD.70.103505
- M. Alishahiha, E. Silverstein and D. Tong, “DBI in the Sky,” Physical Review D, Vol. 70, No. 12, 2004, Article ID: 123505.
- I. Gullu, T. C. Sisman and B. Tekin, “Born-Infeld Extension of New Massive Gravity,” Classical and Quantum Gravity, Vol. 27, No. 16, 2010, Article ID: 162001. doi:10.1088/0264-9381/27/16/162001
- I. Gullu, T. C. Sisman and B. Tekin, “c-Functions in the Born-Infeld Extended New Massive Gravity,” Physical Review D, Vol. 82, No. 2, 2010, Article ID: 024032. doi:10.1103/PhysRevD.82.024032
- A. Ghodsi and D. M. Yekta, “Black Holes in Born-Infeld Extended New Massive Gravity,” Physical Review D, Vol. 83, No. 10, 2011, Article ID: 104004. doi:10.1103/PhysRevD.83.104004
- D. P. Jatkar and A. Sinha, “New Massive Gravity and AdS4 Counterterms,” Physical Review Letters, Vol. 106, No. 17, 2011, Article ID: 171601. doi:10.1103/PhysRevLett.106.171601
- E. A. Bergshoeff, O. Hohm and P. K. Townsend, “Massive Gravity in Three Dimensions,” Physical Review Letters, Vol. 102, No. 20, 2009, Article ID: 201301. doi:10.1103/PhysRevLett.102.201301
- E. A. Bergshoeff, O. Hohm and P. K. Townsend, “More on Massive 3D Gravity,” Physical Review D, Vol. 79, No. 12, 2009, Article ID: 124042. doi:10.1103/PhysRevD.79.124042
- S. Dengiz and B. Tekin, “Higgs Mechanism for New Massive Gravity and Weyl Invariant Extensions of Higher Derivative Theories,” Physical Review D, Vol. 84, No. 2, 2011, Article ID: 024033. doi:10.1103/PhysRevD.84.024033
- T. Moon, J. Lee and P. Oh, “Conformal Invariance in Einstein-Cartan-Weyl Space,” Modern Physics Letters A, Vol. 25, No. 37, 2010, pp. 3129-3143. doi:10.1142/S0217732310034201
- T. Moon, P. Oh and J. Sohn, “Anisotropic Weyl Symmetry and Cosmology,” Journal of Cosmology and Astroparticle Physics, 2010, arXiv: 1002.2549v3.
NOTES
*Corresponding author.
1Of course, only the vector field as the source cannot lead to the exactly isotropic expansion.
2Note that 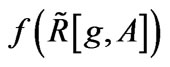 does not bring about substantial nonminimal couplings [5].
does not bring about substantial nonminimal couplings [5].
3Judging from the number of fields and derivatives, the term Φ−4/(D−2) gλμFνλFσμ is allowed in the same order. But this term is different from others in the point that it includes two kinds of fields except for the metric. Therefore we discarded this marginally possible term here.
4If we demand that the terms with lowest derivatives in the expansion (1.6) look like the Lagrangian of scalar-tensor theory, we must choose as α1 + 4α2 > 0 and γ1 + 4γ2 + 4γ3 + 8γ4 > 0, for D = 4.
5Note that 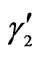 can be tuned by take an appropriate value for γ4.
can be tuned by take an appropriate value for γ4.
6The parameters 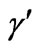 s can be taken to be sufficiently small so that no “antigravity” emerges.
s can be taken to be sufficiently small so that no “antigravity” emerges.

