Applied Mathematics
Vol.3 No.10A(2012), Article ID:24139,6 pages DOI:10.4236/am.2012.330203
A Collaborative Approach for LA-DHBMO
1Department of Information Technology, Sufi Razi Institute of Higher Education, Zanjan, Iran
2Department of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran
Email: V.Azadehgan@sufi.ac.ir, P.Khanteimouri@aut.ac.ir, Akbari.Sorayya@gmail.com, Ghandehari.Niusha@gmail.com
Received July 10, 2012; revised August 10, 2012; accepted August 17, 2012
Keywords: Honey Bees Mating Optimization; Learning Automata; Collaborative Optimization; Function Optimization
ABSTRACT
Honey Bees Mating Optimization (HBMO) is a novel developed method used in different engineering areas. Optimization process in this algorithm is inspired of natural mating behavior between bees. In this paper, we have attempted to createa new collaborative learning automata based honey bees mating optimization (C-LA-DHBMO).In previous model presented by very authors, the same learning automata parameters for all drones were used. However in the presented method, learning automatas with different reward and penalty parameters have been used which enhance reliability of algorithm and also has high convergence speed compared to previous proposed algorithm (LA-DHBMO). Simulation and comparisons based on several well-studied benchmarks demonstrate the effectiveness, efficiency and robustness of the proposed algorithms.
1. Introduction
Hybridization of intelligent techniques, coming from different computational intelligence areas, has become popular because of the growing awareness that such combinations frequently perform better than the individual techniques coming from computational intelligence [1]. Therefore, in this paper a new collaborative algorithm based on honey bees mating optimization and Learning Automaton has been developed.
A very interesting swarm in nature is honey bee swarm that allocates the tasks dynamically and adapts itself in response to changes in the environment in a collective intelligent manner. Honey Bees Mating Optimization (HBMO) algorithm is a typical swarm-based approach to optimization, in which the search algorithm is inspired by the honey bees mating process. The Honey Bees Mating Optimization Algorithm was first presented in [2,3], and since then it was used on a number of different applications [4-6]. HBMO is an evolutionary computation algorithm which simulates the mating process of the queen of the hive. The mating process of the queen begins when the queen flights away from the nest performing the mating flight which the drones follow the queen and mate with her in the air.
Learning Automaton (LA) is a general-purpose stochastic optimization tool, which has been developed as a model for learning systems. They are typically used as the basis oflearning systems, which through interactions with a stochastic unknown environment learn the optimal action for that environment. The learning automaton tries to determine, iteratively, the optimal action to apply to environment from a finite number of actions that are available to it. The environment returns a reinforcement signal that shows the relative quality of action of the learning automaton. This signal is given to learning automaton and learning automaton adjusts itself by a learning algorithm [7,8]. In previous model presented by very authors [9], learning automata parameters were considered constantly which were not suitable enough and it was possible that the final answer might depended on learning automatas parameters value. In new proposed algorithm, different parameters have been attributed to each automata which can produce better Answers by algorithm.
The results of computer sihe rest of this paper is organized as follows: In the next section a short review honey bees mating optimization is presented, Section 3 describes the Learning Automata. mulations show that the proposed algorithm attains better solutions in a faster way for most of the problems. T in Section 6, a proposed algorithm is described in detail. Section 5, indicates experimental setting to show proficiency of suggested algorithm, Section 6 presents results on the benchmark optimization functions. Section 7 contains the concluding remarks and the future work.
2. Honey Bees Mating Optimization
A very interesting swarm in nature is honey bee swarm that allocates the tasks dynamically and adapts itself in response to changes in the environment in a collective intelligent manner [10]. Before presenting the algorithm describing the use of honey bee mating behaviors, behavior of the colony is explained below: Bees are social insects living as colonies. The mating between honey bees includes three different bee categories: queen bee, drones and workers [2,3,10].
Queen bee is the only egg-laying female who is the mother of all the members of the colony. The queen usually mates only once in her life and she stores sperms in spermatheca and use them to produce broods. Drones are the fathers of the colony. Drones die after they mate with the queen. This process has been simulated in the model as a search of global optima. Workers are responsible for conserving the produced bees during mating process between queen and drones. Workers search on produced answers locally in simulated model. The main process in honey bees mating is mating flight. It begins with a dance of queen. During the flight the drones follow the queen and mate with her in the air. Sperm of the drones will be deposited and accumulated in the queen’s spermatheca to form the genetic pool of the potential broods to be produced by the queen.
2.1. Honey-Bees Modeling
The mating-flight may be considered as a set of transitions in possible solutions where the queen moves between the different states in some speed and mates with the drone encountered at each state probabilistically. At the beginning of flight, each queen is initialized by an amount of energy and if this amount reaches a threshold or Zero, or even spermatheca has been filled, the queens will return to the nest. In this algorithm, workers’ task is watching broods. In developed algorithm, workers are implemented as heuristic functions which cause fitness of broods to be increased. A drone mates with a queen probabilistically using below function as [2,3]:

where Prob(Q, D) is the probability of adding the sperm of drone D to the spermatheca of queen Q (that is, the probability of a successful mating); ∆(f) is the absolute difference between the fitness of D (i.e. f(D)) and the fitness of Q (i.e. f(Q)); and S(t) is the speed of the queen at time t. It is apparent that this function acts as an annealing function, where the probability of mating is high when either the queen is still in the start of her mating-flight and therefore her speed is high, or when the fitness of the drone is as good as the queen’s. After each transition in space, the queen’s speed, S(t), and energy, E(t), decay using the following equations:
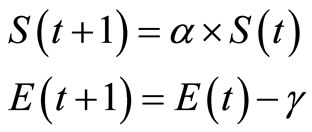
where α is a factor  [0, 1] and γ is the amount of energy reduction after each transition. Thus, Honey Bees Mating Optimization (HBMO) algorithm may be constructed with the following five main stages [4]:
[0, 1] and γ is the amount of energy reduction after each transition. Thus, Honey Bees Mating Optimization (HBMO) algorithm may be constructed with the following five main stages [4]:
1) The algorithm starts with the mating-flight, where a queen (best solution) selects drones probabilistically to form the spermatheca (list of drones). A drone is then selected from the list at random for the creation of broods.
2) Creation of new broods (trial solutions) by crossoverring the drones’ genotypes with the queen’s.
3) Use of workers (heuristics) to conduct local search on broods (trial solutions).
4) Adaptation of workers’ fitness based on the amount of improvement achieved on broods.
5) Replacement of weaker queens by fitter broods.
The algorithm starts with three user-defined parameters and one predefined parameter. The predefined parameter is the number of workers, representing the number of heuristics encoded in the program. The three user-defined parameters are the number of queens, the queen’s spermatheca size and the number of broods that will be born by all queens.
3. Learning Automata
Learning Automata are adaptive decision-making devices operating on unknown random environments. The Learning Automaton has a finite set of actions and each action has a certain probability of getting rewarded by the environment of the automaton. The aim is to learn to choose the optimal action (i.e. the action with the highest probability of being rewarded) through repeated interaction on the system. If the learning algorithm is chosen properly, then the iterative process of interacting on the environment can be made to result in selection of the optimal action. Figure 1 illustrates how a stochastic automaton works in feedback connection with a random environment. Learning Automata can be classified into two main families: fixed structure learning automata and variable structure learning automata (VSLA) [7,8].

Figure 1. The interaction between learning automata and environment.
In the following, the variable structure learning automata is described. A VSLA is a quintuple <α, β, p, T(α, β, p)>, where α, β, pare an action set with s actions, an environment response set and the probability set p containing s probabilities, each being the probability of performing every action in the current internal automaton state, respectively. The function of T is the reinforcement algorithm, which modifies the action probability vector p with respect to the performed action and received response. Let a VSLA operate in an environment with β = {0, l}. Let 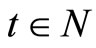 be the set of nonnegative integers. A general linear schema for updating action probabilities can be represented as follows. Let action i be performed. If β(t) = 0 (Reward),
be the set of nonnegative integers. A general linear schema for updating action probabilities can be represented as follows. Let action i be performed. If β(t) = 0 (Reward),
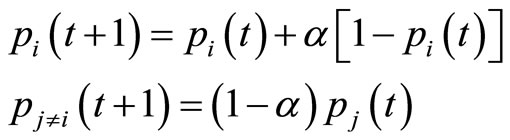
If β (t) = 1 (Penalty),
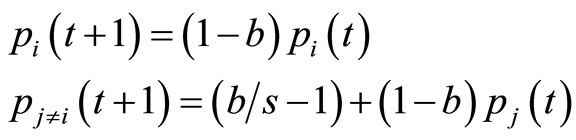
where a and b are reward and penalty parameters. When a = b, automaton is called LRP. If b = 0 the automaton is called LRI and if  the automaton is called LREP.
the automaton is called LREP.
4. Collaborative Honey Bees Mating Optimization Based on Learning Automata
In previous presented paper [9] we introduced a new algorithm based on learning automata is suggested. In this model, each drone has been attributed to a set of learning automata which are responsible for producing better drones. As a result, producing better drones and their mating with queen can produce better broods and it causes to converge faster close to global optima. In this algorithm each drone consists of two parts, Model genome and string genome. Model genome is a set of learning automata. The set of actions selected by the set of learning automata determines the second component of the genome called string genome which a reinforcement signal is produced after mating flight and replacing queens with better broods for every automaton. Each learning automaton based on the received signalupdate its internal structure according to a Learning algorithm. Then each drone generates a new string genome and compares its fitness with the fitness of the string genome of the drone. If the fitness of the generated genome is better than the quality of the sting genome of the drone, the generated string genome becomes the string genome of that drone. This process of generating string genome by the drones is iterated until a termination condition is satisfied. There is a snapshot of Honey Bees Mating Optimization based on Learning Automata presented in Figure 2.
We are going to introduce a new algorithm called Collaborative Honey Bees Mating Optimization based on Learning Automata (C-LA-DHBMO) in this paper. Unlike previous model, in this model learning automatas parameters are not the same and various parameters for learning automatas are considered. The algorithm routine can be defined as this: high parameters are chosen for half of drones and for the rest of them, low parameters will be chosen. In characterized repetition, string genome of each drone with high and low parameter will be changed with each other. This action causes learning automatas not to converge to a specific action and produce better result compared to the first proposed algorithm. The collaboration between drones is presented in Figure 3.

Figure 2. Honey bees mating optimization based on learning automata.

Figure 3. The collaboration between drones, in a specified repetition, the string genomes of drones with different parameters are changed with each other.
Proposed algorithms as the one described algorithm in this paper can be used in any arbitrary finite discrete search space. To simplify the algorithm, we assume that sight search space is a binary finite search space. So the optimization problem can be presented as follows. Assume  be a real function that is to be minimized.
be a real function that is to be minimized.
In order to use the algorithm for the optimization function f first a set of learning automata is associated to each drone. The number of learning automata associated to a drone is the number bits in the string genome representing points of the search space of f. Each automaton has two actions called action 0 and 1. After each mating flight, these set of steps are done:
1) Every automata in a dronei chooses one of its actions using its action probability vector.
2) dronei generates a new string genome, newi, by combining the actions chosen by the learning automata of dronei. The newly generated string genome is obtained by concatenating the actions of the automata (0 or 1) associated to that drone. This section of algorithm is equivalent to learning from previous self-experiences.
3) Every dronei computes the fitness value of string genome newi; if the fitness of this string genome is better than the one in the drone then the new string genome newi becomes the string genome of that cell. That is.
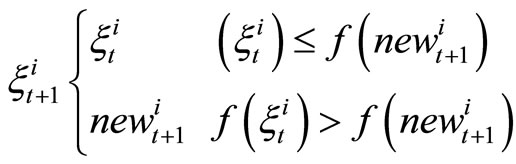
4) Se queens of the hive are selected. This Selection is based on the fitness value of the queens in hive.
5) Based on selected queens a reinforcement vector is generated. This vector becomes the input for the set of learning automata associated to the drones. This section of algorithm is equivalent to learning from experiences of others. Let Qs be set selected queens:
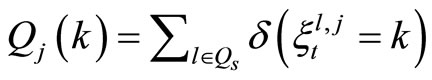
where
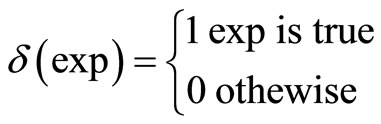
βi,j, the reinforcement signal given to learning automaton j of drone i, is computed as follows:
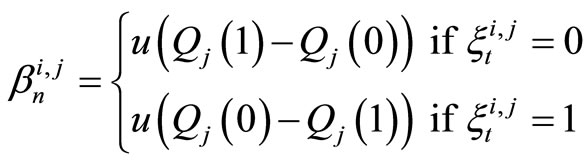
where u(·) is a step function. The proposed algorithm is summarized in the Pseudo code of Figure 4.
5. Experimental Setting
In this section, the efficiency of proposed algorithm is presented. For this purpose, Standard functions borrowed from reference [11] are used to show proficiency of suggested algorithm. In the Table 1, functions with their characteristics are described (All experiments have been done on 10 dimension functions).
The parameters used for C-LA-DHBMO, LA-DHBMO and DHBMO consist of the number of queens set to 5, the spermatheca capacity set to 5, the maximum number of produced broods set to 30, and also the number of workers suggested in paper [2,3] set to 4. Learning automata LRP has been used for algorithms LA-DHBMO and C-LA-DHBMO and they were performed separately with values R = P = 0.01 and R = P = 0.001 for LA-DHBMO and they are shown in results as LA-DHBMORP (0.01, 0.01) and LA-DHBMORP (0.001, 0.001). Automatas which owns reward and high penalty parameters with values of RH = PH = 0.01 and also the ones which owns reward and low penalty parameters with values RL = PL = 0.001 are used for C-LA-DHBMO. They are shown as C-LA-DHBMORP (0.01, 0.01, 0.001, 0.001) in results.
6. Results
To demonstrate reliability of algorithm, the results of algorithm performance on functions of table I have been shown in Tables 2-5. The results indicate better and closer answers to global optima.
To demonstrate high speed of convergence and also escaping from local optimas, acomparison between previous methods and proposed method on functions of Table 1 has been shown in Figures 5-8.
7. Conclusion
In this paper we have strived to present a new model to

Figure 4. Pseudo code ofthe proposed algorithm.

Table 1. Benchmark functions and their characteristics.
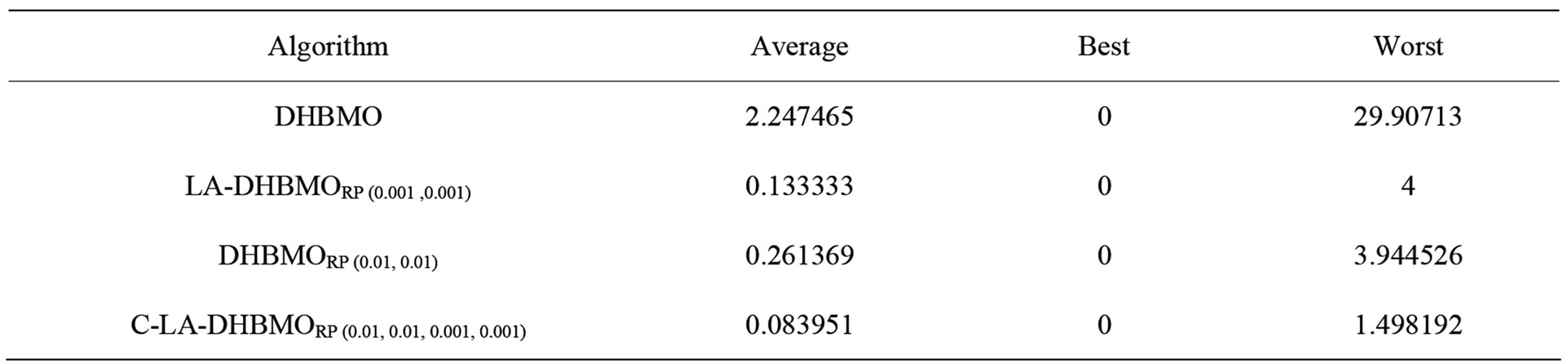
Table 2. Results obtained from 30 independent run by algorithms on De Jong function in 150 mating flights.

Table 3. Results obtained from 30 independent run by algorithms on Rastrigin function in 150 mating flights.
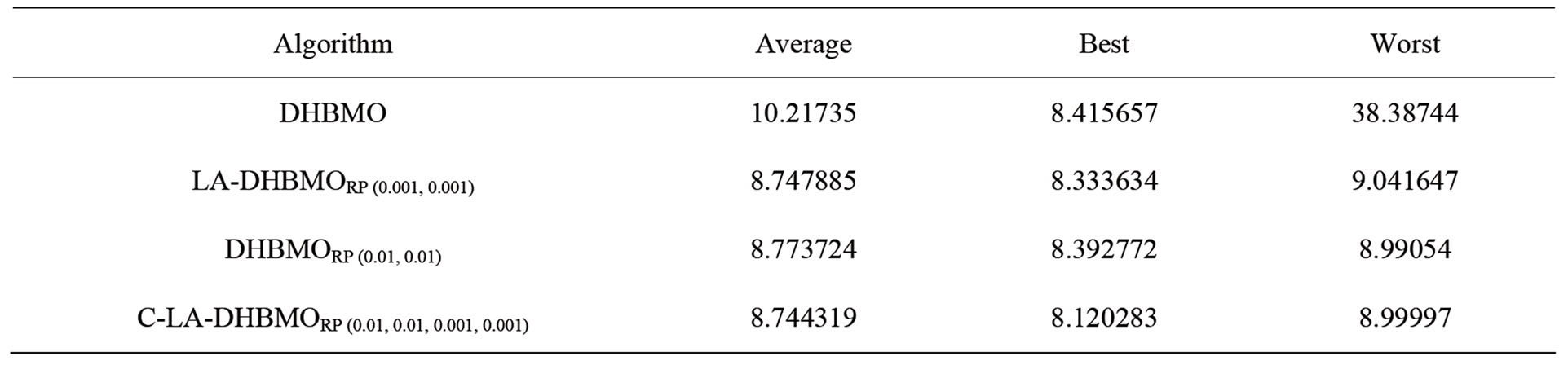
Table 4. Results obtained from 30 independent run by algorithms on Rosenbrock function in 300 mating flights.

Table 5. Results obtained from 30 independent run by algorithms on Ackley function in 200 mating flights.
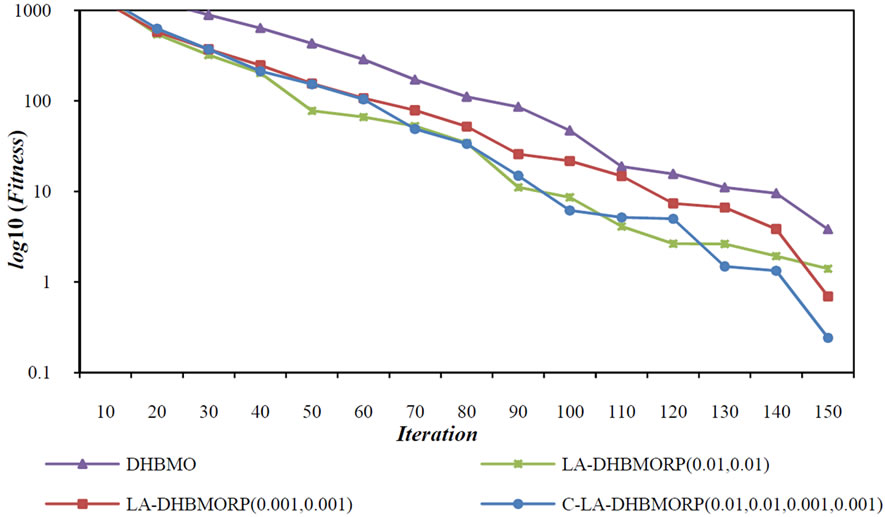
Figure 5. The averaged performances of algorithms on De Jong function in 30 independent run.
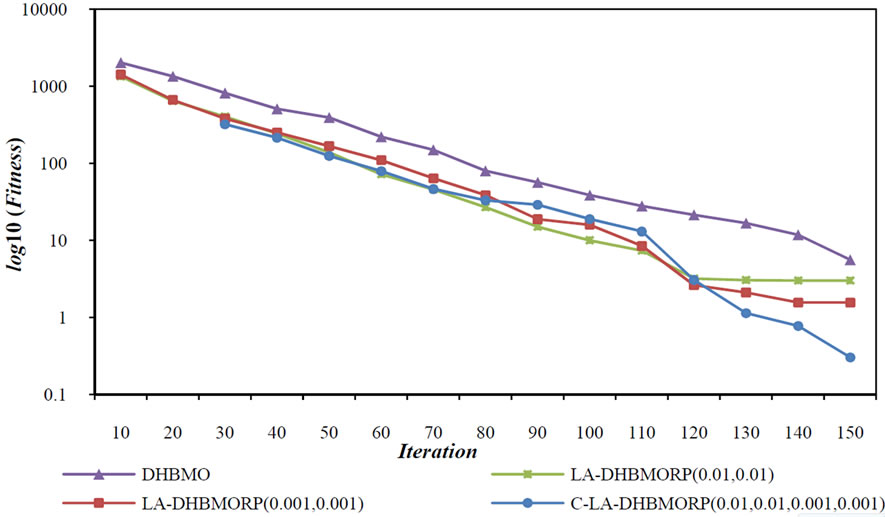
Figure 6. The averaged performances of algorithms on Rastrigin function in 30 independent run.

Figure 7. The averaged performances of algorithms on Rosenbrock function in 30 independent run.
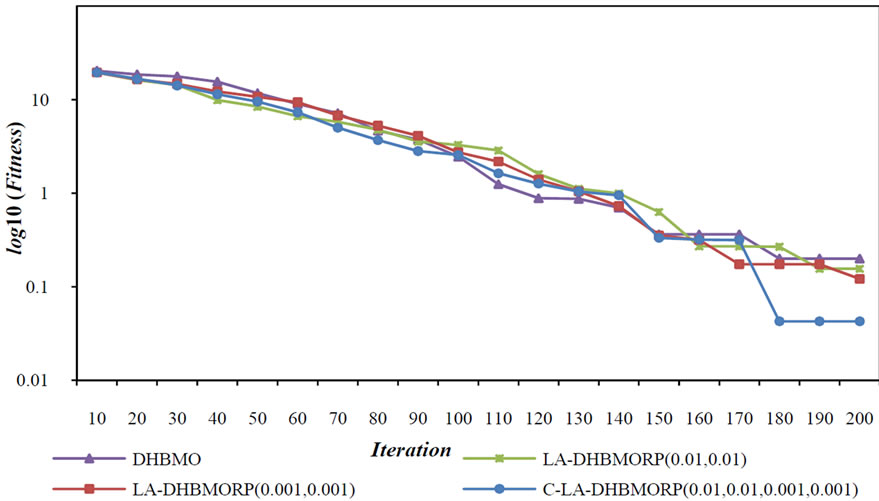
Figure 8. The averaged performances of algorithms on Ackley function in 30 independent run.
improve effectiveness and convergence speed in optimization problems. The new model presented by using learning automata and the concept of collaboration between automatas. Unlike former model, proposed model used learning automatas with different parameters such as reward and penalty. As it is shown in experiments, the presented algorithm has got excellence compared to previous ones. In future researches we will attempt to provide contact possibilities between searching agents to use them better.
REFERENCES
- V. Azadehgan, A. Sooni, N. Jafarian and D. Khateri, “A New Hybrid Algorithm for Multiobjective Optimization,” 23rd IEEE International Conference on Tools with Artificial Intelligence, Boca Raton, 7-9 November 2011, pp. 911-913. doi:10.1109/ICTAI.2011.152
- H. Abbass, “A Monogenous MBO Approach to Satisfiability,” Proceeding of the International Conference on Computational Intelligence for Modelling, Control and Automation, Las Vegas, 2001.
- H. Abbass, “Marriage in Honey-Bee Optimization (MBO): A Haplometrosispolygynous Swarming Approach,” The Congress on Evolutionary Computation (CEC2001), Seoul, 27-30 May 2001, pp. 207-214.
- A. Afshar, O. Bozog Haddad, M. A. Marino and B. J. Adams, “Honey-Bee Mating Optimization (HBMO) Algorithm for Optimal Reservoir Operation,” Journal of the Franklin Institute, Vol. 344, No. 5, 2007, pp. 452-462. doi:10.1016/j.jfranklin.2006.06.001
- M. Fathian, B. Amiri and A. Maroosi, “Application of Honey-Bee Mating Optimization Algorithm on Clustering,” Applied Mathematics and Computation, Vol. 190, No. 2, 2007, pp. 1502-1513.
- Y. Marinakis and M. Marinaki, “A Honey Bees Mating Optimization Algorithm for the Open Vehicle Routing Problem,” Proceedings of GECCO, 2011, pp. 101-108.
- M. A. L. Thathachar and P. S. Sastry, “Varieties of Learning Automata: An Overview,” IEEE Transactions on Systems, Man, and Cybernetics, Part B, Vol. 32, No. 6, 2002, pp. 711-722.
- K. S. Narendra and M. A. L. Thathachar, “Learning Automata: An Introduction,” Printice-Hall Inc., Upper Saddle River, 1989.
- V. Azadehgan, M. R. Meybodi, N. Jafarian and F. Jafarieh, “Discrete Binary Honey Bees Mating Optimization with Capability of Learning,” Computational Intelligence and Information Technology, Communication in Computer and Information Science, Vol. 250, 2011, pp. 630-636.
- D. Karaboga and B. Akay, “A Survey: Algorithms Simulating Bee Swarm Intelligence,” Artificial Intelligence Review, Vol. 31, No .1-4, 2009, pp. 61-85.
- X.-S. Yang, “Test problems in optimization,” In: X.-S. Yang, Ed., Engineering Optimization: An Introduction with Metaheuristic Applications, John Wiley & Sons, Hoboken, 2010. doi:10.1002/9780470640425.app1

